Reliability-Based Design Method of Tunnel Structures Based on Deformation Failure of Surrounding Rock
-
摘要:
为科学地处理隧道工程中由于材料属性和复杂地质环境等带来的不确定性,使支护设计更加安全合理,基于可靠度理论,提出一种实用隧道可靠度设计计算方法. 首先,基于可靠度指标的几何意义,结合Nataf变换和Cholesky分解等考虑参数相关性与非负性,建立约束在原始空间的最优化模型;其次,利用数值软件内嵌的优化函数在不需人为计算偏导数的情况下直接获得设计点;然后,引入重要抽样方法,在设计点处计算失效概率,形成兼顾收敛性和精度的实用可靠度计算方法;再次,通过高度非线性的数值算例和非圆坑道算例验证该方法的有效性和适应性;最后,基于围岩变形失效功能函数,采用本文方法进行隧道支护抗力设计计算. 算例分析结果表明:本文方法能够以较小代价获取设计点,最终结果和蒙特卡洛法结果相对误差小于1.0%,并且能够结合含交叉项响应面函数处理无解析功能函数的非圆坑道可靠度问题;本文方法能够获取准确的支护抗力设计值,与蒙特卡洛法结果相对误差小于0.5%;内摩擦角的敏感性比黏聚力和变形模量的大.
Abstract:In order to scientifically address the uncertainty caused by material properties and complex geological environments in tunnel engineering and make the support design more safe and reasonable, a tunnel reliability design and calculation method based on reliability theory is proposed. Firstly, according to the geometric meaning of the reliability index, an optimization model considering correlation and non-negativity of parameters is established, which is limited in the original space based on Nataf transformation and Cholesky decomposition. Secondly, the design points are obtained directly by using the optimization function embedded in the numerical software without the need to calculate the partial derivatives manually, and the probability of failure is calculated by the important sampling method at the design point, so as to form a real reliability calculation method considering convergence and accuracy. Then, highly nonlinear numerical examples and non-circular tunnel problems are presented to validate the effectiveness and adaptability of the proposed method. Finally, the proposed method is applied to design and calculate the tunnel support resistance based on the performance function concerning the deformation failure of surrounding rock. Results of the example analysis show that the proposed method can obtain design points at a low cost, and the relative error with the results of the Monte Carlo method is less than 1.0%. In addition, the proposed method can address the non-circular tunnel reliability without analytical performance function with the help of response surface function with cross terms. The proposed method can obtain accurate design values of support resistance with a relative error of less than 0.5% with the Monte Carlo method. Additionally, parameter analysis shows that the sensitivity of the internal friction angle is greater than that of the cohesion and deformation modulus.
-
Key words:
- reliability-based design /
- optimization model /
- importance sampling method /
- convergence /
- accuracy
-
表 1 抽样次数
Table 1. Sampling numbers
Pf/% $ \beta $ 抽样方法 N/次 精度 1.00 2.326 0 直接抽样 3.80 × 104 10% (95%) 重要抽样 1.03 × 103 0.10 3.090 0 直接抽样 3.84 × 105 重要抽样 1.34 × 103 0.01 3.719 0 直接抽样 3.84 × 106 重要抽样 1.61 × 103 表 2 计算结果
Table 2. Calculation results
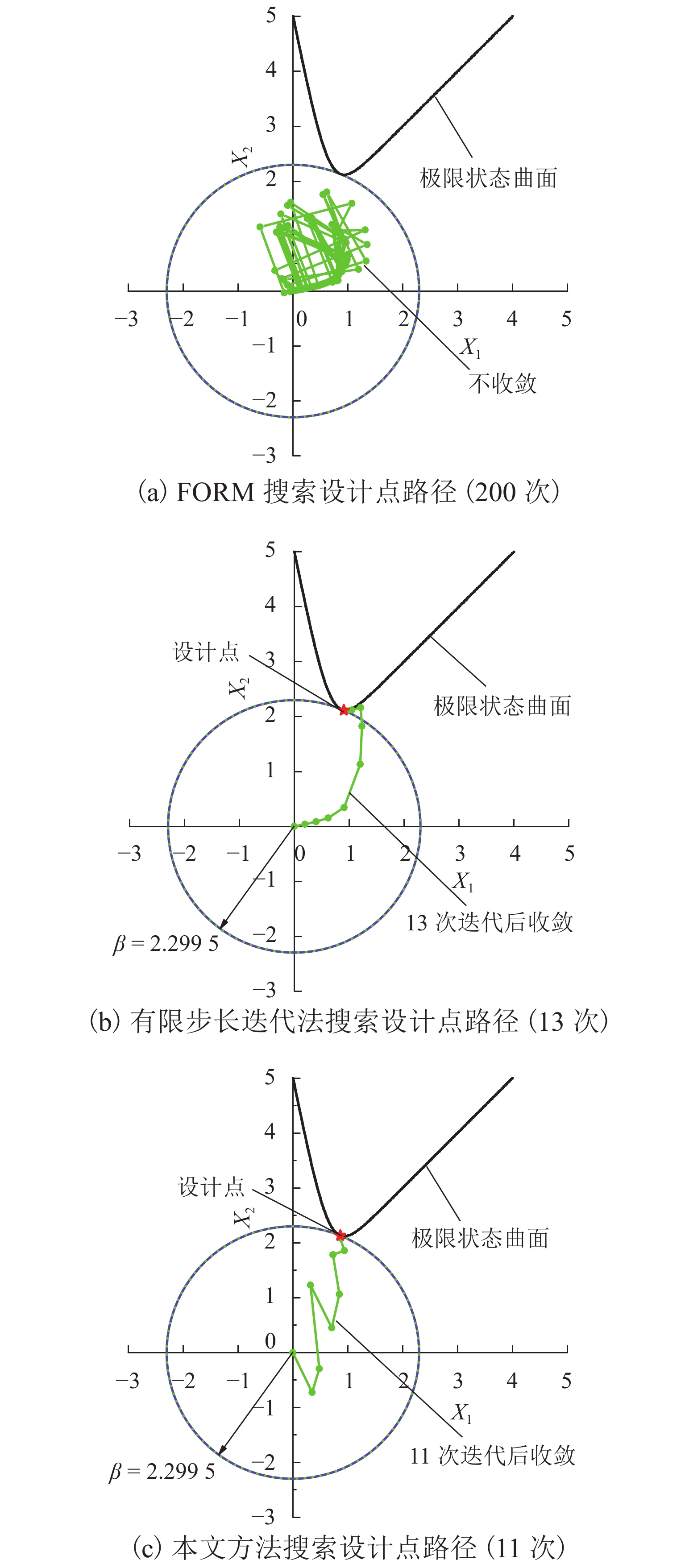
方法 Pf/% 收敛情况 相对误差/% 蒙特卡洛法 0.300 收敛 一次二阶矩法 不收敛 有限步长迭代法 1.070 收敛 256.66 表格算法 1.070 收敛 256.66 本文方法 0.302 收敛 0.66 表 3 围岩统计特征值
Table 3. Statistical characteristics of surrounding rock
类型 c2 φ2 E2 均值 0.451 MPa 30.85° 1.704 GPa 变异系数 0.124 MPa 0.076° 0.109 GPa 分布形态 正态分布 正态分布 正态分布 表 4 抽样点及其计算结果
Table 4. Sampling points and results
E2 /GPa c2 /MPa φ2 /(°) ur /cm Z/cm 1.890 0.451 30.85 10.294 1.846 1.518 0.451 30.85 12.364 −0.224 1.704 0.507 30.85 10.724 1.416 1.704 0.395 30.85 11.941 0.199 1.704 0.451 33.21 10.330 1.810 1.704 0.451 28.49 12.596 −0.456 1.704 0.451 30.85 11.229 0.911 1.704 0.395 28.49 13.744 −1.604 表 5 计算结果
Table 5. Calculation results
% 方法 Pf 相对误差 蒙特卡洛模拟法 33.55 表格算法 30.37 10.48 本文方法 33.58 0.09 表 6 基本随机变量统计特征
Table 6. Statistical characteristics of the basic random variables
类型 $c$ ${\varphi}$ $E$ 均值 0.23 MPa 22.85° 373 MPa 标准差 0.068 MPa 1.310° 48 MPa 分布 正态分布 正态分布 正态分布 表 7 计算结果
Table 7. Calculation results
方法 Pf/% pi /MPa 相对误差/% 蒙特卡洛模拟法 0.01 0.699 2 表格算法 0.01 0.687 5 1.70 本文方法 0.01 0.698 8 0.06 -
[1] DUNCAN J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 307-316. doi: 10.1061/(ASCE)1090-0241(2000)126:4(307) [2] PHOON K K, KULHAWY F H, GRIGORIU M D. Development of a reliability-based design framework for transmission line structure foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 798-806. doi: 10.1061/(ASCE)1090-0241(2003)129:9(798) [3] International Organization for Standardization. 2015 General principles on reliability of structures: ISO 2394[S]. Geneva: [s.n.], 2015. [4] European Committee for Standardization (CEN). Geotechnical design—part 1: general rules: EN 1997−1: 2004[S]. Brussels: [s.n.], 2004. [5] PAIKOWSKY S G, CANNIFF M C, LESNY K, et al. LRFD design and construction of shallow foundations for highway bridge structures[M]. Washington D. C.: National Academies Press, 2010. [6] 中国铁路总公司企业标准. 铁路隧道设计规范(极限状态法): Q/CR 9129—2018 [S]. 北京: 中国铁道出版社, 2019. [7] FENTON G A, GRIFFITHS D V, ZHANG X Y. Load and resistance factor design of shallow foundations against bearing failure[J]. Canadian Geotechnical Journal, 2008, 45(11): 1556-1571. doi: 10.1139/T08-061 [8] SALGADO R, KIM D. Reliability analysis of load and resistance factor design of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(1): 57-73. doi: 10.1061/(ASCE)GT.1943-5606.0000978 [9] 赵万强,宋玉香,赵东平,等. 铁路隧道钢筋混凝土衬砌结构可靠度分析[J]. 铁道工程学报,2015,32(8): 81-86.ZHAO Wanqiang, SONG Yuxiang, ZHAO Dongping, et al. Reliability analysis of reinforced concrete lining structure for railway tunnel[J]. Journal of Railway Engineering Society, 2015, 32(8): 81-86. [10] 喻渝,赵东平,宋玉香,等. 铁路隧道衬砌结构分项系数的优化分析研究[J]. 铁道工程学报,2015,32(6): 57-61.YU Yu, ZHAO Dongping, SONG Yuxiang, et al. Analysis of partial coefficient optimization of lining structure in railway tunnel[J]. Journal of Railway Engineering Society, 2015, 32(6): 57-61. [11] FANG Y, SU Y. On the use of the global sensitivity analysis in the reliability-based design: insights from a tunnel support case[J]. Computers and Geotechnics, 2020, 117: 103280.1-103280.13. [12] 姬建,张哲铭,夏嘉诚,等. 基于逆可靠度分析的隧道开挖面极限支护压力优化设计[J]. 岩土工程学报,2021,43(10): 1825-1833.JI Jian, ZHANG Zheming, XIA Jiacheng, et al. Inverse reliability-based design of limit support pressure for tunnel face stability[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(10): 1825-1833. [13] HASOFER A M, LIND N C. Exact and invariant second-moment code format[J]. Journal of Engineering Mechanics Division, 1974, 100(1): 111-121. doi: 10.1061/JMCEA3.0001848 [14] RACKWITZ R, FLESSLER B. Structural reliability under combined random load sequences[J]. Computers & Structures, 1978, 9(5): 489-494. [15] LIU P L, DER KIUREGHIAN A. Optimization algorithms for structural reliability[J]. Structural Safety, 1991, 9(3): 161-177. doi: 10.1016/0167-4730(91)90041-7 [16] 贡金鑫. 结构可靠指标求解的一种新的迭代方法[J]. 计算结构力学及其应用,1995,12(3): 369-373.GONG Jinxin. A new algorithm for solving the structural reliability index[J]. Chinese Journal of Computational Mechanics, 1995, 12(3): 369-373. [17] ZHANG Y, KIUREGHIAN A D, Finite element reliability methods for inelastic structures[R]. Berkeley: University of California, Berkeley, 1997. [18] SANTOS S R, MATIOLI L C, BECK A T. New optimization algorithms for structural reliability analysis[J]. Computer Modeling in Engineering & Sciences (CMES), 2012, 83(1): 23-55. [19] LOW B K, TANG W H. Efficient spreadsheet algorithm for first-order reliability method[J]. Journal of Engineering Mechanics, 2007, 133(12): 1378-1387. doi: 10.1061/(ASCE)0733-9399(2007)133:12(1378) [20] 李晓军,陈雪琴,朱合华. 基于Spreadsheet法的盾构衬砌截面可靠度分析[J]. 岩土工程学报,2013,35(9): 1642-1649.LI Xiaojun, CHEN Xueqin, ZHU Hehua. Reliability analysis of shield lining sections using Spreadsheet method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(9): 1642-1649. [21] 张道兵,杨小礼,朱川曲,等. 基于最大熵原理与最优化方法的隧道衬砌结构可靠度分析[J]. 中南大学学报(自然科学版),2012,43(2): 663-668.ZHANG Daobing, YANG Xiaoli, ZHU Chuanqu, et al. Structural reliability analysis of tunnel lining based on maximal entropy principle and optimization method[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 663-668. [22] DER KIUREGHIAN A, LIU P L. Structural reliability under incomplete probability information[J]. Journal of Engineering Mechanics, 1986, 112(1): 85-104. doi: 10.1061/(ASCE)0733-9399(1986)112:1(85) [23] LIU P L, DER KIUREGHIAN A. Multivariate distribution models with prescribed marginals and covariances[J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105-112. doi: 10.1016/0266-8920(86)90033-0 [24] RUBINSTEIN R Y. Simulation and the Monte Carlo method[M]. Hoboken: John Wiley & Sons, Inc., 1981. [25] MEYERHOF G G. Development of geotechnical limit state design[J]. Canadian Geotechnical Journal, 1995, 32(1): 128-136. doi: 10.1139/t95-010 [26] LÜ Q, SUN H Y, LOW B K. Reliability analysis of ground-support interaction in circular tunnels using the response surface method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1329-1343. doi: 10.1016/j.ijrmms.2011.09.020 [27] LI H Z, LOW B K. Reliability analysis of circular tunnel under hydrostatic stress field[J]. Computers and Geotechnics, 2010, 37(1/2): 50-58. [28] DUNCAN FAMA M E. Numerical modeling of yield zones in weak rocks[C]//Comprehensive Rock Engineering. Oxford: Pergamon Press, 1993: 49-75. [29] HOEK E. Reliability of Hoek-Brown estimates of rock mass properties and their impact on design[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(1): 63-68. doi: 10.1016/S0148-9062(97)00314-8 [30] MARTIN C D. Seventeenth Canadian geotechnical colloquium: the effect of cohesion loss and stress path on brittle rock strength[J]. Canadian Geotechnical Journal, 1997, 34(5): 698-725. doi: 10.1139/t97-030 -




 下载:
下载: