Three-Dimensional Wheel–Rail Contact Thermal Analysis Considering Temperature-Dependent Material Property
-
摘要:
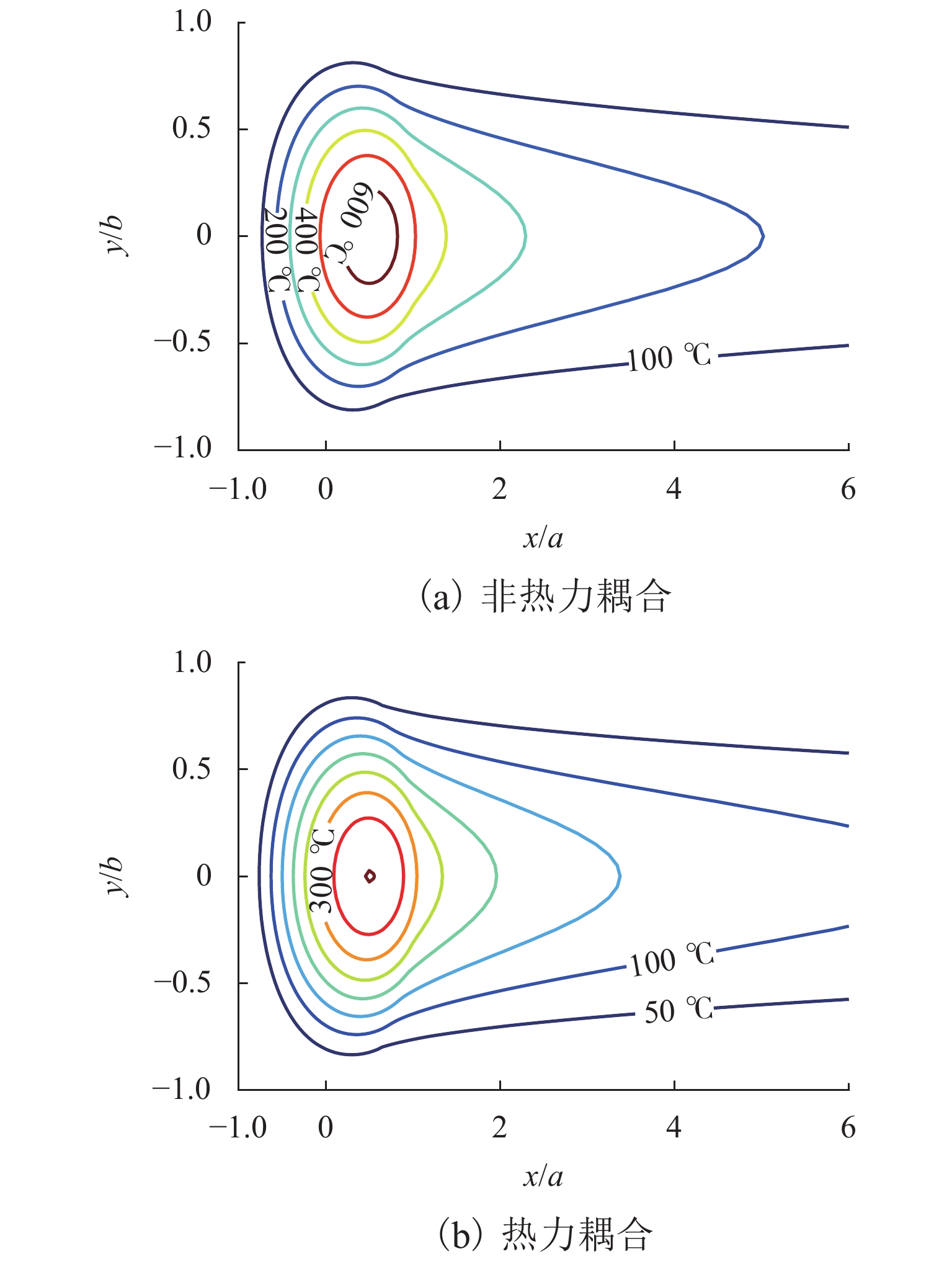
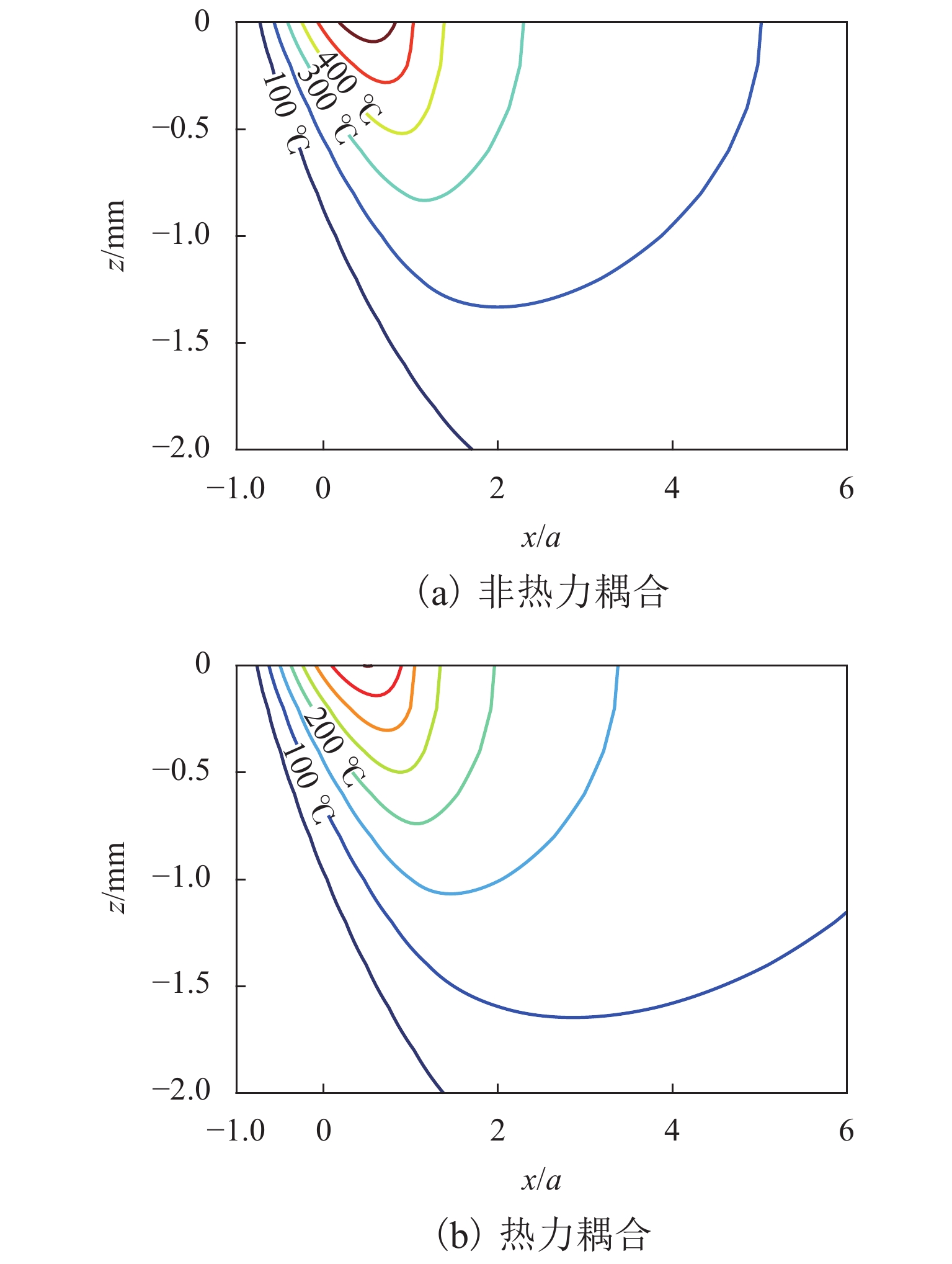
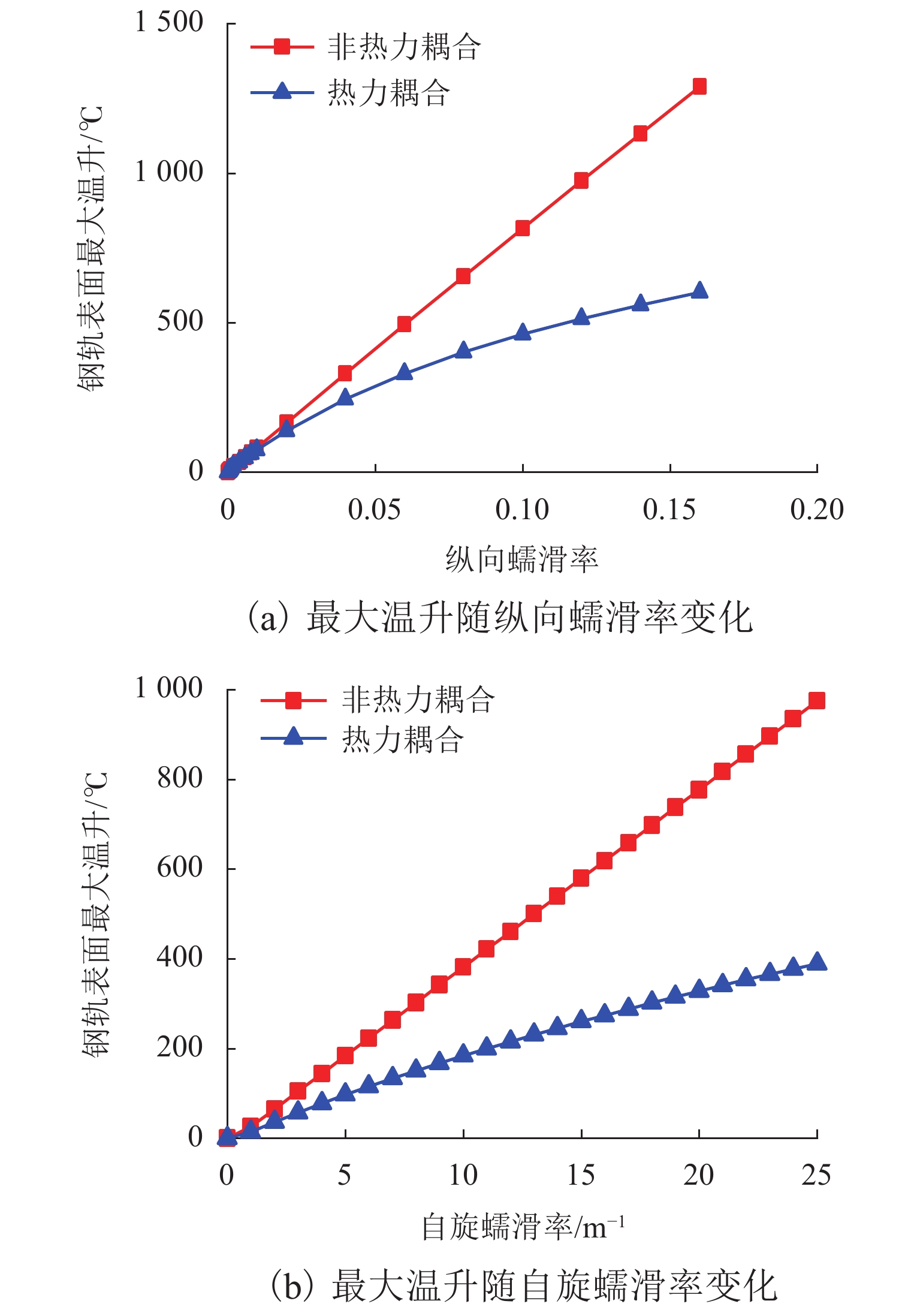
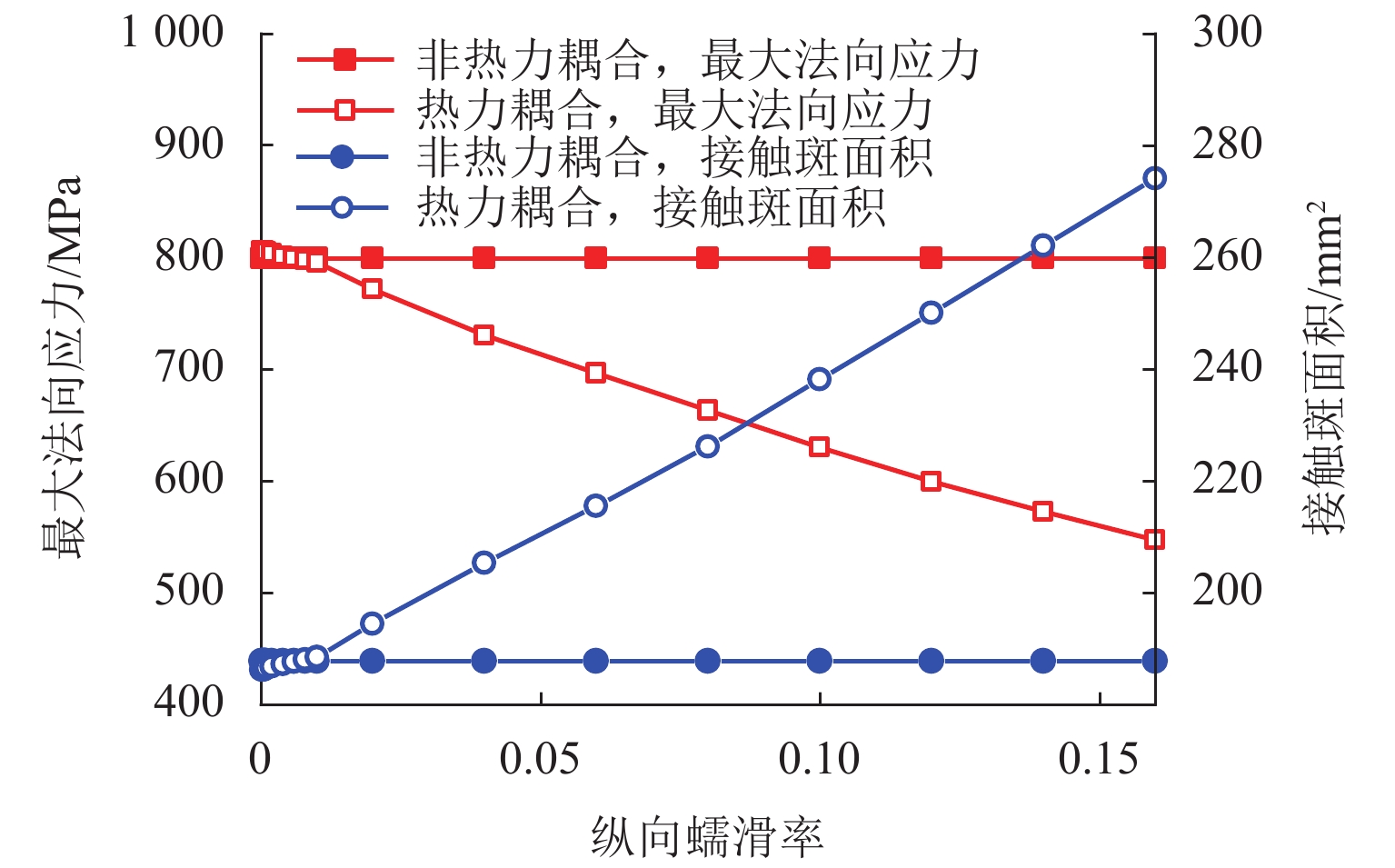
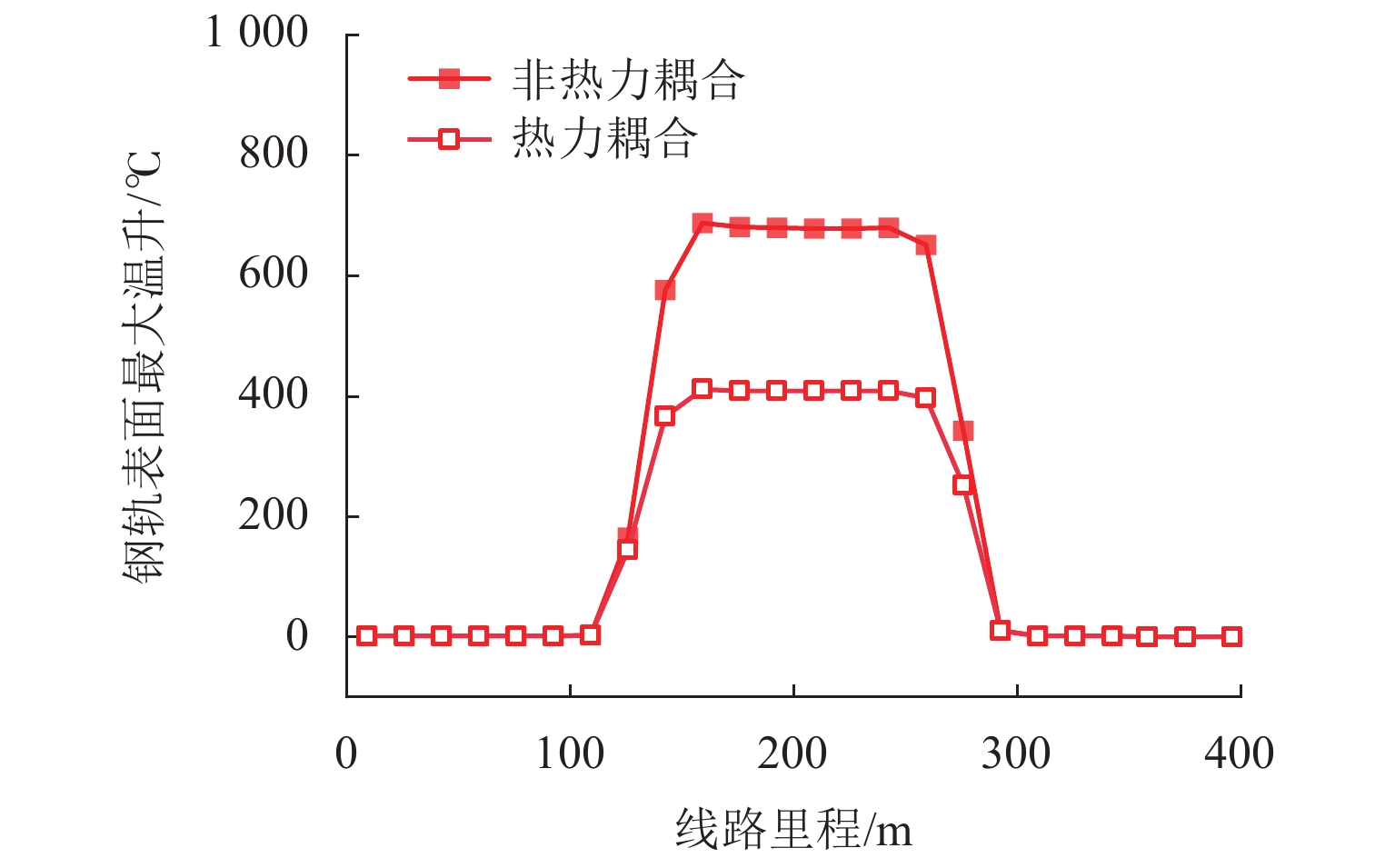
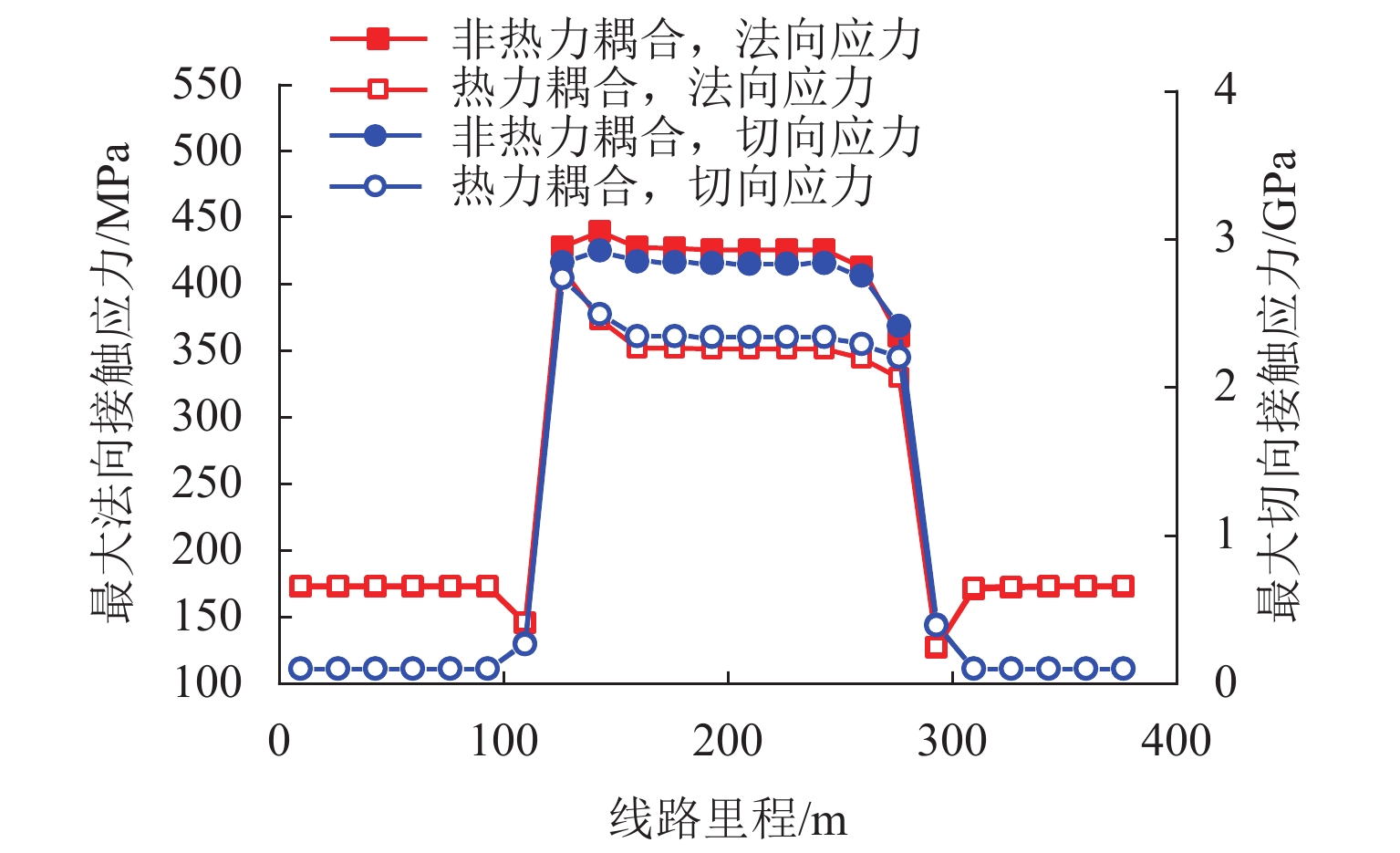
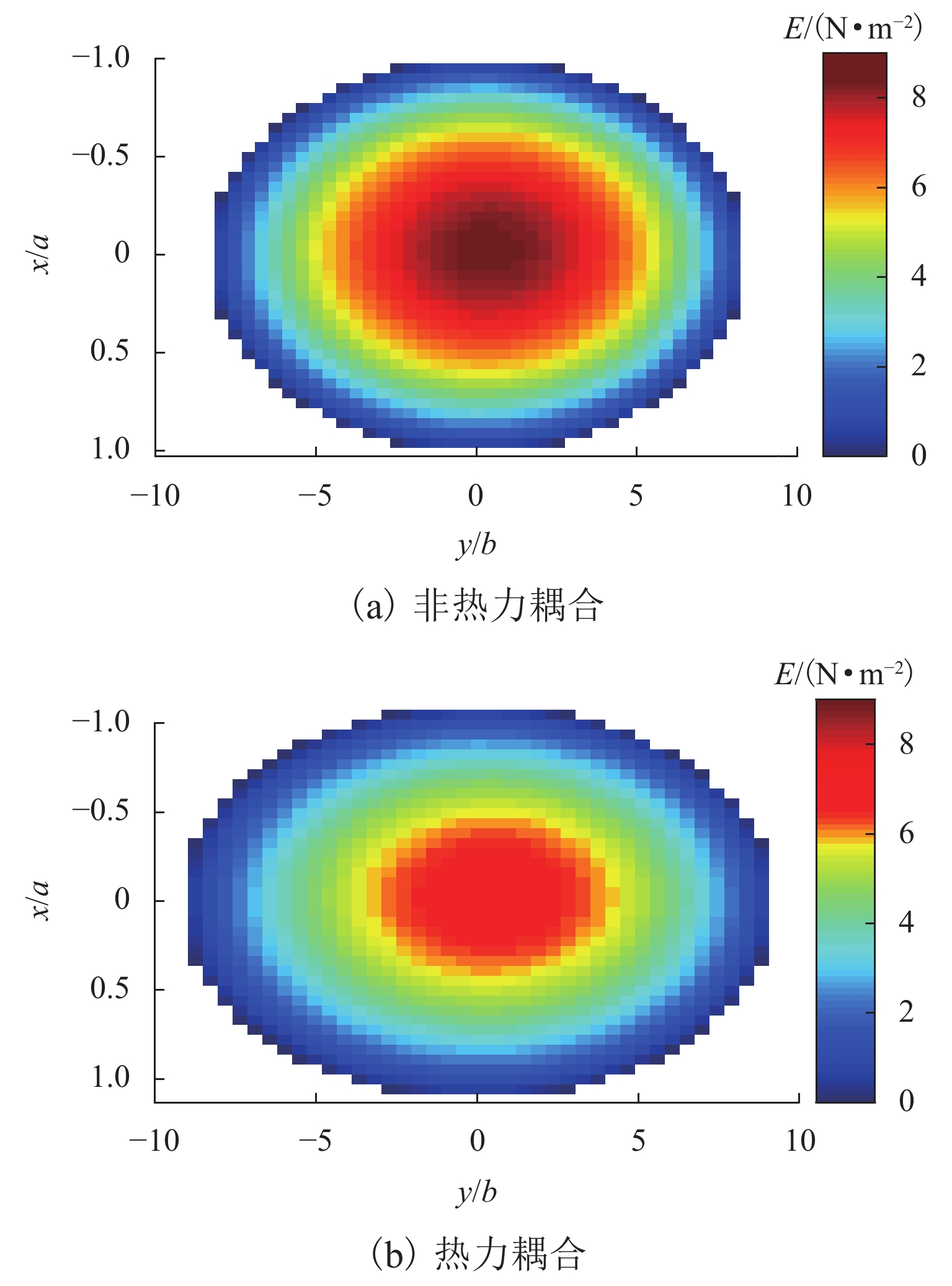
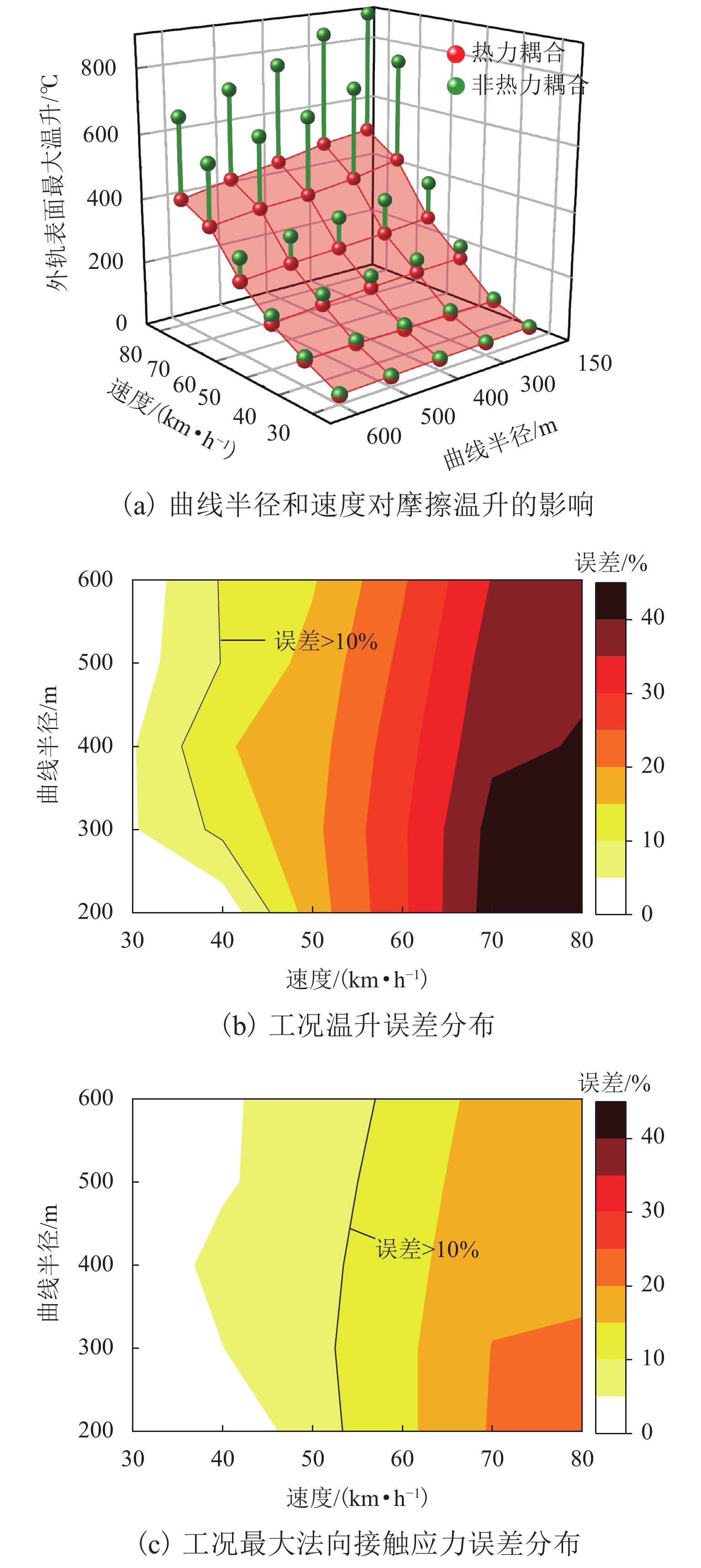
为研究材料温变特性对轮轨接触行为和摩擦温升的影响，提出了一种考虑材料温变特性的三维轮轨热力耦合模型，能够考虑纵、横向蠕滑率和自旋的影响，更为真实地模拟轮轨系统的服役状态. 首先，研究了热力耦合建模方式对轮轨界面摩擦温升及接触应力的影响；随后，将该模型应用于地铁小半径曲线处车辆-轨道相互作用模拟. 结果表明：当轮轨界面温度达到450 ℃时，轮轨接触应力显著降低，降幅可达20%；考虑热力耦合建模后，轮轨界面的预测温升明显低于不考虑热力耦合建模时的结果，在蠕滑率为0.16时，两者的差异可达51%；地铁车辆在小半径曲线线路上运行时轮轨摩擦温升因过大的蠕滑率与自旋会急剧增大到750 ℃，应考虑轮轨热力耦合建模以避免过高估计轮轨摩擦温升以及轮轨接触应力.
-
关键词:
- 摩擦温升 /
- 轮轨接触 /
- 热力耦合 /
- 车辆-轨道耦合动力学 /
- 轮轨损伤
Abstract:In order to study the influence of the temperature-dependent material property on the wheel–rail contact behavior and frictional temperature rise, a three-dimensional wheel–rail thermal-mechanical coupling model considering the temperature-dependent material property was proposed in this paper, which could consider the longitudinal and lateral creepage rates and spins to simulate the service state of the wheel–rail system more realistically. In this paper, the influence of the thermal-mechanical coupling modeling method on the wheel–rail frictional temperature rise and contact stress was first studied. Subsequently, this model was applied to the simulation of vehicle–rail interaction of subways running on a small radius curve. The results show that when the temperature reaches 450 ℃, the wheel–rail contact stress is significantly reduced by 20%. After considering the thermal-mechanical coupling modeling, the predicted temperature rise of wheel–rail interface is significantly lower than that without considering the thermal-mechanical coupling modeling. When the creepage rate is 0.16, the difference between the two can reach 51%. Due to excessive creepage rate and spin, the wheel–rail frictional temperature rise will increase sharply to 750 ℃ when subways run on a small radius curve. Therefore, the wheel–rail thermal-mechanical coupling modeling should be considered to avoid overestimating the wheel–rail frictional temperature rise and wheel–rail contact stress.
-
图 2 2种模拟方式条件下轮轨界面摩擦温升对比
Figure 2. Comparison of frictional temperature rise of wheel–rail interface under two simulation conditions
图 3 2种模拟方式条件下钢轨内部的温度场分布对比
Figure 3. Comparison of temperature field distribution inside the rail under two simulation methods
图 4 钢轨表面最大温升随蠕滑率变化
Figure 4. Variation of maximum temperature rise of rail surface with creepage rate
图 5 接触斑面积与最大法向应力随纵向蠕滑率变化
Figure 5. Variation of contact spot area and maximum normal stress with longitudinal creepage rate
图 7 线路内外侧轮轨蠕滑率变化
Figure 7. Variation of wheel–rail creepage rate inside and outside the line
图 11 工况摩擦温升及误差分布
Figure 11. Frictional temperature rise and error distribution under working conditions
表 1 随温度变化的比热容和导热系数
Table 1. Specific heat capacity and thermal conductivity at different temperatures
温度/℃ 比热容/（J·kg−1·℃−1） 导热系数/（W·m−1·℃−1） 0 419.5 59.71 350 629.5 40.88 703 744.5 30.21 710 652.9 30.00 800 657.7 25.00 950 665.2 27.05 1200 677.3 30.46 
下载: 导出CSV
表 2 随温度变化的材料参数
Table 2. Material parameters at different temperatures
温度/℃ 弹性模量/GPa 泊松比 24 213 0.295 230 201 0.307 358 193 0.314 452 178 0.320 567 102 0.326 900 43 0.345
下载: 导出CSV
-
[1] 陈帅,吴磊,陶功权,等. 基于摩擦温升效应的地铁车轮磨耗特性研究[J]. 机械工程学报,2023,59(4): 213-220. doi: 10.3901/JME.2023.04.213CHEN Shuai, WU Lei, TAO Gongquan, et al. Study of wheel wear characteristic of subway vehicle based on the effect of friction temperature rising[J]. Journal of Mechanical Engineering, 2023, 59(4): 213-220. doi: 10.3901/JME.2023.04.213 [2] 赵鑫,温泽峰,金学松. 表面不平顺对轮轨摩擦温度场的影响[J]. 交通运输工程学报,2005,5(2): 19-22.ZHAO Xin, WEN Zefeng, JIN Xuesong. Influence of surface irregularity on wheel-rail friction temperature field[J]. Journal of Traffic and Transportation Engineering, 2005, 5(2): 19-22. [3] 李伟,温泽峰,吴磊,等. 滚滑接触下钢轨热力耦合分析[J]. 工程力学,2010,27(8): 199-204,216.LI Wei, WEN Zefeng, WU Lei, et al. Thermal-mechanical coupling analysis of rail under rolling-sliding contact[J]. Engineering Mechanics, 2010, 27(8): 199-204,216. [4] 肖乾,张海,王成国,等. 函数型摩擦系数条件下轮轨滚动和滑动接触的热机耦合分析[J]. 中国铁道科学,2013,34(4): 60-65.XIAO Qian, ZHANG Hai, WANG Chengguo, et al. Thermal mechanical coupling analysis of wheel rail rolling and sliding contacts under functional friction coefficient[J]. China Railway Science, 2013, 34(4): 60-65. [5] 刘洋,刘振,吴亚平,等. 考虑变摩擦系数的轮轨系统滑动接触热弹塑性应力分析[J]. 中国铁道科学,2015,36(5): 87-93.LIU Yang, LIU Zhen, WU Yaping, et al. Thermo-elasto-plastic analysis of wheel-rail sliding contact stress with variable friction coefficient[J]. China Railway Science, 2015, 36(5): 87-93. [6] VO K D, TIEU A K, ZHU H T, et al. The influence of high temperature due to high adhesion condition on rail damage[J]. Wear, 2015, 330/331: 571-580. doi: 10.1016/j.wear.2015.01.059 [7] KNOTHE K, LIEBELT S. Determination of temperatures for sliding contact with applications for wheel-rail systems[J]. Wear, 1995, 189(1/2): 91-99. [8] ERTZ M, KNOTHE K. A comparison of analytical and numerical methods for the calculation of temperatures in wheel/rail contact[J]. Wear, 2002, 253(3/4): 498-508. [9] FISCHER F D, DAVES W, WERNER E A. On the temperature in the wheel-rail rolling contact[J]. Fatigue & Fracture of Engineering Materials & Structures, 2003, 26(10): 999-1006. [10] 杨新文,顾少杰,周顺华,等. 30t轴重重载铁路轮轨滑动接触引起的钢轨热相变分析[J]. 铁道学报,2016,38(7): 84-90.YANG Xinwen, GU Shaojie, ZHOU Shunhua, et al. Analysis of rail thermal phase transformation due to wheel-rail sliding contact for heavy-haul railway with 30 t axle-load[J]. Journal of the China Railway Society, 2016, 38(7): 84-90. [11] 徐培娟,张大伟,田抑阳,等. 重载钢轨摩擦热损伤行为研究[J]. 铁道科学与工程学报,2021,18(12): 3155-3163.XU Peijuan, ZHANG Dawei, TIAN Yiyang, et al. Frictional thermal damage behavior of heavy-haul rails[J]. Journal of Railway Science and Engineering, 2021, 18(12): 3155-3163. [12] 伏培林,丁立,赵吉中,等. 考虑材料温度相关性的二维轮轨弹塑性滑动接触温升分析[J]. 力学学报,2020,52(5): 1245-1254.FU Peilin, DING Li, ZHAO Jizhong, et al. Frictional temperature analysis of two-dimensional elasto-plastic wheel-rail sliding contact with temperature-dependent material properties[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(5): 1245-1254. [13] KALKER J J. The rolling contact problem[M]//Three-Dimensional Elastic Bodies in Rolling Contact. Dordrecht: Springer Netherlands, 1990: 1-45. [14] KALKER J J. A fast algorithm for the simplified theory of rolling contact[J]. Vehicle System Dynamics, 1982, 11(1): 1-13. doi: 10.1080/00423118208968684 [15] TANVIR M A. Temperature rise due to slip between wheel and rail—an analytical solution for hertzian contact[J]. Wear, 1980, 61(2): 295-308. doi: 10.1016/0043-1648(80)90293-8 [16] CARSLAW H S, JAEGER J C. Conduction of heat in solids[M]. 2nd Edition. Oxford: Clarendon Press, 1959 [17] 李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008. [18] 肖宏,陈鑫,赵越. 基于摩擦自激理论的单侧钢轨波磨机理分析[J]. 西南交通大学学报,2022,57(1): 83-89,119.XIAO Hong, CHEN Xin, ZHAO Yue. Mechanism analysis of unilateral rail corrugation based on friction self-excitation theory[J]. Journal of Southwest Jiaotong University, 2022, 57(1): 83-89,119. [19] 周宇,韩延彬,木东升,等. 摩擦系数对滚动接触疲劳裂纹萌生和磨耗影响[J]. 同济大学学报(自然科学版),2018,46(10): 1392-1402.ZHOU Yu, HAN Yanbin, MU Dongsheng, et al. Effects of friction coefficient on rolling contact fatigue crack initiation and wear growth[J]. Journal of Tongji University (Natural Science), 2018, 46(10): 1392-1402. [20] DIRKS B, ENBLOM R, EKBERG A, et al. The development of a crack propagation model for railway wheels and rails[J]. Fatigue & Fracture of Engineering Materials & Structures, 2015, 38(12): 1478-1491. -
下载:
点击查看大图
计量
- 文章访问数: 377
- HTML全文浏览量: 80
- PDF下载量: 75
- 被引次数: 0