Method for Compressing Departure Tracking Interval of High-Speed Trains Based on Pre-departure Strategy
-
摘要:
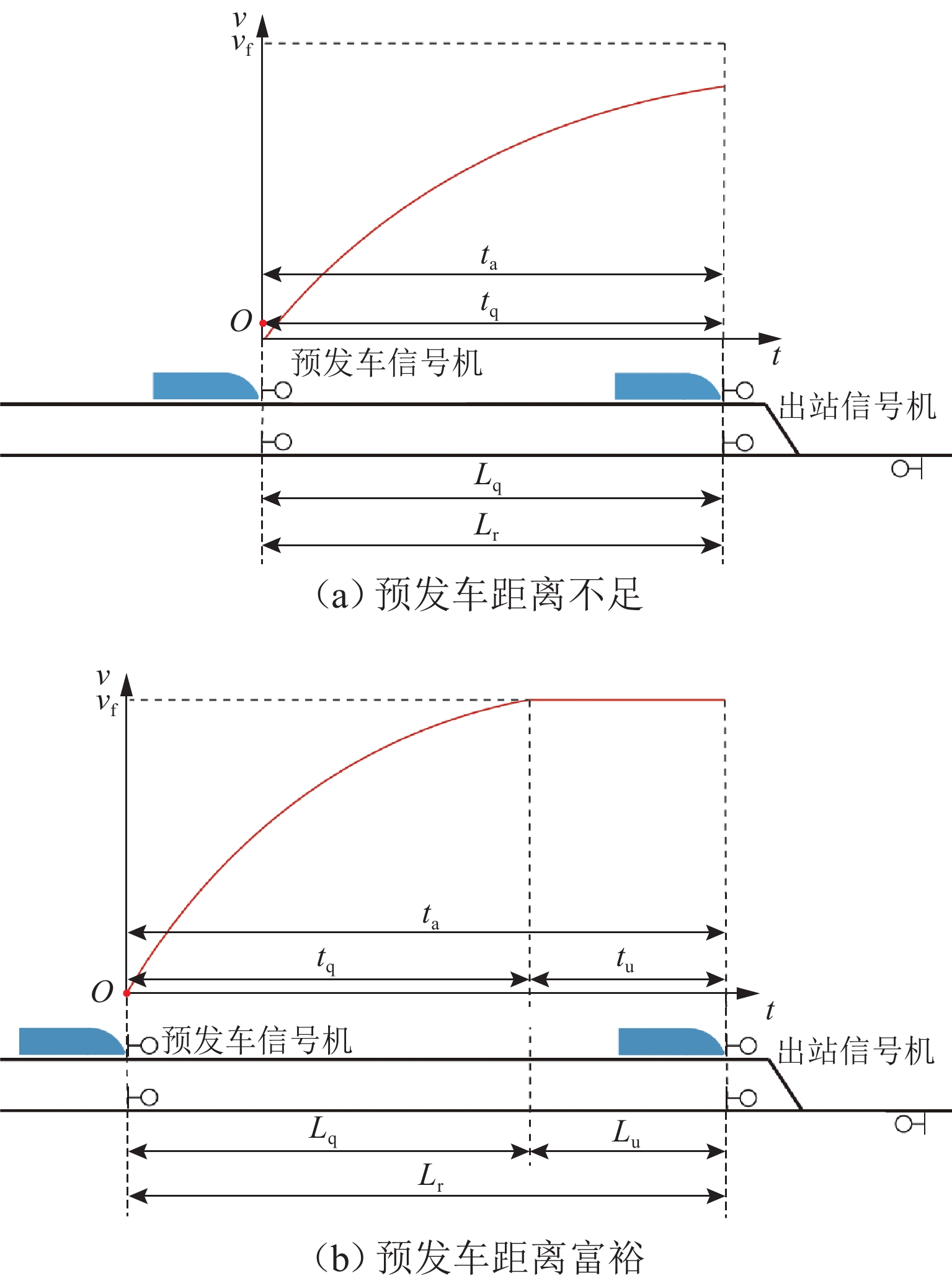
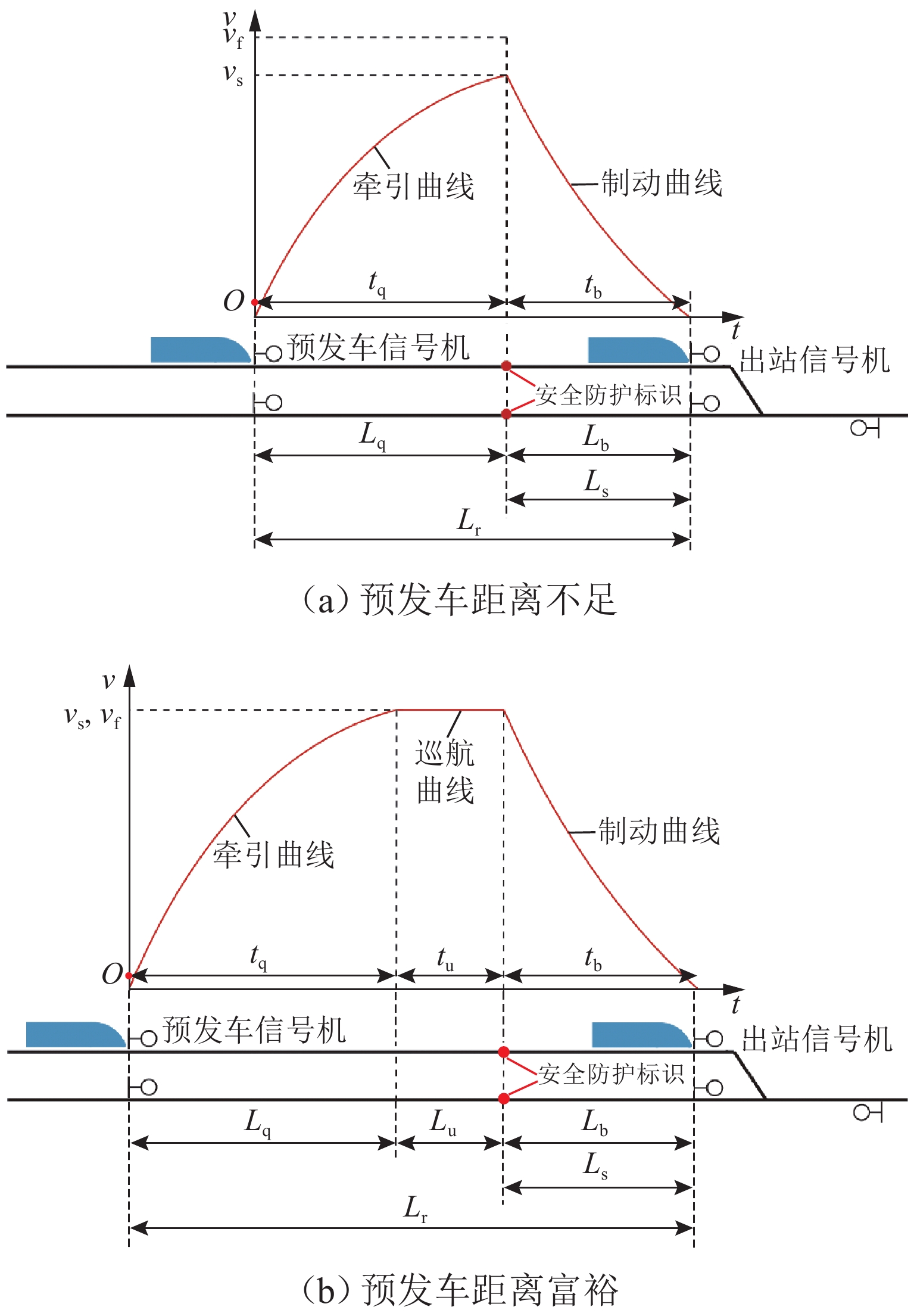
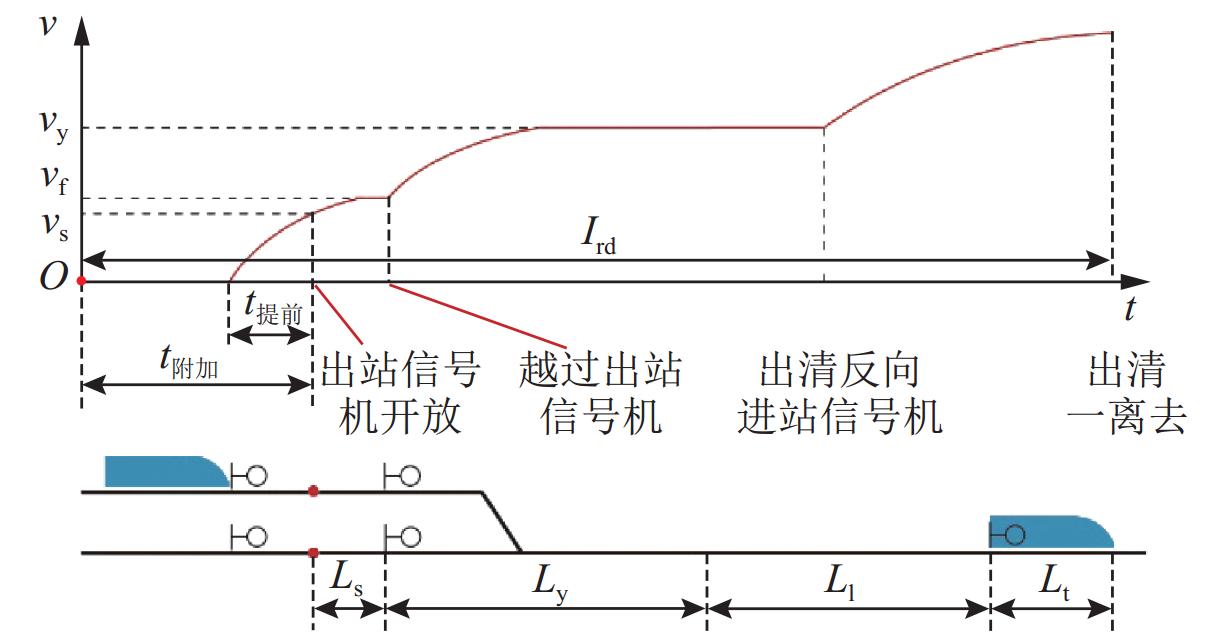
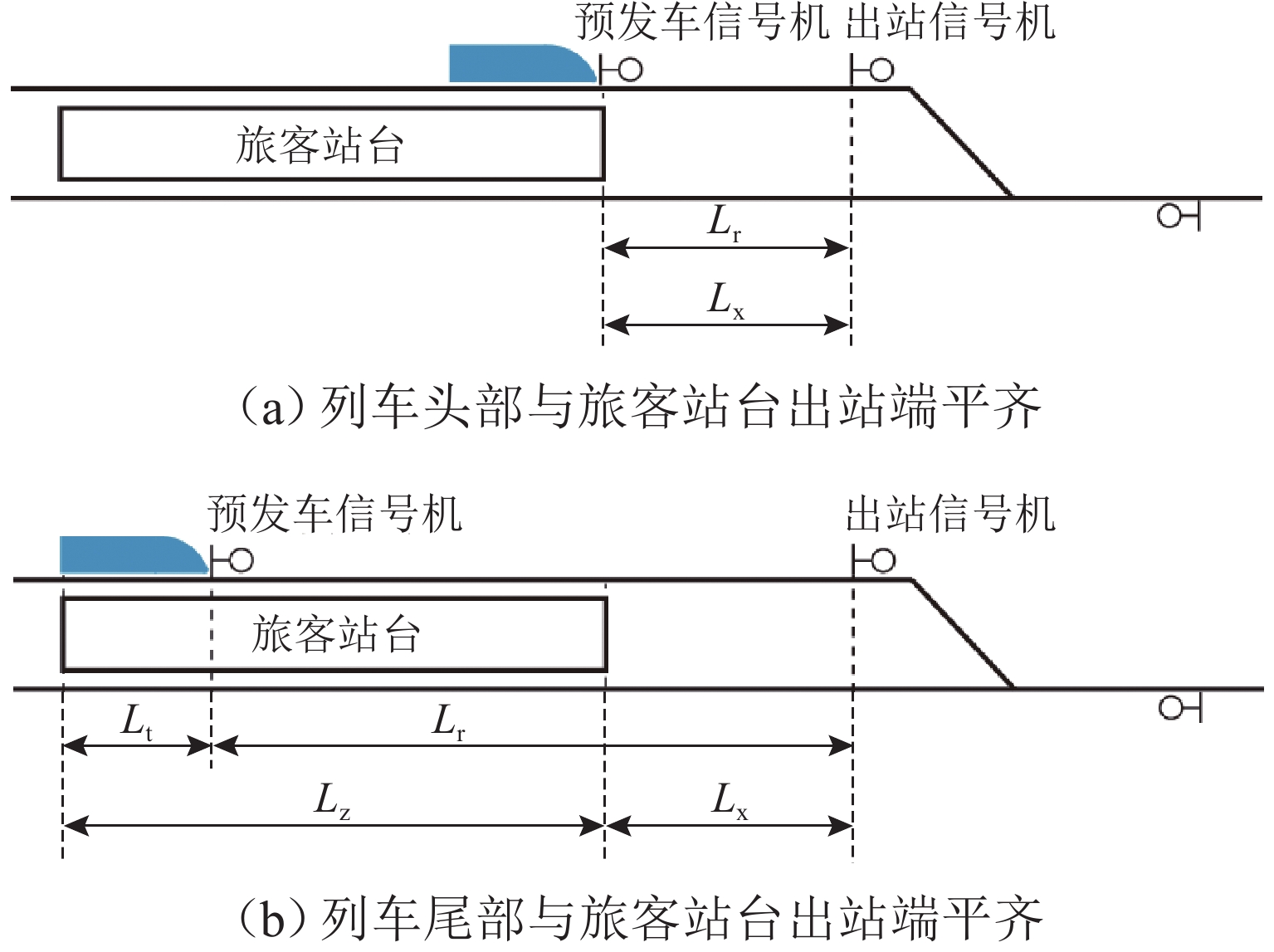
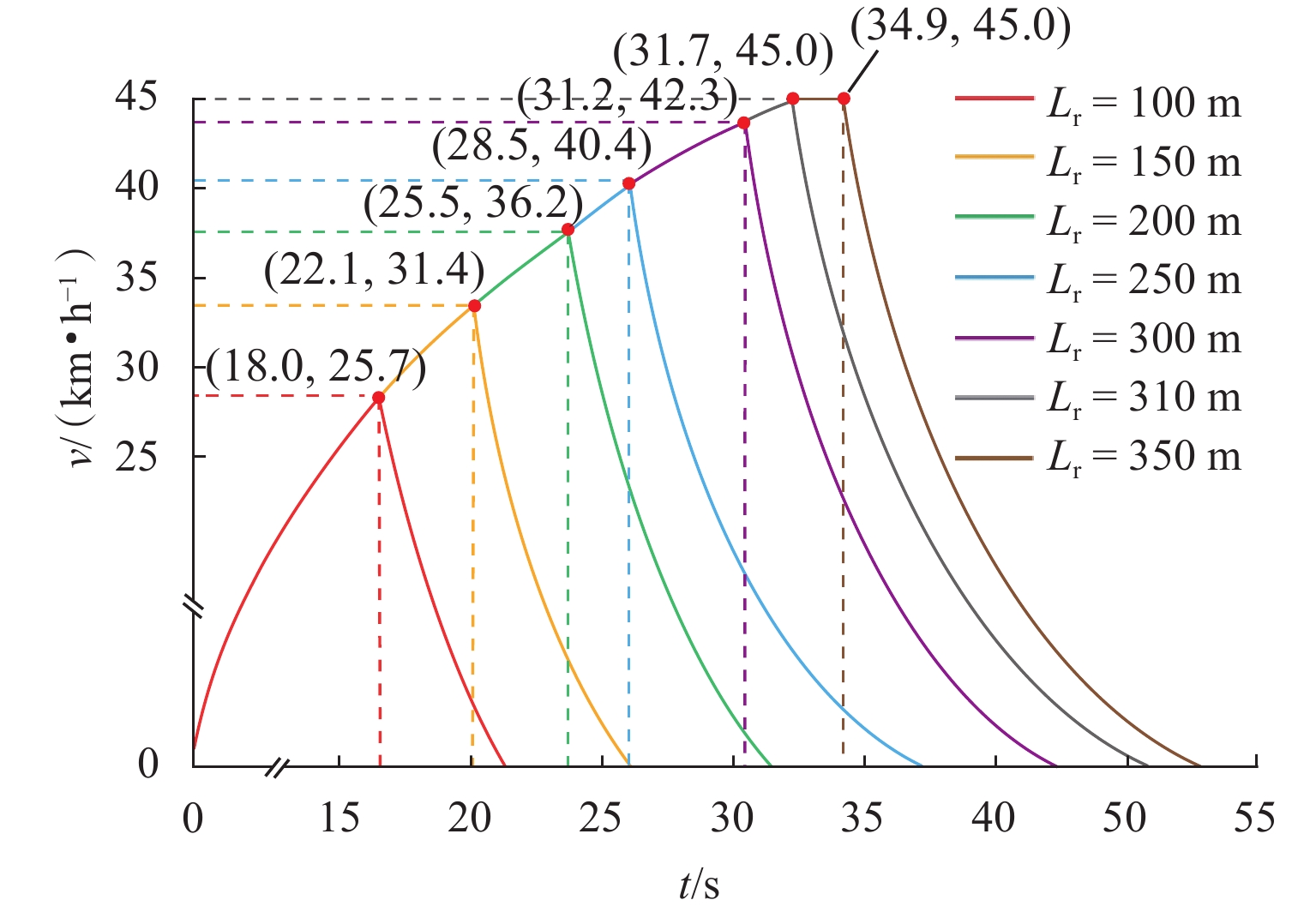
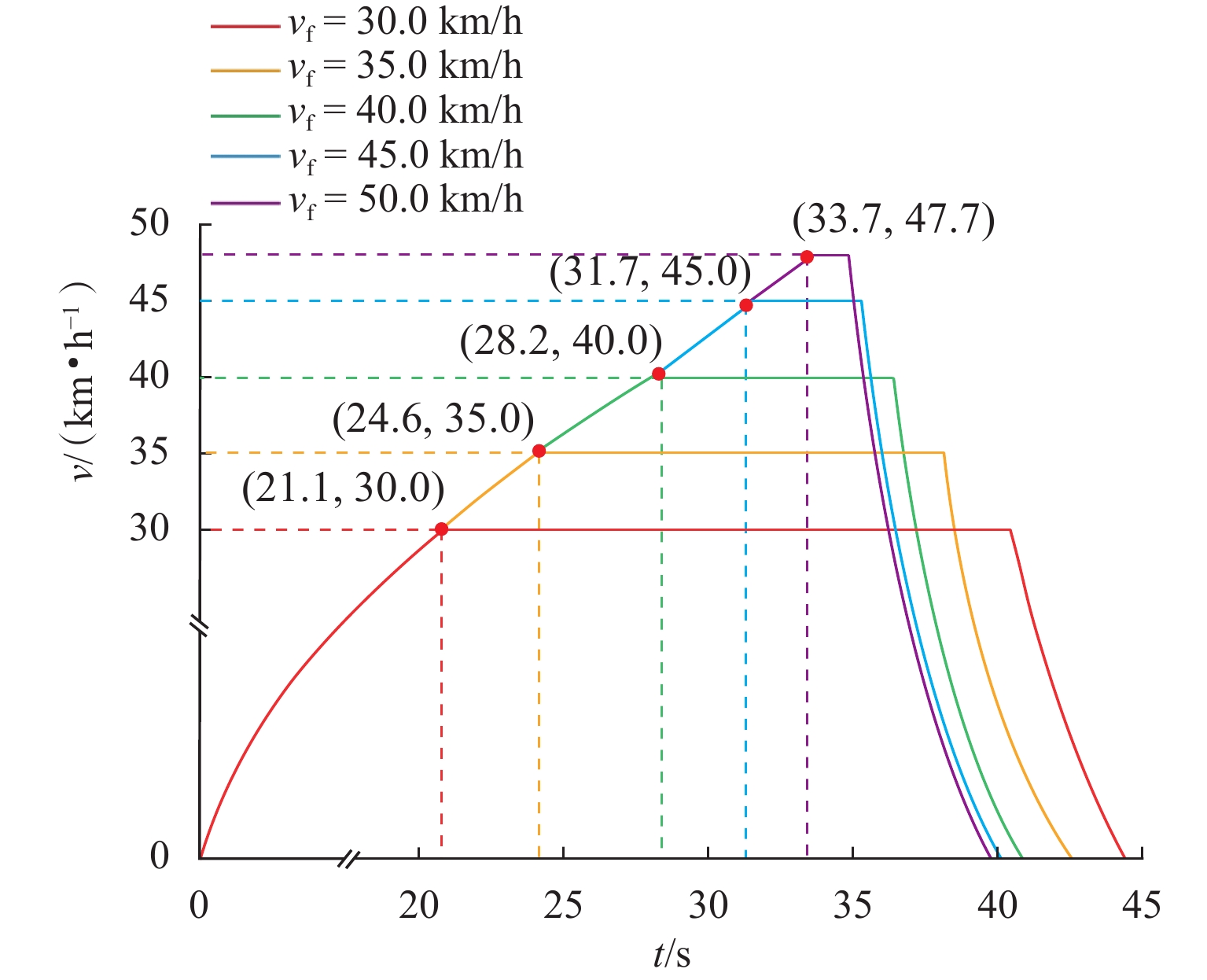
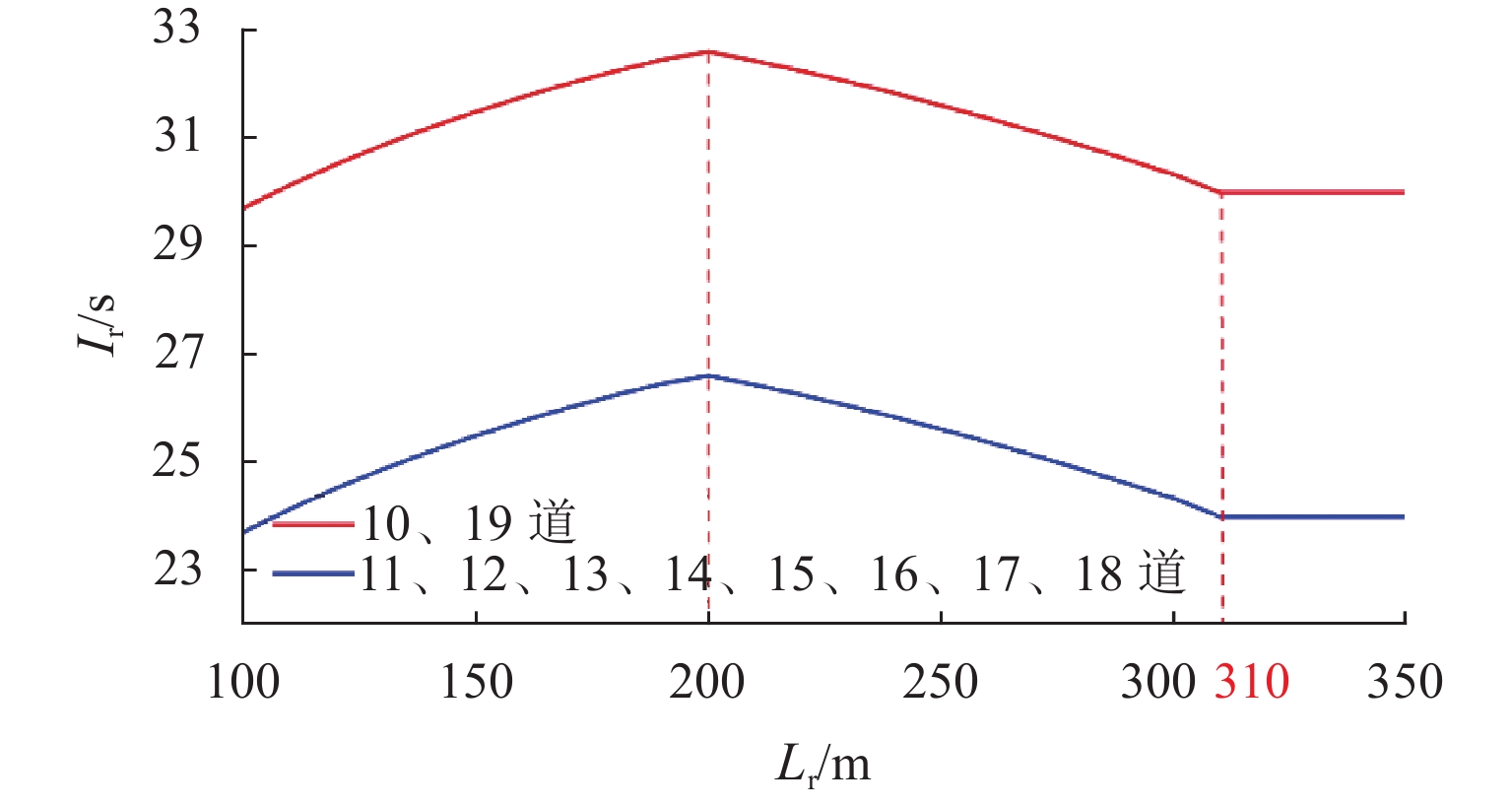
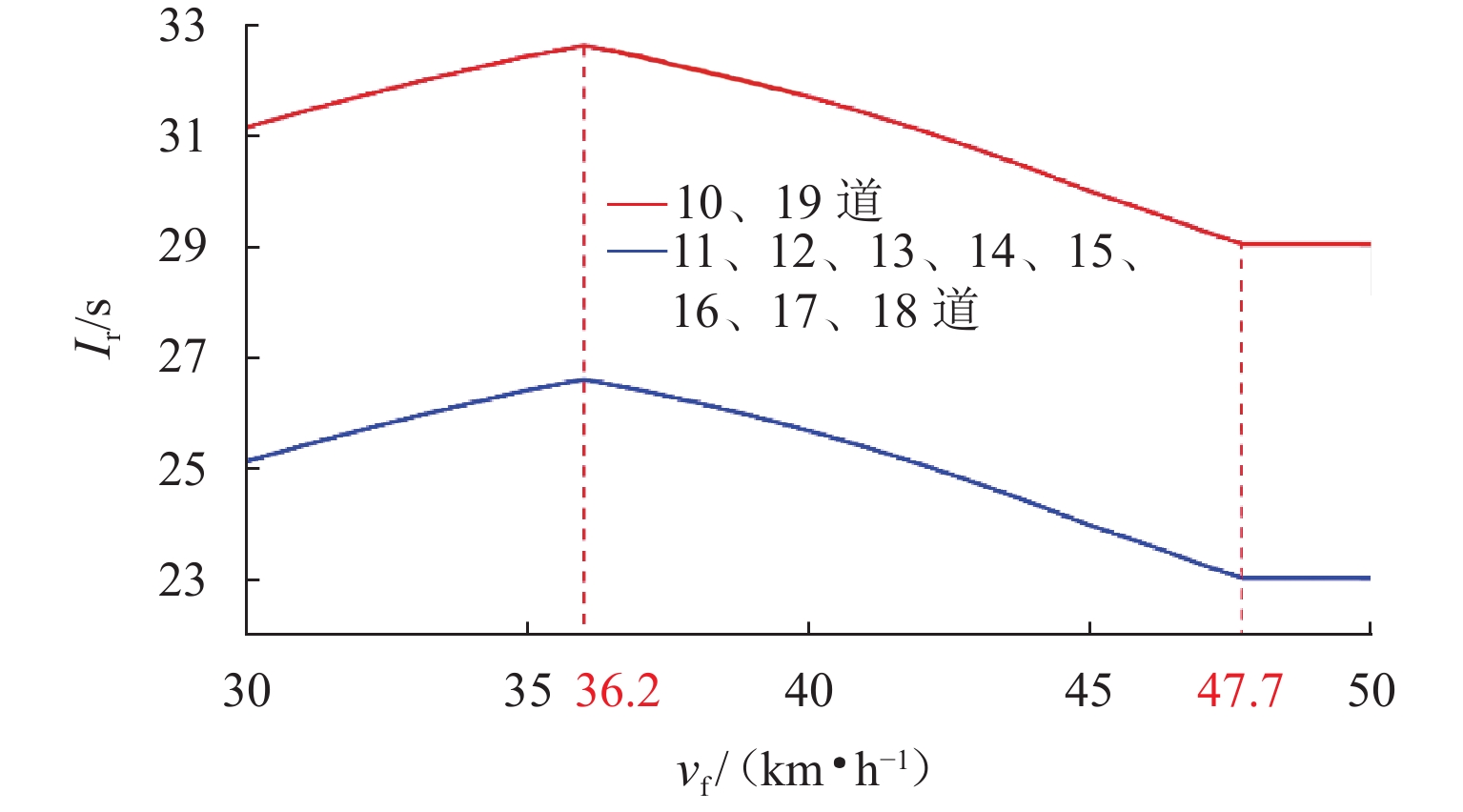
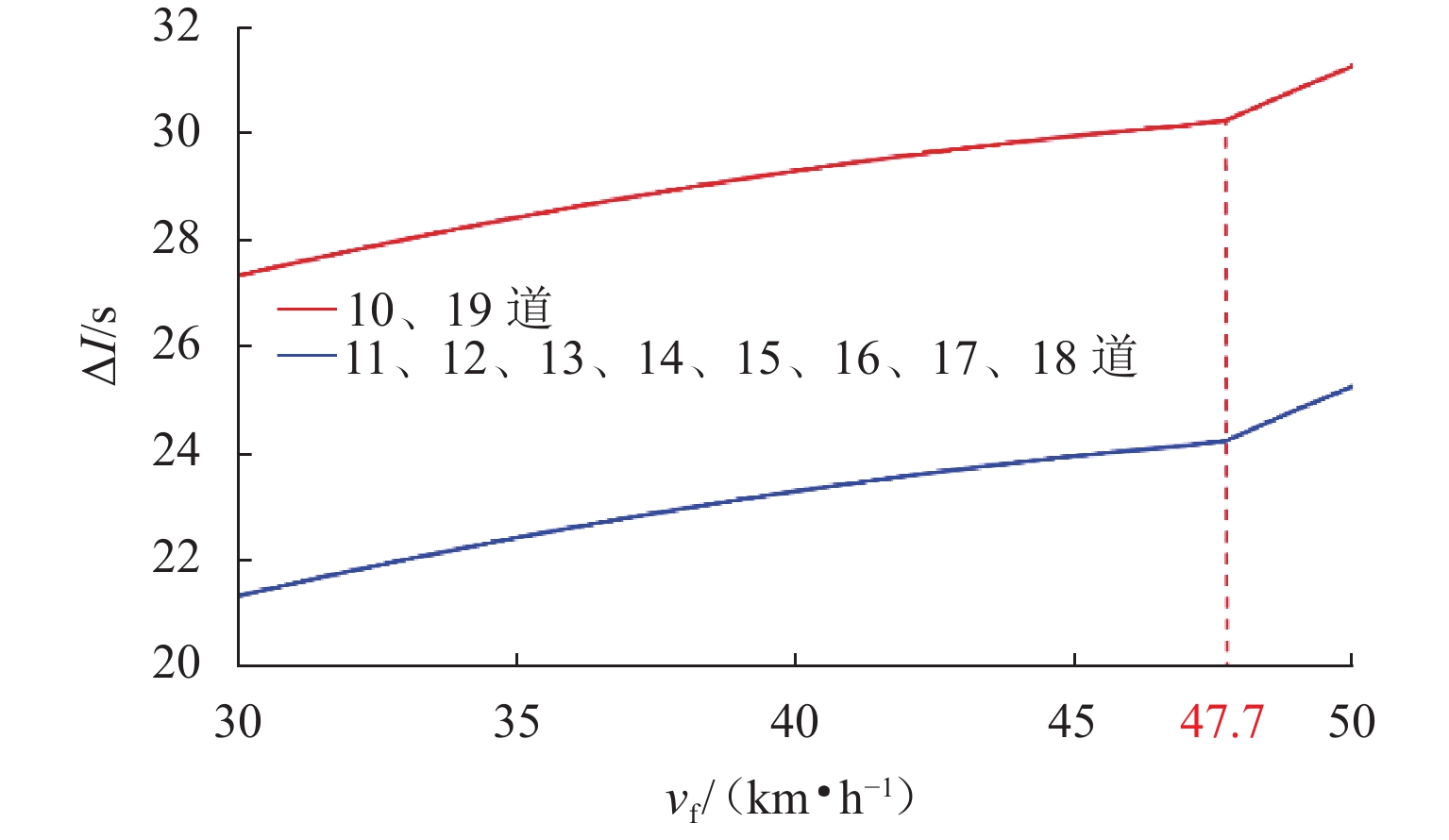
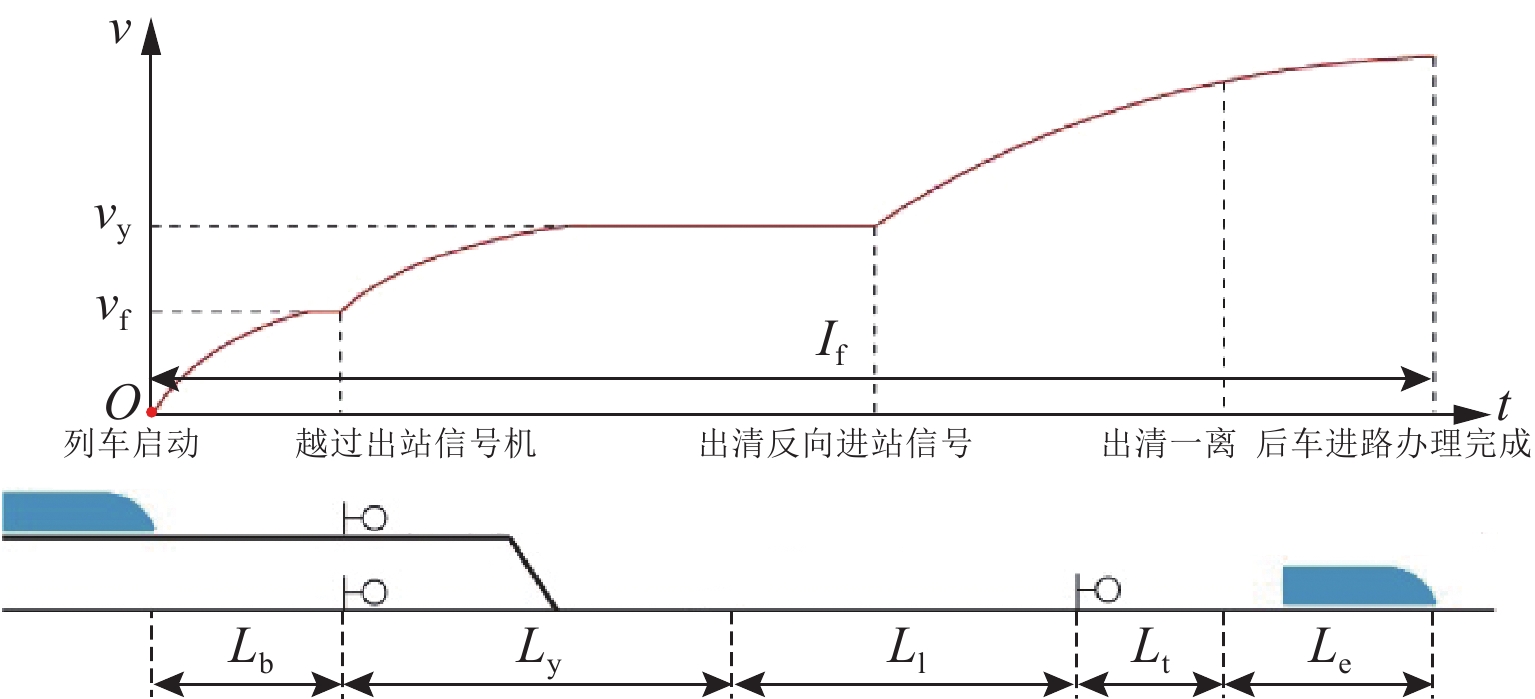
出发追踪间隔时间是限制列车实现3 min追踪运行的主要瓶颈之一，压缩出发追踪间隔时间可有效提高线路通过能力. 首先，分析高速列车出发追踪运行过程，提出在出站信号机内侧一定距离设置预发车信号机，使列车在出站信号机开放时具有一定初速度且剩余出站距离缩短；并设计预发车过程的“故障导向安全”原则以确保列车不冒进出站信号机；然后，在分析影响压缩出发追踪间隔时间因素的基础上，研究不同预发车方案下的列车控车模式曲线；最后，以上海虹桥站高速场为例进行仿真验证. 研究表明：该方法能压缩列车出发追踪间隔时间，压缩效果随预发车距离的增大呈现先上升后下降的趋势；在到发线有效长可提供200 m预发车距离时，最大可压缩列车出发追踪间隔时间26 s以上.
Abstract:The departure tracking interval is one of the main bottlenecks that limit the 3-minute tracking operation of trains, and compressing the departure tracking interval can effectively improve line capacity. The departure tracking process of high-speed trains was first analyzed, and a pre-departure annunciator was set at a certain distance inside the outbound annunciator, making the train have a certain initial speed and shortening the remaining outbound distance when the outbound annunciator was open. At the same time, the principle of “failure-oriented safety” for the pre-departure process was put forward to ensure that the train did not cross the outbound annunciator. Then, based on the analysis of factors affecting the compression of departure tracking interval, the curves of train control mode under different pre-departure schemes were studied. Finally, the high-speed yard of Shanghai Hongqiao Station was studied, and the results show that the departure tracking interval can be compressed by the proposed method. The compression effect increases first and then decreases with the increase in the pre-departure distance, and the maximum compressible departure tracking interval can be more than 26 s if the pre-departure distance reaches 200 m of the effective lengths of the arrival-departure track.
-
随着我国冷弯技术的快速发展，冷弯薄壁型钢凭借其轻质高强、利用率高的优点，在土木工程中的应用日益广泛[1]. 而冷弯薄壁不等肢卷边角钢由于截面简单、工业化程度高、安装简易，常被应用于可拆式箱式房屋以及冷弯型钢结构房屋中.
Adluri等[2]对铰接细长轴压角钢柱弯曲屈曲进行试验研究，表明由于局部屈曲引起有效截面形心的偏移，导致荷载偏心，引起附加弯矩，承载力计算时需考虑其影响；Dinis等[3]也指出，采用北美规范[4]计算角钢柱承载力，仅需考虑L/
1000 的偏心，其中，L为试件几何长度；Young[5]对固接冷弯平板角钢柱进行轴压试验，结果表明，承载力设计应只考虑弱轴的弯曲屈曲，而忽略弹性扭转屈曲和弯扭屈曲以及偏心引起的附加弯矩；De Barros Chodraui等[6]通过有限条法对轴心受压冷弯角钢柱进行分析，表明板件局部屈曲和整体扭转屈曲是一致的；Silvestre等[7]通过理论和有限元分析表明，固接和销轴连接的短、中长等肢角钢柱的屈曲和后屈曲有一定的不同；Ellobody等[8]以及Young等[9]分别对轴心受压平板角钢和卷边角钢屈曲性能进行计算分析，表明北美规范[4]对宽厚比较大构件承载力计算较为保守，而对宽厚比较小构件计算承载力偏于不安全；在此基础上，Young等[10]进行了屈曲强度450 MPa和550 MPa不等肢卷边角钢轴压试验，试件发生了弯扭屈曲以及局部和弯扭屈曲的相关屈曲，结果表明，北美规范[4]偏于保守；Shifferaw等[11]对固接冷弯薄壁等肢角钢柱整体屈曲性能进行理论和有限元分析，表明构件发生整体弯扭屈曲时表现出较为显著的屈曲后强度；Zhang等[12]采用试验和数值模拟研究S690高强角钢柱的弯扭屈曲性能和承载力，表明设计规范均给出了过于保守和分散的弯扭屈曲承载力；姚行友等[13]等对冷弯不等肢复杂卷边角钢进行轴压试验和有限元参数分析，提出考虑整体屈曲后强度的直接强度法修正公式；周宜松[14]对复杂卷边角钢柱进行轴压试验，发现试件越长越容易发生整体失稳，并提出适用复杂卷边不等肢角钢的直接强度法建议公式；徐步洲[15]通过对不等肢卷边角钢进行试验和有限元分析表明，中等长度柱易发生畸变和局部的相关屈曲，分肢宽厚比较大的卷边发生明显的畸变屈曲现象.尽管国内外学者对轴心受压冷弯薄壁型角钢进行了大量研究，但针对不等肢卷边角钢受力性能及设计方法的研究仍相对较少，我国现行国家规范《冷弯薄壁型钢结构技术规范》[16]也缺乏对双轴不对称冷弯薄壁截面构件承载力的设计方法. 鉴于此，本文对32根冷弯薄壁不等肢卷边角钢轴压试件的屈曲性能和极限承载力进行试验研究. 基于验证的有限元模型，分析长细比、宽厚比、肢宽比等参数对其屈曲性能和极限承载力的影响. 基于试验和有限元分析结果提出轴心受压冷弯薄壁不等肢卷边角钢构件承载力计算直接强度法的修正公式.
1. 试验概况
1.1 试件设计
本试验共设计32根冷弯薄壁不等肢卷边角钢试件，试件板材为LQ550镀锌钢板，名义厚度为2 mm，截面形式如图1所示. 图中：b1、b2分别为构件长肢和短肢的宽度，a1、a2为对应卷边的宽度，t为板厚，试件编号形式为LL4030-400-1，其中：LL表示不等肢卷边角钢，40、30分别表示长肢和短肢宽度，400表示角钢长度，1表示相同试件序号. 试件名义几何尺寸和实测尺寸如表1和表2所示.
表 1 试件名义几何尺寸Table 1. Nominal geometric dimension of specimens试件编号 bl/mm b2/mm al/mm a2/mm t/mm b1/t b2/t LL4030 40 30 15 15 2 20 15 LL6040 60 40 20 20 2 30 20 LL9060 90 60 20 20 2 45 30 LL12080 120 80 24 24 2 60 40 表 2 试件实测几何尺寸Table 2. Measured geometric dimensions of specimens试件编号 bl/mm b2/mm al/mm a2/mm t/mm 长度 L/mm 长细比 λ LL4030-400-1 42.13 31.43 15.97 15.54 1.98 400.00 39.19 LL4030-400-2 41.51 31.45 15.56 16.34 1.98 399.27 39.88 LL4030-900-1 42.00 31.61 15.96 14.84 1.99 900.00 87.28 LL4030-900-2 42.25 31.05 15.14 15.79 2.00 900.00 89.45 LL4030-1500-1 41.98 31.48 15.99 15.28 1.97 1498.37 147.14 LL4030-1500-2 41.93 31.42 15.93 15.95 2.00 1499.33 146.65 LL4030-2100-1 42.07 31.32 15.60 15.96 1.98 2101.17 206.51 LL4030-2100-2 42.20 31.59 15.52 15.66 1.98 2101.27 206.93 LL6040-400-1 61.68 41.48 21.63 19.48 1.98 400.00 29.54 LL6040-400-2 61.35 41.52 21.17 21.00 1.97 399.00 29.40 LL6040-900-1 62.05 41.60 21.45 19.37 1.98 900.00 66.46 LL6040-900-2 62.16 41.63 21.54 19.61 2.09 900.00 68.25 LL6040-1500-1 62.10 41.64 21.06 20.48 1.99 1499.43 110.40 LL6040-1500-2 61.80 41.76 21.35 20.98 2.07 1499.27 111.54 LL6040-2100-1 62.24 41.37 21.32 19.86 1.91 2101.10 152.65 LL6040-2100-2 61.44 41.91 20.92 20.47 1.98 2100.00 154.12 LL9060-400-1 91.80 61.41 20.25 20.02 1.97 400.00 22.15 LL9060-400-2 91.92 61.31 20.12 20.50 1.97 399.50 22.16 LL9060-900-1 91.51 61.43 19.90 21.05 1.99 900.00 49.79 LL9060-900-2 91.90 61.89 20.67 20.19 2.00 900.00 49.39 LL9060-1500-1 91.50 62.59 20.51 20.88 2.00 1498.90 81.56 LL9060-1500-2 91.43 62.42 21.08 19.88 1.97 1499.10 81.69 LL9060-2100-1 92.07 61.52 20.99 19.69 1.98 2100.00 115.66 LL9060-2100-2 91.60 61.94 21.83 21.01 2.00 2101.03 113.94 LL12080-400-1 121.53 81.77 24.92 23.98 1.98 400.00 16.95 LL12080-400-2 121.30 81.82 24.19 24.22 1.98 399.27 17.00 LL12080-900-1 122.30 81.71 25.11 24.05 1.97 900.00 38.10 LL12080-900-2 121.87 81.95 23.68 24.90 1.97 900.00 38.23 LL12080-1500-1 121.97 82.20 24.71 24.17 2.00 1498.22 63.34 LL12080-1500-2 122.48 81.87 24.95 24.70 1.97 1499.13 63.33 LL12080-2100-1 122.79 81.89 23.76 24.03 1.98 2101.17 89.38 LL12080-2100-2 121.04 82.24 24.71 24.49 1.97 2100.14 88.61 1.2 材性试验
材性试验共设计3个标准试样，所有试样均来自同一母材，根据《金属材料拉伸试验室温试验第1部分：室温试验方法》[17]中的规定方法进行拉伸试验.
3个标准试样材性试验应力-应变曲线如图2所示. 得到屈服强度fy=403.0 MPa，极限强度fu=522.8 MPa，弹性模量E=2.11 × 1011 Pa，断后伸长率δ=31.3%.
1.3 初始缺陷
试验前采用千分表对所有试件的初始几何缺陷进行量测. 试件纵向初始缺陷量测位置如图3所示. 外凸变形取值为正，内凹变形取值为负，1#、2#、4#、5# 千分表测量试件肢宽边缘10 mm处沿纵向分肢初始局部屈曲缺陷，3# 千分表量测试件整体弯曲初始缺陷. 部分试件沿纵向初始缺陷如图4所示，其他试件初始几何缺陷与其基本一致，并无明显的分布规律. 表3给出所有试件初始几何缺陷测量结果的最大值. 表中：ΔLmax、ΔGmax分别为局部屈曲缺陷与整体屈曲缺陷；Pt、PFE、PD、PMD、PY分别为试件试验极限承载力、试件有限元分析极限承载力、北美规范直接强度法计算极限承载力、修正直接强度法计算极限承载力、文献[18]建议修正公式计算极限承载力；F、L、D、FT分别表示弯曲屈曲、局部屈曲、畸变屈曲和弯扭屈曲. 由表3可知，试件的局部屈曲缺陷值均大于整体屈曲缺陷值，试件的整体初始缺陷均小于L/
1000 .表 3 试验和有限元分析角钢屈曲模式和承载力对比Table 3. Comparisons of buckling modes and bearing capacities of steel angles between test and finite element analysis试件编号 屈曲模式 ΔLmax/
mmΔGmax/
mmPt/kN PFE/kN PD/kN PMD/kN PY/kN Pt/PY Pt/ PFE Pt/ PD Pt/PMD 试验 有限元 一阶模态 LL4030-400-1 FT FT F 0.49 0.28 79.66 83.17 83.77 74.38 72.51 1.0986 0.9578 0.9509 1.0710 LL4030-400-2 FT FT F 0.41 0.34 79.38 82.66 83.67 73.51 73.41 1.0813 0.9603 0.9488 1.0799 LL4030-900-1 FT FT F 1.30 0.83 50.68 53.93 56.47 50.71 27.68 1.8312 0.9397 0.8974 0.9995 LL4030-900-2 FT FT F 1.54 0.77 52.72 54.70 56.90 50.97 27.97 1.8852 0.9638 0.9265 1.0342 LL4030-1500-1 FT FT F 1.30 0.38 40.70 40.93 40.36 42.15 23.01 1.7689 0.9944 1.0085 0.9655 LL4030-1500-2 FT FT F 1.14 0.17 40.98 41.52 41.89 43.75 23.88 1.7159 0.9869 0.9783 0.9366 LL4030-2100-1 FT FT F 1.84 0.08 30.52 31.19 24.48 25.57 13.96 2.1867 0.9786 1.2467 1.1936 LL4030-2100-2 FT FT F 1.10 0.09 29.26 31.35 24.50 25.59 13.97 2.0948 0.9335 1.2343 1.1434 LL6040-400-1 L L L 0.67 0.46 103.70 105.82 102.94 95.81 119.12 0.8706 0.9800 1.0074 1.0824 LL6040-400-2 L L L 0.75 0.31 102.46 105.26 105.33 96.41 121.73 0.8417 0.9734 0.9728 1.0628 LL6040-900-1 FT FT F 1.08 0.63 83.69 85.39 94.17 76.27 52.34 1.5989 0.9800 0.9886 1.0973 LL6040-900-2 FT FT F 1.17 0.74 83.62 84.70 98.45 80.28 54.25 1.5414 0.9872 0.9494 1.0416 LL6040-1500-1 FT FT F 1.15 0.60 59.96 61.98 74.21 61.37 42.31 1.4172 0.9673 0.9480 0.9769 LL6040-1500-2 FT FT F 1.42 0.43 60.82 63.31 78.23 64.30 44.60 1.3638 0.9607 0.9775 0.9459 LL6040-2100-1 FT FT F 1.17 0.24 48.66 50.69 41.59 43.44 23.71 2.0519 0.9600 1.1699 1.1201 LL6040-2100-2 FT FT F 1.42 1.08 49.94 50.96 42.99 44.90 24.51 2.0376 0.9800 1.1617 1.1122 LL9060-400-1 L L L 0.99 0.35 126.76 129.35 104.56 124.03 153.51 0.8257 0.9800 1.2123 1.0220 LL9060-400-2 L L L 0.57 0.57 125.71 129.60 106.03 124.39 155.32 0.8094 0.9700 1.1855 1.0106 LL9060-900-1 FT + L FT + L L 1.12 0.71 94.42 96.00 108.68 101.84 68.10 1.3865 0.9835 0.9688 0.9271 LL9060-900-2 FT + L FT + L L 1.02 0.92 95.60 97.20 107.99 102.07 67.07 1.4253 0.9835 0.9853 0.9366 LL9060-1500-1 FT + L FT + L L 0.79 0.71 77.34 80.36 90.86 94.90 51.80 1.4929 0.9625 0.9512 0.8149 LL9060-1500-2 FT + L FT + L L 0.88 0.83 77.04 78.87 85.54 89.34 48.77 1.5797 0.9768 0.9006 0.8623 LL9060-2100-1 D D F 1.22 0.90 59.95 61.37 48.74 50.90 27.79 2.1574 0.9768 1.2300 1.1776 LL9060-2100-2 D D F 1.08 0.77 61.51 63.42 54.77 57.20 31.22 1.9701 0.9700 1.2232 1.0754 LL12080-400-1 L L L 0.59 0.22 147.54 150.67 117.71 146.76 224.28 0.6578 0.9792 1.2535 1.0053 LL12080-400-2 L L L 0.58 0.14 146.78 150.41 117.29 146.49 223.06 0.6580 0.9759 1.2515 1.0020 LL12080-900-1 FT + L FT + L L 1.20 0.56 136.59 138.37 117.55 118.57 105.70 1.2923 0.9872 1.1620 1.1520 LL12080-900-2 FT + L FT + L L 1.52 1.11 131.36 138.86 118.35 118.60 106.10 1.2380 0.9460 1.1099 1.1075 LL12080-1500-1 FT + L FT + L L 1.20 1.56 97.14 98.99 116.57 104.35 81.31 1.1948 0.9813 0.8334 0.9309 LL12080-1500-2 FT + L FT + L L 1.52 1.11 98.56 98.19 116.67 102.58 83.41 1.1817 1.0038 0.8447 0.9608 LL12080-2100-1 FT + L FT + L L 1.44 1.42 85.43 85.91 73.43 76.89 41.97 2.0354 0.9948 1.2634 1.1110 LL12080-2100-2 FT + L FT + L L 1.45 1.54 85.82 86.48 76.31 80.96 44.19 1.9419 0.9926 1.2246 1.0600 均值 1.4760 0.9741 1.1246 1.0318 方差 0.2060 0.0002 0.0227 0.0077 变异系数 0.1395 0.0002 0.0201 0.0074 1.4 加载装置和测点布置
试验采用自平衡反力系统施加竖向荷载，YJ16静态应变位移采集系统采集数据. 加载端板和底板设10 mm深凹槽，试件插入凹槽后采用垫片将凹槽缝隙填满嵌实以保证试件端部固结. 试验加载装置如图5所示. 采用分级加载的加载方式，每级加载后暂停1 min；当试件发生屈曲或承载力开始下降时，加载速率减半；当试件承载力下降至极限承载力的75%或完全破坏，结束加载. 试件位移计布置如图6所示，D1、D2、D3、D4 4个位移计分别布置在试件中截面处，以量测试件跨中的扭转变形，在试件加载端端部布置位移计D5测量竖向位移.
2. 试验结果及分析
2.1 试验过程和试验现象
2.1.1 长度为400 mm角钢柱
长度为400 mm的不等肢角钢柱屈曲模式如图7所示. 试件在加载初期变形不明显，随着荷载逐渐增大，b2/t=15的试件分肢出现扭转变形且伴有弯曲，达到破坏荷载时长肢扭转变形明显，构件最终表现为弯扭屈曲模式（图7（a））. b2/t=20，30，40的试件出现了明显的局部屈曲，最终表现为塑性折曲破坏（图7（b））.
2.1.2 长度为900、
1500 mm角钢柱长度为900、
1500 mm的试件屈曲模式如图8所示. 在加载初期变形不明显，随着荷载逐渐增大，b2/t=15，20的试件开始整体弯曲，且分肢沿短肢方向出现向内扭转，达到破坏荷载时长短肢出现明显扭转，构件最终表现为弯扭屈曲（图8（a）），b2/t=30，40的试件出现双肢扭转变形且发生整体弯曲，随着长度的增加弯扭现象愈明显，分肢出现局部屈曲，最终表现为整体弯扭和局部相关屈曲（图8（b））.
图 8 长度为900、1500 mm的角钢柱屈曲模式Figure 8. Buckling mode of steel angle with lengths of 900 mm and 1 500 mm2.1.3 长度为
2100 mm角钢柱长度为
2100 mm的不等肢角钢柱屈曲变形如图9所示. 加载初期变形不明显，随着荷载逐渐增大，b2/t=15，20的试件发生明显的弯扭变形，最终表现为弯扭屈曲模式（图9（a）），b2/t=30的试件两肢向内扭转，表现为畸变屈曲（图9（b）），b2/t=40的试件扭转和弯曲变形明显且在构件下端部出现局部屈曲现象，表现为弯扭和局部相关屈曲（图9（c））.由所有试件屈曲模式可知：轴压冷弯薄壁不等肢卷边角钢屈曲模式主要有弯扭屈曲、局部屈曲以及弯扭和局部相关屈曲，个别试件发生了畸变屈曲. 分析发现，长细比大且宽厚比小的试件易发生弯扭屈曲，长细比小且宽厚比大的易发生局部屈曲或者弯扭和局部相关屈曲.
2.2 试验结果
由表3可知，相同试件重复试验的结果非常相近，表明试验结果是可靠的. 相同截面试件的极限承载力随着试件长细比的增加而降低. 相同长度不同截面的试件荷载-位移曲线对比如图10所示：各试件在加载初期处于弹性阶段，荷载变形曲线成线性关系，刚度基本不变，轴向位移随荷载增大而明显增大；试件屈曲后，荷载变形曲线表现为非线性；达到极限荷载后，承载力缓慢降低.
3. 有限元参数化分析
3.1 有限元模型建立
采用ABAQUS有限元软件S4R壳单元和理想弹塑性模型对试件进行数值模拟建模，有限元模型的几何参数及材料特性采用实测值，不考虑残余应力的影响. 建立有限元模型如图11所示，试件上、下端分别耦合于形心RP-1、RP-2位置，上端约束x、y、z方向的平动自由度（Dx、Dy、Dz）以及x、y、z方向的转动自由度（Rx、Ry、Rz），下端约束所有自由度. 有限元分析首先通过弹性特征值屈曲分析获取试件可能出现的第一阶屈曲模态，作为非线性分析的初始几何缺陷形状，图12是试件LL12080-1500-1的一阶弹性屈曲模态，初始缺陷最大值取表3中实测最大值，采用Von-Mises屈服准则，弧长法求解.
3.2 有限元模型验证
通过ABAQUS有限元软件分析得到所有试件的屈曲模式和极限承载力（表3）. 代表性试件的屈曲模式以及荷载-位移曲线对比分别如图13和图14所示. 由表3可知，试件有限元分析屈曲模式与试验结果一致，试验承载力与有限元分析结果比值的平均值和变异系数分别为0.974和
0.0002 . 由图13可知，有限元分析试件LL6040-1500-1和试件LL9060-900-1的弯扭屈曲、弯扭和局部相关屈曲与试验结果一致. 由图14可知，有限元分析试件荷载位移曲线与试验曲线基本一致. 由此表明，本文采用的有限元分析模型是合理可行的.
图 13 试验与有限元分析屈曲模式对比Figure 13. Comparison of buckling modes between test and finite element analysis
图 14 试验与有限元分析荷载-位移曲线对比Figure 14. Comparison of load-displacement curves between test and finite element analysis3.3 参数分析
选取不同截面不等肢卷边角钢分析长细比、宽厚比、肢宽比对其承载力的影响. λ=10，20，40，60，80，100，130，160，200；b2/t=20，30，45，60；b2/b1=0.5，0.6，0.7，0.8，0.9，1.0，共216根角钢构件. 得到不同截面和长细比的不等肢卷边角钢极限承载力. 角钢承载力NFE/Ns与长细比之间的关系如图15所示，其中：NFF为有限元分析承载力，Ns为截面屈服承载力. 由图15可知，不等肢卷边角钢极限承载力随构件长细比的增加而降低，当λ<40时影响稍大，长细比对构件极限承载力的影响随构件宽厚比的增大而减弱.
图 15 极限承载力和长细比关系曲线Figure 15. Relationship between ultimate bearing capacity and slenderness ratio4. 建议计算方法
4.1 现有计算方法
4.1.1 北美规范[4]
北美规范采用直接强度法计算轴心受压冷弯薄壁不等肢卷边角钢构件稳定承载力PD，PD取整体屈曲极限承载力Pne （式（1） ）、局部和整体相关屈曲极限承载力Pnl （式（2） ）的最小值.
Pne={0.658λ2cPy,λc⩽1.5,0.877λ2cPy,λc>1.5, (1) Pnl={Pne,λl⩽0.776,[1−0.15(PcrlPne)0.4](PcrlPne)0.4Pne,λl>0.776, (2) F3cre(r20−x30−y30)−F2cre[r20(σex+σey+σt)−(σeyx20+σexy20)]+Fcrer20(σexσey+σeyσt+σexσt)−(σexσeyσtr20)=0, (3) 式中：Py为构件屈服承载力，$P_{\mathrm{y}}=A_{\mathrm{g}} F_{\mathrm{y}} $，Fy为材料屈服强度，Ag为试件的毛截面面积；$\lambda_{\mathrm{c}} = \sqrt{P_{\mathrm{y}} / P_{{\mathrm{cre}}}} $，Pcre为试件弹性整体屈曲临界力，如式（3）；$\lambda_{\mathrm{l}}=\sqrt{P_{{\mathrm{ne}}} / P_{{\mathrm{crl}}}} ， P_{{\mathrm{crl}}}= A_{\mathrm{g}} F_{{\mathrm{crl}}} $，为试件弹性局部屈曲临界力，Fcrl为试件弹性局部屈曲临界应力；x0和y0分别为沿x主轴和y主轴从剪心到形心的距离；$ {\sigma }_{\mathrm{e}\mathrm{x}} $和$ {\sigma }_{\mathrm{e}\mathrm{y}} $分别为围绕x轴和y轴弹性弯曲屈曲临界应力；${r}_{{\mathrm{0}}} $为弹性扭转屈曲临界应力；$ {\sigma }_{{\mathrm{t}}} $为$ {r}_{{\mathrm{0}}} $的回转半径.
4.1.2 Young[5]计算方法
Young考虑角钢构件的整体屈曲后强度，提出建议式：
Pne={0.5λ2cpy,λc⩽1.5,0.5λ2cpy,λc>1.5. (4) 4.1.3 建议方法
按照北美规范[4]中直接强度法（式（1）～（3））以及Young[5]建议修正式（式（4））计算试件稳定承载力PD和PY，如表3所示. 试件试验极限承载力Pt与北美规范[4]直接强度法计算稳定承载力PD结果之比的均值和变异系数分别为
1.1246 和0.0201 . 试件试验极限承载力Pt和Young[5]建议修正式之比的均值和变异系数分别为1.4760 和0.1395 . 由表3和图16可知，北美规范[4]直接强度法和Young[5]建议方法计算试件稳定承载力偏保守. 图16中，DSM为直接强度法. 为此，基于试验结果及有限元分析结果对直接强度法计算式进行拟合修正，得出
图 16 试验和有限元分析角钢屈曲模式和承载力对比Figure 16. Comparisons of buckling modes and bearing capacities of steel angles between test and finite element analysisPmne={0.761λ2cPy,λc⩽1.174,0.916λ2cPy,λc>1.174, (5) Pmnl={Pne,λ1⩽0.626,[1−0.191(PcrlPne)0.4](PcrlPne)0.4Pne,λ1>0.626, (6) 式中：Pmne、Pmnl分别为整体屈曲极限承载力和局部和整体相关屈曲极限承载力.
采用修正式（5）、（6）计算得到轴心受压冷弯薄壁不等肢卷边角钢构件稳定承载力PMD，如表3所示，其中，PMD为修正式（5）计算的Pmne和修正计算（式（6））的Pmnl的最小值. 试件试验极限承载力Pt与修正直接强度法PMD计算结果之比的均值和变异系数分别为
1.0318 和0.0074 ，表明修正式是准确的.4.2 建议方法可靠度分析
采用建议的直接强度法（式（5）、 （6））对试验试件、有限元分析构件进行稳定承载力计算，得到采用建议公式计算试验试件以及有限元分析构件的承载力与其之比的均值（变异系数）分别为
1.0318 、0.0075 （0.9769 、0.0109 ）. 试件试验极限承载力以及有限元分析的构件承载力与直接强度法曲线及建议公式曲线对比如图16所示. 采用文献[18]一次二阶矩法对冷弯薄壁不等肢卷边角钢设计稳定承载力进行可靠度分析，得到冷弯薄壁型不等肢卷边角钢轴压构件可靠指标如表4所示. 表中：G为恒荷载，L1 和L2分别为办公楼和住宅的活荷载，W为风荷载. 由表4可知，在不同荷载组合下的可靠度指标均大于现行的《冷弯型钢结构技术规范》[16]对LQ550级的冷弯薄壁型钢材的目标可靠指标（3.2）. 由此可知，采用修正直接强度法计算此类冷弯薄壁不等肢卷边角钢轴压承载力是安全可靠的.表 4 冷弯薄壁型不等肢卷边角钢轴压构件可靠指标Table 4. Reliability indexes of CFTWS with unequal-leg lipped angles under axial compression类型 ρ2 组合形式 ρ1=0.5 ρ1=1.0 ρ1=2.0 ρ1=3.0 可靠指标平均值 办公楼 0 1.3G + 1.5L1 4.518 4.467 4.442 4.403 4.457 0.5 1.3G + 0.9 × 1.5 （L1 + W） 4.306 4.298 4.253 4.198 4.264 1.0 1.3G + 0.9 × 1.5 （L1 + W） 4.178 4.161 4.102 4.087 4.132 2.0 1.3G + 0.9 × 1.5 （L1 + W） 4.096 4.011 3.918 3.824 3.962 3.0 1.3G + 0.9 × 1.5 （L1 + W） 3.954 3.898 3.837 3.763 3.863 4.0 1.3G + 0.9 × 1.5 （L1 + W） 3.781 3.675 3.621 3.601 3.670 住宅 0 1.3G + 1.5L2 4.924 4.869 4.841 4.799 4.858 0.5 1.3G + 0.9 × 1.5 （L2 + W） 4.693 4.684 4.635 4.575 4.647 1.0 1.3G + 0.9 × 1.5 （L2 + W） 4.554 4.535 4.471 4.454 4.503 2.0 1.3G + 0.9 × 1.5 （L2 + W） 4.464 4.372 4.270 4.168 4.318 3.0 1.3G + 0.9 × 1.5 （L2 + W） 4.309 4.248 4.182 4.101 4.210 4.0 1.3G + 0.9 × 1.5 （L2 + W） 4.121 4.005 3.947 3.925 3.999 注：ρ1 为活荷载标准值与风荷载标准值之和与恒荷载标准值的比值，ρ2 为风荷载标准值与活荷载标准值的比值. 5. 结 论
本文通过对轴心受压冷弯薄壁不等肢卷边角钢进行屈曲承载力试验和有限元分析，得到如下结论：
1） 长细比较大和宽厚比较小的试件易发生弯扭屈曲，长细比较小和宽厚比较大的试件易发生弯扭和局部相关屈曲. 相同长度试件的极限承载力随着宽厚比的增加而提高；相同截面试件的极限承载力随着试件长度的增加而大幅下降；宽厚比越大，构件长度对构件极限承载力的影响越小.
2） 有限元分析结果与试验结果对比表明，建立的ABAQUS有限元分析模型对分析冷弯薄壁不等肢卷边角钢轴压柱屈曲性能是有效的.
3） 有限元参数分析表明，长细比是影响构件极限承载力和屈曲模式的主要因素. 通过增大构件宽厚比和构件肢宽比可提高构件的极限承载力.
4） 北美规范直接强度法建议方法偏保守，基于试验和有限元分析提出的修正直接强度法具有较好的准确性和可靠度.
-
图 4 故障导向安全的列车预发车控车模式曲线
Figure 4. Pre-departure control curve under principle of “failure-oriented safety”
图 7 不同$ {L}_{{\mathrm{r}}} $下列车预发车过程的控车模式曲线
Figure 7. Pre-departure control curves under different Lr
图 8 不同$ {v}_{{\mathrm{f}}} $下列车预发车过程的控车模式曲线
Figure 8. Pre-departure control curves under different vf
图 9 上海虹桥站高速场上行方向站型图
Figure 9. Layout of upward direction of high-speed yard of Shanghai Hongqiao Station
图 10 各到发线$ {I}_{{\mathrm{r}}} $随$ {L}_{{\mathrm{r}}} $的变化
Figure 10. Variation of Ir with Lr in each arrival-departure track
图 11 各到发线$ {I}_{{\mathrm{r}}} $随$ {v}_{{\mathrm{f}}} $的变化
Figure 11. Variation of Ir with vf in each arrival-departure track
图 12 各到发线$\Delta I$随$ {v}_{{\mathrm{f}}} $的变化
Figure 12. Variation of △I with vf in each arrival-departure track
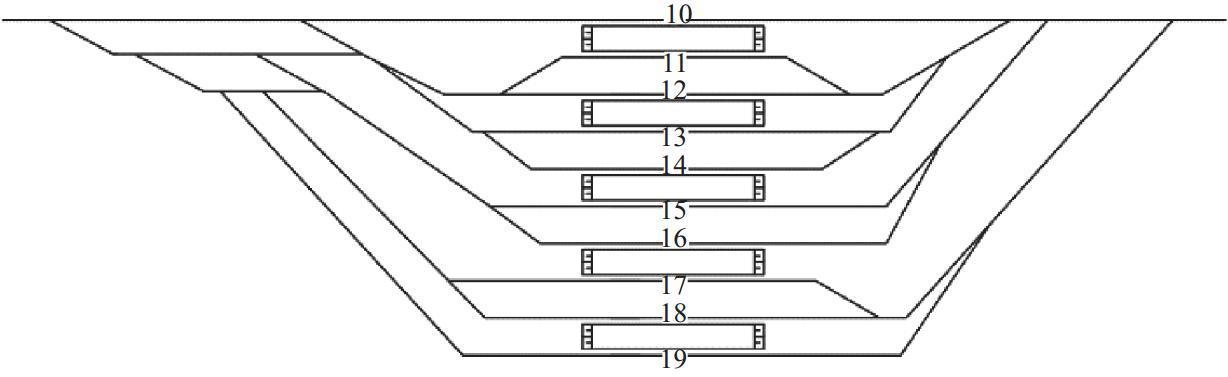
表 1 相关参数
Table 1. Related parameters
股道 发车进路
长度/m$ {L}_{{\mathrm{b}}} $/m $ {t}_{{\mathrm{e}}} $/s $ {v}_{{\mathrm{f}}} $/
（km•h−1）$ {v}_{{\mathrm{y}}} $/
（km•h−1）10 2607 290 51.0 45.0 80.0 11 2903 215 12 2903 215 13 2871 215 14 2871 215 15 2879 215 16 2879 215 17 2936 215 18 2936 215 19 2551 290 
下载: 导出CSV
-
[1] 胡志垚. 进路分段办理压缩大型客站发车追踪间隔时间[J]. 交通科技与经济,2018,20(3): 23-27,65.HU Zhiyao. Compressing departure tracking interval of large passenger railway station with departure route subsection[J]. Technology & Economy in Areas of Communications, 2018, 20(3): 23-27,65. [2] SHANGGUAN W, YAN X H, CAI B G, et al. Multiobjective optimization for train speed trajectory in CTCS high-speed railway with hybrid evolutionary algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 2215-2225. doi: 10.1109/TITS.2015.2402160 [3] YAN X H, CAI B G, NING B, et al. Moving horizon optimization of dynamic trajectory planning for high-speed train operation[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(5): 1258-1270. doi: 10.1109/TITS.2015.2499254 [4] GAO S L, ZHENG Y S. Adjustment of train interval time based on dynamic programming algorithm[C]// 2018 IEEE International Conference of Intelligent Robotic and Control Engineering (IRCE). Lanzhou: IEEE, 2018: 106-110. [5] WAGTER W. Block sections around stations under ETCS: the effect of the block layout on the headways at stations[D]. Enschede:Enschede University of Twente, 2019. [6] VIGNALI V, CUPPI F, LANTIERI C, et al. A methodology for the design of sections block length on ETCS L2 railway networks[J]. Journal of Rail Transport Planning & Management, 2020, 13: 100160.1-100160.22. [7] 田长海,张守帅,张岳松,等. 高速铁路列车追踪间隔时间研究[J]. 铁道学报,2015,37(10): 1-6.TIAN Changhai, ZHANG Shoushuai, ZHANG Yuesong, et al. Study on the train headway on automatic block sections of high speed railway[J]. Journal of the China Railway Society, 2015, 37(10): 1-6. [8] 彭其渊,王超宇,鲁工圆. 基于到发线运用方案的列车到达追踪间隔时间压缩方法及仿真研究[J]. 中国铁道科学,2020,41(2): 131-138.PENG Qiyuan, WANG Chaoyu, LU Gongyuan. Compression method and simulation of train arrival interval based on utilization of arrival-departure track[J]. China Railway Science, 2020, 41(2): 131-138. [9] 鲁工圆,沈子力,彭其渊,等. 基于区间速度控制的列车到达追踪间隔时间压缩方法研究[J]. 铁道学报,2021,43(1): 19-27.LU Gongyuan, SHEN Zili, PENG Qiyuan, et al. Compressing arrival interval of high-speed trains by speed control within railway section[J]. Journal of the China Railway Society, 2021, 43(1): 19-27. [10] 鲁工圆,王超宇,沈子力,等. 面向追踪间隔压缩的高速铁路列车运行时空轨迹优化[J]. 铁道学报,2021,43(7): 10-18.LU Gongyuan, WANG Chaoyu, SHEN Zili, et al. Headway compression oriented space-time trajectory optimization for high-speed railway trains[J]. Journal of the China Railway Society, 2021, 43(7): 10-18. [11] TAKAGI R. Synchronisation control of trains on the railway track controlled by the moving block signalling system[J]. IET Electrical Systems in Transportation, 2012, 2(3): 130-138. doi: 10.1049/iet-est.2011.0053 [12] 张婷. 通过提高列车出站速度压缩高速铁路列车发车追踪间隔时间[J]. 价值工程,2018,37(3): 34-36.ZHANG Ting. Compress the tracing interval of high-speed railway trains by increasing train outbound speed[J]. Value Engineering, 2018, 37(3): 34-36. [13] 聂英杰,胡志垚. 京沪高速铁路北京南站发车追踪间隔研究[J]. 铁道运输与经济,2018,40(11): 28-31.NIE Yingjie, HU Zhiyao. A study on departure headway interval of Beijing South Railway Station of Beijing–Shanghai high-speed railway[J]. Railway Transport and Economy, 2018, 40(11): 28-31. [14] 朱子轩. 高速铁路列车追踪间隔时间压缩策略仿真分析研究[D]. 成都: 西南交通大学,2019. [15] 张岳松,田长海,姜昕良,等. 高速铁路列车间隔时间的计算方法[J]. 中国铁道科学,2013,34(5): 120-125.ZHANG Yuesong, TIAN Changhai, JIANG Xinliang, et al. Calculation method for train headway of high speed railway[J]. China Railway Science, 2013, 34(5): 120-125. [16] 中国铁路总公司. CRH系列动车组操作规则:TG/JW105—2015[S]. 北京: 中国铁路总公司,2015. [17] 赵博. 高铁车站出站信号机与停车标设置方案探讨[J]. 铁道工程学报,2018,35(10): 69-72.ZHAO Bo. Research on the setting scheme of starting signal and train stop sign on high speed railway station[J]. Journal of Railway Engineering Society, 2018, 35(10): 69-72. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 221
- HTML全文浏览量: 66
- PDF下载量: 29
- 被引次数: 0