Traffic Speed Prediction in Merging Zone of Urban Expressway Based on Bidirectional Long Short-Term Memory Network
-
摘要:
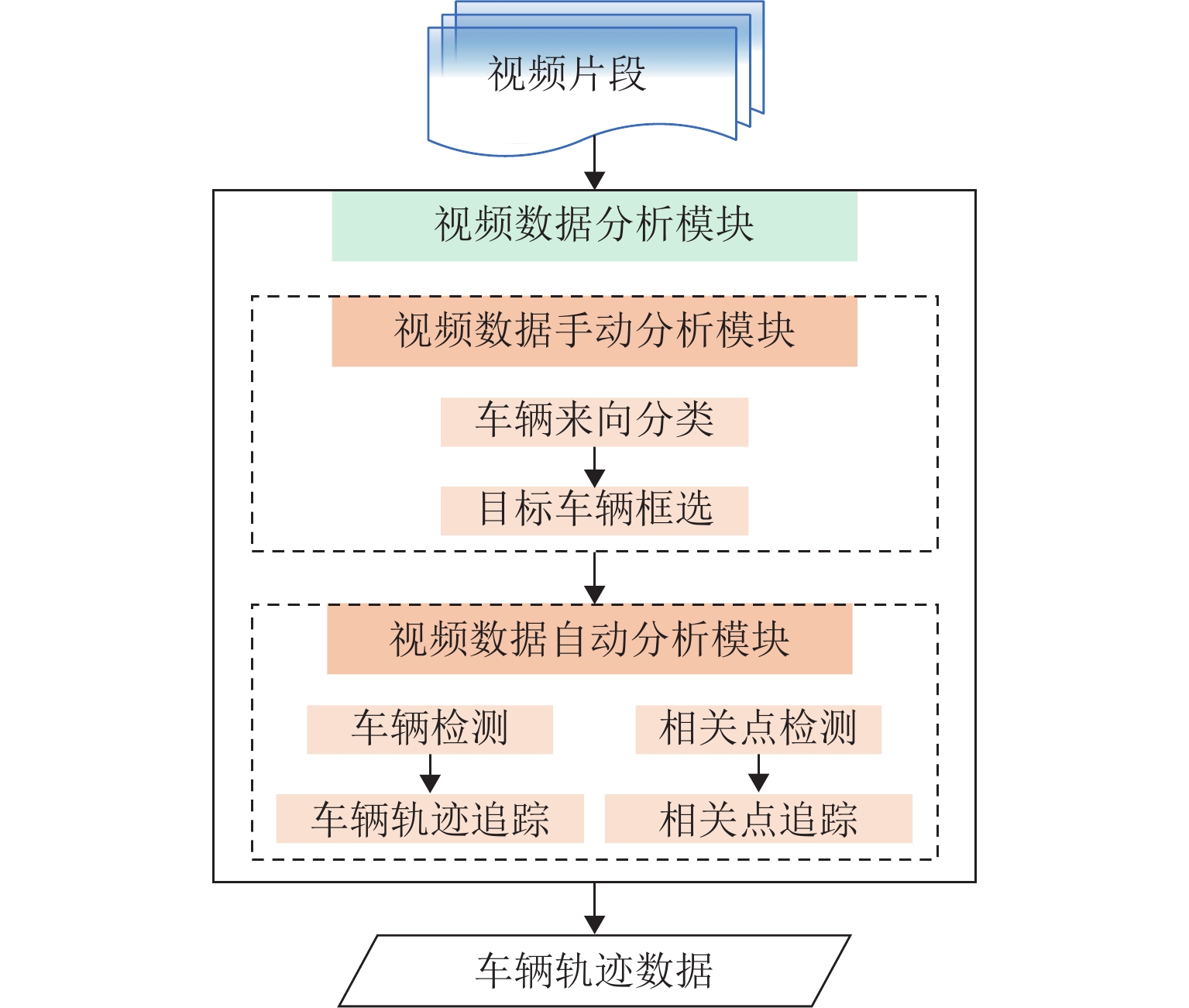
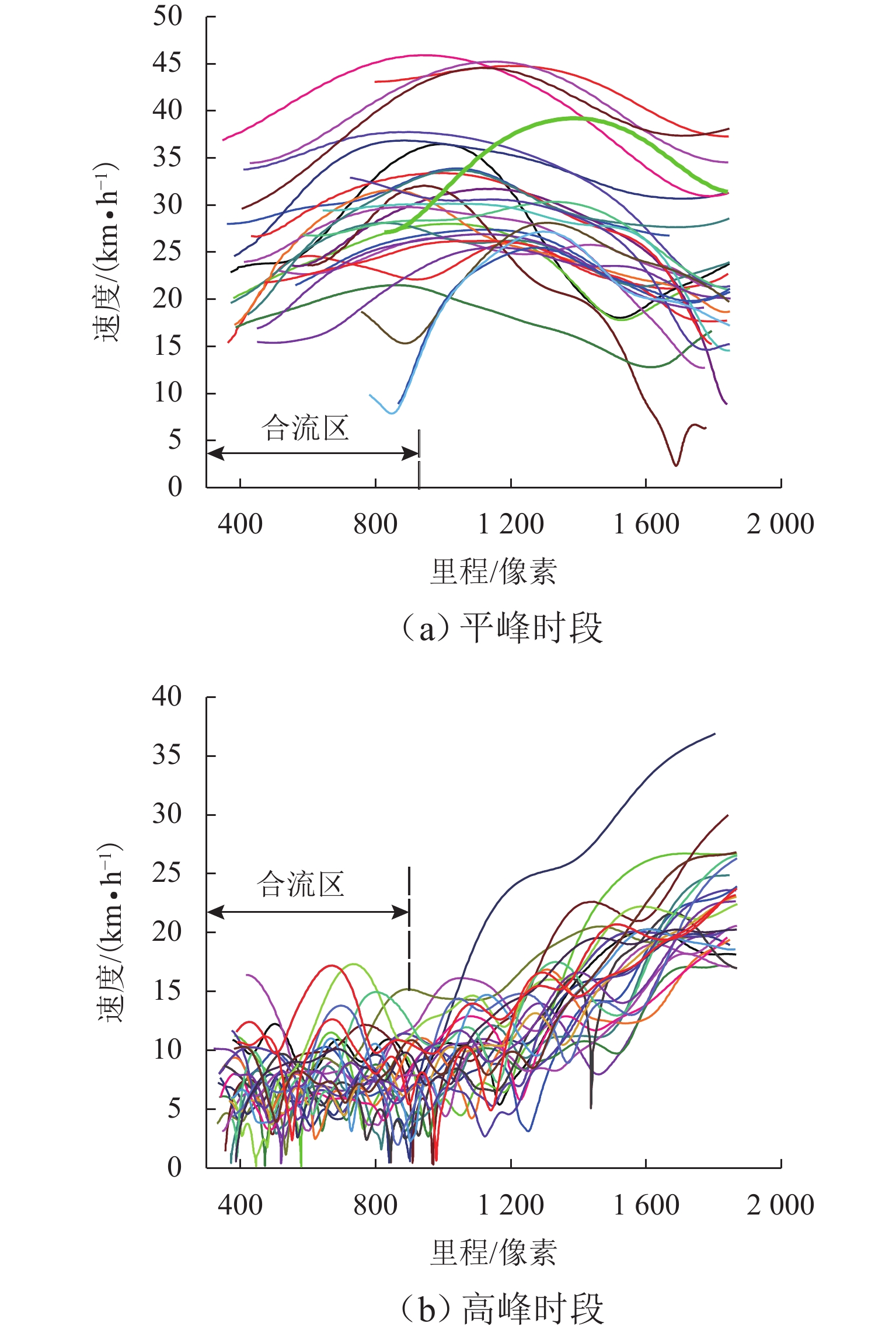
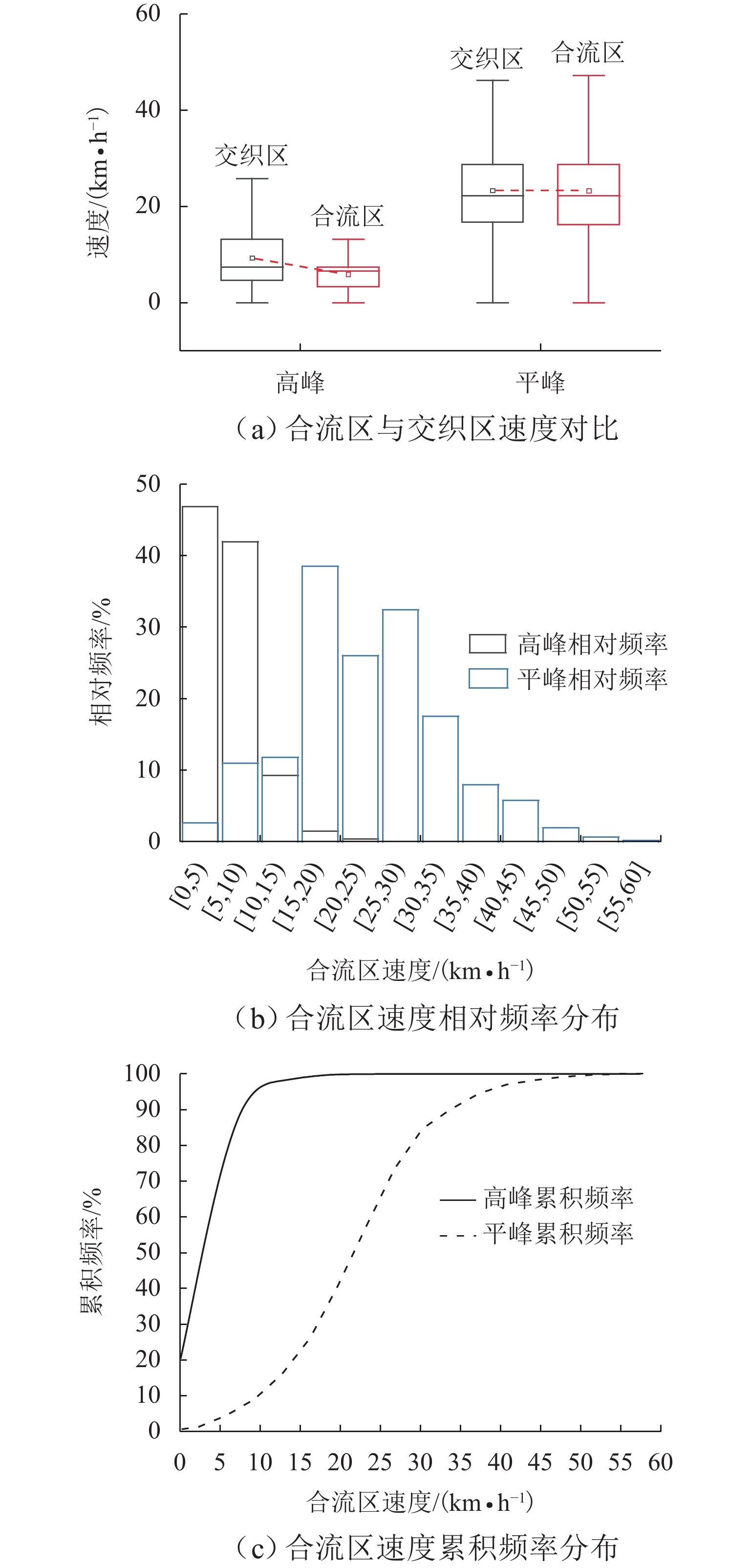
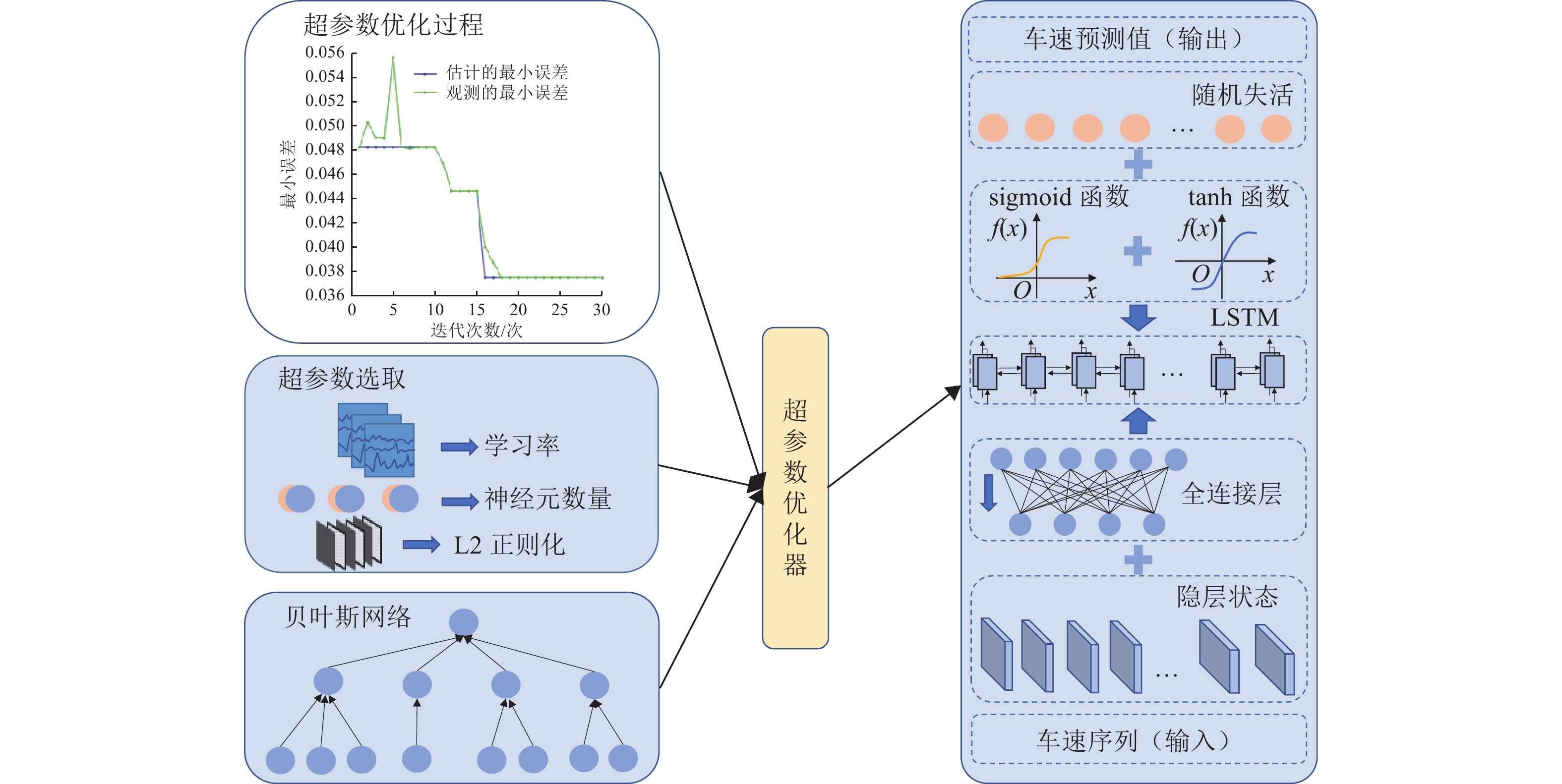
非典型复杂场景微观交通参数的准确预测是保证车路协同系统（IVICS）稳定运行的前提. 为解决IVICS条件下合流区高峰时段瓶颈现象所致的车速分布紊乱而不易预测的问题，首先，基于无人机高空视频，从广域视角提取交织区高峰时段全样本高精度车辆轨迹数据；然后，考虑双向长短期记忆网络（bidirectional long short-term memory，Bi-LSTM）时间较长且人工设置训练参数对模型预测性能影响较大，提出基于贝叶斯超参数(bayesian hyperparameters optimization，BHO)优化的BHO-Bi-LSTM 车速预测集成模型；最后，构建经典多元线性回归车速预测模型、Bi-LSTM车速预测模型作对比. 结果表明：BHO-Bi-LSTM模型表现最优，拟合优度、秩相关度分别为91.05%、94.87%，误差均值、误差的标准差、均方误差、均方根误差、归一化均方根误差分别为
0.056 1 、0.455 6 、0.210 6 、0.458 9 、0.078 5 ，有效改善了合流区高峰时段车速特性复杂而导致不易预测的缺陷.Abstract:Accurate prediction of microscopic traffic parameters in atypical complex scenes is a prerequisite to ensure stable operation of the intelligent vehicle infrastructure cooperative systems (IVICS). To solve the problem of vehicle speed distribution disorder and difficulty in prediction caused by bottleneck phenomenon during peak hours in the merging area under IVICS conditions, First, using the UAV video, the full-sample high-precision vehicle trajectory data of the intertwined area during peak hours are extracted from a wide-area view. Then, as bidirectional long short-term memory (Bi-LSTM) networks cost long time and affect the prediction performance of the model when training parameters are manually set, a BHO-Bi-LSTM (bayesian hyperparameter optimization bidirectional long short-term memory) integrated vehicle speed prediction model based on Bayesian hyperparameters optimization is proposed. Finally, the classical multiple linear regression model and Bi-LSTM model of vehicle speed prediction are constructed for comparison. The results show that the BHO-Bi-LSTM model outperforms other models, with a goodness-of-fit and rank correlation of 91.05% and 94.87%, respectively, and error mean, error standard deviation, mean square error, root mean square error, and normalized root mean square error of
0.0561 ,0.4556 ,0.2106 ,0.4589 , and0.0785 , respectively, which can overcome the disadvantage in prediction of complicated traffic speeds during peak hours.-
Key words:
- traffic engineering /
- speed prediction /
- multiple weaving area /
- trajectory data /
- Bayesian optimization
-
填充墙作为非结构构件，不承担上部结构传来的荷载，仅承担自身的重量，主要起空间的划分与围护作用. 经大量震害调查[1]，地震中许多建筑主体结构完好，作为非结构构件的填充墙却发生严重的平面内或平面外破坏，造成了巨大的经济损失，同时对人民群众的生命安全造成了严重的威胁.
为了明确填充墙的受力机制，减轻地震中填充墙的破坏，减少地震中人员伤亡和经济损失，研究人员针对填充墙内部组成材料与构造、受力机制和力学性能等进行了大量的研究[2-7]. 本课题组通过对带水平滑移层框架空心砖填充墙进行拟静力试验，验证了水平滑移层的设置能有效提高框架空心砖填充墙平面内的抗震性能与耗能能力，解决了空心砖作为填充材料在地震下易于破坏的问题[8]. 其主要原因为墙体中水平滑移层的设置,导致墙体受到地震荷载作用时能够发生相对的滑移，耗散掉地震能量，同时，还削弱了填充墙的斜撑作用，减轻了填充墙体的破坏程度.
为了解带水平滑移层框架空心砖填充墙平面外的承载力和破坏模式，根据既有的平面内试验数据，利用数值分析方法，进行带水平滑移层框架空心砖填充墙平面外力学性能的数值计算和分析，通过与未设置水平滑移层普通框架空心砖填充墙的对比分析，获得带水平滑移层框架空心砖填充墙的平面外性能.
1. 模型的建立
根据既有带水平滑移层框架空心砖填充墙拟静力试验数据，利用数值分析软件，建立带水平滑移层框架空心砖填充墙和普通框架空心砖填充墙平面外分析的有限元模型.
1.1 设计参数
带水平滑移层框架空心砖填充墙的构造如图1所示. 原试验上部框架梁截面尺寸为200 mm × 450 mm，基础框架梁截面尺寸为500 mm × 600 mm，框架柱截面尺寸为400 mm × 400 mm. 梁柱配置HRB335直径16 mm的纵筋和HPB300直径8 mm的箍筋，梁柱混凝土等级为C30. 填充墙体采用 240 mm × 200 mm × 110 mm的MU3.5页岩空心砖，空洞率为47.85%，M5混合砂浆砌筑[8]. 填充墙体与框架柱之间采用HPB300直径8 mm的拉结筋，按照竖向每隔500 mm的间距进行通长布置. 水平滑移层分别设置在墙体高度1/3和2/3高度处，材料为4 mm厚改性沥青防水卷材，宽度同墙体宽. 普通框架空心砖填充墙与带水平滑移层框架空心砖填充墙的区别在于水平滑移层的有无. 各模型的相关参数如表1和表2所示.
表 1 配筋信息Table 1. Reinforcement information of Specimens类型 框架柱纵筋 框架梁纵筋 箍筋/mm 带滑移层墙 6 
4 
普通墙 6 4 钢筋 空心砖 砂浆抗压
强度/MPa混凝土抗压
强度/MPa孔洞
率/%单位重
度/N抗压强
度/MPa屈服强
度/MPa抗拉强
度/MPa屈服强
度/MPa抗拉强
度/MPa402 515 480 602 47.85 49.60 3.50 5.62 33.50 1.2 材料本构模型
1） 混凝土
混凝土单轴受拉时，相关参数由式（1） [9]确定.
{σ=(1−dt)Ecε,dt={1−ρt[1.2−0.2x5],x⩽ (1) 式中：σ、ε、Ec分别为混凝土的应力、应变和弹性模量；
{d}_{\mathrm{t}} 为混凝土单轴受拉损伤演化参数；{a}_{\mathrm{t}} 为混凝土单轴受拉时应力-应变曲线下降段参数；{f}_{\mathrm{t},\mathrm{r}} 为混凝土单轴受拉的强度代表值；{\varepsilon }_{\mathrm{t},\mathrm{r}} 为与{f}_{\mathrm{t},\mathrm{r}} 相对应的峰值受拉应变.混凝土单轴受压时，相关参数由式（2）[9]确定.
\left\{\begin{aligned} &\sigma =(1-{d}_{\mathrm{c}}){E}_{\mathrm{c}}\varepsilon ,\\ &{d}_{\mathrm{c}}=\left\{\begin{array}{l}1-{\rho }_{\mathrm{c}}n/\left(n-1 + {x}^{n}\right),\quad x\leqslant 1, \\ 1-{\rho }_{\mathrm{c}}/[{\alpha }_{\mathrm{c}}(x-1{)}^{2} + x],\quad x > 1,\end{array}\right. \\ &{\rho }_{\mathrm{c}}={f}_{\mathrm{c},\mathrm{r}}/{(E}_{\mathrm{c}}{\varepsilon }_{\mathrm{c},\mathrm{r}}),\\ & n={(E}_{\mathrm{c}}{\varepsilon }_{\mathrm{c},\mathrm{r}})/({E}_{\mathrm{c}}{\varepsilon }_{\mathrm{c},\mathrm{r}}-{f}_{\mathrm{c},\mathrm{r}}),\\ &x=\varepsilon /{\varepsilon }_{\mathrm{c},\mathrm{r}}, \end{aligned}\right. (2) 式中：
{d}_{\mathrm{c}} 为混凝土单轴受压损伤演化参数；{\alpha }_{\mathrm{c}} 为混凝土单轴受压时应力-应变曲线下降段参数；{f}_{\mathrm{c},\mathrm{r}} 为混凝土单轴受压的强度代表值；{\varepsilon }_{\mathrm{c},\mathrm{r}} 为与{f}_{\mathrm{c},\mathrm{r}} 相对应的峰值受压应变.混凝土采用塑性损伤模型. 混凝土密度取2400 kg/m3，杨氏模量取30 000 MPa，泊松比取0.2；在塑性参数定义中，膨胀角取31°，流动势偏移量取0.1，双轴与单轴极限抗压强度之比取1.16，拉伸子午面上与压缩子午面上的第二应力不变量的比值取0.667，黏聚系数取0[10].
2） 钢筋
钢筋本构关系如下[9]：
\left\{\begin{aligned} &{\sigma }_{\mathrm{s}}={E}_{\mathrm{s}}{\varepsilon }_{\mathrm{s}} , \quad {\varepsilon }_{\mathrm{s}}\leqslant {\varepsilon }_{\mathrm{y}} \mathrm{， } \\ &{\sigma }_{\mathrm{s}}={f}_{\mathrm{y},\mathrm{r}} , \quad {\varepsilon }_{\mathrm{y}} < {\varepsilon }_{\mathrm{s}}\leqslant {\varepsilon }_{\mathrm{u}\mathrm{y}} \mathrm{， } \\ &{\sigma }_{\mathrm{s}}={f}_{\mathrm{y},\mathrm{r}} + k\left({\varepsilon }_{\mathrm{s}}-{\varepsilon }_{\mathrm{u}\mathrm{y}}\right),\quad {\varepsilon }_{\mathrm{u}\mathrm{y}} < {\varepsilon }_{\mathrm{s}}\leqslant {\varepsilon }_{\mathrm{u}} \mathrm{， } \\ &{\sigma }_{\mathrm{s}}=0 ,\quad {\varepsilon }_{\mathrm{s}} > {\varepsilon }_{\mathrm{u}} , \end{aligned}\right. (3) 式中：
{E}_{\mathrm{s}} 为钢筋弹模；{\sigma }_{\mathrm{s}} 为钢筋应力；{\varepsilon }_{\mathrm{s}} 为钢筋应变；{f}_{\mathrm{y},\mathrm{r}} 为钢筋屈服强度代表值；{\varepsilon }_{\mathrm{y}} 为钢筋屈服应变；{\varepsilon }_{\mathrm{u}\mathrm{y}} 为钢筋硬化起点应变；{\varepsilon }_{\mathrm{u}} 为钢筋峰值应变；k 为钢筋硬化阶段斜率.钢筋密度取7 850 kg/m3，杨氏模量取2×1011 Pa，泊松比取0.3，钢筋的屈服强度按表2取值，塑性应变取0.
3） 砌体
进行力学分析时，砌块和砂浆组成的砌体的本构关系如下 [11]：
① 上升段
\begin{split} &\sigma /{f}_{\mathrm{m}}=1.15\varepsilon /{\varepsilon }_{0}-0.15(\varepsilon /{\varepsilon }_{0}{)}^{2}, \\ &\quad 0\leqslant \varepsilon /{\varepsilon }_{0}\leqslant1; \end{split} (4) ② 下降段
\begin{split} &\sigma /{f}_{\mathrm{m}}=1.6-0.6\varepsilon /{\varepsilon }_{0}, \quad 1 < \varepsilon /{\varepsilon }_{0}\leqslant4; \end{split} (5) 式（4）、（5）中：
{f}_{\mathrm{m}} 为平均抗压强度；{\varepsilon }_{0} 为平均压应变.由既有试验数据，组合砌体密度取1900 kg/m3，杨氏模量取20 GPa，泊松比取0.15.
4） 滑移层
滑移层材料采用改性沥青防水卷材（SBS），材料属性如表3所示.
表 3 滑移材料属性Table 3. Material characteristics of slip layer质量密度/（kg·m−3） 杨氏模量/MPa 泊松比 1 240.10 9.52 0.43 数值分析中采用滑移层间摩擦系数表征滑移层的滑移特性，摩擦系数取0.32.
1.3 单元选取
框架和内部填充墙砌体采用实体单元，实体单元采用C3D8R单元；内部钢筋采用梁单元，梁单元采用B31单元.
1.4 加载情况
平面外加载前模型的受力与原平面内试验往复加载前的受力一致，考虑相同的柱轴压比[8]. 平面外分析对填充墙施加平面外均布荷载，加载示意和加载制度如图2所示.
1.5 相互作用
不考虑框架梁柱内钢筋和混凝土之间的黏结滑移，而是用嵌入的方式来定义两者的接触关系，认为两者共同工作. 对于砌体部分，砌体与框架柱、框架梁、滑移层之间以及各层砌体之间的相互作用均采用“接触”类型. “接触”的界面条件包括法向接触条件和切向接触条件两部分. 本文采用法线方向“硬接触”与切线方向“摩擦系数”模拟[12]. 砌体与滑移层间摩擦系数取0.32，砌体与砌体之间或砌体与框架梁柱混凝土之间的滑动摩擦系数依据《砌体结构设计规范GB 50003—2011》[13]表3.2.5-3砌体摩擦系数的规定，取0.7.
1.6 模型试验验证
为验证有限元模型参数设置的正确性，选择了文献[14]中的DIWF-J-C填充墙试件，建立了有限元模型，材料依据该文献数据作相应调整. 根据文献先进行面内损伤模拟再施加平面外荷载，试验与数值模拟结果如图3所示. 由图3可知：数值模拟计算的平面外荷载-位移曲线与试验结果吻合较好.
同理，图4为文献[8]中的FIW-2填充墙试件试验与数值模拟的骨架曲线对比.
由图4可知：数值模拟计算的骨架曲线与既有试验结果吻合良好. 图4和图3中存在些许误差，可能是由于施加荷载处的混凝土损伤较大导致的，上述的验证分析显示数值分析参数设置正确，为后续进一步分析奠定了基础.
2. 结果分析
2.1 平面外破坏形式
1） 填充墙体平面外破坏模式
竖向受弯破坏、双向受弯破坏和双向拱承破坏是填充墙的主要破坏形式[15]. 填充墙体破坏状态如图5所示. 由图5可知：未设置滑移层的普通填充墙和带水平滑移层填充墙两者的破坏均始于墙体中部，因中部墙体外凸，中部墙体整体性散失，墙体塌落. 在平面外荷载作用下，未设置滑移层的普通填充墙和带水平滑移层填充墙的破坏由中部点向四周环向扩大，破坏为双向拱承破坏.
未设置滑移层的普通填充墙的“拱”承效应明显，中部破坏范围呈“圆形”分布. 与未设置滑移层的普通填充墙相比，带水平滑移层的“拱”承效应明显弱化，中部破坏区域由“圆形”转变为“矩形”，主要是由于滑移层降低了墙体的整体性，削弱了外部框架对填充墙体的约束作用.
墙体沿框架柱方向的受弯能力明显小于沿框架梁方向的受弯能力，主要是因为墙体的高度小于墙体的宽度，导致墙体受到上、下端框架梁的约束作用更强.
2） 填充墙体等效塑性应变和应力分布
填充墙体受到周边框架的约束作用大小可采用墙体等效塑性应变和应力分布进行分析. 未设置滑移层的普通填充墙体和带水平滑移层填充墙体的等效塑性应变如图6所示，竖向压应力分布如图7所示.
由图6可知：未设置滑移层的普通填充墙的等效塑性应变沿框架四周呈“环状”分布，等效塑性应变的最大值为0.064 95，最大值位于与框架梁的连接处；带水平滑移层填充墙的等效塑性应变呈“C”形分布，受到上端梁和周边柱的约束较下端梁强，等效塑性应变的最大值为0.068 15，最大值位于与框架梁的连接处.
与未设置滑移层的普通填充墙相比，带水平滑移层填充墙的等效塑性应变分布有所变化，等效塑性应变最大值基本接近. 表明整体上带水平滑移层填充墙所受框架的平面外约束比未设置滑移层的普通填充墙小.
图7显示未设置滑移层的普通填充墙承受的竖向压应力为2.996 MPa，带水平滑移层填充墙承受的竖向压应力为1.950 MPa，前者大于后者，表明未设置滑移层的普通填充墙体受到框架梁的平面外约束较大，“拱”承载效应更明显.
3） 框架等效塑性应变
图8为未设置滑移层的普通填充墙和带水平滑移层填充墙框架的等效塑性应变云图.
填充墙受到周边框架的约束作用，由力的相互作用理论，周边框架也同样受到内部填充墙的约束反作用. 由图8可知：未设置滑移层的普通填充墙和带水平滑移层填充墙两者外部框架的等效塑性应变均主要集中在框架梁上，未设置滑移层的普通填充墙的外部框架等效塑性应变最大值为1.789×10−3，带水平滑移层填充墙的等效塑性应变最大值为7.332×10−4，前者大于后者，表明未设置滑移层的普通填充墙体受到外部框架，特别是外部框架梁的平面外约束更大.
2.2 平面外承载力
1） 平面外承载力对比
提取各级平面外均布荷载作用下墙体中心点的平面外位移值，绘制填充墙体平面外荷载-位移曲线，如图9所示.
由图9可知：填充墙体在平面外均布荷载作用下的破坏大致分为3个阶段：第1阶段为弹性阶段，此阶段平面外位移值较小，荷载-位移曲线基本呈斜直线；第2阶段为屈服阶段，墙体由弹性变形转向塑性变形，此阶段平面外位移增长较大，平面外荷载也有较大幅度的增长，荷载-位移曲线基本呈凹曲线；第3阶段为破坏阶段，此阶段平面外位移显著增加，而平面外荷载基本不再增加，荷载-位移曲线基本呈水平直线，继续加载，直至墙体脱出，填充墙随即丧失平面外抵抗能力，墙体破坏.
第1阶段，未设置滑移层的普通填充墙和带水平滑移层填充墙的平面外承载力基本相同，两者荷载-位移曲线基本重叠；第2、3阶段，随着位移的增加，未设置滑移层的普通填充墙平面外荷载值高于带水平滑移层填充墙的平面外荷载值，此阶段带水平滑移层填充墙的荷载-位移曲线位于未设置滑移层的普通填充墙的荷载-位移曲线的下方. 定义第1阶段对应的平面外荷载为墙体开裂荷载，荷载-位移曲线平面外荷载最高点为峰值荷载，将两组模型的开裂荷载与峰值荷载进行对比分析，结果如表4所示. 表中：
{F}_{\mathrm{P}} 为普通墙面外承载力；{F}_{\mathrm{H}} 为带滑移层墙面外承载力.表 4 平面外承载力对比Table 4. Comparison of out-of-plane bearing capacity类型 FP/kPa FH/kPa （FP−FH）/FP/% 开裂荷载值 21.1 12.0 43.1 峰值荷载值 43.2 33.6 22.2 由表4可知：带水平滑移层填充墙体开裂荷载、峰值荷载均小于未设置滑移层的普通填充墙的对应值. 与未设置滑移层的普通填充墙体相比，带水平滑移层填充墙的峰值荷载降低了22.2%，开裂荷载降低了43.1%，主要是因为水平滑移层降低了墙体的整体性，削弱周边框架对墙体的约束作用.
2） 平面外承载力验算分析
为验算带水平滑移层填充墙平面外承载力是否达到规范要求的标准，采用等效侧力法计算填充墙体自身重力产生的地震作用，得到抗震设防烈度为6、7、8、9度时所产生的作用于填充墙最不利方向的水平地震作用，其计算式[16]为
F=\gamma \eta {\zeta }_{1}{\zeta }_{2}{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}G , (6) 式中：F为沿最不利方向作用于非结构构件重心处的水平地震标准值；
\gamma 为非结构构件功能系数；\eta 为非结构构件类别系数；{\zeta }_{1} 、{\zeta }_{2} 分别为状态系数与位置系数；{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}} 为地震影响系数最大值；G 为非结构构件的重力.以抗震设防烈度为8度（0.30g）的多遇地震为例，计算作用于填充墙最不利方向的水平地震作用设计值，由《建筑抗震设计规范》[16]，
\gamma 、\eta 、{\zeta }_{1} 、{\zeta }_{2} 、{\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}} 分别取1.4、0.9、1.0、2.0、0.24，G =21 kN （按空心砖墙重度10\mathrm{k}\mathrm{N}/{\mathrm{m}}^{3} 计），将以上数据代入式（6），得到沿最不利方向作用于非结构构件重心处的水平地震标准值为12.7 kN，再乘分项系数1.3，得到设计值16.5 kN.将表4计算的墙体开裂荷载、峰值荷载与墙体竖向面积相乘，即可得到墙体的开裂荷载、峰值荷载作用力. 定义开裂安全系数、破坏安全系数分别为数值分析获得的开裂荷载、峰值荷载作用力与多遇和罕遇地震作用下规范计算的水平地震力设计值的比值，如表5所示.
表 5 按规范计算的水平地震力及安全系数Table 5. Horizontal seismic force and safety factor类型 抗震设防烈度 规范计算的水平地震力设计值/kN 开裂安全系数（破坏安全系数） 未设滑移层填充墙 设滑移层填充墙 多遇地震 6 度 2.8 80.5（164.8） 45.8（128.2） 7 度（0.15g） 8.3 26.8（54.9） 15.3（42.7） 8 度（0.30g） 16.5 13.4（27.5） 7.6（21.4） 9 度 22.0 10.1（20.6） 5.7（16.0） 罕遇地震 6 度 19.3 11.5（23.5） 6.5（18.3） 7 度（0.15g） 49.5 4.5（9.2） 2.5（7.1） 8 度（0.30g） 82.6 2.7（5.5） 1.5（4.3） 9 度 96.3 2.3（4.7） 1.3（3.7） 由表5可知：7度（0.15g）多遇地震作用时，未设置滑移层普通填充墙的开裂安全系数、破坏安全系数分别为26.8、54.9，带水平滑移层填充墙的开裂安全系数、破坏安全系数分别为15.3、42.7；9度罕遇地震作用时，未设置滑移层普通填充墙的开裂安全系数、破坏安全系数分别为2.3、4.7，带水平滑移层填充墙的开裂安全系数、破坏安全系数分别为1.3、3.7. 带水平滑移层填充墙开裂和破坏安全系数均小于未设置滑移层的普通填充墙相应的安全系数. 更重要的是，带水平滑移层填充墙在多遇和罕遇地震作用下，开裂和破坏的安全系数均大于1.0，可见带水平滑移层填充墙的平面外承载力大于按规范计算要求的平面外承载力.
2.3 平面外位移
在填充墙体上分别加载平面外均布荷载10、20、30 kPa，计算墙体的平面外位移，得到3种荷载作用下沿墙体高度方向分布的平面外位移曲线，如图10所示.
由图10可知：平面外荷载为10、20 、30 kPa时，带水滑移层填充墙的最大面外位移分别为3.08、14.53、70.09 mm，普通填充墙的最大面外位移分别为1.28、3.74 、10.01 mm. 可见，在上述各级荷载作用下，未设置水平滑移层普通墙体的平面外位移均小于带水平滑移层的平面外位移值，且随着平面外荷载的增加，两者平面外位移的差值也随之增大.
2.4 平面外刚度
图11为填充墙体的平面外刚度退化曲线. 由图可知：随着平面外位移的逐渐增大，带水平滑移层填充墙和未设置滑移层普通墙两者平面外刚度均随之降低，但未设置滑移层普通墙平面外刚度降低速率小，主要是因为水平滑移层降低了墙体的整体性，削弱了周边框架对墙体的约束作用.
3. 结论和展望
本文分析了带水平滑移层框架空心砖填充墙、未设置滑移层的普通框架空心砖填充墙在平面外荷载作用下的响应，得到以下结论：
1） 填充墙体中设置水平滑移层将降低墙体整体性，削弱周边框架对墙体的约束作用，墙体“拱”支承效应也随之减弱. 在同等平面外荷载作用下，带水平滑移层的墙体与未设置滑移层的普通填充墙体平面外破坏程度存在差异，前者的破坏程度明显大于后者.
2） 与未设置滑移层普通填充墙相比，带水平滑移层墙的平面外极限荷载降低了22.2%，开裂荷载降低了43.1%.
3） 抗震设防烈度为6、7、8、9度时，带水平滑移层填充墙在多遇和罕遇地震作用下，墙体平面外承载力大于按规范计算要求的平面外承载力，满足规范要求.
考虑填充墙实际复杂的受力工况，可能会同时受到面内外地震作用，其受面内外耦合作用下的性能将是后续研究解决和完善的问题.
-
图 5 平（高）峰时段交织区车速-位置分布曲线
Figure 5. Vehicle speed-position distribution curves in weaving area during flat (high) peak hours
图 6 平（高）峰时段实例合流区车速分布
Figure 6. Distribution of traffic speeds in merging area during peak hours
表 1 模型总体评价指标对比
Table 1. Comparison of overall model evaluation indicators
模型 R2 \mu estD eMSE eRMSE eNRMSE rs 多元线性回归[22]
（模型Ⅰ）0.7980 0.001 7 1.659 5 2.754 2 1.659 6 0.269 0 0.844 0 Bi-LSTM[23]
（模型Ⅱ）0.8882 −0.005 3 0.471 1 0.221 8 0.470 9 0.080 6 0.945 3 BHO-Bi-LSTM
（模型Ⅲ）0.9105 0.056 1 0.455 6 0.210 6 0.458 9 0.078 5 0.948 7 模型Ⅲ对比模型Ⅰ
（提升或下降比例）+ 0.1125
（↑14.10%）+ 0.054 4
（↓3 200%）−1.203 9
（↑72.55%）−2.543 6
（↑92.35%）−1.200 7
（↑72.35%）−0.190 5
（↑70.82%）+ 0.1047
（↑12.35%）模型Ⅲ对比模型Ⅱ
（提升或下降比例）0.2230
（↑3.80%）+ 0.061 4
（↓1158.49%）−0.015 5
（↑3.29%）−0.011 2
（↑5.05%）−0.012 0
（↑2.548%）−0.002 1
（↑2.605%）+ 0.0034
（↑0.40%）注：黑体加粗表示最优指标 
下载: 导出CSV
-
[1] 朱洁玉,马艳丽. 合流区域多车交互风险实时评估方法[J]. 吉林大学学报(工学版),2022,52(7):1574-1578.ZHU Jieyu, MA Yanli. Risk assessment method in real-time of multi-vehicle interaction at themerging area[J]. Journal of Jilin University (Engineering and Technology Edition),2022,52(7):1574-1578. [2] 阎莹,盛彦婷,袁华智,等. 高速公路出入口区域行车风险评价及车速控制[J]. 交通运输工程学报,2011,11(2): 90-96. doi: 10.3969/j.issn.1671-1637.2011.02.015YAN Ying, SHENG Yanting, YUAN Huazhi, et al. Driving risk evaluation and speed control in passageway areas of freeway[J]. Journal of Traffic and Transportation Engineering, 2011, 11(2): 90-96. doi: 10.3969/j.issn.1671-1637.2011.02.015 [3] 贺正冰,徐瑞康,谢东繁,等. 数据驱动跟驰模型综述[J]. 交通运输系统工程与信息,2021,21(5): 102-113.HE Zhengbing, XU Ruikang, XIE Dongfan, et al. A review of data-driven car-following models[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(5): 102-113. [4] 徐进,曾粤. 高速条件下隧道出入口行驶速度特性[J]. 交通运输工程学报,2021,21(4): 197-209.XU Jin, ZENG Yue. Characteristics of driving speed at tunnel entrance and exit at high speed[J]. Journal of Traffic and Transportation Engineering, 2021, 21(4): 197-209. [5] Williams B M, Hoel L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results[J]. Journal of Transportation Engineering, 2003, 129(6): 664-672. doi: 10.1061/(ASCE)0733-947X(2003)129:6(664) [6] Yang J S. A study of travel time modeling via time series analysis[C]//Proceedings of 2005 IEEE Conference on Control Applications, 2005. Toronto: IEEE, 2005:855-860. [7] MIR Z H, FILALI F. An adaptive Kalman filter based traffic prediction algorithm for urban road network[C]//2016 12th International Conference on Innovations in Information Technology (IIT). Arab Emirates: IEEE, 2016:1-6. [8] YAO B, CHEN C, CAO Q, et al. Short-term traffic speed prediction for an urban corridor[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(2): 154-169. doi: 10.1111/mice.12221 [9] 陈孟,干可,李凯,等. 基于实时多模态时空数据的时空图卷积网络精准鲁棒交通流预测模型[J]. 公路交通科技,2021,38(8): 134-139,158. doi: 10.3969/j.issn.1002-0268.2021.08.018CHEN Meng, GAN Ke, LI Kai, et al. A spatial-temporal graph convolutional network model for accurate and robust traffic flow prediction based on real-time multimodal spatial-temporal data[J]. Journal of Highway and Transportation Research and Development, 2021, 38(8): 134-139,158. doi: 10.3969/j.issn.1002-0268.2021.08.018 [10] ZHAO Z, CHEN W, WU X, et al. LSTM network: a deep learning approach for short-term traffic forecast[J]. IET Intelligent Transport Systems, 2017, 11(2): 68-75. doi: 10.1049/iet-its.2016.0208 [11] XU Y, KONG Q J, KLETTE R, et al. Accurate and interpretable bayesian mars for traffic flow prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2457-2469. doi: 10.1109/TITS.2014.2315794 [12] ZHENG L, YANG J, CHEN L, et al. Dynamic spatial-temporal feature optimization with ERI big data for short-term traffic flow prediction[J]. Neurocomputing, 2020, 412: 339-350. doi: 10.1016/j.neucom.2020.05.038 [13] Peng Y, Xiang W. Short-term traffic volume prediction using GA-BP based on wavelet denoising and phase space reconstruction[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 549: 1-14. doi: 10.1016/j.physa.2019.123913 [14] 李桃迎,王婷,张羽琪. 考虑多特征的高速公路交通流预测模型[J]. 交通运输系统工程与信息,2021,21(3): 101-111.LI Taoying, WANG Ting, ZHANG Yuqi. Highway traffic flow prediction model considering multi-features[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(3): 101-111. [15] 陈华伟,邵毅明,敖谷昌,等. 面向在线地图的GCN-LSTM神经网络速度预测[J]. 交通运输工程学报,2021,21(4):183-196.CHEN Huawei, SHAO Yiming, AO Guchang, et al. On-line map oriented GCN-LSTM neural network speed prediction[J]. Journal of Traffic and Transportation Engineering,2021,21(4):183-196. [16] LI T, NI A, ZHANG C, et al. Short-term traffic congestion prediction with Conv-BiLSTM considering spatio-temporal features[J]. IET Intelligent Transport Systems, 2021, 14(14): 1978-1986. [17] BERGSTRA J , BENGGIO Y. Random search for hyper-parameter optimization[J]. Journal of Machine Learning Research,2012,13(1):281-305. [18] JIA W, CHEN X Y, et al. Hyperparameter optimization for machine learning models based on bayesian optimization[J]. Journal of Electronic Science and Technology,2019, 17(1):26-40. [19] 崔佳旭,杨博. 贝叶斯优化方法和应用综述[J]. 软件学报,2018,29(10): 3068-3090.CUI Jiaxu, YANG Bo. Survey on bayesian optimization methodology and applications[J]. Journal of Software, 2018, 29(10): 3068-3090. [20] SHAHRIARI B , SWERSKY K , WANG Z , et al. Taking the human out of the loop: a review of bayesian optimization[J]. Proceedings of the IEEE,2015,104(1):148-175. [21] 徐进, 陈莹, 张晓波, 等. 回头曲线路段的轨迹曲率特性和汽车过弯方式[J]. 西南交通大学学报,2021,56(06):1143-1152.XU Jin, CHEN Ying, ZHANG Xiaobo, et al. Longitudinal acceleration performance of passenger cars on complex mountain highways[J]. Journal of Southwest Jiaotong University,2021,56(06):1143-1152. [22] 朱云波, 夏玉兰, 王玥然, 等. 基于生态驾驶的道路合流区车辆运行状态估计[J]. 北京工业大学学报,2023,49(7):785-791.ZHU Yunbo, XIA Yulan, WANG Yueran, et al. Estimation of vehicle operating states in merging areas of roads based on eco-driving[J]. Journal of Beijing University of Technology,2023,49(7):785-791. [23] 秦雅琴, 夏玉兰, 钱正富, 等. 微观轨迹信息驱动的Bi-LSTM合流区车速预测[J]. 重庆大学学报,2023,46(4):120-128.QIN Yaqin, XIA Yulan, QIAN Zhengfu, et al. Bi-LSTM merging area speed prediction driven by microscopic trajectory information[J]. Journal of Chongqing University, 2023,46(4):120-128. 期刊类型引用(0)
其他类型引用(3)
-
下载:
下载:
点击查看大图
计量
- 文章访问数: 551
- HTML全文浏览量: 191
- PDF下载量: 85
- 被引次数: 3