Damage Evolution Law of Layered Rock Mass Considering Residual Strength
-
摘要:
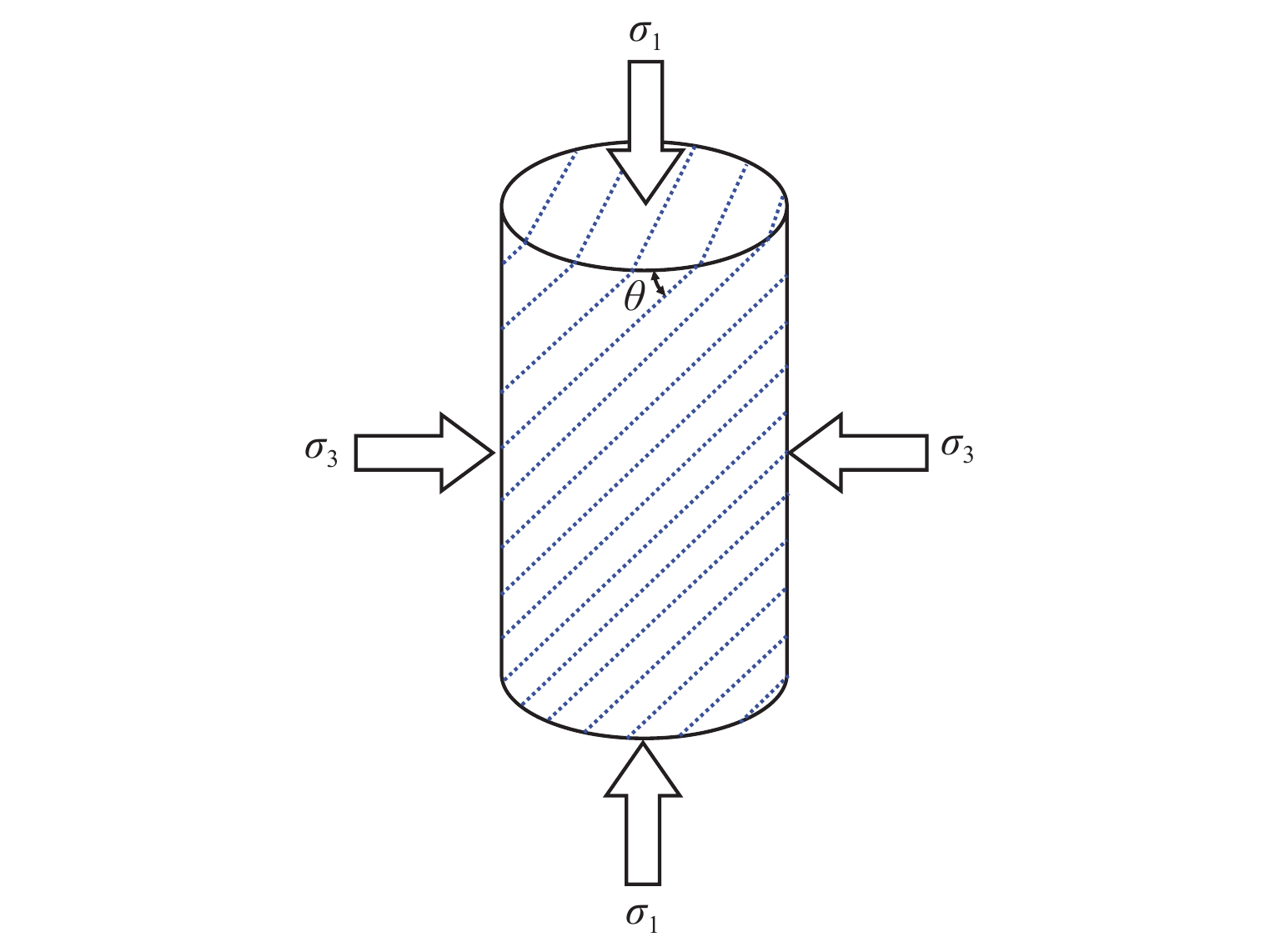
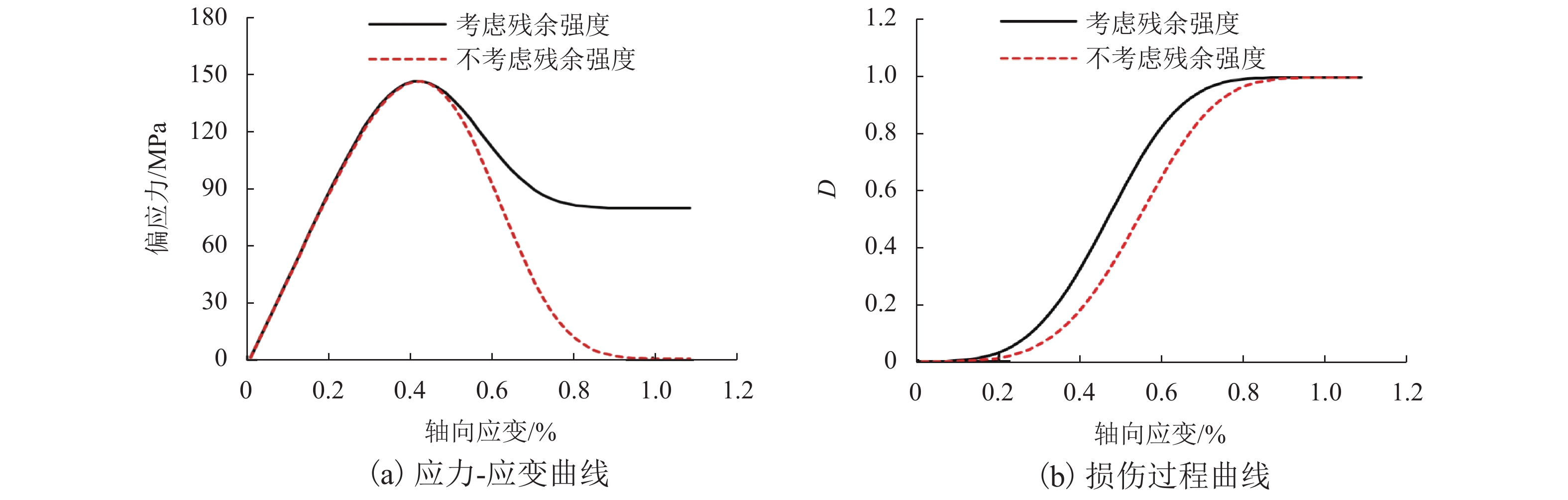
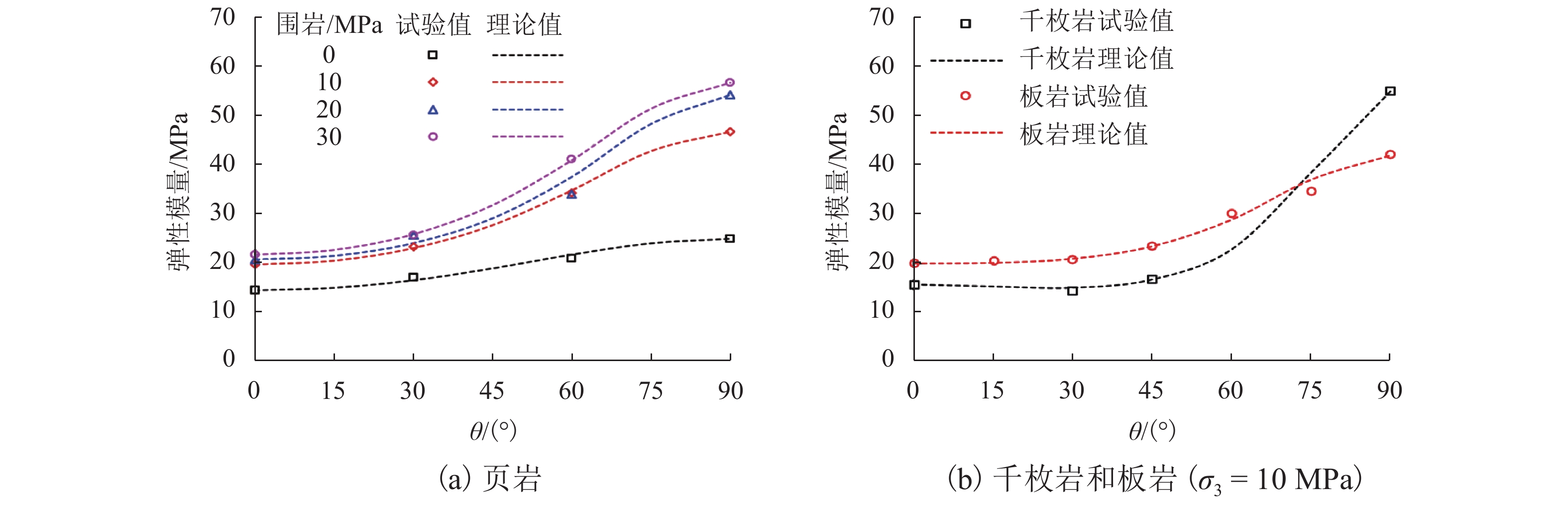
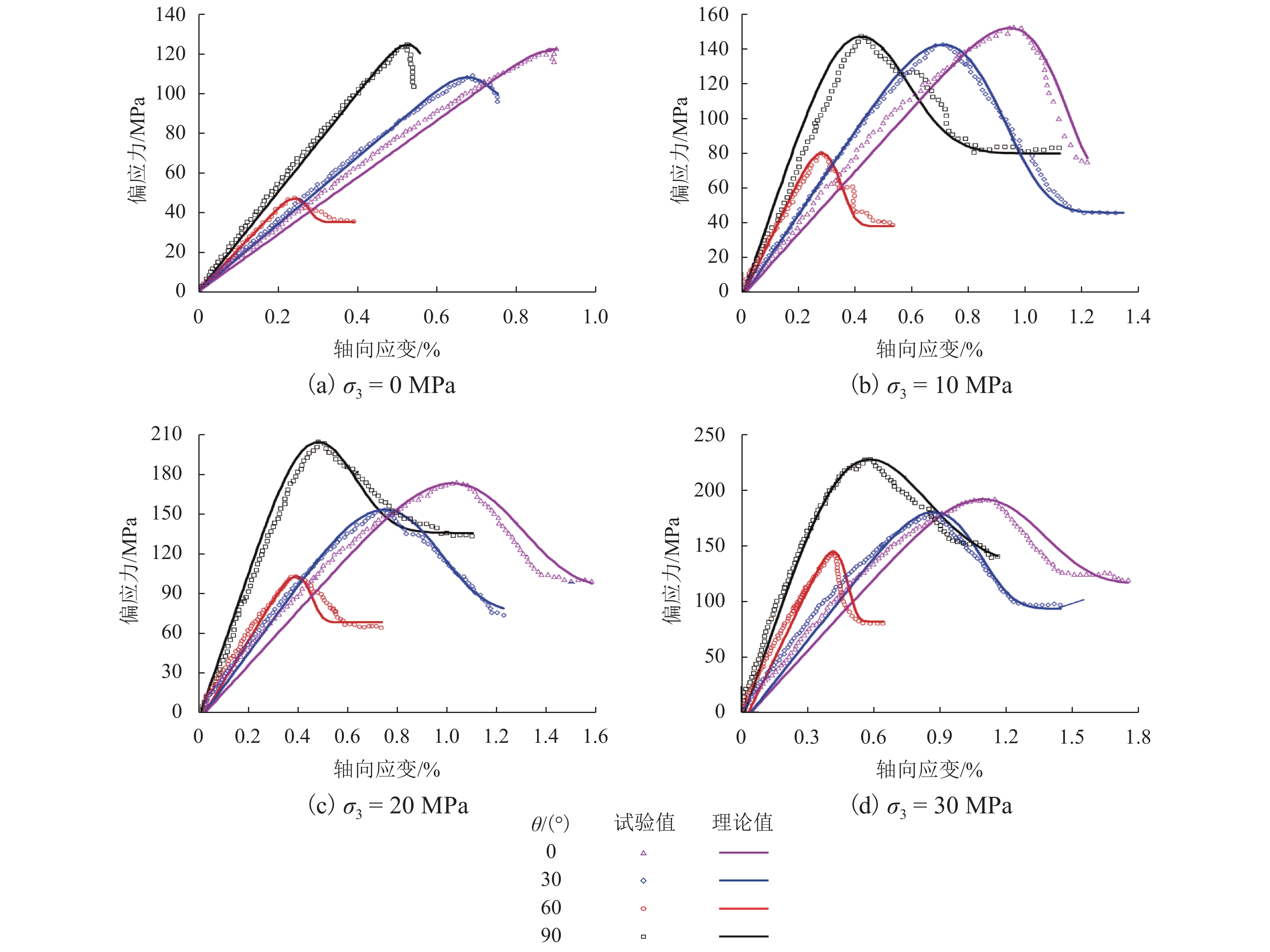
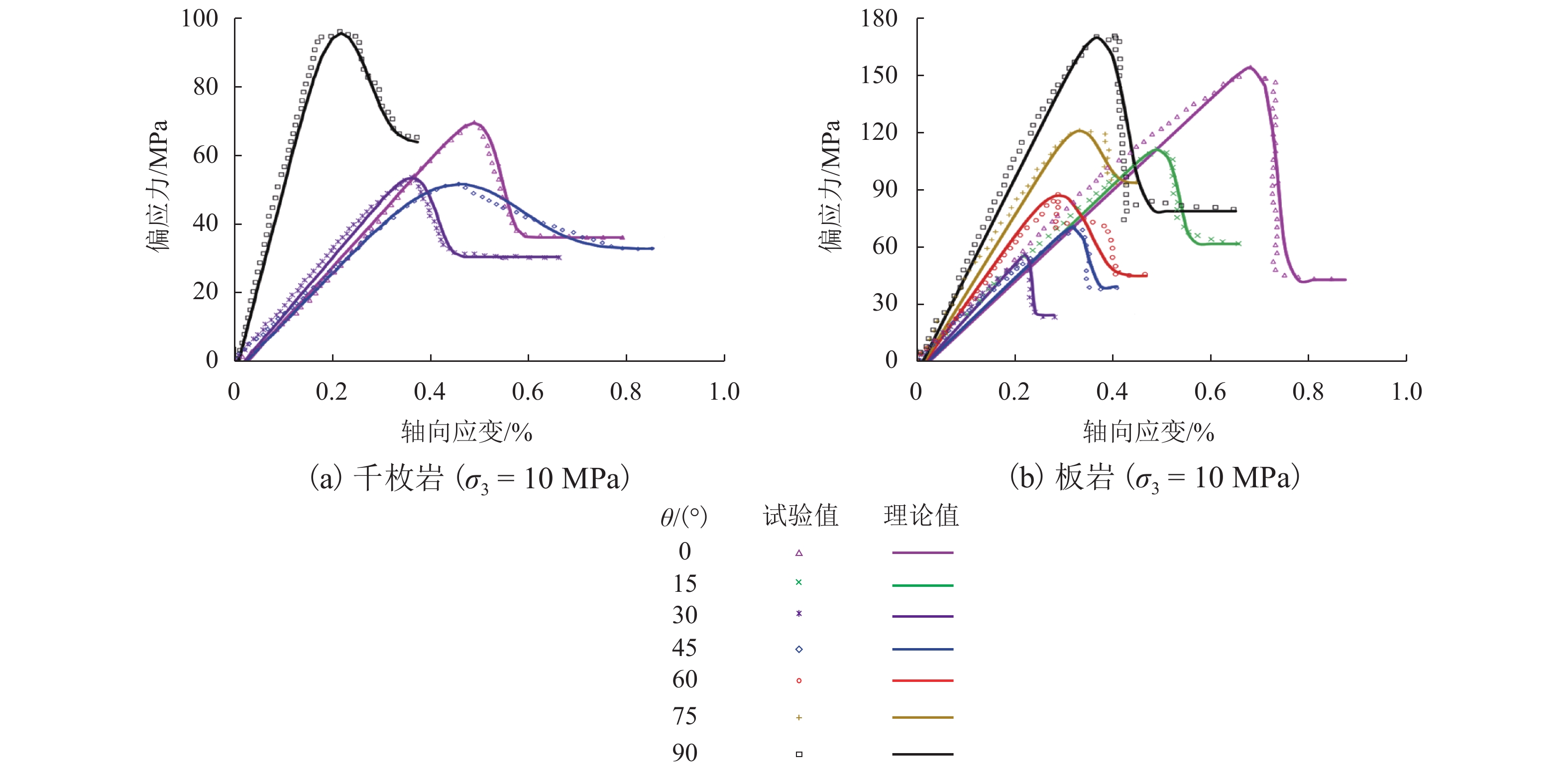
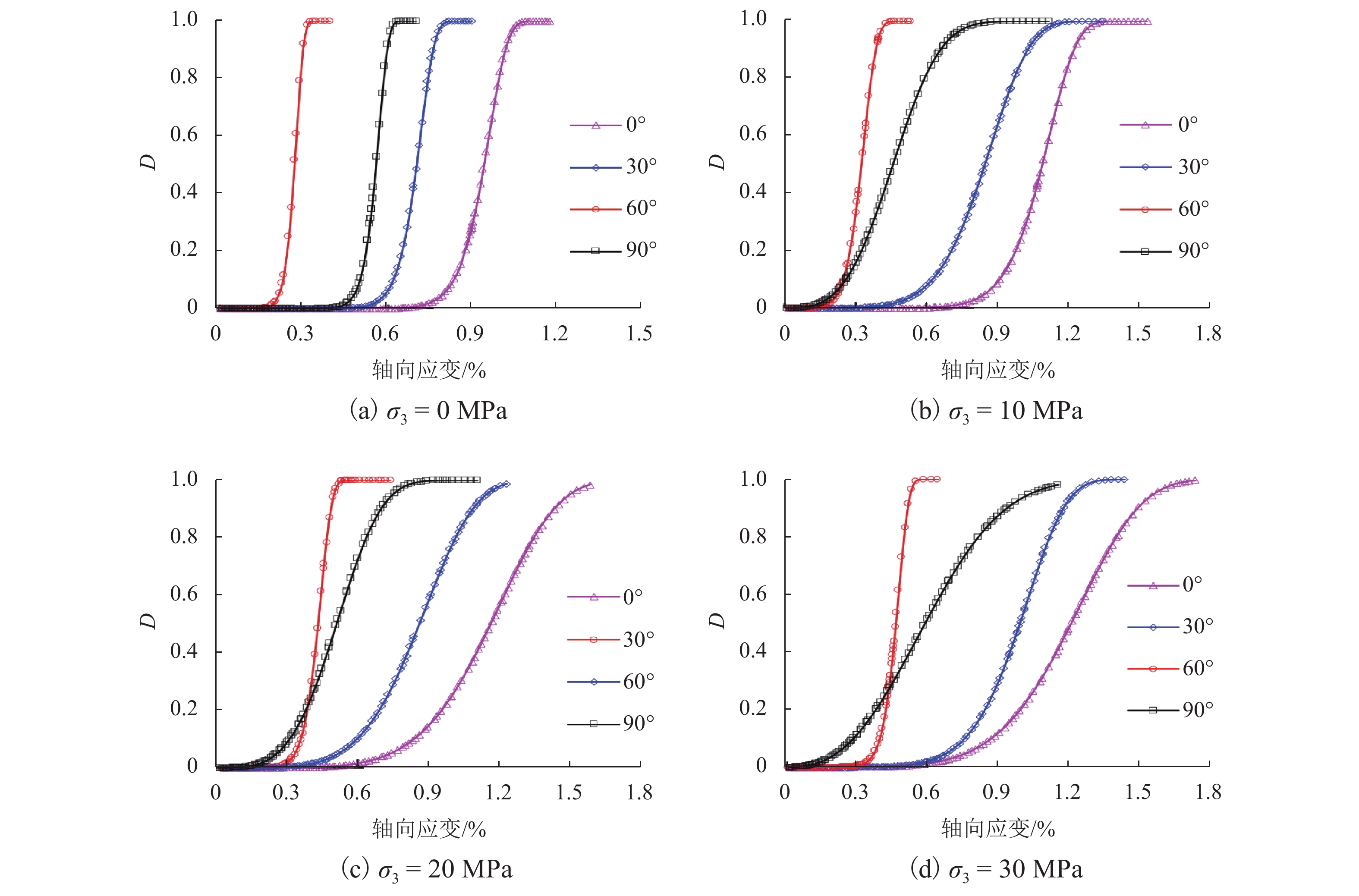
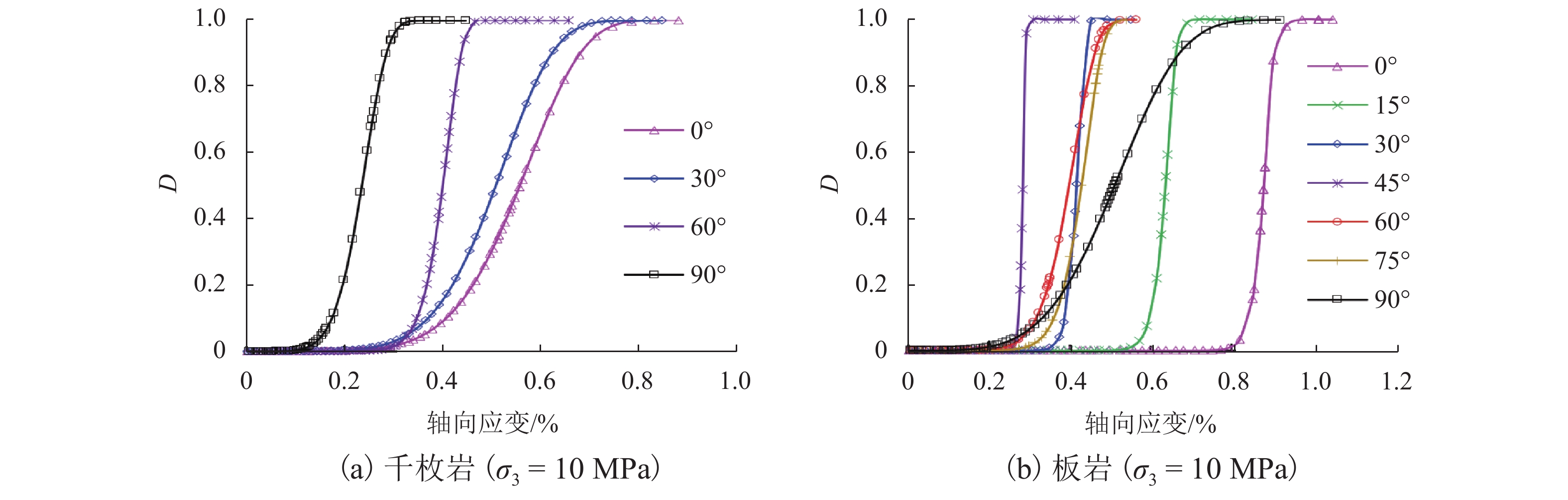
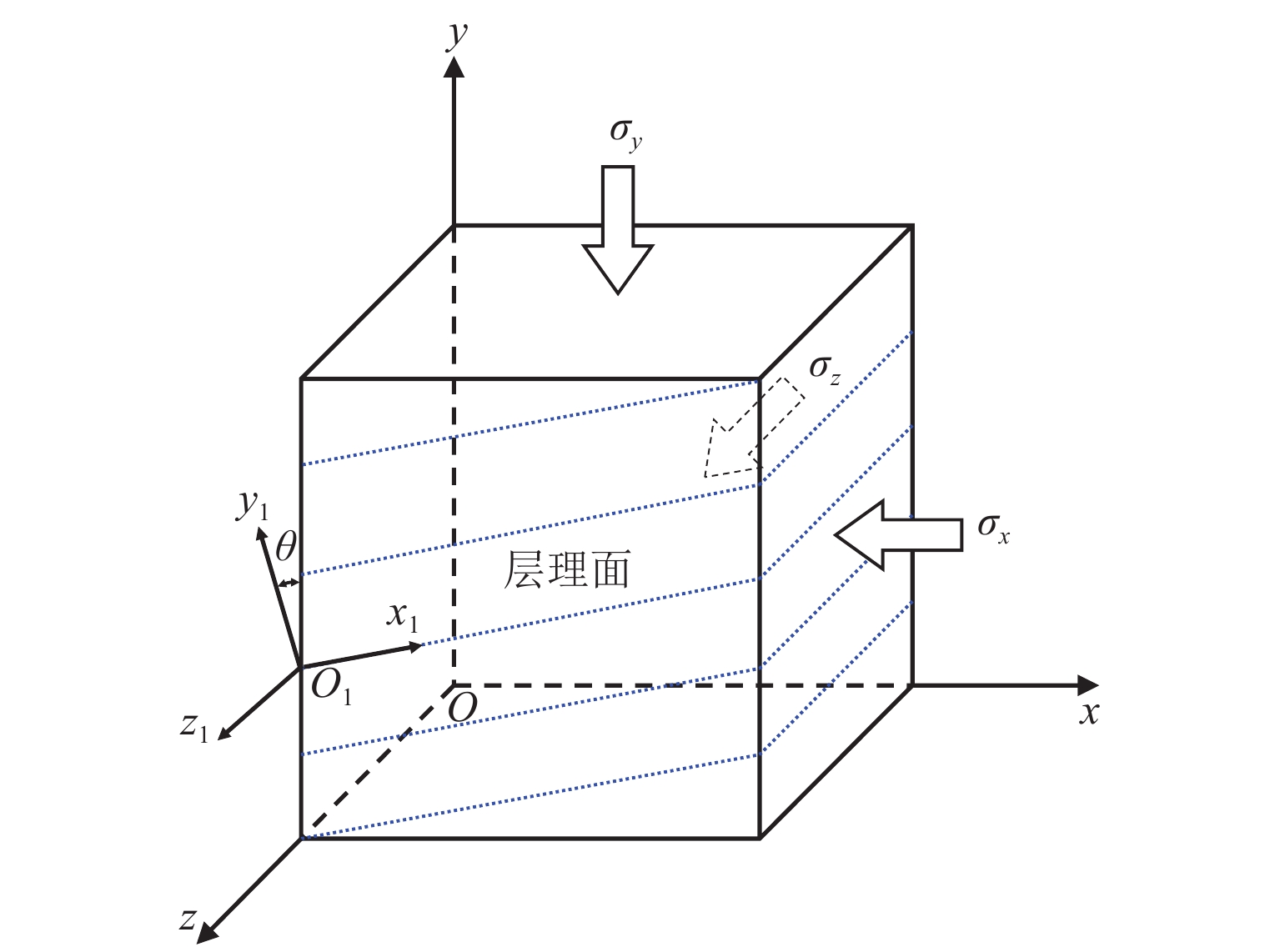
为更加真实准确地描述层状岩体的损伤演化过程，结合横观各向同性材料的弹性理论和损伤力学理论，采用修正的Lemaitre应变等价假设，建立了考虑残余强度的层状岩体损伤本构模型，通过页岩、千枚岩和板岩的三轴试验数据验证了模型的准确性，并分析了不同层理角度岩体的全过程损伤演化规律. 研究表明：模型既可以描述层状岩体的弹性变形，又可以较好地反映峰后应变软化过程；在初期加载过程中岩体的损伤值基本为0，随着应力增加，损伤值呈现出缓慢增长、加速增长、减速增长以及达到残余强度后稳定于1；页岩层理角度为60° 时损伤演化曲线最陡，损伤发展速度最快，最先破坏，千枚岩层厚较薄，强度更低，层理角度为90° 时最先破坏，而板岩相对较厚，强度更高，层理角度为45° 时最先破坏；岩体层理弱面的存在，导致了力学性能和破坏模式的各向异性，损伤演化规律也表现出明显的差异性.
Abstract:In order to describe the damage evolution process of layered rock mass more truly and accurately, a damage constitutive model for layered rock mass considering the residual strength was established, which adopted modified Lemaitre strain equivalence hypothesis, combining the elastic theory of transversely isotropic materials and the damage mechanics theory. The accuracy of the model was verified by the triaxial test data of shale, phyllite, and slate, and the whole process damage evolution law of rock mass with different bedding angles was analyzed. The research results showed that the model could describe the elastic deformation of layered rock mass, but also reflect the post-peak strain softening process well. In the initial loading process, the damage value of rock mass was near zero. With the increase of stress, the damage value showed slow growth, accelerated growth, and decelerated growth, until it reached the residual strength and then stabilized at one. When the bedding angle of the shale was 60°, the damage evolution curve was the steepest, the damage speed was the fastest, and it shale failed first. Because the phyllite was thinner in thickness and lower in strength, it failed first when the bedding angle was 90°. However, the slate was relatively thick and had higher strength, and it failed first when the bedding angle was 45°. The existence of a weak bedding surface of rock mass led to the anisotropy of mechanical properties and failure modes, and the damage evolution law showed remarkable differences.
-
Key words:
- layered rock mass /
- anisotropy /
- constitutive model /
- residual strength /
- damage evolution
-
图 1 横观各向同性材料坐标示意
Figure 1. Diagram of coordinate system for the transversely isotropic materials
图 3 考虑残余强度与不考虑残余强度对比
Figure 3. Comparison between the considered and unconsidered residual strengths
图 4 弹性模量的理论值与试验值对比
Figure 4. Comparison between theoretical and experimental values of elastic modulus
图 5 页岩应力-应变关系的理论值与试验值对比
Figure 5. Comparison between theoretical and experimental values of stress-strain curves for shale
图 6 千枚岩、板岩应力-应变关系的理论值与试验值对比
Figure 6. Comparison between theoretical and experimental values of stress-strain curves for phyllite and slate
围压/MPa 层理角度/（°） 峰值应力/MPa 峰值应变/% 弹性模量/GPa 残余强度/MPa m ε0/% 0 0 120.87 0.891 14.07 117.1 15.476 0.965 30 108.63 0.687 16.67 95.8 14.929 0.720 60 47.18 0.238 20.53 35.3 11.163 0.275 90 124.07 0.525 24.61 103.3 17.374 0.569 10 0 152.76 0.961 19.50 114.9 5.463 1.190 30 142.62 0.710 24.10 99.5 6.181 0.901 60 80.02 0.282 34.10 38.5 7.013 0.342 90 147.29 0.422 46.64 83.4 3.291 0.513 20 0 173.87 1.042 20.52 99.1 5.770 1.242 30 153.05 0.751 25.57 75.2 5.148 0.925 60 102.59 0.395 33.93 64.7 10.159 0.450 90 204.14 0.485 54.13 132.7 3.841 0.563 30 0 191.47 1.094 21.50 125.5 5.720 1.300 30 180.17 0.872 25.57 96.7 6.979 1.051 60 144.11 0.416 41.05 79.6 11.682 0.479 90 227.50 0.584 56.60 138.9 2.576 0.684 
下载: 导出CSV
表 2 千枚岩、板岩三轴压缩试验的主要参数[22-23] （σ3=10 MPa）
Table 2. Main parameters of triaxial compression test for phyllite and slate [22-23] （σ3 = 10 MPa）
岩性 层理角度/（°） 峰值应力/MPa 峰值应变/% 弹性模量/GPa 残余强度/MPa m ε0/% 千枚岩[22] 0 69.29 0.489 15.7 40.0 20.726 0.547 30 51.55 0.459 14.4 36.0 4.642 0.539 45 53.39 0.362 16.7 33.5 14.487 0.412 90 95.46 0.217 55.0 68.0 4.848 0.253 板岩[23] 0 154.19 0.820 20.0 49.0 42.896 0.887 15 111.41 0.590 20.5 67.5 29.327 0.644 30 70.26 0.384 20.6 45.0 22.803 0.425 45 55.82 0.267 23.5 30.0 50.078 0.285 60 87.26 0.349 30.0 51.0 8.212 0.415 75 121.25 0.400 34.5 100.0 10.882 0.443 90 170.35 0.487 42.0 87.0 17.038 0.505
下载: 导出CSV
-
[1] 吴永胜,谭忠盛,喻渝,等. 川西北茂县群千枚岩各向异性力学特性[J]. 岩土力学,2018,39(1): 207-215.WU Yongsheng, TAN Zhongsheng, YU Yu, et al. Anisotropically mechanical characteristics of Maoxian group phyllite in northwest of Sichuan province[J]. Rock and Soil Mechanics, 2018, 39(1): 207-215. [2] 陈子全,何川,吴迪,等. 高地应力层状软岩隧道大变形预测分级研究[J]. 西南交通大学学报,2018,53(6): 1237-1244. doi: 10.3969/j.issn.0258-2724.2018.06.020CHEN Ziquan, HE Chuan, WU Di, et al. Study of large deformation classification criterion for layered soft rock tunnels under high geostress[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1237-1244. doi: 10.3969/j.issn.0258-2724.2018.06.020 [3] 刘运思,王世鸣,郭志广,等. 横观各向同性岩体内时损伤本构模型研究[J]. 铁道科学与工程学报,2017,14(7): 1407-1414. doi: 10.3969/j.issn.1672-7029.2017.07.009LIU Yunsi, WANG Shiming, GUO Zhiguang, et al. Endchronic damage constitutive model of transversely isotropic rock[J]. Journal of Railway Science and Engineering, 2017, 14(7): 1407-1414. doi: 10.3969/j.issn.1672-7029.2017.07.009 [4] 史越,傅鹤林,伍毅敏,等. 层状岩石单轴压缩损伤本构模型研究[J]. 华中科技大学学报(自然科学版),2020,48(9): 126-132.SHI Yue, FU Helin, WU Yimin, et al. Study on damage constitutive model of layered rock under uniaxial compression[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2020, 48(9): 126-132. [5] WANG Z, ZONG Z, QIAO L, et al. Elastoplastic model for transversely isotropic rocks[J]. International Journal of Geomechanics, 2018, 18(2): 04017149.1-04017149.15. [6] SAROGLOU H, TSIAMBAOS G. A modified Hoek-Brown failure criterion for anisotropic intact rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 223-234. doi: 10.1016/j.ijrmms.2007.05.004 [7] SHI X C, YANG X, MENG Y F, et al. Modified Hoek-Brown failure criterion for anisotropic rocks[J]. Environmental Earth Sciences, 2016, 75(11): 1-11. [8] LI K H, YIN Z Y, HAN D Y, et al. Size effect and anisotropy in a transversely isotropic rock under compressive conditions[J]. Rock Mechanics and Rock Engineering, 2021, 54(9): 4639-4662. doi: 10.1007/s00603-021-02558-0 [9] POURAGHA M, EGHBALIAN M, WAN R. Micromechanical correlation between elasticity and strength characteristics of anisotropic rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 125: 104154.1-104154.8. [10] GHOLAMI R, RASOULI V. Mechanical and elastic properties of transversely isotropic slate[J]. Rock Mechanics and Rock Engineering, 2014, 47(5): 1763-1773. doi: 10.1007/s00603-013-0488-2 [11] 衡帅,杨春和,张保平,等. 页岩各向异性特征的试验研究[J]. 岩土力学,2015,36(3): 609-616.HENG Shuai, YANG Chunhe, ZHANG Baoping, et al. Experimental research on anisotropic properties of shale[J]. Rock and Soil Mechanics, 2015, 36(3): 609-616. [12] 储超群,吴顺川,张诗淮,等. 层状砂岩力学行为各向异性与破裂特征[J]. 中南大学学报(自然科学版),2020,51(8): 2232-2246.CHU Chaoqun, WU Shunchuan, ZHANG Shihuai, et al. Mechanical behavior anisotropy and fracture characteristics of bedded sandstone[J]. Journal of Central South University (Science and Technology), 2020, 51(8): 2232-2246. [13] 邓华锋,王伟,李建林,等. 层状砂岩各向异性力学特性试验研究[J]. 岩石力学与工程学报,2018,37(1): 112-120.DENG Huafeng, WANG Wei, LI Jianlin, et al. Experimental study on anisotropic characteristics of bedded sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 112-120. [14] 邓华锋,李涛,李建林,等. 层状岩体各向异性声学和力学参数计算方法研究[J]. 岩石力学与工程学报,2020,39(增1): 2725-2732.DENG Huafeng, LI Tao, LI Jianlin, et al. Study on calculation method of anisotropic acoustic and mechanical parameters of layered rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S1): 2725-2732. [15] 陈子全,何川,吴迪,等. 深埋碳质千枚岩力学特性及其能量损伤演化机制[J]. 岩土力学,2018,39(2): 445-456.CHEN Ziquan, HE Chuan, WU Di, et al. Mechanical properties and energy damage evolution mechanism of deep-buried carbonaceous phyllite[J]. Rock and Soil Mechanics, 2018, 39(2): 445-456. [16] 刘冬桥,王焯,张晓云. 岩石应变软化变形特性及损伤本构模型研究[J]. 岩土力学,2017,38(10): 2901-2908.LIU Dongqiao, WANG Zhuo, ZHANG Xiaoyun. Characteristics of strain softening of rocks and its damage constitutive model[J]. Rock and Soil Mechanics, 2017, 38(10): 2901-2908. [17] 温韬,唐辉明,马俊伟,等. 考虑初始损伤和残余强度的岩石变形过程模拟[J]. 地球科学,2019,44(2): 652-663.WEN Tao, TANG Huiming, MA Junwei, et al. Deformation simulation for rock in consideration of initial damage and residual strength[J]. Earth Science, 2019, 44(2): 652-663. [18] 曹文贵,赵衡,李翔,等. 基于残余强度变形阶段特征的岩石变形全过程统计损伤模拟方法[J]. 土木工程学报,2012,45(6): 139-145.CAO Wengui, ZHAO Heng, LI Xiang, et al. A statistical damage simulation method for rock full deformation process with consideration of the deformation characteristics of residual strength phase[J]. China Civil Engineering Journal, 2012, 45(6): 139-145. [19] 李海潮,张升. 基于修正Lemaitre应变等价性假设的岩石损伤模型[J]. 岩土力学,2017,38(5): 1321-1326, 1334.LI Haichao, ZHAGN Sheng. A constitutive damage model of rock based on the assumption of modified Lemaitre strain equivalence hypothesis[J]. Rock and Soil Mechanics, 2017, 38(5): 1321-1326, 1334. [20] 汪杰,宋卫东,付建新. 考虑节理倾角的岩体损伤本构模型及强度准则[J]. 岩石力学与工程学报,2018,37(10): 2253-2263.WANG Jie, SONG Weidong, FU Jianxin. A damage constitutive model and strength criterion of rock mass considering the dip angle of joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2253-2263. [21] 贾长贵,陈军海,郭印同,等. 层状页岩力学特性及其破坏模式研究[J]. 岩土力学,2013,34(增2): 57-61.JIA Changgui, CHEN Junhai, GUO Yintong, et al. Research on mechanical behaviors and failure modes of layer shale[J]. Rock and Soil Mechanics, 2013, 34(S2): 57-61. [22] 唐克东,王甲亮,管俊峰,等. 层状岩体在三轴加载下的扩容及塑性应变特性[J]. 水利学报,2021,52(1): 42-50.TANG Kedong, WANG Jialiang, GUAN Junfeng, et al. Dilatancy and plastic strain characteristics of layered rock mass under triaxial compressive test[J]. Journal of Hydraulic Engineering, 2021, 52(1): 42-50. [23] CHEN Y F, WEI K, LIU W, et al. Experimental characterization and micromechanical modelling of anisotropic slates[J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3541-3557. doi: 10.1007/s00603-016-1009-x -
下载:
点击查看大图
计量
- 文章访问数: 458
- HTML全文浏览量: 96
- PDF下载量: 68
- 被引次数: 0