Influence of Fastener Stiffness Nonlinearity on Wheel–Rail Transient Rolling Contact Behavior in Corrugated Area
-
摘要:
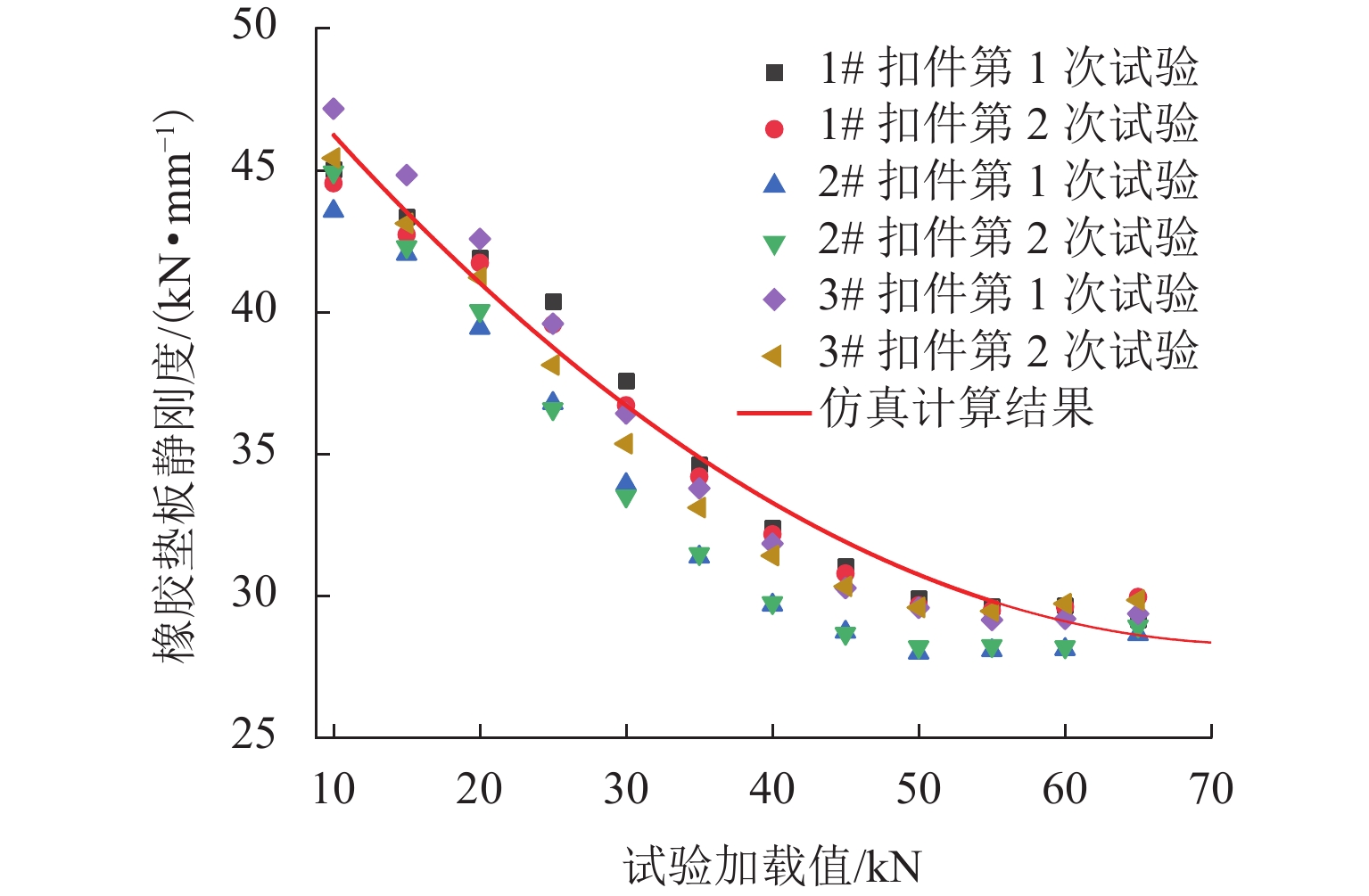
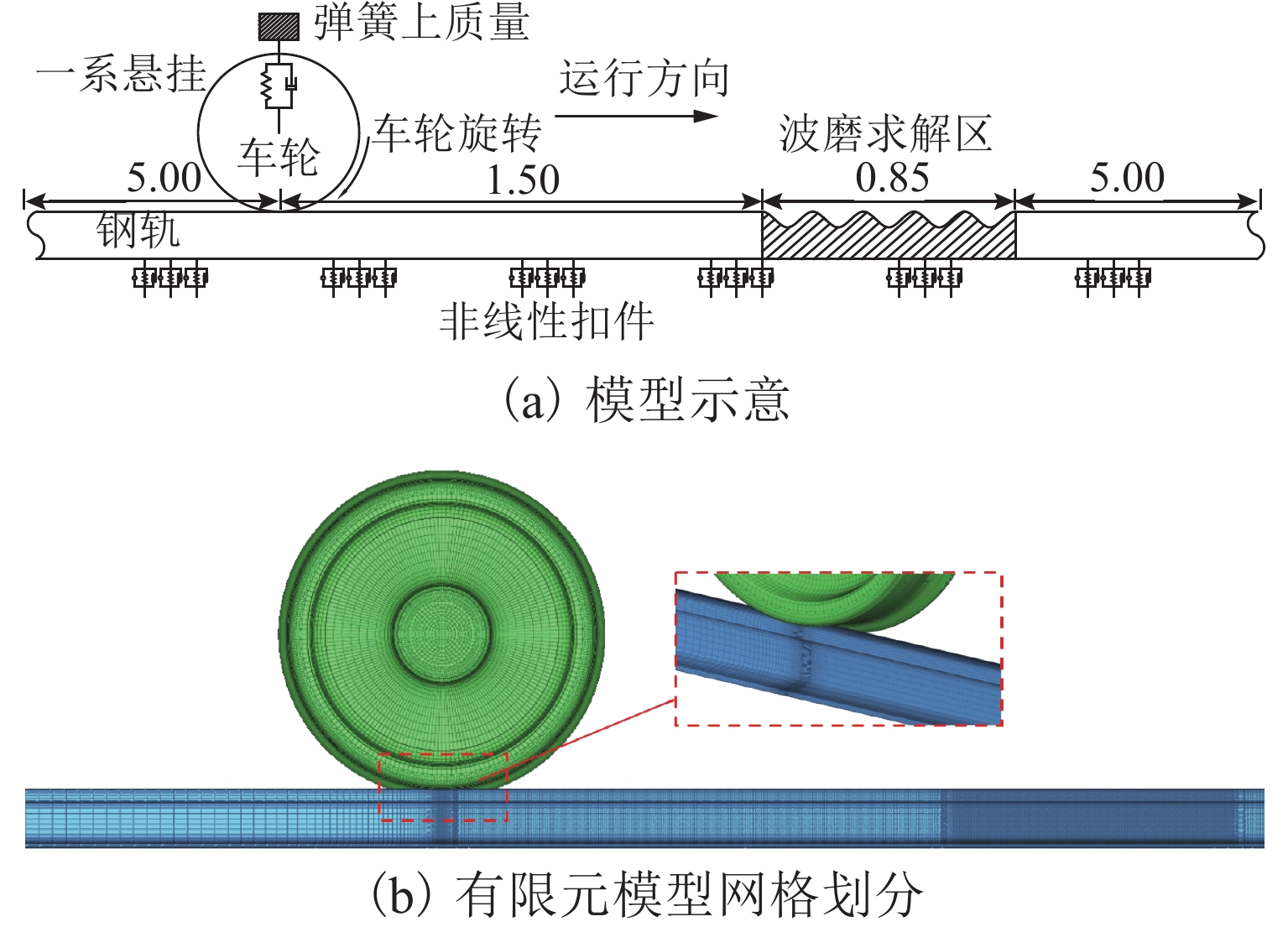
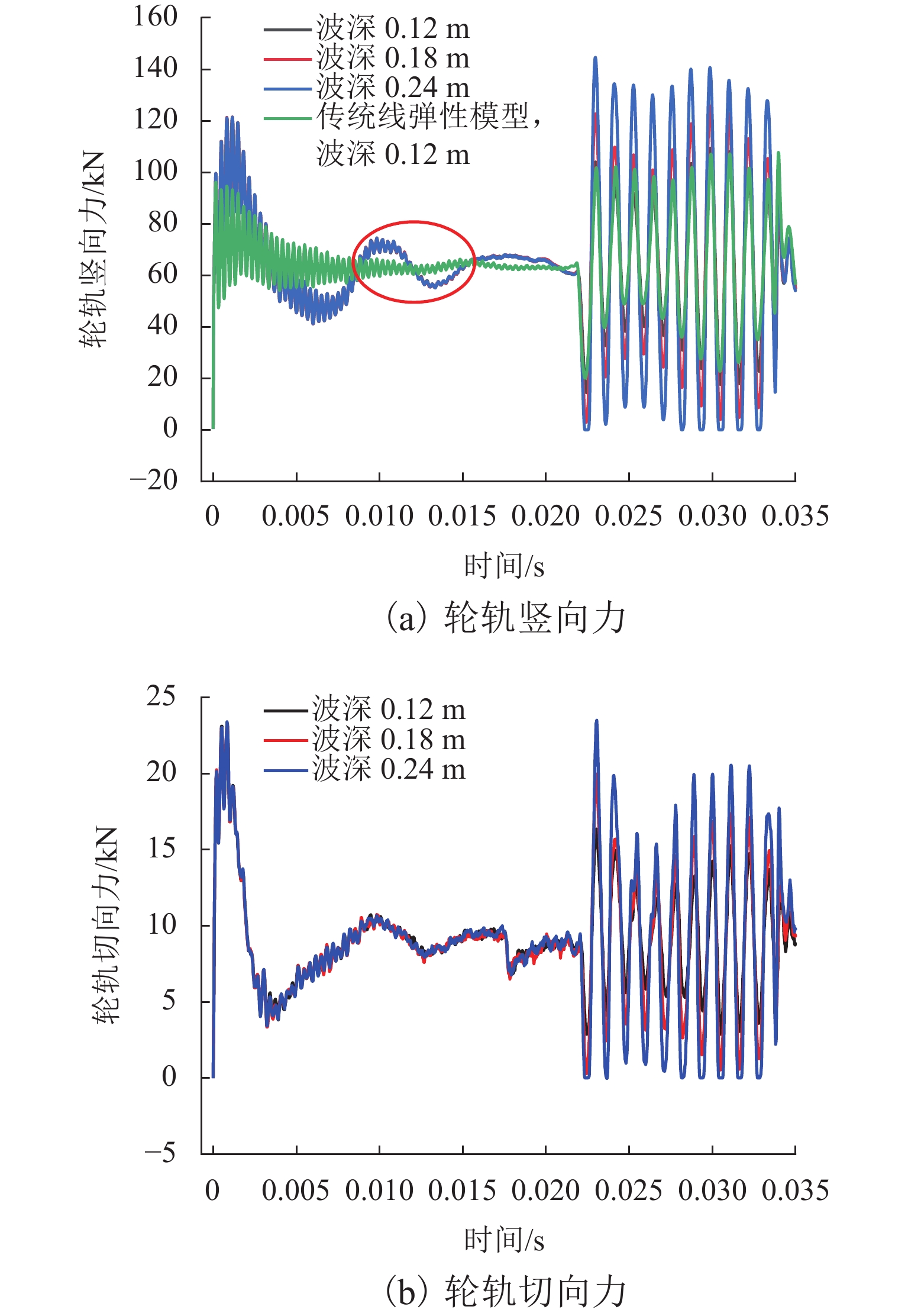
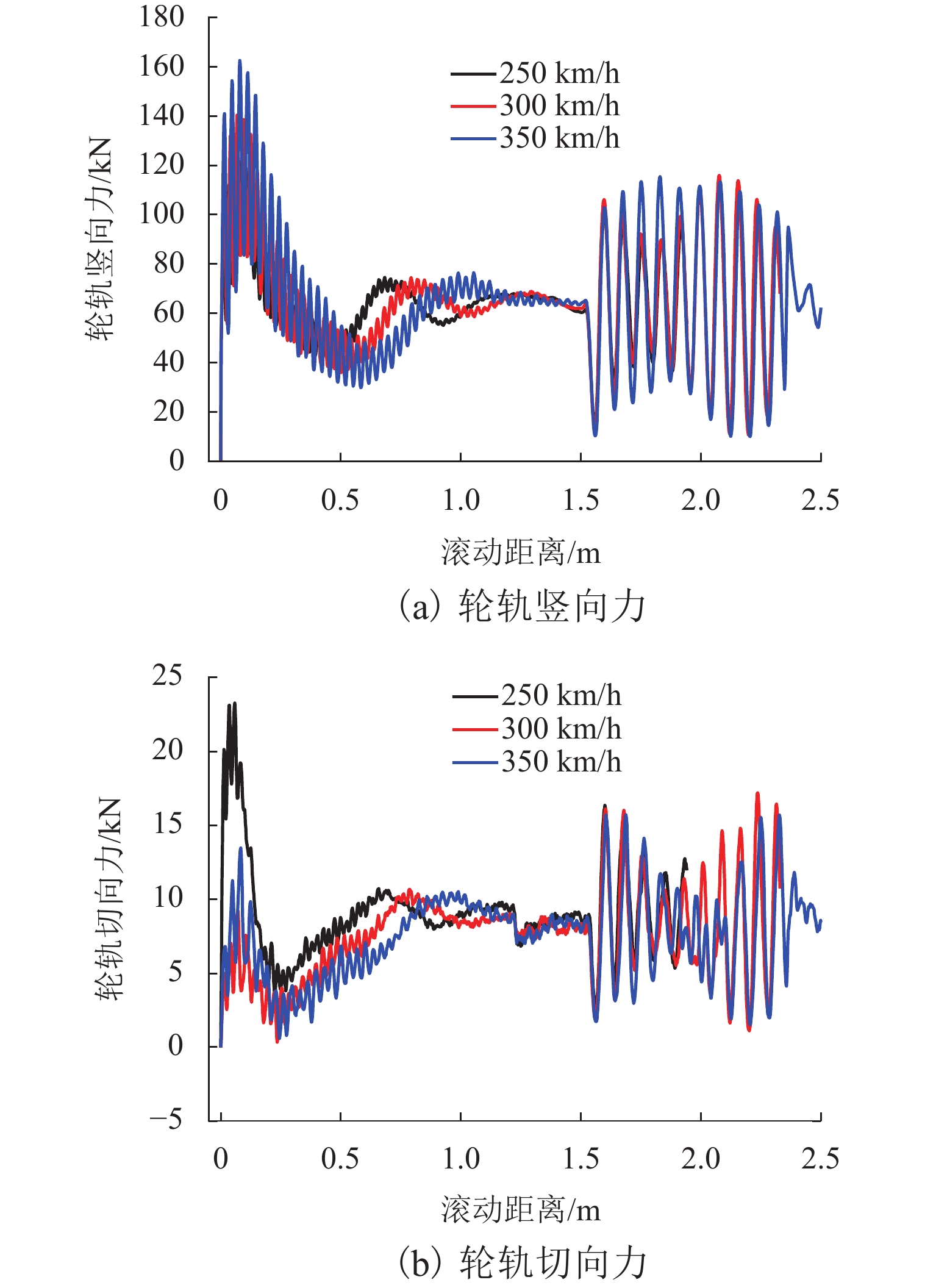
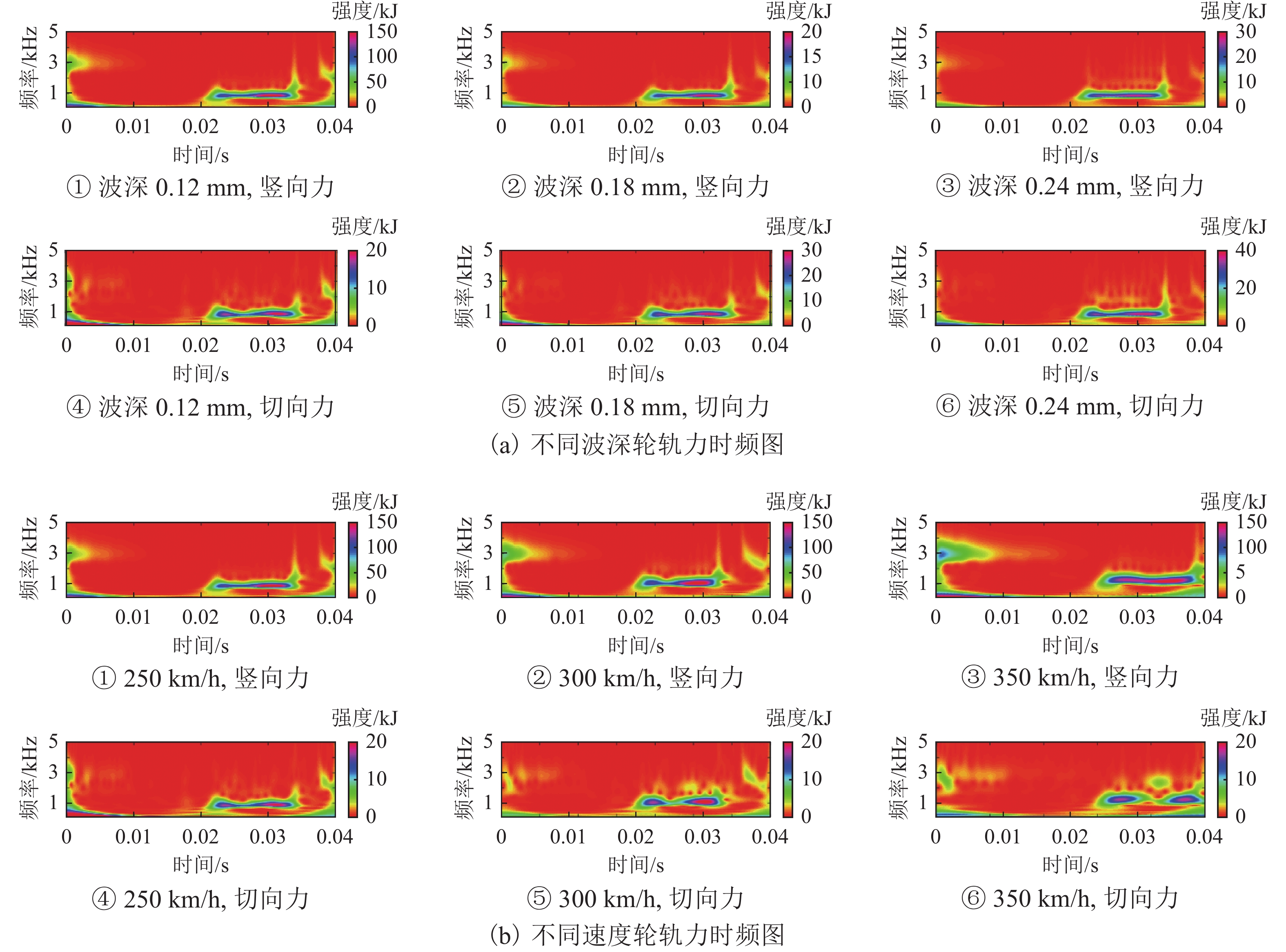
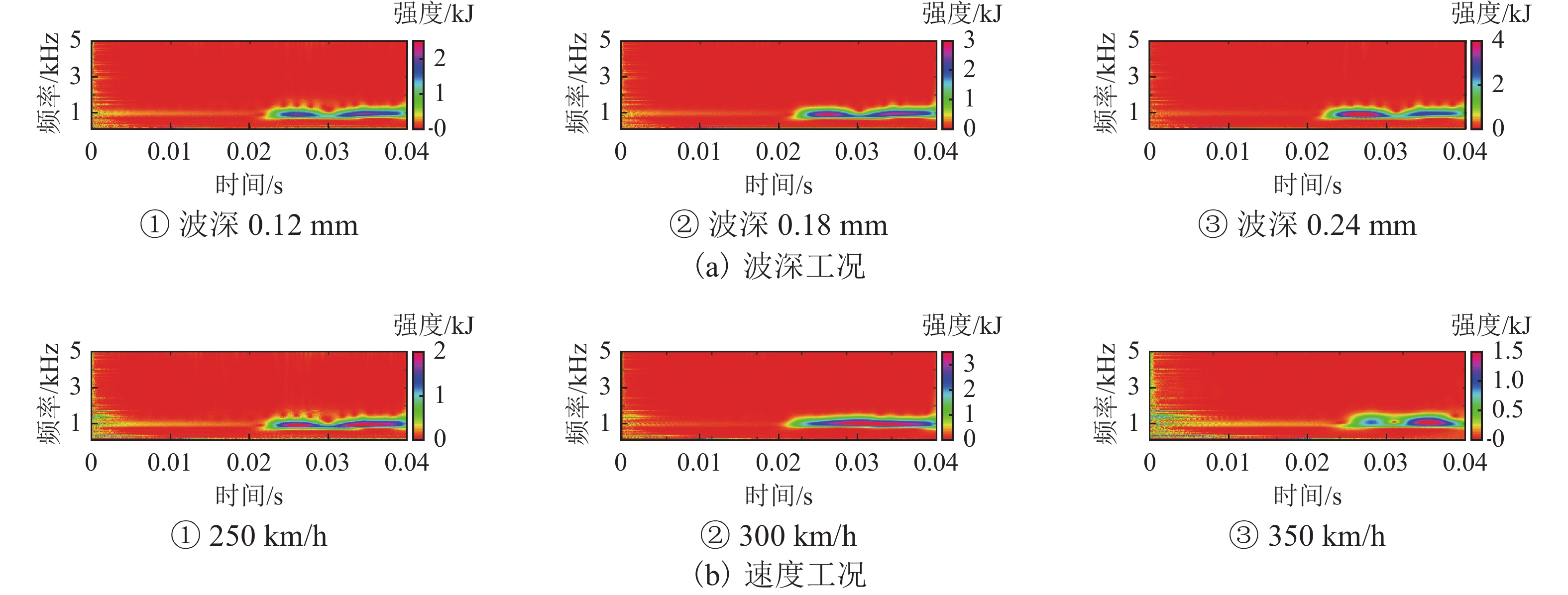
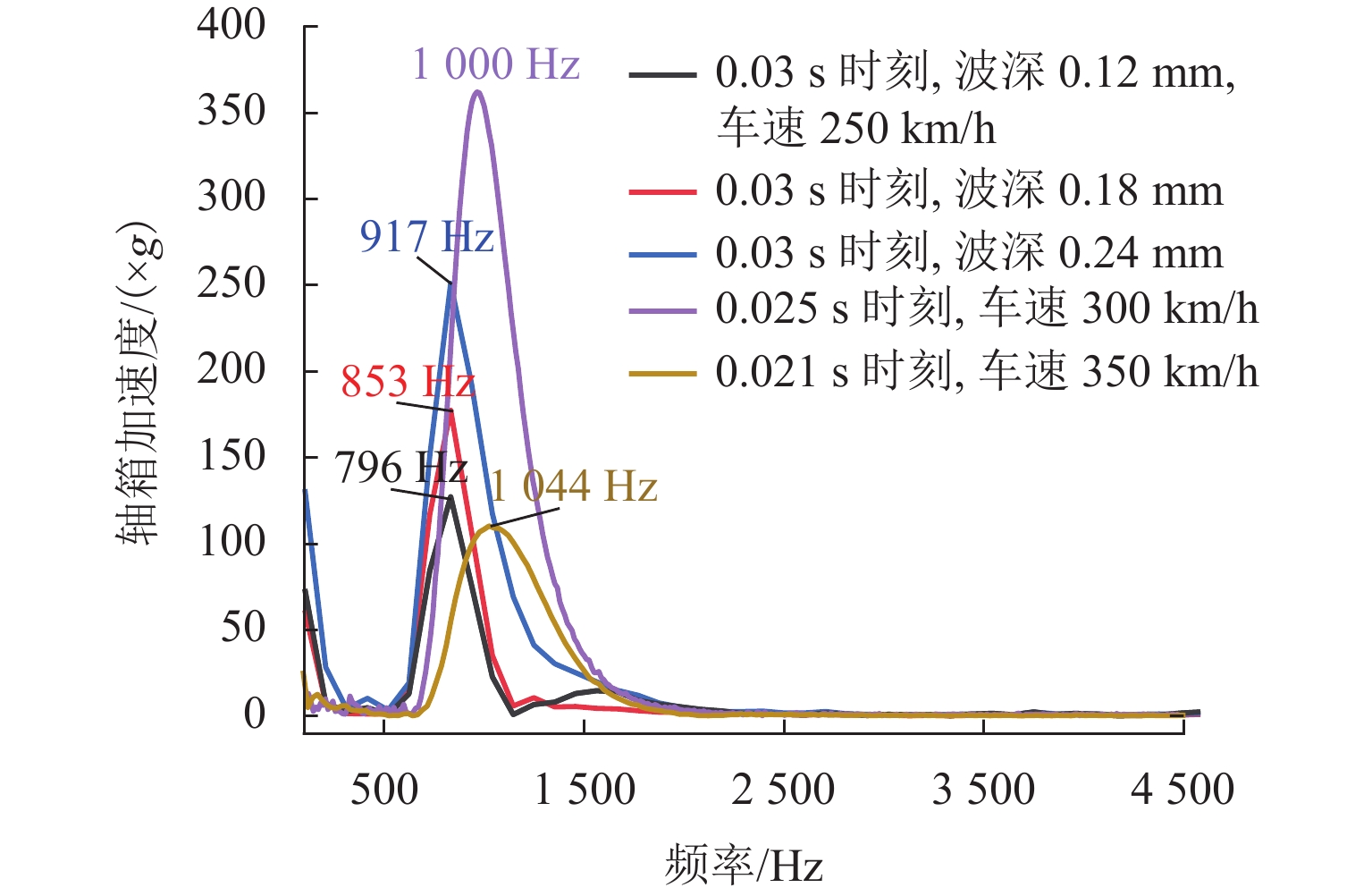
WJ-8型扣件橡胶垫板刚度在长期服役过程中表现出非线性特征，静刚度随荷载增加而降低，为提高三维瞬态滚动接触有限元模型计算精确性，本文以LMA踏面车轮及CHN60型钢轨为基础，基于显式积分算法，将以往研究中线弹性扣件转化为非线性扣件，建立考虑扣件刚度非线性特征的三维轮轨瞬态滚动接触有限元模型，研究刚度非线性对车轮与钢轨波磨间高频动态响应及瞬态接触行为的影响，并重点分析了波磨工况下时频域内轮轨接触力、轴箱加速度的变化信息. 结果表明：扣件非线性对轮轨接触力变化影响明显，主要表现为车轮行驶至扣件前端时强振动导致橡胶垫板表现为柔软特性使轮轨接触力减小，车轮行驶至扣件上方时在轴重作用下振动减弱表现为刚硬特性使轮轨接触力增大，轮轨力变化差异最大达到13.1%.
Abstract:The stiffness of the rubber pad of the WJ-8 fastener exhibits nonlinear characteristics during long-term service, and the static stiffness decreases with the increase in the load. In order to improve the calculation accuracy of the three-dimensional transient rolling contact finite element model, the LMA tread wheel and CHN60 rail were used. Based on the explicit integration algorithm, the linear elastic fasteners in the previous research were transformed into nonlinear fasteners to establish a three-dimensional wheel–rail transient rolling contact finite element model considering the nonlinear characteristics of fastener stiffness. The influence of stiffness nonlinearity on the high-frequency dynamic response and transient contact behavior between wheel and rail corrugation was studied, and the change of wheel–rail contact force and axle box acceleration in the time-frequency domain under corrugation conditions was analyzed. The results show that the nonlinearity of the fastener has an obvious effect on the change of the wheel–rail contact force. The main manifestation is that when the wheel travels to the front end of the fastener, the strong vibration makes the rubber pad soft, which reduces the contact force of the wheel and rail. In addition, when the wheel travels above the fastener, the vibration is weakened under the action of the axle load; the stiffness characteristic increases the wheel-rail contact force, and the difference between the wheel–rail force changes is up to 13.1%.
-
图 2 试验测得扣件静刚度与荷载拟合曲线
Figure 2. Fitting curve between static stiffness and load of fasteners measured by test
图 3 三维轮轨瞬态滚动有限元模型
Figure 3. Finite element model of three-dimensional wheel–rail transient rolling
图 5 不同波深轮轨力时程曲线
Figure 5. Time history curves of wheel–rail force with different corrugation depths
图 6 不同运行速度轮轨力时程曲线
Figure 6. Time history curves of wheel–rail force at different operating speeds
图 7 不同波深/运行速度轮轨力时频图
Figure 7. Time-frequency diagrams of wheel–rail force at different corrugation depths/operating speeds
图 8 不同波深/运行速度轮轨力功率谱曲线
Figure 8. Power spectrum curves of wheel–rail force at different corrugation depths/operating speeds
图 9 不同波深/运行速度轴箱加速度时程曲线
Figure 9. Time history curves of axle box acceleration at different corrugation depths/operating speeds
图 11 不同波深/运行速度轴箱加速度功率谱曲线
Figure 11. Power spectrum curves of axle box acceleration at different corrugation depths/operating speeds
表 1 模型参数
Table 1. Model parameters
簧上质量/kg 车辆一系悬挂 簧下质量 车轮及钢轨材料 刚度/
（MN·m−1）阻尼/
（kN·s·m−1）车轮质量/kg 轮下附属部件质量/kg 弹性模量/
GPa密度/
（kg·m−3）泊松比 阻尼常数 6000 0.88 4 656 340 210 7790 0.3 0.0001 
下载: 导出CSV
-
[1] 朱胜阳. 高速铁路无砟轨道结构伤损行为及其对动态性能的影响[D]. 成都: 西南交通大学, 2015. [2] BRUNI S, COLLINA A. Modelling the viscoelastic behaviour of elastomeric components: an application to the simulation of train-track interaction[J]. Vehicle System Dynamics, 2000, 34(4): 283-301. doi: 10.1076/vesd.34.4.283.2061 [3] GIL-NEGRETE N, VIÑOLAS J, KARI L. A nonlinear rubber material model combining fractional order viscoelasticity and amplitude dependent effects[J]. Journal of Applied Mechanics, 2009, 76: 011009.1-011009.9. [4] SJÖBERG M M, KARI L. Non-linear behavior of a rubber isolator system using fractional derivatives[J]. Vehicle System Dynamics, 2002, 37(3): 217-236. doi: 10.1076/vesd.37.3.217.3532 [5] 吴杰,上官文斌. 采用黏弹性分数导数模型的橡胶隔振器动态特性的建模及应用[J]. 工程力学,2008,25(1): 161-166.WU Jie, SHANGGUAN Wenbin. Modeling and applications of dynamic characteristics for rubber isolators using viscoelastic fractional derivative model[J]. Engineering Mechanics, 2008, 25(1): 161-166. [6] WU T X, THOMPSON D J. Theoretical investigation of wheel/rail non-linear interaction due to roughness excitation[J]. Vehicle System Dynamics, 2000, 34(4): 261-282. doi: 10.1076/vesd.34.4.261.2060 [7] YANG Z, BOOGAARD A, WEI Z L, et al. Numerical study of wheel-rail impact contact solutions at an insulated rail joint[J]. International Journal of Mechanical Sciences, 2018, 138/139: 310-322. doi: 10.1016/j.ijmecsci.2018.02.025 [8] BERG M. A non-linear rubber spring model for rail vehicle dynamics analysis[J]. Vehicle System Dynamics, 1998, 30(3/4): 197-212. [9] ZHU S Y, CAI C B, SPANOS P D. A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab track systems[J]. Journal of Sound and Vibration, 2015, 335: 304-320. doi: 10.1016/j.jsv.2014.09.034 [10] 张大伟,翟婉明,朱胜阳,等. 基于橡胶弹簧非线性模型的重载车辆轮轨动力特征分析[J]. 铁道学报,2016,38(12): 19-27.ZHANG Dawei, ZHAI Wanming, ZHU Shengyang, et al. Wheel/rail dynamic interaction between heavy-haul freight car and ballasted track based on a nonlinear rubber spring model[J]. Journal of the China Railway Society, 2016, 38(12): 19-27. [11] BAGLEY R L, TORVIK P J. Fractional calculus-A different approach to the analysis of viscoelastically damped structures[J]. AIAA Journal, 1983, 21(5): 741-748. doi: 10.2514/3.8142 [12] 赵鑫,温泽峰,王衡禹,等. 三维高速轮轨瞬态滚动接触有限元模型及其应用[J]. 机械工程学报,2013,49(18): 1-7. doi: 10.3901/JME.2013.18.001ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. 3D transient finite element model for high-speed wheel-rail rolling contact and its application[J]. Journal of Mechanical Engineering, 2013, 49(18): 1-7. doi: 10.3901/JME.2013.18.001 [13] 谷永磊. 高速铁路无砟轨道钢轨波浪形磨损机理研究[D]. 北京: 北京交通大学, 2017. [14] 徐井芒,王凯,高原,等. 高速铁路无缝钢轨断缝瞬态冲击行为分析[J]. 西南交通大学学报,2020,55(6): 1348-1354.XU Jingmang, WANG Kai, GAO Yuan, et al. Transient impact behavior analysis of rail broken gap on high-speed continuous welded rail[J]. Journal of Southwest Jiaotong University, 2020, 55(6): 1348-1354. [15] 韩立,伍向阳,刘兰华,等. 基于Morlet小波分析的高速铁路轮轨粗糙度声学特征[J]. 铁道建筑,2020,60(5): 89-93.HAN Li, WU Xiangyang, LIU Lanhua, et al. Acoustic characteristics of high speed railway wheel-rail roughness based on morlet wavelet analysis[J]. Railway Engineering, 2020, 60(5): 89-93. [16] 李伟. 地铁钢轨波磨成因及其对车辆/轨道行为的影响[D]. 成都: 西南交通大学, 2015. -
下载:
点击查看大图
计量
- 文章访问数: 290
- HTML全文浏览量: 50
- PDF下载量: 68
- 被引次数: 0