Track Condition Evaluation for Multi-vehicle Performance Prediction Model Based on Convolutional Neural Network and Gated Recurrent Unit
-
摘要:
不同车型高速综合检测列车的动力学传递特性不同,使得其对同一线路的车体加速度评价结果存在一定差异. 为解决上述问题,本文基于多列动检车的检测数据,将卷积神经网络(convolutional neural network,CNN)与门控循环单元(gated recurrent unit,GRU)相结合,建立了多车型车辆动力学响应预测模型,通过输入多项实测轨道不平顺和车速预测各车型的车体垂向和横向加速度,并将多车型车体加速度预测值的最大包络作为轨道状态评价依据. 结果表明:将高低、轨向不平顺等8项轨道不平顺和车速共同作为输入参数的模型预测性能最优,车体垂向和横向加速度预测的评估指标分别提升了5%~13%和25%~36%;CNN-GRU模型所预测的车体加速度在时域和频域均与实测结果吻合较好,相关系数最大达到0.902;且相比于BP (back propagation)神经网络,各项车体垂向和横向加速度预测的评估指标分别提升了36%~109%和11%~167%;针对某轨道几何状态不良区段应用效果,预测6种车型中有4种车型达到车体垂向加速度Ⅰ级或Ⅱ级超限,有1种车型达到车体横向加速度Ⅰ级超限,提高了轨道状态评价的准确性和一致性.
-
关键词:
- 轨道不平顺 /
- 车体加速度 /
- 轨道状态评价 /
- 门控循环单元(GRU) /
- 卷积神经网络(CNN)
Abstract:The dynamic transmission characteristics of different types of high-speed track inspection vehicles are different, which makes the evaluation results of vehicle body acceleration on the same railway line different. To solve the above problem, the convolutional neural network (CNN) is combined with the gated recurrent unit (GRU) to establish a dynamic response prediction model for multi-vehicle dynamic response, which predicts the vertical and lateral acceleration of each vehicle by inputting a number of measured track irregularities and vehicle speeds, and uses the maximum envelope of the predicted values of multi-vehicle acceleration as the basis for track state evaluation. The results show that the model with eight track irregularities and vehicle speed, such as longitudinal irregularity, horizontal irregularity, as input parameters has the best prediction performance, and the evaluation indices of vertical and lateral vehicle acceleration prediction are increased by 5%–13% and 25%–36%, respectively. The vehicle acceleration predicted by the CNN-GRU model is in good agreement with the measured results in both time domain and frequency domains, with the maximum correlation coefficient of 0.902. Compared with back propagation (BP) neural network, CNN-GRU improves the evaluation indices of vertical and lateral vehicle acceleration prediction by 36%–109% and 11%–167%, respectively. The application result in a section with poor track geometry state shows that four out of the six vehicle types reach the level Ⅰ or Ⅱ overrun of the vehicle vertical acceleration, and one vehicle type reaches the level Ⅰ overrun of the vehicle lateral acceleration, which improves the accuracy and consistency of the track state evaluation.
-
轨道不平顺作为车辆-轨道耦合系统的主要激扰源,是加剧车体浮沉、点头、侧摆等响应以及诱发列车脱轨的主要原因. 常用的轨道不平顺评价方法有局部幅值超限扣分、轨道质量指数、轨道不平顺功率谱、车辆动态响应等[1]. 近年来,结合轨道不平顺和车辆动力学响应共同评价轨道状态成为研究热点. 这就要求寻找一个能够将轨道不平顺与车辆响应有效关联的预测模型,在关注轨道不平顺幅值的同时,利用车辆动态响应辅助评价轨道状态,及时消除复合的、与敏感波长相关的、发展较快和变化较大的轨道不平顺.
从研究方法角度可将基于轨道不平顺预测车辆动力学响应概括为4类:车辆-轨道耦合动力学建模、系统辨识、车辆-轨道耦合动力学建模与系统辨识相结合、机器学习方法. 车辆-轨道耦合动力学建模方法通过建立各种车辆-轨道耦合动力学机理模型,仿真模拟轨道不平顺激励下的车辆动力学响应[2],建模过程对复杂非线性系统进行了简化和近似,影响模型精度. 系统辨识方法借助信号处理理论建立轨道不平顺与车辆响应间的传递函数. Luber等[3-4]基于频域内信号分解等方法建立传递函数,通过滤波技术获得车辆响应. Furukawa等[5-6]建立ARX (auto regressive exogenous)模型和状态空间模型,分别预测车体加速度和轮重减载率. 系统辨识方法不足之处是将车辆-轨道系统近似为线性系统[4,6],虽然大多数情况下车体垂向振动可视为线性系统,但车体横向振动一般为非线性系统[6],并且该方法只适用于列车匀速行驶条件,在变速和非线性因素的情况下,表征输入与输出关系的有效性降低. Li等[7-9]将车辆-轨道动力学建模与系统辨识相结合,通过轨道不平顺预测轮轨力. 这种方法能对不同车型、车速建模,但还停滞在对轮轨力的预测,研究方法并不成熟. 机器学习方法中,神经网络具有任意函数逼近器特性,因此,利用机器学习模型可以表达建立轨道不平顺与车辆响应的非线性关系. Wang等[10-11]建立了BP (back propagation)神经网络,预测由轨道不平顺与列车速度激励下的车体加速度和轮轨力. 徐磊等[12]构建扭曲和水平不平顺的25个时域和频域统计特征,例如绝对均值、方根均值、最大值和方根幅值等,使用主成分分析法(principal component analysis,PCA)对其进行参数降维和信息优化后,构建支持向量机(support vector machine, SVM)分类器预测6种车辆振动状态:极差、恶化、合格、中等、良好、优秀. 柴晓冬等[13-14]将模拟或实测的多项不平顺参数作为输入,采用多体动力学模型仿真得到响应数据,基于BP或径向基函数(radial basis function,RBF)神经网络来建立车体垂向及横向振动加速度预测模型. 车辆响应除与轨道不平顺、车辆动力学参数、速度密切相关外,还受车辆载荷和悬挂状态等多因素共同影响,基于仿真的数据建模难以全面反映这些情况. 而传统机器学习需要人工确定特征,也难以捕捉车辆-轨道之间复杂的动力学关系,因此所得到的模型性能受限.
深度学习是近10年来蓬勃发展起来的机器学习新方法,在计算机视觉和自然语言处理等领域取得了巨大的成功,推动了人工智能的飞速发展. 深度学习能够自动提取特征,具有较强的非线性建模能力,可以有效提高模型的预测性能. 刘秀波等[15-16]基于长短时记忆网络(long short-term memory networks,LSTM)方法实现了逐点预测车体加速度,然后又结合卷积神经网络(convolutional neural network,CNN)形成CNN-LSTM方法,进一步提高了模型预测性能. 但由于LSTM是一种结构复杂的循环神经网络,训练和推理阶段会比较耗时,并且未考虑车速对模型性能影响,难以适应速度变化较大的情况.
由于不同车型高速综合检测列车动力学传递特性不同,使得不同车型对同一目标轨道状态的评价结果有所区别. 而实际中往往有多种车型服役在同一条高铁线路上,因此,利用单一车型的车体加速度评价轨道状态,其可靠性不足. 针对上述问题,本文提出一种基于多车型预测模型的轨道状态评价方法. 通过建立多车型CNN与门控循环单元(gated recurrent unit,GRU)相结合的车辆响应预测模型,将多项实测轨道不平顺和车速作为输入,输出6种车型的车体垂向和横向加速度预测值,根据多车型车体加速度预测值的最大包络来评价轨道状态,以期为科学评价轨道状态提供一种新的技术手段.
1. CNN-GRU模型建立
1.1 CNN网络
CNN是为处理二维图像数据而研发的一种神经网络,采用局部连接和共享权值的方式[17],直接从原始数据中通过卷积层和池化层交替使用获取有效表征,自动提取数据的局部特征.
针对一维轨道不平顺数据建立了一维CNN网络,如图1所示. 卷积层用于提取轨道不平顺波形特征;最大池化层减小卷积层输出维度大小,用于提取最显著的特征;扁平层将多维特征向量转为一维特征向量,作为全局特征提取. CNN可以有效地自动提取和学习一维轨道不平顺波形特征,这些特征包含在局部轨道不平顺波形中,并与车体加速度相关[16]. 由于轨道不平顺包含多波段成分,因此,通过交替堆叠卷积层和最大池化层,提取到不同尺度的轨道不平顺波形特征.
1.2 GRU网络
轨道不平顺与车体加速度是按照0.25 m等空间间隔采样的序列型数据,适合采用循环神经网络(recurrent neural network,RNN)建模. 传统RNN处理长序列数据时存在梯度消失或梯度爆炸的问题, LSTM较好地解决了这个问题,在时序序列处理中获得广泛应用[18]. 2014年Cho等[19]又提出了GRU,这是LSTM的一种变体,成功应用于语音识别、机器翻译等领域. Chung等[20]对GRU和LSTM作了详细比较,两者基本上具有同等效果,都能解决RNN梯度消失或梯度爆炸问题,但GRU比LSTM更简单,计算和更新效率更高.
GRU单元结构如图2所示,内部的信息传播过程见式(1)~(4). GRU有两个门:更新门
zt 和重置门rt . xt、yt分别为时刻t的输入、输出;ht为时刻t隐藏层状态,来源于时刻t−1隐藏层状态ht−1 和时刻t候选隐藏层状态˜ht ,并由更新门zt 分配重要性;˜ht 由隐藏层状态ht−1 、重置门rt 与输入xt 共同决定;而更新门zt 用来控制当前的状态需要遗忘多少历史信息和接受多少新信息;重置门rt 用来控制候选状态中有多少信息是从历史信息中得到. 通过这种方式,GRU不断吸收新的重要信息并丢弃不相关的信息,以捕获长期依赖关系.ht=(1−zt)⊗ht−1+zt⊗˜ht, (1) ˜ht=tanh(W1xt+W2(rt⊗ht−1)), (2) zt=σ(W3xt+W4ht−1), (3) rt=σ(W5xt+W6ht−1), (4) 式中:
W1 为输入信息权重;W2 为隐藏层权重;W3 为更新门输入信息权重;W4 为隐藏层下更新门权重;W5 为重置门输入信息权重;W6 为隐藏层状态下重置门权重;⊗ 为逐元素相乘;σ(•) 为sigmoid函数.1.3 CNN-GRU网络
相邻空间里程点的轨道不平顺具有时序依赖关系,GRU能够学习到这种依赖关系. 通过建立多个GRU单元,使GRU网络能够学习到轨道不平顺的空间变化趋势. 但轨道不平顺包含多波段成分,GRU难以有效学习到轨道不平顺与车体加速度之间不同波长的复杂关系.
因此,本文将具有学习轨道不平顺多波段波形特征的CNN网络与GRU相结合,建立的CNN-GRU网络结构如图3所示,其中,第1层GRU网络的每个GRU单元接入相同的CNN网络结构.
y(1)t 、y(2)t 分别为第1层、第2层GRU在时刻t 的输出;T为训练序列长度. 对于时刻t轨道不平顺采样点,CNN-GRU的输入是时刻t及之前的采样点总数为L−1的轨道不平顺和车速:x=(xt−L+1,xt−L+2,⋯,xt−1,xt) ,对应的输出ˆyt 为时刻t的车体垂向或横向加速度. 这种输入模式可以使CNN学习到波形特征以及提高CNN-GRU学习长距离空间变化趋势的能力.本文CNN的结构和参数如下:有2层卷积层,卷积核数目依次为4、8,卷积核大小为1 × 5,步长为1,采用零填充. 卷积层的输出采用relu(•)激活函数来增加网络的非线性表达能力. 在池化层中,采用与卷积层交替的2层最大池化,池大小为2,步长为2,通过卷积层中的特征映射使用最大池化来提取最显著特征和减小输出维度大小. 经过连续2次交替卷积和最大池化操作,提取出显著的轨道不平顺特征. 最后一层最大池化的输出采用扁平层操作,其作用是将CNN提取到的多维特征向量压成一维特征向量,作为全局特征提取.
GRU负责学习轨道不平顺中的时序特征并预测车体加速度. 为增强特征学习能力,如图2所示,构建了2层GRU,神经元个数依次为64、128个,采用tanh(•)激活函数. GRU之后是全连接层,全连接层使用线性激活函数,最终恒等变化输出预测的车体加速度.
在前向和反向传播中,CNN-GRU网络采用均方误差损失值,如式(15)所示.
l=1TT∑t=1lt=1TT∑t=1(yt,t−ˆyt,t)2, (5) 式中:lt为时刻t的均方误差损失值;
yt,t 、ˆyt,t 分别为时刻t车体加速度训练序列的真实值、预测值.CNN-GRU模型训练使用Adam优化算法[20],是一种计算每个参数的自适应学习率方法.
2. CNN-GRU超参数选择
2.1 模型评估指标
采用平均绝对误差
EMAE (mean absolute error,MAE)、均方根误差ERMSE (root mean square error,RMSE)、希尔不等系数UTIC 和相关系数ρ作为CNN-GRU评估指标[16],各指标的定义如下:EMAE=1KK∑k=1|ym,k−ˆym,k|, (6) ERMSE=√1KK∑k=1(ym,k−ˆym,k)2, (7) UTIC=√1KK∑k=1(ym,k−ˆym,k)2√1KK∑k=1y2m,k+√1KK∑k=1ˆy2m,k, (8) ρ=cov(ym,ˆym)√var(ym)√var(ˆym), (9) 式中:
ym,k 和ˆym,k 分别为时刻t第k个车体加速度测试序列的实测值和预测值;K为测试数据容量;ym=(ym,1,ym,2,⋯,ym,k,⋯,ym,K) ;ˆym=(ˆym,1,ˆym,2,⋯,ˆym,k,⋯,ˆym,K) .EMAE 和ERMSE 反映了模型预测的绝对准确度,值越小,准确度越高;UTIC 和ρ为相对准确度指标,UTIC 在0和1之间,其值越接近0,模型预测准确度越高;ρ在 −1和1之间,其值越接近1,模型预测准确度越高.2.2 模型超参数
以某高速铁路长300 km的动态检测数据为分析对象,其中,200 km作为训练集,100 km作为测试集,检测速度基本保持在280~310 km/h. 采用控制变量法调节超参数,探讨输入组合、CNN超参数、输入长度L、序列长度T、GRU深度的影响.
1) 输入组合
本文探讨了7组输入组合方式,模型评估指标如表1所示. 表中:高低(或长波高低)是指左、右轨高低不平顺(或长波高低不平顺)的平均值;轨向(或长波轨向)指左、右轨轨向不平顺(或长波轨向不平顺)的平均值;垂加、横加分别指垂向加速度、横向加速度. 对比表1第 ① 组~第 ⑥ 组看出:第 ⑥ 组的模型性能达到最佳效果;第 ⑥ 组相比于第 ① 组而言,对于车体垂向加速度的预测,
EMAE 、ERMSE 、UTIC 和ρ分别提升13%、12%、13%和5%;对于车体横向加速度的预测,上述4个指标性能分别提升36%、34%、36%和25%. 每一项轨道不平顺指标都会对车辆响应产生不同程度的贡献,因此,各项轨道不平顺共同激励下模型性能得以提升,车体横向加速度预测精度的提升效果更为显著.表 1 轨道不平顺输入组合的CNN-GRU评价指标Table 1. CNN-GRU evaluation index of track irregularity input combination组号 输入 加速度 EMAE/
(m·s−2)ERMSE/
(m·s−2)UTIC ρ ① 车速 + 长波高低 + 长波轨向 垂向 0.078 0.098 0.291 0.839 横向 0.053 0.067 0.404 0.701 ② ① + 高低 + 轨向 垂向 0.074 0.093 0.274 0.858 横向 0.049 0.062 0.389 0.737 ③ ② + 水平 垂向 0.069 0.087 0.259 0.875 横向 0.040 0.051 0.294 0.855 ④ ③ + 三角坑 垂向 0.070 0.088 0.257 0.875 横向 0.041 0.053 0.312 0.831 ⑤ ④ + 超高 垂向 0.070 0.088 0.262 0.872 横向 0.038 0.049 0.279 0.847 ⑥ ⑤ + 轨距 垂向 0.068 0.086 0.253 0.880 横向 0.034 0.044 0.256 0.879 ⑦ ⑥ (去除车速) 垂向 0.071 0.089 0.264 0.869 横向 0.038 0.049 0.289 0.848 此外,车速与车体的振动幅度密切相关,车速越大,车辆动力学响应越剧烈. 表1中第 ⑥ 组和第 ⑦ 组分别为轨道不平顺组合输入时有、无速度输入下的CNN-GRU评价指标. 可以看出:有速度输入时的性能明显优于没有速度输入的;对于车体垂向加速度的预测,
EMAE 、ERMSE 、UTIC 和ρ分别提升了4%、3%、4%和1%;对于车体横向加速度的预测,上述4个指标分别提升了12%、11%、13%和4%,可见对车体横向加速度预测精度的提升效果更为显著. 因此,为了更准确模拟列车变速运行情况,本文加入速度特征,将其与轨道不平顺组合作为模型输入. 通过比较,最终确定CNN-GRU的输入特征为第 ⑥ 组:车速和8项轨道不平顺组合.2) CNN超参数
CNN的深度为2层,非线性激活函数为Relu,卷积核大小为1 × 5,池化层为最大池化.
3) 输入长度L
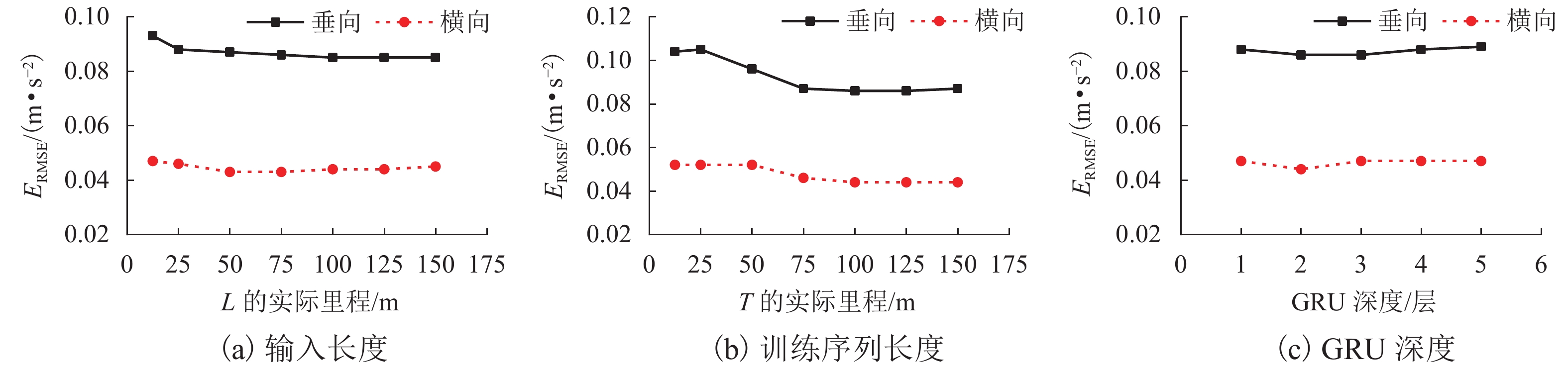
以
ERMSE 为评估指标,探讨输入长度L对CNN-GRU预测性能的影响. L不可过长或过短. L过长,会引入过多无关信息和弱化模型对中短波的学习;L过短,模型难以有效学习到轨道不平顺长波信息. 数据采样间隔为0.25 m,共模拟了7种不同的L,换算成实际里程长度分别为12.5、25.0、50.0、75.0、100.0、125.0、150.0 m,ERMSE 结果如图4(a).当L的实际里程长度大于50.0 m时,L对模型性能的影响较小. 动检车检测轨道不平顺的最大截止波长为120.0 m,因此,选取L的实际里程长度为120.0 m,对应L = 480.4) 序列长度T
模拟了7种不同的序列长度T,换算成实际里程长度分别为12.5、25.0、50.0、75.0、100.0、125.0、150.0 m,
ERMSE 结果如图4(b). 当T的实际里程长度不大于75.0 m时,误差较大;当实际里程长度为100.0~150.0 m时,误差较小. T取值不宜过大或过小,T过大有可能造成GRU远距离记忆丢失. T的实际里程长度宜取75.0~100.0 m[15-16],本文通过实验取T的实际里程长度为100.0 m,对应T = 400.5) GRU深度
堆叠多层GRU有利于学习更抽象的序列数据特征,本文对比了1~5层GRU对CNN-GRU性能的影响,
ERMSE 结果如图4(c). 随着GRU深度的加深,CNN-GRU性能呈现先变好后变差的趋势,其中GRU深度为2时误差最小. 因此,本文堆叠2层GRU.3. 多车型CNN-GRU模型评价轨道状态
3.1 评价方法
本文提出基于多种车型预测模型的轨道状态评价方法,具体评价过程如下:
1) 获取不同车型动检车检测的轨道不平顺和车体加速度数据.
2) 基于GRU学习轨道不平顺的时序特征,并结合具有波形特征学习能力和自适应滤波功能的CNN,建立CNN-GRU车辆响应预测模型. 该模型以轨道不平顺和车速为输入,以车体垂向和横向振动加速度为输出.
3) 基于不同车型动检车的轨道不平顺和车体加速度数据,利用CNN-GRU建立多车型模型.
4) 以同一段目标轨道不平顺的数据为输入,利用多车型CNN-GRU模型生成多组车体加速度波形.
5) 对生成的多组车体加速度波形进行最大包络拟合,分别对车体垂向和横向加速度峰值评价.
3.2 检测数据的预处理
以6列动检车为建模分析对象,各车型的训练集和测试集如表2所示. 使用的高铁动态检测数据涵盖如下车速:200、250、300、350 km/h. 考虑到轨道不平顺管理波长最大到120.0 m,并且轨距、超高、车体横向加速度等容易出现波长120.0 m以上的低频成分,容易影响CNN-GRU对轨道不平顺与车体加速度的正常关系表征,因此,对实测数据剔除波长120.0 m以上的趋势项. 动检车检测轨道不平顺的最小截止波长为1.5 m,为了对轨道不平顺评判时尽可能考虑到短波长成分,将下截止波长取为2.0 m.
表 2 不同车型的训练集和测试集里程Table 2. Kilometrages of training set and test set for various track inspection vehicleskm 序号 车型 训练集总里程 测试集总里程 1 CRH2A-2010 400 (上行) 200 (上行) 2 CRH2C-2150 840 (上行) 200 (下行) 3 CRH380BJ-A-0504 400 (上行) 210 (上行) 4 CRH5J-0501 400 (下行) 100 (下行) 5 CRH380AJ-0201 940 (上行) 200 (上行) 6 CRH380BJ-0301 200 (下行) 100 (上行) 本文使用小波分析技术Mallat分解与重构算法滤除波长2.0 m以下和120.0 m以上的成分[21]. 轨道不平顺和车体加速度采样间隔为0.25 m,对应空间频率为4 m−1,要剔除波长120.0 m以上的成分,需将小波分解到第8层,小波分解层及对应的波长区段见表3.
表 3 小波分解层及波长范围Table 3. Wavelet decomposition layer and wavelength range小波层 D1 D2 D3 D4 D5 D6 D7 D8 A8 波长范围/m (0.5, 1.0] (1.0, 2.0] (2.0, 4.0] (4.0, 8.0] (8.0, 16.0] (16.0, 32.0] (32.0, 64.0] (64.0, 128.0] >128.0 3.3 各车型CNN-GRU模型评估与验证
本文对每一种车型的CNN-GRU模型进行评估,以便确定各车型CNN-GRU模型的实际性能,同时建立各车型的BP神经网络、GRU与CNN-GRU对比. BP结构由输入层、双隐藏层和输出层组成,每层节点数与GRU保持一致. 通过3种建模方法得到的各车型预测模型评估指标结果见表4.
表 4 多车型的不同模型评估指标对比Table 4. Comparison of the evaluation index of different models for multi-vehicle模型 车型 加速度 EMAE/
(m·s−2)ERMSE/
(m·s−2)UTIC ρ BP CRH2A-2010 垂向 0.113 0.152 0.692 0.214 横向 0.059 0.078 0.698 0.233 CRH2C-2150 垂向 0.118 0.151 0.716 0.343 横向 0.054 0.071 0.693 0.345 CRH380BJ-A-0504 垂向 0.064 0.081 0.618 0.468 横向 0.060 0.064 0.752 0.161 CRH5J-0501 垂向 0.051 0.066 0.633 0.440 横向 0.055 0.071 0.855 0.223 CRH380AJ-0201 垂向 0.116 0.148 0.739 0.434 横向 0.045 0.059 0.893 0.139 CRH380BJ-0301 垂向 0.070 0.091 0.682 0.339 横向 0.060 0.081 0.780 0.104 GRU CRH2A-2010 垂向 0.065 0.086 0.317 0.820 横向 0.041 0.056 0.396 0.711 CRH2C-2150 垂向 0.083 0.106 0.366 0.753 横向 0.045 0.061 0.485 0.600 CRH380BJ-A-0504 垂向 0.055 0.070 0.413 0.670 横向 0.037 0.048 0.346 0.782 CRH5J-0501 垂向 0.041 0.052 0.413 0.701 横向 0.054 0.071 0.620 0.333 CRH380AJ-0201 垂向 0.069 0.088 0.296 0.841 横向 0.043 0.056 0.611 0.383 CRH380BJ-0301 垂向 0.056 0.074 0.420 0.667 横向 0.053 0.071 0.543 0.491 CNN-GRU CRH2A-2010 垂向 0.050 0.065 0.227 0.902 横向 0.044 0.059 0.426 0.671 CRH2C-2150 垂向 0.079 0.100 0.337 0.789 横向 0.046 0.061 0.443 0.621 CRH380BJ-A-0504 垂向 0.054 0.068 0.408 0.691 横向 0.037 0.048 0.350 0.784 CRH5J-0501 垂向 0.041 0.052 0.391 0.714 横向 0.060 0.078 0.631 0.243 CRH380AJ-0201 垂向 0.058 0.074 0.245 0.888 横向 0.041 0.053 0.547 0.479 CRH380BJ-0301 垂向 0.056 0.073 0.398 0.693 横向 0.062 0.080 0.545 0.416 分别将同一方法建模的6种不同车型各项评估指标求平均数,GRU相比于BP神经网络而言,对于车体垂向加速度的预测,
EMAE 、ERMSE 、UTIC 和ρ分别提升30%、30%、45%和99%;对于车体横向加速度的预测,上述4个指标性能分别提升18%、14%、36%和174%. CNN-GRU相比于BP神经网络而言,对于车体垂向加速度的预测,上述4个指标性能分别提升36%、37%、51%和109%;对于车体横向加速度的预测,4个指标性能分别提升13%、11%、37%和167%. GRU和CNN-GRU各项评估指标均明显优于BP神经网络. BP神经网络的性能相对较差,这是因为BP神经网络不具有反馈连接,从而使相邻的数据之间彼此独立,忽略了动态检测数据前后的空间依赖关系.CNN-GRU相比于GRU而言,对于车体垂向加速度的预测,CNN-GRU模型的各个指标性能表现均更优;对于车体横向加速度的预测,虽然GRU和CNN-GRU各项指标各有优劣,但CNN-GRU的指标总体上比GRU好.
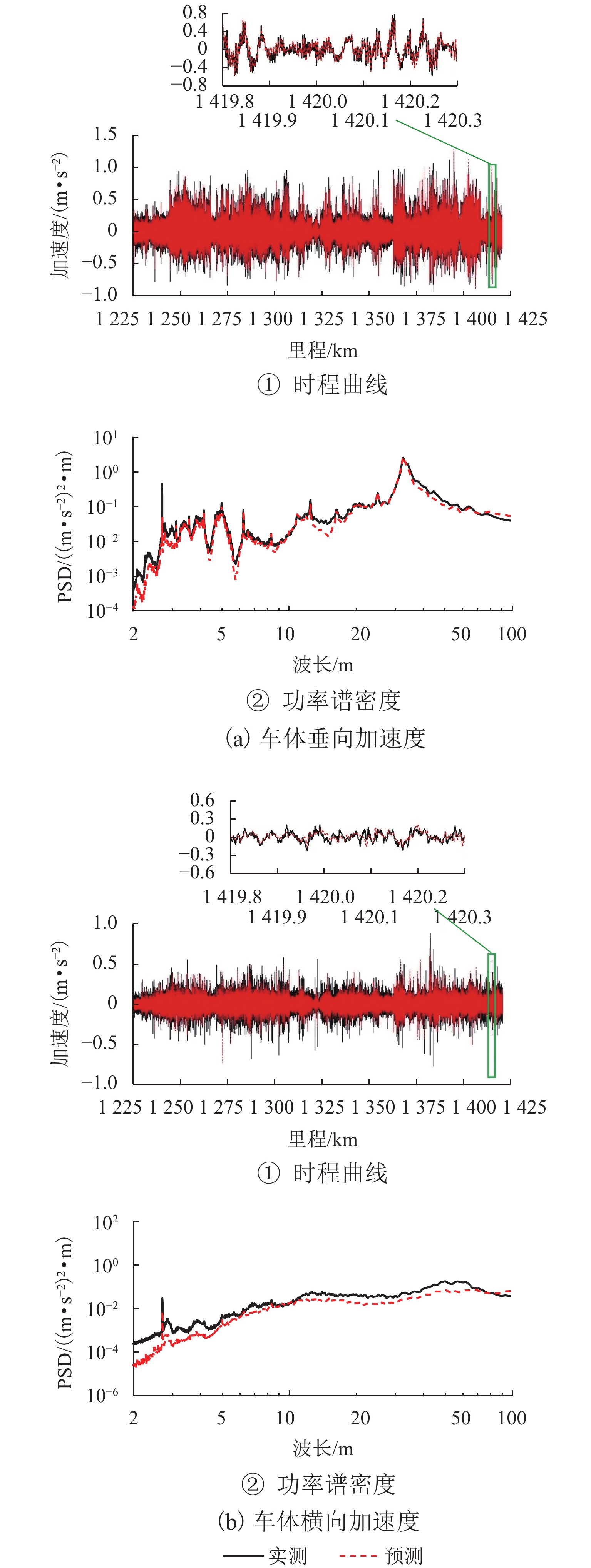
为进一步直观评估CNN-GRU模型的预测效果,限于篇幅,仅绘制出CRH2A-2010模型的预测结果,预测和实测的车体加速度及其功率谱(PSD)图5所示.
由图5可以看出:CNN-GRU预测的车体加速度波形与实测加速度波形的相关度较高,预测波形基本能反映出真实加速度波形的幅度和变化趋势;预测值和实测值在各个波段的功率谱幅值和变化趋势重合性较好,说明模型能够较为准确预测车体加速度随机性成分. 此外,预测值和实测值在由梁长为32.6 m的简支梁和周长为2.7 m的车轮一阶不圆等引起的车体加速度谱峰幅值基本吻合,表明模型能够有效预测周期性的车体垂向和横向振动响应. 综上可得,CNN-GRU能较好预测出轨道不平顺激励下的车体随机性振动和周期性振动响应成分.
3.4 基于多车型预测模型的轨道状态评价效果
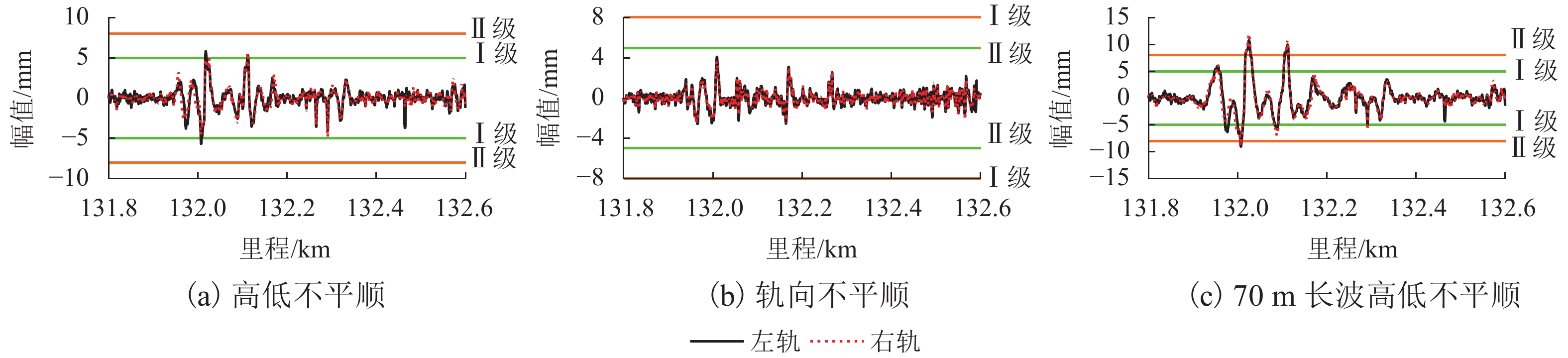
以某高速铁路实测轨道不平顺数据作为输入,其中,高低不平顺、轨向不平顺和70 m长波高低不平顺如图6所示. 该区段为路桥过渡段,由于降雨致使轨道不平顺迅速劣化,高低不平顺最大值为5.84 mm,到Ⅰ级超限;轨向不平顺最大值为4.11 mm,未超限;70 m长波高低不平顺最大值为11.97 mm,达到Ⅱ级超限.
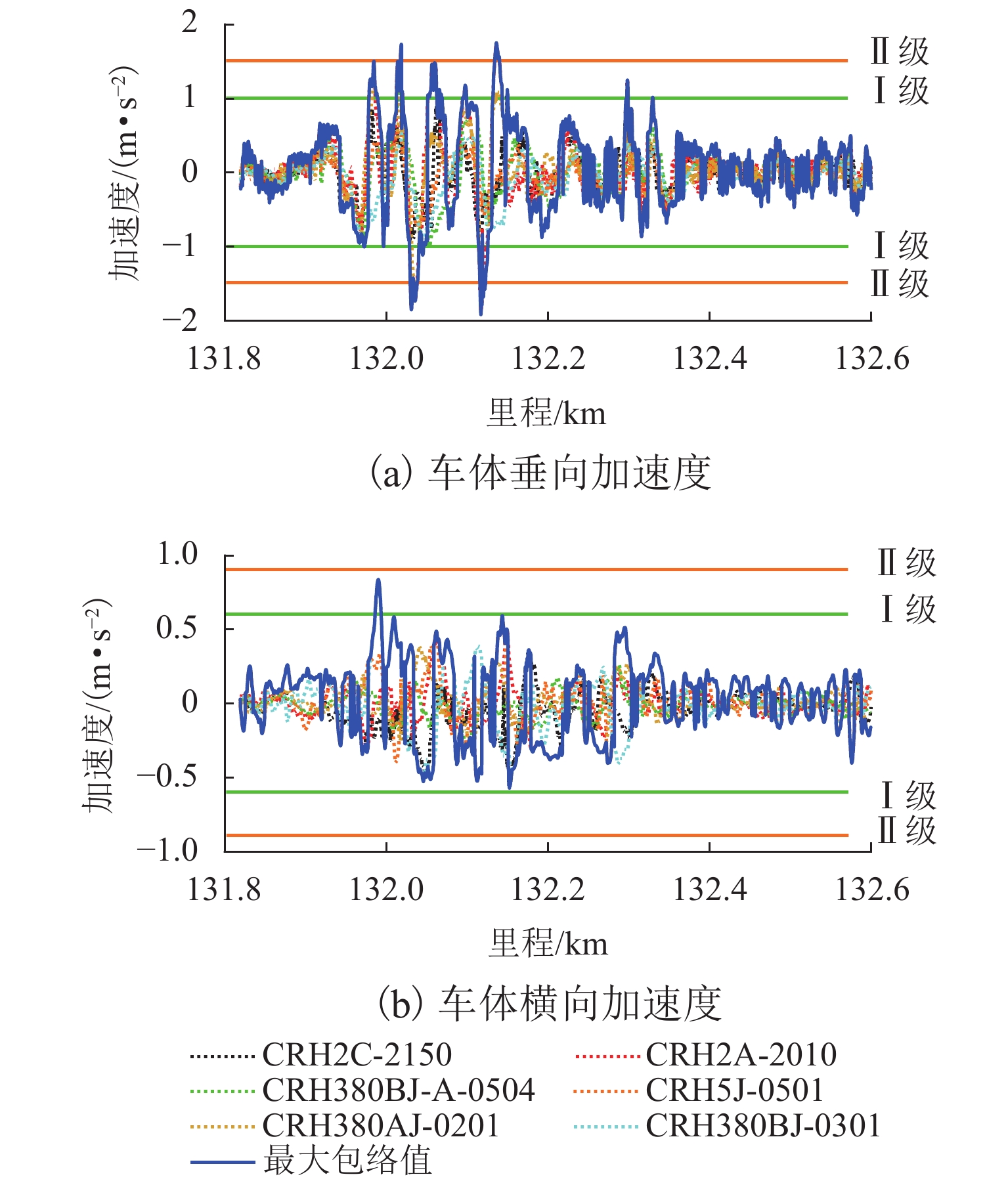
利用建好的6种车型CNN-GRU模型预测出6个车体加速度时域波形;然后,对这6个加速度波形取最大包络值,结果如图7所示;最后,对最大包络值进行车体加速度的峰值评判,得到各车型模型预测的车体加速度最大幅值及偏差等级见表5.
表 5 各车型预测的加速度最大幅度值及偏差等级Table 5. Maximum amplitude value and deviation level of the acceleration predicted by each track inspection vehicle车型 垂向加速度/
(m·s−2)横向加速度/
(m·s−2)最大值 超限等级 最大值 超限等级 CRH2A-2150 1.12 Ⅰ 0.57 未超限 CRH2C-2010 1.92 Ⅱ 0.53 未超限 CRH380BJ-A-0504 1.22 Ⅰ 0.30 未超限 CRH5J-0501 0.73 未超限 0.59 未超限 CRH380AJ-0201 1.58 Ⅱ 0.40 未超限 CRH380BJ-0301 0.98 未超限 0.84 Ⅰ 由表5得出,仅采用单车型CNN-GRU模型预测,不同车型的动检车预测出的车体加速度响应评价结果并不完全一致,但都在K131 + 900—K132 +200区段内响应较大. 对于车体垂向加速度而言,多车模型中CRH2C-2150、CRH2A-2010、CRH380BJ-0504、CRH380AJ-0201这4个车型模型预测到车体垂向加速度幅值至少达到Ⅰ级超限. 其中,CRH2A-2010车体垂向加速度响应最大,其峰值为1.92 m/s2,到Ⅱ级超限. CRH5J-0501和CRH380BJ-0301模型在该处车体垂向加速度虽有较大响应,但没有超限. 对于车体横向加速度而言,除了CRH380BJ-A-0504模型预测的车体横向加速度仅为0.30 m/s2外,其余5个车型预测的车体横向加速度幅值更大,其中,CRH380BJ-0301模型预测的车体横向加速度最大为0.84 m/s2,达到Ⅰ级超限.
采用多车型CNN-GRU模型预测得到多车型车体加速度最大包络值,结果显示该区段车体垂向加速度最大幅值为1.92 m/s2,达到Ⅱ级超限;车体横向加速度最大幅值为0.84 m/s2,达到Ⅰ级超限. 现场复核发现,存在超限的区段为路桥过渡段,由于降雨导致高低和轨向不平顺急剧增加,车载晃车仪垂向加速度报警,铁路工务人员添乘明显感觉列车不舒适,这与基于多车型CNN-GRU模型的预测结果一致,现场安排捣固作业.
综合来看,不同车型对同一轨道不平顺的响应有所区别,导致不同的单车型CNN-GRU模型预测的车体加速度结果也不相同. 但通过最大包络值将各组结果结合起来的基于多车型CNN-GRU预测模型可以提高舒适性评价和轨道状态评判的准确性,比单车模型更及时、更可靠,保证线路的及时维修.
4. 结 论
1) 各项轨道不平顺和车速都与车体加速度有不同程度的关联,从而对CNN-GRU预测模型的性能产生影响. 将高低、轨向不平顺等8项轨道不平顺和车速共同作为输入参数,使各项车体垂向和横向加速度预测的评估指标分别提升了5%~13%和25%~36%. 输入参数车速的引入使各项车体垂向和横向加速度预测的评估指标分别提升了1%~4%和4%~12%.
2) CNN-GRU相比于BP神经网络而言,各项车体垂向和横向加速度预测的评估指标分别提升了36%~109%和11%~167%,其性能明显优于BP神经网络和GRU.
3) 从预测的时域波形看,CNN-GRU预测的车体加速度幅值和变化趋势与实测结果很接近,相关系数最大达到0.902;从预测波形功率谱看,CNN-GRU能较好地反映出车体随机性振动和周期性振动特征.
4) 针对某轨道几何状态不良区段应用效果显示,预测6种车型中有4种车型达到车体垂向加速度Ⅰ级或Ⅱ级超限,有1种车型达到车体横向加速度Ⅰ级超限. 通过多车型CNN-GRU预测模型综合评判,提高了轨道状态评价的准确性和一致性.
致谢:中国铁道科学研究院集团有限公司科技研究开发计划(2021YJ022)的支持.
-
表 1 轨道不平顺输入组合的CNN-GRU评价指标
Table 1. CNN-GRU evaluation index of track irregularity input combination
组号 输入 加速度 EMAE/
(m·s−2)ERMSE/
(m·s−2)UTIC ρ ① 车速 + 长波高低 + 长波轨向 垂向 0.078 0.098 0.291 0.839 横向 0.053 0.067 0.404 0.701 ② ① + 高低 + 轨向 垂向 0.074 0.093 0.274 0.858 横向 0.049 0.062 0.389 0.737 ③ ② + 水平 垂向 0.069 0.087 0.259 0.875 横向 0.040 0.051 0.294 0.855 ④ ③ + 三角坑 垂向 0.070 0.088 0.257 0.875 横向 0.041 0.053 0.312 0.831 ⑤ ④ + 超高 垂向 0.070 0.088 0.262 0.872 横向 0.038 0.049 0.279 0.847 ⑥ ⑤ + 轨距 垂向 0.068 0.086 0.253 0.880 横向 0.034 0.044 0.256 0.879 ⑦ ⑥ (去除车速) 垂向 0.071 0.089 0.264 0.869 横向 0.038 0.049 0.289 0.848 表 2 不同车型的训练集和测试集里程
Table 2. Kilometrages of training set and test set for various track inspection vehicles
km 序号 车型 训练集总里程 测试集总里程 1 CRH2A-2010 400 (上行) 200 (上行) 2 CRH2C-2150 840 (上行) 200 (下行) 3 CRH380BJ-A-0504 400 (上行) 210 (上行) 4 CRH5J-0501 400 (下行) 100 (下行) 5 CRH380AJ-0201 940 (上行) 200 (上行) 6 CRH380BJ-0301 200 (下行) 100 (上行) 表 3 小波分解层及波长范围
Table 3. Wavelet decomposition layer and wavelength range
小波层 D1 D2 D3 D4 D5 D6 D7 D8 A8 波长范围/m (0.5, 1.0] (1.0, 2.0] (2.0, 4.0] (4.0, 8.0] (8.0, 16.0] (16.0, 32.0] (32.0, 64.0] (64.0, 128.0] >128.0 表 4 多车型的不同模型评估指标对比
Table 4. Comparison of the evaluation index of different models for multi-vehicle
模型 车型 加速度 EMAE/
(m·s−2)ERMSE/
(m·s−2)UTIC ρ BP CRH2A-2010 垂向 0.113 0.152 0.692 0.214 横向 0.059 0.078 0.698 0.233 CRH2C-2150 垂向 0.118 0.151 0.716 0.343 横向 0.054 0.071 0.693 0.345 CRH380BJ-A-0504 垂向 0.064 0.081 0.618 0.468 横向 0.060 0.064 0.752 0.161 CRH5J-0501 垂向 0.051 0.066 0.633 0.440 横向 0.055 0.071 0.855 0.223 CRH380AJ-0201 垂向 0.116 0.148 0.739 0.434 横向 0.045 0.059 0.893 0.139 CRH380BJ-0301 垂向 0.070 0.091 0.682 0.339 横向 0.060 0.081 0.780 0.104 GRU CRH2A-2010 垂向 0.065 0.086 0.317 0.820 横向 0.041 0.056 0.396 0.711 CRH2C-2150 垂向 0.083 0.106 0.366 0.753 横向 0.045 0.061 0.485 0.600 CRH380BJ-A-0504 垂向 0.055 0.070 0.413 0.670 横向 0.037 0.048 0.346 0.782 CRH5J-0501 垂向 0.041 0.052 0.413 0.701 横向 0.054 0.071 0.620 0.333 CRH380AJ-0201 垂向 0.069 0.088 0.296 0.841 横向 0.043 0.056 0.611 0.383 CRH380BJ-0301 垂向 0.056 0.074 0.420 0.667 横向 0.053 0.071 0.543 0.491 CNN-GRU CRH2A-2010 垂向 0.050 0.065 0.227 0.902 横向 0.044 0.059 0.426 0.671 CRH2C-2150 垂向 0.079 0.100 0.337 0.789 横向 0.046 0.061 0.443 0.621 CRH380BJ-A-0504 垂向 0.054 0.068 0.408 0.691 横向 0.037 0.048 0.350 0.784 CRH5J-0501 垂向 0.041 0.052 0.391 0.714 横向 0.060 0.078 0.631 0.243 CRH380AJ-0201 垂向 0.058 0.074 0.245 0.888 横向 0.041 0.053 0.547 0.479 CRH380BJ-0301 垂向 0.056 0.073 0.398 0.693 横向 0.062 0.080 0.545 0.416 表 5 各车型预测的加速度最大幅度值及偏差等级
Table 5. Maximum amplitude value and deviation level of the acceleration predicted by each track inspection vehicle
车型 垂向加速度/
(m·s−2)横向加速度/
(m·s−2)最大值 超限等级 最大值 超限等级 CRH2A-2150 1.12 Ⅰ 0.57 未超限 CRH2C-2010 1.92 Ⅱ 0.53 未超限 CRH380BJ-A-0504 1.22 Ⅰ 0.30 未超限 CRH5J-0501 0.73 未超限 0.59 未超限 CRH380AJ-0201 1.58 Ⅱ 0.40 未超限 CRH380BJ-0301 0.98 未超限 0.84 Ⅰ -
[1] 刘金朝,刘秀波. 轨道质量状态评价方法[J]. 铁路技术创新,2012(1): 106-109. doi: 10.19550/j.issn.1672-061x.2012.01.030 [2] 关庆华,赵鑫,温泽峰,等. 基于Hertz接触理论的法向接触刚度计算方法[J]. 西南交通大学学报,2021,56(4): 883-890.GUAN Qinghua, ZHAO Xin, WEN Zefeng, et al. Calculation method of hertz normal contact stiffness[J]. Journal of Southwest Jiaotong University, 2021, 56(4): 883-890. [3] LUBER B. Railway track quality assessment method based on vehicle system identification[J]. e & i Elektrotechnik und Informationstechnik, 2009, 126(5): 180-185. [4] LUBER B, HAIGERMOSER A, GRABNER G. Track geometry evaluation method based on vehicle response prediction[J]. Vehicle System Dynamics, 2010, 48(S1): 157-173. [5] FURUKAWA A, YOSHIMURA A. A method to predict track geometry-induced vertical vehicle motion[J]. Quarterly Report of RTRI, 2004, 45(3): 142-148. doi: 10.2219/rtriqr.45.142 [6] FURUKAWA A. A method to predict vertical vehicle motion caused by track irregularities[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2017, 231(4): 431-443. doi: 10.1177/0954409716634394 [7] LI M X D, BERGGREN E G, BERG M, et al. Assessing track geometry quality based on wavelength spectra and track-vehicle dynamic interaction[J]. Vehicle System Dynamics, 2008, 46(S1): 261-276. [8] BERGGREN E G, LI M X D, SPÄNNAR J. A new approach to the analysis and presentation of vertical track geometry quality and rail roughness[J]. Wear, 2008, 265(9/10): 1488-1496. [9] LI M X D, BERGGREN E G, BERG M. Assessment of vertical track geometry quality based on simulations of dynamic track-vehicle interaction[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(2): 131-139. doi: 10.1243/09544097JRRT220 [10] WANG J K, HE Y L, LU H Y, et al. Study on vibration acceleration prediction model of track inspection vehicle based on BP neural network[J]. IOP Conference Series: Materials Science and Engineering, 2018, 435: 012041.1-012041.8. [11] LI D, MEDDAH A, HASS K, et al. Relating track geometry to vehicle performance using neural network approach[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2006, 220(3): 273-281. doi: 10.1243/09544097JRRT39 [12] 徐磊,陈宪麦. 轨道不平顺作用下铁路列车车体振动状态的PCA-SVM预测分析[J]. 铁道学报,2014,36(7): 16-23. doi: 10.3969/j.issn.1001-8360.2014.07.003XU Lei, CHEN Xianmai. PCA-SVM forecast of car-body vibration states of railway locomotives and vehicles under the action of track irregularities[J]. Journal of the China Railway Society, 2014, 36(7): 16-23. doi: 10.3969/j.issn.1001-8360.2014.07.003 [13] 耿松,柴晓冬,郑树彬. 基于递阶神经网络的轨道车辆振动状态预测[J]. 城市轨道交通研究,2015,18(12): 94-98. doi: 10.16037/j.1007-869x.2015.12.021GENG Song, CHAI Xiaodong, ZHENG Shubin. Prediction of rail transit vehicle vibration state based on hierarchical neural network[J]. Urban Mass Transit, 2015, 18(12): 94-98. doi: 10.16037/j.1007-869x.2015.12.021 [14] 李立明,柴晓冬,郑树彬. 基于径向基函数神经网络的轨道交通车辆振动状态预测[J]. 城市轨道交通研究,2017,20(12): 18-21. doi: 10.16037/j.1007-869x.2017.12.005LI Liming, CHAI Xiaodong, ZHENG Shubin. Prediction of rail vehicle vibration state based on radial basis function nerve network[J]. Urban Mass Transit, 2017, 20(12): 18-21. doi: 10.16037/j.1007-869x.2017.12.005 [15] 刘秀波, 马帅, 高利民, 等. 基于轨道几何和LSTM的车辆响应预测模型[C]//第十三届全国振动理论及应用学术会议. 西安: 中国振动工程学会, 2019: 15-21. [16] MA S, GAO L, LIU X B, et al. Deep learning for track quality evaluation of high-speed railway based on vehicle-body vibration prediction[J]. IEEE Access, 2019, 7: 185099-185107. doi: 10.1109/ACCESS.2019.2960537 [17] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. doi: 10.1109/5.726791 [18] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. doi: 10.1162/neco.1997.9.8.1735 [19] CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Doha: Association for Computational Linguistics, 2014: 1724-1734 [20] CHUNG J, GULCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL]. (2014-12-11)[2021-11-10]. https://arxiv.org/abs/1412.3555. [21] 康熊,刘秀波,李红艳,等. 高速铁路无砟轨道不平顺谱[J]. 中国科学(技术科学),2014,44(7): 687-696. doi: 10.1360/N092014-00088KANG Xiong, LIU Xiubo, LI Hongyan, et al. PSD of ballastless track irregularities of high-speed railway[J]. Scientia Sinica (Technologica), 2014, 44(7): 687-696. doi: 10.1360/N092014-00088 -






 下载:
下载:

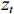
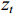
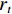
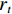

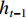
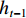
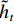
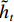


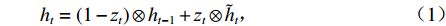
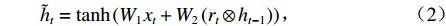
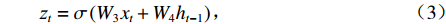
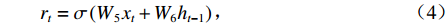
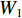

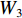
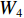




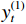
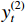
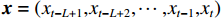
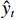

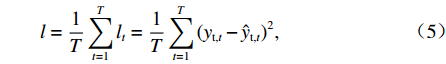
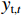



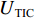


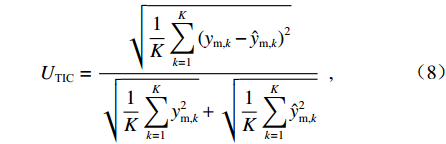
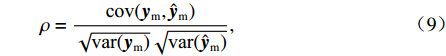
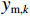
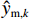

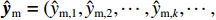

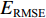
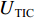
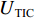
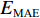

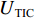

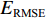
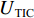

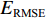

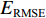








 下载:
下载: