Power Allocation Algorithm in T2T and T2G Hybrid Network
-
摘要:
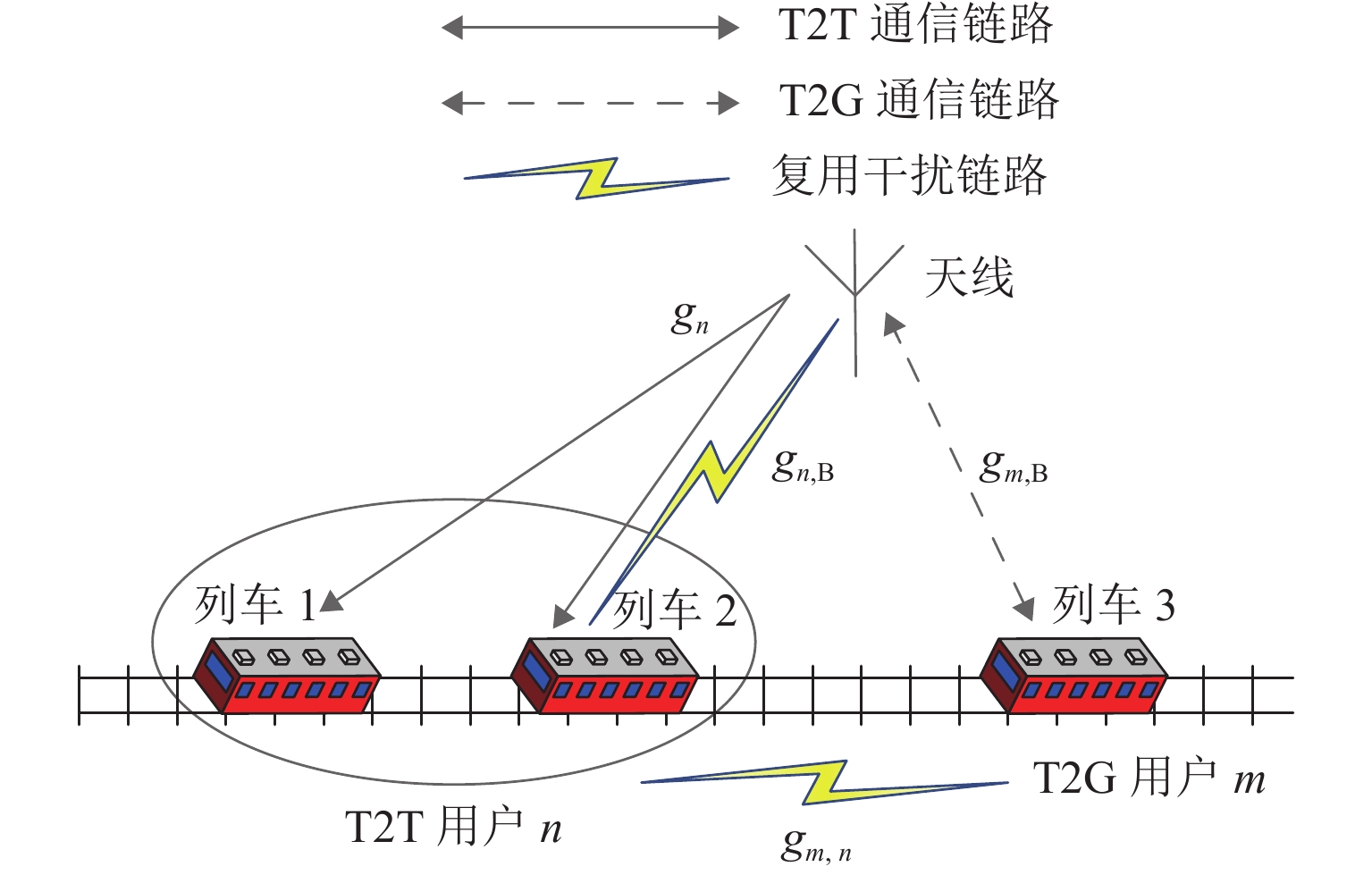
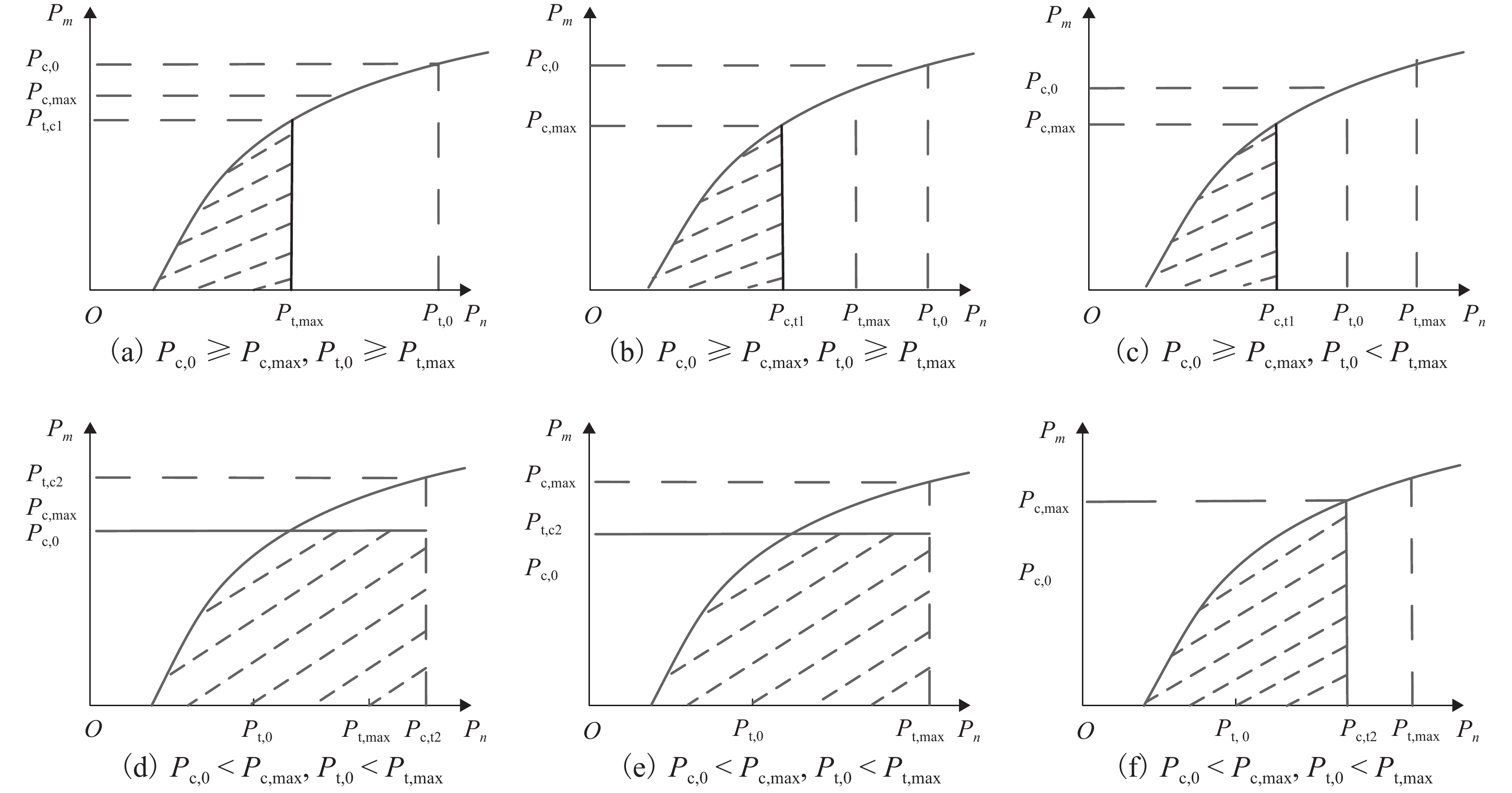
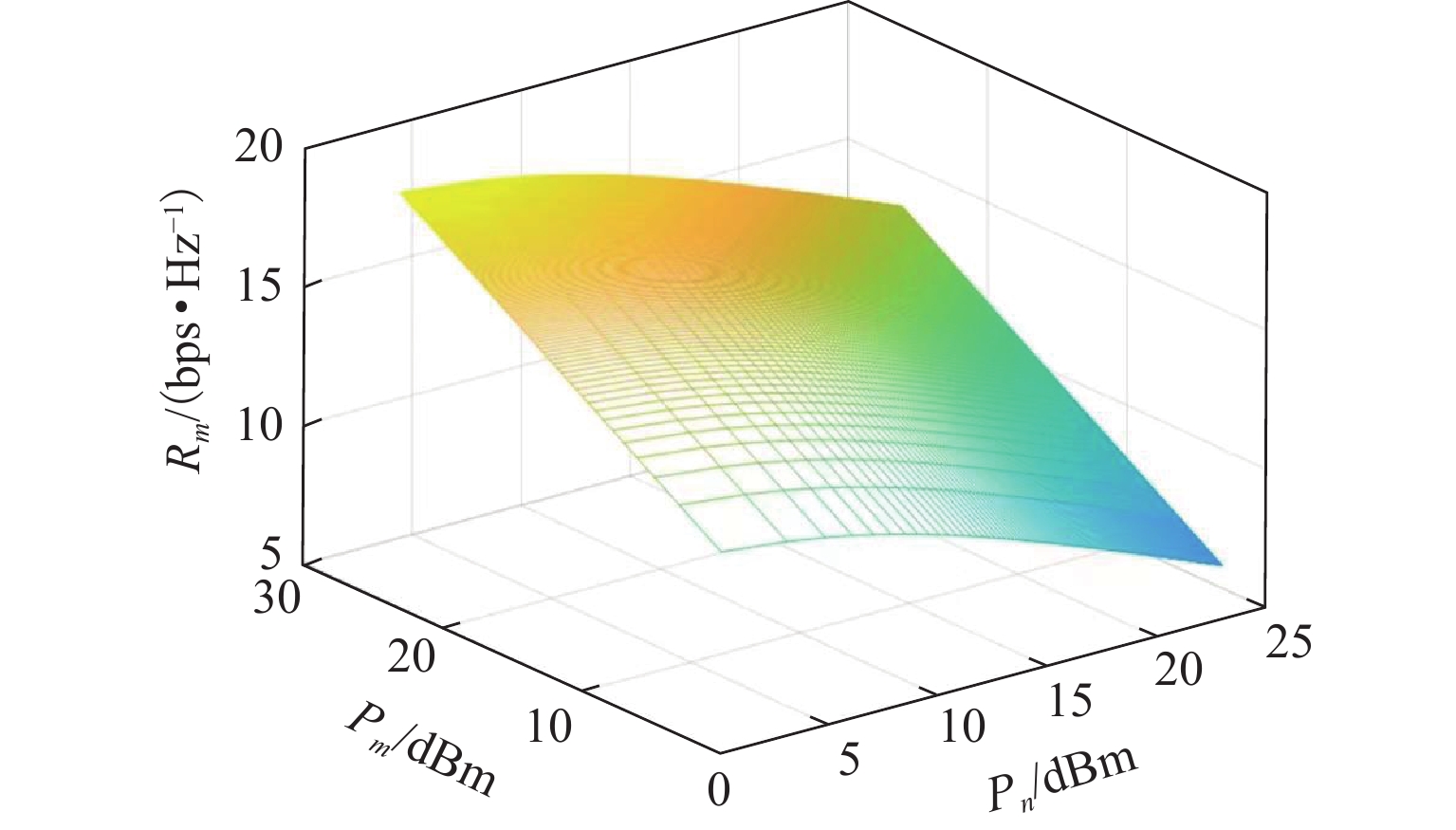
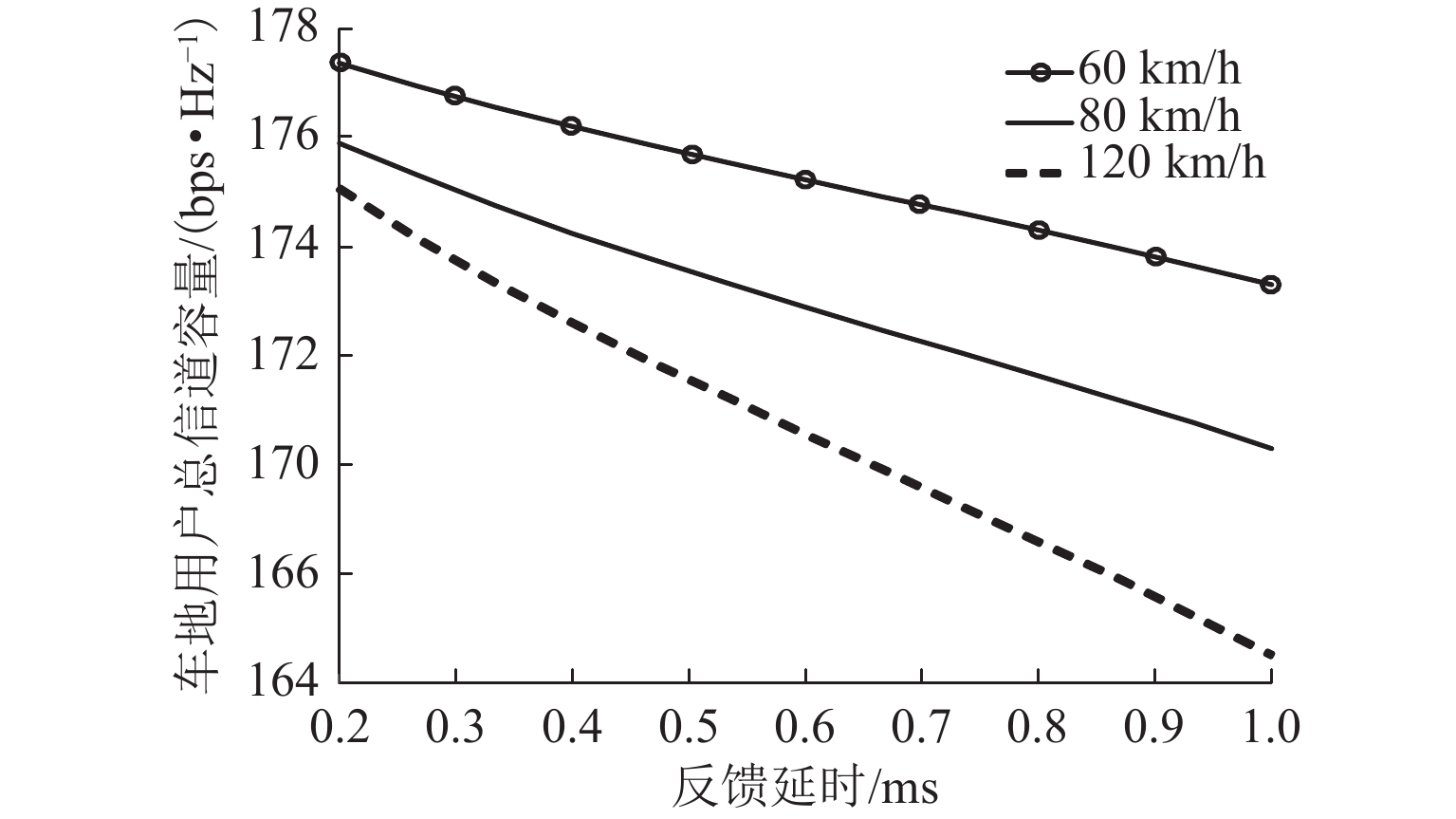
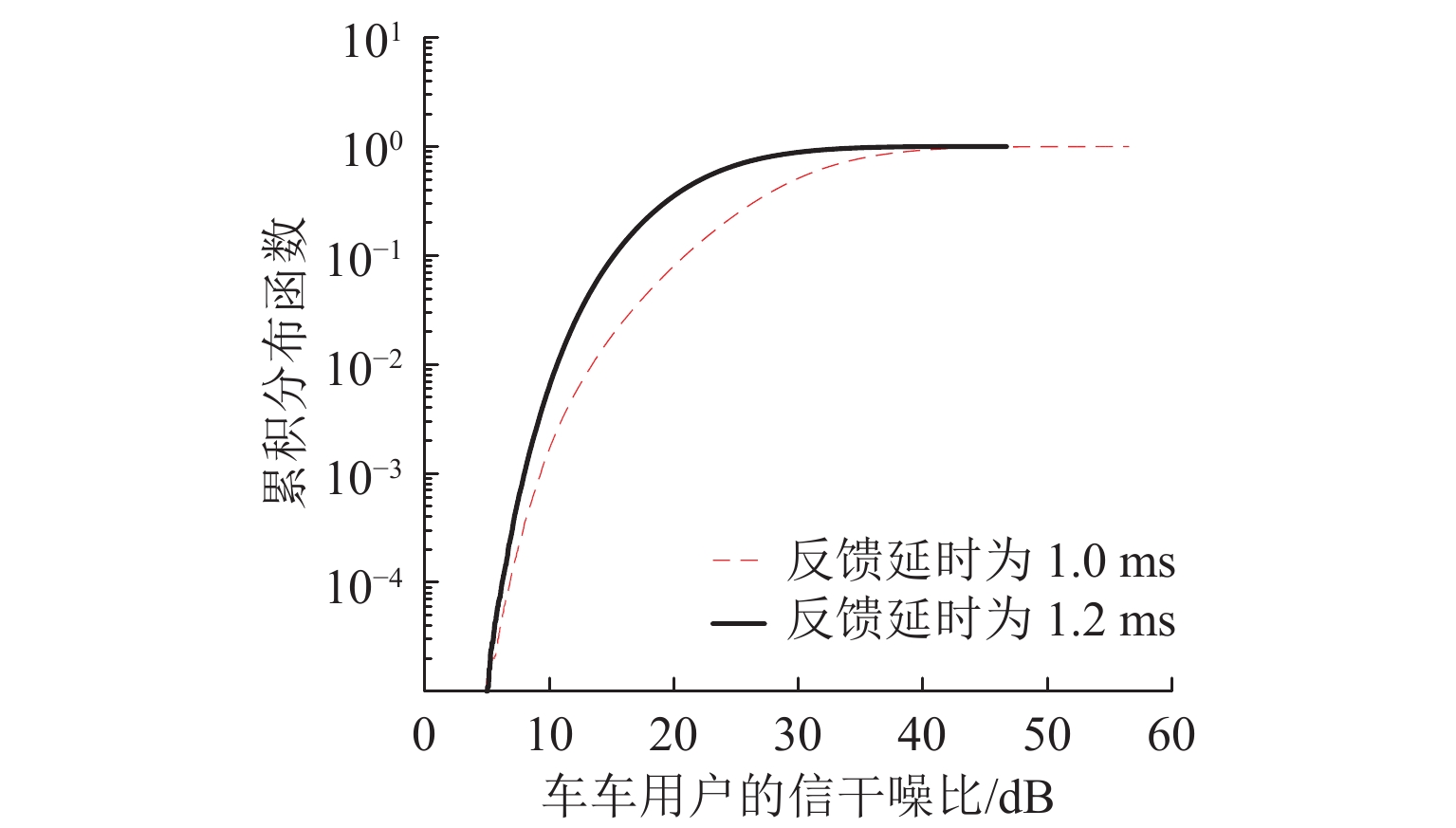
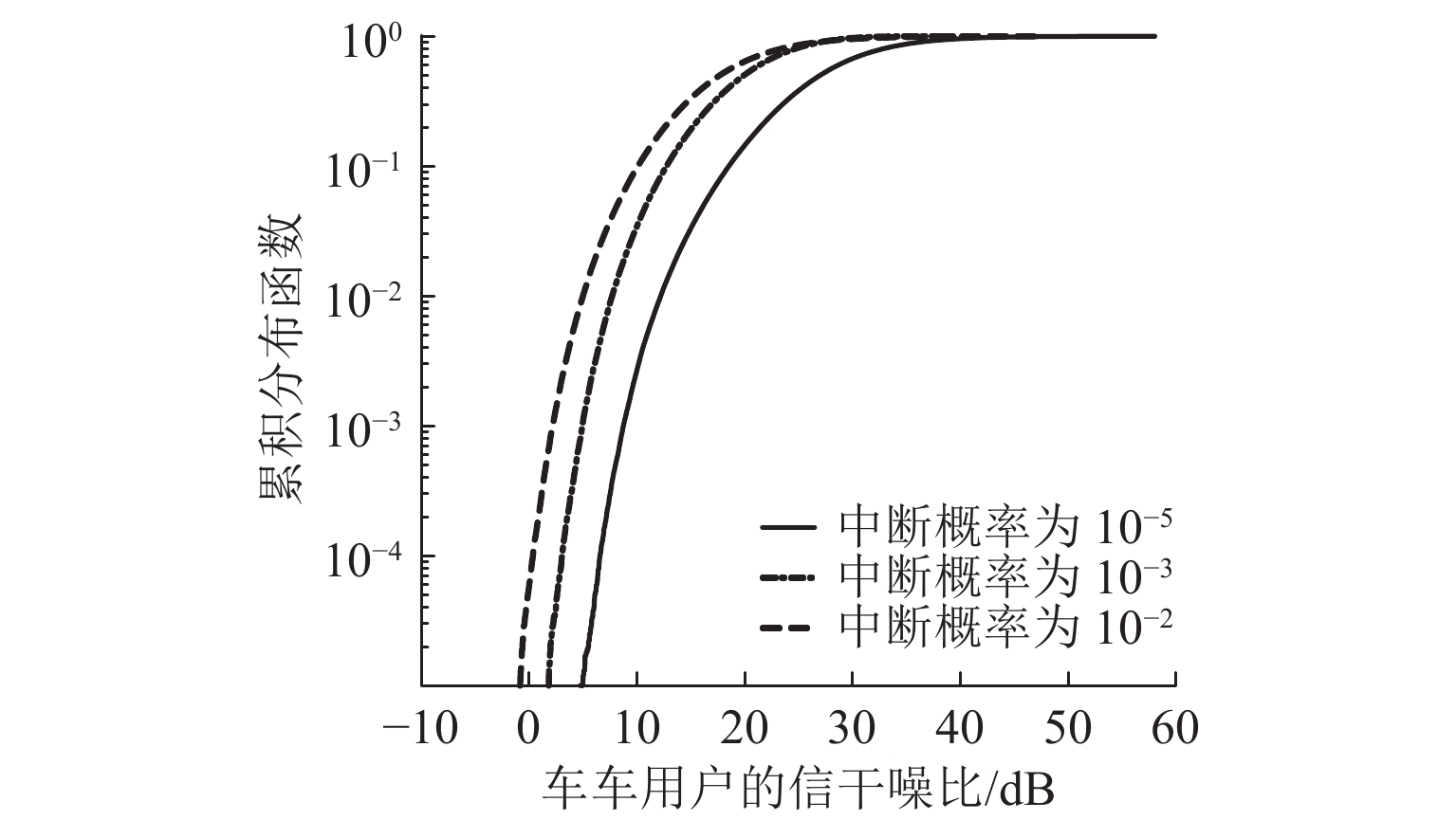
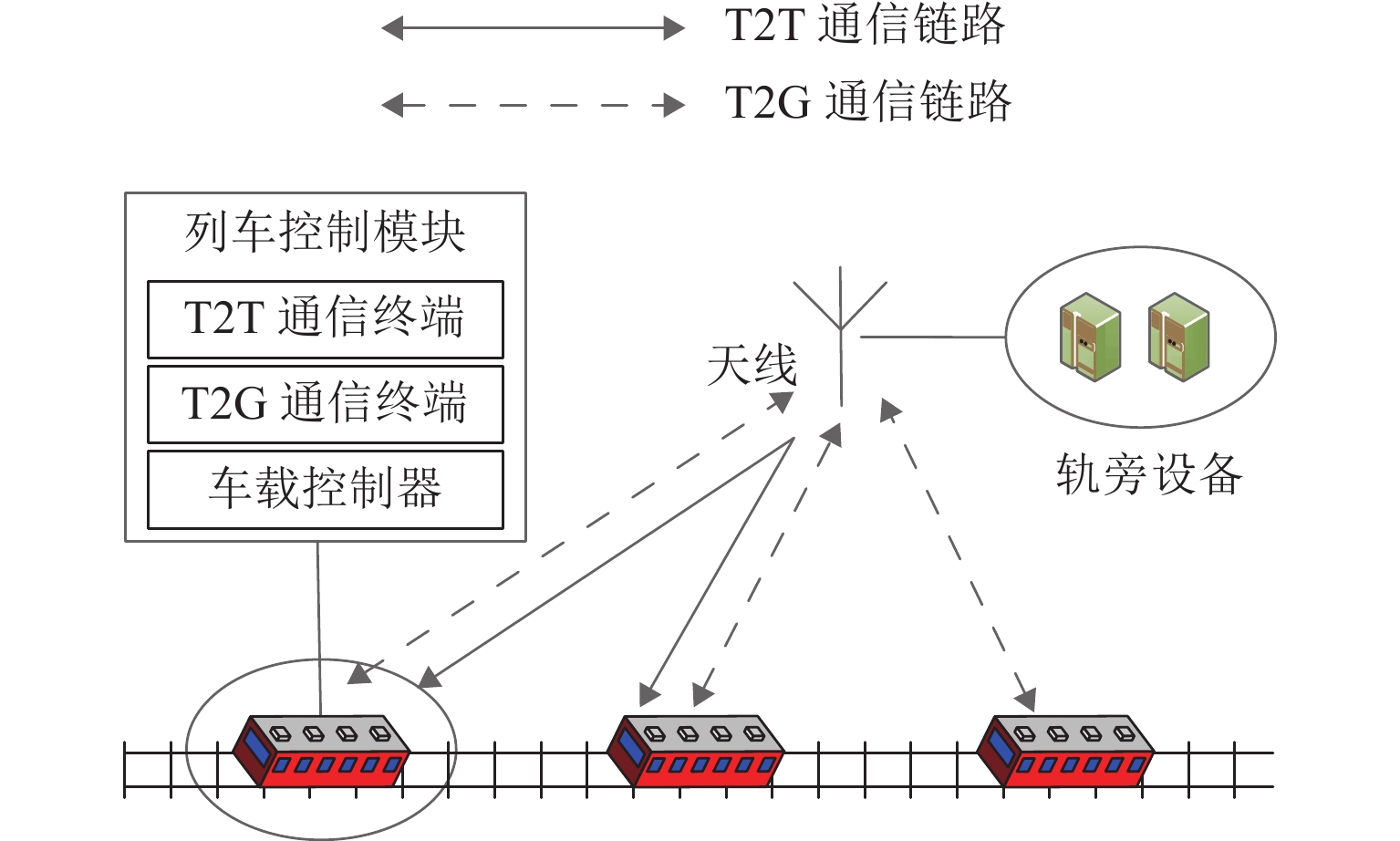
现有功率分配算法大多基于理想信道状态信息(CSI)实现性能优化，在列车对列车(T2T)双移动端通信场景中并不适用. 针对城市轨道交通系统T2T和车地(T2G)混合网络场景，引入CSI反馈延时，研究非理想状态时仍可保障通信质量的功率分配算法. 考虑单蜂窝用户复用单T2T用户对情况，以T2G用户传输速率总和最大化为优化目标，构建多约束条件下的功率分配模型. 首先，根据分步思想将非凸模型简化为最优分配功率计算和最佳复用用户匹配2个子模型；其次，利用线性规划分析可行域内目标函数的最优解及最优值，并通过二分法求解最优分配功率；最后，筛选出可行复用对集合后，利用匈牙利算法进行二分图匹配. 仿真结果表明：该算法兼顾城市轨道交通系统中T2T通信中断概率约束和T2G用户传输速率，且可实现1.0 ms内的CSI反馈延时.
Abstract:Most of power allocation algorithms are based on ideal channel state information (CSI) to achieve performance optimization, which is not applicable in train-to-train (T2T) dual mobile terminal communication. For the hybrid network scenario of T2T and train-to-ground (T2G) in urban rail transit system, the CSI feedback delay is introduced to study the power allocation algorithm that can still guarantee the communication quality under non-ideal conditions. Given the situation that a single T2G user reuse a single T2T user pair, the optimization goal is to maximize the total transmission rate of T2G users, and a power allocation model is constructed under multiple constraints. First, according to a step-by-step concept, the non-convex model is divided into two sub-models of optimal allocated power calculation and optimal multiplexing users matching. Second, the optimal solution and the optimal value of the objective function in the feasible region are analyzed through linear programming, and the optimal distribution power is solved by the dichotomy. Finally, after screening the set of feasible multiplex pairs, the Hungarian algorithm is used for matching. Simulation results show that the proposed algorithm allows for the interruption probability constraint of T2T communication and the total transmission rate of T2G users in the urban rail transit system, and controls CSI feedback delay within 1.0 ms.
-
图 2 城市轨道交通系统T2T和T2G混合网络模型
Figure 2. T2T and T2G hybrid network model for urban rail transit system
图 6 不同反馈延时下T2T用户信干噪比的累积分布函数
Figure 6. CDF of SINR for T2T users in different feedback delays
图 7 不同中断概率下T2T用户信干噪比的累积分布函数
Figure 7. CDF of SINR for T2T users under different outage probabilities
表 1 仿真参数设置
Table 1. Simulation parameter setting
仿真参数 数值 Bf/MHz 10 fc/GHz 2 GB/dBi 8 GT/dBi 3 Pc,max/dBm 23 Pt,max/dBm 23 ε 10−6 $ {\gamma _0} $/dB 5 r0/(bps·Hz−1) 0.5 N0/dBm −114 $ {\xi _{{\text{T2T}}}} $/dB 3 $ {\xi _{{\text{T2G}}}} $/dB 8 
下载: 导出CSV
-
[1] GAO Y B, TIAN Z Y, LI M Q, et al. Channel characteristics analysis of train-to-train wireless communication[J]. Journal of Measurement Science and Instrumentation, 2021, 12(3): 331-339. [2] STRANG T, MEYEIZU H M, GU X. A railway collision avoidance systems exploiting ad-hoc inter-vehicle communications and galileo[C]//13th World Congress on Intelligent Transportation Systems. London: IEEE, 2006: 45-47. [3] CRISTINA R G, ANDREAS L, THOMAS S, et al. Channel model for train communication using the 400 MHz band[C]//IEEE Vehicular Technology Conference. Singapore: IEEE, 2008: 3082-3086 [4] AI B, CHENG X, KURNER T, et al. Challenges towards wireless communications for high speed railway[J]. IEEE Communications Magazine, 2015, 53(10): 62-68. doi: 10.1109/MCOM.2015.7295465 [5] YANG X Z. A multilevel soft frequency reuse technique for wireless communication systems[J]. IEEE Communications Letters, 2014, 18(11): 1983-1986. doi: 10.1109/LCOMM.2014.2361533 [6] 李翠然,杜欣怡,谢健骊. 高铁环境下基于QoS用户业务的公平性功率分配算法[J]. 铁道学报,2020,42(5): 99-104. doi: 10.3969/j.issn.1001-8360.2020.05.013LI Cuiran, DU Xinyi, XIE Jianli. Power control algorithm based on fairness and QoS in high-speed railway scenarios[J]. Journal of the China Railway Society, 2020, 42(5): 99-104. doi: 10.3969/j.issn.1001-8360.2020.05.013 [7] 同钊,李兵兵,惠永涛. 蜂窝与D2D混合网络中的无线资源分配[J]. 北京理工大学学报,2017,37(4): 396-400,429. doi: 10.15918/j.tbit1001-0645.2017.04.013TONG Zhao, LI Bingbing, HUI Yongtao. Radio resource allocation for cellular and device-to-device communication hybrid networks[J]. Transactions of Beijing Institute of Technology, 2017, 37(4): 396-400,429. doi: 10.15918/j.tbit1001-0645.2017.04.013 [8] LI X Q, HE C L, FENG D Q, et al. Power allocation criteria for distributed antenna systems with D2D communication[J]. AEU-International Journal of Electronics and Communications, 2018, 93: 109-115. doi: 10.1016/j.aeue.2018.05.036 [9] 田春生,钱志鸿,阎双叶,等. D2D通信中联合链路共享与功率分配算法研究[J]. 电子学报,2019,47(4): 769-774. doi: 10.3969/j.issn.0372-2112.2019.04.001TIAN Chunsheng, QIAN Zhihong, YAN Shuangye, et al. Research on joint link sharing and power allocation algorithm for device-to-device communications[J]. Acta Electronica Sinica, 2019, 47(4): 769-774. doi: 10.3969/j.issn.0372-2112.2019.04.001 [10] 范康康,董颖,钱志鸿,等. D2D通信的干扰控制和资源分配算法研究[J]. 通信学报,2018,39(11): 198-206. doi: 10.11959/j.issn.1000-436x.2018240FAN Kangkang, DONG Ying, QIAN Zhihong, et al. Research on the interference control and resource allocation in D2D communication[J]. Journal on Communications, 2018, 39(11): 198-206. doi: 10.11959/j.issn.1000-436x.2018240 [11] LIANG L, GEOFFREY Y L, XU W. Meeting different QoS requirements of vehicular networks: a D2D-based approach[C]//2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans: IEEE, 2017: 3734-3738. [12] LIANG L, XIE S J, GEOFFREY Y L, et al. Graph-based radio resourse management for vehicular networks[C]//2018 IEEE International Conference on Commumications. Kansas City: IEEE, 2018: 1-6. [13] LIANG L, LI G Y, XU W. Resource allocation for D2D-enabled vehicular communications[J]. IEEE Transactions on Communications, 2017, 65(7): 3186-3197. doi: 10.1109/TCOMM.2017.2699194 [14] 滕昌敏. 端到端通信在列控系统中应用的研究[D]. 北京: 北京交通大学, 2017. [15] 陈垚,赵军辉,张青苗,等. 车车通信中通信模式选择与资源分配算法[J]. 计算机工程与应用,2022,58(10): 93-100. doi: 10.3778/j.issn.1002-8331.2012-0104CHEN Yao, ZHAO Junhui, ZHANG Qingmiao, et al. Communication mode selection and resource allocation algorithm in vehicle-to-vehicle communication[J]. Computer Engineering and Applications, 2022, 58(10): 93-100. doi: 10.3778/j.issn.1002-8331.2012-0104 [16] KIM T, LOVE D J, CLERCKX B. Does frequent low resolution feedback outperform infrequent high resolution feedback for multiple antenna beamforming systems?[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1654-1669. doi: 10.1109/TSP.2010.2099222 [17] HUSSAIN F, HASSAN M Y, HOSSEN M S, et al. System capacity maximization with efficient resource allocation algorithms in D2D communication[J]. IEEE Access, 2018, 6: 32409-32424. [18] LIANG L, KIM J, JHA S C, et al. Spectrum and power allocation for vehicular communications with delayed CSI feedback[J]. IEEE Wireless Communications Letters, 2017, 6(4): 458-461. doi: 10.1109/LWC.2017.2702747 [19] 张友鹏. 可靠性理论与工程技术应用[M]. 兰州: 兰州大学出版社, 2004. [20] 褚衍东, 常迎香, 张建刚. 数值计算方法[M]. 北京: 科学出版社, 2016. [21] 徐桂贤,马卫国,任余维. 比例公平保证的MIMO-OFDM系统能效资源分配[J]. 北京邮电大学学报,2015,38(4): 68-73. doi: 10.13190/j.jbupt.2015.04.015XU Guixian, MA Weiguo, REN Yuwei. Proportional fairness-guaranteed energy-efficient resource allocation for MIMO-OFDM systems[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(4): 68-73. doi: 10.13190/j.jbupt.2015.04.015 -
下载:
点击查看大图
计量
- 文章访问数: 297
- HTML全文浏览量: 94
- PDF下载量: 12
- 被引次数: 0