Analysis of Generation and Evolution Characteristics of Wheel High-Order Polygonal Wear
-
摘要:
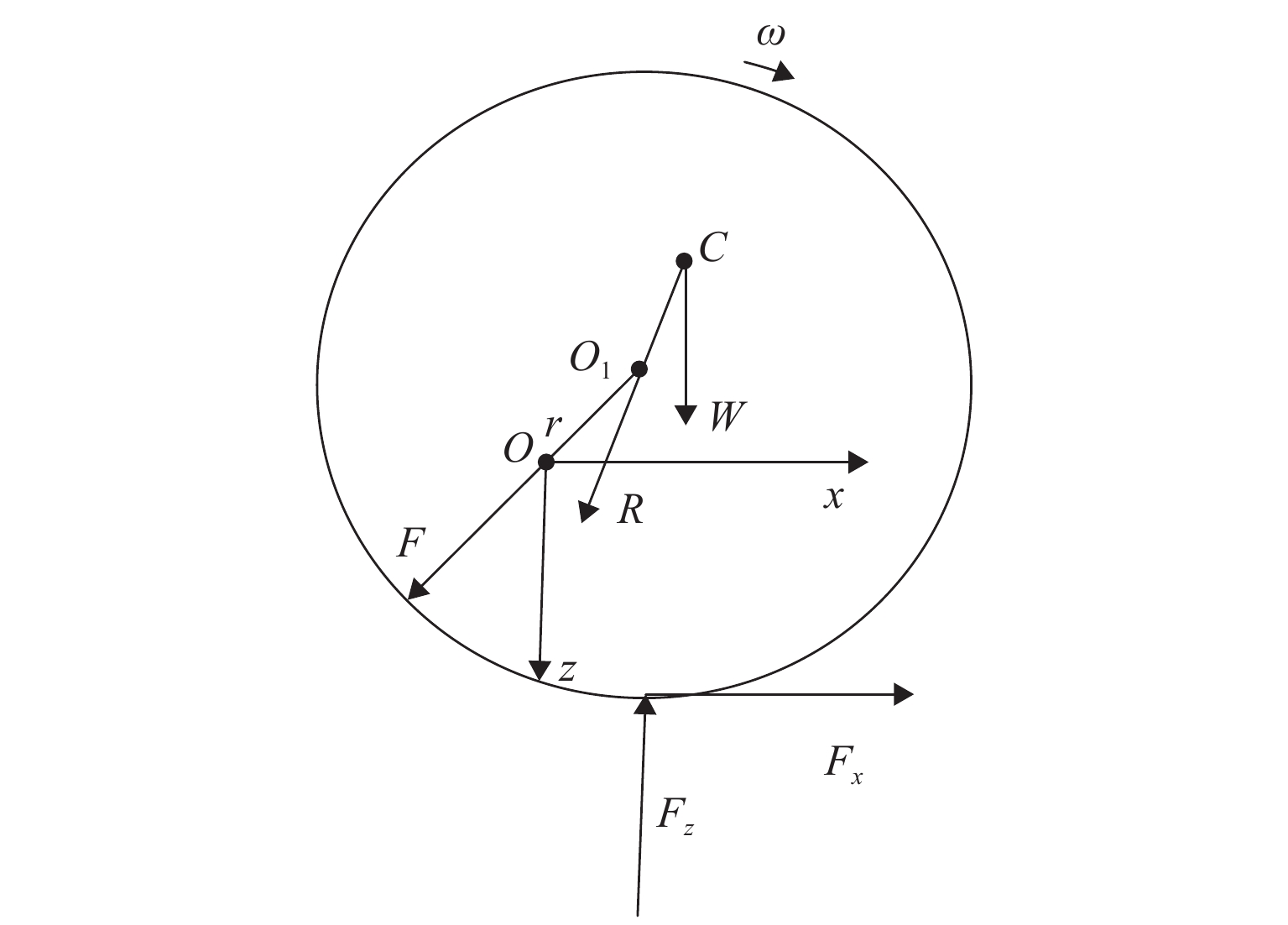
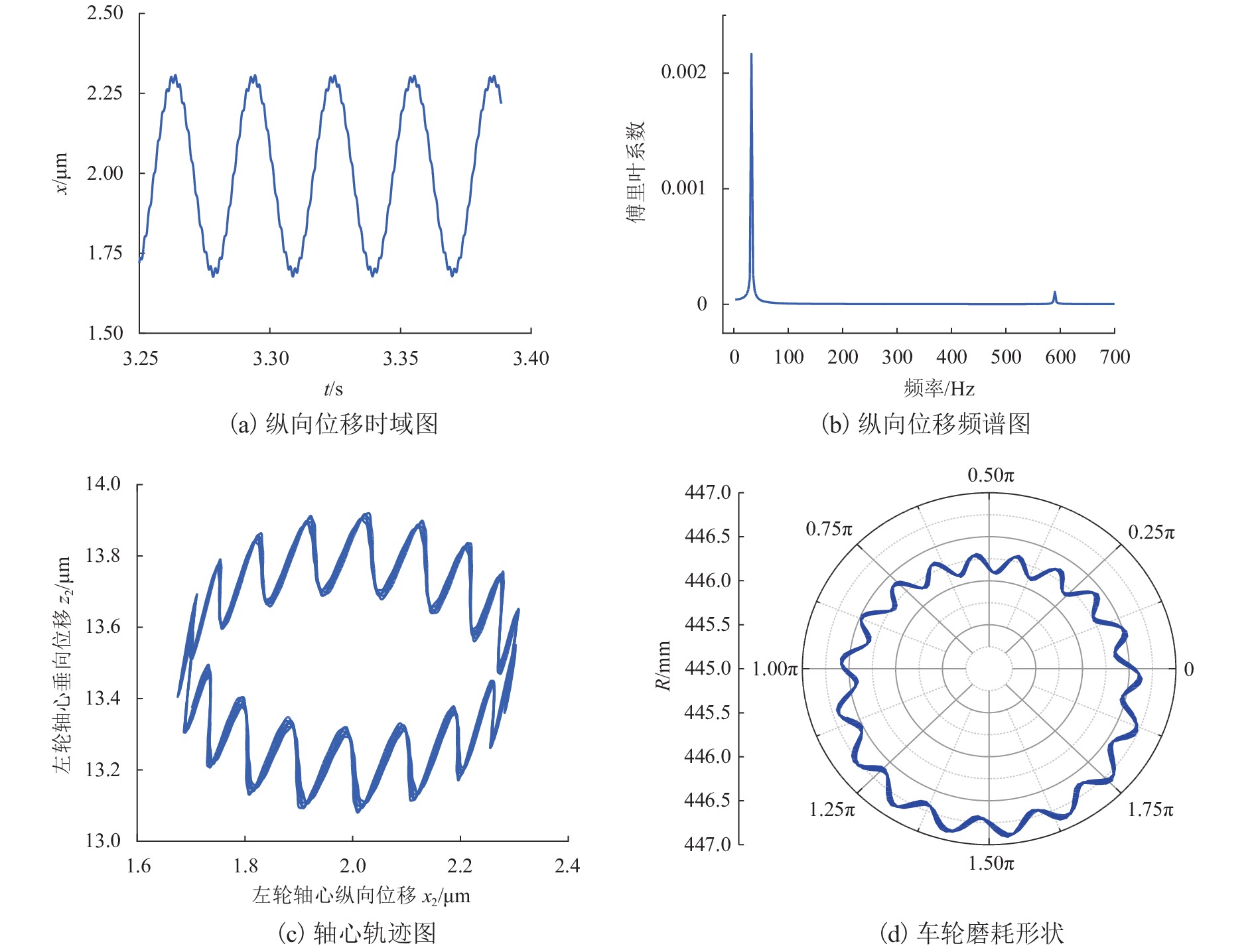
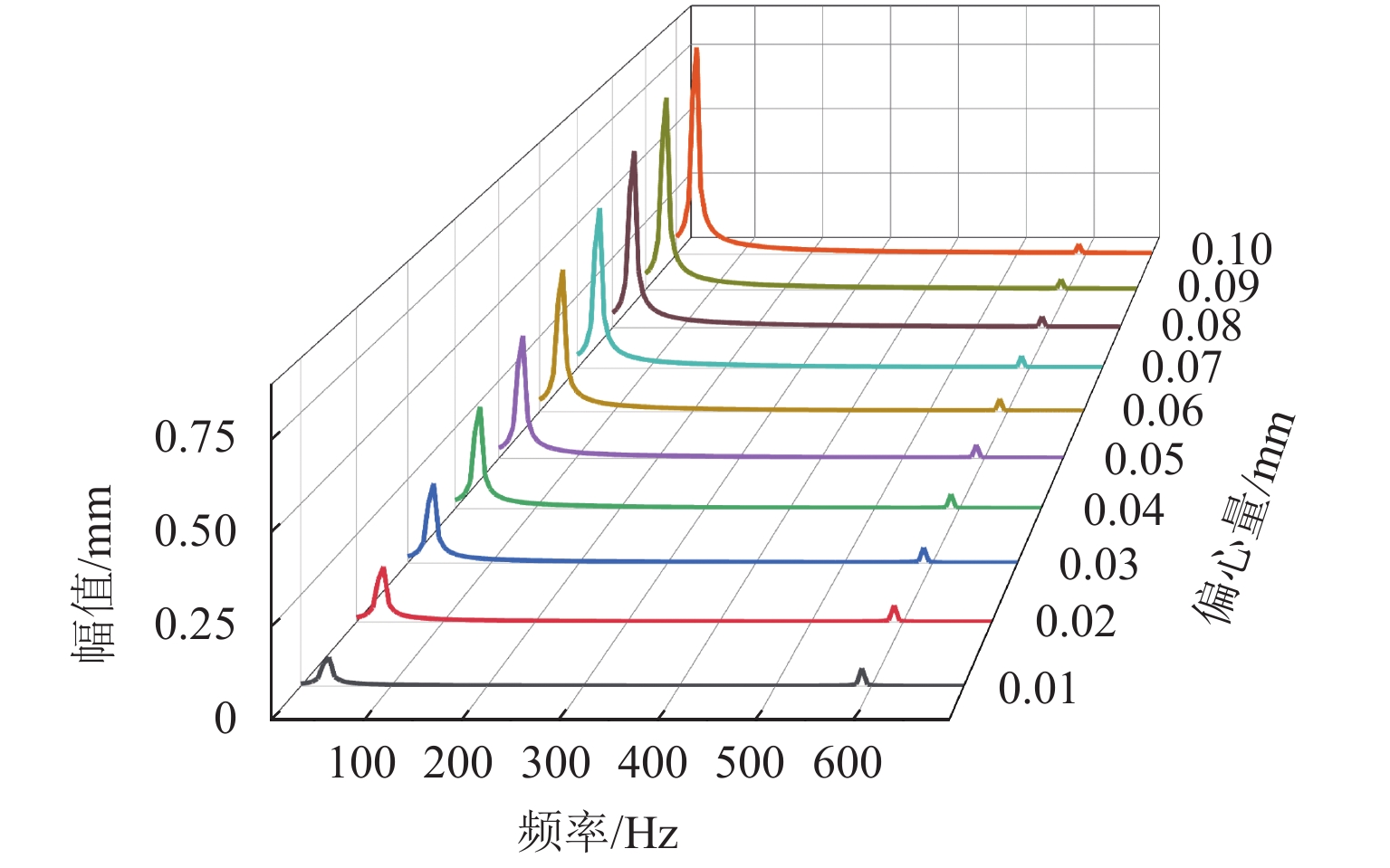
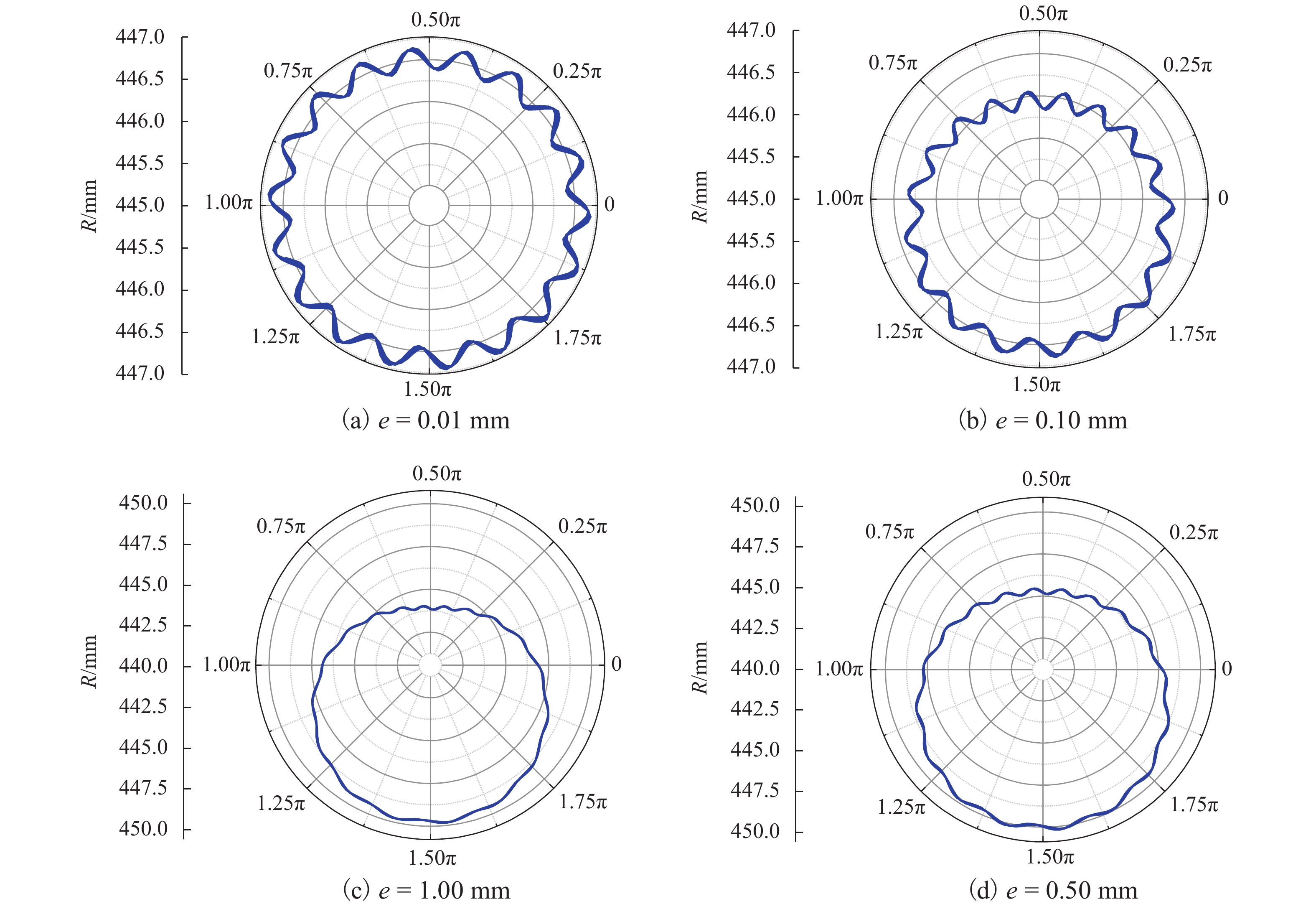
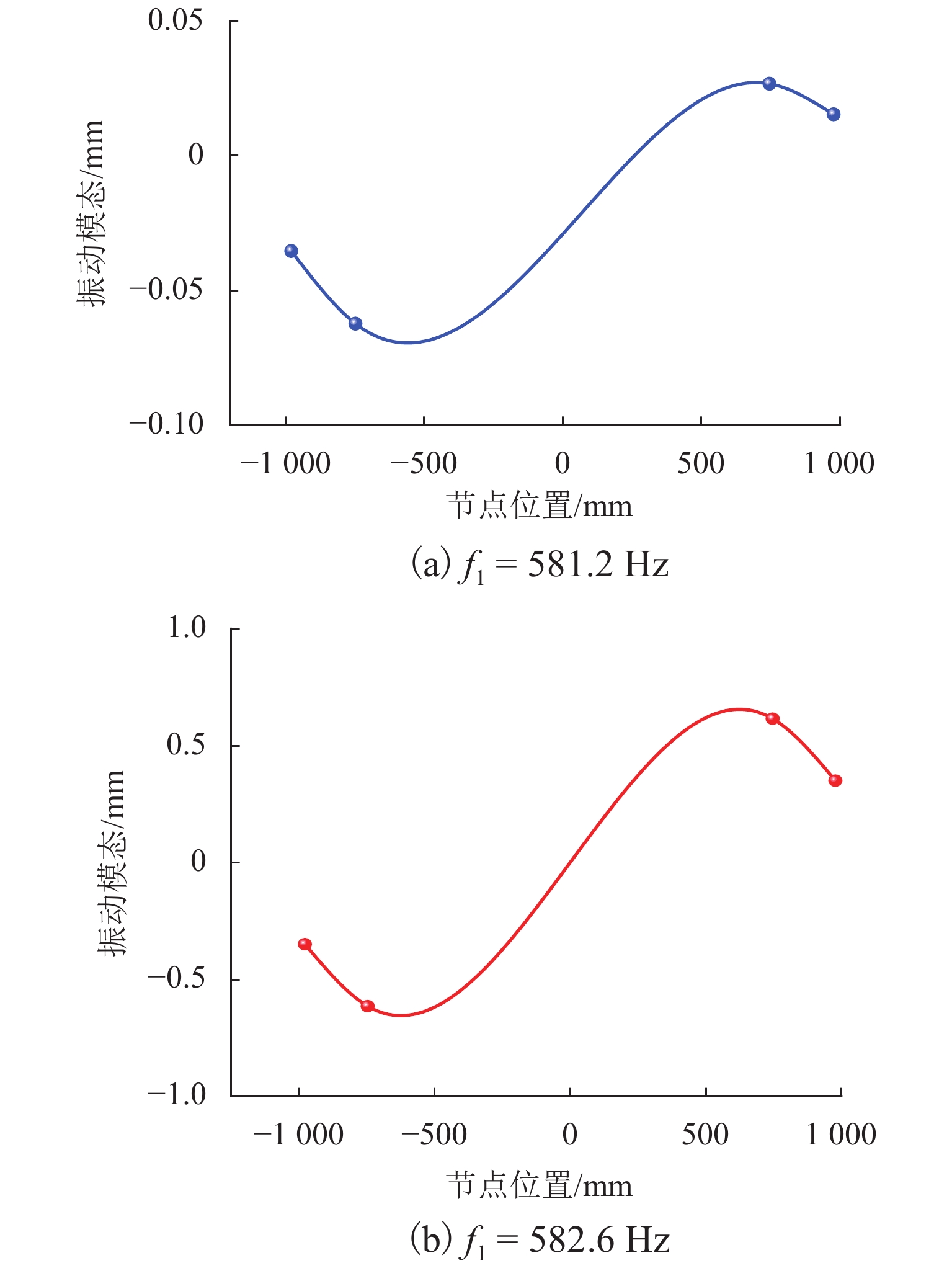
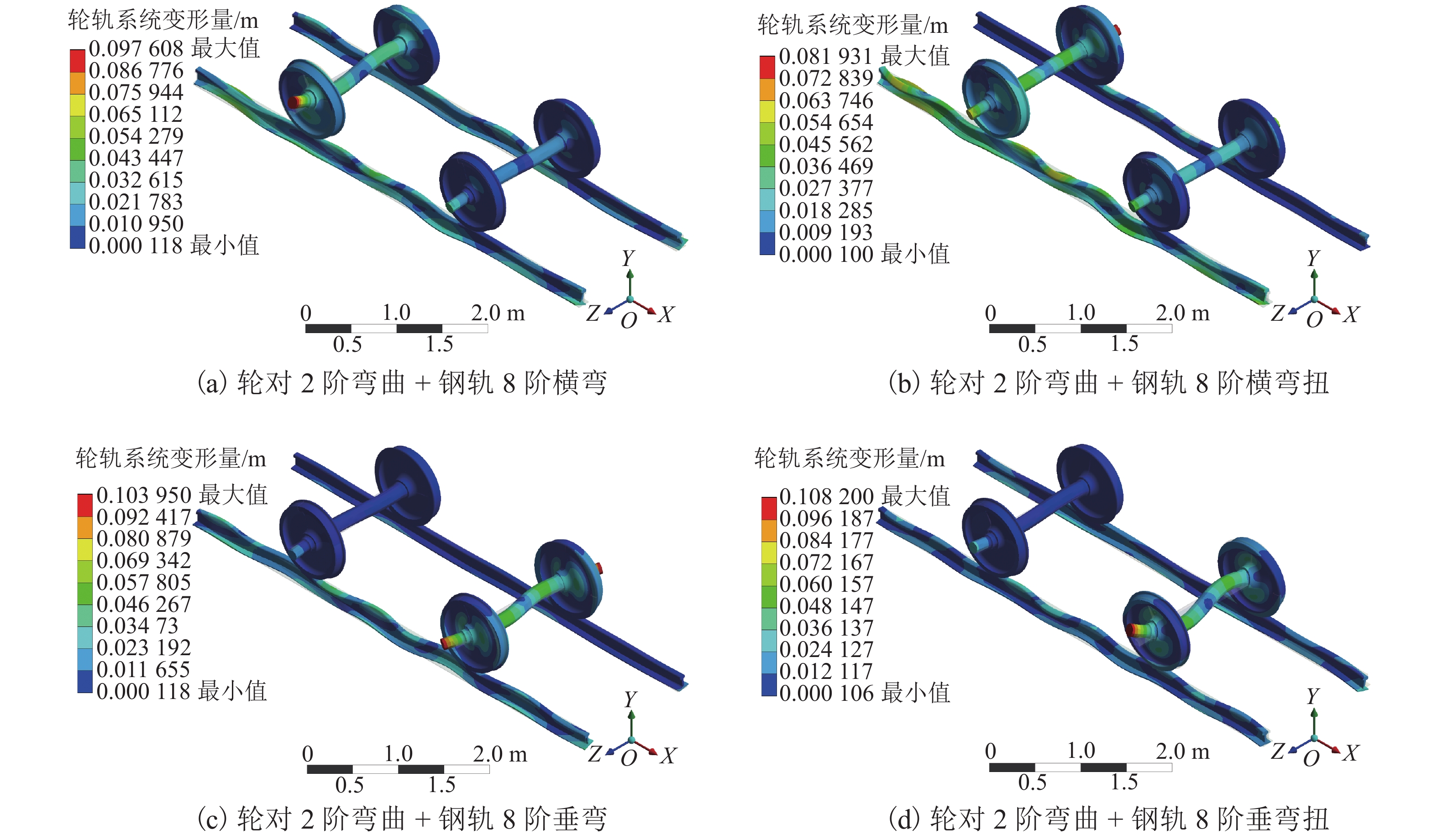
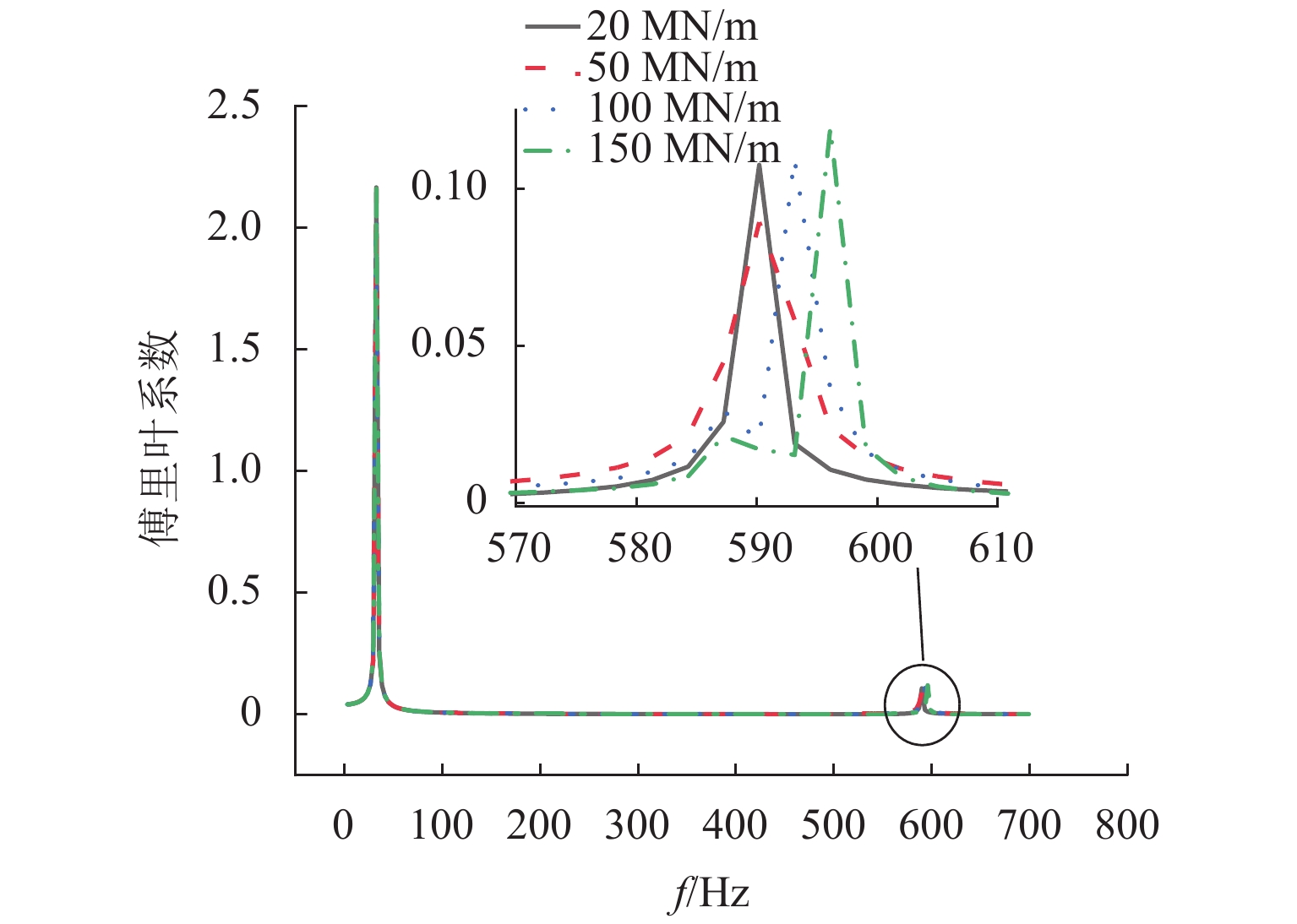
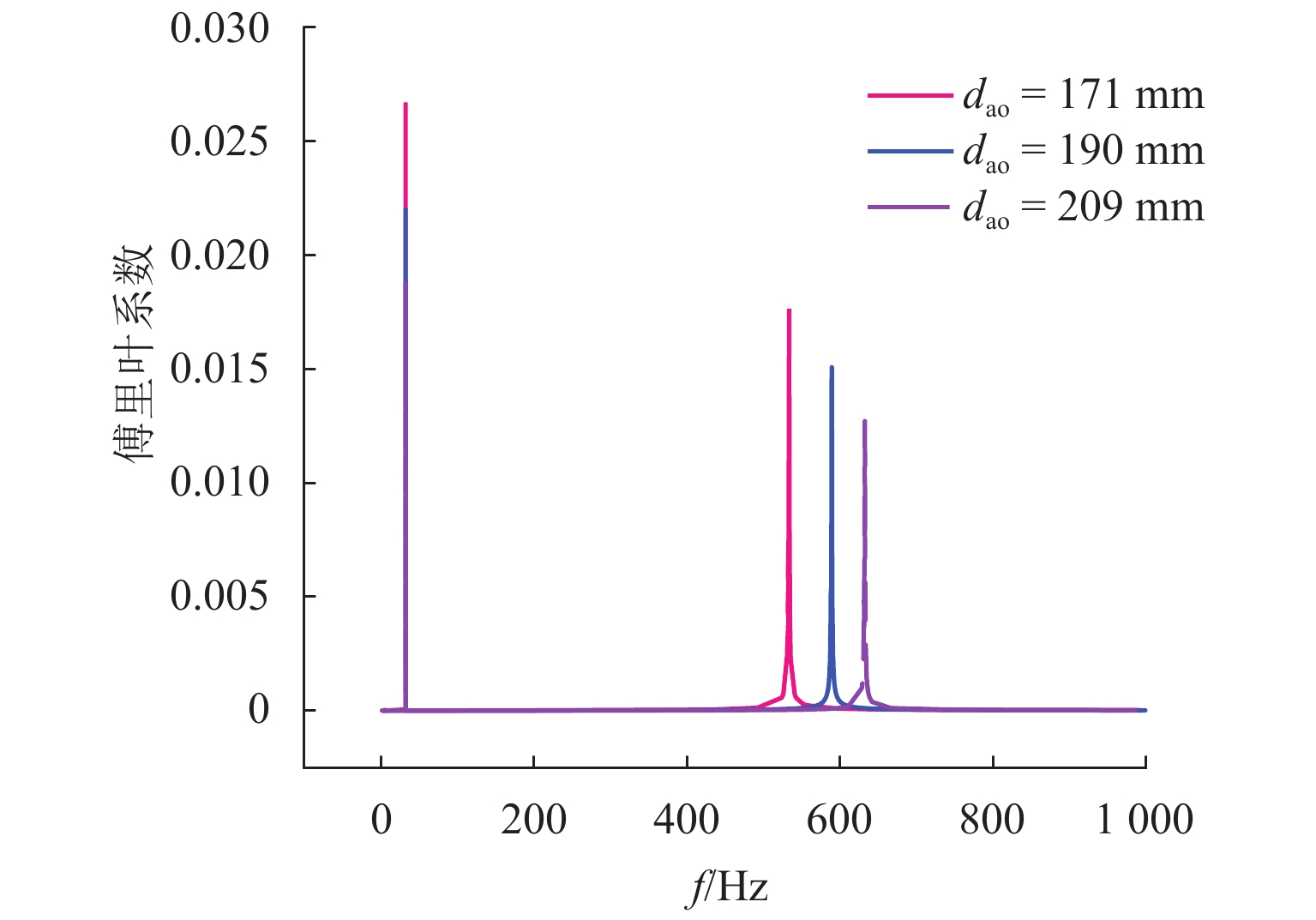
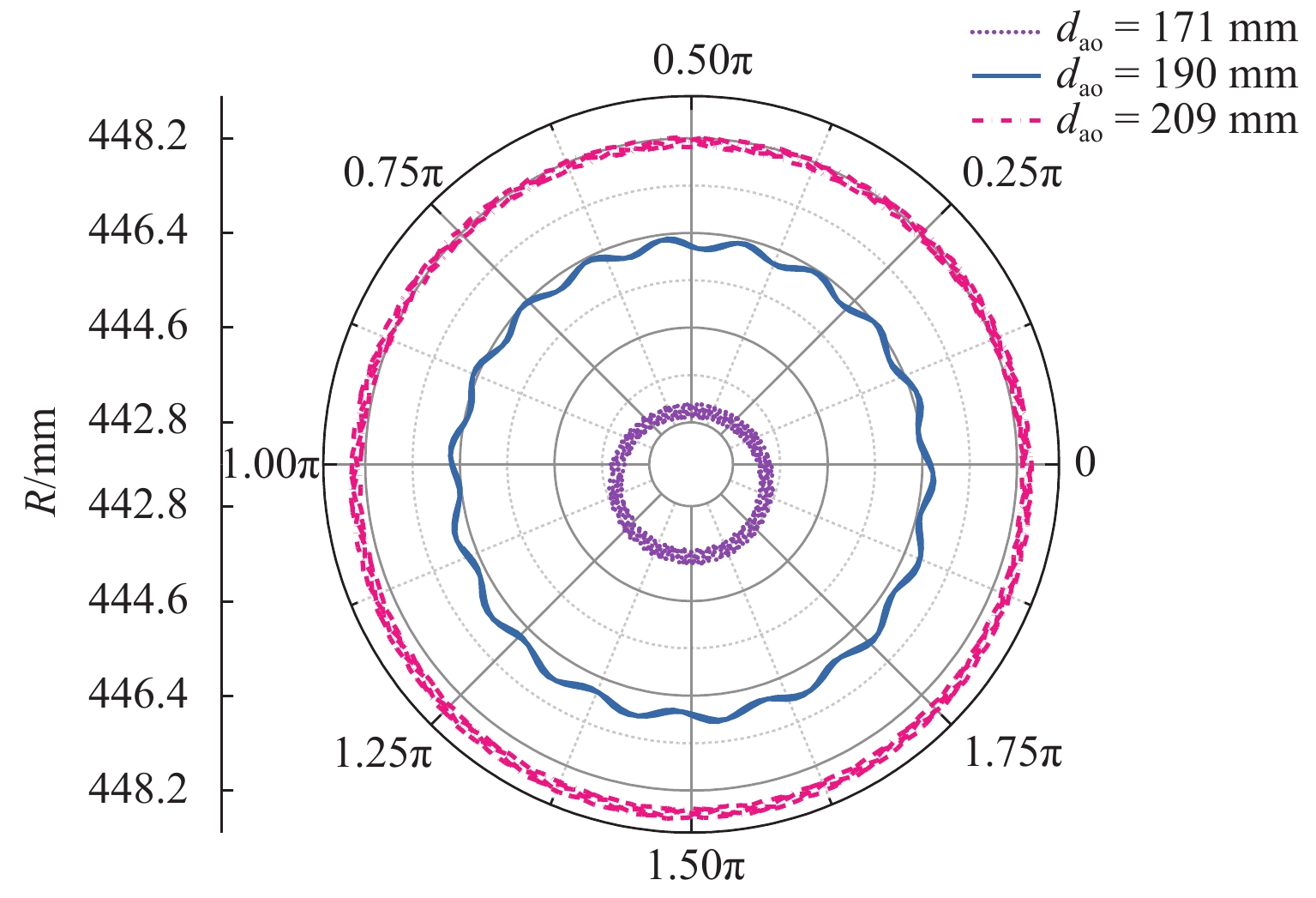
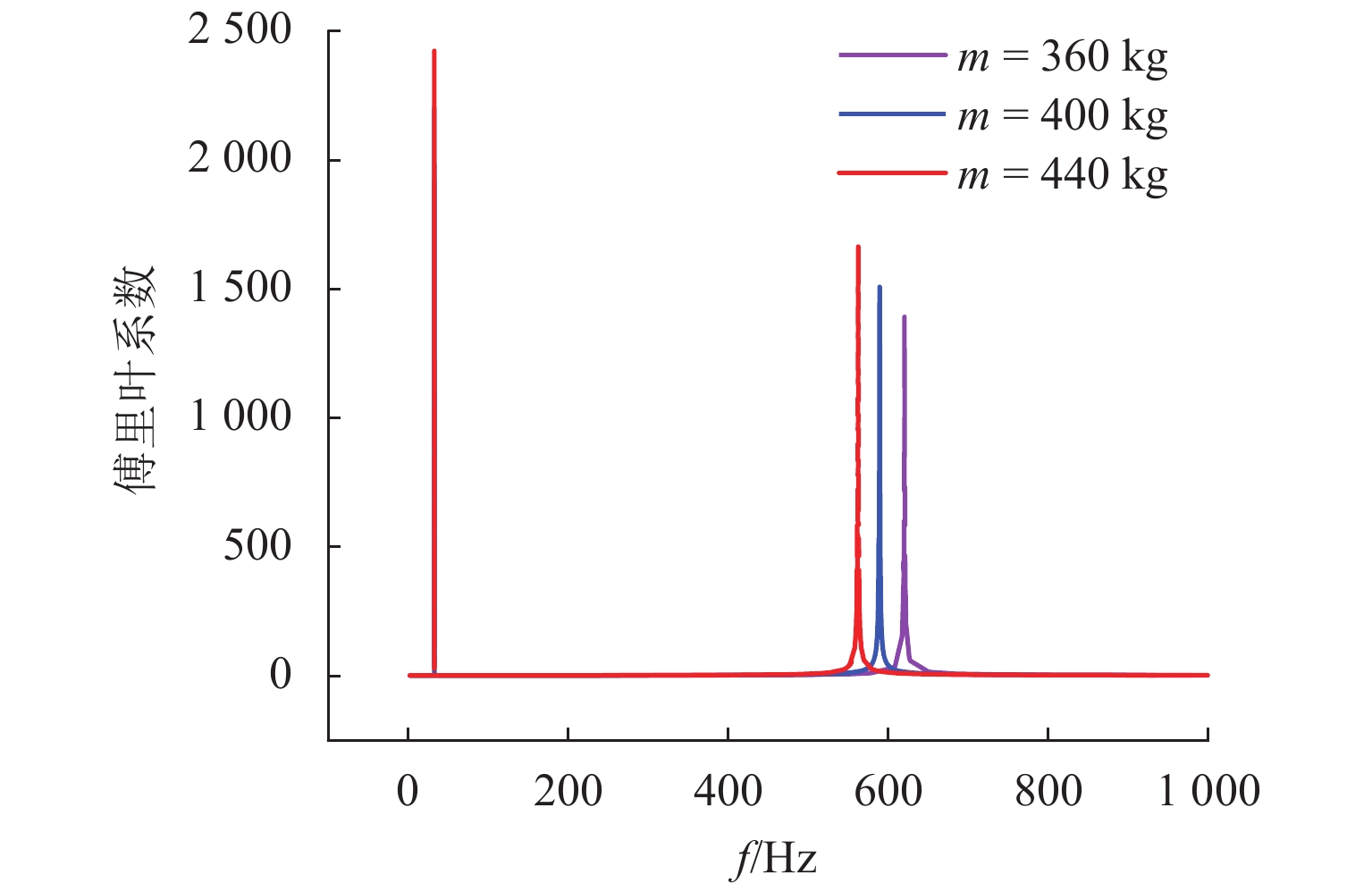
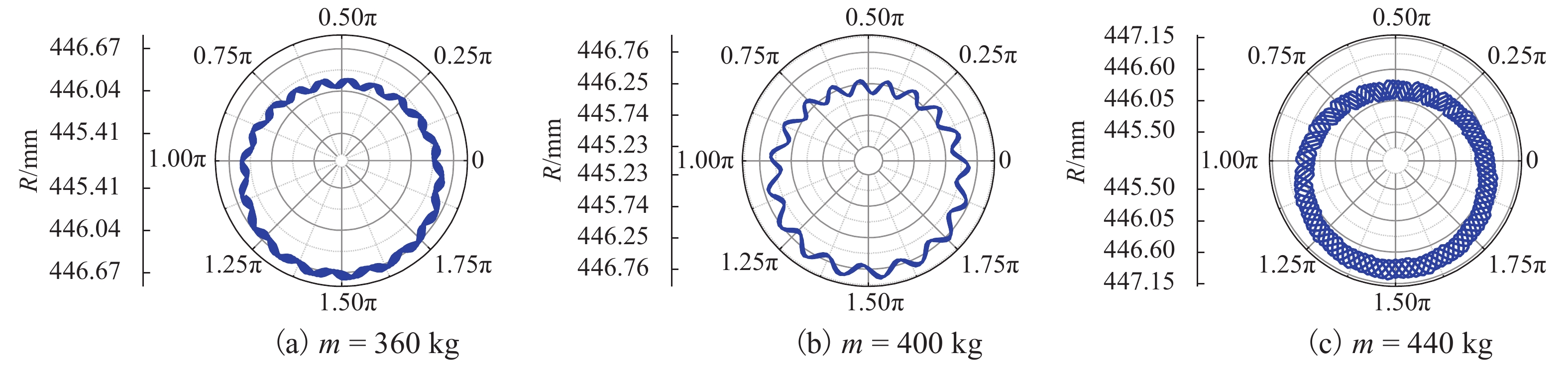
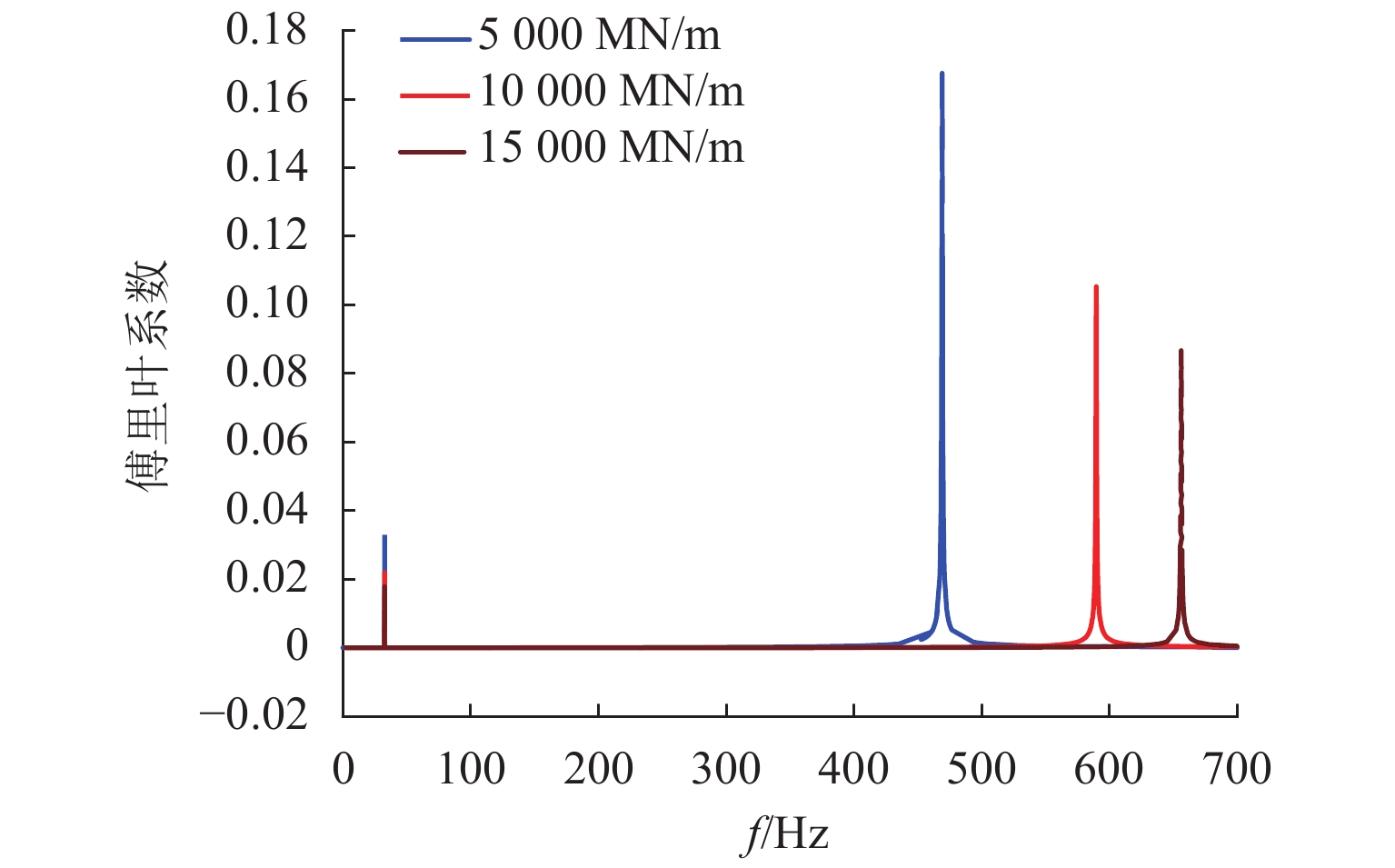
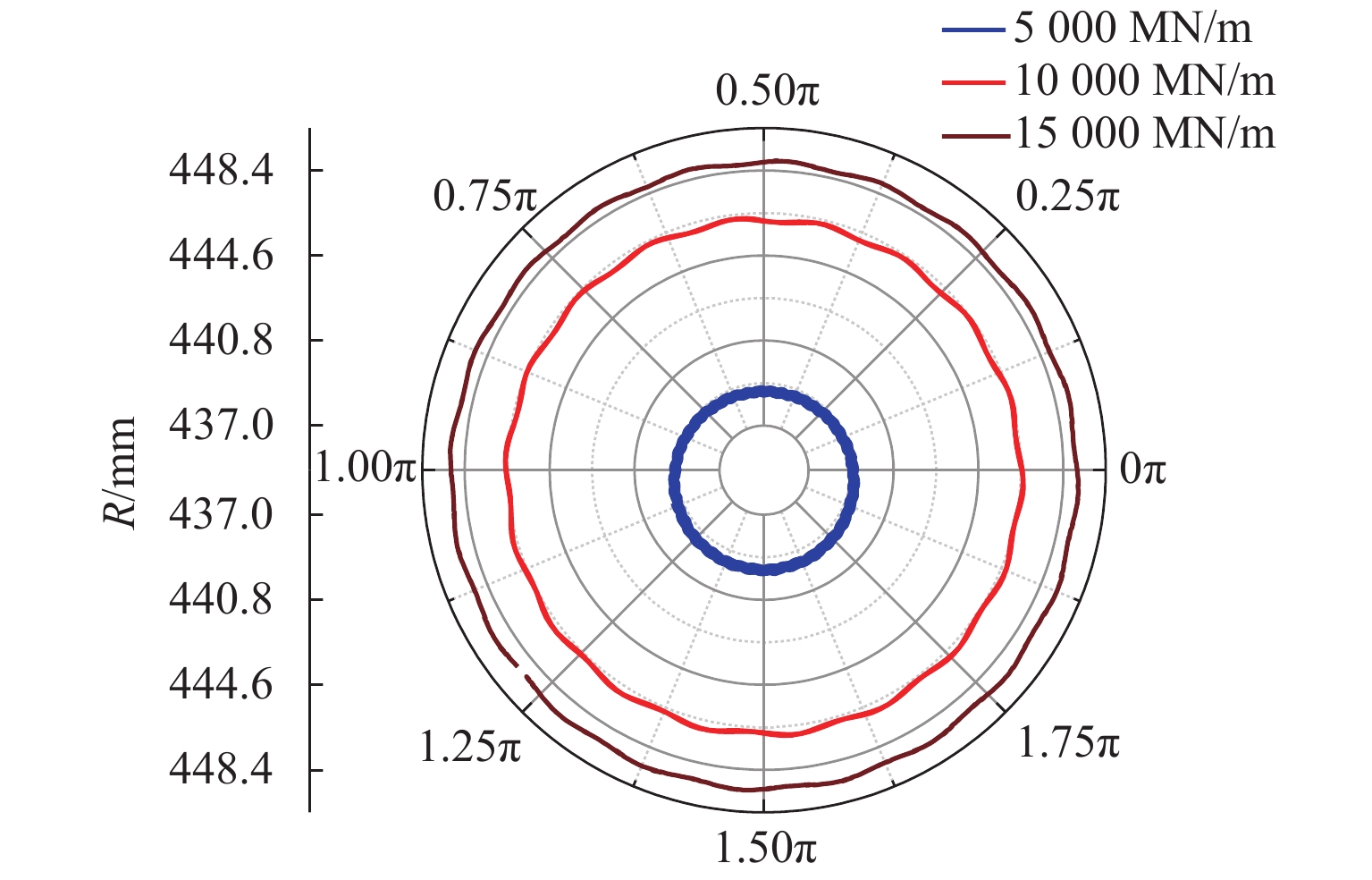
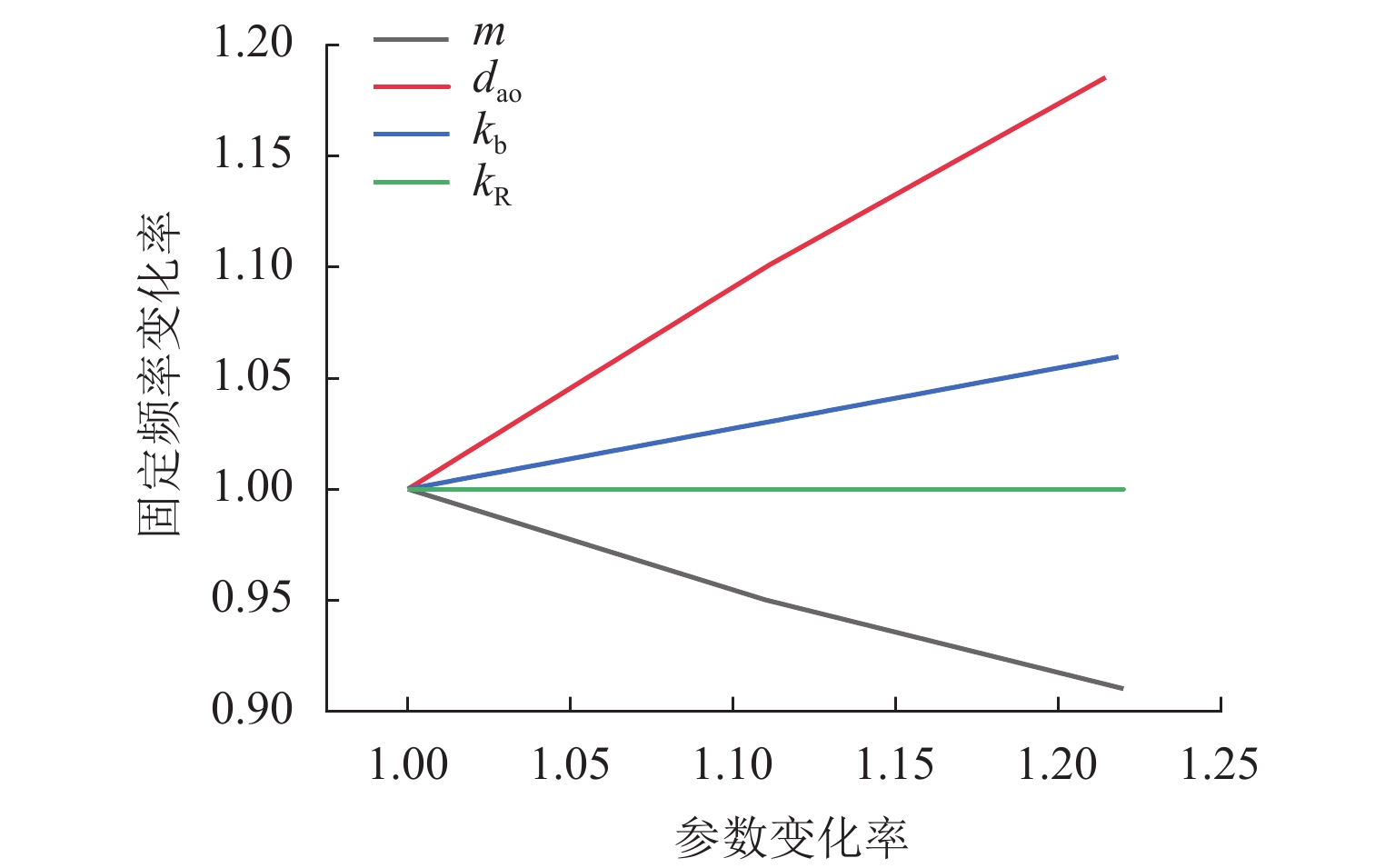
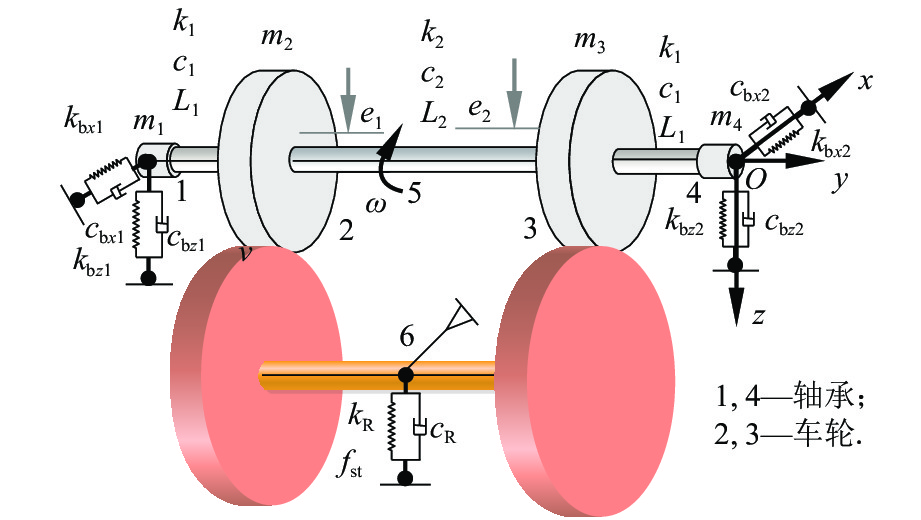
针对日益突出的车轮高阶多边形磨耗问题，基于轮轨系统转子动力学模型、轮轨接触模型和车轮圆周磨耗深度模型，建立车轮多边形磨耗发生与演化模型；分析列车运行速度和车轮质量偏心的变化，揭示车轮多边形磨耗发生与演化的规律，并进行现场跟踪实测数据验证；通过模态和灵敏度分析研究系统参数对多边形磨耗的影响. 研究结果表明：车轮高阶多边形磨耗的产生和演化遵循“定频整分”规律，即580 Hz左右的固定频率整分轮对转频时，车轮磨耗会演化成19阶左右的多边形，否则车轮磨耗将趋于均匀；该固定频率主要来源于轮对的2阶弯曲模态，且对车轴直径的灵敏度最大，通过定转速运行、增大车轴直径等措施改变固定频率可有效抑制车轮多边形磨耗.
Abstract:Aiming at the increasingly serious problem of high-order wheel polygonal wear, based on the wheel-rail system rotor dynamics model, wheel-rail contact model and wear depth model, the generation and evolution model of wheel polygonal wear is established. By analyzing the variation of speed and wheel mass eccentricity, the regularity of generation and evolution of wheel polygonal wear are revealed, and the field tracking data are verified. The influence of system parameters on polygonal wear is studied by modal analysis and sensitivity analysis. The results show that the generation and evolution of high order wheel polygonal wear follows the law of “fixed frequency and divisible”. When the fixed frequency of 580 Hz divides wheelset rotation frequency, the wheel wear will evolve into 19th order polygonal, otherwise it will tend to be uniform. This fixed frequency is mainly derived from the 2nd-order bending mode of the wheelset and has the greatest sensitivity to the axle diameter. The fixed frequency of the wheel can be changed by running at constant rotating speed and increasing the axle diameter, which can effectively suppress the polygonal wear of the wheel.
-
Key words:
- high-order polygonal /
- wear /
- fixed frequency and divisible /
- sensitivity
-
自动定理证明是人工智能的核心部分之一，致力于生成高效的计算机程序，从而使计算机能够完全或几乎完全自动地进行推理. 即，将形式化为一阶逻辑公式的前提和结论作为计算机程序的输入，并试图利用程序自动从前提中推导出结论. 这样的程序通常被称为自动定理证明器（automated theorem prover，ATP）.
随着形式化技术的发展，ATP的应用范围从理论上的数学定理逐渐拓展到知识编译[1]、软（硬）件模型检验[2-5]、管理规划[6-7]、集成电路设计[8-10]及软件测试[11]等实际问题上. 因此，旨在推理小规模数学问题的ATP越来越多面对从一些大型知识库（CYC[12]、SUMO[13]以及Mizar[14]等）和实际应用中转换而成的大规模的问题. 这些大规模问题通常被称为大理论（large theory），通常包含成千上万个前提，但是仅有非常少的一部分前提才对问题结论的证明有用. 大规模的冗余前提集会使得ATP在证明问题时搜索空间呈指数型增长，甚至可能立即超出计算机的运行能力，这大大地限制ATP自动推理能力. 假设可以直接使用在证明中出现的前提，ATP则能够轻松快速地证明问题的结论. 因此，从问题中去除不必要的前提，可以减少搜索空间，并降低搜索难度. 在ATP开始证明之前选择出对问题结论证明有用的前提的过程被称为前提选择（premise selection）. 前提选择是ATP预处理中非常关键的一环，对解决大理论的自动推理至关重要.
早期的前提选择方法[15-16]通过不断对当前选择的前提和结论否定的模型进行语义分析来指导前提的选择. 然而，基于语义的前提选择方法非常耗时，且严重依赖模型检查器的能力. 随后，一些基于符号相关性的前提选择方法[17-19]不断被提出. 此类方法主要通过计算和比较出现在公式（前提和结论）符号中，分析公式间的相关性. 当前，一些机器学习[20-22]和深度学习[23-27]技术也开始应用在前提选择中. 基于学习的前提选择方法强烈地依赖于大规模成功证明的领域经验，需要从形式化证明构造不同领域（如集合论、代数以及管理等）问题的语料库. 然而，在形式化时不同领域问题使用的符号是随机制定的，使得对应的语料库无法在学习训练中跨领域通用. 因此，当ATP面临一个新领域中的大规模问题时，由于缺乏新领域中的形式化证明，将导致当此类学习方法在前提选择任务中失效.
因此，从效率和可行性出发，当前ATP主要使用基于符号相关性的方法作为主要前提选择方法. 然而，当前方法终止前提选择过程的条件是，无法再选择任何的前提作为相关前提. 在此情况下，现有方法缺少在选择过程中对所选择前提的充分性进行判断，因此，可能在已经充分选择了相关前提的情况下，仍不会停止选择过程. 这直接导致当前选择过程将大量与结论证明无关的前提标记为相关的. 此外，当前的方法在选择前提时仍需人工设置相关度边界，这导致相关度边界值不具有普遍性和广泛适用性.
针对以上问题，本文提出了一种新的基于符号权重的一阶逻辑前提选择方法SymbolWeight. 新方法通过考虑问题中符号出现的频率，为每个符号赋予不同的权重. 在新的权重定义下，若符号是通用符号（高频符号），其权重就越小；若符号是稀有符号（低频符号），其权重就越大. 新定义符号的权重能够削弱通用符号造成的负面影响，以及体现稀有符号的重要性，从而保证基于新权重的相关度计算更加稳定. 同时，为减少手工参数的数量，提高前提选择的精确度，新方法提出一种自适应相关度边界，用于判断前提是否与结论相关. 此外，为了在充分选择相关前提的情况下及时停止前提选择过程，新方法交互结合了前提选择过程和结论自动推理过程. 实验结果表明，和自动定理证明器中广泛使用的通用前提选择方法相比，新方法能够帮助自动定理证明器E在MPTP2078基准测试集上提高10%以上的证明率.
1. 预备工作
在一阶逻辑[28]中，给定一个变元符号集
$ \mathcal{V} $ 、一个函数符号集$\mathcal{{{F}}}$ 、一个谓词集$ \mathcal{P} $ . 一阶逻辑项是一个变量项$v\;（v\in \mathcal{V} ）$ 或者形如$f\left({t}_{\mathrm{u}1},{t}_{\mathrm{u}2},\cdots ,{t}_{\mathrm{u}{{g}}}\right)$ 的函数项. 其中：$ f({\text{•}})\in \mathcal{F} $ ，是$ g $ （$ g\geqslant 0 $ ）元函数符；$ {t}_{\mathrm{u}1} $ ,$ {t}_{\mathrm{u}2} $ ,…,${t}_{\mathrm{u}{{g}}}$ 是项. 一阶逻辑原子（atom）形如${p}_{\mathrm{r}\mathrm{e}\mathrm{d}}\left({t}_{\mathrm{r}1},{t}_{\mathrm{r}2},\cdots ,{t}_{\mathrm{r}{{o}}}\right)$ ，其中：$ {p}_{\mathrm{r}\mathrm{e}\mathrm{d}}({\text{•}})\in \mathcal{P} $ ，是$ o $ （$ o\geqslant 0 $ ）元谓词符；$ {t}_{\mathrm{r}1} $ ，$ {t}_{\mathrm{r}2} $ ，…，$ {t}_{\mathrm{r}{\rm{o}}} $ 是项. 一阶逻辑公式是由一阶逻辑联结词$\mathcal{C}= \{ ～ ,\wedge ,\vee ,\to , \leftrightarrow \}$ 、量词$ {Q}=\{\forall ,\exists \} $ 和原子联结而成. 其中：$～$ 表示否定；$ \wedge $ 表示且；$ \vee $ 表示或；$ \to $ 表示蕴含；$\leftrightarrow$ 表示等价；$ \forall $ 表示全称量词；$ \exists $ 表示存在量词.在自动定理证明中，问题的前提和结论均被形式化为一阶逻辑公式. 因此，符号是前提和结论最直观的特征. 若要为大理论问题的结论选择最相关的前提，最自然的方法是使用基于符号的前提选择方法.
2. 前提选择方法
基于符号相关性的前提选择方法意味着需要根据出现在前提中符号计算前提与当前结论证明的相关性，并据对应的相关度对前提进行选择.
2.1 基本思想
令c和P分别为一个大理论问题中的结论和前提集，基于符号相关性的前提选择方法的基本框架为：
1） 若符号s出现在c中，则s与c是1度相关的；
2） 若前提
$ p\in P $ 中的符号（或符号集）与c是k度相关的，则p是$ k + 1 $ 度相关的；3） 若p与c是k度相关的，则p中的所有符号与c是k度相关的.
在此过程中，首先需要定义两个相关集，即相关前提集
$ {R}_{\mathrm{p}} $ 和相关符号集$ {R}_{\mathrm{s}} $ .$ {R}_{\mathrm{p}} $ 包含结论及与结论证明相关的前提.$ {R}_{\mathrm{s}} $ 包含$ {R}_{\mathrm{p}} $ 中所有公式的所有符号，即Rs=⋃func∈RpF(func), (1) 式中：
$ {f}_{\mathrm{u}\mathrm{n}\mathrm{c}} $ 为结论c或与结论证明相关的任意前提p；$ F\left({f}_{\mathrm{u}\mathrm{n}\mathrm{c}}\right) $ 为$ {f}_{\mathrm{u}\mathrm{n}\mathrm{c}} $ 中所有符号组成的集合.开始时，
$ {R}_{\mathrm{p}} $ 仅包含结论c，$ {R}_{\mathrm{s}} $ 仅包含c中所有的符号. 即初始时，$ {R}_{\mathrm{p}}=\left\{c\right\} $ ，$ {R}_{\mathrm{s}}=F\left(c\right) $ . 前提选择方法基于每个前提p的符号集$ F\left(p\right) $ 和当前$ {R}_{\mathrm{s}} $ , 计算p与c的相关度，不断地选择新的p加入$ {R}_{\mathrm{p}} $ 中，同时更新$ {R}_{\mathrm{s}} $ ，直到无法再将任何前提加入$ {R}_{\mathrm{p}} $ 中. 在完成前提选择后，由相关前提集$ {R}_{\mathrm{p}} $ 中的所有前提和结论组成的缩减问题将作为自动定理证明器新的输入，用于自动地证明问题的结论. 现有基于符号相关性的前提选择方法的通用流程如算法1所示.算法1 现有的基于符号相关性的前提选择方法
输入：结论c、前提P、相关前提集
$ {R}_{\mathrm{p}} $ 、相关符号集
$ {R}_{\mathrm{s}} $ 、无关前提集$ {I}_{\mathrm{p}} $ 、选择前提集SP、相关度阈值h、循环标记
$ {F}_{\mathrm{l}\mathrm{a}\mathrm{g}} $ 输出：
$ {R}_{\mathrm{p}} $ ${R}_{\mathrm{p}}=c$ ，$ {R}_{\mathrm{s}}=F\left(c\right) $ ，$ {I}_{\mathrm{p}}=P $ ，$ {S}_{\mathrm{p}}=\varnothing $ ，${F}_{\mathrm{l}\mathrm{a}\mathrm{g}}=\mathrm{T}\mathrm{r}\mathrm{u}\mathrm{e}$ while
$ {F}_{\mathrm{l}\mathrm{a}\mathrm{g}} $ dofor
$ p\in {I}_{\mathrm{p}} $ do根据当前的
$ {R}_{\mathrm{s}} $ ，计算$ p $ 的相关度if
$ p $ 的相关度$ \geqslant h $ then$ {S}_{\mathrm{p}}:={S}_{\mathrm{p}}\cup \left\{p\right\} $ end if
end for
if
$ {S}_{\mathrm{p}}=\varnothing $ then$ {F}_{\mathrm{l}\mathrm{a}\mathrm{g}}=\mathrm{F}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e} $ else
${R}_{\mathrm{p}}:={R}_{\mathrm{p}}\cup {S}_{\mathrm{p}}$ ，${R}_{\mathrm{s}}:=({\bigcup }_{p\in {S}_{\mathrm{p}}}F(p))\cup {R}_{\mathrm{s}}$ ，${I}_{\mathrm{p}}:={I}_{\mathrm{p}}|{S}_{\mathrm{p}}$ $ {S}_{\mathrm{p}}=\varnothing $ end if
end while
完整的前提选择方法必须包含两个部分：前提选择和结论证明. 给定一个大理论，前提选择方法首先需要对大理论中的前提进行选择，随后利用自动定理证明器在选定的前提集上对问题的结论进行自动推理. 现有基于符号相关性的前提选择方法均将这两个部分分离开来，即，必须在结束前提选择过程之后，再利用自动定理证明器证明缩减后的问题. 尽管通过调整和添加实验参数对选择前提的数量进行限制，现有方法最后选择的前提仍有大量是与结论证明无关的.
2.2 基于符号权重的前提选择方法
由算法1可知，如何计算前提和相关符号集相关度是基于符号相关性的前提选择方法的重点. 简单地，可通过前提中的符号是否出现在相关符号集中，从而确定前提的相关性. 如果前提至少包含相关符号集中的一个符号，则可认为该前提是相关的. 在此情况下，若前提包含相关符号集中的一个符号，则该前提中的所有符号都会变为相关符号（加入相关符号集中）. 这种做法的弊端在于，几次迭代后，问题中几乎所有的前提都将被选择加入相关前提集中. 其中，最主要的原因是大理论问题中某些符号（通常被称为通用符号）频繁地出现在不同的前提中. 若通用符号被标记为相关符号，则所有包含此类符号的前提都将被认为是与结论证明相关的. 因此，前提的选择方法的重心应该放在解决通用符号的问题上.
与通过符号对应的是稀有符号，即在问题中出现的频率较低，基于此类符号的选择方法能够避免选择过多的前提. 因此，符号的权重定义应该遵循两个原则：削弱通用符号造成的负面影响，以及体现稀有符号的重要性. 给定一个前提集
$ P $ ，任意符号$s\in \bigcup\limits_{p \in P}F\left(p\right)$ 的权重$ w\left(s\right) $ 定义为w(s)=1−occ(s)|P|+1， (2) 式中：
$ {o}_{\mathrm{c}\mathrm{c}}\left(s\right) $ 为包含符号s的所有前提数量；$ \left|P\right| $ 为P中的前提总数.显而易见，对任意符号
$ s $ ，$ 0 < w\left(s\right) < 1 $ .$ w\left(s\right) $ 满足符号权重定义的两个原则. 若符号s是通用符号，则s的权重就越小；若符号s是稀有符号，则s的权重就越大. 式（2）定义的符号权重均在区间$ \left(\mathrm{0,1}\right) $ ，这能够保证基于该符号权重的相关度更加稳定.给定相关符号集
$ {R}_{\mathrm{s}} $ ，前提$ p $ 在$ {R}_{\mathrm{s}} $ 下与结论证明的相关度为r(p)=∑si∈Rs∩F(p)w(si)∑sj∈F(p)w(sj), (3) 式中：
$ {s}_{\mathrm{i}} $ 为$ {R}_{\mathrm{s}} $ 与$ F\left(p\right) $ 的交集中的任意符号；$ {s}_{\mathrm{j}} $ 为$ F\left(p\right) $ 中的任意符号.前提p与结论证明的相关度
$ r\left(p\right) $ 是在区间$ \left[\mathrm{0,1}\right] $ 内的实数. 如果p中的符号均不在相关符号集$ {R}_{\mathrm{s}} $ 中，则p与结论证明的相关度为0. 这说明p与当前的相关前提集$ {R}_{\mathrm{p}} $ 毫无符号上的关联. 如果p中的符号均在$ {R}_{\mathrm{s}} $ 中，则p与结论证明的相关度为1. 这说明p与当前的相关前提集$ {R}_{\mathrm{p}} $ 在符号上非常相关. 值得注意的是，随着相关前提集$ {R}_{\mathrm{p}} $ 和相关符号集$ {R}_{\mathrm{s}} $ 的变化，前提p的相关度也会发生变化.由式（3）可知，每个前提都存在一个基于当前相关符号集的相关度. 给定任意两个前提，通过比较其与结论证明的相关度大小，可以形式化两个前提间“更相关”的关系. 根据相关度的高低能够将对应的前提进行排序，但不能直接形式化“最相关前提”这一概念. 最相关前提的相关度大于最不相关前提的相关度, 因此，最直观的做法是设定一个相关度边界，用于区分最相关前提和最不相关前提.
定义1 给定一个相关度边界h（
$0\leqslant h\leqslant 1$ ），前提p被标记为最相关前提, 当且仅当$r\left(p\right)\leqslant h$ .由定义1可知，如果将h设置为0，所有的前提均为最相关前提. 如果将h设置为1，仅有非常少（甚至为0）的前提被标记为最相关的. 显然，相关度边界值过大或过小都会直接影响选择的结果，甚至问题结论的证明. 通过人工设置的相关度边界不具有普遍性和广泛适用性.
为解决以上问题，本文提出了一种自适应相关度边界. 该边界仅由当前选择过程中前提的相关度而决定，从而不再需要提前进行人工设置.
假定问题中包含n个前提
$ {p}_{1} $ ,$ {p}_{2} $ ,…,${p}_{{{{{n}}}}}$ ，$n \in {{{\bf{N}}}}, n \geqslant 1$ ，其对应的相关度分别为$ r\left({p}_{1}\right) $ ,$ r\left({p}_{2}\right) $ ,…,$ r\left({p}_{{n}}\right) $ . 在n个相关度中，部分相关度的值相同. 因此，合并相同的相关度值，能够从$ r\left({p}_{1}\right) $ ,$ r\left({p}_{2}\right) $ ,…,$ r\left({p}_{{n}}\right) $ 中获取M个不同的数值,$M \in {\bf{N}},1 \leqslant M \leqslant n$ . 这里将M个数值从高到低进行排序，序号为m的数值即为第m级自适应相关度边界$ {h}_{m} $ ，$m \in {\bf{N}},1 \leqslant m \leqslant M$ .显然，自适应相关度边界因问题而异，且会随着选择过程的变化而变化. 在选择过程中，所有相关度小于
$ {h}_{m} $ 的前提均不会被选择.前提选择方法的主旨在于选择尽可能少但充分与问题结论证明相关的前提. 一种可能的方法是选择一级自适应相关度边界
$ {h}_{1} $ 作为选择前提的条件. 实验发现，在大部分情况下，$ {h}_{1}=1 $ . 由式（3）可知，若一个前提的相关度为1，则该前提的所有符号均在相关符号集中. 若在相关前提集中加入相关度为1的前提，并不会使对应的相关符号集$ {R}_{s} $ 发生任何变化（加入新的符号）. 因此，仅选择相关度为1的前提作为最相关前提，会导致选择的前提不够充分. 因此，本文进一步细化地定义了自适应相关度边界$ {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}} $ .定义2 给定一个前提集和前提对应的相关度，
1） 若第1级自适应相关度边界
$ {h}_{1}=1 $ ，则自适应相关度边界为第2级自适应相关度边界，即$ {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}={h}_{2} $ ；2） 此外，自适应相关度边界为第1级自适应相关度边界，即
$ {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}={h}_{1} $ .由定义2可知，利用自适应相关度边界
$ {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}} $ ，新提出的基于符号权重的前提选择方法不再依赖任何人工设置的相关度边界.给定一个前提集
$ P $ ，现在可以根据前提$ p\in P $ 的相关度和自适应相关度边界，从$ P $ 中选择最相关前提. 然而，当前仍无法直观地判断所选择的前提对问题的结论证明是否足够充分. 因此，本文将前提选择过程和ATP的证明过程进行交互地结合. 在新的框架下，每一次选择的结果均将作为ATP的输入，开始尝试证明问题的结论. 若结论能够被自动地证明，则说明当前选择的前提是充分的，且整个过程可以停止.新提出的基于符号权重的前提选择算法流程如算法2所示. 最初的相关前提集仅包含问题的结论，对应的相关符号集仅包含结论中的符号，且无关前提集为问题的整个前提集. 在每次选择结束后，当前相关前提集中的前提和结论组成了新的缩减问题，ATP开始尝试在给定的CPU （central processing unit）运行时间内对该缩减问题进行证明. 若ATP能够证明该问题的结论，则不需要再继续选择前提，整个选择和证明过程立即停止. 否则，开始基于当前的相关符号集计算前提的相关度，并依据相关度边界, 将符合条件的前提标记为选择前提. 在旋转过程中，若没有满足条件的前提，则整个过程立即停止；否则, 利用当前新选择的前提更新相关前提集和相对应的关符号集，并从无关前提集中移除新选择的前提. 因此，整个过程将在K次循环后停止，
$k \in {\bf{N}}, k \geqslant 1$ .算法2 基于符号权重的前提选择算法
输入： 结论c、前提P、相关前提集
$ {R}_{\mathrm{p}} $ 、相关符 号集$ {R}_{\mathrm{s}} $ 、无关前提集IP、选择前提集SP、 相关度集R、自动定理证明器${{A}}_{\mathrm{T}\mathrm{P}}$ 、迭代 次数K、 CPU运行时间T输出：
$ {R}_{\mathrm{p}} $ $ {R}_{\mathrm{p}}=c $ ，$ {R}_{\mathrm{s}}=F\left(c\right) $ ，$ {I}_{\mathrm{p}}=P $ ，$ {S}_{\mathrm{p}}=\varnothing，R=\varnothing $ for
$ k\in [\mathrm{1,2},\dots ,K] $ do利用
$ {{A}}_{\mathrm{T}\mathrm{P}} $ 尝试在时间T内证明由$ {R}_{\mathrm{p}} $ 中的前提（和结论）组成的缩减问题
if 问题被
${{A}}_{\mathrm{T}\mathrm{P}}$ 证明 then停止
else
for
$ p\in {I}_{\mathrm{p}} $ do根据当前的
$ {R}_{\mathrm{s}} $ ，计算$ p $ 的相关度$ r\left(p\right) $ $ R:=R\cup \left\{r\left(p\right)\right\} $ end for
根据R决定自适应相关度
$ {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}} $ for
$ p\in {I}_{\mathrm{p}} $ doif
$r\left(p\right)\geqslant {h}_{\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}}$ then$ {S}_{\mathrm{p}}:={S}_{\mathrm{p}}\cup \left\{p\right\} $ end if
end for
if
$ {S}_{\mathrm{p}}=\varnothing $ then停止
else
$ {R}_{\mathrm{p}}:={R}_{\mathrm{p}}\cup {S}_{\mathrm{p}} $ ，${R}_{\mathrm{s}}:=(\bigcup\limits_{p \in {S_{\rm{p}}}} {F(p)} )\cup {R}_{\mathrm{s}}$ ，$ {I}_{\mathrm{p}}:={I}_{\mathrm{p}}|{S}_{\mathrm{p}} $ $ {S}_{\mathrm{p}}=\varnothing $ ，$ R=\varnothing $ end if
end if
end for
3. 实验和分析
本节使用MPTP2078问题库作为实验的基准测试集. MPTP2078问题库一共包含2078个问题，均来自Mizar问题库与Bolzano-Weierstrass定理相关的问题. 问题库中, 所有问题的前提和结论均被形式化为一阶逻辑公式，且公式按照其在Mizar数学库中出现的顺序线性排序. 即出现在每一个结论之前的公式（前提和其他结论）均可作为证明该结论的前提. 问题的前提数量在区间
$ \left[\mathrm{10,4\;563}\right] $ 内，且前提的平均数量为1876个. 有关问题库前提数量和符号的具体分析见表1.表 1 MPTP2078问题库描述Table 1. Description of MPTP2078 benchmark个 项目 公式 结论 最小前提 最大前提 平均前提 符号 数量 4564 2078 10 4563 1876 784 在本文的实验中，使用的操作系统为CentOS Linux 7.4.1708；CPU为octa-core Intel（R） Xeon（R） E5-2667 3.20 GHz；内存128 G. 使用自动定理证明器E作为实验默认ATP. 除证明结论的数量外，还使用选择精准度
${S} _{\mathrm{p}\mathrm{r}\mathrm{e}}$ （selected precision）和选择度${S} _{\mathrm{e}\mathrm{l}}$ （selectivity）[29]作为评估各种选择方法性能的指标, 如式（4）、（5）所示.${S} _{\mathrm{p}\mathrm{r}\mathrm{e}}$ 的值越高越好，而${S} _{\mathrm{e}\mathrm{l}}$ 的值越低越好.Spre=1|Proved|∑prob∈ProvedNUiP(prob)NSel(prob)， (4) Sel=1|Proved|∑prob∈ProvedNSel(prob)NAxP(prob)， (5) 式中：
$ {P}_{\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}} $ 为被证明的问题集；$ {p}_{\mathrm{r}\mathrm{o}\mathrm{b}}\in {P}_{\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}} $ ，是$ {P}_{\mathrm{r}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}} $ 中的一个被证明的问题；$ {N}_{\mathrm{U}\mathrm{i}\mathrm{P}}\left({p}_{\mathrm{r}\mathrm{o}\mathrm{b}}\right) $ 为出现在$ {p}_{\mathrm{r}\mathrm{o}\mathrm{b}} $ 证明中的有用前提的数量；${N}_{{\rm{S}}\mathrm{e}\mathrm{l}}\left({p}_{\mathrm{r}\mathrm{o}\mathrm{b}}\right)$ 为选择的前提的数量；$ {N}_{\mathrm{A}\mathrm{x}\mathrm{P}}\left({p}_{\mathrm{r}\mathrm{o}\mathrm{b}}\right) $ 为$ {p}_{\mathrm{r}\mathrm{o}\mathrm{b}} $ 包含的原始前提的数量.表2列出了实验所涉及的基于符号的前提选择方法. 为了保证实验的公平性，本文将每个问题在自动定理证明器E上运行的CPU时间设定为60 s. 若一个问题的选择过程迭代K次，则每次迭代后生成的缩减问题仅在自动定理证明器E上运行
$ 60/K $ s. 显然地，需要权衡每次自动定理证明器运行的CPU时间和选择的迭代次数.表 2 参与实验的基于符号的前提选择方法的说明Table 2. Description of symbol-based premise selection methods in experiments提出的SymbolWeight能够根据前提的相当度自动地决定合适的相关度边界. 因此，SymbolWeight的性能仅与选择的迭代次数K有关. 表3评估了其在不同迭代次数K下对自动定理证明器E的性能影响. 由于每个问题运行CPU的时间最多为60 s，继续增加迭代次数会使得每次迭代中证明问题的CPU时间过小. 因此，SymbolWeight在实验中的最大迭代次数设置为30次. 随着K的不断增加，证明问题的数量在不断增加. 当
$ K= 30 $ 时，自动定理证明器E能够证明1077个问题. 值得注意的是，增加迭代次数并不会限制SymbolWeight的选择能力. 实验发现，SymbolWeight能够大大地减少选择前提的数量. 即使当K增加到30时，SymbolWeight平均选择前提数仅约为174个. 这表明，提出的自适应相关度边界在不损害自动定理证明器E证明能力的前提下，能够有效解决相关度边界的阈值设定问题. 随着K的增加，自动定理证明器CPU时间在逐渐减少（${{K}}=30$ 时，CPU时间仅为2 s）. 然而，证明问题的数量在不断增加. 这说明如果能够正确地选择出证明大理论问题结论所需要的全部前提，自动定理证明器E能够轻易地搜索到结论的证明. 因此，有效的前提选择方法能够大大地帮助证明器提高证明问题的能力.表 3 自动定理证明器E在SymbolWeight下的证明性能Table 3. Performance of automated theorem prover E with SymbolWeight$ K $ 证明数
量/个平均选择前提数量/个 选择精
确度选择度 2 288 13.0 0.358 0.054 4 599 22.6 0.336 0.060 6 818 33.3 0.322 0.054 8 862 44.5 0.309 0.053 10 920 55.9 0.302 0.055 12 932 68.4 0.295 0.057 14 967 81.1 0.288 0.059 16 980 94.0 0.285 0.060 18 1003 106.3 0.280 0.061 20 1014 117.3 0.278 0.061 22 1028 128.7 0.275 0.064 24 1045 140.7 0.271 0.068 26 1057 151.5 0.268 0.070 28 1071 162.4 0.265 0.074 30 1077 174.2 0.264 0.076 表4比较了自动定理证明器E在不同基于符号的前提选择方法下的证明性能. E-SInE和Vampire-SInE分别表示在证明器E和Vampire中的SInE[19]方法. 自动定理证明器E在使用SymbolWeight作为前提选择方法时能够证明MPTP2078问题库中超过半数的问题. 与E-SInE和Vampire-SInE相比，SymbolWeight能够帮助自动定理证明器E在MPTP2078基准测试集上分别提高19.49%和10.49%的证明率.
表 4 自动定理证明器E在不同的基于符号的前提选择方法下的证明性能Table 4. Performance of automated theorem prover E with different symbol-based premise selection methods前提选择方法 证明数量/个 证明率/% no-selection 663 30.90 E-SInE 672 32.34 Vampire-SInE 859 41.34 SymbolWeight 1077 51.83 4. 结 论
1） 提出了新的符号权重和相关度计算方法，并基于此设计并实现了用于解决大理论问题的前提选择的方法；
2） 提出了自适应相关度边界，解决了在基于符号的前提选择方法中需要人工地设置相关度边界的问题；
3） 新提出的前提选择方法能够大大地提高自动定理证明器E在MPTP2078问题库上的证明能力.
-
图 9 考虑转动效应下轮轨耦合系统振动模态
Figure 9. Vibration modes of wheel-rail coupling system considering rotation effect
图 10 不同扣件刚度幅频图
Figure 10. Amplitude-frequency diagram under different fastener stiffnesses
图 16 不同支承刚度的幅频图
Figure 16. Amplitude-frequency diagram under different support stiffnesses
表 1 车轮多边形磨耗参数分析
Table 1. Analysis of wheel polygonal wear parameters
n D/mm ω/（rad·s−1） f2/Hz fx/Hz 20 915 182.1 29.0 580.1 19 875 190.5 30.3 576.3 18 830 200.8 32.0 575.6 
下载: 导出CSV
表 2 轮轨耦合系统的固有频率
Table 2. Natural frequency of rotor system of wheel set
Hz 不考虑转动效应 考虑转动效应 刚轮柔轨 柔轮刚轨 柔轮柔轨 柔轮柔轨 519.40 567.16 565.42 565.42 559.49 567.19 580.73 580.61 574.77 577.74 583.07 582.97 593.11 578.03 584.48 584.37 605.90 585.43 585.47 585.65 608.93 585.45 586.78 586.94 622.27 748.22 591.33 591.35 648.97 769.92 621.80 621.81
下载: 导出CSV
-
[1] 金学松,吴越,梁树林,等. 高速列车车轮多边形磨耗、机理、影响和对策分析[J]. 机械工程学报,2020,56(16): 118-136. doi: 10.3901/JME.2020.16.118JIN Xuesong, WU Yue, LIANG Shulin, et al. Characteristics, mechanism, influences and countermeasures of polygonal wear of high-speed train wheels[J]. Journal of Mechanical Engineering, 2020, 56(16): 118-136. doi: 10.3901/JME.2020.16.118 [2] 陶功权,温泽峰,金学松. 铁道车辆车轮非圆化磨耗形成机理及控制措施研究进展[J]. 机械工程学报,2021,57(6): 106-120. doi: 10.3901/JME.2021.06.106TAO Gongquan, WEN Zefeng, JIN Xuesong. Advances in formation mechanism and mitigation measures of out-of-round railway vehicle wheels[J]. Journal of Mechanical Engineering, 2021, 57(6): 106-120. doi: 10.3901/JME.2021.06.106 [3] TAO G Q, WEN Z F, JIN X S, et al. Polygonisation of railway wheels: a critical review[J]. Railway Engineering Science, 2020, 28(4): 317-345. doi: 10.1007/s40534-020-00222-x [4] MORYS B. Enlargement of out-of-round wheel profiles on high speed trains[J]. Journal of Sound and Vibration, 1999, 227(5): 965-978. doi: 10.1006/jsvi.1999.2055 [5] MEYWERK M. Polygonalization of railway wheels[J]. Archive of Applied Mechanics, 1999, 69(2): 105-120. doi: 10.1007/s004190050208 [6] JOHANSSON A, ANDERSSON C. Out-of-round railway wheels—a study of wheel polygonalization through simulation of three-dimensional wheel-rail interaction and wear[J]. Vehicle System Dynamics, 2005, 43(8): 539-559. doi: 10.1080/00423110500184649 [7] WU X W, RAKHEJA S, CAI W B, et al. A study of formation of high order wheel polygonalization[J]. Wear, 2019, 424/425: 1-14. doi: 10.1016/j.wear.2019.01.099 [8] CAI W B, CHI M R, WU X W, et al. Experimental and numerical analysis of the polygonal wear of high-speed trains[J]. Wear, 2019, 440/441: 203079.1-203079.12. [9] MEINKE P, MEINKE S. Polygonalization of wheel treads caused by static and dynamic imbalances[J]. Journal of Sound and Vibration, 1999, 227(5): 979-986. doi: 10.1006/jsvi.1999.2590 [10] 胡晓依,任海星,成棣,等. 动车组车轮多边形磨耗形成与发展过程仿真研究[J]. 中国铁道科学,2021,42(2): 107-115.HU Xiaoyi, REN Haixing, CHENG Di, et al. Numerical simulation on the formation and development of polygonal wear of EMU wheels[J]. China Railway Science, 2021, 42(2): 107-115. [11] 宋志坤,任海星,胡晓依,等. 动车组车轮多边形磨耗发展历程模拟及车轮粗糙度的影响[J]. 铁道学报,2021,43(6): 23-28. doi: 10.3969/j.issn.1001-8360.2021.06.004SONG Zhikun, REN Haixing, HU Xiaoyi, et al. Research on development process simulation and influencing factors of polygonal wear of high-speed train wheels[J]. Journal of the China Railway Society, 2021, 43(6): 23-28. doi: 10.3969/j.issn.1001-8360.2021.06.004 [12] ZHAO X N, CHEN G X, LV J Z, et al. Study on the mechanism for the wheel polygonal wear of high-speed trains in terms of the frictional self-excited vibration theory[J]. Wear, 2019, 426/427: 1820-1827. doi: 10.1016/j.wear.2019.01.020 [13] 关庆华,赵鑫,温泽峰,等. 基于Hertz接触理论的法向接触刚度计算方法[J]. 西南交通大学学报,2021,56(4): 883-888.GUAN Qinghua, ZHAO Xin, WEN Zefeng, et al. Calculation method of Hertz normal contact stiffness[J]. Journal of Southwest Jiaotong University, 2021, 56(4): 883-888. [14] 王玉丰,沈钢. 几种铁路轮轨蠕滑力计算方法的比较[J]. 上海铁道大学学报(理工辑),1999(10): 27-32.WANG Yufeng, SHEN Gang. Comparison of several calculation methods of wheel/rail creep force[J]. Journal of Shanghai Tiedao University (Science and Technology), 1999(10): 27-32. [15] 张卫华,金学松,薛弼一. 单轮对试验台试验及轮轨蠕滑力计算模型的验证[J]. 铁道车辆,1997,35(5): 3-6,11.ZHANG Weihua, JIN Xuesong, XUE Biyi. Single wheelset test and verification of wheel-rail creep force calculation model[J]. Journal of Railway Vehicle, 1997, 35(5): 3-6,11. [16] 曹树谦,陈予恕. 多跨不平衡轴系的非线性动力学建模[J]. 非线性动力学学报,2002,9(1): 26-32.CAO Shuqian, CHEN Yushu. Nonlinear dynamics modeling of multi-span unbalanced shafting[J]. Journal of Nonlinear Dynamics, 2002, 9(1): 26-32. [17] 丁军君,杨九河,胡静涛,等. 高速列车车轮多边形磨耗演变行为[J]. 机械工程学报,2020,56(22): 184-189. doi: 10.3901/JME.2020.22.184DING Junjun, YANG Jiuhe, HU Jingtao, et al. Evolution of the polygonal wear of high-speed train wheels[J]. Journal of Mechanical Engineering, 2020, 56(22): 184-189. doi: 10.3901/JME.2020.22.184 [18] WU Y, JIN X S, CAI W B, et al. Key factors of the initiation and development of polygonal wear in the wheels of a high-speed train[J]. Applied Sciences, 2020, 10(17): 10175880.1-10175880.22. doi: 10.3390/app10175880 [19] 金学松,吴越,梁树林,等. 车轮非圆化磨耗问题研究进展[J]. 西南交通大学学报,2018,53(1): 1-14. doi: 10.3969/j.issn.0258-2724.2018.01.001JIN Xuesong, WU Yue, LIANG Shulin, et al. Mechanisms and countermeasures of out-of-roundness wear on railway vehicle wheels[J]. Journal of Southwest Jiaotong University, 2018, 53(1): 1-14. doi: 10.3969/j.issn.0258-2724.2018.01.001 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 692
- HTML全文浏览量: 218
- PDF下载量: 88
- 被引次数: 0