Mechanical Properties of Scroll Compressor with Permanent Magnetic Compliance Mechanism
-
摘要:
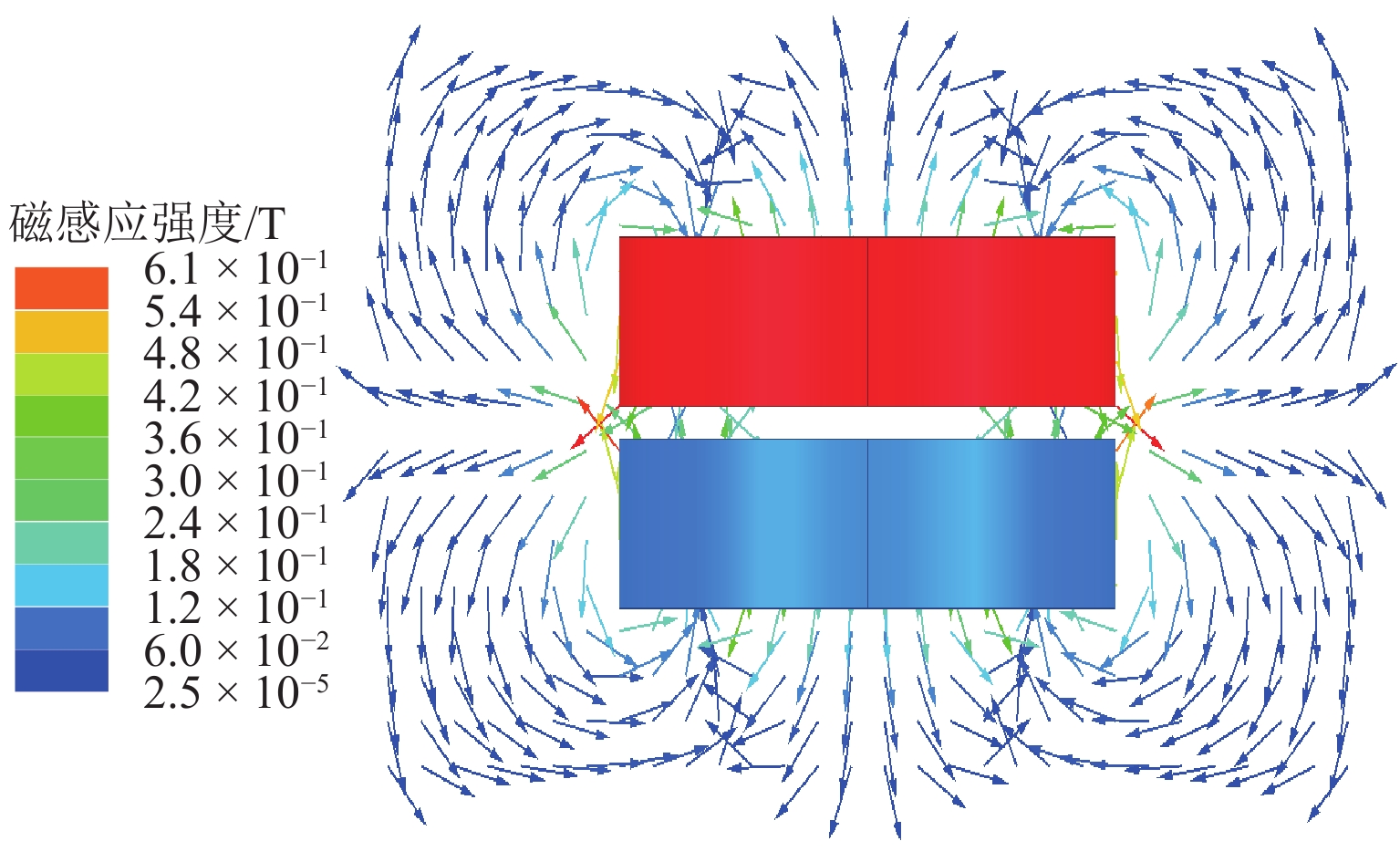
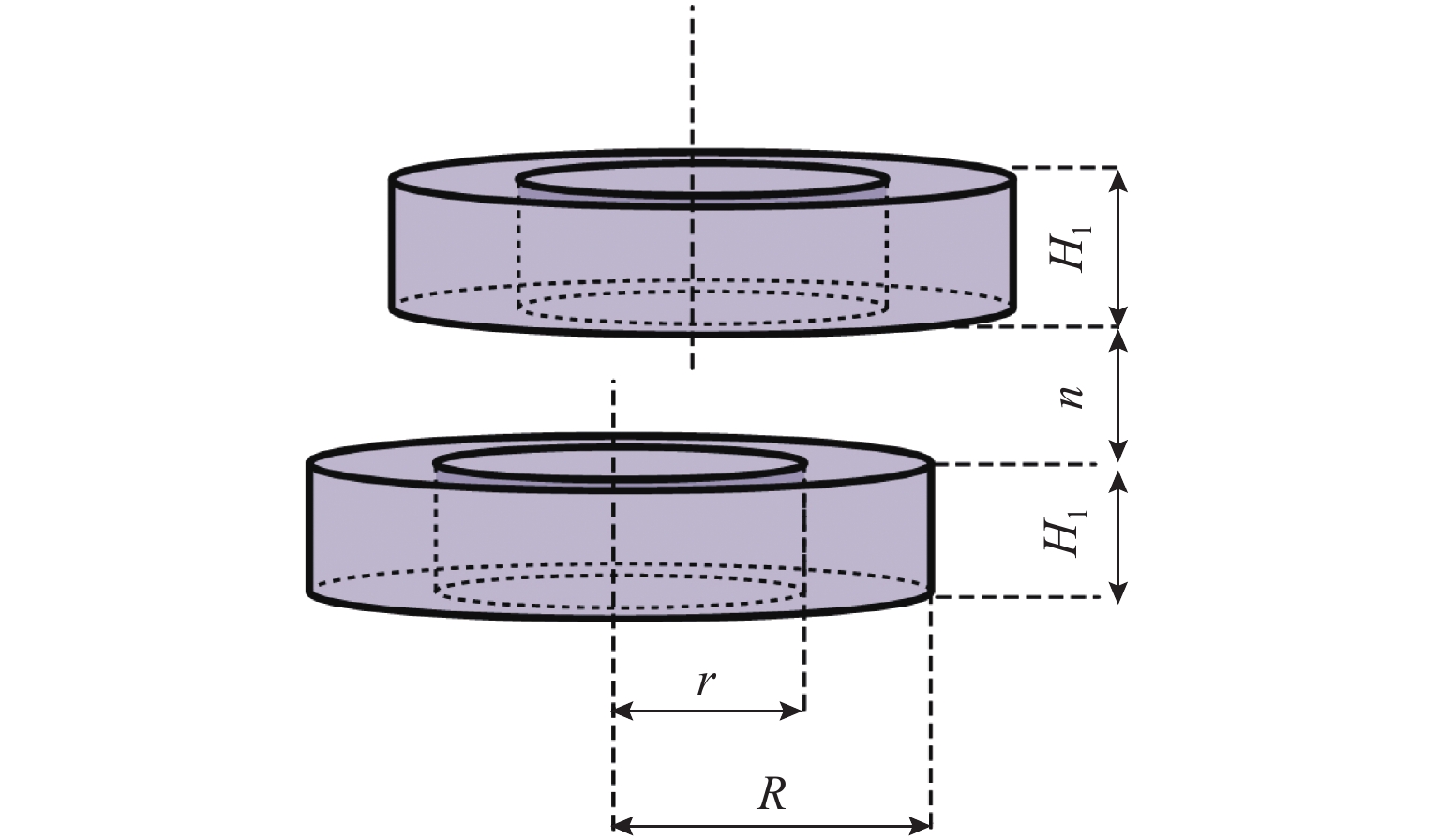
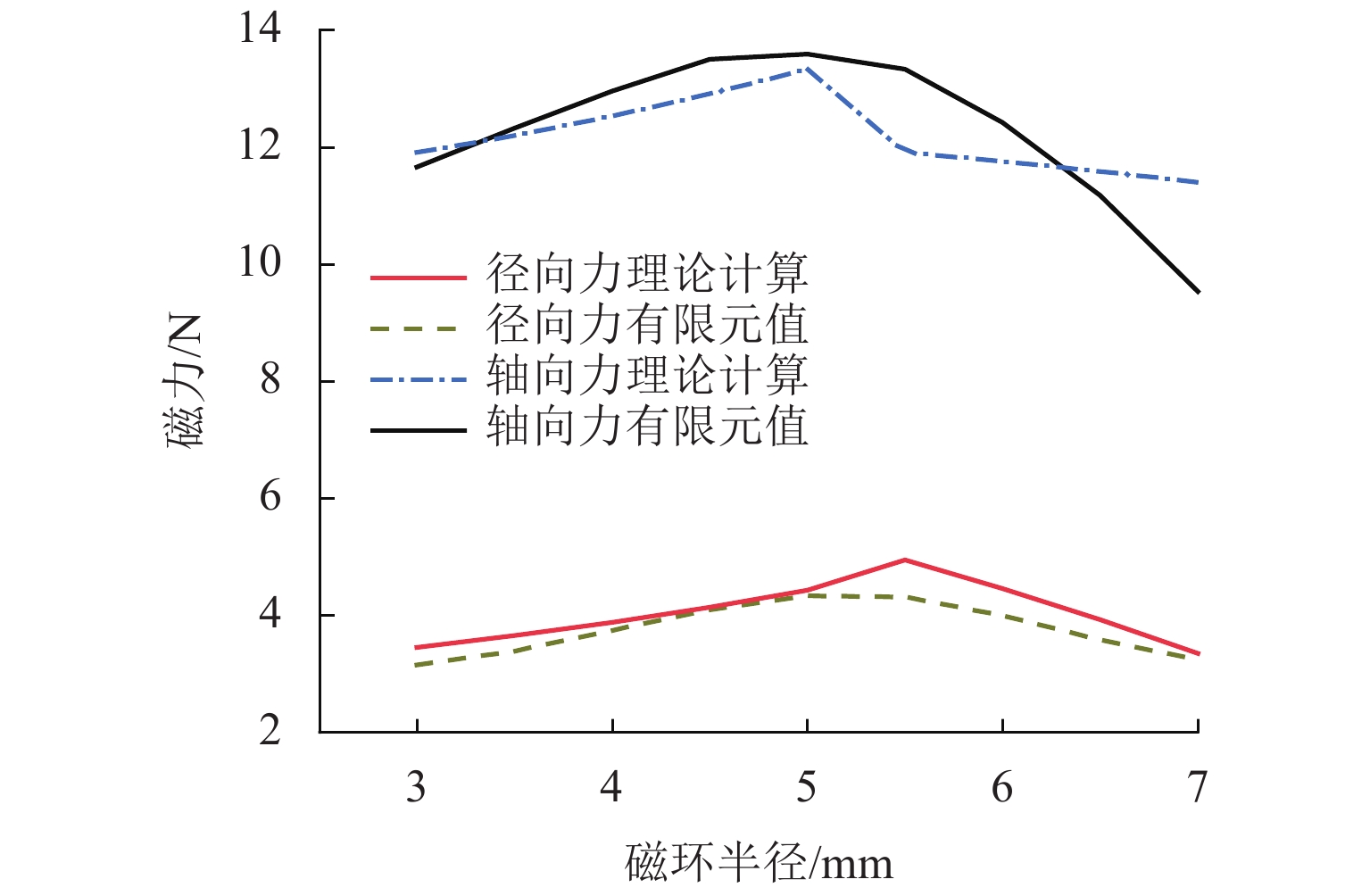
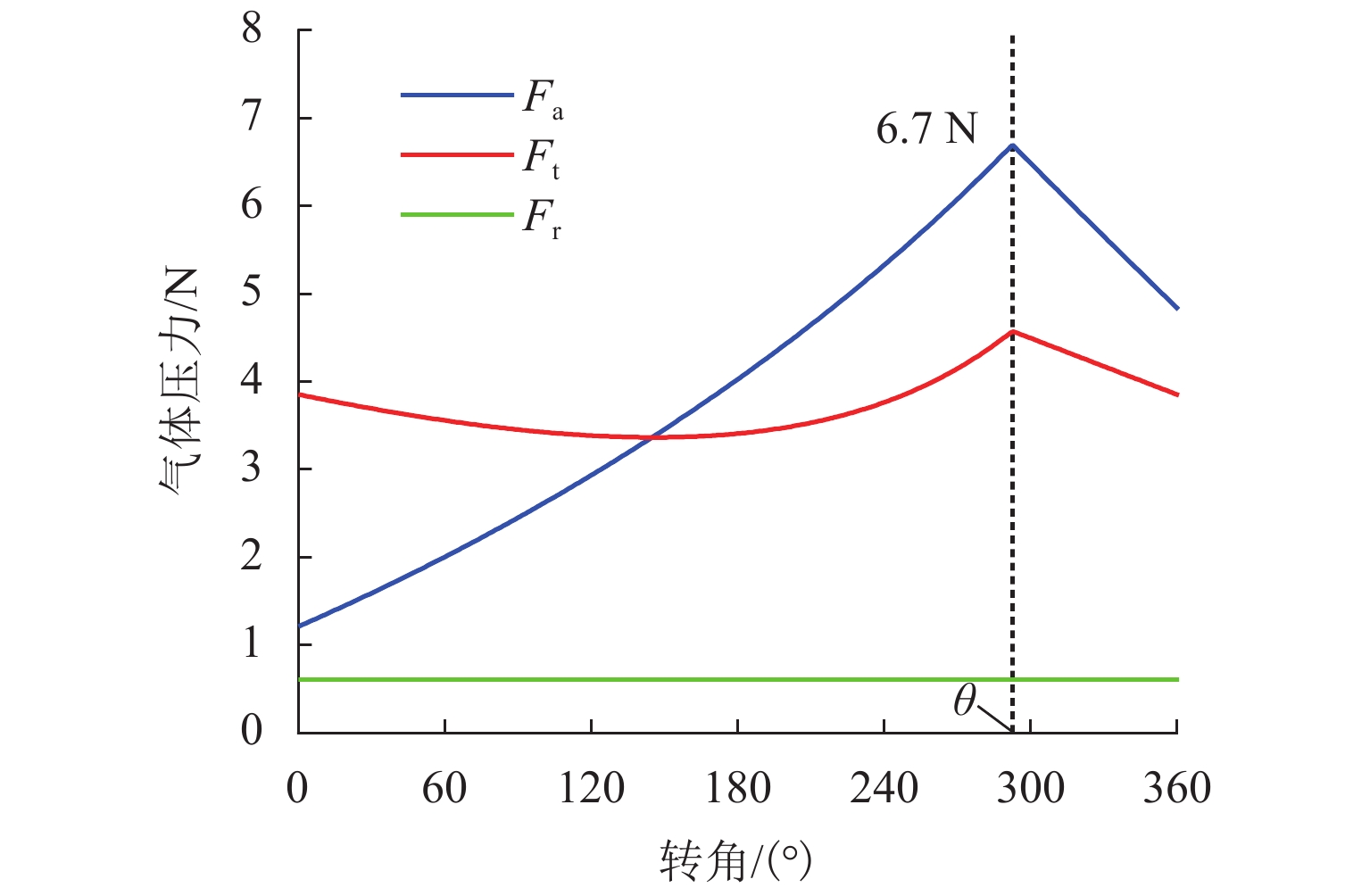
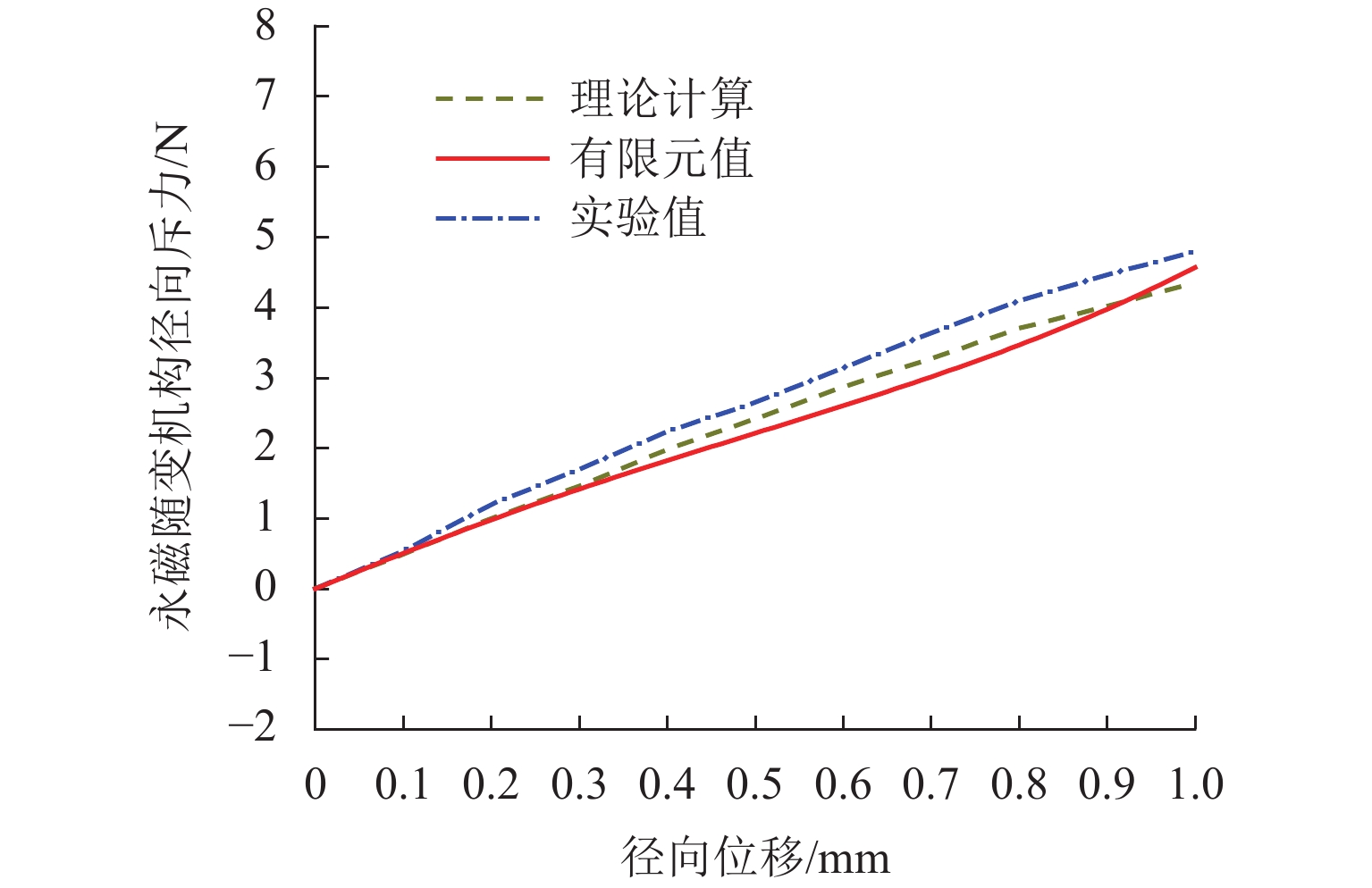
为减少涡旋压缩机运行时的机械接触，针对无油涡旋压缩机的结构特点提出一种永磁随变机构，并分析其力学特性. 首先，分析永磁随变机构的工作原理，采用虚位移法建立磁力模型，运用理论公式、有限元仿真和实验分析永磁随变机构工作气隙处的磁感应强度；其次，通过理论公式和有限元仿真，分析永磁随变机构结构参数与力学特性的关系；最后，通过磁力涡旋压缩机的性能参数和磁力测试实验对永磁随变机构的力学性能进行验证. 结果表明：永磁随变机构的径向磁力在一定范围内随着径向位移的增加而增加，随着轴向位移的增大而减小；在永磁随变机构工作中，径向位移与永磁随变机构刚度系数近似呈线性关系；在工作距离内永磁随变机构单组磁环的最小轴向磁力为8.73 N，在工作轨迹上的径向力为4.8 N，满足磁力涡旋压缩机的工作需求.
Abstract:To reduce the mechanical contact of scroll compressor during operation, a novel permanent magnetic compliance mechanism is proposed according to the structural characteristics of oil-free scroll compressor, and its mechanical properties are analyzed. Firstly, the working principle of the permanent magnetic compliance mechanism is analyzed, the magnetic force model is established by the virtual displacement method, and the magnetic induction intensity at the working air gap of permanent magnetic compliance mechanism is analyzed by using theoretical formula, finite element simulation and experimental measurements. Secondly, the relationship between structural parameters and mechanical characteristics of permanent magnetic compliance mechanism is analyzed by theoretical formula calculation and finite element simulation. Finally, the mechanical properties of the permanent magnetic compliance mechanism are verified by the performance parameters of the magnetic scroll compressor and the magnetic force test. The results show that within a certain range, the radial magnetic force of the permanent magnetic compliance mechanism is proportional to the radial displacement and inversely proportional to the axial displacement. Radial displacement has approximately linear relationship with stiffness coefficient when permanent magnetic compliance mechanism works. Within the working distance, the minimum axial magnetic force of the single group magnetic ring with permanent magnetic compliance mechanism is 8.73 N, and the radial force on working trajectory is 4.8 N, which meets the working requirements of the magnetic scroll compressor.
-
图 6 永磁随变机构的结构参数
Figure 6. Structural parameters of permanent magnetic compliance mechanism
图 7 径向磁力和轴向磁力与磁环内径的关系
Figure 7. Relationship between radial magnetic force, axialmagnetic force and inner diameter of magnetic ring
图 8 径向磁力和轴向磁力与磁环高度的关系
Figure 8. Relationship between radial magnetic force, axial magnetic force and height of magnetic ring
图 9 径向磁力和轴向磁力与轴向位移的关系
Figure 9. Relationship between radial magnetic force, axialmagnetic force and axial displacement
图 11 轴向磁力与径向位移关系
Figure 11. Relationship between axial magnetic force and radial displacement
图 12 径向磁力与径向位移关系
Figure 12. Relationship between radial magnetic force and radial displacement
表 1 压缩机型线参数
Table 1. Parameters of scroll compressor profile
参数 取值 节距/mm 8 齿高/mm 10 齿厚/mm 3 圈数/圈 2 旋转半径/mm 1 基圆半径/mm 1.27 吸气角/（°） 0 θ/（°） 293 压缩比 3 泄露系数 1.2 排气量/mm3 1508 
下载: 导出CSV
-
[1] 李超,赵荣珍,刘振全. 涡旋压缩机径向随变机构动力学模型研究[J]. 压缩机技术,2004(3): 7-8,22. doi: 10.3969/j.issn.1006-2971.2004.03.003LI Chao, ZHAO Rongzhen, LIU Zhenquan. Study of kinetics model of scroll compressor with radial compliance mechanism[J]. Compressor Technology, 2004(3): 7-8,22. doi: 10.3969/j.issn.1006-2971.2004.03.003 [2] 刘兴旺,王华,刘振全,等. 一种变频涡旋压缩机的径向密封机构[J]. 压缩机技术,2007(4): 1-3. doi: 10.3969/j.issn.1006-2971.2007.04.001LIU Xingwang, WANG Hua, LIU Zhenquan, et al. A radial sealing mechanism of inverter scroll compressor[J]. Compressor Technology, 2007(4): 1-3. doi: 10.3969/j.issn.1006-2971.2007.04.001 [3] 赵嫚,李超,俞树荣,等. 径向随变机构对涡旋压缩机转子系平衡影响分析[J]. 化工机械,2012,39(6): 732-735. doi: 10.3969/j.issn.0254-6094.2012.06.012ZHAO Man, LI Chao, YU Shurong, et al. Radial compliance mechanism effect on rotor balancing system for scroll compressor[J]. Chemical Engineering & Machinery, 2012, 39(6): 732-735. doi: 10.3969/j.issn.0254-6094.2012.06.012 [4] 陶文. 涡旋机械涡旋槽式轴向随变机构的动态特性研究[D]. 兰州: 兰州理工大学, 2013. [5] FORNI R J. Scroll pump having axially compliant spring element: US9360013[P]. 2016-06-07. [6] TANG Y, HUNG C, CHANG Y. Performance improvements in low side scroll compressor with extended operation speeds[J]. Applied Thermal Engineering, 2011, 31(16): 3542-3551. doi: 10.1016/j.applthermaleng.2011.07.009 [7] JU J T, WANG J A, WANG Y F, et al. Suspension force analysis of six-pole radial-axial magnetic bearing for energy storage flywheel[J]. International Journal of Modern Physics B, 2020, 34(1/2/3): 2040066.1-2040066.7. [8] ZHANG X, LIU X, HAN B C, et al. Magnetic circuit designing and structural optimisation for a three degree-of-freedom hybrid magnetic bearing[J]. IET Electric Power Applications, 2018, 12(8): 1082-1089. doi: 10.1049/iet-epa.2017.0792 [9] 黎松奇,张昆仑. 单磁铁悬浮系统自激振动的稳定性分析及抑制[J]. 西南交通大学学报,2015,50(3): 410-416. doi: 10.3969/j.issn.0258-2724.2015.03.004LI Songqi, ZHANG Kunlun. Self-excited vibration of single-magnet suspension system: stability analysis and inhibition[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 410-416. doi: 10.3969/j.issn.0258-2724.2015.03.004 [10] ZHU H Q, WANG S S. Decoupling control based on linear/non-linear active disturbance rejection switching for three-degree-of-freedom six-pole active magnetic bearing[J]. IET Electric Power Applications, 2020, 14(10): 1818-1827. doi: 10.1049/iet-epa.2019.0448 [11] SHEH ZAD H, KHAN T I, LAZOGLU I. Design and adaptive sliding-mode control of hybrid magnetic bearings[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2537-2547. doi: 10.1109/TIE.2017.2739682 [12] KANDIL A. Investigation of the whirling motion and rub/impact occurrence in a 16-pole rotor active magnetic bearings system with constant stiffness[J]. Nonlinear Dynamics, 2020, 102(4): 2247-2265. doi: 10.1007/s11071-020-06071-x [13] 孙凤,张明,孙兴伟,等. 3自由度等刚度永磁弹簧的尺寸参数特性研究[J]. 机械设计与制造,2018(9): 41-44. doi: 10.3969/j.issn.1001-3997.2018.09.011SUN Feng, ZHANG Ming, SUN Xingwei, et al. Study on dimensional parameters’ characteristics of 3 DOF same-stiffness permanent magnetic spring[J]. Machinery Design & Manufacture, 2018(9): 41-44. doi: 10.3969/j.issn.1001-3997.2018.09.011 [14] 孙凤,张明,孙兴伟,等. 三自由度等刚度永磁弹簧的力学特性研究[J]. 中国机械工程,2015,26(8): 1005-1009. doi: 10.3969/j.issn.1004-132X.2015.08.003SUN Feng, ZHANG Ming, SUN Xingwei, et al. Study on mechanics characteristics of 3-DOF same-stiffness permanent magnetic spring[J]. China Mechanical Engineering, 2015, 26(8): 1005-1009. doi: 10.3969/j.issn.1004-132X.2015.08.003 [15] KIM K B, IM S H, UM D Y, et al. Comparison of magnetic levitation systems using ring-shaped permanent magnets[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-4. [16] 刘强,赵明师,韩邦成,等. 永磁偏置径向磁轴承能量优化与实验[J]. 光学 精密工程,2019,27(11): 2420-2428. doi: 10.3788/OPE.20192711.2420LIU Qiang, ZHAO Mingshi, HAN Bangcheng, et al. Energy optimization and experimental for a permanent magnet-biased redial magnetic bearing[J]. Optics and Precision Engineering, 2019, 27(11): 2420-2428. doi: 10.3788/OPE.20192711.2420 [17] 孙凤,唐敬虎,李强,等. 可变磁路式永磁悬浮系统刚度特性分析及变刚度控制[J]. 振动与冲击,2020,39(7): 132-139.SUN Feng, TANG Jinghu, LI Qiang, et al. Stiffness characteristics analysis and variable stiffness control for a permanent magnetic levitation system with variable magnetic circuit[J]. Journal of Vibration and Shock, 2020, 39(7): 132-139. [18] XU F Q, LU X, ZHENG T, et al. Motion control of a magnetic levitation actuator based on a wrench model considering yaw angle[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8545-8554. doi: 10.1109/TIE.2019.2949519 [19] ZHANG X D, TRAKARNCHAIYO C, ZHANG H, et al. MagTable:a tabletop system for 6-DOF large range and completely contactless operation using magnetic levitation[J]. Mechatronics, 2021, 77: 102600.1-102600.10. doi: 10.1016/j.mechatronics.2021.102600 [20] 刘振全. 涡旋式流体机械与涡旋压缩机[M]. 北京: 机械工业出版社, 2009. -
下载:
点击查看大图
计量
- 文章访问数: 201
- HTML全文浏览量: 98
- PDF下载量: 5
- 被引次数: 0