Floating Control Method for Permanent Magnetic Levitation Platform with Variable Flux Path
-
摘要:
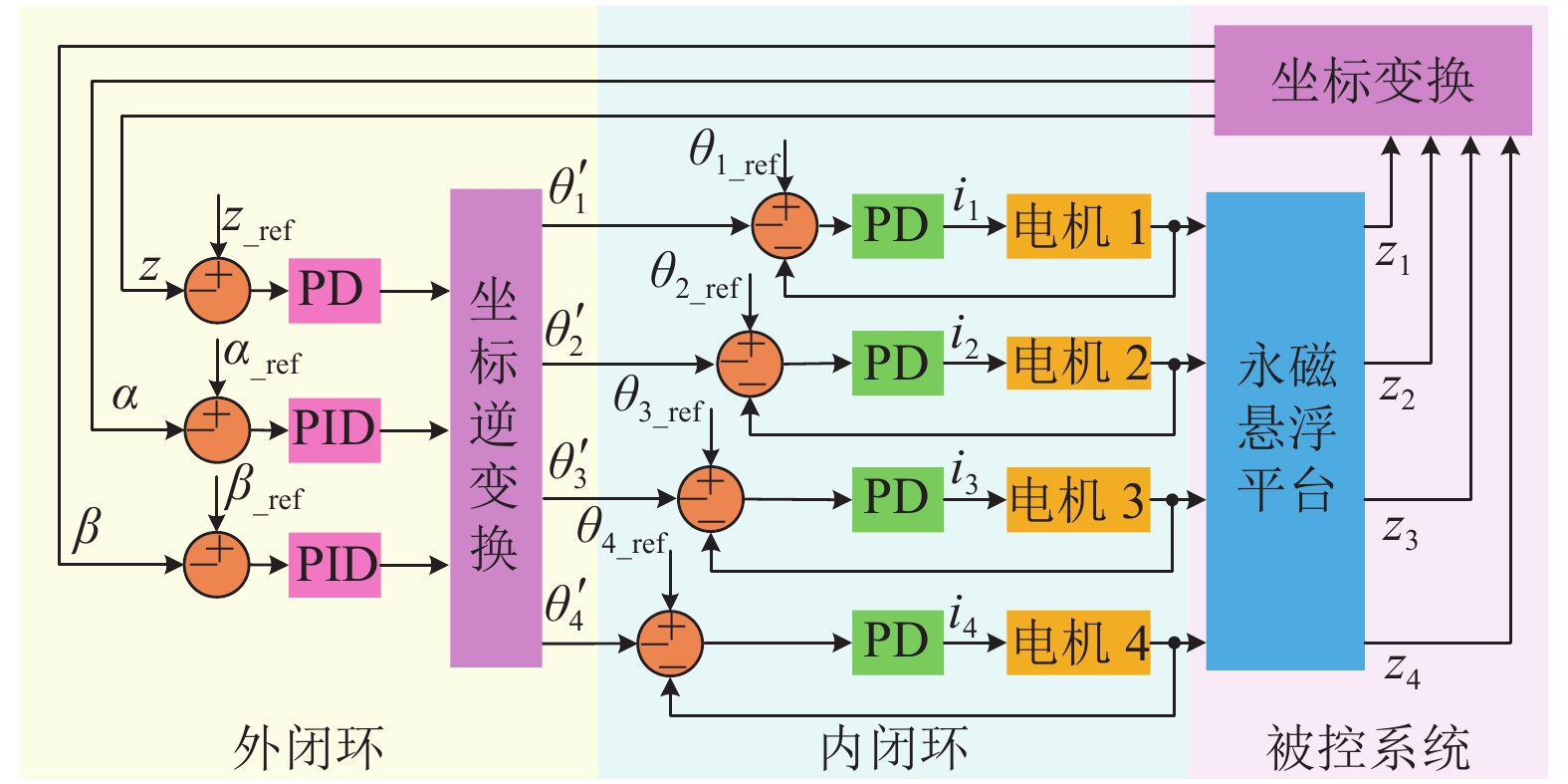
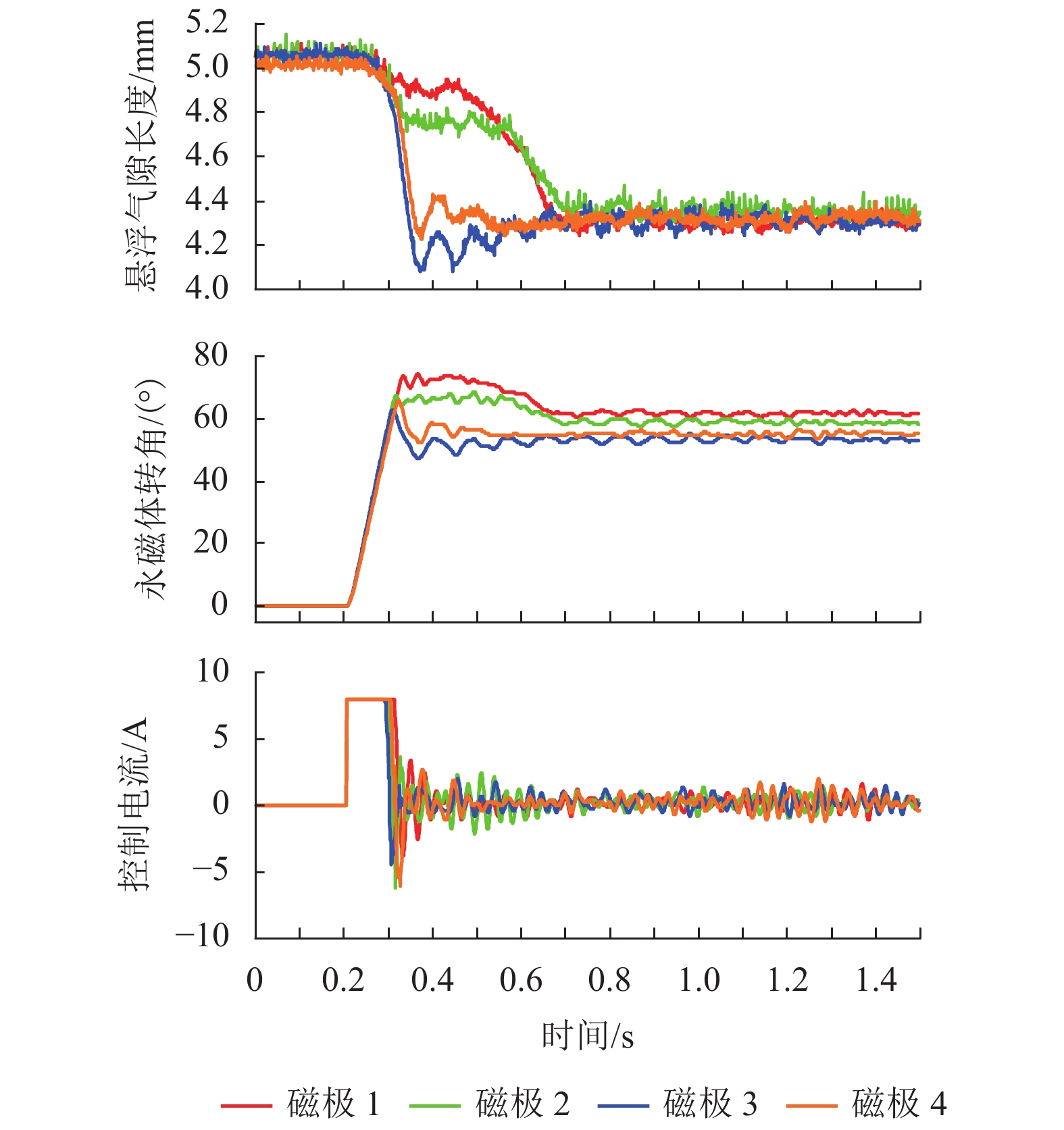
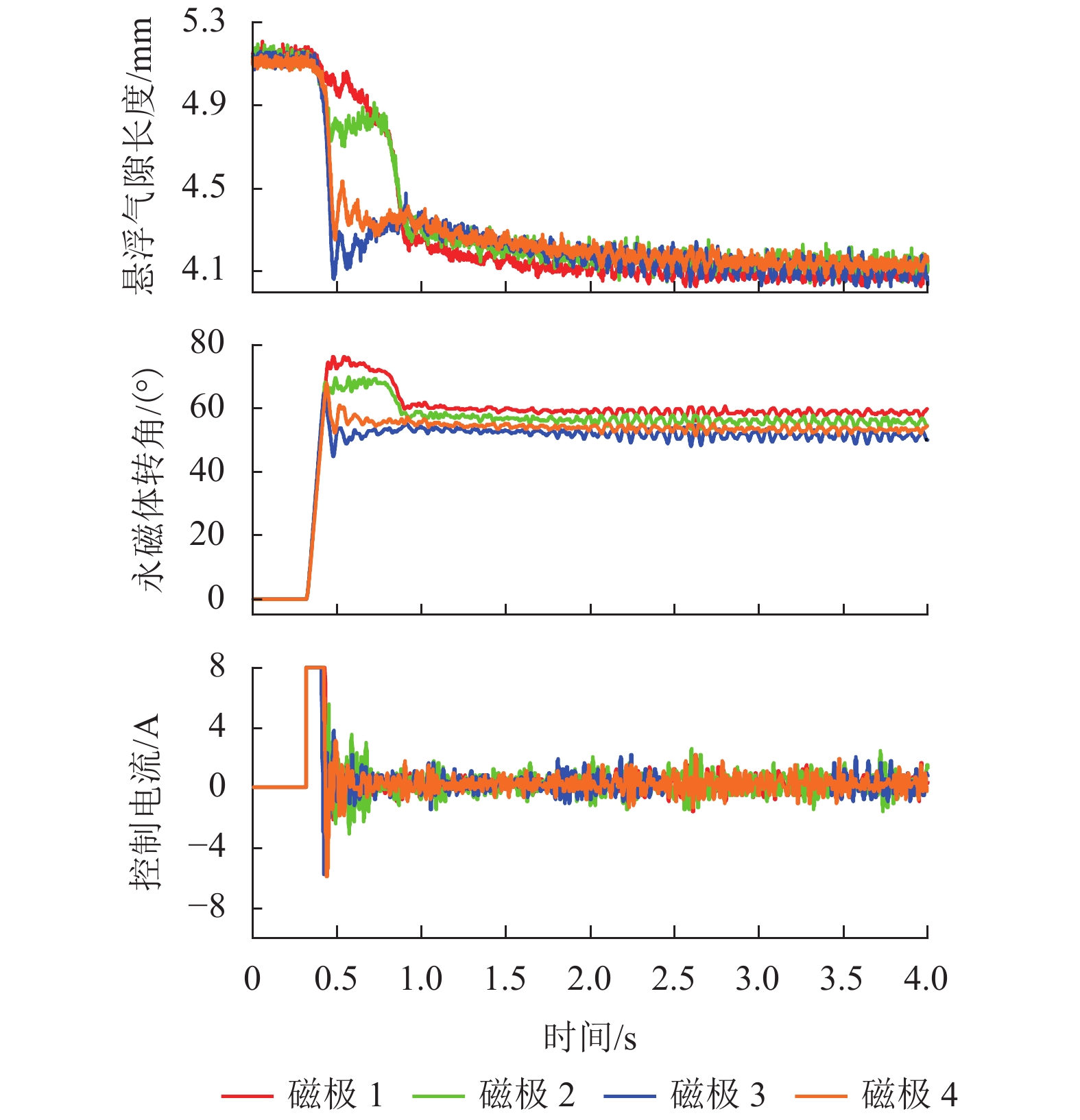
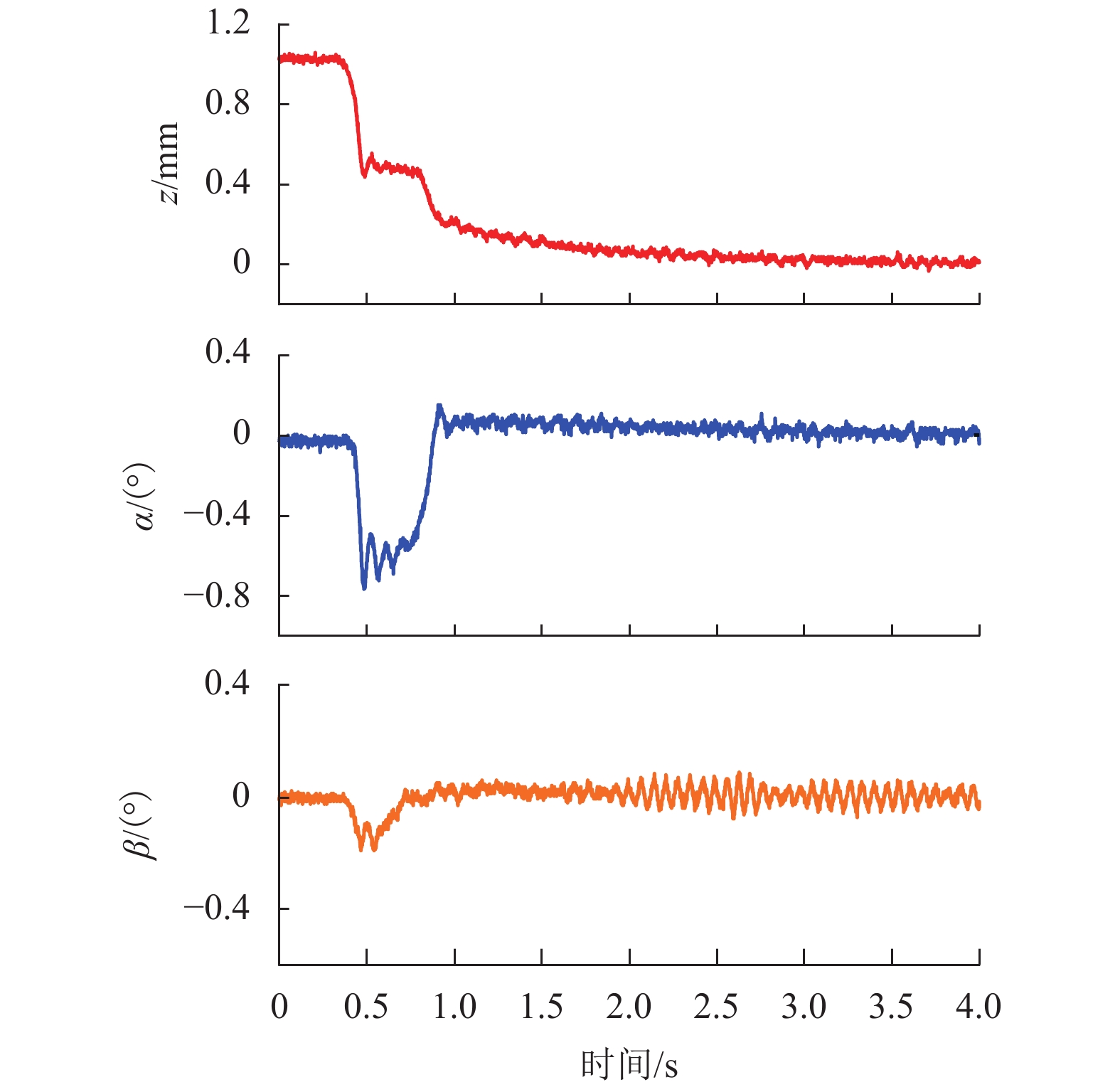
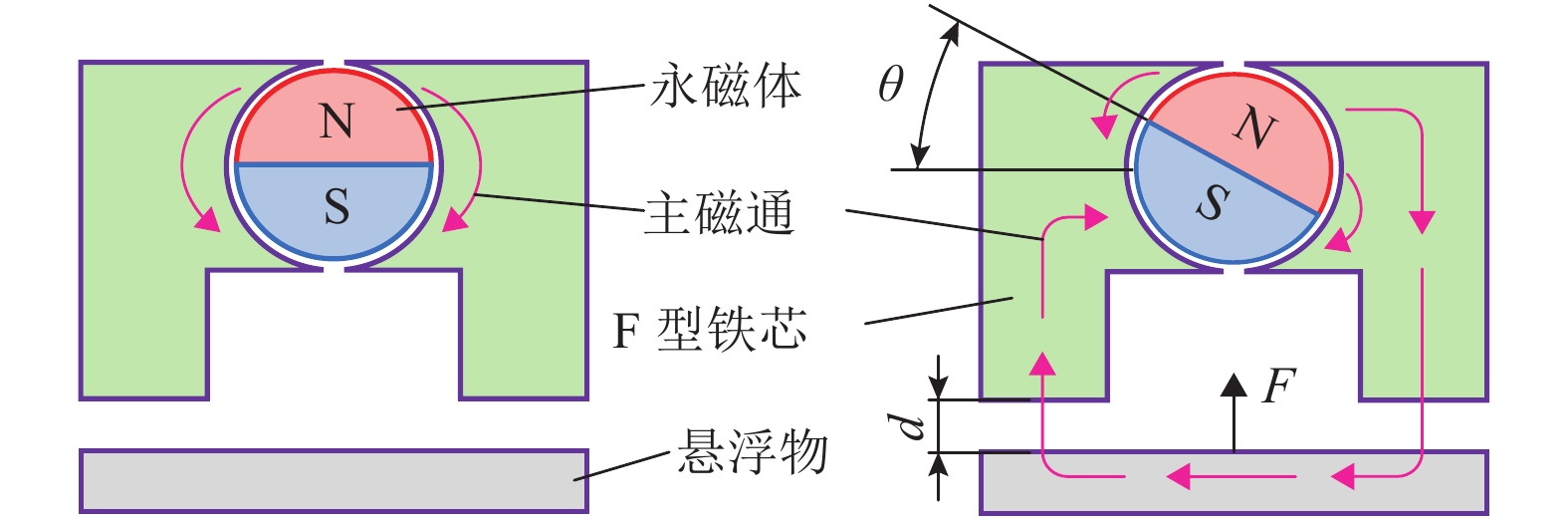
磁悬浮技术应用于超洁净传送，可有效减少粉尘污染. 可变磁路式永磁悬浮平台具有低功耗、抗吸附的特性，可避免电磁悬浮传送平台温升大和混合磁悬浮平台安全性差的弊端. 为解决永磁悬浮平台起浮过程易发散的问题，提出并验证分散控制、集中控制和积分分离法3种起浮控制方法. 首先，分析可变磁路式永磁悬浮平台的磁力控制原理，建立系统动力学模型，并采用分散控制实现悬浮平台起浮；然后，针对起浮后平台倾斜的问题，提出了三自由度集中控制方法，其中平台的垂向控制为PD （proportional differential），侧倾与俯仰方向为PID（proportional integral differential ）；最后，应用积分分离法进行分段控制，以实现垂向的精确定位. 研究结果表明：集中控制方法实现了平台倾斜角的自纠偏，可有效解决分散控制下各磁极磁力特性差异引起的平台倾斜问题，调节时间为0.5 s；垂向采用积分分离方法后，平台垂向的稳态误差由0.23 mm可减小为0，调节时间为3.0 s.
Abstract:Application of the magnetic levitation technology in ultra-clean transmission can effectively reduce dust pollution. The permanent magnetic levitation platform with a variable flux path has the characteristics of low-power consumption and anti-adsorption, which can avoid the large temperature rise in electromagnetic levitation systems and poor safety of hybrid electromagnetic levitation systems. To avoid the instability in the floating, three floating control methods are presented and validated, which are decentralized control, centralized control and integral separation. At first, the magnetic-force control mechanism of the platform is analyzed to build its dynamic model, and the decentralized control strategy is adopted to realize the floating. Furthermore, a 3-DOF centralized control strategy is proposed to prevent platform tilt, in which the vertical controller is PD (proportional differential) and the rolling and pitching are controlled by PID (proportional integral differential). Finally, the integral separation method is used for subsection control to realize the accurate vertical positioning. The results indicate that the centralized control method realizes the self-correction of the platform tilt angle with the adjustment time of 0.5 s, which solves the platform tilt caused by the magnetic characteristics difference of each pole in the decentralized control. Moreover, when using the integral separation method, the vertical steady-state error of the platform can be reduced from 0.23 mm to 0 with the adjustment time of 3.0 s.
-
图 14 积分分离控制起浮实验结果
Figure 14. Results of floating experiments with integral separation method
-
[1] 邓自刚,张勇,王博,等. 真空管道运输系统发展现状及展望[J]. 西南交通大学学报,2019,54(5): 1063-1072. doi: 10.3969/j.issn.0258-2724.20180204DENG Zigang, ZHANG Yong, WANG Bo, et al. Present situation and prospect of evacuated tube transportation system[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 1063-1072. doi: 10.3969/j.issn.0258-2724.20180204 [2] 徐园平,周瑾,金超武,等. 抗磁悬浮研究综述[J]. 机械工程学报,2019,55(2): 214-222.XU Yuanping, ZHOU Jin, JIN Chaowu, et al. Diamagnetic levitation: a review[J]. Journal of Mechanical Engineering, 2019, 55(2): 214-222. [3] 巩磊,杨智,祝长生. 主动电磁轴承-刚性转子系统加速响应的鲁棒性[J]. 电工技术学报,2021,36(2): 268-281.GONG Lei, YANG Zhi, ZHU Changsheng. Acceleration responses robustness of active magnetic bearings-rigid rotor system[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 268-281. [4] 段吉安,郭宁平,周海波. 一种新型磁悬浮直线运动平台的热分析[J]. 中国电机工程学报,2011,31(15): 114-120.DUAN Ji’an, GUO Ningping, ZHOU Haibo. Thermal analysis of a novel linear maglev transportation platform[J]. Proceedings of the CSEE, 2011, 31(15): 114-120. [5] KIM J, HA C W, KING G B, et al. Experimental development of levitation control for a high-accuracy magnetic levitation transport system[J]. ISA Transactions, 2020, 101: 358-365. [6] COEY J M D. Perspective and prospects for rare earth permanent magnets[J]. Engineering, 2020, 6(2): 119-131. [7] MORISHITA M, AZUKIZAWA T, KANDA S, et al. A new MAGLEV system for magnetically levitated carrier system[J]. IEEE Transactions on Vehicular Technology, 1989, 38(4): 230-236. [8] KIM K J, HAN H S, KIM C H, et al. Dynamic analysis of a maglev conveyor using an EM-PM hybrid magnet[J]. Journal of Electrical Engineering and Technology, 2013, 8(6): 1571-1578. [9] OKA K, TOSHIRO H, TAKUYA S. Hanging type MAGLEV system with permanent magnet motion control[J]. IEEJ Transactions on Industry Applications, 1999, 119(3): 291-297. [10] 孙凤,韦伟,金嘉琦,等. 永磁悬浮非接触回转驱动系统[J]. 机械工程学报,2017,53(20): 192-201.SUN Feng, WEI Wei, JIN Jiaqi, et al. Non-contact rotation driving system using permanent-magnetic suspension[J]. Journal of Mechanical Engineering, 2017, 53(20): 192-201. [11] LIN J, OKA K, HARADA A. Zero-power tip-tilt control of a magnetically levitated platform by lateral displacement of hybrid-electromagnets[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 66(1): 63-74. [12] ZHAO C, OKA K, SUN F, et al. Design of zero-power control strategy with resisting tilt of hybrid magnetic levitation system[J/OL]. IEEE Transactions on Industrial Electronics, 2021: 3121670.1-3121670.10.[2021-10-22]. https://ieeexplore.ieee.org/document/9592690 [13] UENO T, HIGUCHI T. Zero-power magnetic levitation using composite of magnetostrictive/piezoelectric materials[J]. IEEE Transactions on Magnetics, 2007, 43(8): 3477-3482. [14] ISHIBASHI N, MIZUNO T, ISHINO Y, et al. The proposal of magnetic suspension using laterally control flux-path mechanism[J]. Actuators, 2017, 6(1): 11. [15] OKA K, YAMAMOTO K, HARADA A. Magnetic suspension mechanism using rotary permanent magnets[J]. International Journal of Applied Electromagnetics and Mechanics, 2020, 64(1/2/3/4): 977-983. [16] SUN F, OKA K, JIN J J. A zero suspension force improvement method of a permanent magnetic suspension device[J]. International Journal of Applied Electromagnetics and Mechanics, 2013, 41(1): 1-12. [17] 李强,唐敬虎,孙凤,等. 可变磁路式永磁悬浮系统的防跌落防吸附控制[J]. 仪器仪表学报,2019,40(3): 246-254.LI Q, TANG J H, SUN F, et al. Anti-fall and anti-adsorption control of permanent magnetism levitation system with flux path control[J]. Chinese Journal of Scientific Instrument, 2019, 40(3): 246-254. [18] ZHAO C, SUN F, JIN J J, et al. Analysis of quasi-zero power characteristic for a permanent magnetic levitation system with a variable flux path control mechanism[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(1): 437-447. -
下载:
点击查看大图
计量
- 文章访问数: 346
- HTML全文浏览量: 137
- PDF下载量: 24
- 被引次数: 0