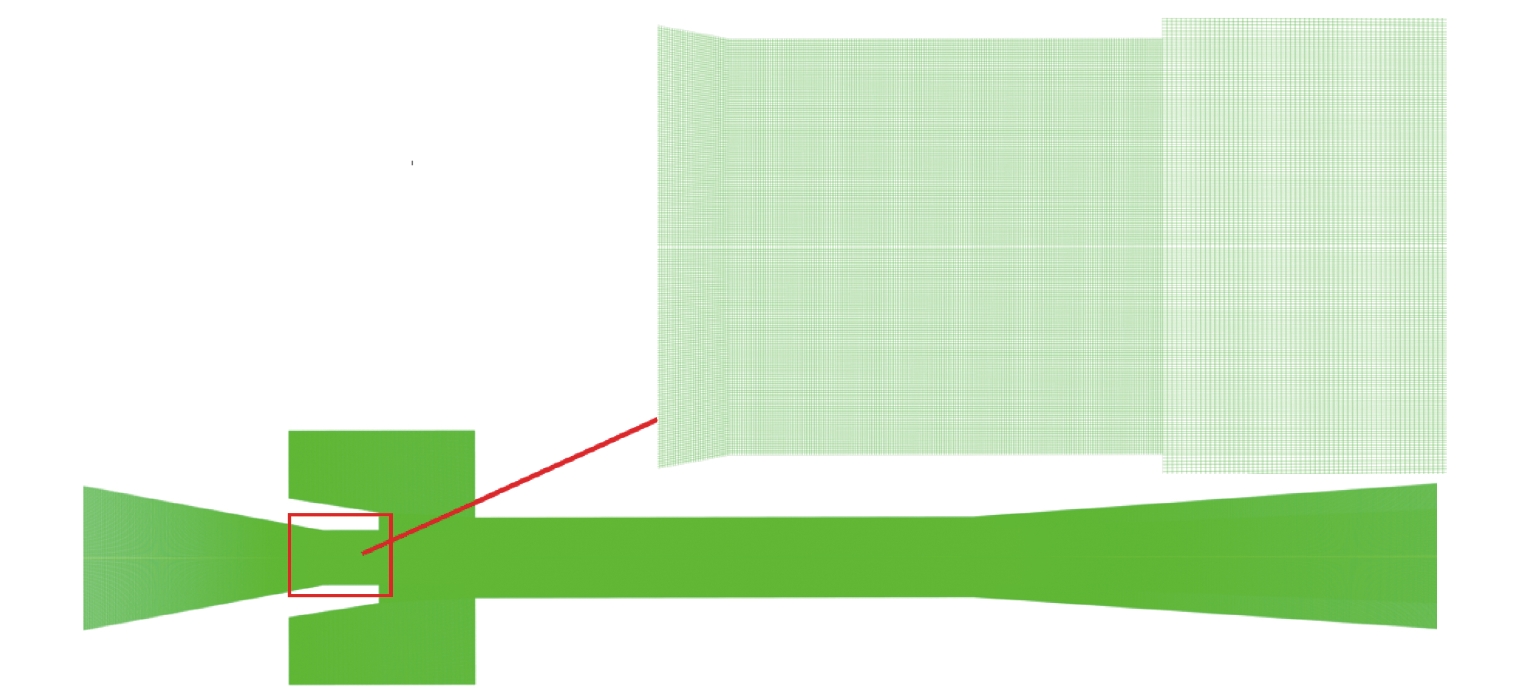
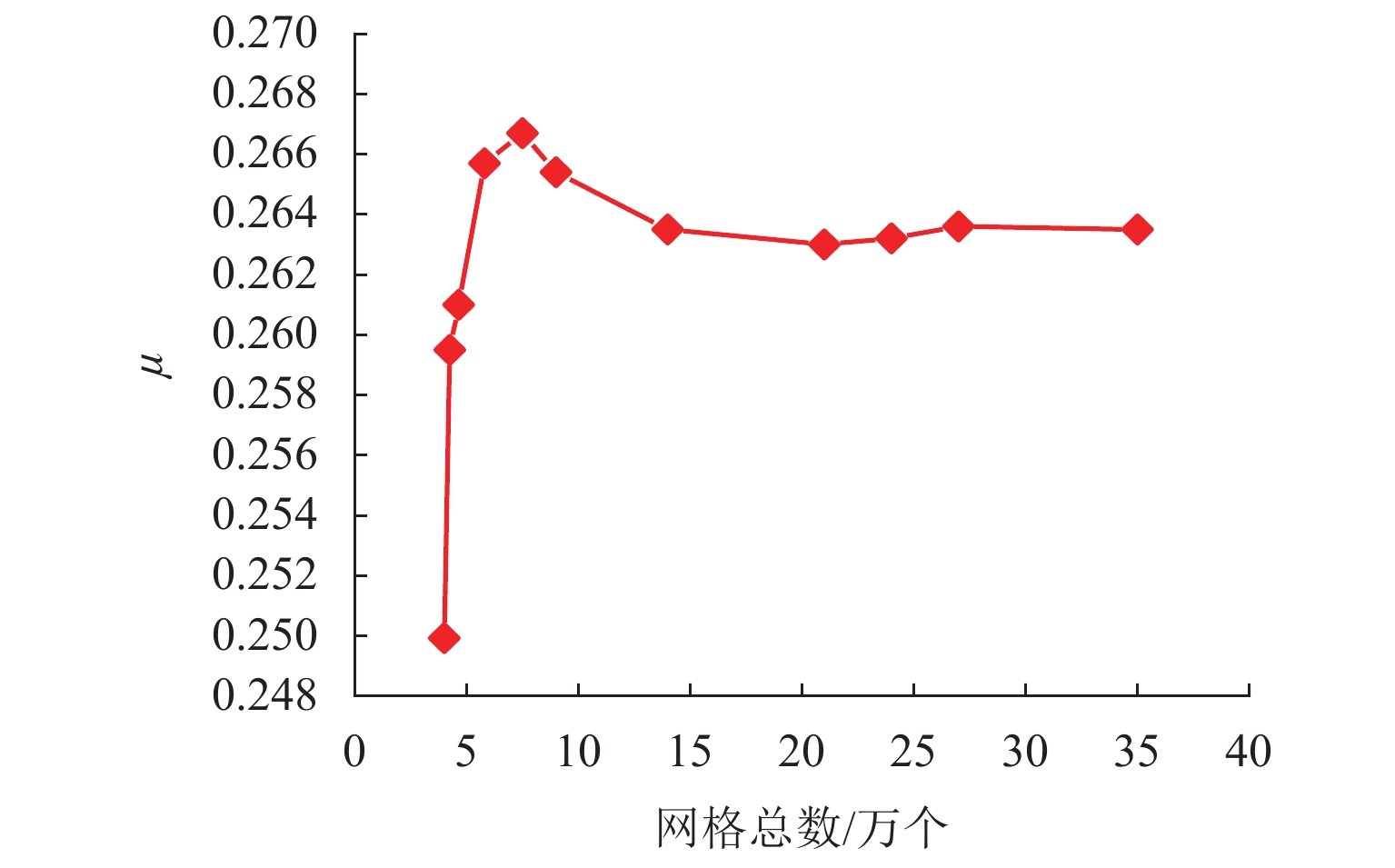
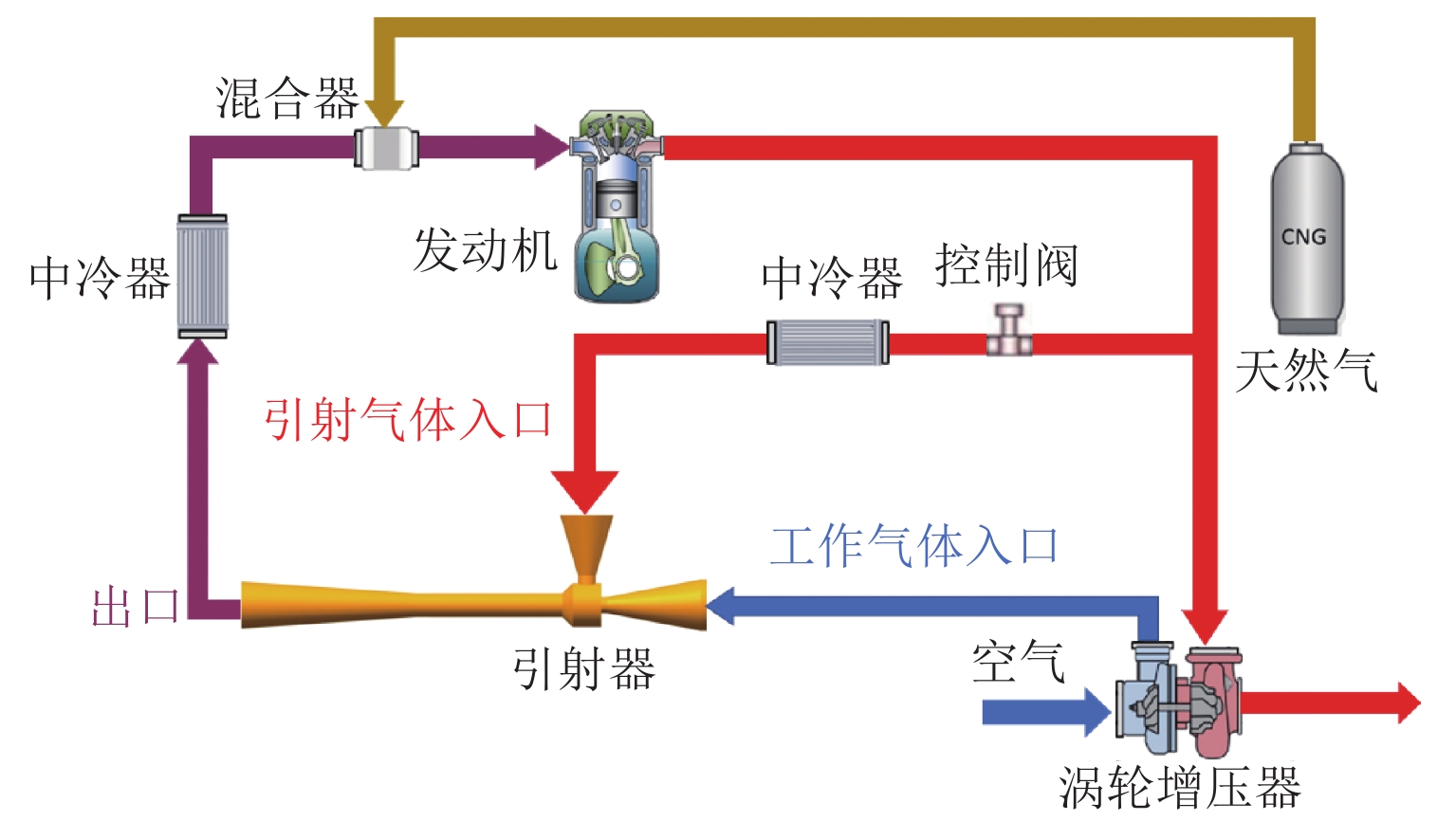
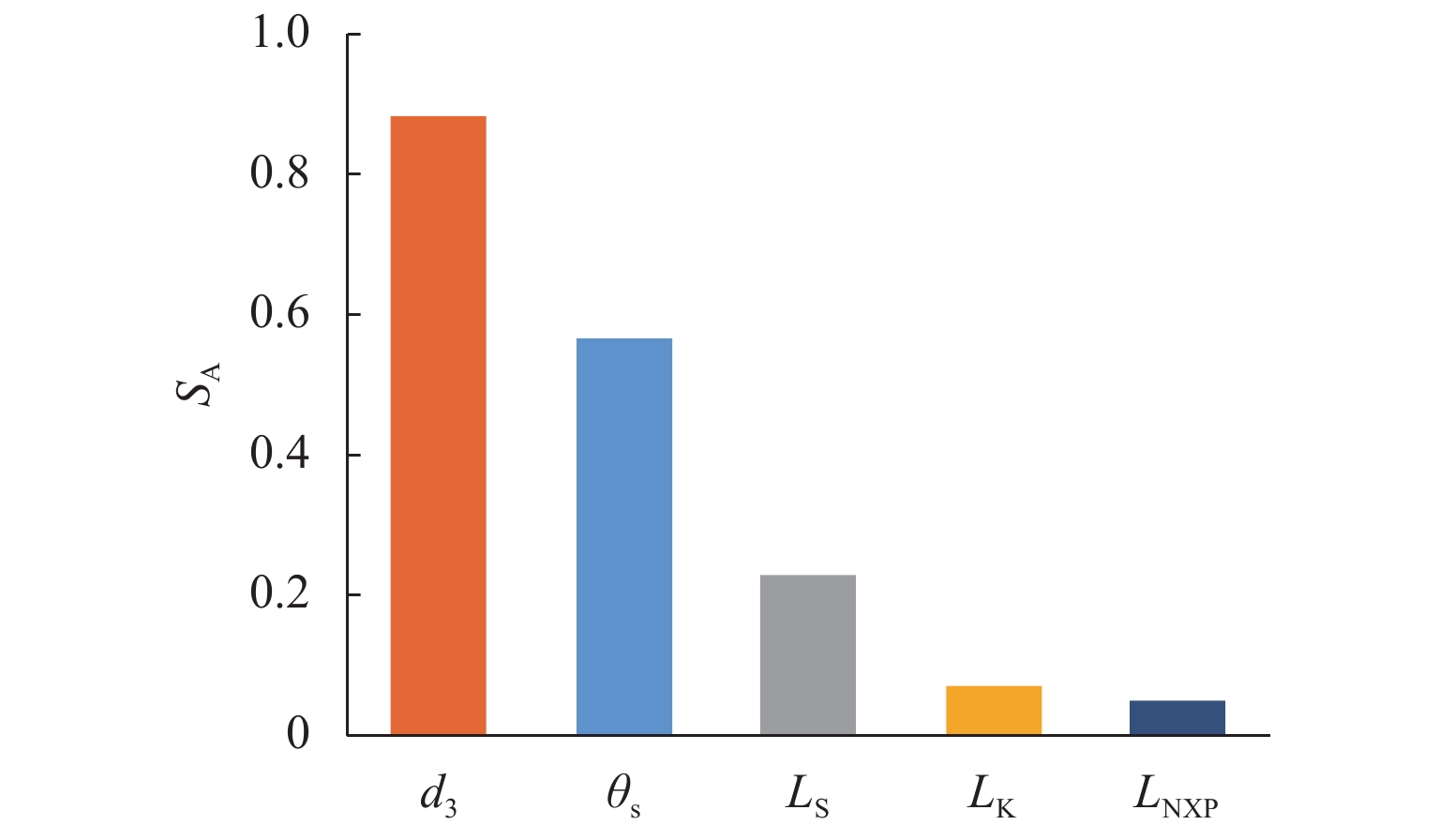Simulation Research on Ejector for Natural Gas Engine with High Exhaust Gas Recirculation Rate
-
摘要:
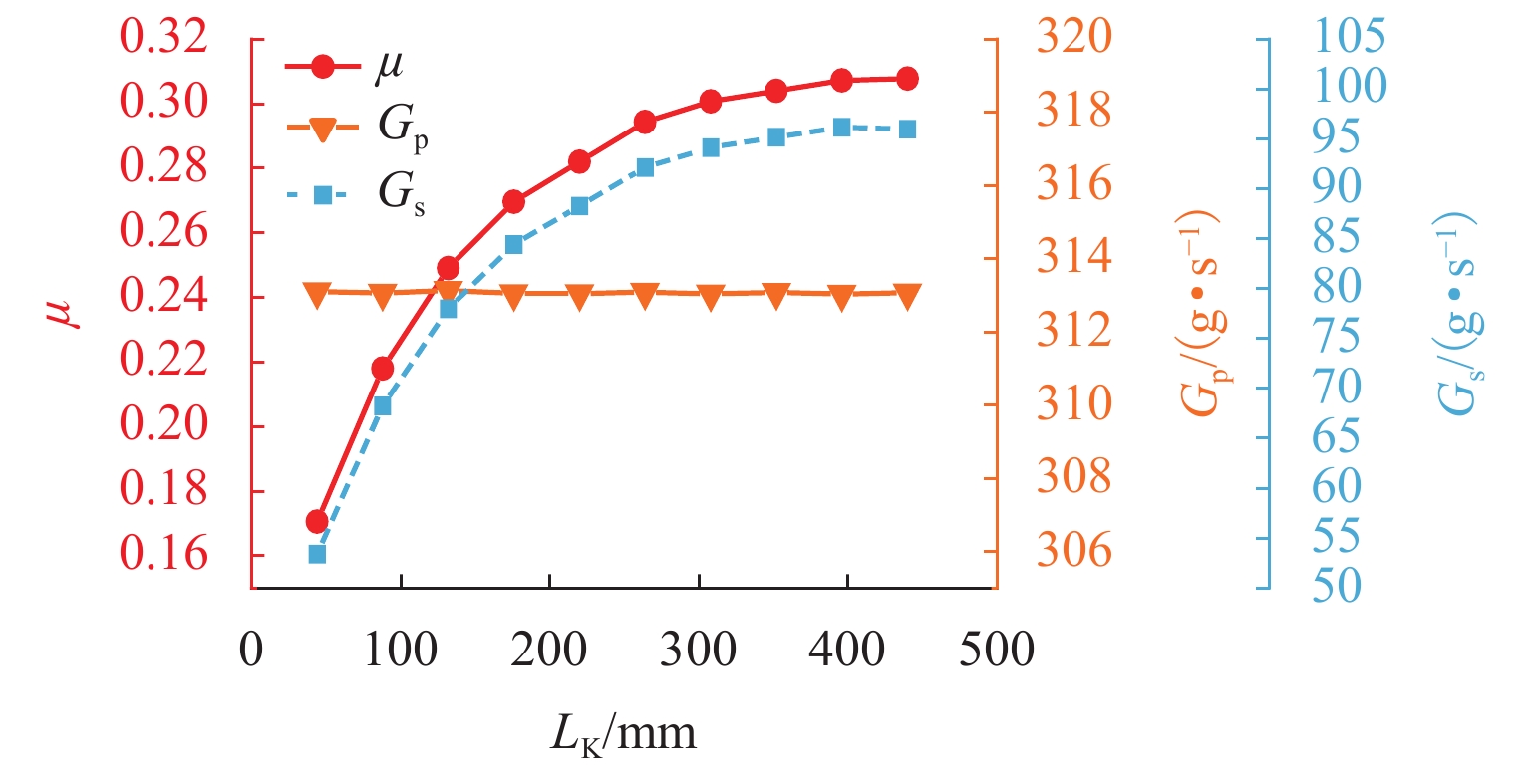
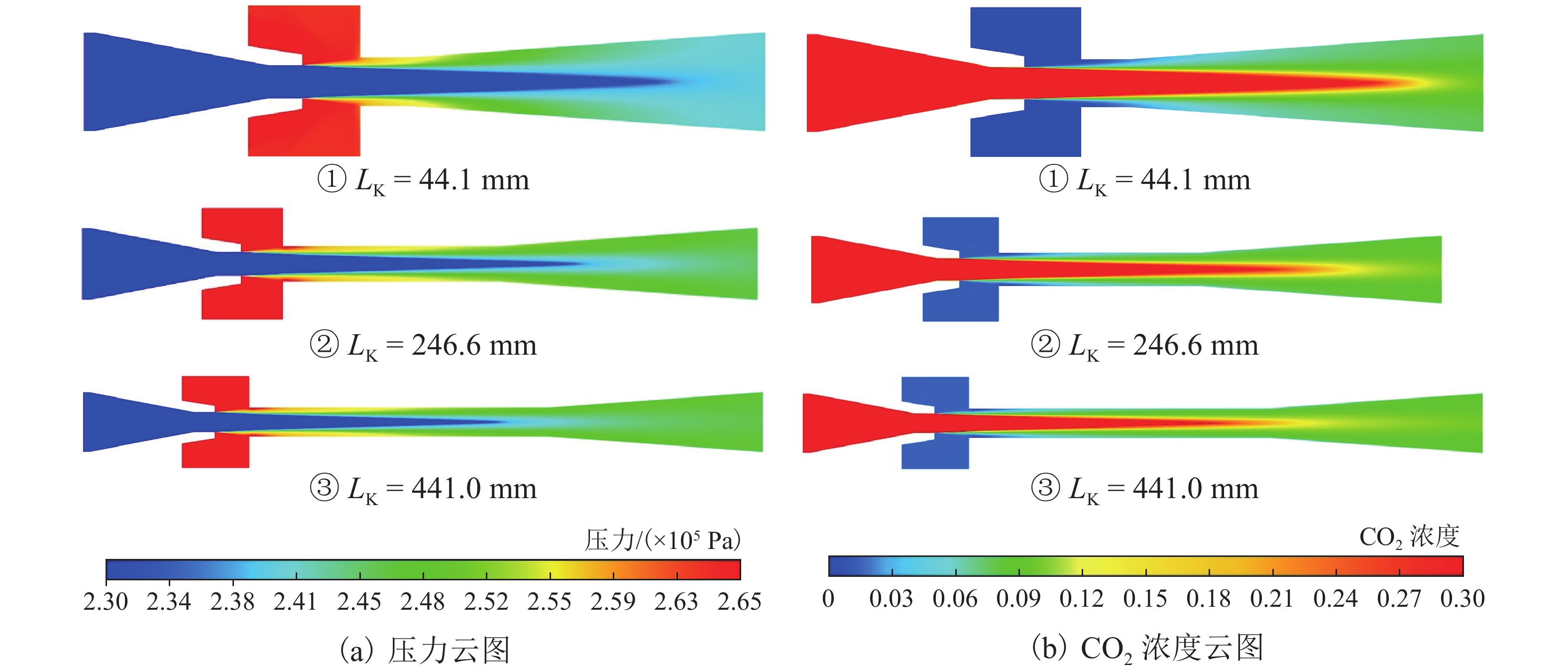
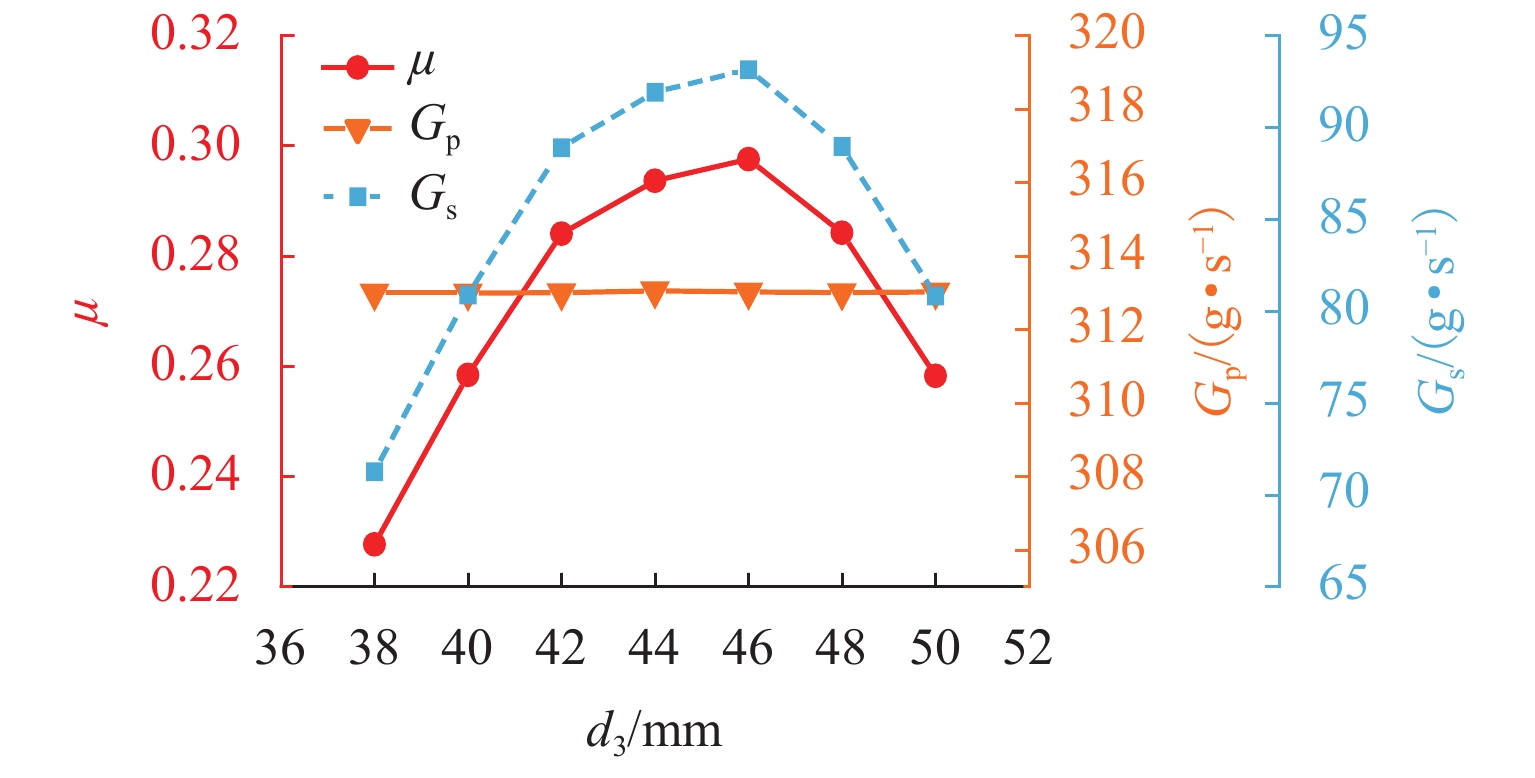
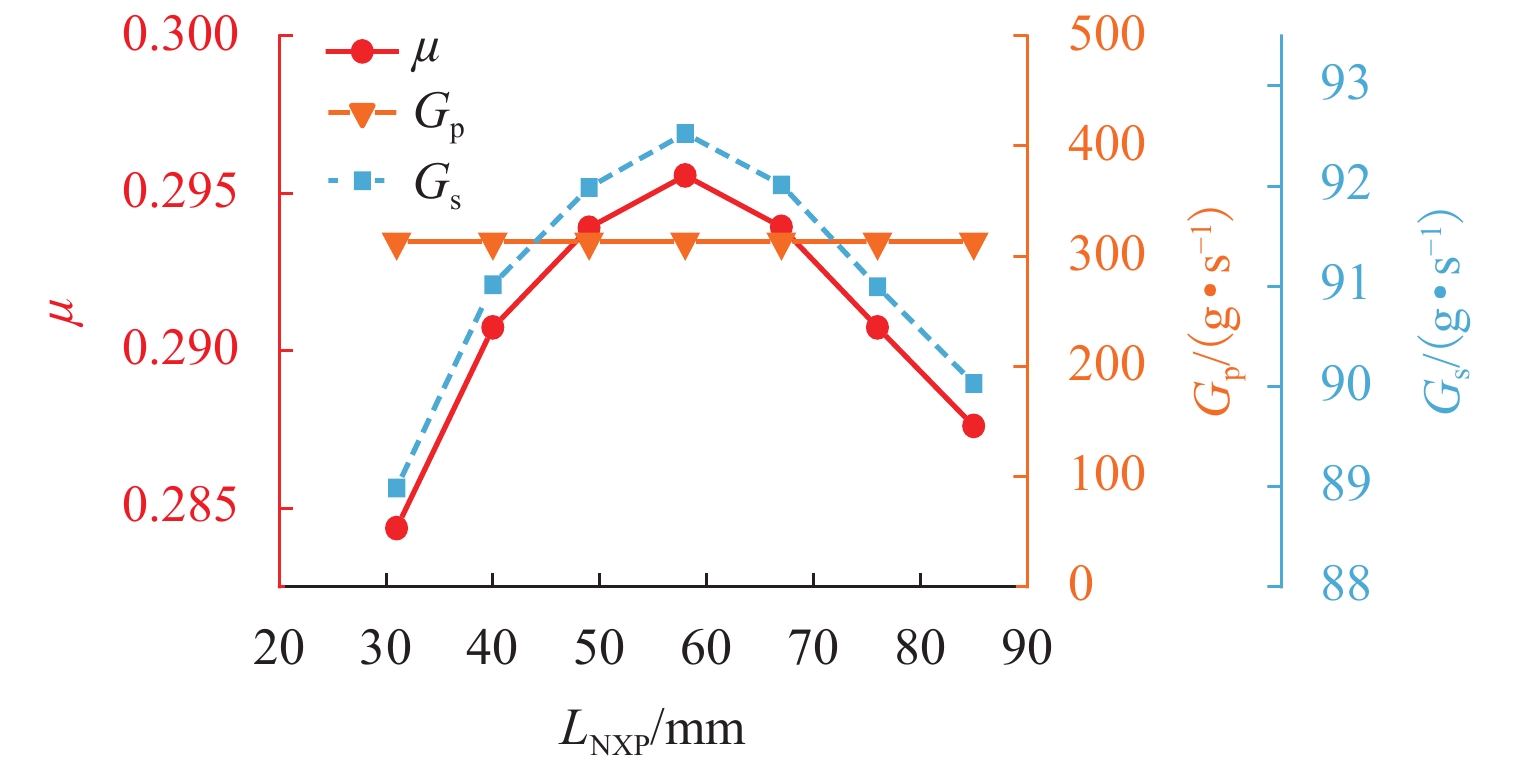
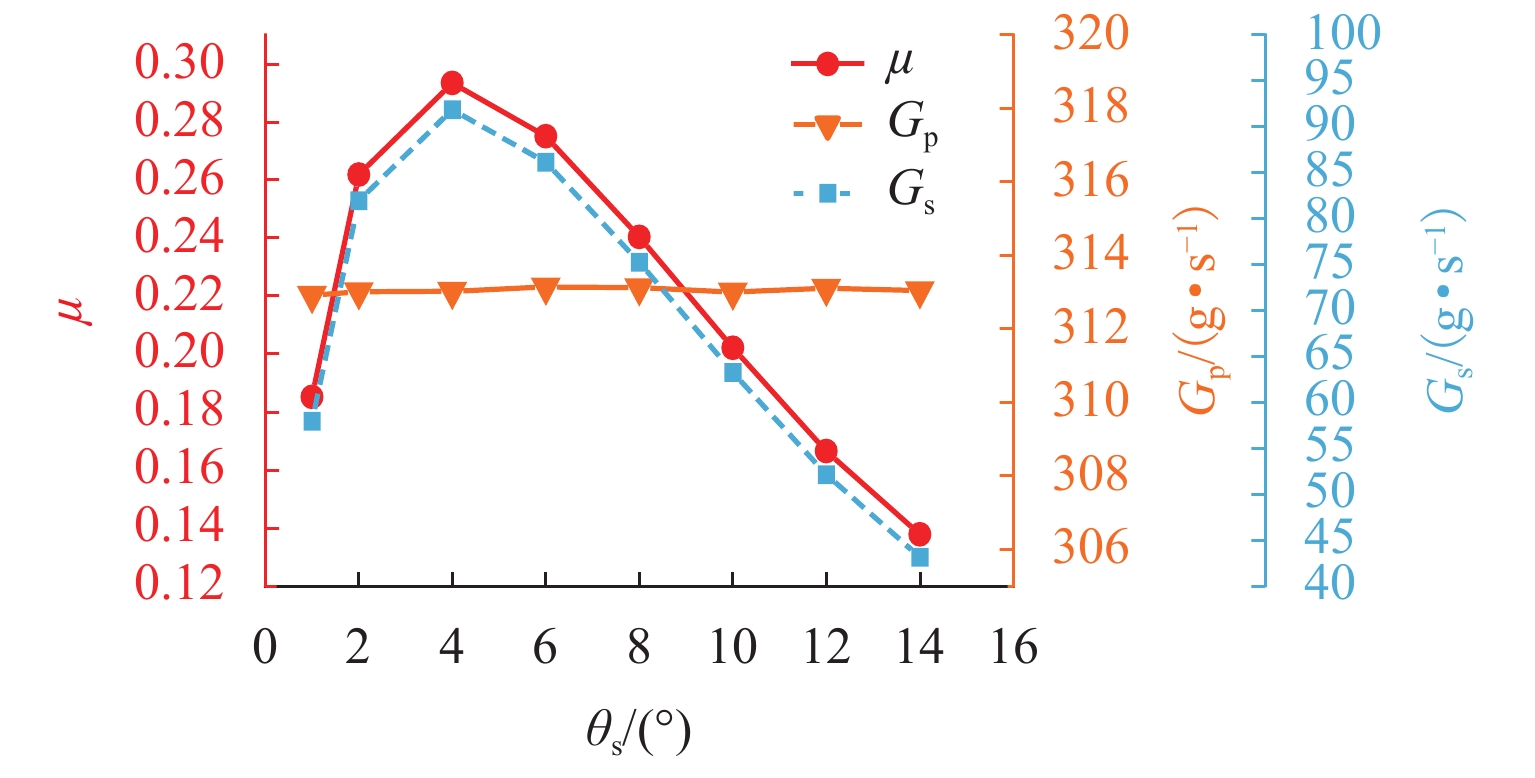
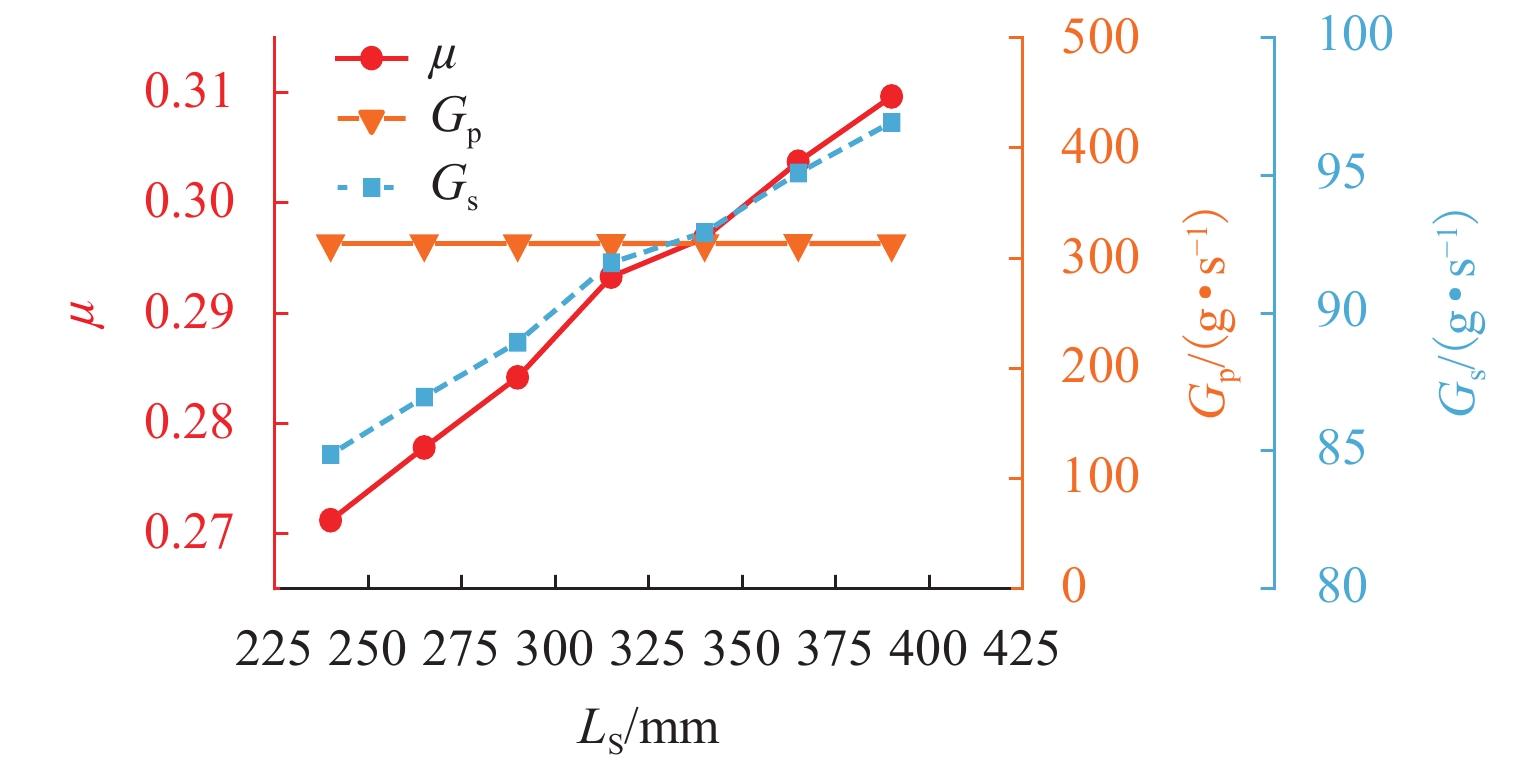
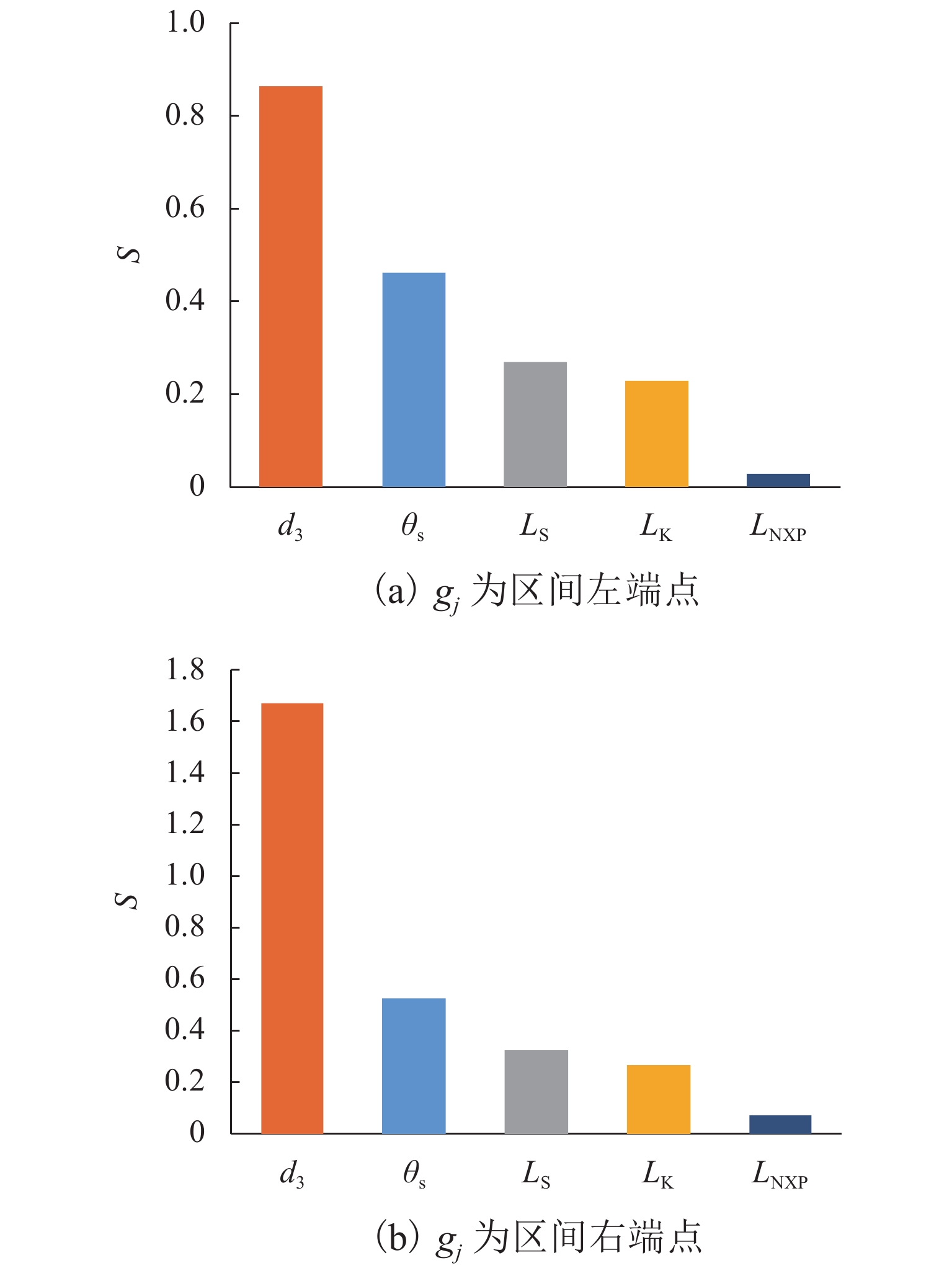
针对发动机抑制爆震的难题，提出采用无功耗的引射器实现天然气发动机高废气再循环（EGR）率的技术方案. 首先，完成设计工况下的引射器结构参数设计计算；然后，建立引射器仿真模型，并根据实验数据开展引射器计算模型的校核与验证；其次，对引射器引射性能随结构参数的改变进行分析，获取各结构参数对引射性能的影响规律；最后，提出了一种新的结构参数敏感性评价指标，研究了结构参数对引射性能的影响程度. 研究结果表明：随着混合段长度和扩压段长度的增加，引射系数（
μ ）会随之增大；混合段直径（d 3）、扩压段角度（θ s）和喷嘴出口至混合段距离（L NXP）的增加会导致μ 先增加后减小，μ 的最大值分别出现在d 3=46.1 mm、θ s=4° 和L NXP=57.33 mm处；对μ 影响最大的结构参数为d 3，对应的敏感性指标为0.88，而L NXP对μ 的影响程度最小，敏感性指标为0.05.Abstract:In view of engine knock, a technical solution was proposed to achieve a natural gas engine with a high exhaust gas recirculation (EGR) rate by utilizing a zero-power consumption ejector. Firstly, the structural parameters of the ejector were designed and calculated under specified operating conditions. Subsequently, the ejector simulation model was established, and the model was verified using experimental data. Furthermore, the ejection performance variations of the ejector with structural parameters were analyzed, and the influence of structural parameters on ejection performance was obtained. Lastly, a novel sensitivity evaluation index for structural parameters was introduced to examine the extent of their influence on ejection performance. The results show that as the length of the mixing section and the diffuser section increase, the entrainment coefficient (
μ ) increases. Conversely, as the diameter of the mixing section (d 3), the angle of the diffuser section (θ s), and the distance from the nozzle outlet to the mixing section (L NXP) increase,μ increases first and then decreases. The maximum value ofμ is observed atd 3 = 46.1 mm,θ s = 4°, andL NXP = 57.33 mm, respectively. Among the structural parameters,d 3 exhibits the most significant influence onμ , with a corresponding sensitivity index of 0.88. However,L NXP had the least impact onμ , with a sensitivity index of 0.05. -
图 1 基于引射器的发动机高EGR技术方案
Figure 1. Technical scheme for realizing natural gas engine with high EGR rate based on ejector
图 7 流量计算结果与实验数据的对比
Figure 7. Comparison of flow calculation results with experimental data
图 9 不同LK下引射器CO2浓度和压力分布云图
Figure 9. Contours of CO2 concentration and pressure of ejector under different LK
图 14 采用S评价指标得到的结构参数敏感性
Figure 14. Sensitivity of structural parameters obtained by S evaluation index
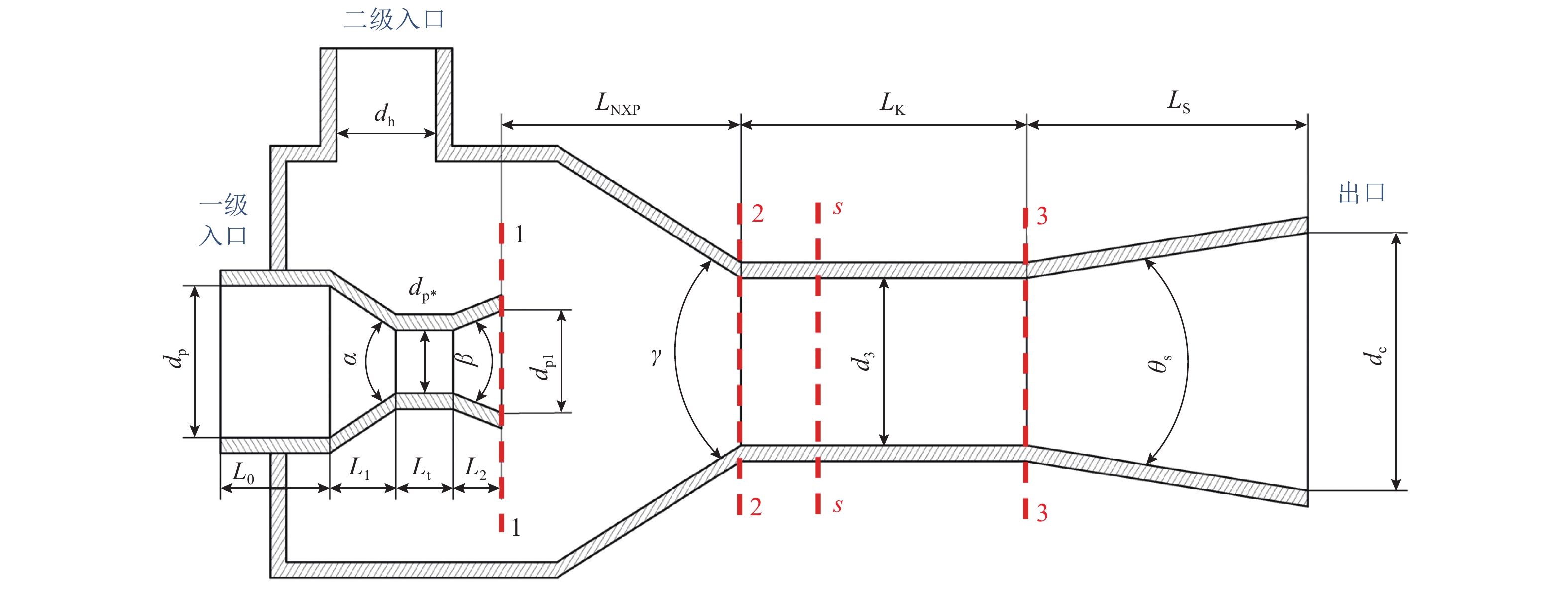
表 1 引射器结构示意图符号含义
Table 1. Symbolic meaning of ejector structure
变量 含义 dp/mm 喷嘴入口直径 dp*/mm 喷嘴临界直径 dp1/mm 喷嘴出口直径 dh/mm 引射气体入口直径 d3/mm 混合段直径 dc/mm 扩压段出口直径 L0/mm 喷嘴入口段长度 L1/mm 喷嘴收缩段长度 Lt/mm 喷嘴喉部长度 L2/mm 喷嘴扩张段长度 LK/mm 混合段长度 LS/mm 扩压段长度 α/（°） 喷嘴收缩角 β/（°） 喷嘴扩散角 γ/（°） 接收段夹角 θs/（°） 扩压段扩散角 
下载: 导出CSV
表 2 Nikiforow的引射器实验数据
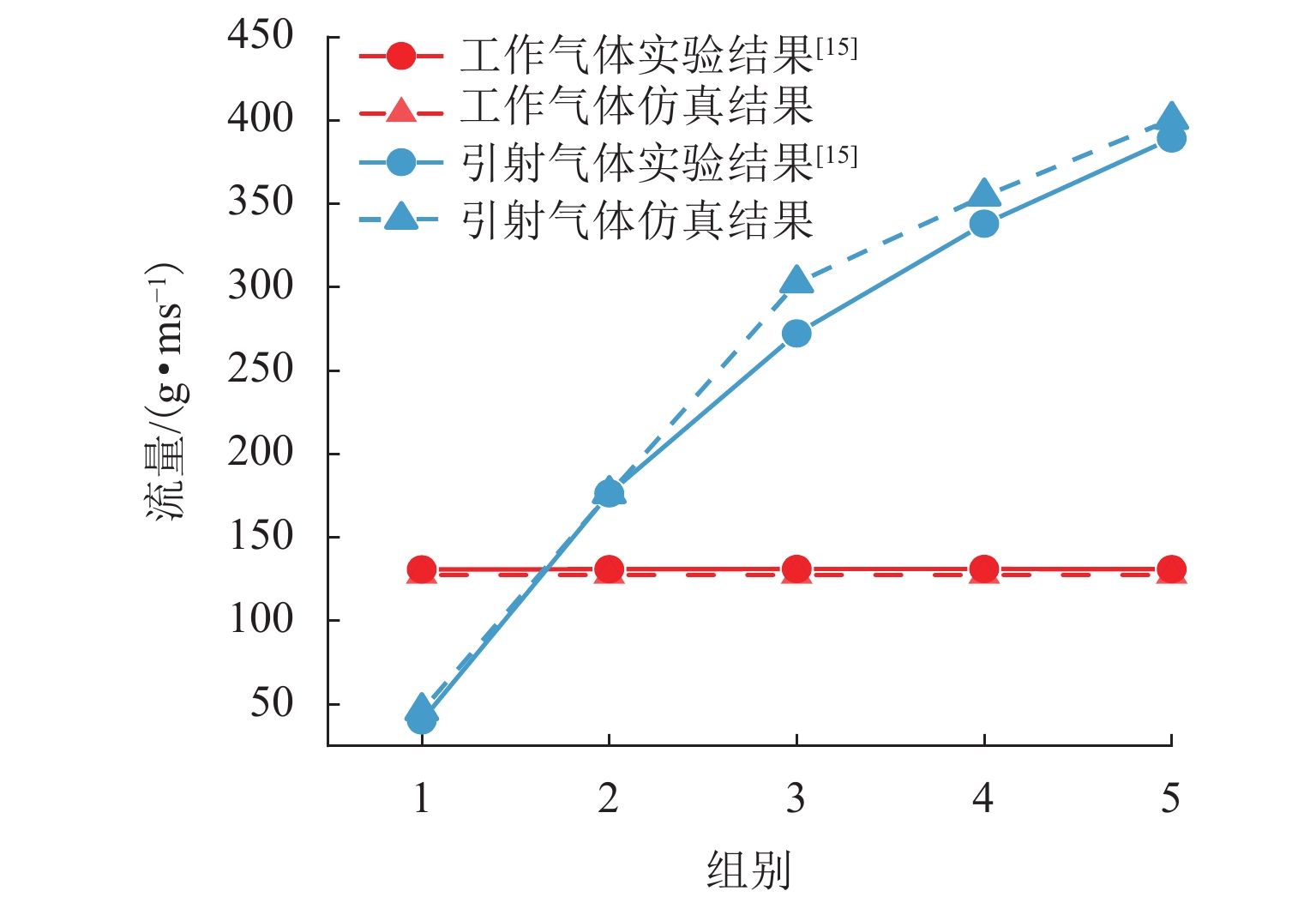
Table 2. Experimental data of Nikiforow’s ejector
组别 Pp/MPa Ps/MPa Gp/（g·ms−1） Gs/（g·ms−1） 1 2.00 0.0851 130.70 40.2 2 2.00 0.9000 1.75 176.3 3 2.00 0.9500 2.00 272.1 4 2.00 0.0975 2.50 337.9 5 0.20 0.0999 3.01 389.0
下载: 导出CSV
表 3 几何参数取值范围
Table 3. Geometric parameter value range
项目 LK/mm d3/mm LNXP/mm θd/（°） LS/mm 基准值 264.6 44.1 57.33 8 315 取值范围 44.1～441.0 38.1～50.1 30.87～83.79 2～14 240～390
下载: 导出CSV
-
[1] 赵建辉, 刘伟龙, 陈修旻. 一种气体机爆震抑制装置及其抑制方法: CN 112211759A[P]. 2021-01-12. [2] 张心悦,张海伦,王雷. 燃料电池氢循环喷射器性能分析与结构优化[J]. 仪器仪表学报,2021,42(6): 152-160. doi: 10.19650/j.cnki.cjsi.J2107613ZHANG Xinyue, ZHANG Hailun, WANG Lei. Performance analysis and structure optimization of ejector in PEMFC hydrogen cycle[J]. Chinese Journal of Scientific Instrument, 2021, 42(6): 152-160. doi: 10.19650/j.cnki.cjsi.J2107613 [3] ZHANG B, SONG X, LV J, et al. Study on the key ejector structures of the waste heat-driven ejector air conditioning system with R236fa as working fluid[J]. Energy and Buildings, 2012, 49: 209-215. [4] ZHU Y, CAI W, WEN C, et al. Numerical investigation of geometry parameters for design of high performance ejectors[J]. Applied Thermal Engineering, 2009, 29(5/6): 898-905. [5] 于文艳,王海博,田瑞. 混合室轴向结构参数对蒸气喷射器性能的影响[J]. 真空科学与技术学报,2018,38(6): 455-458. doi: 10.13922/j.cnki.cjovst.2018.06.03YU Wenyan, WANG Haibo, TIAN Rui. Effect of mixing chamber geometry on steam ejector performance[J]. Chinese Journal of Vacuum Science and Technology, 2018, 38(6): 455-458. doi: 10.13922/j.cnki.cjovst.2018.06.03 [6] MAZZELLI F, LITTLE A, GARIMELLA S, et al. Computational and experimental analysis of supersonic air ejector: turbulence modeling and assessment of 3D effects[J]. International Journal of Heat and Fluid Flow, 2015, 56: 305-316. doi: 10.1016/j.ijheatfluidflow.2015.08.003 [7] 孙淮清, 王建中. 流量测量节流装置设计手册[M]. 2版. 北京: 化学工业出版社, 2005: 1-35. [8] 张恒. 质子交换膜燃料电池氢气引射器设计及性能研究[D]. 武汉: 武汉理工大学, 2018. [9] 索科洛夫. 喷射器[M]. 黄秋云译. 北京: 科学出版社, 1977. [10] 刘成炎. 双流体喷射制冷系统的理论与实验研究[D]. 杭州: 浙江大学, 2017. [11] BARTOSIEWICZ Y, AIDOUN Z, DESEVAUX P, et al. Numerical and experimental investigations on supersonic ejectors[J]. International Journal of Heat and Fluid Flow, 2005, 26(1): 56-70. doi: 10.1016/j.ijheatfluidflow.2004.07.003 [12] YU F. Drop-in replacement in a R134 ejector refrigeration cycle by HFO refrigerants[J]. International Journal of Refrigeration, 2017, 77: 87-98. doi: 10.1016/j.ijrefrig.2017.02.028 [13] Inc A. ANSYS Fluent Theory Guide[M]. Commonwealth of Pennsylvania: [s.n.], 2021. [14] SHARIFI N, BOROOMAND M. An investigation of thermo-compressor design by analysis and experiment: part 1. validation of the numerical method[J]. Energy Conversion and Management, 2013, 69: 217-227. doi: 10.1016/j.enconman.2012.12.009 [15] NIKIFOROW K, KOSKI P, KARIMAKI H, et al. Designing a hydrogen gas ejector for 5 kW stationary PEMFC system-CFD-modeling and experimental validation[J]. International Journal of Hydrogen Energy, 2016, 41(33): 14952-14970. doi: 10.1016/j.ijhydene.2016.06.122 [16] LI S, YAN J, LIU Z, et al. Optimization on crucial ejector geometries in a multi-evaporator refrigeration system for tropical region refrigerated trucks[J]. Energy, 2019, 189: 1-14. [17] SUN Y. Sensitivity analysis of macro-parameters in the system design of net zero energy building[J]. Energy and Buildings, 2015, 86: 464-477. doi: 10.1016/j.enbuild.2014.10.031 -
下载:
点击查看大图
计量
- 文章访问数: 314
- HTML全文浏览量: 80
- PDF下载量: 21
- 被引次数: 0