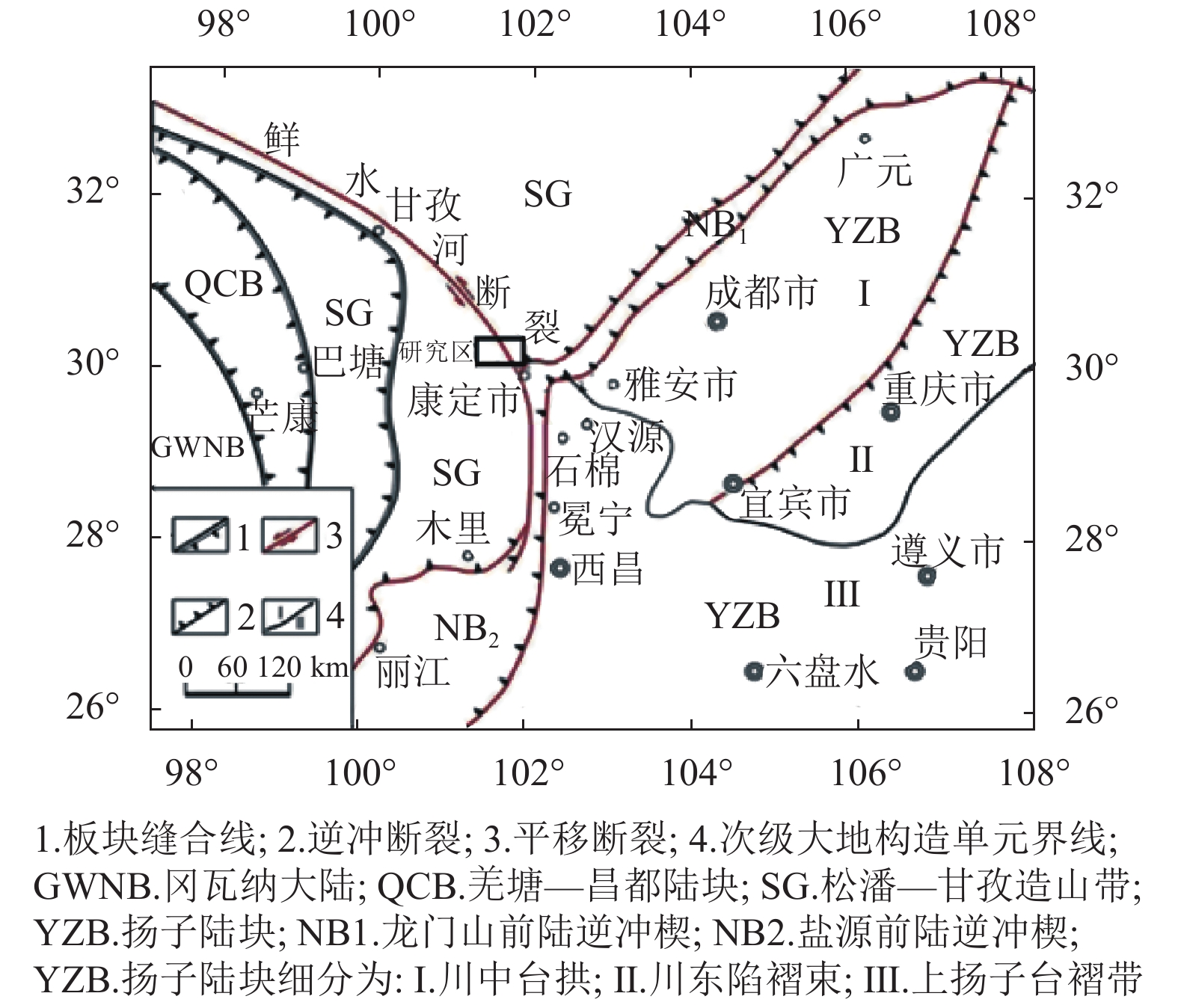
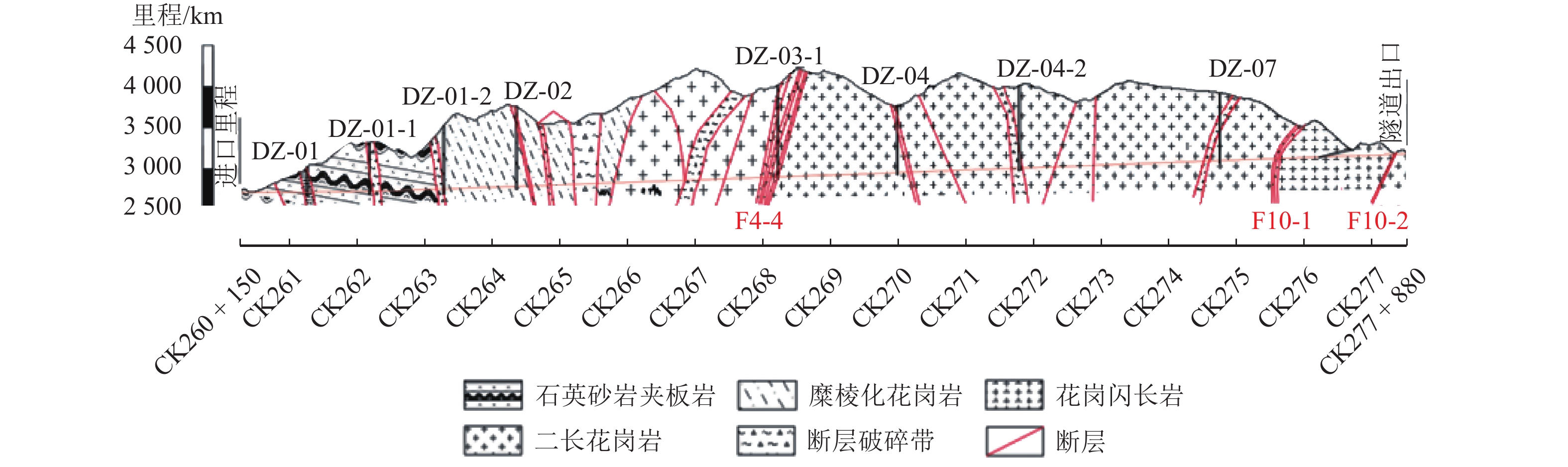
Back-Calculation of In-situ Stress of Railway Tunnel in Xianshuihe Fault Belt
-
摘要:
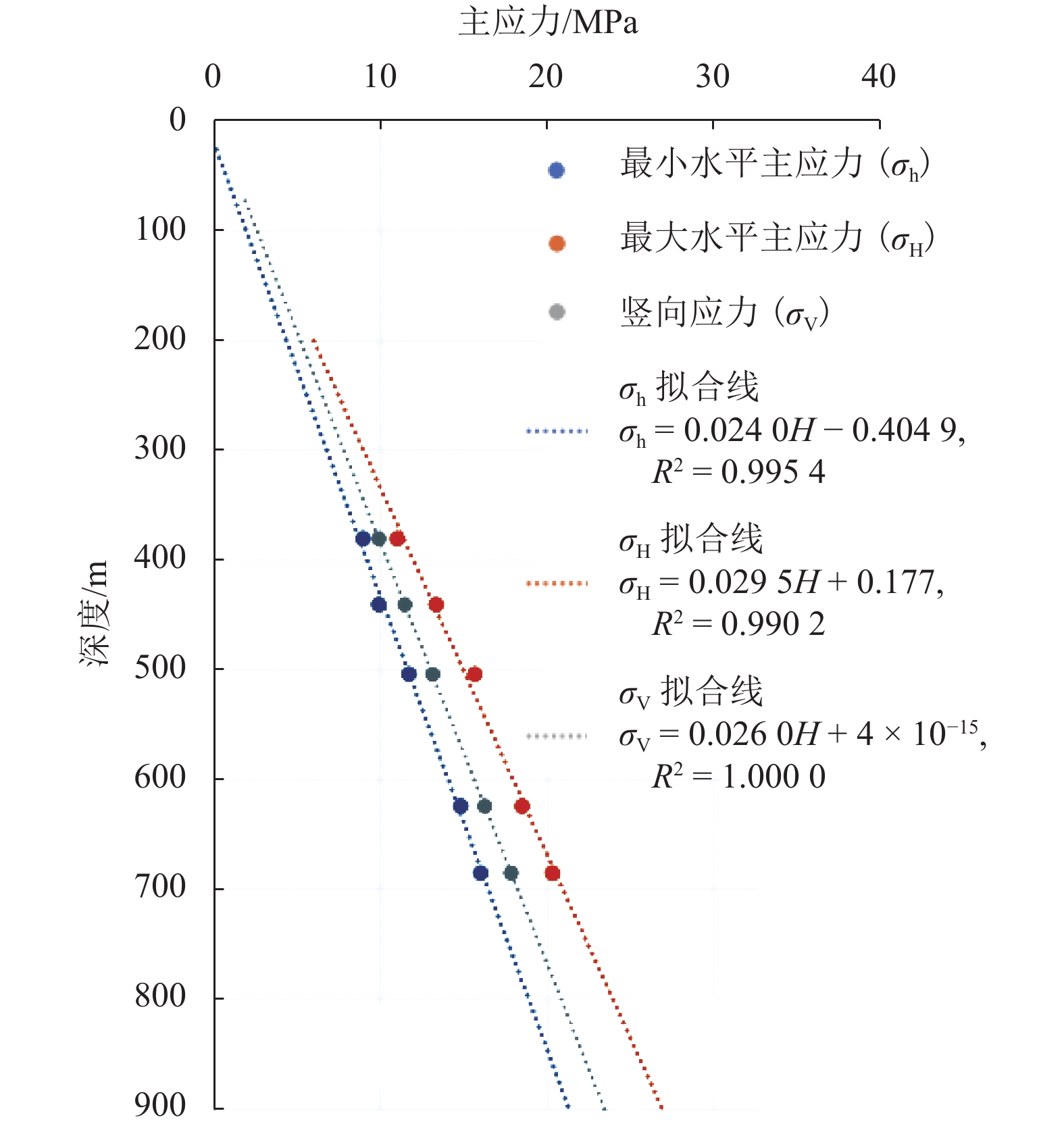
地应力的分布规律严重影响地下工程建设，获得开展工程区域地应力场分布对指导支护结构的设计具有重要意义.在鲜水河断裂带某隧道工程区采用钻孔水压致裂法进行了深孔地应力测试，基于地应力测试结果，得到了开展工程区域地应力随深度的变化规律，并利用数值模拟进行地应力反演. 结果表明：地应力随深度的增加而逐渐增加，其中最大水平地应力的递增梯度为0.385 MPa/km，最小水平主应力递增梯度为0.257 MPa/km；隧道纵断面水平最大主应力为41.69 MPa，最小主应力为29.84 MPa，侧压力系数为1.363～1.438，围岩应力以水平应力为主；地应力在断层部位得到了一定程度的释放，断层两侧的完整岩体应力存在一定程度的集中，应力值较高.
Abstract:The distribution law of ground stress has a very important role in the construction of underground engineering, and obtaining the distribution of ground stress field in the construction area is of great significance to guide the design of support structure. The borehole hydraulic fracturing method was used to test the in-situ stress in the project area of a railway tunnel in Xianshuihe fault belt. Based on the in-situ stress results, the variation law of in-situ stress with depth was obtained and the in-situ stress inversion was carried out by numerical simulation. The results show that the in-situ stress increases gradually with the increase of depth, in which the increasing gradient of the maximum horizontal in-situ stress is 0.385 MPa/km, and that of the minimum horizontal principal stress is 0.257 MPa/km. The maximum and minimum horizontal principal stress values of the tunnel profile are 41.69 and 29.84 MPa, respectively. The lateral pressure coefficient is 1.363−1.438, and the surrounding rock stress is dominated by horizontal stress. Generally, the in-situ stress has been released to a certain extent in the fault area, and the stress of the intact rock mass on both sides of the fault is concentrated to a certain extent with a high stress value.
-
Key words:
- hydraulic fracturing /
- in-situ stress /
- back-calculation /
- numerical simulation
-
图 3 隧道纵剖面及地应力测孔
Figure 3. Tunnel profile and borehole map for in-situ stress measurement
图 4 DZ-04号测孔地应力沿深度分布规律
Figure 4. Distribution law of ground stress along depth in dZ-04 measuring hole
图 7 隧道最大主应力云图及数值折线图
Figure 7. Cloud diagram and numerical broken-line diagram of maximum principal stress of tunnel
表 1 DZ-04号测孔水压致裂地应力测量结果
Table 1. Measurement results of ground stress caused by water pressure in borehole DZ-04
测段序号 测段中心深度/m 压裂参数/MPa 应力值/MPa 破裂方向/（°） P0 Pb Pr Ps T σH σh σv 1 685.0～685.7 15.98 26.20 20.95 19.21 5.25 20.28 15.98 17.81 N53W 2 624.0～624.7 14.78 24.26 19.76 18.13 4.50 18.46 14.78 16.22 N58W 3 504.0～504.7 11.69 18.00 14.50 13.29 3.50 15.63 11.69 13.10 N65W 4 440.0～440.7 9.88 15.43 12.01 11.49 3.42 13.32 9.88 11.44 5 380.0～380.7 8.94 13.50 12.11 10.34 1.39 10.99 8.94 9.88 
下载: 导出CSV
表 2 不同钻孔地应力拟合结果
Table 2. In-situ stress fitting results of different boreholes
孔号 拟合公式 最大值/
MPa最小值/
MPaDZ-01 σH=0.031 2H−8.027 0
σh=0.010 9H + 0.328 014.24 11.19 DZ-01-1 σH=0.022 8H−1.417 0
σh=0.009 1H + 3.226 017.88 10.84 DZ-01-2 σH=0.023 3H−0.188 4
σh=0.014 1H + 1.029 911.44 7.91 DZ-02 σH=0.042 6H−6.773 9
σh=0.031 9H−4.133 336.91 28.53 DZ-03-1 σH=0.038 9H−2.014 1
σh=0.025 4H + 1.037 841.69 29.84 DZ-04 σH=0.033 9H−0.106 7
σh=0.027 3H−0.073 827.85 22.12 DZ-04-2 σH=0.040 2H−2.167 2
σh=0.027 2H + 0.383 127.86 20.39 DZ07 σH=0.018 4H + 3.284 6
σh=0.013 4H + 1.547 318.65 13.49
下载: 导出CSV
表 3 隧道围岩物理力学参数
Table 3. Physical and mechanical parameters of tunnel surrounding rock
地层 围岩
级别弹性模量/GPa 泊松比 体积模量/GPa 剪切模量/GPa 密度/
（kg•m−3）板岩 Ⅳ 20 0.32 18.52 13.20 2 630 Ⅴ 6 0.35 6.67 4.05 2 600 花岗岩 Ⅲ 50 0.25 33.33 31.25 2 750 Ⅳ 20 0.30 16.67 13.00 2 650 Ⅴ 6 0.35 6.67 4.05 2 600 糜棱岩 Ⅳ 22 0.30 18.33 14.30 2 650 Ⅴ 8 0.35 8.89 5.40 2 620
下载: 导出CSV
表 4 隧道断层破碎带力学参数
Table 4. Mechanical parameters of tunnel fault fracture zone
断层 弹性模量/
GPa泊松比 体积模量/
GPa剪切模量/
GPa密度/
（kg•m−3）F1 9.0 0.24 5.77 3.63 2 250 F2 8.5 0.25 5.67 3.40 2 250 F4 8.1 0.25 5.40 3.24 2 250 F5 8.2 0.25 5.47 3.28 2 250 F6 7.9 0.26 5.49 3.13 2 250 F7 7.5 0.26 5.21 2.98 2 250
下载: 导出CSV
表 5 DZ-04应力计算结果与实测应力值对比
Table 5. Comparison between calculated and measured results of dZ-04 horizontal principal stress
测段序号 深度/m $\sigma_{\rm{H}} $ $\sigma_{\rm{h}} $ $\sigma_{\rm{v}} $ 实测/MPa 计算/MPa 拟合度/% 实测/MPa 计算/MPa 拟合度/% 实测/MPa 计算/MPa 拟合度/% 1 835.7 27.85 30.8 111 22.12 21.87 99 21.71 23.45 108 2 705.7 24.23 27.56 114 20.45 19.45 95 18.33 20.22 110 3 635.7 21.27 22.35 105 16.74 17.36 104 16.51 14.53 88 4 540.7 18.80 18.56 99 14.58 15.98 110 14.04 12.56 89 5 455.7 14.78 14.32 97 12.23 13.65 112 11.83 9.76 83
下载: 导出CSV
表 6 DZ-07应力计算结果与实测应力值对比
Table 6. Comparison between calculated and measured results of dZ-07 maximum horizontal principal stress
测段序号 深度/m $\sigma_{\rm{H}} $ $\sigma_{\rm{h}} $ $\sigma_{\rm{v}} $ 实测/MPa 计算/MPa 拟合度/% 实测/MPa 计算/MPa 拟合度/% 实测/MPa 计算/MPa 拟合度/% 1 294.5 8.91 8.45 95 5.85 6.21 106 7.80 8.32 107 2 382.5 10.39 11.20 108 7.13 8.02 112 10.14 11.23 111 3 546.6 13.03 12.67 97 9.07 10.08 111 14.48 15.64 108 4 659.5 15.06 14.76 98 10.80 11.78 109 17.48 18.56 106 5 758.5 17.75 16.87 95 12.69 13.65 108 20.10 21.47 107 6 835.0 18.65 19.19 103 13.49 15.04 111 22.13 24.51 111
下载: 导出CSV
表 7 隧道各里程段最大主应力值
Table 7. Maximum principal stress in each mileage section of tunnel
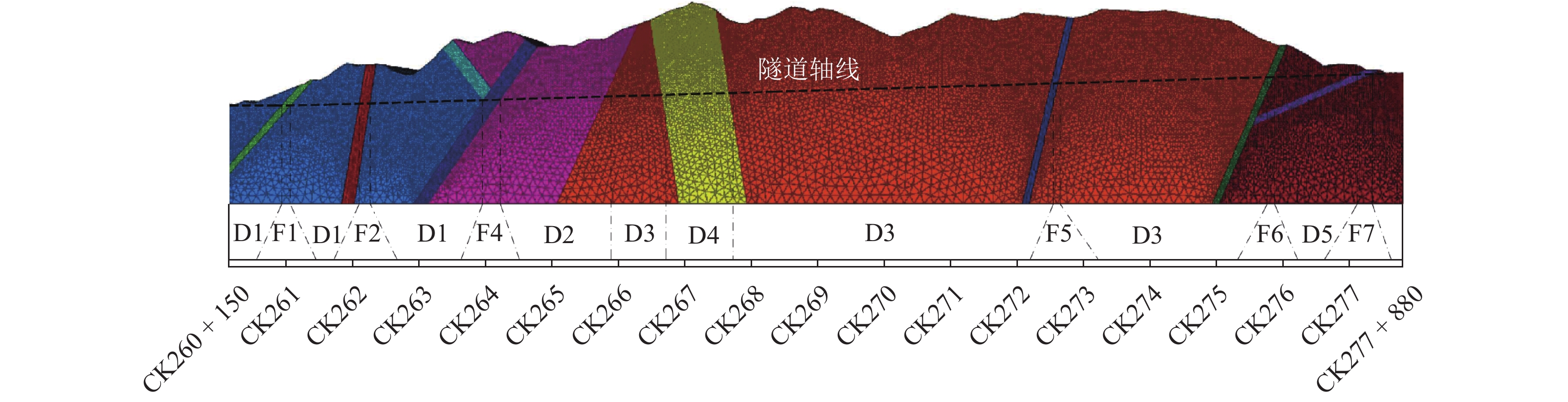
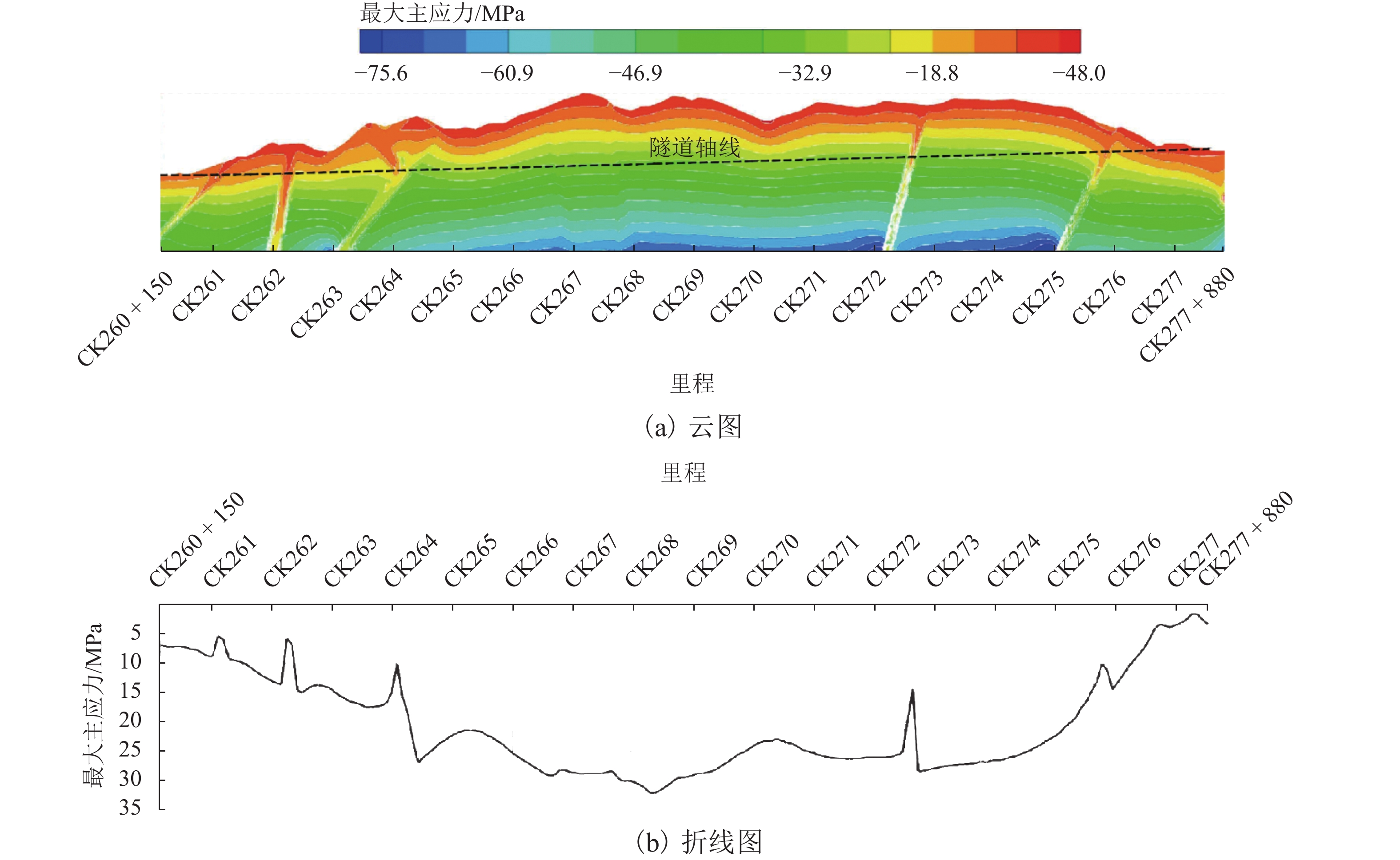
地层或断层编号 里程段 最大主应力
值/MPaD1 CK260 + 150～CK261 + 000 6.86～9.02 F1 CK261 + 000～CK261 + 200 3.80～7.97 D1 CK261 + 200～CK262 + 154 8.75～13.57 F2 CK262 + 154～CK262 + 405 4.53～14.33 D1 CK262 + 405～CK263 + 960 13.60～17.48 F4 CK263 + 960～CK264 + 412 9.47～27.13 D2 CK264 + 412～CK265 + 892 21.32～26.62 D3 CK265 + 892～CK266 + 717 25.80～30.15 D4 CK266 + 717～CK267 + 726 25.80～30.15 D3 CK267 + 726～CK267 + 873 25.80～30.15 D3 CK267 + 873～CK268 + 652 30.01～32.14 D3 CK268 + 652～CK272 + 488 22.94～29.83 F5 CK272 + 488～CK272 + 639 10.58～18.84 D3 CK272 + 639～CK275 + 648 13.63～21.40 F6 CK275 + 648～CK275 + 954 8.86～14.36 D5 CK275 + 954～CK277 + 880 1.49～12.81
下载: 导出CSV
-
[1] 朱光仪,郭小红,陈卫忠,等. 雪峰山公路隧道地应力场反演及工程应用[J]. 中南公路工程,2006,31(1): 71-75.ZHU Guangyi, GUO Xiaohong, CHEN Weizhong, et al. Inversion of in situ Stress and its application in xuefengshan roadway tunnel[J]. Gentral South Highway Engineering, 2006, 31(1): 71-75. [2] 邱祥波,李术才,李树忱. 三维地应力回归分析方法与工程应用[J]. 岩石力学与工程学报,2003(10): 1613-1617. doi: 10.3321/j.issn:1000-6915.2003.10.007QIU Xiangbo, LI Shucai, LI Shuchen, et al. 3D Geostress regression analysis method and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2003(10): 1613-1617. doi: 10.3321/j.issn:1000-6915.2003.10.007 [3] 郭运华,朱维申,李新平,等. 基于FLAC3D改进的初始地应力场回归方法[J]. 岩土工程学报,2014,36(5): 892-898. doi: 10.11779/CJGE201405012GUO Yunhua, ZHU Weishen, LI Xinping, et al. Improved regression method for initial geostress based on FLAC3D[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 892-898. doi: 10.11779/CJGE201405012 [4] 李金锁,彭华,马秀敏,等. 大丽线铁路隧道工程地应力三维有限元数值模拟分析[J]. 岩土工程学报,2006,28(6): 800-803. doi: 10.3321/j.issn:1000-4548.2006.06.025LI Jinsuo, PENG Hua, MA Xiumin, et al. Three-dimensional finite element numerical simulation of geo-stress in Da-Li Railway tunnel of Yunnan[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 800-803. doi: 10.3321/j.issn:1000-4548.2006.06.025 [5] 白世伟,韩昌瑞,顾义磊,等. 隧道应力扰动区地应力测试及反演研究[J]. 岩土力学,2008,29(11): 2887-2891. doi: 10.3969/j.issn.1000-7598.2008.11.001BAI Shiwei, HAN Changrui, GU Yilei, et al. Researth on crustral strese measurement and inversion of stress disturbed area of a tunnel[J]. Rock and Soil Mechanics, 2008, 29(11): 2887-2891. doi: 10.3969/j.issn.1000-7598.2008.11.001 [6] 赵跃堂,范斌,梁晖,等. 大型深埋隧道初始地应力状态的确定[J]. 地下空间与工程学报,2008,4(1): 147-151.ZHAO Yuetang, FAN Bin, LIANG Hui, et al. Determination of initial earth stress of large deeply-buried tunnel[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(1): 147-151. [7] 夏彬伟,李晓红,韩昌瑞,等. 深埋隧道层状岩体地应力反演研究[J]. 水文地质工程地质,2009,36(4): 75-79. doi: 10.3969/j.issn.1000-3665.2009.04.017XIA Binwei, LI Xiaohong, HAN CHangrui, et al. Study on inversion of in-situ stress of layered rockmass in buried tunnel[J]. Hydrogeology & Engineering Geology, 2009, 36(4): 75-79. doi: 10.3969/j.issn.1000-3665.2009.04.017 [8] 田勇,俞然刚,张能,等. 基于ANSYS软件地应力反演的数值实验技术[J]. 实验技术与管理,2019,36(2): 168-170.TIAN Yong, YU Rangang, ZHANG Neng, et al. Numerical experimental technology for geo-stress inversion based on ANSYS software[J]. Experimental Technology and Management, 2019, 36(2): 168-170. [9] 刘宁,张春生,褚卫江,等. 超深埋长隧道地应力场综合反分析方法与应用[J]. 中国公路学报,2018,31(10): 69-78. doi: 10.3969/j.issn.1001-7372.2018.10.007LIU Ning, ZHANG Chunsheng, CHU Weijiang, et al. Comprehensive inversion analysis method and application of deep buried long tunnel geo-stress field[J]. China Journal of Highway and Transport, 2018, 31(10): 69-78. doi: 10.3969/j.issn.1001-7372.2018.10.007 -
下载:
点击查看大图
计量
- 文章访问数: 193
- HTML全文浏览量: 90
- PDF下载量: 20
- 被引次数: 0