Global Fast Terminal Sliding Mode Control for Maglev Ball System Based on Disturbance Observer
-
摘要:
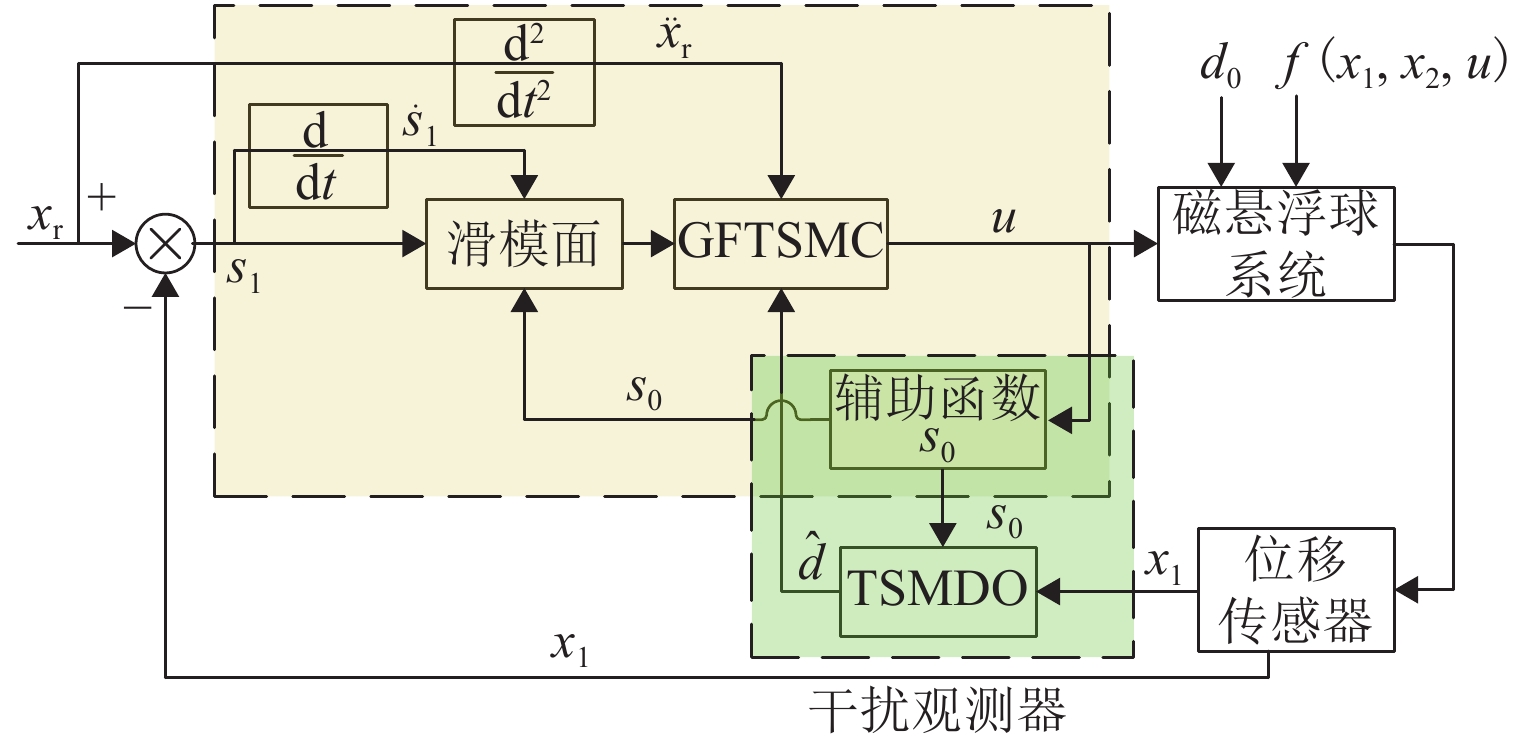
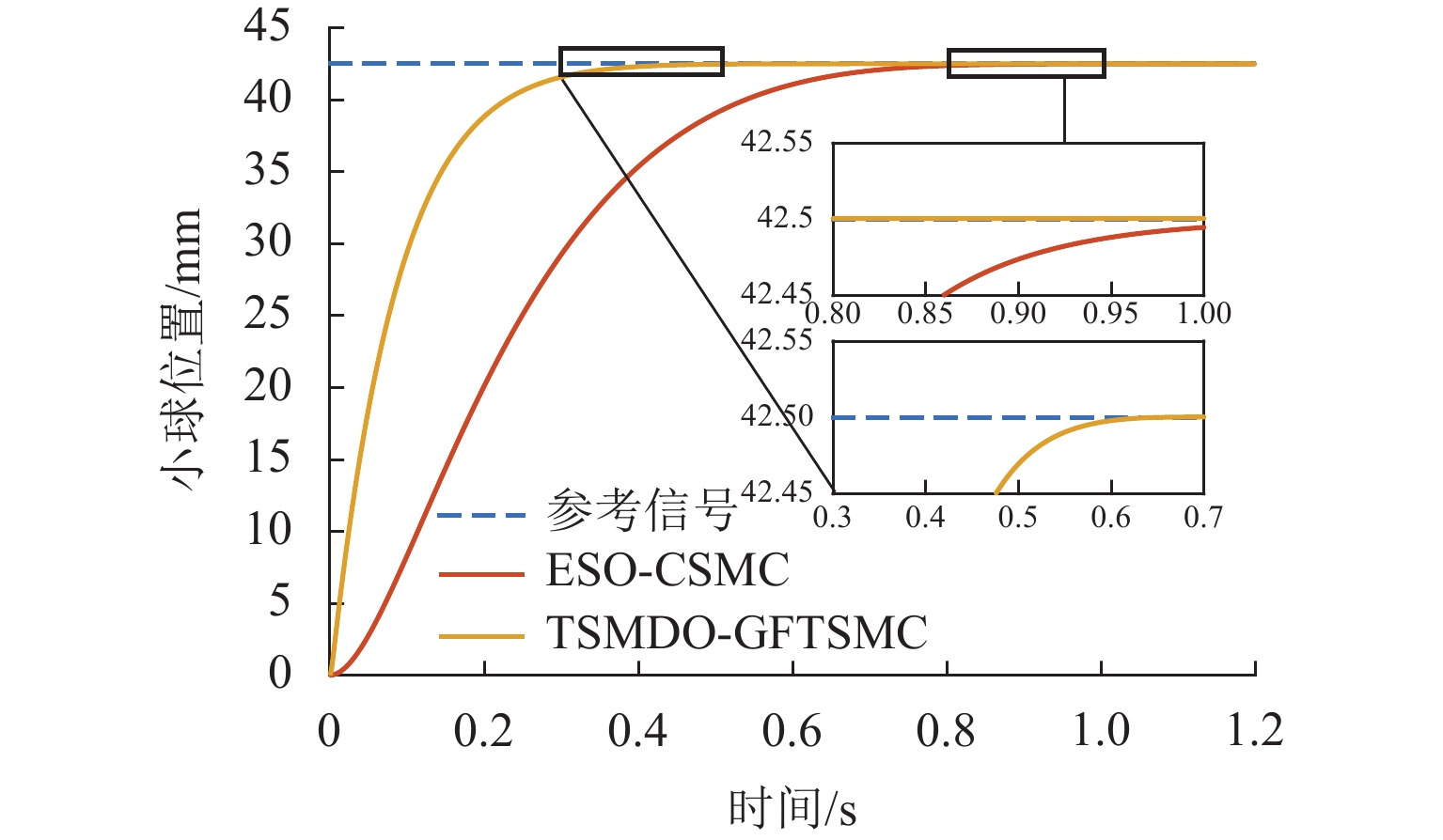
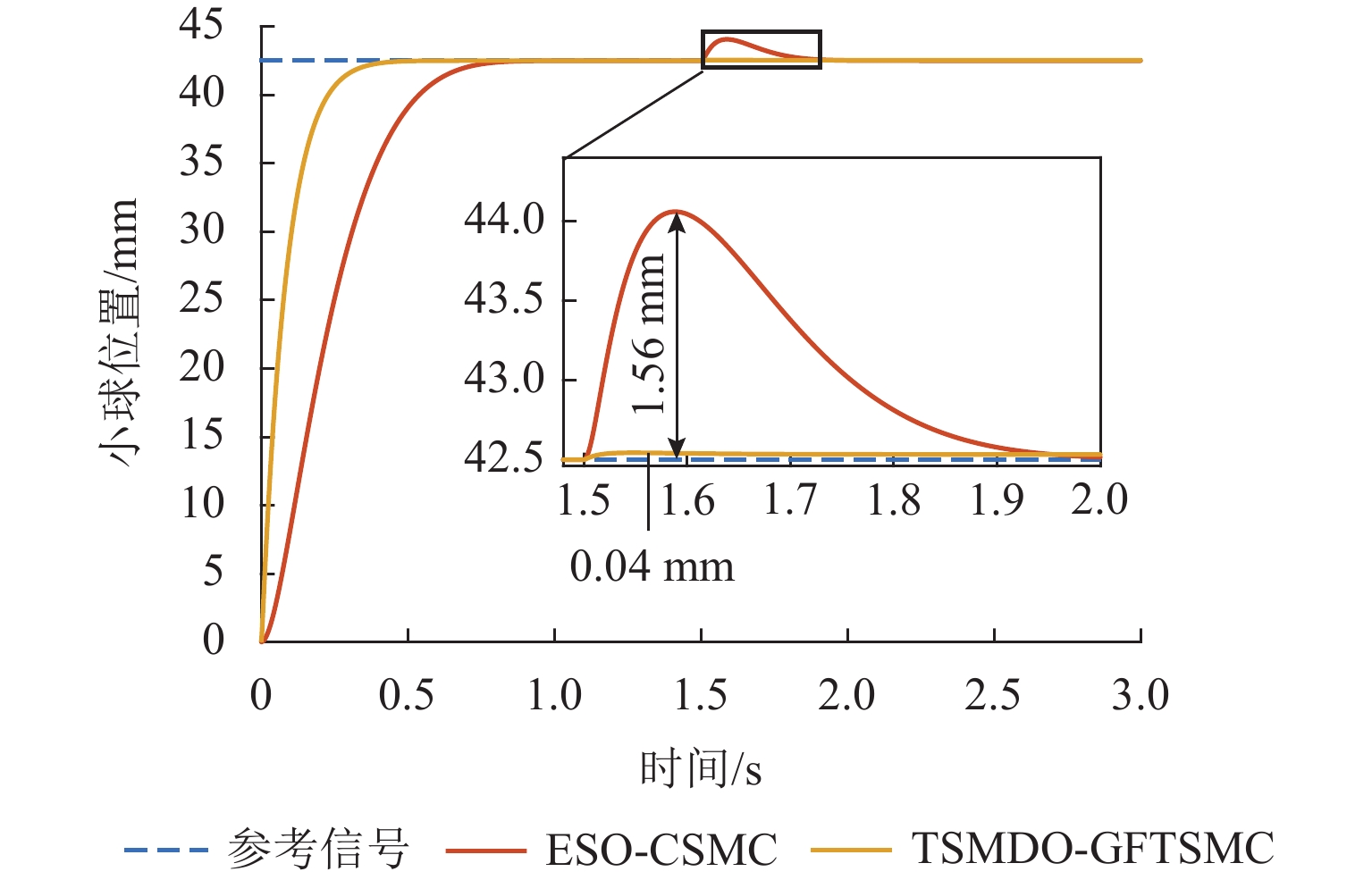
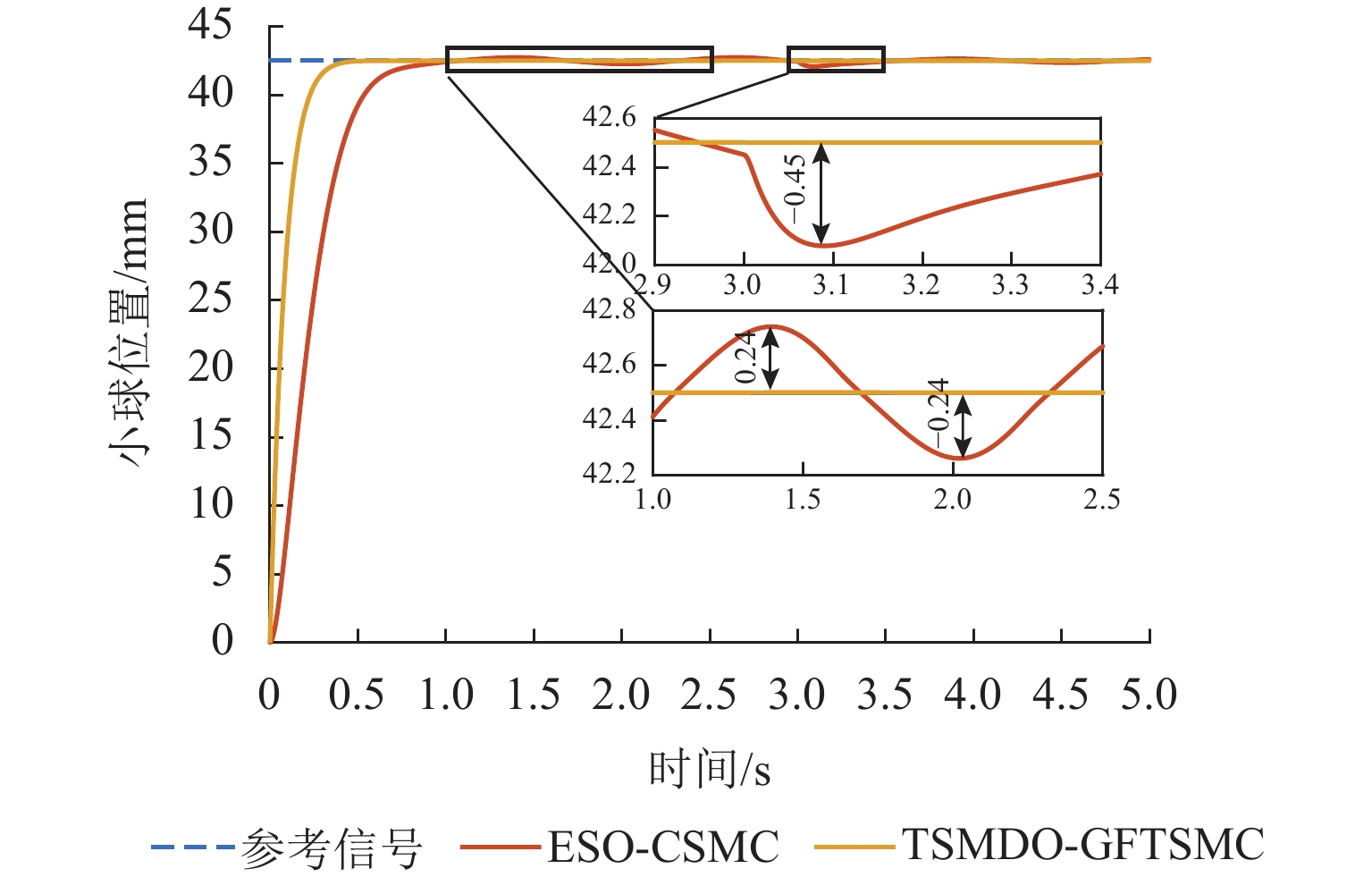
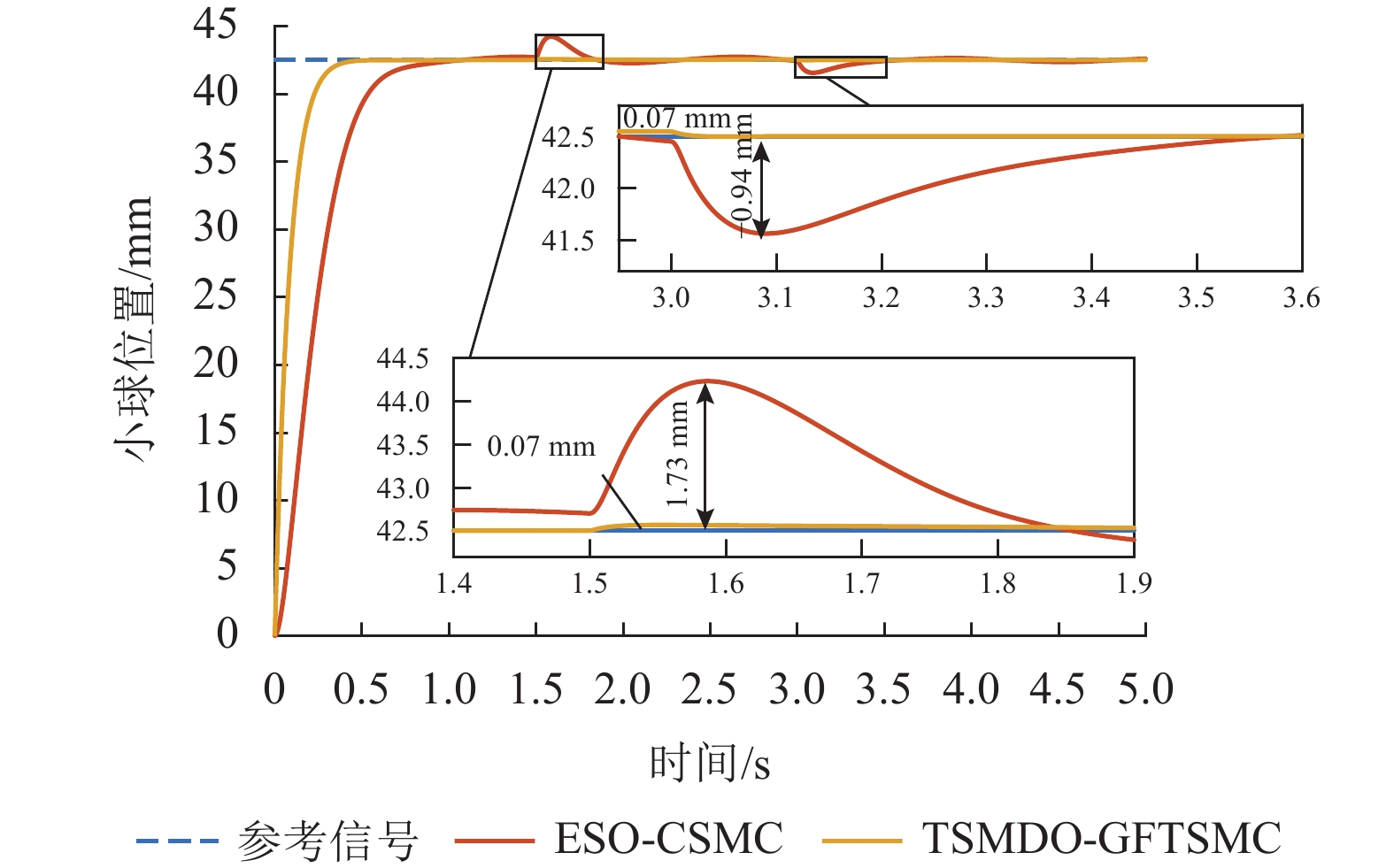
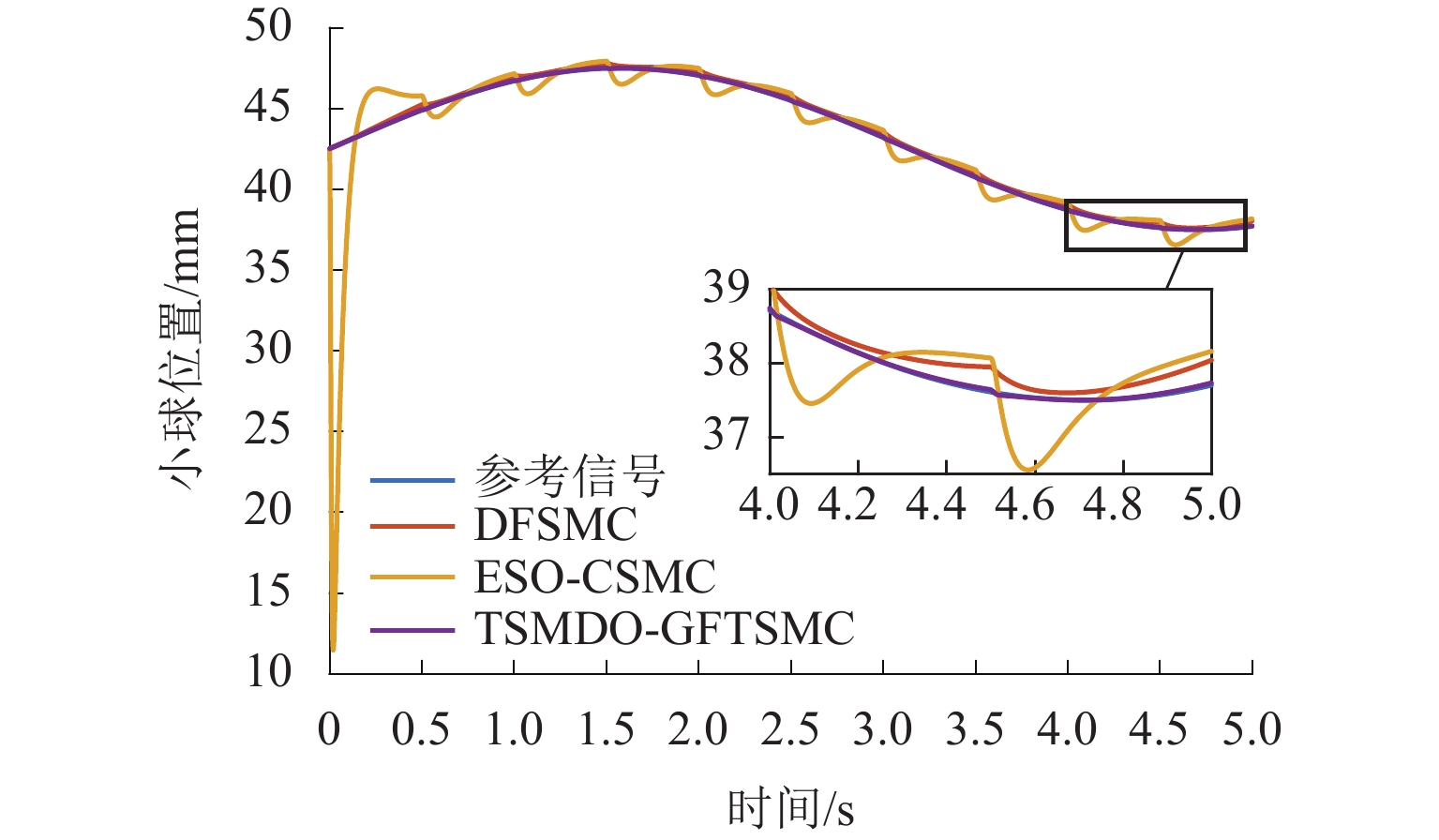
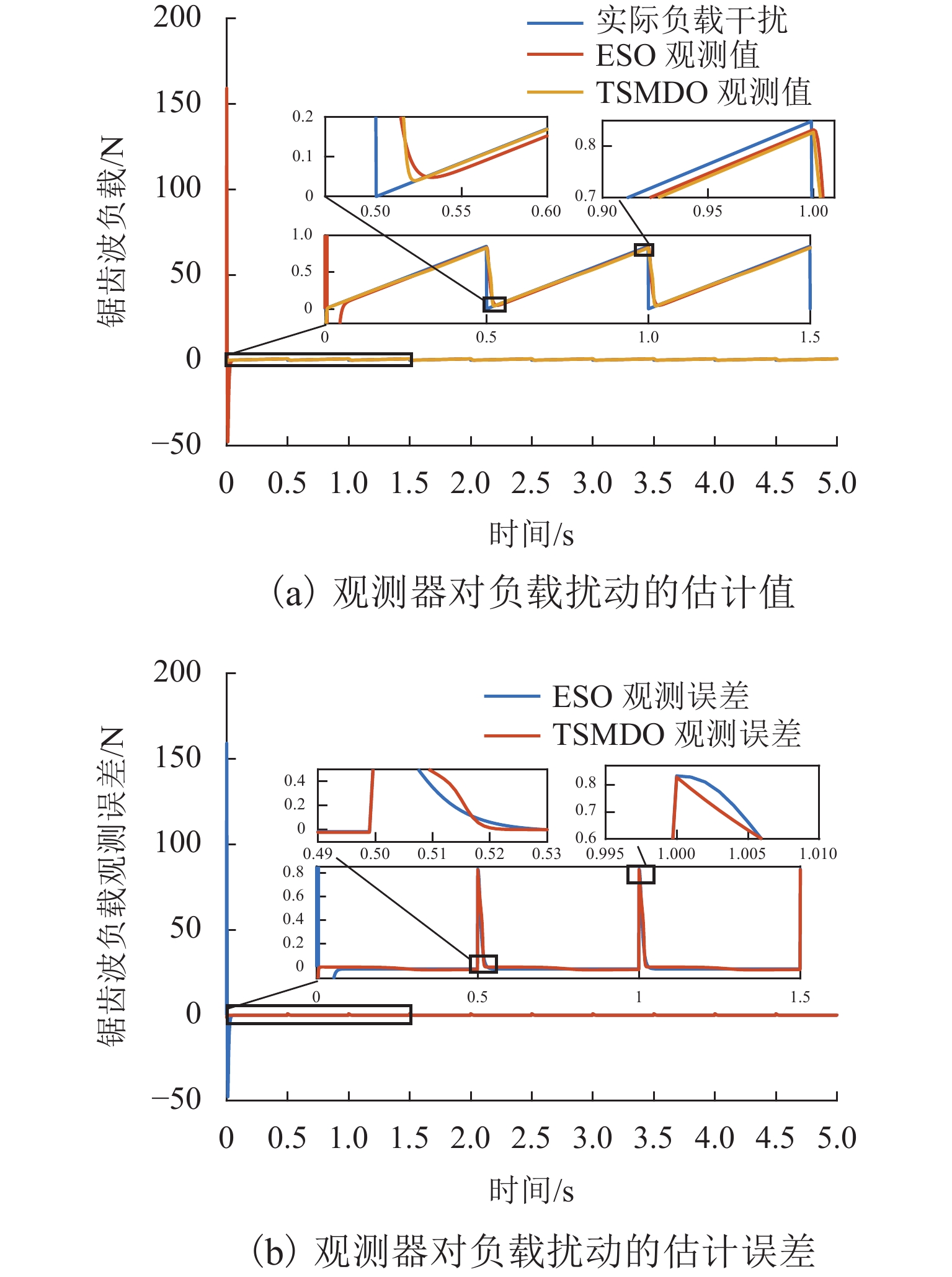
为解决磁悬浮球系统模型不确定性和易受外部干扰影响的问题，提出一种基于终端滑模干扰观测器的全局快速终端滑模控制（GFTSMC）方法. 首先，分析了磁悬浮球系统的数学模型并建立动态方程；然后，设计终端滑模干扰观测器（TSMDO），用以观测和估计系统所受到的扰动，经证明，该观测器对扰动的估计误差能在有限时间内收敛；其次，为克服系统不确定性和外部干扰的影响，设计了基于终端滑模干扰观测器的全局快速终端滑模控制器，可以实现系统的全局快速收敛，所设计的控制律不含切换项，能削弱抖振，以提高系统的抗干扰性和鲁棒性；最后，对所提出的TSMDO-GFTSMC进行了仿真验证，结果表明：与基于扩张状态观测器的连续滑模控制方法相比，采用本文方法，磁悬浮小球的起浮响应时间缩短0.38 s，位移偏差减小90%，跟踪误差由0.420 mm减小为0.032 mm；本文方法提高了对干扰的观测精度，优化了磁悬浮球系统的控制效果，增强了系统的鲁棒性.
-
关键词:
- 磁悬浮球系统 /
- 全局快速终端滑模控制 /
- 干扰观测器 /
- 抗干扰性 /
- 鲁棒性
Abstract:In order to solve model uncertainty and susceptibility to external disturbances of the maglev ball system, a global fast terminal sliding mode control (GFTSMC) method based on a terminal sliding mode disturbance observer (TSMDO) was proposed. Firstly, the mathematical model of the maglev ball system was analyzed, and its dynamic equation was established. Then, a TSMDO was designed to observe and estimate system disturbances. It was proven that the estimated disturbance error of the observer converged in finite time. Secondly, in order to overcome the influence of system uncertainty and external disturbance, a global fast terminal sliding-mode controller (GFTSMC) based on a TSMDO was developed to realize the global fast convergence. The designed control law did not include switching terms, which could weaken the chattering and improve the anti-disturbance and robustness of the system. Finally, the effectiveness of the proposed TSMDO-GFTSMC was verified by simulation. The results show that compared with the continuous sliding mode control method based on the extended state observer, the response time of the maglev ball floating is shortened by 0.38 s, and the displacement deviation is reduced by 90%. The tracking error is reduced from 0.420 mm to 0.032 mm. The proposed method improves the observation accuracy against disturbance, optimizes the control effect of the maglev ball system, and enhances the robustness of the system.
-
图 3 小球在理想条件下起浮响应轨迹
Figure 3. Response trajectory of ball floating under ideal conditions
图 4 外部负载扰动下磁悬浮小球响应轨迹
Figure 4. Response trajectory of maglev ball under external load disturbance
图 5 内部参数扰动下磁悬浮小球响应轨迹
Figure 5. Response trajectory of maglev ball under internal parameter disturbance
图 6 复合扰动下磁悬浮小球响应轨迹
Figure 6. Response trajectory of maglev ball under complex disturbance
图 7 外部负载扰动下磁悬浮小球正弦响应轨迹
Figure 7. Sinusoidal response trajectory of maglev ball under external load disturbance
图 8 锯齿波扰动下观测器对扰动的估计与观测误差
Figure 8. Estimated and observed disturbance errors of observer under sawtooth waves
表 1 磁悬浮球系统相关参数
Table 1. Relevant parameters of maglev ball system
参数 符号 数值 小球质量 m/g 170 小球半径 r/m 0.03 线圈电感 L/mH 46.7 线圈电阻 R/Ω 13.577 线圈匝数 N/匝 1057 平衡位置 δ0/m 0.0425 平衡位置电流 i0/A 0.633 真空磁导率 μ0/(H·m−1) 4π×10−7 磁导截面积 S/m2 9π×10−4 
下载: 导出CSV
-
[1] 熊嘉阳,邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报,2021,21(1): 177-198.XIONG Jiayang, DENG Zigang. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177-198. [2] 刘强,赵明师,韩邦成,等. 磁悬浮框架飞轮磁轴承技术研究与发展现状[J]. 宇航学报,2019,40(11): 1251-1261.LIU Qiang, ZHAO Mingshi, HAN Bangcheng, et al. Research and development status of magnetic bearing technology on magnetically suspended gimballing flywheel[J]. Journal of Astronautics, 2019, 40(11): 1251-1261. [3] DING H F, ZHU H Q, HUA Y Z. Optimization design of bearingless synchronous reluctance motor[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5. [4] GHOSH A, KRISHNAN T R, TEJASWY P, et al. Design and implementation of a 2-DOF PID compensation for magnetic levitation systems[J]. ISA Transactions, 2014, 53(4): 1216-1222. doi: 10.1016/j.isatra.2014.05.015 [5] 彭辉,徐锦华,侯海良. 模糊控制在磁悬浮球系统实时控制中的应用[J]. 控制工程,2009,16(3): 278-281.PENG Hui, XU Jinhua, HOU Hailiang. Application of fuzzy control to real-time control of magnetic levitation ball system[J]. Control Engineering of China, 2009, 16(3): 278-281. [6] 朱坚民,沈正强,李孝茹,等. 基于神经网络反馈补偿控制的磁悬浮球位置控制[J]. 仪器仪表学报,2014,35(5): 976-986.ZHU Jianmin, SHEN Zhengqiang, LI Xiaoru, et al. Magnetic levitation ball position control based on neural network feedback compensation control[J]. Chinese Journal of Scientific Instrument, 2014, 35(5): 976-986. [7] 李广. 磁悬浮球系统的鲁棒控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. [8] 沈莹雅,张建生,张远,等. 主动磁悬浮轴承的鲁棒反演滑模控制[J]. 机械制造与自动化,2016,45(1): 194-198.SHEN Yingya, ZHANG Jiansheng, ZHANG Yuan, et al. Robust backstepping sliding-mode control of active magnetic bearing[J]. Machine Building & Automation, 2016, 45(1): 194-198. [9] 刘金琨,孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用,2007,24(3): 407-418.LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418. [10] 张井岗,方线伟,赵志诚. 磁悬浮球系统的分数阶滑模控制[J]. 南京理工大学学报,2014,38(1): 72-77.ZHANG Jinggang, FANG Xianwei, ZHAO Zhicheng. Fractional order sliding mode control of magnetic levitation ball system[J]. Journal of Nanjing University of Science and Technology, 2014, 38(1): 72-77. [11] 赵磊,王军晓,黄光普,等. 基于扩张状态观测器的磁悬浮球连续滑模控制[J]. 高技术通讯,2020,30(5): 480-486.ZHAO Lei, WANG Junxiao, HUANG Guangpu, et al. Continuous sliding mode control of magnetic levitation ball based on extended state observer[J]. Chinese High Technology Letters, 2020, 30(5): 480-486. [12] 赵磊. 磁悬浮球系统滑模控制方法研究[D]. 杭州: 浙江工业大学, 2020. [13] 王军晓,陈林杰,俞立. 基于等价输入干扰滑模观测器的磁悬浮球系统模型预测控制[J]. 控制理论与应用,2021,38(1): 137-146.WANG Junxiao, CHEN Linjie, YU Li. Model predictive control for magnetic levitation ball system based on equivalent input disturbance sliding mode observer[J]. Control Theory & Applications, 2021, 38(1): 137-146. [14] 孙佃升,章跃进. 一种抑制初始微分峰值现象的改进型三阶时变参数扩张状态观测器[J]. 电机与控制学报,2017,21(9): 55-62.SUN Diansheng, ZHANG Yuejin. Improved third-order time-varying parameters nonlinear ESO restraining the derivative peaking phenomenon[J]. Electric Machines and Control, 2017, 21(9): 55-62. [15] 韩俊庆,吴爱国,董娜. 基于滑模干扰观测器的机械臂终端滑模控制[J]. 中南大学学报(自然科学版),2020,51(10): 2749-2757.HAN Junqing, WU Aiguo, DONG Na. Terminal sliding mode control for robotic manipulator based on sliding mode disturbance observer[J]. Journal of Central South University (Science and Technology), 2020, 51(10): 2749-2757. [16] CHEN M, WU Q X, CUI R X. Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems[J]. ISA Transactions, 2013, 52(2): 198-206. doi: 10.1016/j.isatra.2012.09.009 [17] 李鹏,马建军,郑志强. 采用幂次趋近律的滑模控制稳态误差界[J]. 控制理论与应用,2011,28(5): 619-624.LI Peng, MA Jianjun, ZHENG Zhiqiang. Sliding mode control approach based on nonlinear integrator[J]. Control Theory & Applications, 2011, 28(5): 619-624. [18] 李鹏. 传统和高阶滑模控制研究及其应用[D]. 长沙: 国防科学技术大学, 2011. -
下载:
点击查看大图
计量
- 文章访问数: 386
- HTML全文浏览量: 110
- PDF下载量: 25
- 被引次数: 0