长期循环荷载下土的动力学特性与本构模型研究进展

李琼林; 青于蓝; 崔凯; 张东杰; 李庞举

doi:10.3969/j.issn.0258-2724.20210928

长期循环荷载下土的动力学特性与本构模型研究进展

doi: 10.3969/j.issn.0258-2724.20210928

西南交通大学土木工程学院，四川成都 610031

基金项目: 国家自然科学基金（52178356, 42177128）

详细信息

作者简介:
李琼林（1986—），男，副教授，研究方向为土动力学与寒区岩土工程，E-mail：qionglin_li@swjtu.edu.cn

通讯作者:
崔凯（1979—），男，教授，博士生导师，研究方向为岩土工程，E-mail：cuikai@swjtu.cn

中图分类号: U461；TP308
计量
- 文章访问数: 1330
- HTML全文浏览量: 230
- PDF下载量: 242
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-16
- 修回日期: 2022-03-10
- 网络出版日期: 2023-09-15
- 刊出日期: 2022-03-14

Review of Dynamic Behaviors and Constitutive Model of Soil Under Long-Term Cyclic Loading

School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
随着交通基础设施的快速发展，长期循环荷载下土体的动力性能与相应的本构模型体系愈发受到关注，其能为该类荷载下地基或者岩土构筑物的动力稳定性和服役性能评估提供理论基础与技术支撑. 最近20年来，国内外相关学者已开展了大量的室内试验探索长期循环荷载下土的动力特性与影响因素，建立相应的理论模型描述土体的长期循环变形特征，并努力将其应用于工程实践. 目前，对长期循环荷载下土体动力学性能与主要影响因素的研究基本明确，但在如何减少本构模型参数，增强本构模型在变幅值、变频率等复杂实际工况时的适用性等研究尚需进一步加强. 本文通过对该方向研究发展的总结，明确了未来的发展方向，并提出了当前研究局限的可能解决思路，有利于进一步推进相关研究成果应用于工程实践的进程.
- 长期循环荷载 /
- 加载模式 /
- 累积应变 /
- 动态模量 /
- 本构模型
Abstract:
With the rapid development of transport infrastructure, the dynamic properties of soil under long-term cyclic loading and the corresponding constitutive model system are receiving increased attention, which can provide a theoretical basis and technical support for the assessment of the dynamic stability and service performance of foundations or geotechnical structures under such loading. In the past 20 years, Chinese and foreign scholars have carried out a large number of indoor experiments to explore the dynamic behaviors and influencing factors of soil under long-term cyclic loading, established corresponding theoretical models to describe the characteristics of long-term cyclic deformation of soil, and applied them to engineering practice. At present, the research on dynamic performance and the main influencing factors of soil under long-term cyclic loading is sufficient. However, how to reduce the parameters of these constitutive models and enhance their applicability in complex working conditions with variable amplitudes and frequencies needs to be further studied. Through the summary of research development, this paper clarified the development direction of this topic and proposed some possible solutions to the current research limitations, which was beneficial for applying research findings in engineering practice.
- long-term cyclic loading /
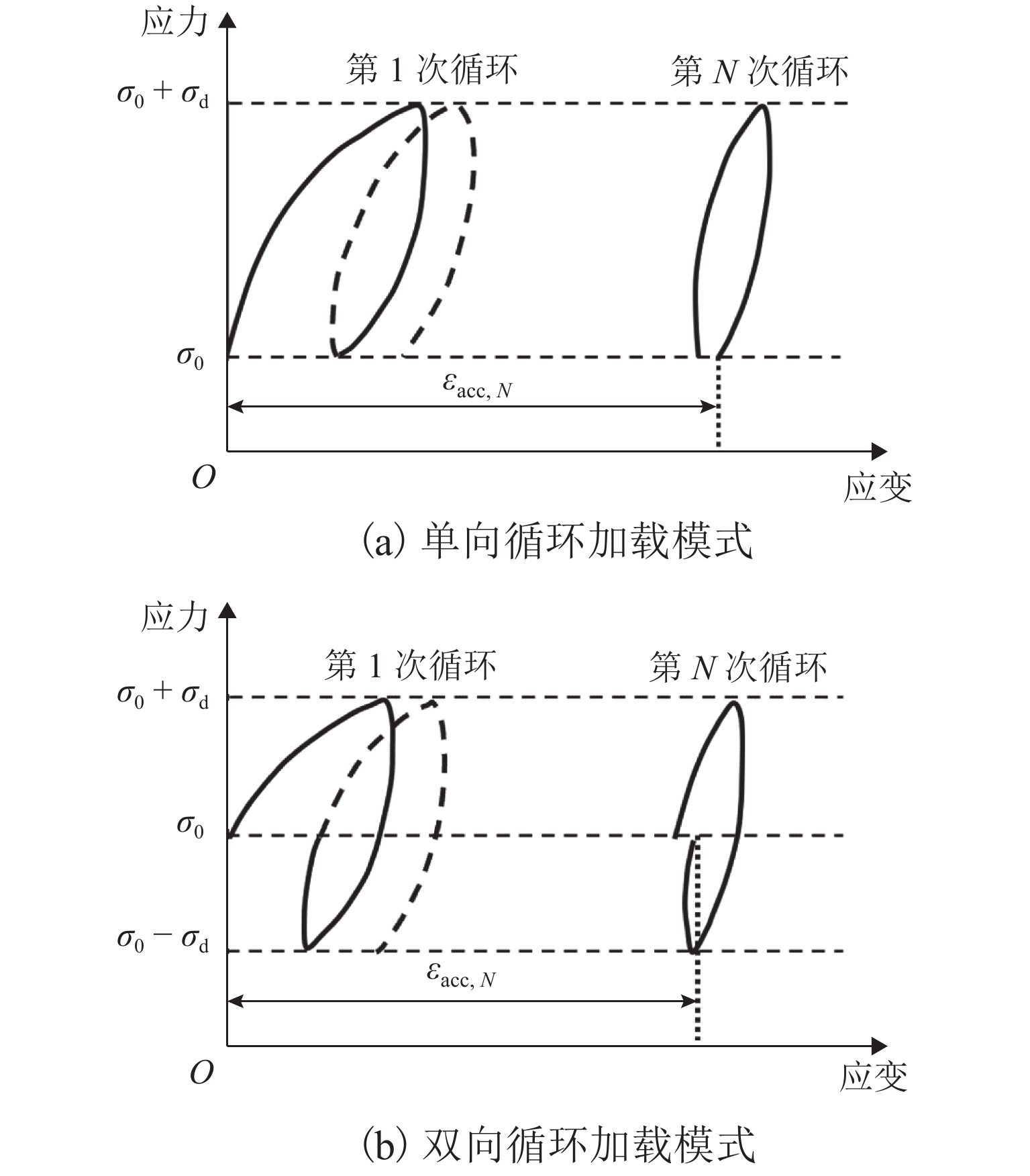
- loading modes /
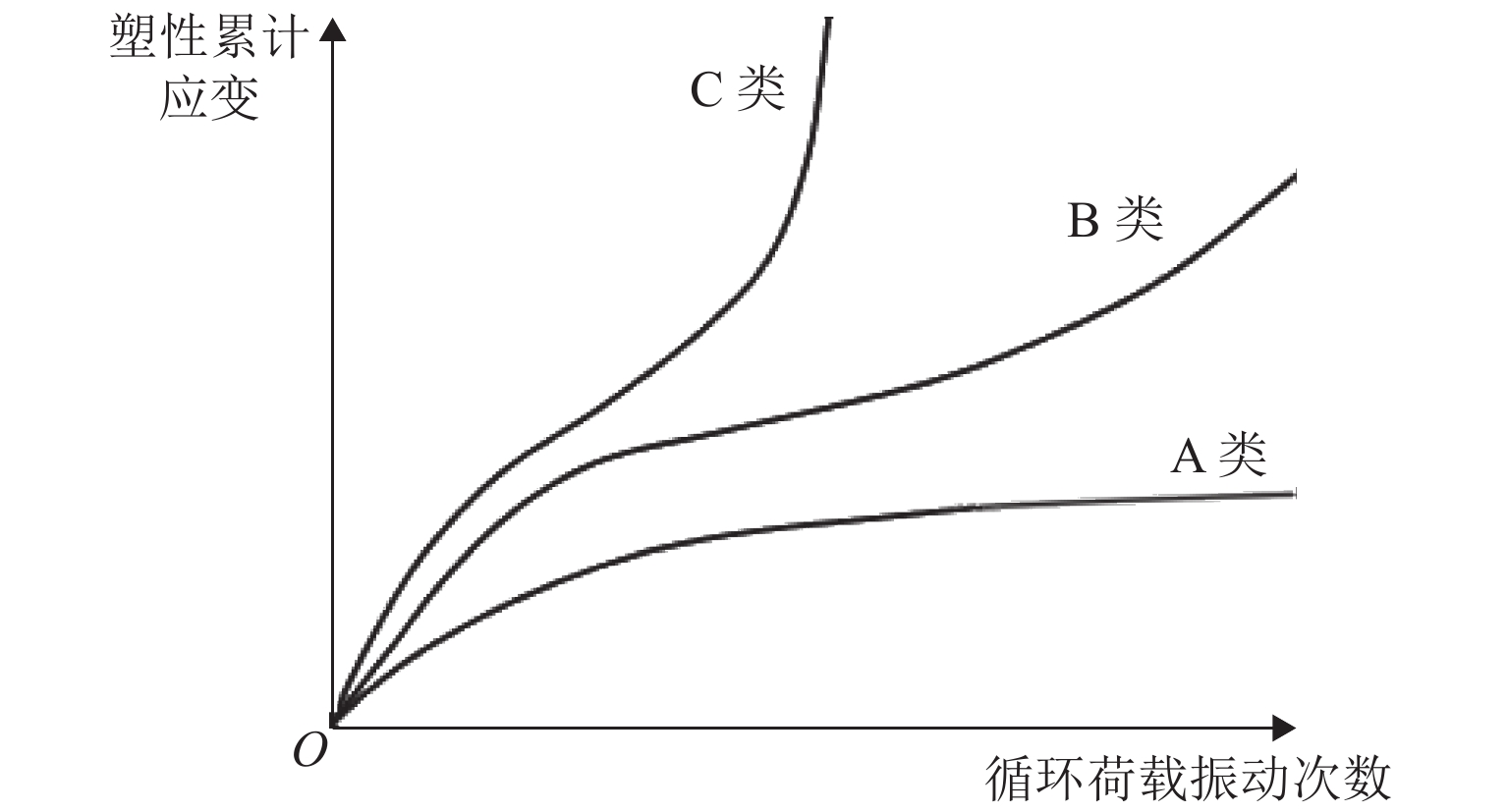
- accumulative strain /
- dynamic modulus /
- constitutive model

HTML全文

基础冲刷是引起桥梁结构坍塌破坏的重要因素之一. 根据Wardhana等^[1]的调查， 1989年—2000年统计的美国503座损毁桥梁中，有一半左右的桥梁毁坏是由基础冲刷引起的. 自1986年以来，哥伦比亚的桥梁损毁有35%与基础冲刷有关^[2]. 同样地，易仁彦等^[3]对国内2000年—2014年桥梁的损毁事故进行调查发现，有超过30%的桥梁毁坏与基础冲刷有关. 大跨桥梁具有较小的刚度和较低的阻尼，因此，对风以及车辆等运营阶段荷载和地震极端作用非常敏感. 基础冲刷会减弱桥梁下部结构的横向约束，改变桥梁结构的性能，从而影响桥梁结构在不同荷载组合作用下的动力响应. 因此，研究冲刷效应对大跨桥梁车-桥系统动力响应的影响和评估桥梁结构和桥上行驶车辆的安全性具有重要意义.

近年来，已有许多学者针对基础冲刷对结构动力性能的影响展开研究：商宇等^[4]研究基础冲刷对桩基动力性能的影响发现，基础冲刷使得桩基的自由长度增加，从而减小了桩基的刚度，增加了桩基的自振周期；通过施加瞬时激励的方式，梁发云等^[5]研究了桥墩冲刷程度对简支梁桥频谱幅值的影响；基于结构的振型和自振频率，熊文等^[6]分析了基础冲刷对结构刚度的影响，并提出了一种基于结构柔度矩阵的识别基础冲刷的参数；Chen等^[7]通过对大跨斜拉桥在日常环境作用下的振动进行测量，分析了基础冲刷深度对主梁和桥墩模态频率的影响；通过进行室内实验和建立数值模型，Bao等^[8]针对不同特性的地基土，研究了基础冲刷对桥墩固有频率的影响；Malekjafarian等^[9]提出了一种模态振型比的冲刷指标，并研究了基础冲刷对模态振型比的影响，研究发现，模态振型比对基础冲刷的敏感性要高于普遍研究的固有频率；基于振型分解法，Khan等^[10]通过数值和实验研究基础冲刷对结构模态振型的影响发现，随着基础冲刷程度的增加，健康模态振型与冲刷模态振型的均方根差几乎呈线性增加. 基础冲刷改变了结构的振动特性，从而影响结构在不同荷载作用下的动力性能. 利用有限元方法，李克冰等^[11]分析了基础冲刷对车-桥系统动力性能的影响，并对比了基础冲刷前后列车运行的安全性，研究发现基础冲刷使得桥梁结构跨中的振动响应明显增大，同时降低了桥上行驶车辆的安全性；基于建立的车-桥-波浪耦合振动系统，Kong等^[12]研究在波浪作用下不同冲刷深度对车-桥系统动力响应的影响发现，基础冲刷使得桥梁结构的自振周期增大，从而改变了车-桥系统的动力响应，基础的冲刷程度可以通过结构自振特性和车-桥系统动力响应的变化来进行识别；Wang等^[13]研究了冲刷效应对多跨简支、多跨连续和连续刚构3种类型钢筋混凝土箱梁桥的动力特性和抗震性能的影响，研究结果表明，多跨简支类型的箱梁桥受基础冲刷的影响最大. 同时，在地震频发地区，可以通过增大桥梁结构的基础刚度来减少基础冲刷引起的结构损坏；杨婷婷等^[14]通过小波包能量分析方法研究了车辆制动激励作用下基础冲刷和桥梁结构的动力响应关系，通过该方法可以确定基础冲刷的位置和程度；李岩等^[15]研究匀速、制动和变速行驶车辆激励作用下基础冲刷对桥梁动力行为的影响规律发现，车辆制动激励下基础冲刷引起的结构动力响应的变化幅度最大；Wei等^[16]开发了一种基于持续时间法的地震易损性分析框架，并利用开发的框架研究了基础冲刷对一座大跨斜拉桥地震易损性的影响.

基础冲刷会导致下部结构的承载力大大降低，使得桥梁结构在不同荷载组合作用下的动力响应加剧，从而威胁到桥梁和桥上行驶车辆的安全性. 大跨桥梁日常运营阶段常受到风荷载和车辆荷载的共同作用，当突发地震时，在桥上行驶的车辆还来不及撤离桥梁，此时车、桥、风、地震4个要素构成了复杂的地震-风-车-桥耦合动力系统. 由于大跨桥梁具有跨度大、阻尼低和刚度小的特性，在计算车-桥系统在地震作用下的动力响应时，忽略日常环境荷载的作用可能使计算结果偏于不安全. 目前，已有桥梁结构的冲刷研究多是针对运营阶段（冲刷、车辆、风荷载）或地震作用（冲刷、地震）下大跨桥梁的动力响应，而全面系统地开展考虑基础冲刷效应的桥梁结构-运营阶段荷载-极端地震耦合系统振动的研究还很少见. 本文旨在建立一个运营阶段的大跨桥梁在突发地震作用下的动力系统，该系统可全面地考虑地震发生前后（运营荷载、运营荷载和地震联合作用）基础冲刷对车桥耦合系统动力响应的影响，为更加精细地分析桥梁和桥上行驶车辆的安全性提供参考依据. 针对常见的车辆和风等日常运营荷载和破坏性较大的地震作用，将建立可以考虑基础冲刷效应的地震-风-车-桥耦合振动模型. 该耦合振动模型可以用于更加精细的动态行为，对全寿命设计和风险评估具有重要意义.

以江顺大桥为例，采用有限元分析软件ANSYS建立桥梁三维模型，基于MATLAB编程软件建立的地震-风-车-桥耦合振动系统，利用p-y曲线（p为土阻力，y为变形）折减法考虑不同冲刷深度的桩土荷载-位移关系，根据桩土荷载-位移关系和冲刷深度更新桩基的侧向支撑刚度和长度，由此建立了考虑基础冲刷深度的地震-风-车-桥耦合振动系统. 基于该系统，分析比较了桥梁结构的自振频率和车-桥系统动力响应的时频特性的变化，探究了冲刷效应对地震-风-车-桥动力系统的影响规律.

1. 工程概况和冲刷效应的模拟

1.1 工程概况

江顺大桥为60 m + 176 m + 700 m + 176 m + 60 m双塔双索面半漂浮体系斜拉桥，主梁宽40 m的扁平流线型箱梁，中间3跨为钢箱梁，最外侧两边跨为预应力混凝土箱梁，如图1所示. 江顺大桥两侧共有4个辅助墩，主塔（N3、N4）和辅助墩（N1、N2、N5、N6）如图1（a）所示. 2个H形桥塔由群桩基础支撑，每个群桩基础由30根直径为3 m的钻孔灌注桩构成，如图2所示. 桥梁结构的振型和自振频率如表1所示. 可以看出，桥梁结构的自振频率较低，自身振动对地震、风和车辆等动力作用比较敏感. 根据桥址处的河床演变规律、桥墩布置和水流特征值，计算得到设计期内桥址处的最大冲刷深度可达20 m. 桥址处地震基本烈度为Ⅵ度，常年风速在6级以上，江顺大桥在运营期间极有可能受到冲刷、地震、风和车辆的联合作用. 因此，本文以江顺大桥为研究对象，探究冲刷效应对地震-风-车-桥动力系统的影响规律.

图 1 斜拉桥模型（单位：m）

Figure 1. Prototype of cable-stayed bridge （unit: m）

下载: 全尺寸图片幻灯片

1.2 冲刷效应的模拟

本文采用p-y曲线来考虑地基土的侧向力，并利用计算程序LPILE^[17]来计算桩-土的p-y曲线，通过输入土层的物理参数和土层厚度可以计算得出土层任一深度位置处的桩-土p-y曲线. p-y曲线法将桩前土体简化为离散的非线性弹簧，通过弹簧的刚度-变形关系来描述桩土间的相互作用. 有限元模型中，将桩基础离散为单位长度的单元，在单元节点施加非线性弹簧，弹簧的刚度-位移关系即为利用计算程序LPILE计算得到的不同深度下桩土的p-y曲线，单元节点施加的弹簧力即为p-y曲线中节点位移和刚度曲线围成的面积.

图 2 带有群桩基础的桥塔模型（单位：m）

Figure 2. Prototype of bridge tower with group-pile foundation （unit: m）

下载: 全尺寸图片幻灯片

由于p-y曲线能够合理地考虑土体的塑性和桩土间的非线性相互作用，因而在岩土工程领域和其他相关工程领域得到了广泛应用^[18]. 针对群桩基础，可采用p因子修正系数来考虑群桩效应，即将单桩的p-y曲线乘以折减系数得到群桩的p-y曲线. 对于黏性黏土和无黏性砂土，Yang等^[19-20]基于最优曲线法提出了p因子修正系数，如式（1）、（2）.

${R}_{1}={\left(\frac{{S}/{D}-1}{7}\right)}^{0.043\left(10-\frac{H}{D}\right)},\quad S\leqslant 8D,\text{ }H \leqslant 10D,$

(1)

${R}_{2}={\left(\frac{{S}/{D}-1}{7}\right)}^{0.056\left(10-\frac{H}{D}\right)},\quad S\leqslant 8D,\text{ }H\leqslant 10D,$

(2)

式中：R₁、R₂分别为黏性黏土和无黏性砂土的修正系数；S、D和H分别为桩间距、桩径和地表下地基土的深度，当桩间距和基础埋深满足S≤8D和H≤10D时，需要考虑群桩修正系数.

表 1 桥梁结构的前十阶自振频率和振型

Table 1. First 10 natural vibration frequencies and modes of bridge

振型数	自振频率/Hz	振型
1	0.0905	纵飘（主梁）
2	0.2029	1 阶对称侧弯（主梁、桥塔）
3	0.2572	1 阶反对称侧弯（主梁、桥塔）
4	0.2917	2 阶对称侧弯（主梁、桥塔）
5	0.2944	1 阶对称竖弯（主梁）
6	0.3331	1 阶反对称竖弯（主梁）
7	0.3450	2 阶对称竖弯（主梁）
8	0.3890	2 阶反对称竖弯（主梁）
9	0.4138	2 阶反对称侧弯（主梁、桥塔）
10	0.4274	1 阶对称扭转（主梁）

下载: 导出CSV

| 显示表格

本文通过修改桩基础周围土体非线性弹簧单元的参数来模拟基础的冲刷效应. 随着冲刷深度的增加，桩基础的侧向约束长度会减小. 同时，土层厚度的减小会引起地基土的应力释放，从而使得剩余基土的刚度发生变化. 在模拟过程中，当基础冲刷发生时，去除冲刷土层的弹簧单元，并根据基础冲刷后的地面高程重新计算剩余地基土的p-y曲线. 根据冲刷后的p-y曲线和桩基侧向约束的长度来更新桩基侧向支撑的刚度和长度，从而在桥梁仿真模型中实现由于基础冲刷引起的地基土对结构侧向约束的变化. 基础冲刷的模拟示意如图3所示.

图 3 模拟示意

Figure 3. Simulation

下载: 全尺寸图片幻灯片

基础冲刷主要包括一般冲刷和局部冲刷. 局部冲刷的物理机理比较复杂，且目前没有能够准确预测局部冲刷深度的数学公式. 本文主要研究了冲刷效应对车-桥耦合动力系统的影响，因此，忽略了局部冲刷的影响，假设所有桩基具有相同的冲刷深度，局部冲刷对车-桥动力系统的影响不在本文的研究范围内.

2. 地震-风-车-桥耦合振动模型

采用有限元法建立桥梁模型，桥墩、桥塔、桩基和主梁利用空间梁单元模拟，斜拉索利用空间杆单元模拟，桩土间的相互作用利用非线性弹簧单元模拟. 本文将车辆模型模拟为质量-弹簧-阻尼系统，采用具有17个独立自由度的两轴四轮车辆模型^[21]. 根据力的平衡关系，车-桥相互作用力 ${\boldsymbol{F}}_{{\rm{vb}}}$ 和 ${\boldsymbol{F}}_{{\rm{bv}}}^{}$ （b表示桥，v表示车，vb表示桥对车，bv表示车对桥，后文同）是一对大小相等且方向相反的力，基于车轮接触点处力的平衡条件，并考虑车辆的重力，车-桥相互作用力采用了Baker^[22]提出的力学模型.

桥梁结构受到的风力由平均风引起的静风力以及脉动风引起的抖振风力和自激风力构成，每种风力又可进一步分解为升力、阻力和扭矩分量^[23]，如式（3）.

${{\boldsymbol{F}}_{{\rm{bwind}}}}{\text{ = }} \left[ \begin{gathered} {\kern 1pt} {\kern 1pt} {{\boldsymbol{L}}_{\rm{b}}}(x,t) \\ {{\boldsymbol{D}}_{\rm{b}}}(x,t) \\ {{\boldsymbol{M}}_{\rm{b}}}(x,t) \\ \end{gathered} \right] = \left[ \begin{array}{c} {{\boldsymbol{L}}_{{\rm{st}}}} + {{\boldsymbol{L}}_{{\rm{se}}}}(x,t) + {{\boldsymbol{L}}_{{\rm{bu}}}}(x,t) \\ {{\boldsymbol{D}}_{{\rm{st}}}} + {{\boldsymbol{D}}_{{\rm{se}}}}(x,t) + {{\boldsymbol{D}}_{{\rm{bu}}}}(x,t) \\ {{\boldsymbol{M}}_{{\rm{st}}}} + {{\boldsymbol{M}}_{{\rm{se}}}}(x,t) + {{\boldsymbol{M}}_{{\rm{bu}}}}(x,t) \end{array} \right],$

(3)

式中：F_bwind为作用在桥梁结构上的风力；L、D和M分别为升力分量、阻力分量和扭矩分量，下标st、se和bu分别为静风力、自激力和抖振力，可利用准静态方法求解车辆受到的风力^[22].

桥梁结构受到的地震作用力可利用大质量法进行施加，施加在结构上的等效地震力^[24]为

${{\boldsymbol{F}}_{{\rm{be}}}} = - {{\boldsymbol{C}}_{{{as}}}}{\dot {\boldsymbol{U}}_{\rm{g}}} - {{\boldsymbol{K}}_{{{as}}}}{{\boldsymbol{U}}_{\rm{g}}},$

(4)

式中：K_as（C_as）为刚度矩阵（阻尼矩阵），为在第s自由度发生单位位移或转角（单位速度或角速度）时，在第a自由度上产生的力或力矩； ${{\boldsymbol{U}}_{\rm{g}}}$ 和 $\dot{{{\boldsymbol U}}_{\rm{g}}}$ 分别为地震动的位移和速度时程.

通过建立桥梁和车辆模型，并考虑作用在车-桥系统上的作用力，得到地震-风-车-桥耦合振动系统的运动方程为

$\left\{ \begin{gathered} {\boldsymbol{M}}_{\rm{v}}^{(i)}\ddot {\boldsymbol{d}}_{\rm{v}}^{(i)} + {\boldsymbol{C}}_{\rm{v}}^{(i)}\dot {\boldsymbol{d}}_{\rm{v}}^{(i)} + {{\boldsymbol{K}}_{\rm{v}}}{\boldsymbol{d}}_{\rm{v}}^{(i)} = {\boldsymbol{F}}_{{\rm{vb}}}^{(i)} + {\boldsymbol{F}}_{{\rm{vG}}}^{(i)} + {\boldsymbol{F}}_{{\rm{vwind}}}^{(i)}, \\ {{\boldsymbol{M}}_{\rm{b}}}{{\ddot {\boldsymbol{d}}}_{\rm{b}}}{\text{ + }}{{\boldsymbol{C}}_{\rm{b}}}{{\dot {\boldsymbol{d}}}_{\rm{b}}}{\text{ + }}{{\boldsymbol{K}}_{\rm{b}}}{{\boldsymbol{d}}_{\rm{b}}}{\text{ = }}\sum\limits_{i = 1}^n {{\boldsymbol{F}}_{{\rm{bv}}}^{(i)}} + {{\boldsymbol{F}}_{{\rm{bG}}}} + {{\boldsymbol{F}}_{{\rm{bwind}}}} , \\ \end{gathered} \right.$

(5)

式中：M、C和K分别为质量、阻尼和刚度矩阵； ${\boldsymbol{ d}}$ 、 $\dot {\boldsymbol{d}}$ 和 ${\boldsymbol{\ddot d}}$ 分别为位移、速度和加速度矢量； ${\boldsymbol{F}}_{{\rm{vb}}}^{(i)}$ $({\boldsymbol{F}}_{{\rm{bv}}}^{(i)})$ 为第i辆车与桥梁之间的相互作用力， $i=1,2,\cdots，n$ ； ${\boldsymbol{F}}_{{\rm{vG}}}^{(i)}$ 和 ${\boldsymbol{F}}_{{\rm{vwind}}}^{(i)}$ 分别为作用在第i辆车上的重力和风荷载；F_bG为作用在桥上的重力.

采用数值积分方法分别求解式（5）中车辆和桥梁的运动方程，并通过不断迭代得到满足桥梁和车辆间耦合关系的动力响应.

3. 数值算例

3.1 工况设置

表2给出了桥址处地基土的物理参数，图4显示了不同土层的p-y曲线. 从图4（a）中可以看出：无黏性砂土的p-y曲线由3个阶段构成，前2个阶段的土体抗力和桩的侧向变形几乎成线性关系，第3阶段的土体抗力不再随着变形的增加而增加；黏性土p-y曲线的土体抗力在较小变形时迅速增大到峰值，然后，随着变形的增加土体抗力减小到一个相对的低值，随后保持不变. 软岩p-y曲线土体抗力随着桩的侧向变形的增加而迅速增大到峰值，随后基本保持不变，如图4（b）所示.

表 2 群桩基础处不同土层的物理和力学参数

Table 2. Physical and mechanical properties of different soil layers at group-pile foundation

土层	地基土的类别	土层厚度/m	重度/ （kN·m⁻³）	排水剪切强度/kPa	内摩擦角/（°）	泊松比	弹性模量/ MPa	单轴抗压强度/MPa	最大主应力为50% 的应变	应变因子
1	无黏性砂土	7.5	18		30	0.30	3
2	黏性土	10.0	20	93.8		0.35	21		0.007
3	软岩	29.5	22			0.25	7240	3.45		0.0005

下载: 导出CSV

| 显示表格

桥面上车流布置为双向车流，本算例的车型采用轻型卡车^[21]，每车道布置15辆车，前后车距为50 m，车速设置为20 m/s. 桥塔和主梁分别均布了11个和83个风场点，桥址处日常风速取10 m/s，图5给出了主梁跨中的水平和竖向脉动风速（u(t)和w(t)）时程. 在本研究中，考虑到车辆和桥梁的气动干扰，通过实验确定了车辆和桥梁的气动力系数^[25-26]，以便更好地预测其动态响应. 桥址处场地的特征周期为0.35 s，特征频率为17.952 rad/s，地震动水平方向的加速度峰值为0.1g，竖向分量取水平分量的2/3^[27]. 假定地震的传播方向与桥梁主梁轴线夹角为45°，行波波速为1000 m/s，图6给出了辅助墩N1、N5和主塔N3支撑点处水平方向的地震动加速度时程.

图 4 桥址处桩土的p-y曲线

Figure 4. p-y curves of soil for piles at bridge site

下载: 全尺寸图片幻灯片

图 5 主梁跨中的u(t)时程和w(t)时程

Figure 5. Horizontal turbulent wind velocity time history and vertical turbulent wind velocity time history at bridge mid-span

下载: 全尺寸图片幻灯片

图 6 桥梁支撑点N1、N3和N5位置处水平方向的地震动加速度时程

Figure 6. Seismic acceleration time histories of support points N1, N3, and N5 along horizontal direction

下载: 全尺寸图片幻灯片

3.2 冲刷深度对自振特性的影响

根据桥址处的水文条件，桥址处的最大冲刷深度为20 m. 由于局部冲刷的物理机理比较复杂且难以预测，同时，重点关注冲刷效应对车桥耦合动力系统的影响，因此，忽略了局部冲刷的影响. 本文假设所有桩基具有相同的冲刷深度. 为了研究冲刷深度对结构自振特性的影响，考虑了0 （无冲刷）、5、10、15、20 m 5个冲刷深度. 表3给出了不同冲刷深度下结构的自振频率. 由表可知，基础冲刷并没有改变结构的相关振型，但结构的自振频率随着基础冲刷深度的增加而不断减小. 对桥梁主梁纵向、侧向和竖向贡献最大的振型为振型1、振型2和振型5，相应振型的自振频率最大分别降低了1.22%、6.01%和1.53%. 因此，基础冲刷对结构的侧向振型影响最大，这主要是因为基础冲刷减弱了地基土对结构的侧向约束.

表 3 不同冲刷深度时桥梁的自振频率

Table 3. Natural frequencies of the bridge under various scour depths Hz

振型序号	冲刷深度
振型序号	0	5 m	10 m	15 m	20 m
1	0.0905	0.0903	0.0902	0.0901	0.0894
2	0.2029	0.1994	0.1987	0.1984	0.1907
3	0.2572	0.2531	0.2523	0.2520	0.2428
4	0.2917	0.2912	0.2911	0.2910	0.2835
5	0.2944	0.2933	0.2928	0.2926	0.2899
6	0.3331	0.3261	0.3240	0.3229	0.2988
7	0.3450	0.3366	0.3342	0.3331	0.3138
8	0.3890	0.3860	0.3852	0.3848	0.3796
9	0.4138	0.4070	0.4058	0.4053	0.3864
10	0.4274	0.4179	0.4152	0.4139	0.3907

下载: 导出CSV

| 显示表格

3.3 考虑冲刷效应的桥梁响应

基础冲刷改变了结构的自振特性，从而影响了结构在不同荷载作用下的动力响应. 本节研究了考虑冲刷效应时车-桥系统在地震与风联合作用下的动力性能. 本节采用3.1节的工况设置，对比分析了冲刷深度分别为0、10、20 m时桥梁结构的动力性能. 为了便于观察桥梁结构在运营车辆和风荷载作用下的初始振动状态，假定地震在车流上桥第30 s时发生并持续了60 s.

图7为冲刷深度0、10、20 m时主梁跨中的横向和竖向位移时程. 如图7（a）所示：在运营车辆和风荷载作用（0～30 s）下，结构的横向位移响应受基础冲刷的影响很小；在地震发生后（30～90 s），结构横向位移的变化明显增大，结构的横向地震位移响应对基础冲刷更加敏感，且随着冲刷深度的增加，结构的横向位移响应极值不断增大；与无冲刷下的动力响应相比，冲刷深度20 m时主梁的横向位移响应极值增大了9.1%. 与主梁跨中横向位移响应的规律不同，主梁的竖向位移响应受基础冲刷的影响很小，可以忽略，如图7（b）所示.

图 7 地震和运营荷载作用下主梁跨中的位移响应

Figure 7. Displacement responses at bridge mid-span under and seismic and operational loads

下载: 全尺寸图片幻灯片

为进一步观察基础冲刷对结构动力特性的影响，利用快速傅里叶变换给出了桥梁主梁跨中在冲刷深度0、10、20 m下的横向和竖向位移响应谱，如图8所示. 对于结构的横向响应，与无冲刷情况相比，在基础冲刷深度为10 m和20 m时，一阶对称横向振型的频率从0.2029 Hz分别减小到0.1987 Hz和0.1907 Hz，分别降低了2.07%和6.01%. 0.1907 Hz（冲刷深度20 m）、0.1987 Hz （冲刷深度10 m）和0.2029 Hz （无冲刷）的显著峰值分别为0.116、0.103和0.088，如图8（a）所示. 此外，由图8（b）可以看出，基础冲刷深度0、10、20 m下的竖向位移响应谱几乎是相同的，这也说明了基础冲刷对桥梁竖向振动特性的影响很小，可以忽略.

图 8 地震和运营荷载作用下主梁跨中的位移响应谱

Figure 8. Displacement response spectrum at bridge mid-span under seismic and operational loads

下载: 全尺寸图片幻灯片

冲刷深度0、10、20 m时桥梁左塔塔顶的横向位移时程及频谱如图9和图10所示. 与桥梁主梁动力响应的变化类似，基础冲刷使得结构的横向动力响应变大，且相应响应谱的幅值增大.

图 9 地震和运营荷载作用下左桥塔顶的横向位移响应

Figure 9. Lateral displacement responses at left tower top under seismic and operational loads

下载: 全尺寸图片幻灯片

3.4 考虑冲刷效应的车辆响应

车辆的安全性主要取决于车辆的加速度响应. 本节采用与3.3节相同的荷载工况，同时选取车道1沿X轴正向行驶的第1辆车作为代表车辆来研究车辆的动力响应. 图11给出了地震前后车辆的横向和竖向加速度时程. 如图11（a）所示，在风荷载作用下（0～30 s），车辆加速度响应受基础冲刷的影响很小，可以忽略；在地震发生后（30～90 s），车辆的横向加速度响应有所降低，冲刷深度20 m时车辆的横向加速度响应极值比无冲刷时减小了7.7%. 然而，基础冲刷对地震发生前后车辆的竖向加速度响应影响都很小，如图11（b）所示.

图 10 地震和运营荷载作用下左桥塔顶的横向位移响应谱

Figure 10. Lateral displacement response spectrum at left tower top under seismic and operational loads

下载: 全尺寸图片幻灯片

图 11 地震和运营荷载作用下代表车辆的加速度响应

Figure 11. Acceleration responses of representative vehicle under seismic and operational loads

下载: 全尺寸图片幻灯片

4. 结　论

本文基于建立的考虑基础冲刷的地震-风-车-桥耦合振动系统，计算并分析了桥梁自振特性和车-桥系统时频特性，探究了基础冲刷对地震-风-车-桥耦合振动系统的影响规律，所得结论如下：

1）结构的自振频率随着基础冲刷深度的增加而不断减小. 同时，基础冲刷对结构的侧向振型影响最大，这主要是因为基础冲刷减弱了地基土对结构的侧向约束.

2）在运营车辆和风荷载作用下，结构的横向位移响应受基础冲刷的影响很小. 在地震发生后，结构横向位移的变化明显增大，结构的横向地震位移响应对基础冲刷更加敏感，且随着冲刷深度的增加结构的横向位移响应极值不断增大，结构的横向位移响应谱也相应增大.

3）地震发生前后，结构的竖向振动受基础冲刷的影响均很小. 同时，不同冲刷深度下结构的竖向位移响应谱几乎是相同的.

4）基础冲刷可能减小车辆横向加速度的响应，然而车辆竖向加速度响应随着冲刷深度的增加几乎没有发生变化.

图 1 循环荷载下土体累积应变发展模式分类^[12]

Figure 1. Classification of soil cumulative strain development modes under cyclic loading^[12]

下载: 全尺寸图片幻灯片

图 2 循环荷载下土体的累积应变

Figure 2. Accumulative strain of soil under cyclic loading

下载: 全尺寸图片幻灯片

图 3 土体p-q空间中的应力状态

Figure 3. Stress state of soil in p-q plane

下载: 全尺寸图片幻灯片

表 1 影响因素分类与表征指标

Table 1. Classification and characterization of influence factors

类别	考察指标
初始应力状态	主应力空间	围压 ${\sigma _3}$ 、轴向应力 ${\sigma _1}$ 、固结应力比 $k = {{{\sigma _1}} \mathord{\left/ {\vphantom {{{\sigma _1}} {{\sigma _3}}}} \right. } {{\sigma _3}}}$
初始应力状态	$p {\text{-}} q$ 空间	初始平均主应力 ${p_0}$ 、初始剪应力 ${q_0}$ 、初始应力比 ${\eta _0} = {{{q_0}} / {{p_0}}}$
循环应力特征	加载频率、循环应力波形、循环应力幅值、循环应力的偏振、主应力轴旋转等
土的物理特征	土的类型与级配特征，土的颗粒骨架的组构形式，初始孔隙比（相对密实度、压实度），含水量（饱和度），温度（冻结与否）

下载: 导出CSV

参考文献(111)

[1]	谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011.
[2]	FUJIKAWA K, MIURA N, BEPPU I. Field investigation on the settlement of low embankment due to traffic load and its prediction[J]. Soils and Foundations, 1996, 36(4): 147-153. doi: 10.3208/sandf.36.4_147
[3]	SAMANG L, MIURA N, SAKAI A. Long-term measurements of traffic load induced settlement of pavement surface in saga airport highway, Japan[J]. Jurnal Teknik Sipil, 2010, 12(4): 275-285. doi: 10.5614/jts.2005.12.4.5
[4]	WICHTMANN T. Explicit accumulation model for non-cohesive soils under cyclic loading[D]. [S.l.]: Thesis, Ruhr-University Bochum, 2005.
[5]	凌建明,王伟,邬洪波. 行车荷载作用下湿软路基残余变形的研究[J]. 同济大学学报(自然科学版),2002,30(11): 1315-1320. doi: 10.3321/j.issn:0253-374X.2002.11.007 LING Jianming, WANG Wei, WU Hongbo. On residual deformation of saturated clay subgrade under vehicle load[J]. Journal of Tongji University (Natural Science), 2002, 30(11): 1315-1320. doi: 10.3321/j.issn:0253-374X.2002.11.007
[6]	曹国安,邸旺亮,蒋永莉,等. 牙林线多年冻土地区路基下沉机理及整治研究[J]. 路基工程,1996(5): 40-42.
[7]	朱占元. 青藏铁路列车行驶多年冻土场地路基振动反应与振陷预测[D]. 哈尔滨: 哈尔滨工业大学, 2009.
[8]	牛富俊,林战举,鲁嘉濠,等. 青藏铁路路桥过渡段沉降变形影响因素分析[J]. 岩土力学,2011,32(增2): 372-377. NIU Fujun, LIN Zhanju, LU Jiahao, et al. Study of the influencing factors of roadbed settlement in embankment-bridge transition section along Qinghai—Tibet Railway[J]. Rock and Soil Mechanics, 2011, 32(S2): 372-377.
[9]	陈亮,沈军辉,沈中超,等. 川汶公路K95+300~K95+490段堰塞湖相沉积地层路基变形机制研究[J]. 中外公路,2017,37(5): 22-25. CHEN Liang, SHEN Junhui, SHEN Zhongchao, et al. The control of subgrade settlement in the sedimentary stratigraphy of barrier lake from K95+300 to K95+490 of Chuanwen highway[J]. Journal of China & Foreign Highway, 2017, 37(5): 22-25.
[10]	金辰. 基于路面开裂状况的薄沥青路面半刚性基层模量评估[J]. 公路工程,2022,47(2): 97-102. JIN Chen. Modulus evaluation of semi-rigid base of thin asphalt pavement based on pavement cracking[J]. Highway Engineering, 2022, 47(2): 97-102.
[11]	李振存. 在役高速公路路基性能评价及快速检测技术[D]. 长沙: 长沙理工大学, 2014.
[12]	CHEN W B, FENG W Q, YIN J H, et al. Characterization of permanent axial strain of granular materials subjected to cyclic loading based on shakedown theory[J]. Construction and Building Materials, 2018, 198(20): 751-761.
[13]	GU F, ZHANG Y Q, LUO X, et al. Characterization and prediction of permanent deformation properties of unbound granular materials for pavement ME Design[J]. Construction and Building Materials., 2017, 155: 584-592. doi: 10.1016/j.conbuildmat.2017.08.116
[14]	王康宇,庄妍,耿雪玉. 铁路路基粗粒土填料临界动应力试验研究[J]. 岩土力学,2020,41(6): 1865-1873. WANG Kangyu, ZHUANG Yan, GENG Xueyu. Experimental study on critical dynamic stress of coarse-grained soil in railway subgrade[J]. Rock and Soil Mechanics, 2020, 41(6): 1865-1873.
[15]	SILVER M L, SEED H B. Deformation characteristics of sands under cyclic loading[J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(8): 1081-1098. doi: 10.1061/JSFEAQ.0001648
[16]	TARHOUNI M A A, HAWLADER B. Monotonic and cyclic behaviour of sand in direct simple shear test conditions considering low stresses[J]. Soil Dynamics and Earthquake Engineering, 2021, 150(11): 106931.1-106931.13.
[17]	高广运,聂春晓,顾晓强. 砂土震陷室内试验研究综述[J]. 水利水电科技进展,2016,36(6): 1-7. GAO Guangyun, NIE Chunxiao, GU Xiaoqiang. A review of recent research in laboratory test of seismic compression of sands[J]. Advances in Science and Technology of Water Resources, 2016, 36(6): 1-7.
[18]	鲁丽雪. Bouc-Wen土体动力本构模型及其阈值应变研究[D]. 大连: 大连理工大学, 2013.
[19]	SORALUMP S, PRASOMSRI J. Cyclic pore water pressure generation and stiffness degradation in compacted clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1): 1-13.
[20]	XU L, WONG K K, FABBRI A, et al. Loading-unloading shear behavior of rammed earth upon varying clay content and relative humidity conditions[J]. Soils and Foundations, 2018, 58(4): 1001-1015. doi: 10.1016/j.sandf.2018.05.005
[21]	刘启旺,杨正权,刘小生,等. 超深厚覆盖层中深埋细粒土地震残余变形特性振动三轴试验研究[J]. 地震工程学报,2015,37(1): 21-26. doi: 10.3969/j.issn.1000-0844.2015.01.0021 LIU Qiwang, YANG Zhengquan, LIU Xiaosheng, et al. Dynamic triaxial tests on seismic residual deformation characteristics of the fine-grained soil in super-deep overburden layer[J]. China Earthquake Engineering Journal, 2015, 37(1): 21-26. doi: 10.3969/j.issn.1000-0844.2015.01.0021
[22]	李扬波,张家生,朱志辉,等. 循环荷载作用下铁路路基级配碎石填料累积变形研究[J]. 工程科学与技术,2018,50(5): 130-137. LI Yangbo, ZHANG Jiasheng, ZHU Zhihui, et al. Accumulated deformation of gravel filler of subgrade under cyclic loading[J]. Advanced Engineering Sciences, 2018, 50(5): 130-137.
[23]	陈方敏,丁智,李绍朗,等. 地铁荷载作用下水泥土应变监测模型试验研究[J]. 现代隧道技术,2018,55(2): 127-133. doi: 10.13807/j.cnki.mtt.2018.02.018 CHEN Fangmin, DING Zhi, LI Shaolang, et al. Model test of strain development in cement soil under subway loading[J]. Modern Tunnelling Technology, 2018, 55(2): 127-133. doi: 10.13807/j.cnki.mtt.2018.02.018
[24]	陈靖宇. 公路路基填料长期动力特性试验研究与累积应变模型[D]. 杭州: 浙江大学, 2018.
[25]	HELM J, LAUE J, TRIANTAFYLLIDIS T. Untersuchungen an der RUB zur verformungsentwicklung von Böden unter zyklischen belastungen beiträge zum workshop: boden unter fast zyklischer belastung: erfahrungen und forschungsergebnisse[R]. Bochum: Institute of Soil Mechanics and Foundation Engineering, Ruhr-University, 2000.
[26]	GOTSCHOL A. Veränderlich elastisches und plastisches verhalten nichtbindiger böden und schotter unter zyklisch-dynamischer beanspruchung[D]. Kassel: University Kassel, 2000.
[27]	LEI H Y, SONG Y J, QI Z Y, et al. Accumulative plastic strain behaviors and microscopic structural characters of artificially freeze-thaw soft clay under dynamic cyclic loading[J]. Cold Regions Science and Technology, 2019, 168: 102895. doi: 10.1016/j.coldregions.2019.102895
[28]	MEI H H, SATVATI S, LENG W M. Experimental study on permanent deformation characteristics of coarse-grained soil under repeated dynamic loading[J]. Railway Engineering Science, 2021, 29(1): 94-107. doi: 10.1007/s40534-021-00233-2
[29]	庄心善,赵汉文,陶高梁,等. 循环荷载下弱膨胀土累积变形与动强度特性试验研究[J]. 岩土力学,2020,41(10): 3192-3200. doi: 10.16285/j.rsm.2019.2180 ZHUANG Xinshan, ZHAO Hanwen, TAO Gaoliang, et al. Accumulated deformation and dynamic strength properties of weak expansive soil under cyclic loading[J]. Rock and Soil Mechanics, 2020, 41(10): 3192-3200. doi: 10.16285/j.rsm.2019.2180
[30]	SAWICKI A, MIERCZYŃSKI J, ŚWIDZIŃSKI W. Strains in sand due to cyclic loading in triaxial conditions[J]. Archives of Hydro-Engineering and Environmental Mechanics, 2009, 56(1/2): 85-98.
[31]	WANG J H, LING X Z, LI Q L, et al. Accumulated permanent strain and critical dynamic stress of frozen silty clay under cyclic loading[J]. Cold Regions Science and Technology, 2018, 153: 130-143. doi: 10.1016/j.coldregions.2018.05.007
[32]	WICHTMANN T, NIEMUNIS A, TRIANTAFYLLIDIS T. Strain accumulation in sand due to cyclic loading: drained triaxial tests[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(12): 967-979. doi: 10.1016/j.soildyn.2005.02.022
[33]	YANG J Q, CUI Z D. Influences of train speed on permanent deformation of saturated soft soil under partial drainage conditions[J]. Soil Dynamics and Earthquake Engineering, 2020, 133: 106120.1-106120.12.
[34]	OZEL M R, MOHAJERANI A. Permanent deformation behaviour of two Victorian subgrade soils under repeated loading[J]. Journal and News of the Australian Geomechanics Society, 2002, 37(3): 41-50.
[35]	HUANG J, CHEN J, LU Y, et al. Deformation behaviors and dynamic backbone curve model of saturated soft clay under bidirectional cyclic loading[J]. International Journal of Geomechanics, 2020, 20(4): 1-12.
[36]	BENOOT J, HAEGEMAN W, FRANÇOIS S, et al. Experimental study of strain accumulation of silica sand in a cyclic triaxial test[C]//Proceedings of the 23rd European Young Geotechnical Engineers Conference. Barcelona: [s.n.], 2014: 3-6.
[37]	CHEN C, XUA G F, ZHOU Z M, et al. Undrained dynamic behaviour of peaty organic soil under long-term cyclic loading, part Ⅱ: constitutive model and simulation[J]. Soil Dynamics and Earthquake Engineering, 2020, 129: 1-10.
[38]	XIONG Y L, LIU G B, ZHENG R Y, et al. Study on dynamic undrained mechanical behavior of saturated soft clay considering temperature effect[J]. Soil Dynamics and Earthquake Engineering, 2018, 115: 673-684. doi: 10.1016/j.soildyn.2018.09.026
[39]	聂如松,李亚峰,冷伍明,等. 列车间歇荷载作用下路基细粒土填料的塑性变形行为及临界动应力研究[J]. 岩石力学与工程学报,2021,40(4): 828-841. doi: 10.13722/j.cnki.jrme.2020.0778 NIE Rusong, LI Yafeng, LENG Wuming, et al. Plastic deformation and critical dynamic stress of fine-grained soils under intermittent loading of trains[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(4): 828-841. doi: 10.13722/j.cnki.jrme.2020.0778
[40]	丁智,郑勇,魏新江,等. 不同加载频率及循环应力水平对人工冻融软土动力特性影响试验研究[J]. 铁道学报,2020,42(3): 122-128. doi: 10.3969/j.issn.1001-8360.2020.03.015 DING Zhi, ZHENG Yong, WEI Xinjiang, et al. Experimental study on the effect of different loading frequency and cyclic stress level for dynamic behaviour of artificial frozen-thawed soft soil[J]. Journal of the China Railway Society, 2020, 42(3): 122-128. doi: 10.3969/j.issn.1001-8360.2020.03.015
[41]	ZHANG X, ZHAO C F, ZHAI W M. Importance of load frequency in applying cyclic loads to investigate ballast deformation under high-speed train loads[J]. Soil Dynamics and Earthquake Engineering, 2019, 120: 28-38. doi: 10.1016/j.soildyn.2019.01.023
[42]	贾鹏飞,孔令伟. 高周循环荷载作用过程中土体塑性包络的弹塑性累积模型[J]. 岩石力学与工程学报,2015,34(12): 2542-2549. doi: 10.13722/j.cnki.jrme.2014.1422 JIA Pengfei, KONG Lingwei. Elastoplastic accumulation model for predicting soil plastic envelope due to high-cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(12): 2542-2549. doi: 10.13722/j.cnki.jrme.2014.1422
[43]	WICHTMANN T, NIEMUNIS A, TRIANTAFYLLIDIS T. Flow rule in a high-cycle accumulation model backed by cyclic test data of 22 sands[J]. Acta Geotechnica, 2014, 9: 695-709. doi: 10.1007/s11440-014-0302-7
[44]	WICHTMANN T, NIEMUNIS A, TRIANTAFYLLIDIS T. Experimental evidence of a unique flow rule of non-cohesive soils under high-cyclic loading[J]. Acta Geotechnica, 2006, 1(1): 59-73. doi: 10.1007/s11440-006-0006-8
[45]	WICHTMANN T. Soil behavior under low- and high-cycle loading—Element tests vs. constitutive models[J]. Geomechanics for Energy and the Environment, 2021, 27: 1-18.
[46]	PANG Y X, GU C, WANG J, et al. Strain evolution of saturated clays under cyclic loadings in three-dimensional stress condition[J]. Engineering Geology, 2020, 278: 1-16.
[47]	FAKHARIAN K, AHMAD A. Effect of anisotropic consolidation and rubber content on dynamic parameters of granulated rubber-sand mixtures[J]. Soil Dynamics and Earthquake Engineering, 2021, 141: 1-14.
[48]	ZHOU W, CHEN Y, MA G, et al. A modified dynamic shear modulus model for rockfill materials under a wide range of shear strain amplitudes[J]. Soil Dynamics and Earthquake Engineering, 2017, 92: 229-238. doi: 10.1016/j.soildyn.2016.10.027
[49]	GU C, WANG J, CAI Y Q, et al. Influence of cyclic loading history on small strain shear modulus of saturated clays[J]. Soil Dynamics and Earthquake Engineering, 2014, 66: 1-12. doi: 10.1016/j.soildyn.2014.06.027
[50]	HU X Q, ZHANG Y, GUO L, et al. Cyclic behavior of saturated soft clay under stress path with bidirectional shear stresses[J]. Soil Dynamics and Earthquake Engineering, 2018, 104: 319-328. doi: 10.1016/j.soildyn.2017.10.016
[51]	CHEN G X, ZHOU Z L, PAN H, et al. The influence of undrained cyclic loading patterns and consolidation states on the deformation features of saturated fine sand over a wide strain range[J]. Engineering Geology, 2016, 204: 77-93. doi: 10.1016/j.enggeo.2016.02.008
[52]	梁珂,何杨,陈国兴. 南沙珊瑚砂的动剪切模量和阻尼比特性试验研究[J]. 岩土力学,2020,41(1): 23-31,38. LIANG Ke, HE Yang, CHEN Guoxing. Experimental study of dynamic shear modulus and damping ratio characteristics of coral sand from Nansha Islands[J]. Rock and Soil Mechanics, 2020, 41(1): 23-31,38.
[53]	陈国兴,杨文保,岳文泽,等. 金塘海峡海洋土动剪切模量与阻尼比特性研究[J]. 防灾减灾工程学报,2020,40(1): 1-8. doi: 10.13409/j.cnki.jdpme.2020.01.001 CHEN Guoxing, YANG Wenbao, YUE Wenze, et al. Experimental studies on the dynamic shear modulus and damping ratio characteristics of marine soils in the Jintang strait[J]. Journal of Disaster Prevention and Mitigation Engineering, 2020, 40(1): 1-8. doi: 10.13409/j.cnki.jdpme.2020.01.001
[54]	刘方成,尚守平,王海东. 循环荷载下黏土应变积累积强化模型研究[J]. 岩土力学,2008(9): 2457-2462. doi: 10.3969/j.issn.1000-7598.2008.09.027 LIU Fangcheng, SHANG Shouping, WANG Haidong. Study of strain accumulation strengthened model for clay under cyclic loadings[J]. Rock and Soil Mechanics, 2008(9): 2457-2462. doi: 10.3969/j.issn.1000-7598.2008.09.027
[55]	黄博,施明雄,陈云敏,等. 循环振动对饱和粉土初始动剪模量的影响[J]. 岩土工程学报,2009,31(5): 764-771. doi: 10.3321/j.issn:1000-4548.2009.05.020 HUANG Bo, SHI Mingxiong, CHEN Yunmin, et al. Effects of seismic vibration on small strain shear modulus of saturated silt[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5): 764-771. doi: 10.3321/j.issn:1000-4548.2009.05.020
[56]	LBIBB S, MANZARI M T. Stress-strain behavior of Ottawa sand in cyclic direct simple shear and modeling of cyclic strength using artificial neural networks[J]. Soil Dynamics and Earthquake Engineering, 2022, 164: 1-17.
[57]	STAMATOPOULOS K, PETRIDIS P, ALLKJA P S, et al. Improvement of dynamic soil properties induced by preloading verified by a field test and embankment failure[J]. Engineering Geology, 2013, 163: 101-112.
[58]	尚守平,刘方成,杜运兴,等. 应变累积对黏土动剪模量和阻尼比影响的试验研究[J]. 岩土力学,2006,27(5): 683-688. doi: 10.3969/j.issn.1000-7598.2006.05.001 SHANG Shouping, LIU Fangcheng, DU Yunxing, et al. Experimental study on effect of shear strain accumulation on dynamic shear modulus and damping ratio of clay soil[J]. Rock and Soil Mechanics, 2006, 27(5): 683-688. doi: 10.3969/j.issn.1000-7598.2006.05.001
[59]	张炜,李亚,周松望,等. 南海北部区域黏土循环动力特性试验研究[J]. 岩土力学,2018,39(7): 2413-2423. doi: 10.16285/j.rsm.2016.2242 ZHANG Wei, LI Ya, ZHOU Songwang, et al. Experimental research on cyclic behaviors of clay in the northern region of South China Sea[J]. Rock and Soil Mechanics, 2018, 39(7): 2413-2423. doi: 10.16285/j.rsm.2016.2242
[60]	YE Y, CAI D, YAO J, et al. Review on dynamic modulus of coarse-grained soil filling for high-speed railway subgrade[J]. Transportation Geotechnics, 2020, 27(6): 1-6.
[61]	SOLTANI-JIGHEH H, SOROUSH A. Cyclic behavior of mixed clayey soils[J]. International Journal of Civil Engineering, 2010, 8(2): 99-106.
[62]	ZHOU Y G, CHEN Y M. Influence of seismic cyclic loading history on small strain shear modulus of saturated sands[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(5): 341-353. doi: 10.1016/j.soildyn.2005.03.001
[63]	LIN B, ZHANG F, FENG D C, et al. Dynamic shear modulus and damping ratio of thawed saturated clay under long-term cyclic loading[J]. Cold Regions Science and Technology, 2018, 145: 93-105. doi: 10.1016/j.coldregions.2017.10.003
[64]	VUCETIC M. Cyclic threshold shear strains in soils[J]. Journal of Geotechnical Engineering, 1994, 120(12): 2208-2228. doi: 10.1061/(ASCE)0733-9410(1994)120:12(2208)
[65]	柏立懂. 荷载历史对砂土最大剪切模量影响的共振柱试验研究[J]. 岩石力学与工程学报,2011,30(11): 2366-2374. BAI Lidong. Effects of loading history on maximum shear modulus of sand by resonant column tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2366-2374.
[66]	WICHTMANN T, TRIANTAFYLLIDIS T. Influence of a cyclic and dynamic loading history on dynamic properties of dry sand, part Ⅰ: cyclic and dynamic torsional prestraining[J]. Soil Dynamics and Earthquake Engineering, 2004, 24(2): 127-147. doi: 10.1016/j.soildyn.2003.10.004
[67]	WICHTMANN T, TRIANTAFYLLIDIS T. Influence of a cyclic and dynamic loading history on dynamic properties of dry sand, part Ⅱ: cyclic axial preloading[J]. Soil Dynamics and Earthquake Engineering, 2004, 24(11): 789-803. doi: 10.1016/j.soildyn.2004.05.002
[68]	KARG C, HAEGEMAN W. Elasto-plastic long-term behavior of granular soils: experimental investigation[J]. Soil Dynamics and Earthquake Engineering, 2009, 29(1): 155-172. doi: 10.1016/j.soildyn.2008.01.001
[69]	黄茂松,李帅. 长期往复荷载作用下近海饱和软黏土强度和刚度的弱化特性[J]. 岩土工程学报,2010,32(10): 1491-1498. HUANG Maosong, LI Shuai. Degradation of stiffness and strength of offshore saturated soft clay under long-term cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1491-1498.
[70]	LING X Z, LI Q L, WANG L N, et al. Stiffness and damping radio evolution of frozen clays under long-term low-level repeated cyclic loading: experimental evidence and evolution model[J]. Cold Regions Science and Technology, 2013, 86: 45-54. doi: 10.1016/j.coldregions.2012.11.002
[71]	NIE R S, SUN B L, LENG W M, et al. Resilient modulus of coarse-grained subgrade soil for heavy-haul railway: an experimental study[J]. Soil Dynamics and Earthquake Engineering, 2021, 150(4): 1-10.
[72]	MUHAMMAD N, SIDDIQUA S. Moisture-dependent resilient modulus of chemically treated subgrade soil[J]. Engineering Geology, 2021, 285: 1-13.
[73]	LIU X L, ZHANG X M, WANG H, et al. Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors[J]. Construction and Building Materials, 2019, 195: 178-186. doi: 10.1016/j.conbuildmat.2018.11.061
[74]	SU Y, CUI Y J, DUPLA J C, et al. Effect of water content on resilient modulus and damping ratio of fine/coarse soil mixtures with varying coarse grain contents[J]. Transportation Geotechnics, 2020, 26: 1-11.
[75]	BOZBEY I, KUBILAY KELESOGLU M, DEMIR D, et al. Effects of soil pulverization level on resilient modulus and freeze and thaw resistance of a lime stabilized clay[J]. Cold Regions Science and Technology, 2018, 151: 323-334. doi: 10.1016/j.coldregions.2018.03.023
[76]	HAN Z, VANAPALLI S K. Relationship between resilient modulus and suction for compacted subgrade soils[J]. Engineering Geology, 2016, 211: 85-97. doi: 10.1016/j.enggeo.2016.06.020
[77]	REN J P, VANAPALLI S K. Empirical model for predicting the resilient modulus of frozen unbound road materials using a hyperbolic function[J]. Transportation Geotechnics, 2018, 17: 66-74. doi: 10.1016/j.trgeo.2018.09.011
[78]	FAN C, ZHANG W, LAI Y, et al. Mechanical behaviors of frozen clay under dynamic cyclic loadings with freeze-thaw cycles[J]. Cold Regions Science and Technology, 2021, 181: 1-10.
[79]	LACKENBY J, INDRARATNA B, MCDOWELL G, et al. Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading[J]. Geotechnique, 2007, 57: 527-536. doi: 10.1680/geot.2007.57.6.527
[80]	ATTIA M, ABDELRAHMAN M. Sensitivity of untreated reclaimed asphalt pavement to moisture, density, and freeze thaw[J]. Journal of Materials in Civil Engineering, 2010, 22(12): 1260-1269. doi: 10.1061/(ASCE)MT.1943-5533.0000135
[81]	CORONADO O, CAICEDO B, TAIBI S, et al. Effect of water content on the resilient behavior of non standard unbound granular materials[J]. Transportation Geotechnics, 2016, 7: 29-39. doi: 10.1016/j.trgeo.2016.04.004
[82]	NG C W W, ZHOU C, YUAN Q, et al. Resilient modulus of unsaturated subgrade soil: experimental and theoretical investigations[J]. Canadian Geotechnical Journal, 2013, 50: 223-232. doi: 10.1139/cgj-2012-0052
[83]	ALNEDAWI A, ULLAH S, AZAM A, et al. Integrated and holistic knowledge map of resilient modulus studies for pavement materials: a scientometric analysis and bibliometric review of research frontiers and prospects[J]. Transportation Geotechnics, 2021, 33: 1-22.
[84]	郭林,蔡袁强,王军,等. 长期循环荷载作用下温州结构性软黏土的应变特性研究[J]. 岩土工程学报,2012,34(12): 2249-2254. GUO Lin, CAI Yuanqiang, WANG Jun, et al. Long-term cyclic strain behavior of Wenzhou structural soft clay[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2249-2254.
[85]	SUIKER A S J, SELIG E T, FRENKEL R. Static and cyclic triaxial testing of ballast and subballast[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(6): 771-782. doi: 10.1061/(ASCE)1090-0241(2005)131:6(771)
[86]	ZHOU C. Cyclic behaviour of an unsaturated silt at various suctions and temperatures[J]. Geotechnique, 2014, 64: 709-720. doi: 10.1680/geot.14.P.015
[87]	SINGHA A, AL FARUQUE M A, BALACHANDAR R. Vortices and large-scale structures in a rough open-channel flow subjected to bed suction and injection[J]. Journal of Engineering Mechanics, 2012, 138(5): 491-501.
[88]	YANG C, CUI Y J, PEREIRA J M, et al. A constitutive model for unsaturated cemented soils under cyclic loading[J]. Computers and Geotechnics, 2008, 35(6): 853-859. doi: 10.1016/j.compgeo.2008.08.005
[89]	GAO Z, ZHAO J. Constitutive modeling of artificially cemented sand by considering fabric anisotropy[J]. Computers and Geotechnics, 2012, 41: 57-69. doi: 10.1016/j.compgeo.2011.10.007
[90]	GAO Z, ZHAO J, LI X S, et al. A critical state sand plasticity model accounting for fabric evolution[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 2014, 38(4): 370-390.
[91]	SINGH A K, SAHOO J P. Rutting prediction models for flexible pavement structures: a review of historical and recent developments[J]. Journal of Traffic and Transportation Engineering (English Edition), 2021, 8(3): 315-338. doi: 10.1016/j.jtte.2021.04.003
[92]	龙尧,张家生,丁建源,等. 粗粒土路基循环荷载试验及累积变形模型研究[J]. 振动与冲击,2017,36(16): 128-133. doi: 10.13465/j.cnki.jvs.2017.16.020 LONG Yao, ZHANG Jiasheng, DING Jianyuan, et al. The cyclic load experiments and an accumulated deformation model for coarse-grained soil filling[J]. Journal of Vibration and Shock, 2017, 36(16): 128-133. doi: 10.13465/j.cnki.jvs.2017.16.020
[93]	GUO L, WANG J, CAI Y Q, et al. Undrained deformation behavior of saturated soft clay under long-term cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 2013, 50(7): 28-37.
[94]	FRANÇOIS S, KARG C, HAEGEMAN W, et al. A numerical model for foundation settlements due to deformation accumulation in granular soils under repeated small amplitude dynamic loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 34(3): 273-296.
[95]	LI D, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering, 1996, 122(12): 1006-1013. doi: 10.1061/(ASCE)0733-9410(1996)122:12(1006)
[96]	ULLDITZ P. Mathematical model for pavement performance under moving wheel load[C]//Transportation Research Record. 1384, Transportation Research Board. Washington, D. C.: [s.n.], 1993: 94-99.
[97]	PUPPALA A J, SARIDE S, CHOMTID S. Experimental and modeling studies of permanent strains of subgrade soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1379-1389. doi: 10.1061/(ASCE)GT.1943-5606.0000163
[98]	CHAI J C, MIURA N. Traffic-load-induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(11): 907-916. doi: 10.1061/(ASCE)1090-0241(2002)128:11(907)
[99]	黄茂松,姚兆明. 循环荷载下饱和软黏土的累积变形显式模型[J]. 岩土工程学报,2011,33(3): 325-331. HUANG Maosong, YAO Zhaoming. Explicit model for cumulative strain of saturated clay subjected to cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 325-331.
[100]	GIDEL G. A new approach for investigating the permanent deformation behaviour of unbound granular material using the repeated load triaxial apparatus[J]. Bulletin des Laboratoires des Ponts et Chaussees, 2001, 233: 5-21.
[101]	NIEMUNIS A, WICHTMANN T, TRIANTAFYLLIDIS T. A high-cycle accumulation model for sand[J]. Computers and Geotechnics, 2005, 32(4): 245-263. doi: 10.1016/j.compgeo.2005.03.002
[102]	LI Q L, LING X Z, SHENG D C. Elasto-plastic behaviour of frozen soil subjected to long-term low-level repeated loading, part Ⅱ: constitutive modelling[J]. Cold Regions Science and Technology, 2016, 122: 58-70. doi: 10.1016/j.coldregions.2015.11.009
[103]	PASTEN C, SHIN H, CARLOS SANTAMARINA J. Long-term foundation response to repetitive loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 140(4): 1-11.
[104]	QIAN J, LI S, GU X, et al. A unified model for estimating the permanent deformation of sand under a large number of cyclic loads[J]. Ocean Engineering, 2019, 181: 293-302. doi: 10.1016/j.oceaneng.2019.03.051
[105]	WU Z X, YIN Z Y, DANO C, et al. Cyclic volumetric strain accumulation for sand under drained simple shear condition[J]. Applied Ocean Research, 2020, 101: 1-10.
[106]	SUN Q D, INDRARATNA B, NIMBALKAR S. Deformation and degradation mechanisms of railway ballast under high frequency cyclic loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 142(1): 04015056.1-04015056.12.
[107]	MIAO Y, ZHANG H, HE H J, et al. In-situ properties of Poisson’s ratio based on KiK-net seismic observations[J]. Engineering Geology, 2022, 296: 1-14.
[108]	LIU Z, HE Z H, ZHANG W Z, et al. Laboratory test and prediction model of dynamic resilient modulus of carbonaceous mudstone coarse-grained soil[J]. Case Studies in Construction Materials, 2022, 18: 1-15.
[109]	XIA P X, SHAO L T, DENG W. Stress-state dependency of the strain ratio of quasi-elastic granular soils under cyclic loading[J]. Geomechanics for Energy and the Environment, 2022, 34(3): 1-14.
[110]	汤大明,曾纪全,胡应德,等. 关于泊松比的试验和取值讨论[J]. 岩石力学与工程学报,2001(增1): 1772-1775. doi: 10.3321/j.issn:1000-6915.2001.z1.035 TANG Daming, ZENG Jiquan, HU Yingde, et al. Discussion on testing and interpretation for poisson’s ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2001(S1): 1772-1775. doi: 10.3321/j.issn:1000-6915.2001.z1.035
[111]	GAO H M, BU C Y, WANG Z H, et al. Dynamic characteristics of expanded polystyrene composite soil under traffic loadings considering initial consolidation state[J]. Soil Dynamics and Earthquake Engineering, 2017, 102: 86-98. doi: 10.1016/j.soildyn.2017.08.012

施引文献

附加材料(0)

访问统计

点击查看大图

图(3) / 表(1)

计量

文章访问数: 1330
HTML全文浏览量: 230
PDF下载量: 242
被引次数: 0

1. 工程概况和冲刷效应的模拟
1.1 工程概况
1.2 冲刷效应的模拟
2. 地震-风-车-桥耦合振动模型
3. 数值算例
3.1 工况设置
3.2 冲刷深度对自振特性的影响
3.3 考虑冲刷效应的桥梁响应
3.4 考虑冲刷效应的车辆响应
4. 结　论

长期循环荷载下土的动力学特性与本构模型研究进展

doi: 10.3969/j.issn.0258-2724.20210928

作者简介: 李琼林（1986—），男，副教授，研究方向为土动力学与寒区岩土工程，E-mail：qionglin_li@swjtu.edu.cn

通讯作者: 崔凯（1979—），男，教授，博士生导师，研究方向为岩土工程，E-mail：cuikai@swjtu.cn

计量

出版历程