Effects of Longitudinal Reinforcement Ratio on Flexural Capacity of One-Way Slab of UHPC Waffle Bridge Deck
-
摘要:
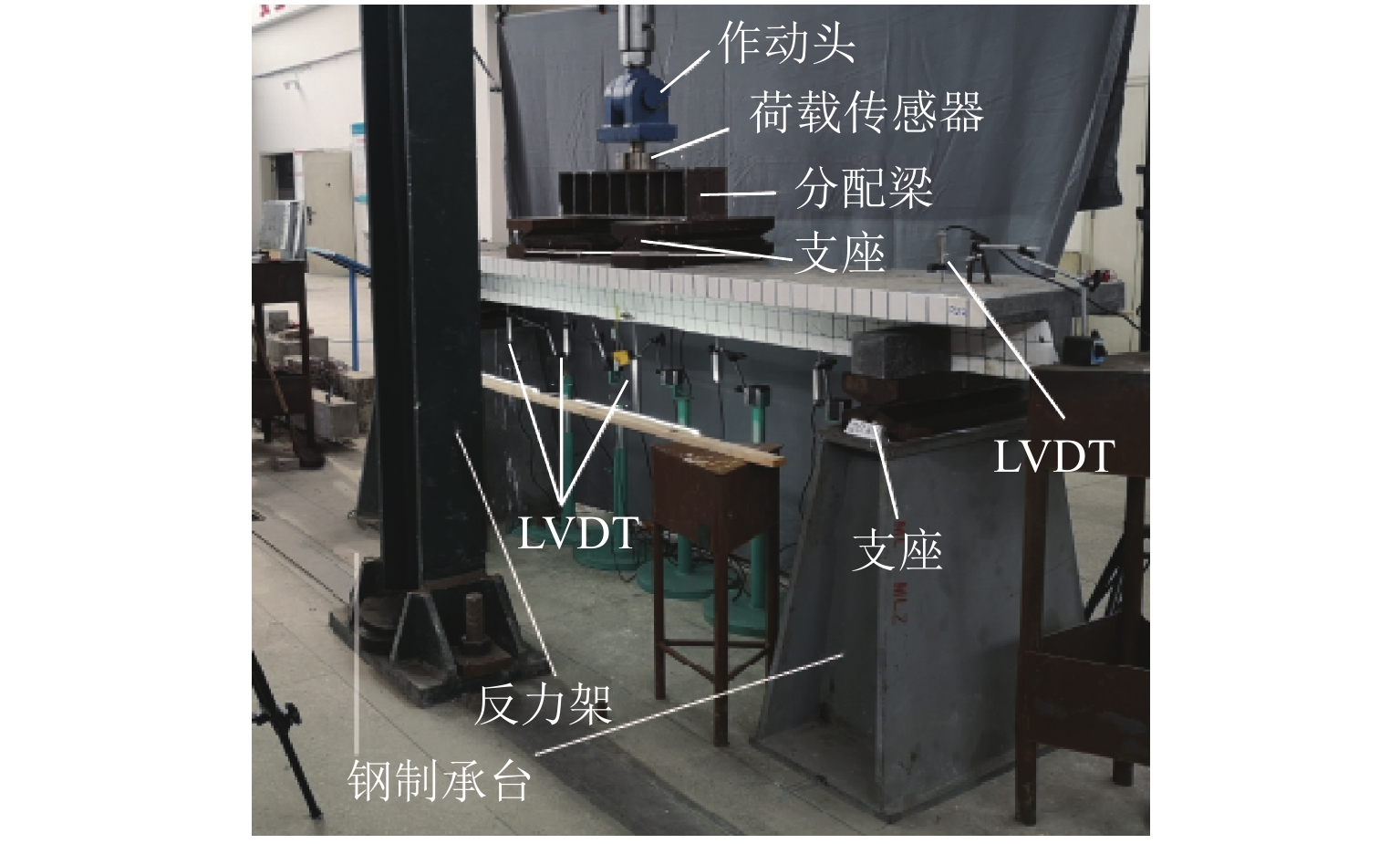
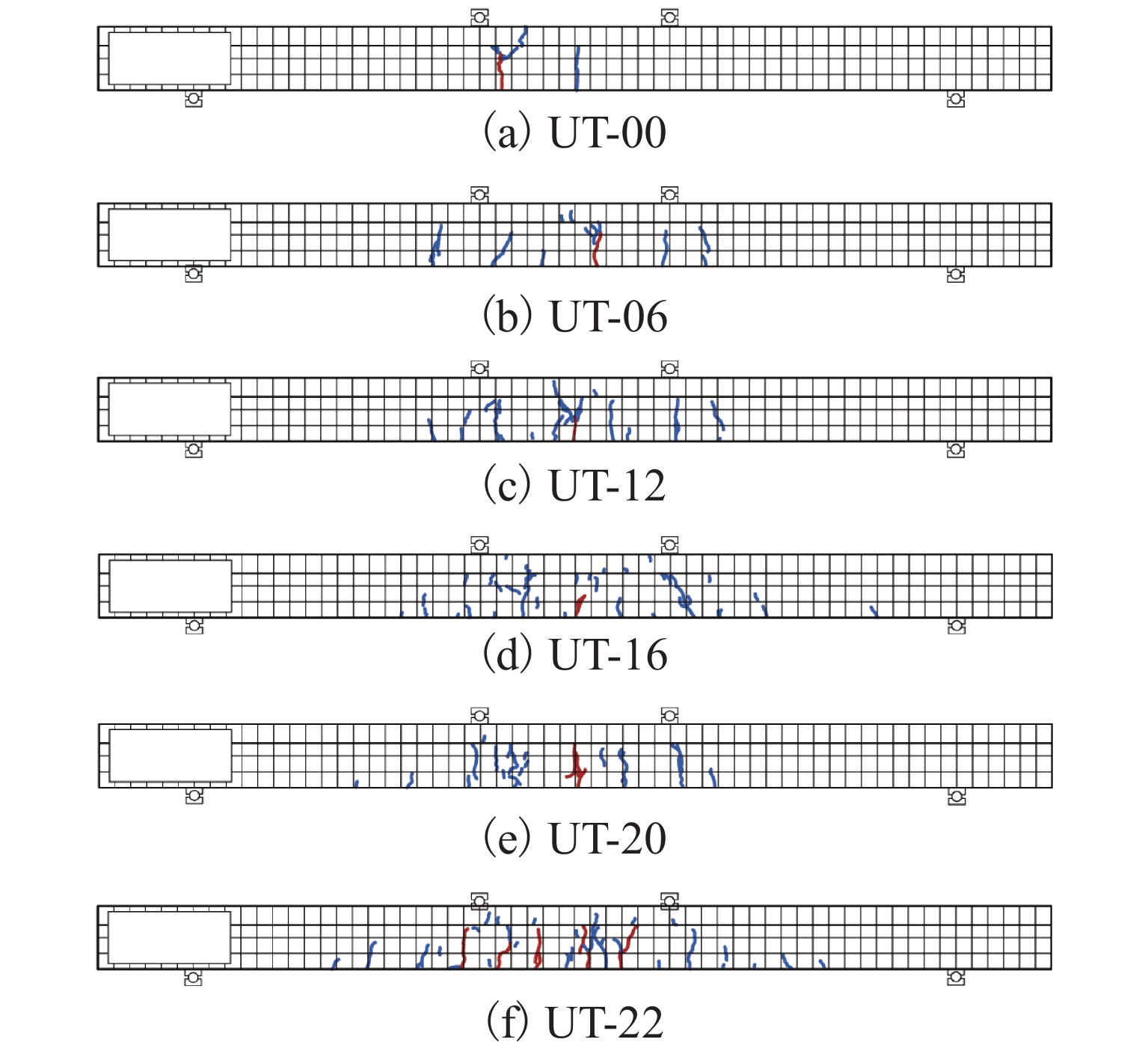
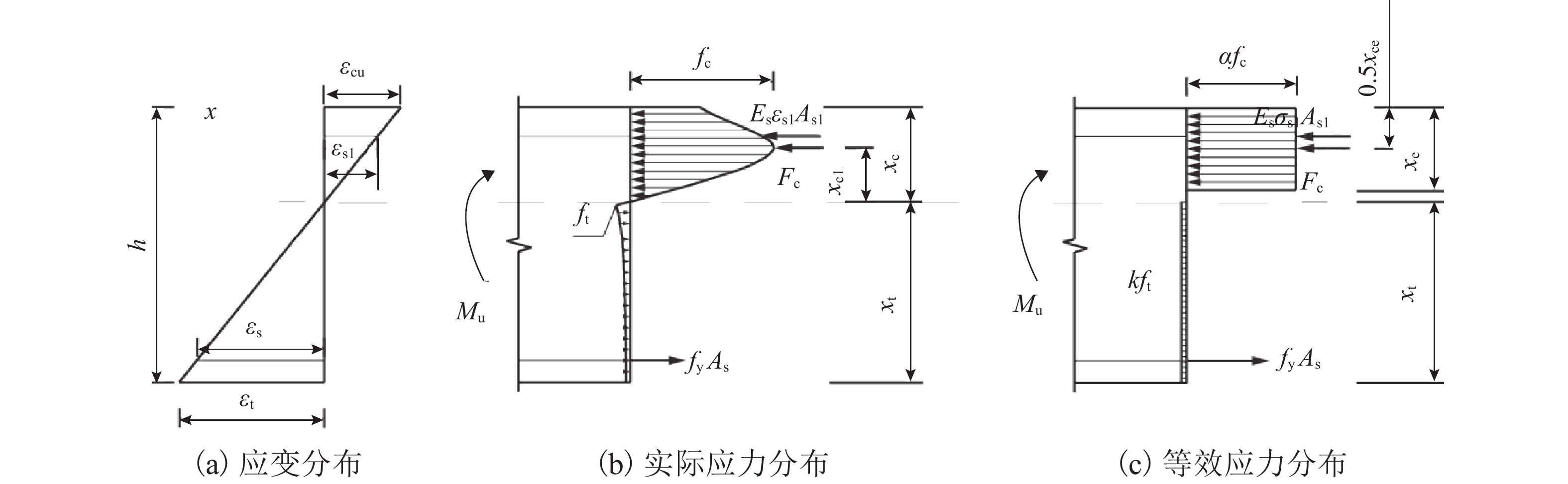
为研究超高性能混凝土(UHPC)华夫桥面单向板中纵筋率对其抗弯承载力的影响,利用等效宽度的原理对其进行简化,设计制作了6根不同纵筋率的足尺T梁模型. 首先,通过加载试验分别对UHPC的基本力学性能和T型截面UHPC梁的抗弯性能和破坏模式进行研究;其次,根据材料性能试验结果,提出UHPC抗拉与抗压的本构模型,并通过截面分析推导T型截面UHPC梁的极限抗弯承载力计算公式;最后,基于既有研究结果,对所提出的T形截面UHPC梁极限抗弯承载力计算公式进行适用性验证. 研究结果表明:由于UHPC具有优异的抗拉强度和拉伸韧性,尽管减小纵筋率会降低T形截面UHPC梁的极限抗弯承载力和延性,但不会改变构件的破坏形式,即T形截面UHPC梁在纵筋率较少甚至不配筋的情况下依然具备延性破坏的特征;根据截面分析推导结果,受拉侧UHPC极限抗拉强度变化系数与纵筋率成正比关系,纵筋率的增大可以更加显著地发挥UHPC的抗拉作用;所提出的公式具有良好的适用性.
Abstract:To study the effect of longitudinal reinforcement ratio on the flexural capacity of a one-way slab of an ultra-high performance concrete (UHPC) wafer bridge deck, six full-scale T-beam models with varying longitudinal reinforcement ratios were produced by using the principle of equivalent width to simplify the analysis. Firstly, the basic mechanical properties of UHPC were studied, followed by the flexural behavior and failure mode of T-shaped UHPC beams through loading experiments. Secondly, a constitutive model for the tensile and compressive strength of UHPC was proposed based on the results of material performance tests. Through section analysis, a formula for calculating the ultimate flexural capacity of T-shaped UHPC beams was derived. Finally, the applicability of the proposed formula was validated based on previous research results. The research findings indicate that although reducing the longitudinal reinforcement ratio will weaken the ultimate flexural capacity and ductility of T-shaped UHPC beams, the failure mode of the components will not change, and T-shaped UHPC beams will still exhibit ductile failure characteristics, even with low or no reinforcement, due to the excellent tensile strength and toughness of UHPC. Moreover, the results of section analysis derivation indicate that the coefficient of variation of the ultimate tensile strength of UHPC under tension is proportional to the longitudinal reinforcement ratio. Therefore, increasing the longitudinal reinforcement ratio can significantly enhance the tensile strength of UHPC. The proposed formula was found to be applicable.
-
表 1 钢纤维特性
Table 1. Properties of steel fibers
参数 长度/mm 直径/mm 抗拉强度/MPa 形状 表面 取值 13 0.2 ≥2 850 直线 光滑 表 2 UHPC配合比
Table 2. Mix proportion of UHPC
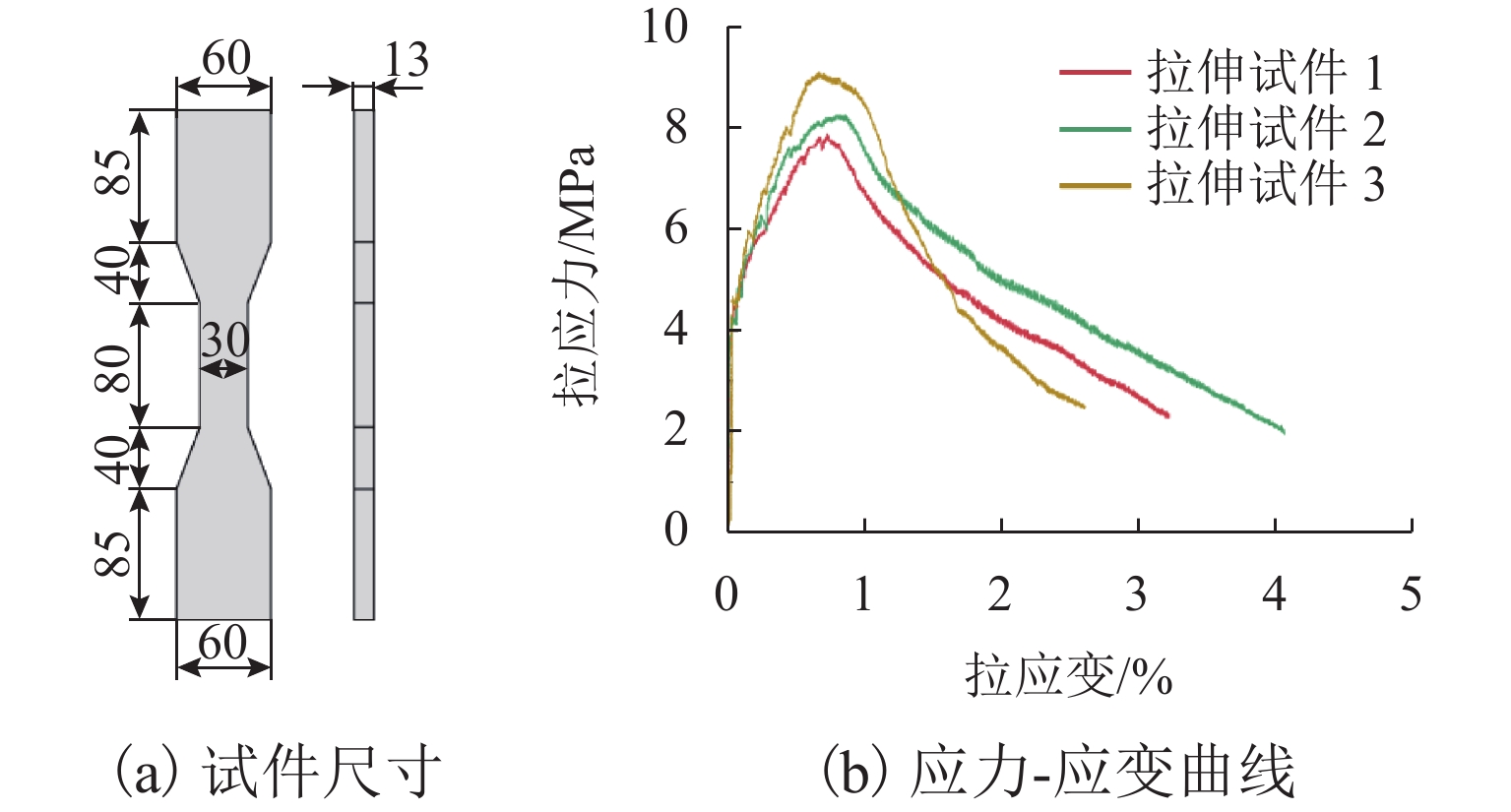
名称 水 预拌料 钢纤维 配比 1.000 11.161 1.036 表 3 UHPC的单轴拉伸性能
Table 3. Uniaxial tensile behavior of UHPC
参数 初裂强度/
MPa初裂
应变极限强度/
MPa极限强度
对应应变取值 4.14 0.0001 8.42 0.0071 表 4 钢筋的抗拉力学性能
Table 4. Tensile properties of steel bars
直径/mm 屈服强度/MPa 极限强度/MPa 表面 6 529.7 537.0 螺纹 10 519.9 623.6 12 479.2 662.2 16 429.9 618.6 20 415.5 604.1 22 470.5 651.0 表 5 试件设计参数
Table 5. Design parameters of specimens
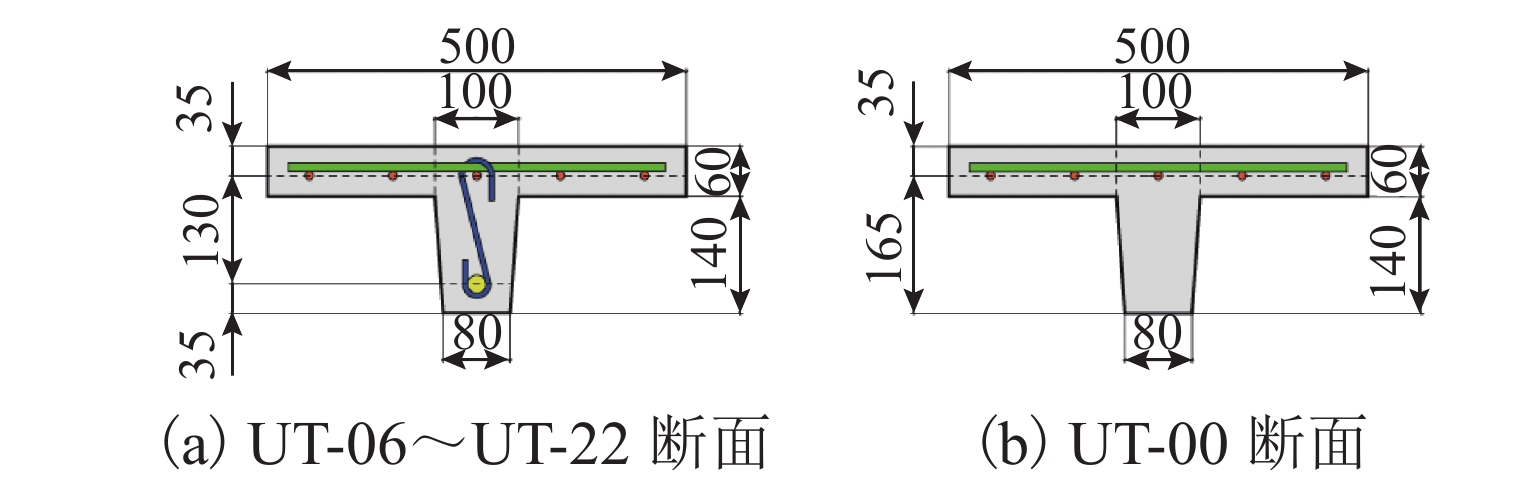
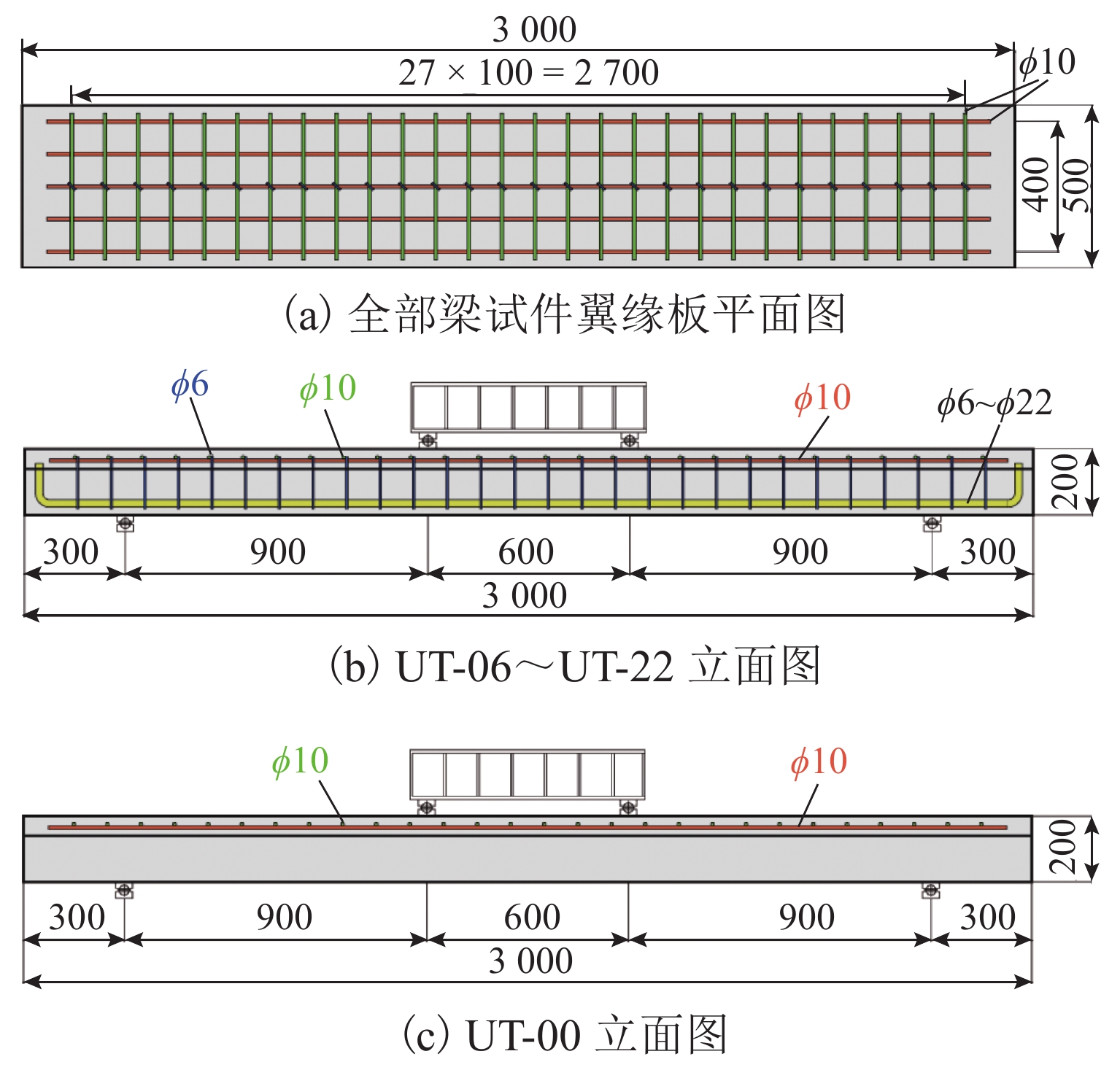
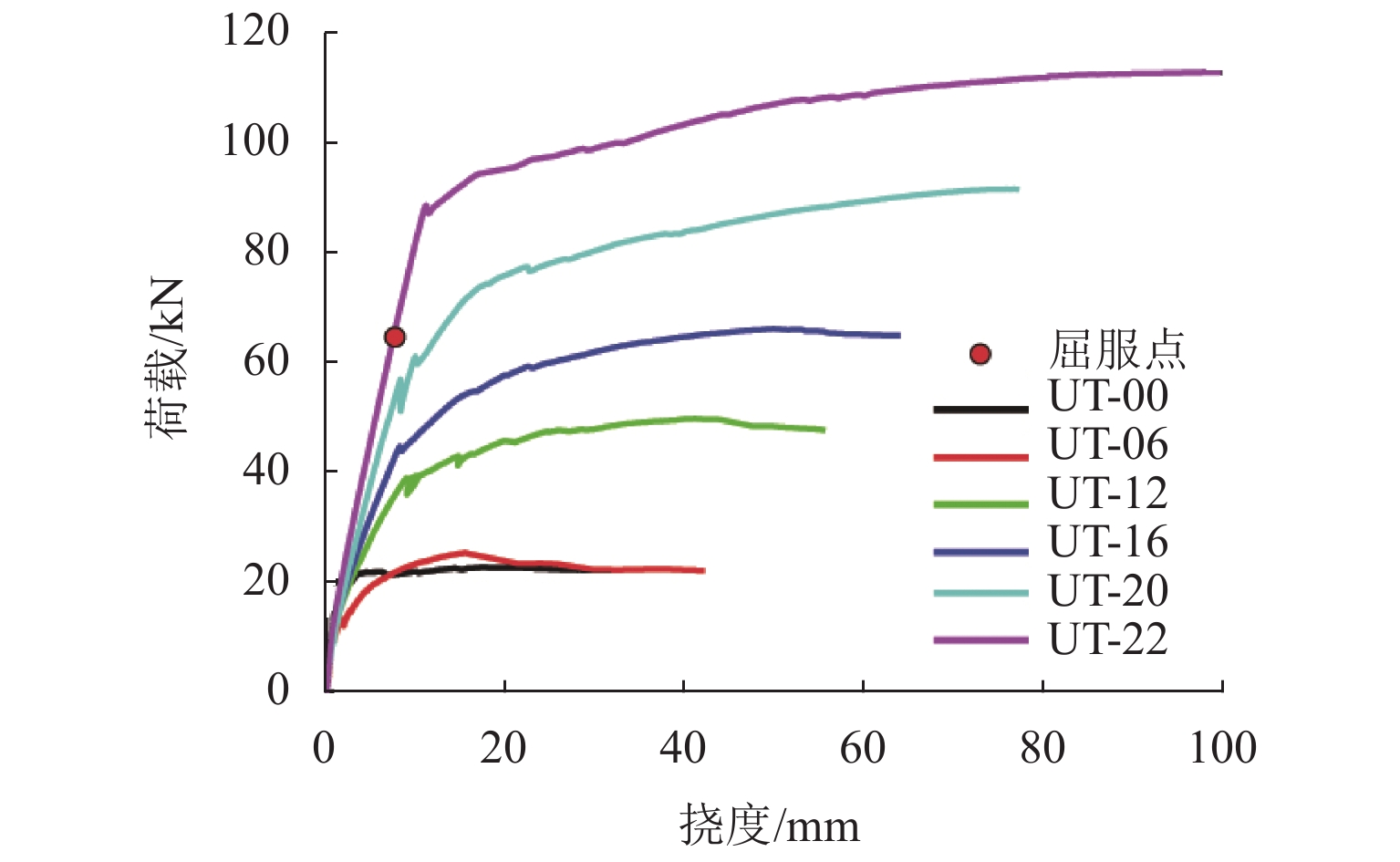
试件编号 底部纵筋 纵筋率$\mathop \rho \nolimits_1 $/% 顶部纵筋 UT-00 无 0 5$\phi $10@100 UT-06 1D6 0.15 UT-12 1D12 0.61 UT-16 1D16 1.08 UT-20 1D20 1.69 UT-22 1D22 2.04 表 6 T梁试验结果
Table 6. Results of T-shaped beam tests
kN 试件编号 开裂荷载 屈服荷载 峰值荷载 UT-00 17.0 22.6 UT-06 14.0 14.7 26.4 UT-12 19.0 29.1 50.5 UT-16 23.0 38.1 66.7 UT-20 27.0 44.3 91.8 UT-22 43.0 63.4 112.7 表 7 T梁受弯承载力计算值与试验值对比
Table 7. Comparison between calculated and experimental flexural capacity of T-shaped UHPC beams
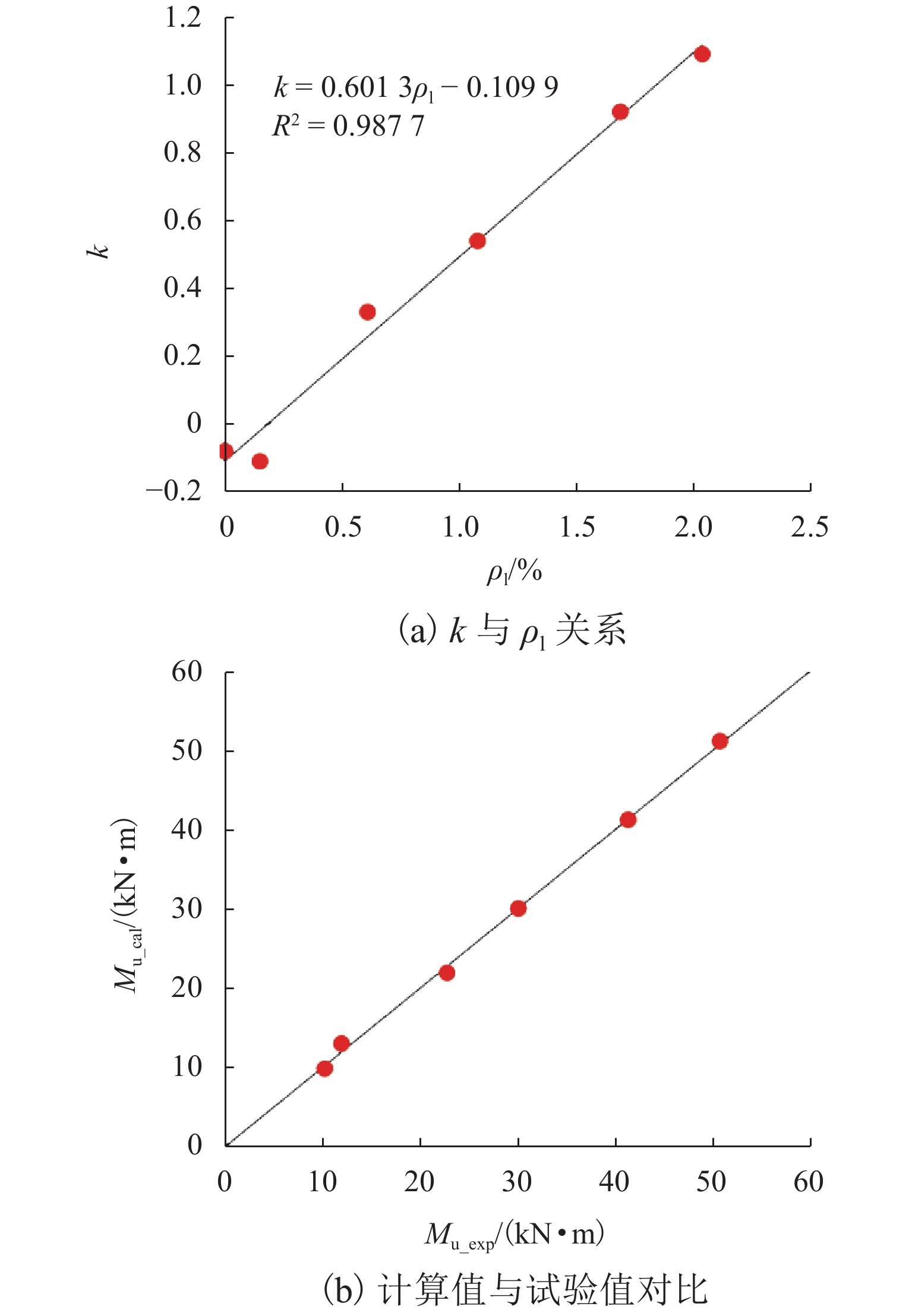
试件
编号xe/mm k Mu_exp/
(kN•m)Mu_cal/
(kN•m)Mu_cal/
Mu_expUT-00 6.91 −0.11 10.17 9.78 0.96 UT-06 7.28 −0.12 11.88 12.92 1.09 UT-12 8.48 0.26 22.73 21.84 0.96 UT-16 9.75 0.54 30.02 29.97 1.00 UT-20 11.60 0.91 41.31 41.18 1.00 UT-22 13.05 1.12 50.72 51.12 1.01 表 8 既有文献的公式验证
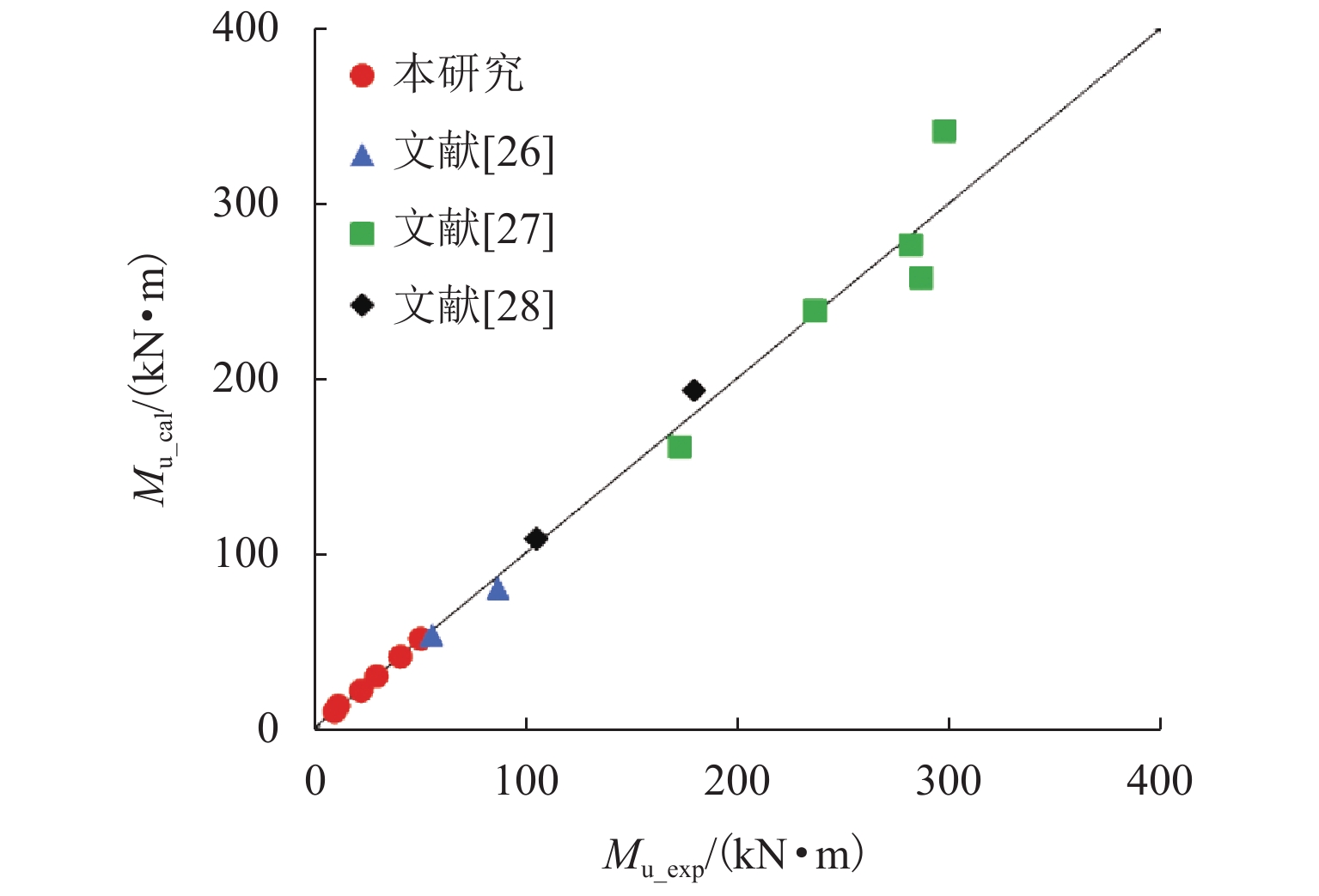
Table 8. Validation of proposed equations in previous studies
来源 试件 xe
/mmk Mu_exp/
(kN•m)Mu_cal/
(kN•m)Mu_cal/ Mu_exp 文献[23] B-S65-16 13.49 0.37 56.16 53.19 0.95 B-S65-20 16.44 0.64 87.21 79.98 0.92 文献[24] T-1 30.38 0.95 172.94 160.61 0.93 T-2 44.23 1.64 236.43 238.17 1.01 T-3 48.76 2.04 286.47 256.84 0.90 T-4 59.73 2.54 297.32 340.77 1.15 T-5 48.18 1.64 281.61 275.65 0.98 文献[25] T1 20.49 0.62 105.12 108.22 1.03 T2 38.76 2.07 179.42 192.62 1.07 -
[1] 聂建国,陶慕轩,吴丽丽,等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报,2012,45(6): 110-122.NIE Jianguo, TAO Muxuan, WU Lili, et al. Advances of research on steel-concrete composite bridges[J]. China Civil Engineering Journal, 2012, 45(6): 110-122. [2] 邓万栋. 钢混组合梁桥病害成因及其加固措施探讨[J]. 人民交通,2019,368(3): 88,90. [3] BASTIEN-MASSE M, DENARIÉ E, BRÜHWILER E. Effect of fiber orientation on the in-plane tensile response of UHPFRC reinforcement layers[J]. Cement and Concrete Composites, 2016, 67: 111-125. doi: 10.1016/j.cemconcomp.2016.01.001 [4] NIWA J. Recommendations for design and construction of ultra high strength fiber reinforced concrete structures[M]. Tokyo: Japan Society of Civil Engineers, 2006. [5] BACHE H H. Compact reinforced composite basic principles[R]. Denmark: Aalborg Portland, 1987. [6] LEE M G, WANG Y C, CHIU C T. A preliminary study of reactive powder concrete as a new repair material[J]. Construction and Building Materials, 2007, 21(1): 182-189. doi: 10.1016/j.conbuildmat.2005.06.024 [7] 邵旭东,曹君辉,易笃韬,等. 正交异性钢板-薄层RPC组合桥面基本性能研究[J]. 中国公路学报,2012,25(2): 40-45.SHAO Xudong, CAO Junhui, YI Dutao, et al. Research on basic performance of composite bridge deck system with orthotropic steel deck and thin RPC layer[J]. China Journal of Highway and Transport, 2012, 25(2): 40-45. [8] TOUTLEMONDE F, RESPLENDINO J, SORELLI L, et al. Innovative design of ultra high-performance fiber reinforced concrete ribbed slab: experimental validation and preliminary detailed analyses[J]. Special Publication, 2005, 228: 1187-1206. [9] GARCIA H M. Analysis of an ultra-high performance concrete two-way ribbed bridge deck slab[R]. Washington D. C.: Federal Highway Administration, 2007. [10] AALETI S, PETERSEN B, SRITHARAN S. Design guide for precast UHPC waffle deck panel system, including connections[R]. Washington D. C.: Federal Highway Administration, 2013. [11] AALETI S, HONARVAR E, SRITHARAN S. Structural characterization of UHPC waffle bridge deck and coonections[R]. Washington D. C.: Federal Highway Administration, 2014. [12] GHASEMI S, ZOHREVAND P, MIRMIRAN A, et al. A super lightweight UHPC-HSS deck panel for movable bridges[J]. Engineering Structures, 2016, 113: 186-193. doi: 10.1016/j.engstruct.2016.01.046 [13] GHASEMI S, MIRMIRAN A, XIAO Y L, et al. Novel UHPC-CFRP waffle deck panel system for accelerated bridge construction[J]. Journal of Composites for Construction, 2016, 20(1): 1-10. [14] BAGHI H, MENKULASI F, PARKER J, et al. Development of a high-performance concrete deck for Louisiana’s movable bridges: numerical study[J]. Journal of Bridge Engineering, 2017, 22(7): 1-18. [15] HADI B, FATMIR M, CARLOS M, et al. Four high performance nonproprietary concrete deck configurations for movable bridges[J]. Engineering Structures, 2018, 168: 559-575. doi: 10.1016/j.engstruct.2018.05.016 [16] 邵旭东, 胡建华. 钢-超高性能混凝土轻型组合桥梁结构[M]. 北京: 人民交通出版社, 2015. [17] 邵旭东,吴佳佳,刘榕,等. 钢-UHPC轻型组合桥梁结构华夫桥面板的基本性能[J]. 中国公路学报,2017,30(3): 218-225,245.SHAO Xudong, WU Jiajia, LIU Rong, et al. Basic performance of waffle deck panel of lightweight steel-UHPC composite bridge[J]. China Journal of Highway and Transport, 2017, 30(3): 218-225,245. [18] 邓舒文,邵旭东,晏班夫,等. 全预制快速架设钢-UHPC轻型组合城市桥梁[J]. 中国公路学报,2017,30(3): 159-166.DENG Shuwen, SHAO Xudong, YAN Banfu, et al. Lightweight steel-UHPC composite bridge with overall prefabrication and fast erection in city[J]. China Journal of Highway and Transport, 2017, 30(3): 159-166. [19] 张清华,韩少辉,贾东林,等. 新型装配式UHPC华夫型上翼缘组合梁受力性能[J]. 西南交通大学学报,2019,54(3): 445-452.ZHANG Qinghua, HAN Shaohui, JIA Donglin, et al. Mechanical performance of novel prefabricated composite girder with top flange of ultra hight performance concrete waffle deck panel[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 445-452. [20] 朱劲松,王永光,郭晓宇,等. 钢-UHPC华夫板组合梁抗剪性能试验研究[J]. 中国公路学报,2020,33(11): 169-181.ZHU Jinsong, WANG Yongguang, GUO Xiaoyu, et al. Experimental study on shear behaviors of steel-UHPC composite beams with waffle slab[J]. China Journal of Highway and Transport, 2020, 33(11): 169-181. [21] 邵旭东,李玉祺,廖子南,等. UHPC华夫桥面板抗弯性能试验及有限元分析[J]. 长安大学学报(自然科学版),2018,38(3): 52-63.SHAO Xudong, LI Yuqi, LIAO Zinan, et al. Test and finite element analysis on bending performance of UHPC Waffle deck panel[J]. Journal of Chang’an University (Natural Science Edition), 2018, 38(3): 52-63. [22] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. [23] QIU M H, SHAO X D, WILLE K, et al. Experimental investigation on flexural behavior of reinforced ultra high performance concrete low-profile T-beams[J]. International Journal of Concrete Structures and Materials, 2020, 14(1): 1-20. doi: 10.1186/s40069-019-0376-6 [24] 邓宗才,王义超,肖锐,等. 高强钢筋UHPC梁抗弯性能试验研究与理论分析[J]. 应用基础与工程科学学报,2015,23(1): 68-78.DENG Zongcai, WANG Yichao, XIAO Rui, et al. Flexural test and theoretical analysis of UHPC beams with high strength rebars[J]. Journal of Basic Science and Engineering, 2015, 23(1): 68-78. [25] 刘超,黄钰豪,马汝杰,等. 高应变强化超高性能混凝土T形梁抗弯承载力[J]. 同济大学学报(自然科学版),2018,46(6): 744-750.LIU Chao, HUANG Yuhao, MA Rujie, et al. Calculation method for flexural capacity of high strain-hardening UHPC T-beams[J]. Journal of Tongji University (Natural Science), 2018, 46(6): 744-750. -




 下载:
下载: