常导电磁型高速磁浮列车主动导向能力的评估与验证

翟明达; 朱朋博; 李晓龙; 龙志强; 刘信; 杨宾

doi:10.3969/j.issn.0258-2724.20210920

常导电磁型高速磁浮列车主动导向能力的评估与验证

doi: 10.3969/j.issn.0258-2724.20210920

翟明达^1,,
朱朋博^{1, 2},
李晓龙^1, ,,
龙志强¹,
刘信¹,
杨宾²

1.
国防科技大学智能科学学院，湖南长沙 410000
2.
63898部队，河南济源 454650

基金项目: 国家重点研发计划（2016YFB1200601，2016YFB1200602）

详细信息

作者简介:
翟明达（1990—），男，助理研究员，博士，研究方向为磁浮列车控制与优化，E-mail：zhaimd@126.com

通讯作者:
李晓龙（1979—），男，副研究员，研究方向为电磁悬浮与推进，E-mail：13787786254@163.com

中图分类号: TP273
计量
- 文章访问数: 427
- HTML全文浏览量: 203
- PDF下载量: 29
- 被引次数: 9
出版历程
- 收稿日期: 2021-11-15
- 修回日期: 2022-04-11
- 刊出日期: 2022-04-14

Evaluation and Verification for Active Guidance Ability of EMS Maglev Train

ZHAI Mingda^1
,,
ZHU Pengbo^{1, 2},
LI Xiaolong^{1
, ,},
LONG Zhiqiang¹,
LIU Xin¹,
YANG Bin²

1.
College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410000, China
2.
63898 Troops, Jiyuan 454650, China

摘要

摘要:
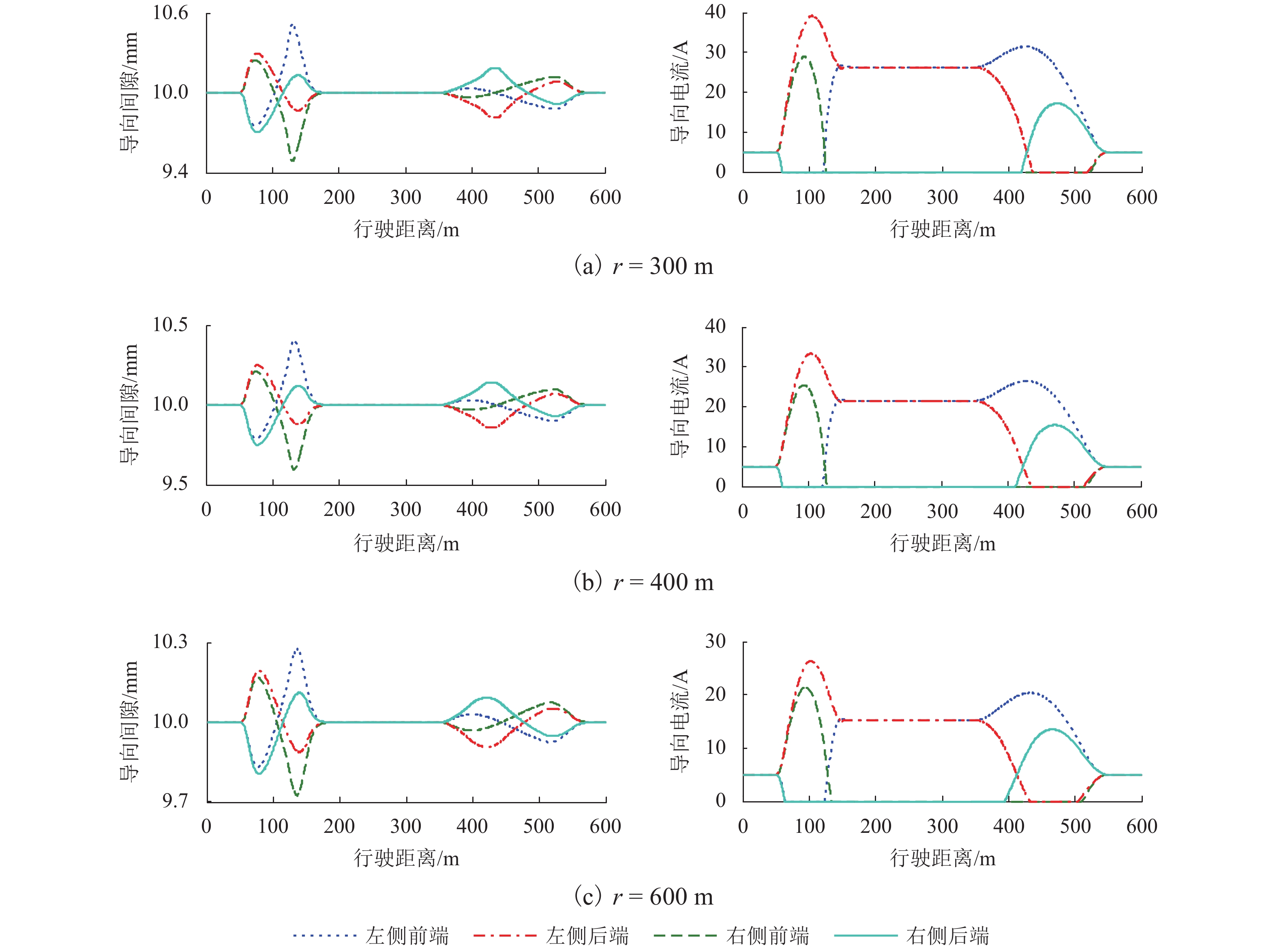
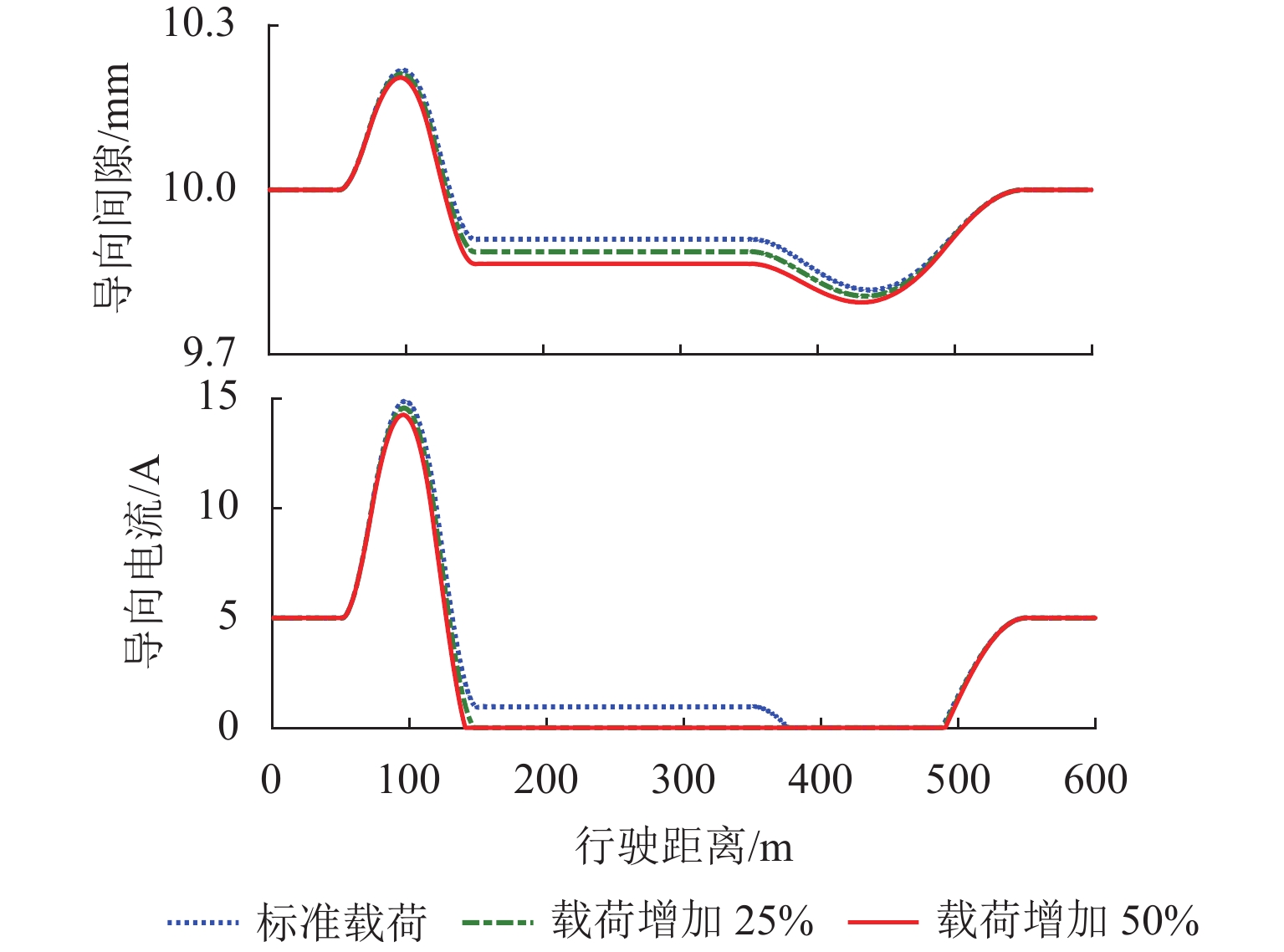
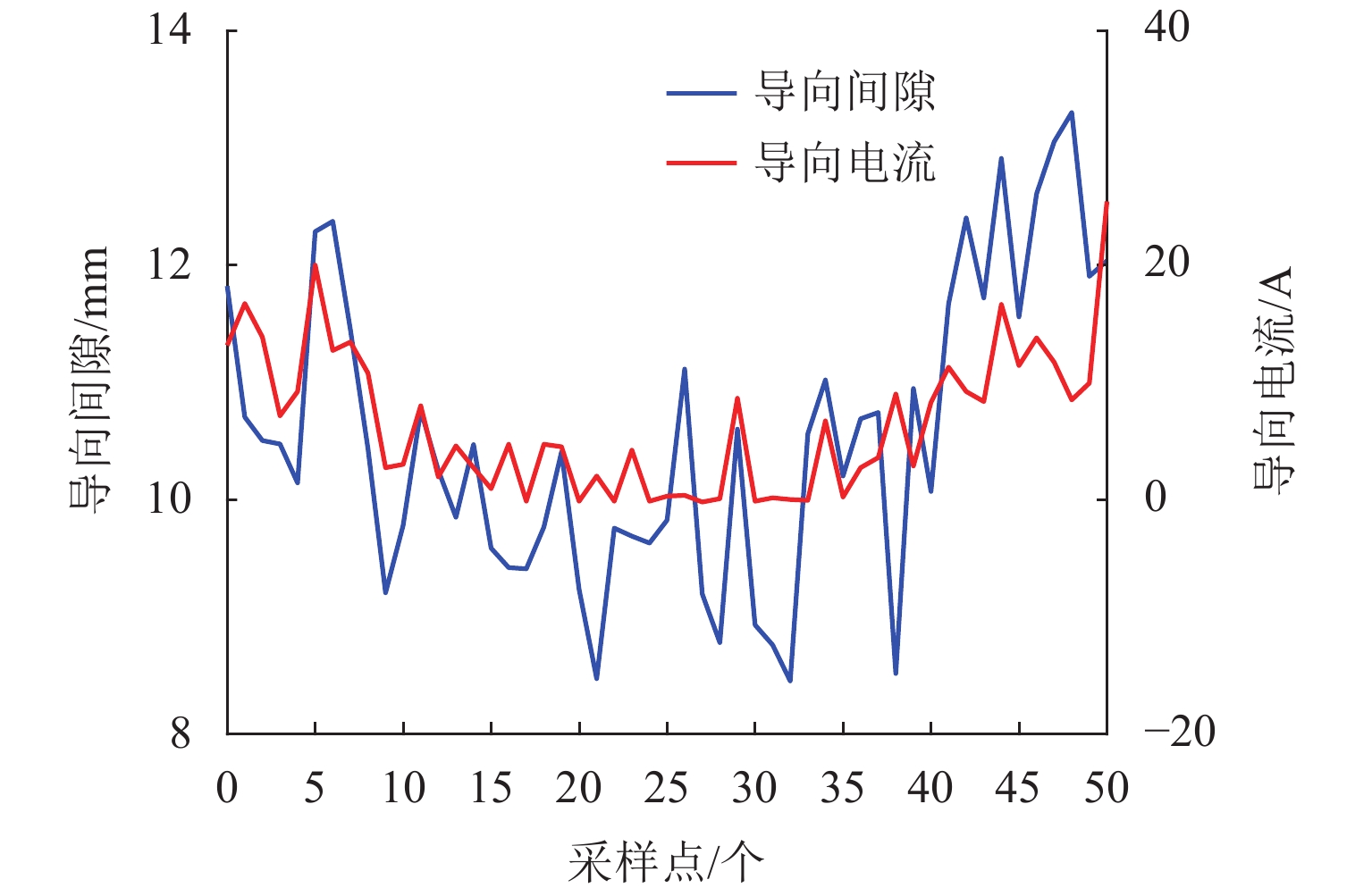
为科学准确地分析和评估常导电磁型高速磁浮列车通过平面曲线线路的能力，利用高速磁浮列车运行中的导向间隙、电流以及加速度等状态信息，基于模糊综合评价法提出了可量化的评价指标；在不同的曲线半径、运行速度和有效载荷下，利用本文提出的评价指标对列车的主动导向能力进行了分析和评估；最后，通过实际线路测试验证了评估结果的有效性. 研究结果表明：常导电磁型高速磁浮列车的主动导向能力不仅与导向系统本身的能力有关，还与线路半径、列车运行速度等因素密切相关；提出的方法可以对常导电磁型高速磁浮列车的主动导向能力进行评估，为检验导向系统的实际效用和应用边界提供参考依据.
- 磁浮列车 /
- 导向 /
- 模糊综合评价 /
- 平面曲线
Abstract:
In order to scientifically and accurately analyze and evaluate the ability of electromagnetic high-speed maglev train passing through the plane curve line, a novel quantifiable evaluation index system is proposed based on fuzzy comprehensive evaluation method by using the state information of guide gap, current and acceleration in maglev train operation. The evaluation index is proposed to analyze and evaluate the active guidance ability of the train under different curve radiuses, running speeds and payloads. The effectiveness of evaluation results is verified by the actual line test. The results indicate that the active guidance ability of the electromagnetic high-speed maglev train is closely related not only to the ability of the guidance system itself, but also to the line radius, running speed and other factors. The proposed method is able to evaluate the active guidance ability, and provide a reference basis for verifying the actual utility and application boundary of the guidance system.
- maglev /
- guidance /
- fuzzy comprehensive evaluation /
- plane curve

HTML全文

图 1 车辆总体结构

Figure 1. Overall vehicle structure

下载: 全尺寸图片幻灯片

图 2 导向电磁铁模块

Figure 2. Module of guidance electromagnet

下载: 全尺寸图片幻灯片

图 3 导向模块工作示意

Figure 3. Working diagram of guidance module

下载: 全尺寸图片幻灯片

图 4 高速磁浮线路平面曲线

Figure 4. Plane curve of high-speed maglev line

下载: 全尺寸图片幻灯片

图 5 隶属度函数

Figure 5. Membership function

下载: 全尺寸图片幻灯片

图 6 曲线半径不同时的导向间隙和电流

Figure 6. Guidance gap and current with different curve radiuses

下载: 全尺寸图片幻灯片

图 7 运行速度不同时导向间隙和电流

Figure 7. Guidance gap and current with different speeds

下载: 全尺寸图片幻灯片

图 8 载荷不同时的导向间隙和电流

Figure 8. Guidance gap and current with different loads

下载: 全尺寸图片幻灯片

图 9 同济大学高速磁浮试验线

Figure 9. High-speed maglev test line at Tongji university

下载: 全尺寸图片幻灯片

图 10 实测运行中的导向间隙和电流

Figure 10. Guidance gap and current in measured opertation

下载: 全尺寸图片幻灯片

表 1 评分结果

Table 1. Grading results

参数	C₁	C₂	C₃	C₄
C₁	1	${9^{{1 \mathord{\left/ {\vphantom {1 9}} \right. } 9}}}$	${9^{{4 \mathord{\left/ {\vphantom {4 9}} \right. } 9}}}$	9^2/3
C₂	9^−1/9	1	${9^{{2 \mathord{\left/ {\vphantom {2 9}} \right. } 9}}}$	${9^{{4 \mathord{\left/ {\vphantom {4 9}} \right. } 9}}}$
C₃	9^−4/9	9^−2/9	1	${9^{{2 \mathord{\left/ {\vphantom {2 9}} \right. } 9}}}$
C₄	9^−2/3	9^−4/9	9^−2/9	1

下载: 导出CSV

参考文献(13)

[1]	JANIC M. Multicriteria evaluation of high-speed rail, transrapid maglev and air passenger transport in Europe[J]. Transportation Planning and Technology, 2003, 26(6): 491-512. doi: 10.1080/0308106032000167373
[2]	GUTIERREZ H M, LUIJTEN H. 5-DOF real-time control of active electrodynamic MAGLEV[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7468-7476. doi: 10.1109/TIE.2018.2795520
[3]	YAN L G. Development and application of the maglev transportation system[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 92-99. doi: 10.1109/TASC.2008.922239
[4]	沈通,马志文,杜晓洁,等. 世界高速磁悬浮铁路发展现状与趋势分析[J]. 中国铁路,2020(11): 94-99. SHEN Tong, MA Zhiwen, DU Xiaojie, et al. Development status and trend analysis of high speed maglev railways worldwide[J]. China Railway, 2020(11): 94-99.
[5]	刘少克,龙长林,陈贵荣,等. 高速磁悬浮列车新型导向电磁铁分析[J]. 机车电传动,2010(1): 49-51. LIU Shaoke, LONG Changlin, CHEN Guirong, et al. Analysis of new guide electromagnet for high-speed maglev train[J]. Electric Drive for Locomotives, 2010(1): 49-51.
[6]	吴云飞. EMS型高速磁浮列车导向控制系统及其仿真[J]. 黑龙江科技学院学报,2006,16(4): 244-247. WU Yunfei. Guidance control system and simulation research of EMS type high-speed maglev vehicle[J]. Journal of Heilongjiang Institute of Science and Technology, 2006, 16(4): 244-247.
[7]	蔡力律. 城市轨道交通磁浮线路最小曲线半径研究[J]. 四川建筑,2008,28(3): 46-47. doi: 10.3969/j.issn.1007-8983.2008.03.021 AI Lilv. Research on the minimum curve radius of maglev line of urban rail transit[J]. Sichuan Architecture, 2008, 28(3): 46-47. doi: 10.3969/j.issn.1007-8983.2008.03.021
[8]	赵春霞. EMS型高速磁浮列车导向动力学研究[D]. 长沙: 国防科学技术大学, 2014.
[9]	郝阿明,龙志强,常文森. 高速磁浮列车导向系统的鲁棒控制器设计[J]. 铁道学报,2008,30(6): 40-45. doi: 10.3321/j.issn:1001-8360.2008.06.008 HAO Aming, LONG Zhiqiang, CHANG Wensen. Design of the robust controller of the guidance system in high-speed maglev train[J]. Journal of the China Railway Society, 2008, 30(6): 40-45. doi: 10.3321/j.issn:1001-8360.2008.06.008
[10]	ZHAI M D, HAO A M, LI X L, et al. Research on the active guidance control system in high speed maglev train[J]. IEEE Access, 2019, 7: 741-752. doi: 10.1109/ACCESS.2018.2885784
[11]	郝阿明,佘龙华,常文森. EMS型高速磁浮列车自适应导向控制器设计[J]. 控制工程,2008,15(2): 116-119,170. doi: 10.3969/j.issn.1671-7848.2008.02.002 HAO Aming, SHE Longhua, CHANG Wensen. Adaptive controller design of guidance system of EMS high speed maglev train[J]. Control Engineering of China, 2008, 15(2): 116-119,170. doi: 10.3969/j.issn.1671-7848.2008.02.002
[12]	王汝宁,程虎,李云钢. 高速磁悬浮列车转向能力研究[J]. 机车电传动,2011(1): 40-42,46. WANG Runing, CHENG Hu, LI Yungang. Research on turning ability of high-speed maglev train[J]. Electric Drive for Locomotives, 2011(1): 40-42,46.
[13]	侯岳衡,沈德家. 指数标度及其与几种标度的比较[J]. 系统工程理论与实践,1995,15(10): 43-49. doi: 10.3321/j.issn:1000-6788.1995.10.008 HOU Yueheng, SHEN Dejia. Index number scale and comparison with other scales[J]. Systems Engineering —Theory & Practice, 1995, 15(10): 43-49. doi: 10.3321/j.issn:1000-6788.1995.10.008

施引文献

期刊类型引用(3)

1.	袁中原，周弦，李海涛，刘国清，全雨杰，罗洋浩，酒芳恒. 新型导磁型永磁混合电磁铁优化设计. 现代交通与冶金材料. 2025(02): 16-21 . 百度学术
2.	卜秀孟，王力东，黎清蓉，胡朋，韩艳. 高速磁浮车-桥耦合振动控制参数影响分析. 西南交通大学学报. 2024(04): 848-857+866 . 本站查看
3.	林国斌，刘万明，徐俊起，孙友刚. 中国高速磁浮交通的发展机遇与挑战. 前瞻科技. 2023(04): 7-18 . 百度学术