Core Loss Analysis of Three Degree-of-Freedom Hybrid Magnetic Bearing with Novel Rotor Structure
-
摘要:
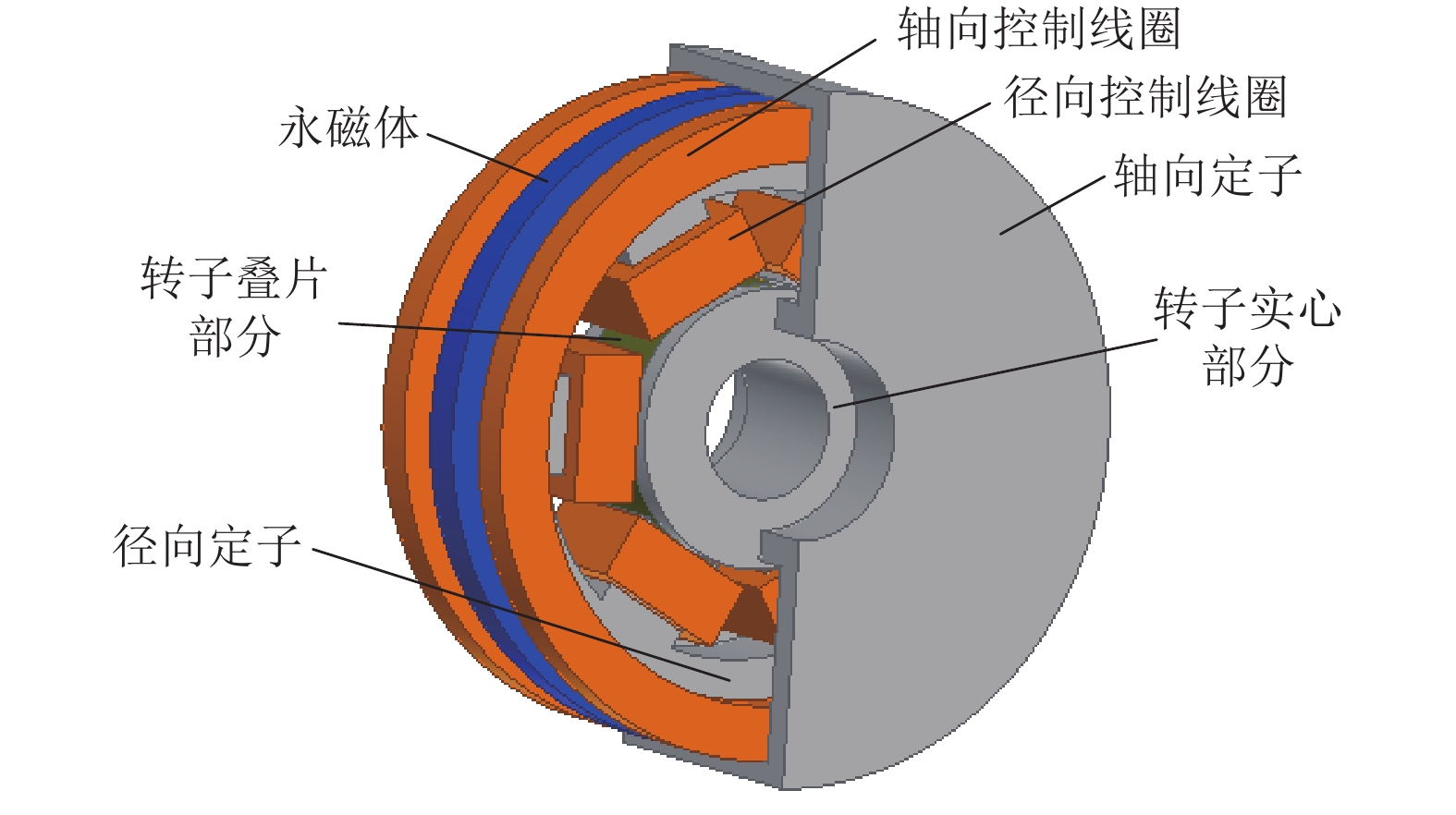
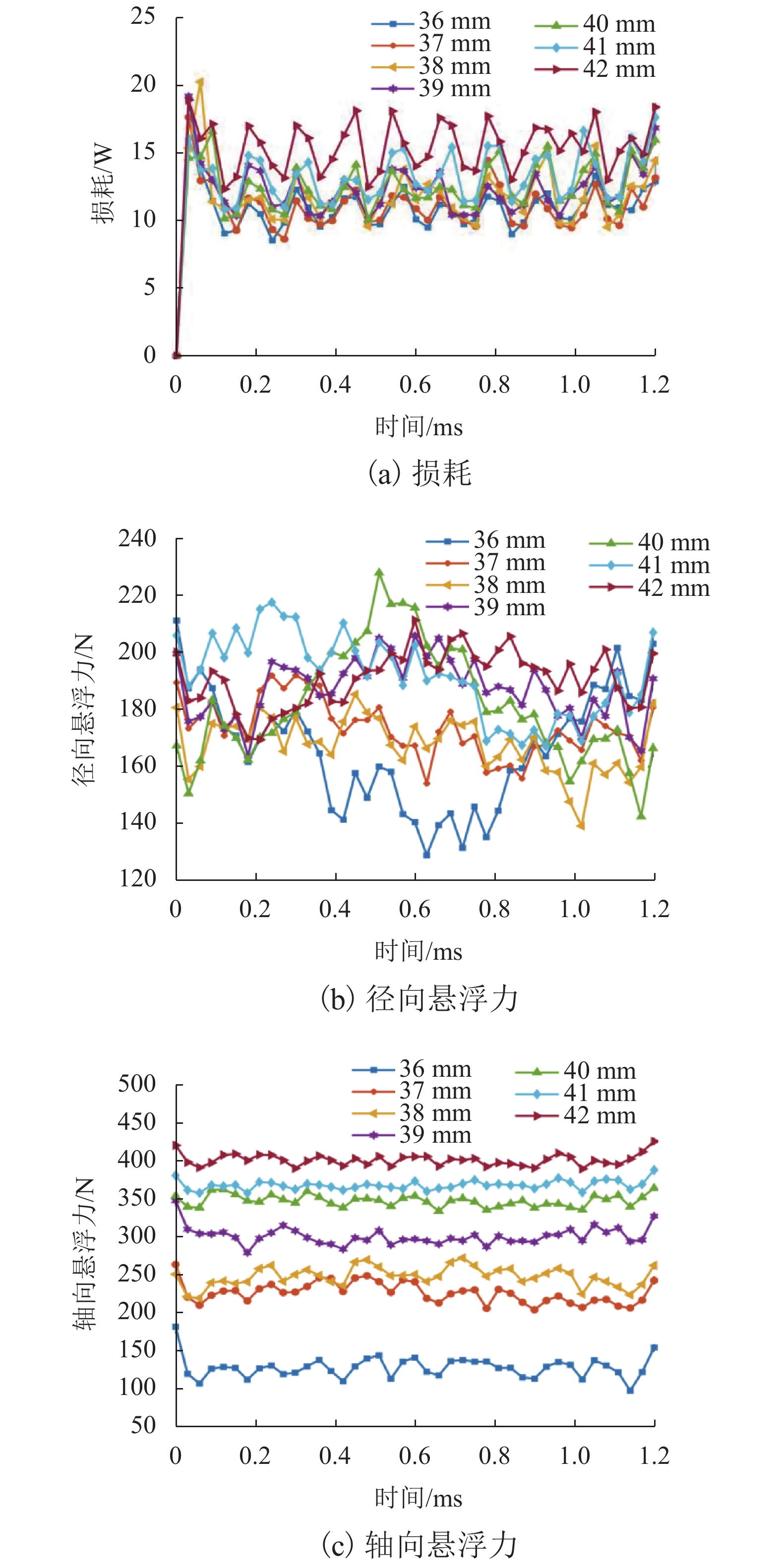
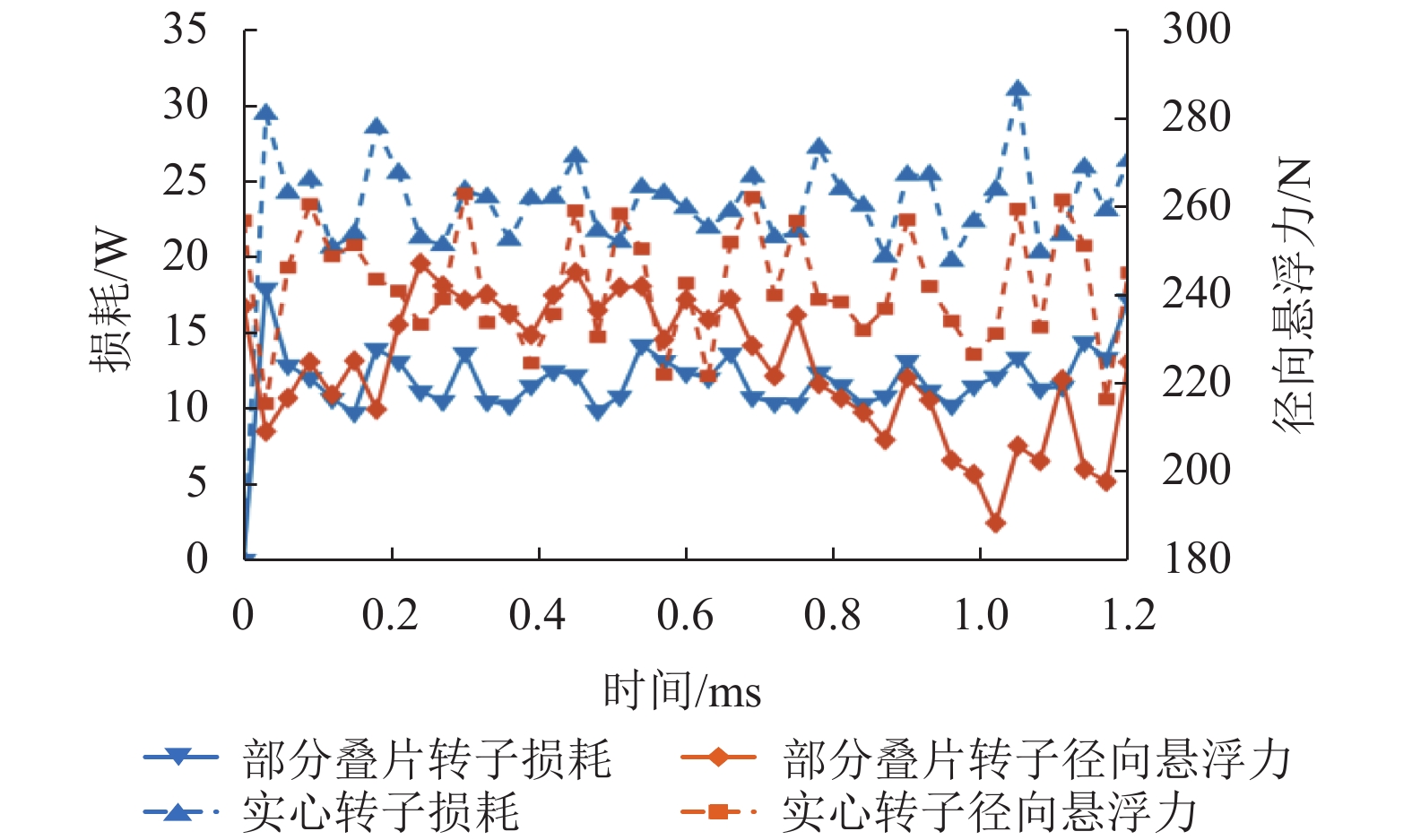
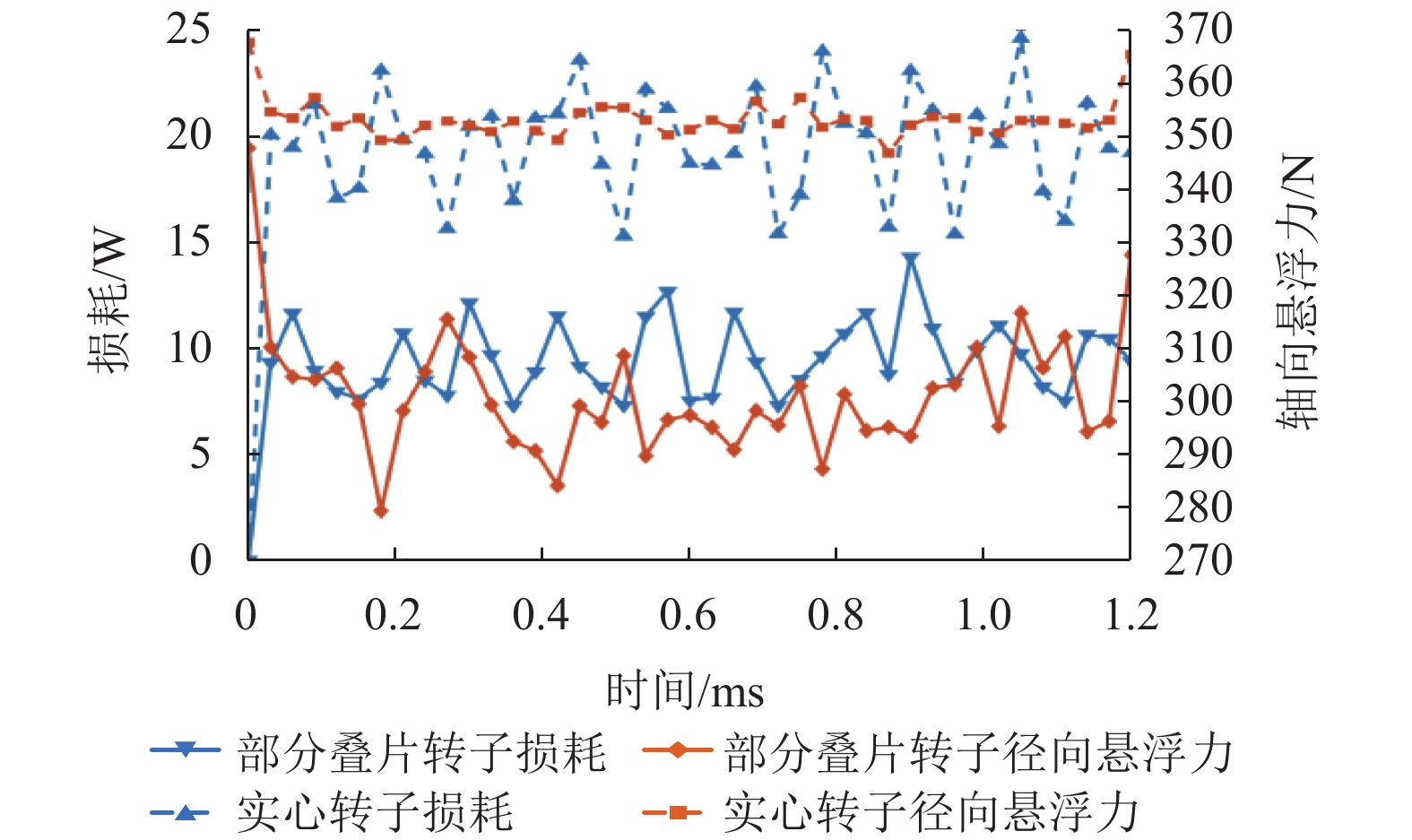
为减少六极径向-轴向混合磁轴承（radial-axial hybrid magnetic bearing，RAHBM）高速下转子产生的损耗，提出了一种部分叠片的转子结构. 首先，用等效磁路法推导了六极RAHMB的悬浮力数学模型，依据该模型设计磁轴承结构参数，对不同转子叠片深度下的铁损和悬浮力进行仿真分析，选择叠片深度最优值；然后，在有限元仿真软件中设定转子转速为50000 r/min，向六极RAHMB分别施加径向和轴向最大控制电流，分析磁轴承产生最大承载力情况下实心转子与部分叠片转子的损耗；最后，对部分叠片转子在正弦扰动电流下的涡流损耗和磁滞损耗进行计算和仿真. 研究结果表明：在产生最大承载力条件下，部分叠片转子结构能够将损耗降低69.7%，虽然轴向承载力减小了14.7%，但仍能够满足设计要求；部分叠片转子可将正弦扰动电流下铁损降低55.4%.
Abstract:To reduce the core loss of six-pole RAHMB (radial-axial hybrid magnetic bearing) at high rotation speeds, a novel partially laminated rotor is proposed. Firstly, the suspension force model of six-pole RAHMB is built by using equivalent magnetic circuit method. The structure parameters of six-pole RAHMB are designed according to the mathematical model of suspension force. The core loss and suspension force under different depths of lamination part are analyzed to select the optimal depth value. Then, in the finite element analysis, the rotation speed of rotor is set to be 50000 r/min, and the maximum radial and axial control currents are injected to six-pole RAHMB respectively to analyze the core losses of the solid rotor and partially laminated rotor when the magnetic bearing generates maximum suspension force. Finally, the eddy current loss and hysteresis loss of laminated rotors are simulated and calculated under sinusoidal disturbance current. The results show that the partially laminated rotor can reduce the core loss by 69.7% while producing the maximum bearing capacity; although the axial bearing capacity is reduced by 14.7%, it still meets the design requirement; besides, the core loss is reduced by 55.4% under sinusoidal disturbance current.
-
Key words:
- magnetic bearings /
- core loss /
- eddy current loss /
- hysteresis loss /
- three degree-of-freedom
-
图 3 叠片转子内径优化仿真结果
Figure 3. Simulation results of inner diameter optimization for laminated rotors
图 4 最大径向电流激励下铁损与径向悬浮力对比
Figure 4. Comparison of core loss and radial suspension force under excitation of maximum radial current
图 5 最大轴向电流激励下涡流损耗与悬浮力对比
Figure 5. Comparison of core loss and axial suspension force under excitation of maximum axial current
图 6 最大径向、轴向电流激励下铁损与悬浮力对比
Figure 6. Comparison of core loss and suspension force under excitation of maximum radial and axial current
图 9 正弦激励下的铁损仿真与计算结果对比
Figure 9. Comparison between calculation and simulation results of core loss under sinusoidal excitation
表 1 六极RAHMB主要参数
Table 1. Main parameters of six-pole RAHMB
参数 值 δr，δz /mm 0.5 Sr /mm2 233 Sz /mm2 600 轴向线圈最大安匝数 /（A·匝） 200 径向线圈最大安匝数 /（A·匝) 300 Θm /（A·匝） 320 径向饱和磁感应强度 /T 1.20 径向偏置磁感应强度 /T 0.60 轴向饱和磁感应强度 /T 1.15 轴向偏置磁感应强度/T 0.70 转子外径 /mm 46 转子轴向宽度 /mm 27 径向定子轭外径/mm 93 永磁体外径/mm 107 轴向定子盘外宽度/mm 53 轴向定子筒外径/mm 114 
下载: 导出CSV
表 2 正弦电流激励下铁损计算与仿真结果
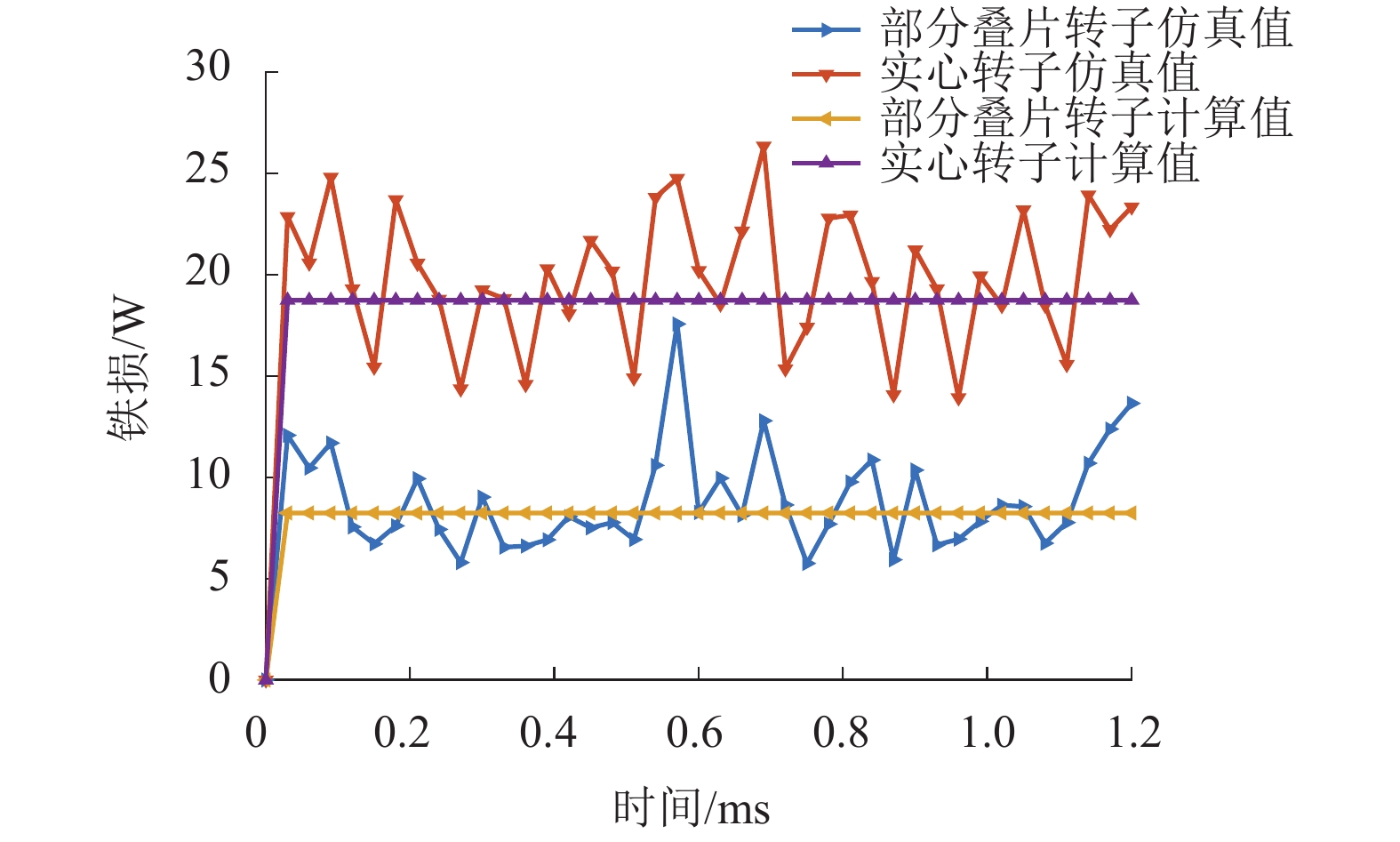
Table 2. Calculation and simulation results of core loss excited by sinusoidal current
转子 计算值/W 仿真值/W 误差/% 涡流
损耗磁滞
损耗铁损 部分叠片转子 8.16 0.0864 8.25 8.66 4.7 实心转子 18.57 0.1778 18.75 19.52 3.9
下载: 导出CSV
-
[1] ZHU R Z, XU W, YE C Y, et al. Novel heteropolar radial hybrid magnetic bearing with low rotor core loss[J]. IEEE Transactions on Magnetics, 2017, 53(11): 1-5. [2] 朱熀秋,龙勇. 交流径向-轴向六极混合磁轴承结构及其悬浮力特性分析[J]. 中国电机工程学报,2019,39(6): 1815-1824,1877.ZHU Huangqiu, LONG Yong. Structure and suspension force characteristics analysis of AC radial-axial six-pole hybrid magnetic bearing[J]. Proceedings of the CSEE, 2019, 39(6): 1815-1824,1877. [3] 张斌,胡业发,丁国平,等. 径向磁力轴承涡流损耗分析与计算[J]. 机械制造,2007,45(7): 36-38. doi: 10.3969/j.issn.1000-4998.2007.07.013 [4] KIM H Y, LEE C W. Analysis of eddy-current loss for design of small active magnetic bearings with solid core and rotor[J]. IEEE Transactions on Magnetics, 2004, 40(5): 3293-3301. doi: 10.1109/TMAG.2004.834620 [5] 孙岩桦,虞烈. 实心转子电磁轴承涡流损耗分析[J]. 中国电机工程学报,2002,22(2): 116-120. doi: 10.3321/j.issn:0258-8013.2002.02.024SUN Yanhua, YU Lie. Eddy Current loss analysis in radial magnetic bearings with solid rotor[J]. Proceedings of the CSEE, 2002, 22(2): 116-120. doi: 10.3321/j.issn:0258-8013.2002.02.024 [6] 石庆才,谢振宇,吴凯锋,等. 同极型和异极型磁轴承的磁场分布和功率损耗分析[J]. 机械设计,2011,28(11): 22-27.SHI Qingcai, XIE Zhenyu, WU Kaifeng, et al. Analysis on electromagnetic field and power loss of homopolar and heteropolar magnetic bearing[J]. Journal of Machine Design, 2011, 28(11): 22-27. [7] 胡小飞,刘刚,孙津济,等. 轴向磁轴承涡流损耗分析[J]. 轴承,2013(3): 22-27. doi: 10.3969/j.issn.1000-3762.2013.03.009HU Xiaofei, LIU Gang, SUN Jinji, et al. Analysis on eddy current loss for axial magnetic bearings[J]. Bearing, 2013(3): 22-27. doi: 10.3969/j.issn.1000-3762.2013.03.009 [8] 胡小飞,刘刚,孙津济,等. Homopolar型径向磁轴承转子涡流损耗的分析与优化[J]. 系统仿真学报,2013,25(12): 2961-2966,2972.HU Xiaofei, LIU Gang, SUN Jinji, et al. Analysis and optimization of rotor eddy current loss in homopolar radial magnetic bearings[J]. Journal of System Simulation, 2013, 25(12): 2961-2966,2972. [9] REN X J, LE Y, HAN B C. System electromagnetic loss analysis and temperature field estimate of a magnetically suspended motor[J]. Progress in Electromagnetics Research M, 2017, 55: 51-61. doi: 10.2528/PIERM17010904 [10] REN X J, LE Y, HAN B C, et al. Loss optimization and thermal analysis of a heteropolar magnetic bearing for a vacuum turbo-molecular pump[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 54(4): 673-690. doi: 10.3233/JAE-170009 [11] 韩邦成,彭松,贺赞,等. 磁悬浮控制力矩陀螺高速电机绕组涡流损耗计算及热分析[J]. 光学 精密工程,2020,28(1): 130-140. doi: 10.3788/OPE.20202801.0130HAN Bangcheng, PENG Song, HE Zan, et al. Eddy Current loss calculation and thermal analysis of high-speed motor winding in magnetically suspended control moment gyroscope[J]. Optics and Precision Engineering, 2020, 28(1): 130-140. doi: 10.3788/OPE.20202801.0130 [12] ZHANG P F, WANG Z H, XI G. A multi-objective optimal design methodology for solid core no-thrust-disk/thrust hybrid magnetic bearings considering eddy-current effects and leakage[J]. International Journal of Applied Electromagnetics and Mechanics, 2019, 61(1): 13-42. doi: 10.3233/JAE-180062 -
下载:
点击查看大图
计量
- 文章访问数: 208
- HTML全文浏览量: 165
- PDF下载量: 17
- 被引次数: 0