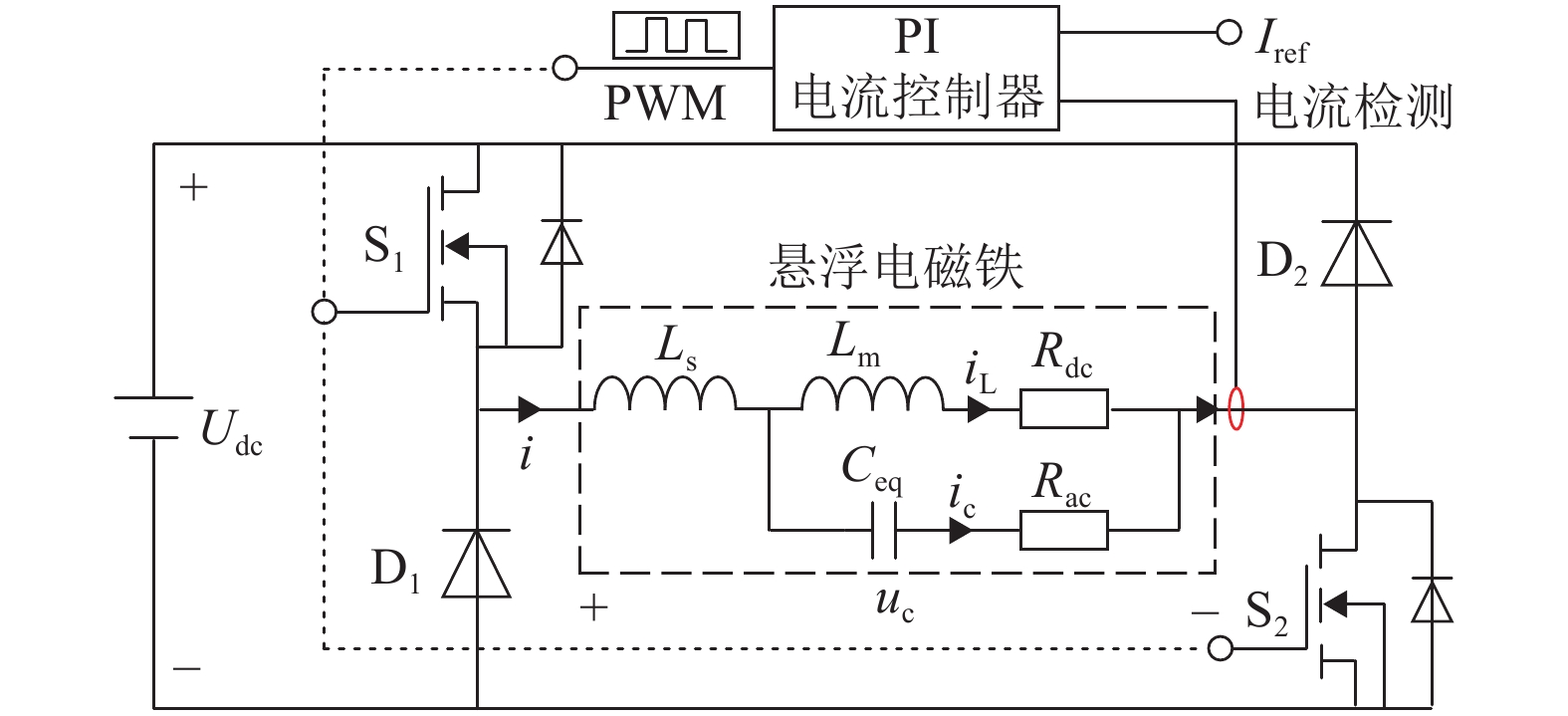
Equivalent Circuit Model of Suspension Electromagnet with Current Ringing Characteristics
-
摘要:
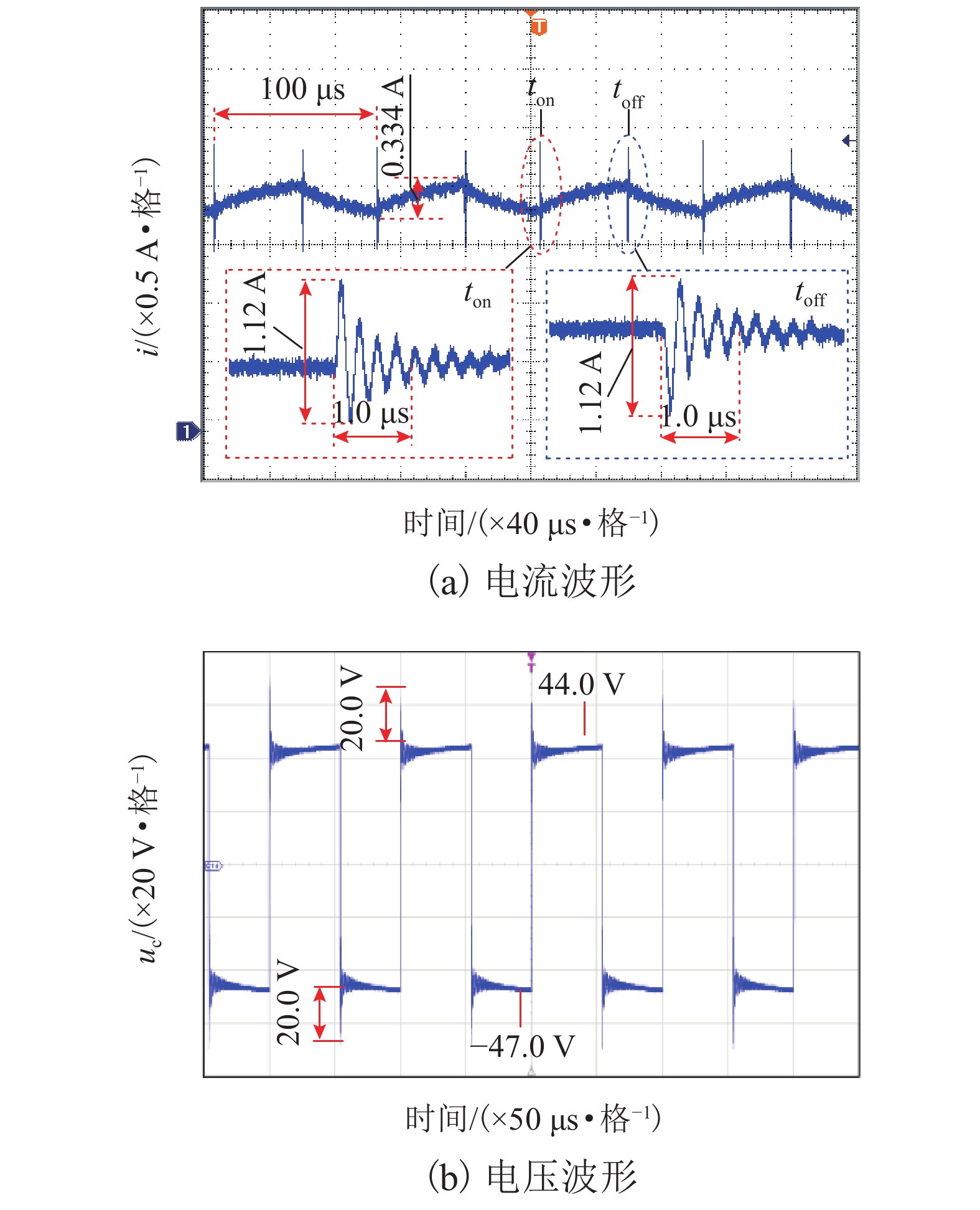
电磁悬浮型(electromagnetic suspension,EMS)磁浮列车通过悬浮斩波器调节悬浮电磁铁电流,进而控制悬浮力,使车体稳定悬浮. 悬浮斩波器驱动悬浮电磁铁过程中所产生的电流振铃会增加开关损耗,造成电磁干扰(electromagnetic interference,EMI),甚至影响悬浮控制效果. 研究悬浮电磁铁电流振铃的产生机理,能为其抑制措施的设计予以指导. 为此,提出了一种考虑电流振铃特性的悬浮电磁铁等效电路模型. 首先,用策动点函数法推导了悬浮电磁铁导抗函数的一般形式,并结合悬浮电磁铁电流的单位阶跃响应特性确定了其导抗函数的最简表达式以及对应的等效电路模型;接着,用判别式法和仿真法分析了不同电路参数对电流振铃特性的影响;最后,比较了同一悬浮电磁铁电流振铃的仿真和实验波形. 结果表明:在所给参数条件下,实验所得悬浮电磁铁电流纹波幅值、振铃峰峰值和振铃频率分别比仿真结果小9.7%、20%和11%;此外,仿真的电流振铃衰减时间约为1 μs,与实验结果接近;仿真和实验所得悬浮电磁铁电流振铃的幅值、频率和衰减特性均能较好吻合,证明了所提电路模型的正确性.
Abstract:Electromagnetic suspension (EMS) type maglev trains adjust currents of suspension electromagnets through maglev choppers and then control the suspension force to keep the car body stable suspension. The suspension electromagnet current ringing generated by the maglev chopper will increase the switching loss, cause electromagnetic interference (EMI), and even affect the suspension control. Studying the suspension electromagnet current ringing’s generation mechanism is helpful to find its suppression measures. An equivalent circuit model of suspension electromagnet is proposed in view of the current ringing characteristics. Firstly, the general form of the suspension electromagnet’s impedance function is derived by the driving-point function method. Then, based on the suspension electromagnet current’s unit-step response characteristics, the simplest expression of the impedance function and the corresponding equivalent circuit model are determined. Next, the influences of different circuit parameters on current ringing characteristics are analyzed by discriminant and simulation methods. Finally, with the same suspension electromagnet, the simulation and experimental waveforms of the current ringing are compared. The results show that for the specified parameters, the current ripple amplitude, ringing peak value, and ringing frequency of the suspension electromagnet obtained from the experiment are 9.7%, 20%, and 11% lower than the simulation results, respectively. In addition, the simulated current ringing attenuation time is about 1 μs, which is close to the experimental results. The simulation and experimental results of the suspension electromagnet current ringing are in good agreement in terms of the amplitude, frequency, and attenuation characteristics, validating the proposed circuit model.
-
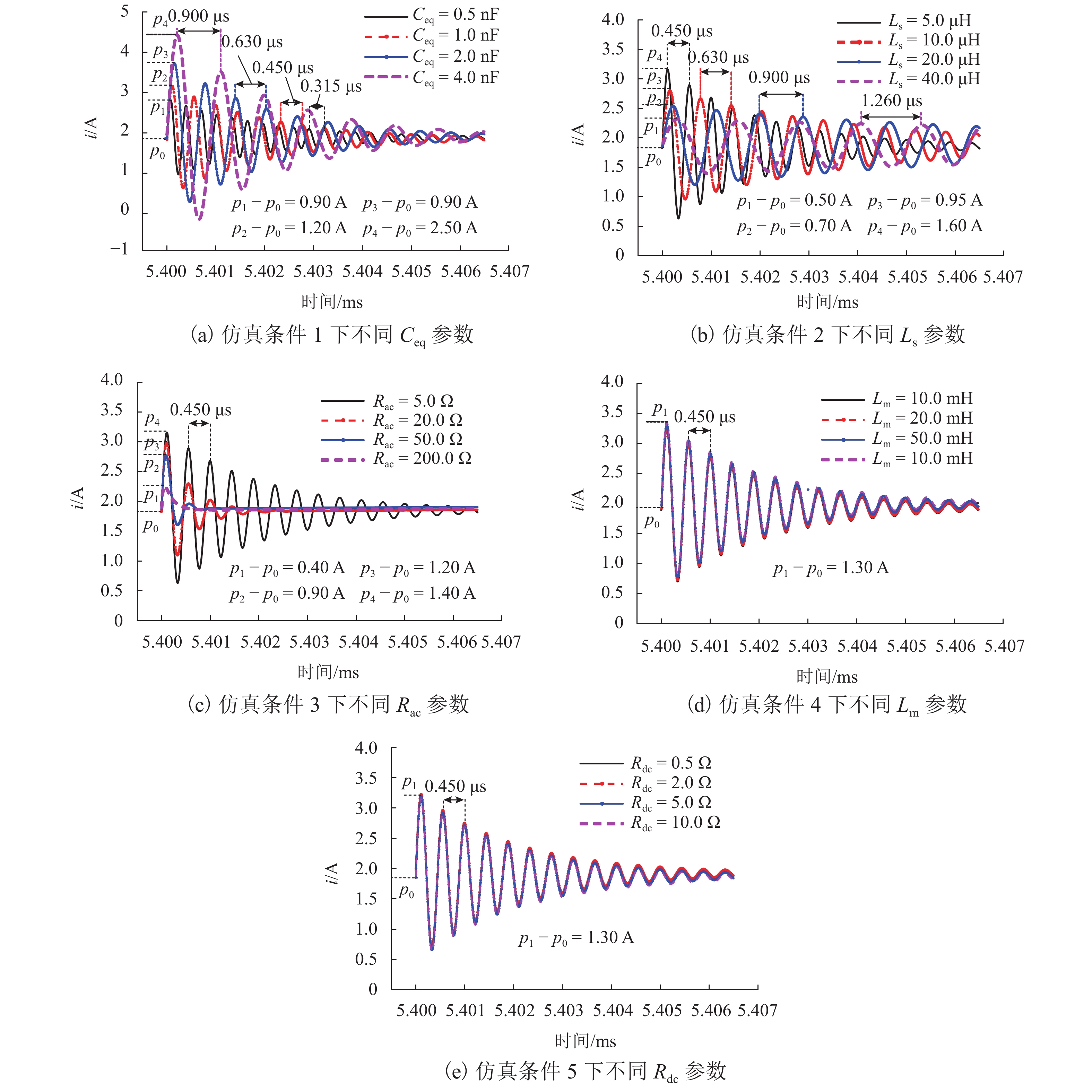
表 1 仿真参数设置
Table 1. Sinulation parameter setting
仿真条件 Ceq/nf Ls/μH Rac/Ω Lm/mH Rdc/Ω 1 变化 5.0 5.0 10.0 2.0 2 1.0 变化 5.0 10.0 2.0 3 1.0 5.0 变化 10.0 2.0 4 1.0 5.0 5.0 变化 2.0 5 1.0 5.0 5.0 10.0 变化 -
[1] SUN Y G, XU J Q, LIN G B, et al. RBF neural network-based supervisor control for maglev vehicles on an elastic track with network time delay[J]. IEEE Transactions on Industrial Informatics, 2022, 18(1): 509-519. doi: 10.1109/TII.2020.3032235 [2] WANG P, LONG Z Q, XU Y S. Component-level fault detection for suspension system of maglev trains based on autocorrelation length and stable kernel representation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(8): 7594-7604. doi: 10.1109/TVT.2021.3096732 [3] WANG J J, CHUNG H S H, LI R T H. Characterization and experimental assessment of the effects of parasitic elements on the MOSFET switching performance[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 573-590. doi: 10.1109/TPEL.2012.2195332 [4] GAITO A, SCOLLO R, PANEBIANCO G, et al. Impact of the source-path parasitic inductance on the MOSFET commutations[C]//2012 IEEE Energy Conversion Congress and Exposition. Raleigh: IEEE, 2012: 1367-1373. [5] BI C, LU R B, LI H. Prediction of electromagnetic interference noise in SiC MOSFET module[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2019, 66(5): 853-857. doi: 10.1109/TCSII.2019.2908971 [6] SUN Y G, XU J Q, QIANG H Y, et al. Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental verification[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8589-8599. doi: 10.1109/TIE.2019.2891409 [7] NI F, MU S Y, KANG J S, et al. Robust controller design for maglev suspension systems based on improved suspension force model[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 1765-1779. doi: 10.1109/TTE.2021.3058137 [8] 蒋祥宇,王昊文,王雪琪,等. 不对称三电平悬浮斩波器[J]. 电力电子技术,2020,54(6): 132-135.JIANG Xiangyu, WANG Haowen, WANG Xueqi, et al. Asymmetric three-level suspension chopper[J]. Power Electronics, 2020, 54(6): 132-135. [9] DING J F, YANG X, LONG Z Q, et al. Three-dimensional numerical analysis and optimization of electromagnetic suspension system for 200 km/h maglev train considering eddy current effect[J]. IEEE Access, 2018, 6: 61547-61555. doi: 10.1109/ACCESS.2018.2876599 [10] LIU T J, NING R T, WONG T T Y, et al. Modeling and analysis of SiC MOSFET switching oscillations[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(3): 747-756. [11] LIU T J, WONG T T Y, SHEN Z J. A survey on switching oscillations in power converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 893-908. doi: 10.1109/JESTPE.2019.2897764 [12] 周庭阳, 张红岩. 电网络理论[M]. 杭州: 浙江大学出版社, 1997. [13] 范盛金. 一元三次方程的新求根公式与新判别式[J]. 海南师范学院学报(自然科学版),1989,2(2): 91-98.FAN Shengjin. A new extracting formula and a new distinguishing means on the one variable cubic equation[J]. Journal of Hainan Normal University (Natural Science), 1989, 2(2): 91-98. [14] JOSIFOVIĆ I, POPOVIĆ-GERBER J, FERREIRA J A. Improving SiC JFET switching behavior under influence of circuit parasitics[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3843-3854. doi: 10.1109/TPEL.2012.2185951 [15] SAITO K, MIYOSHI T, KAWASE D, et al. Simplified model analysis of self-excited oscillation and its suppression in a high-voltage common package for Si-IGBT and SiC-MOS[J]. IEEE Transactions on Electron Devices, 2018, 65(3): 1063-1071. doi: 10.1109/TED.2018.2796314 -





 下载:
下载: