Research on Dynamic Characteristics and Control of Axial-Radial Hybrid Magnetic Bearing
-
摘要:
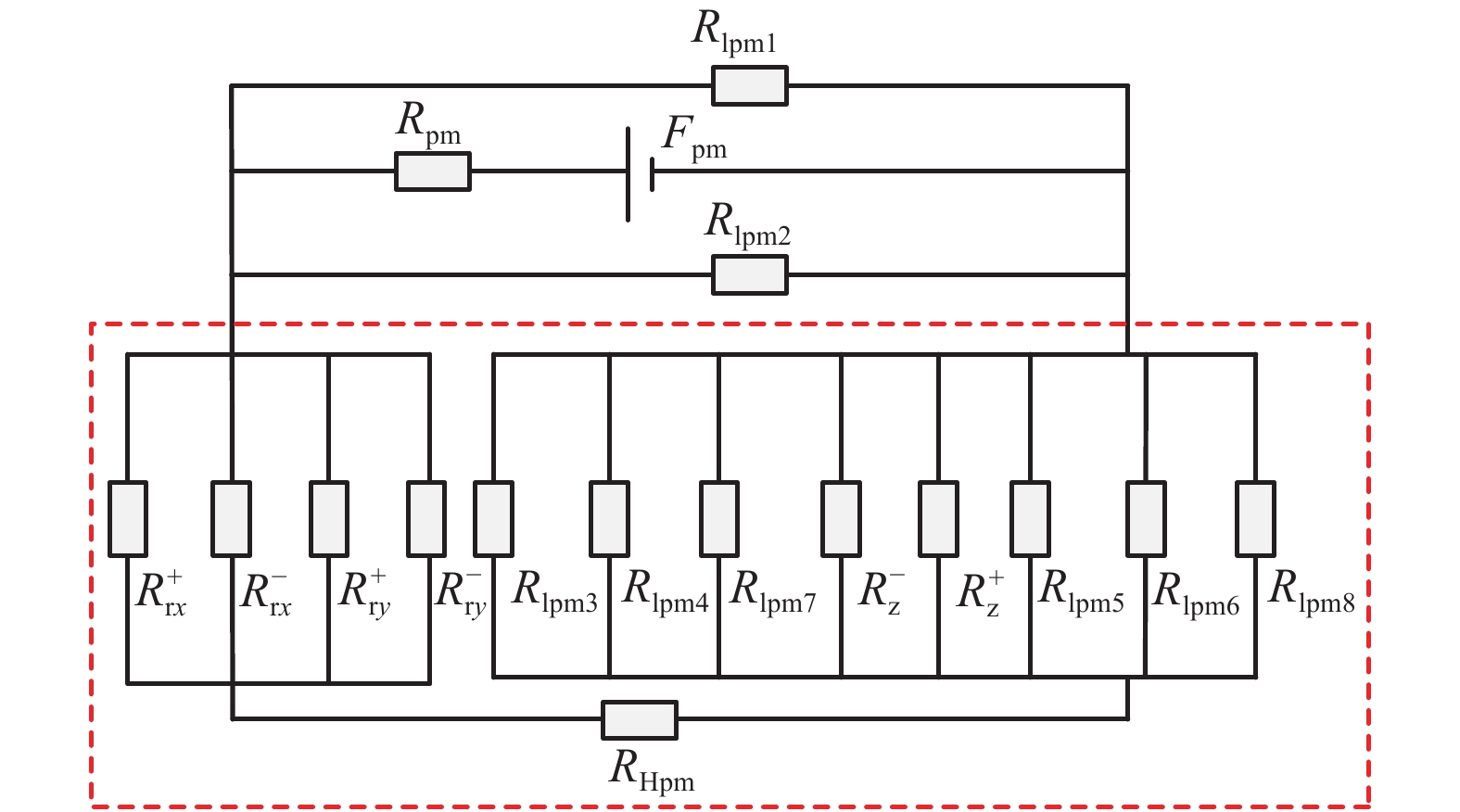
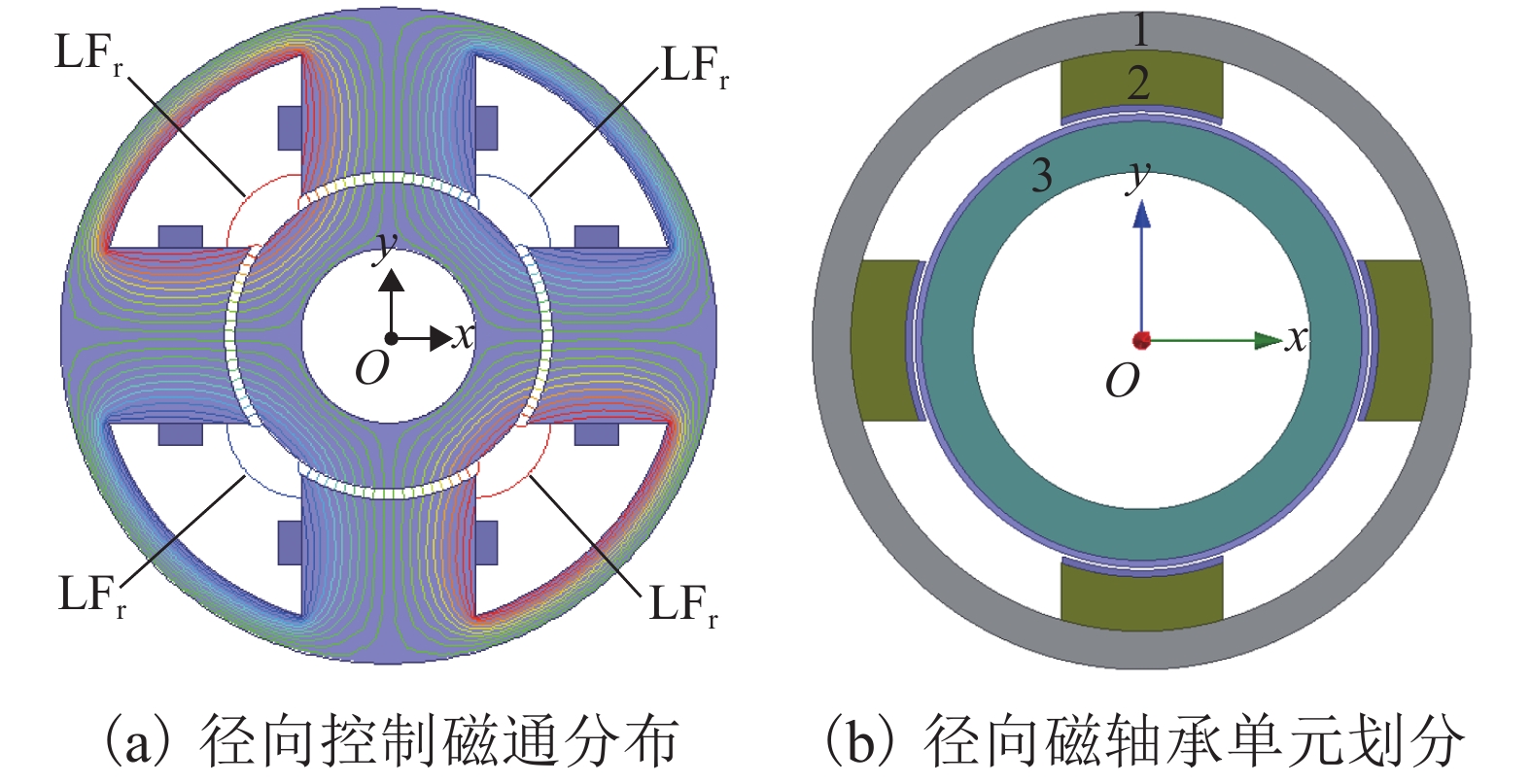
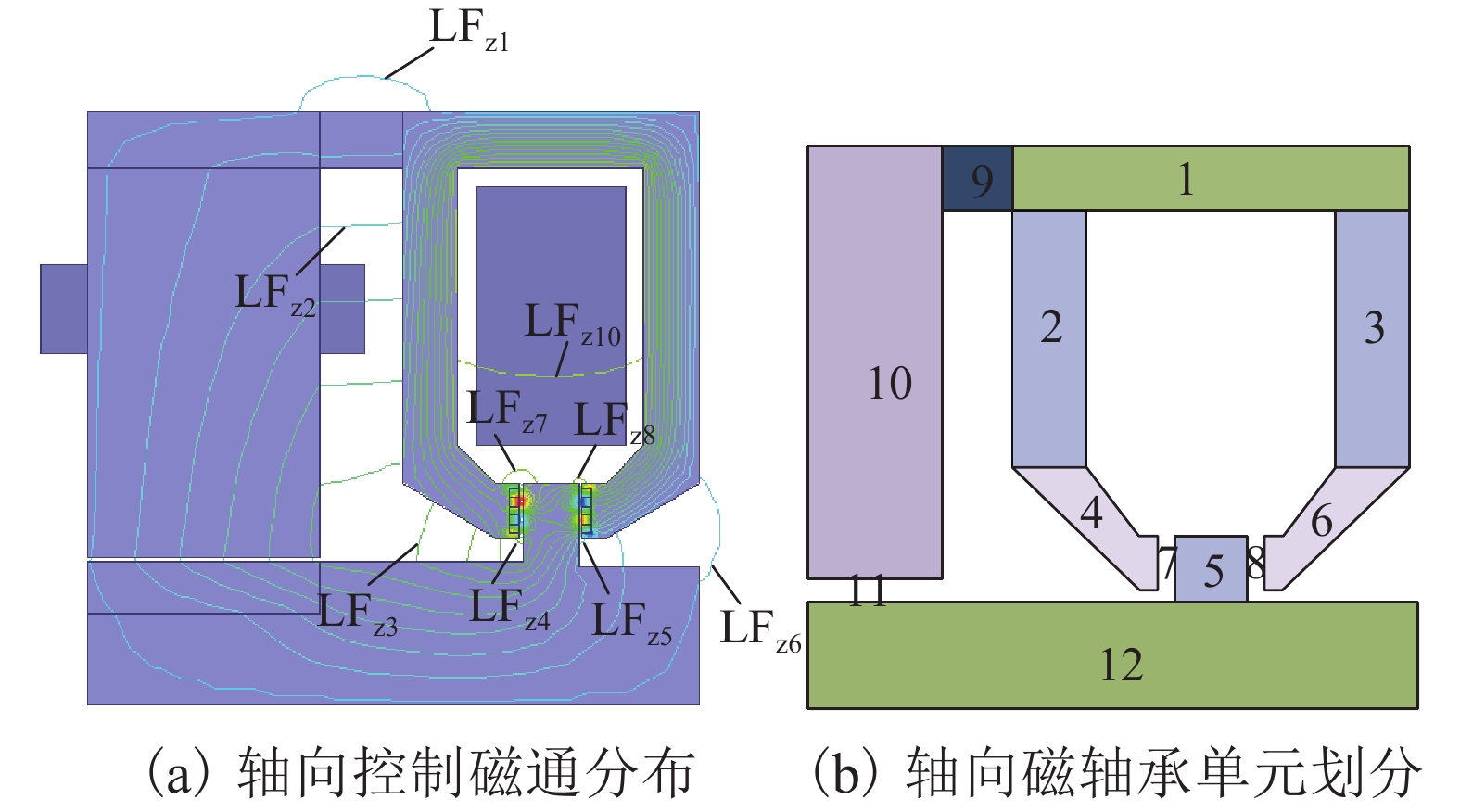
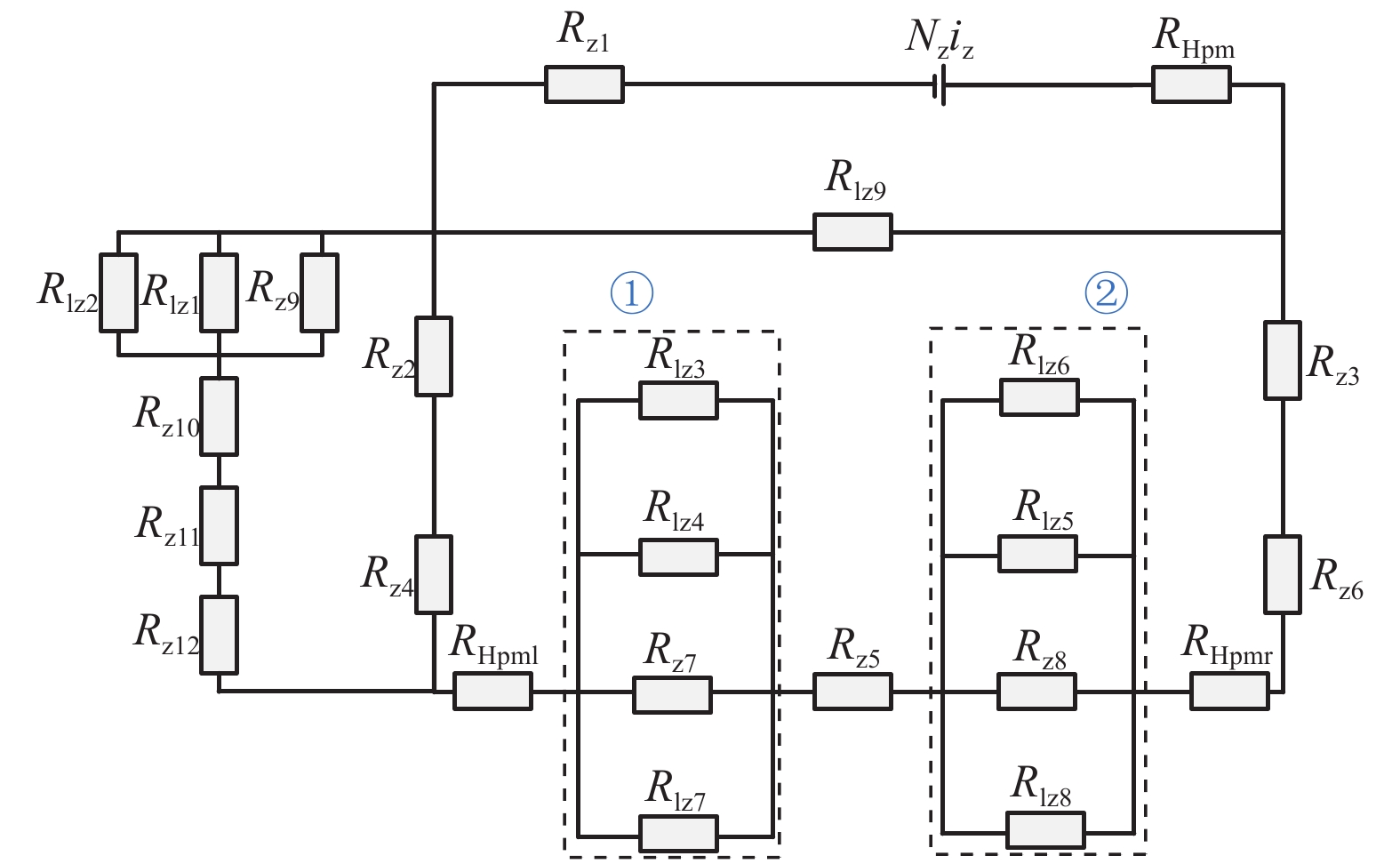
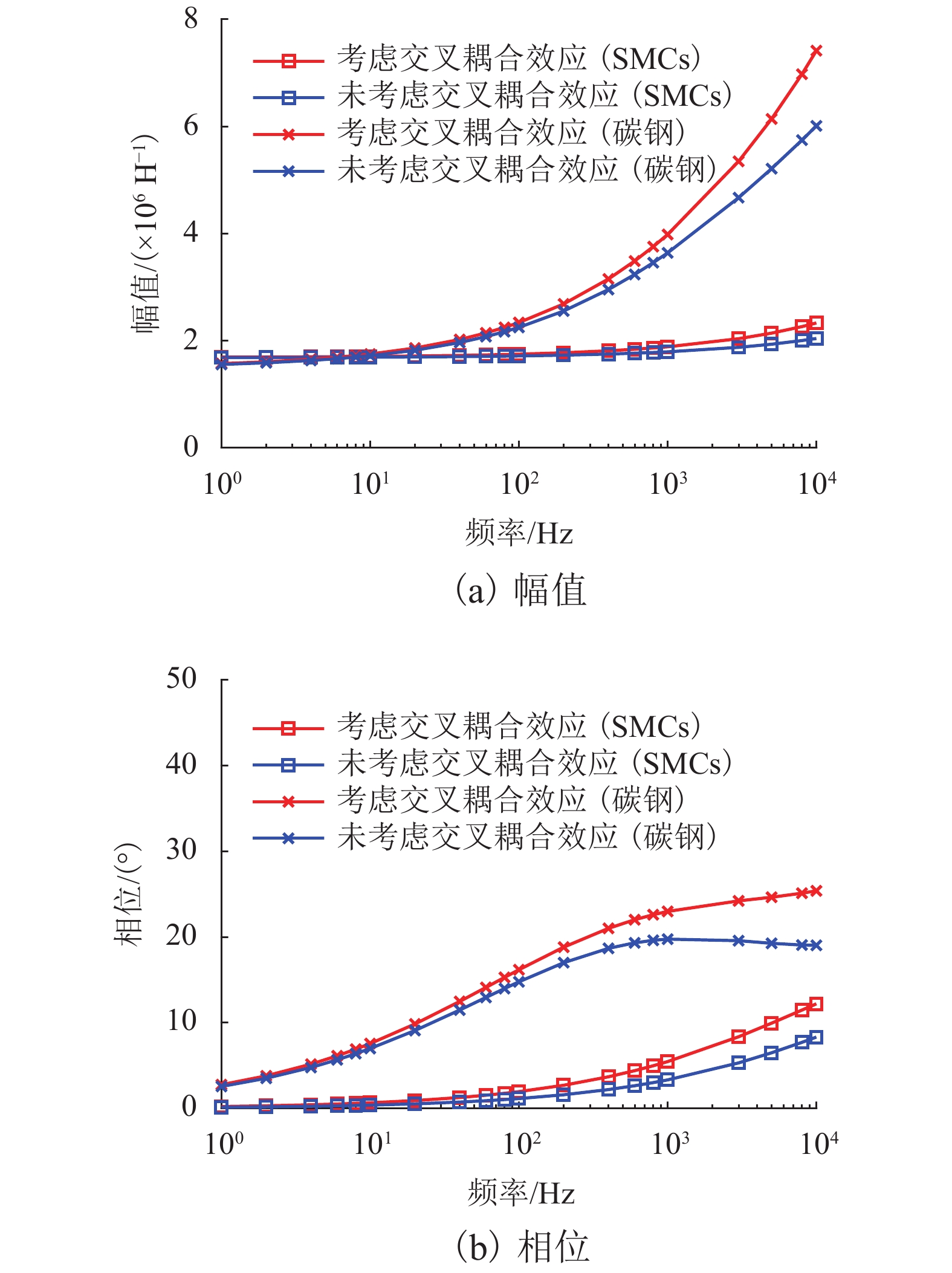
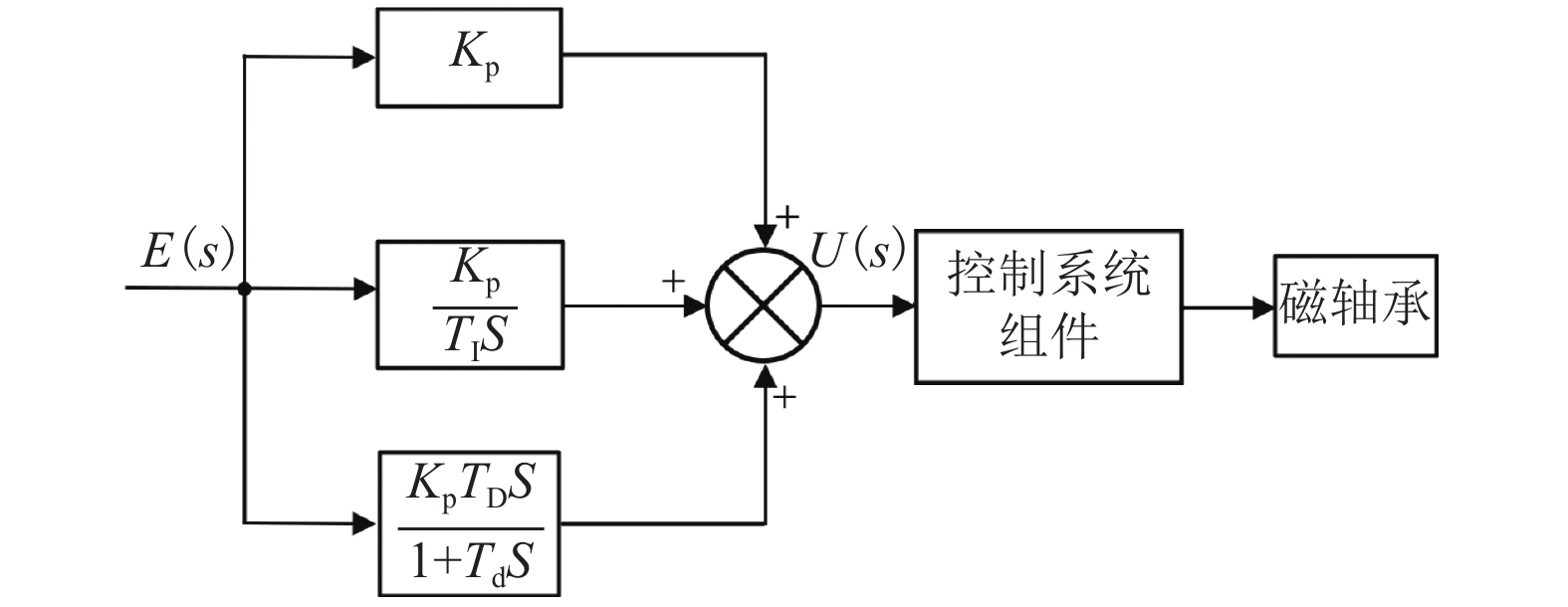
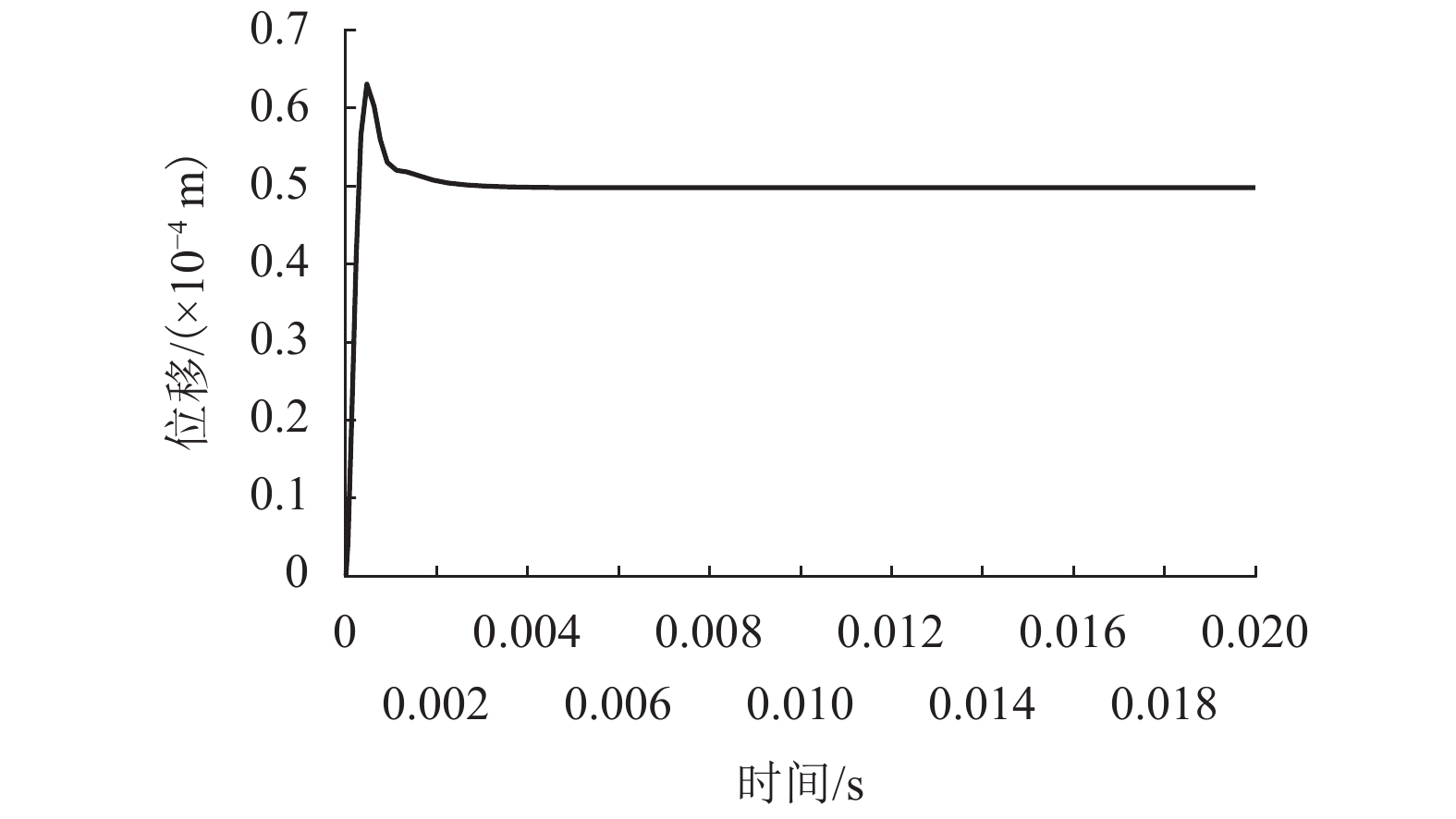
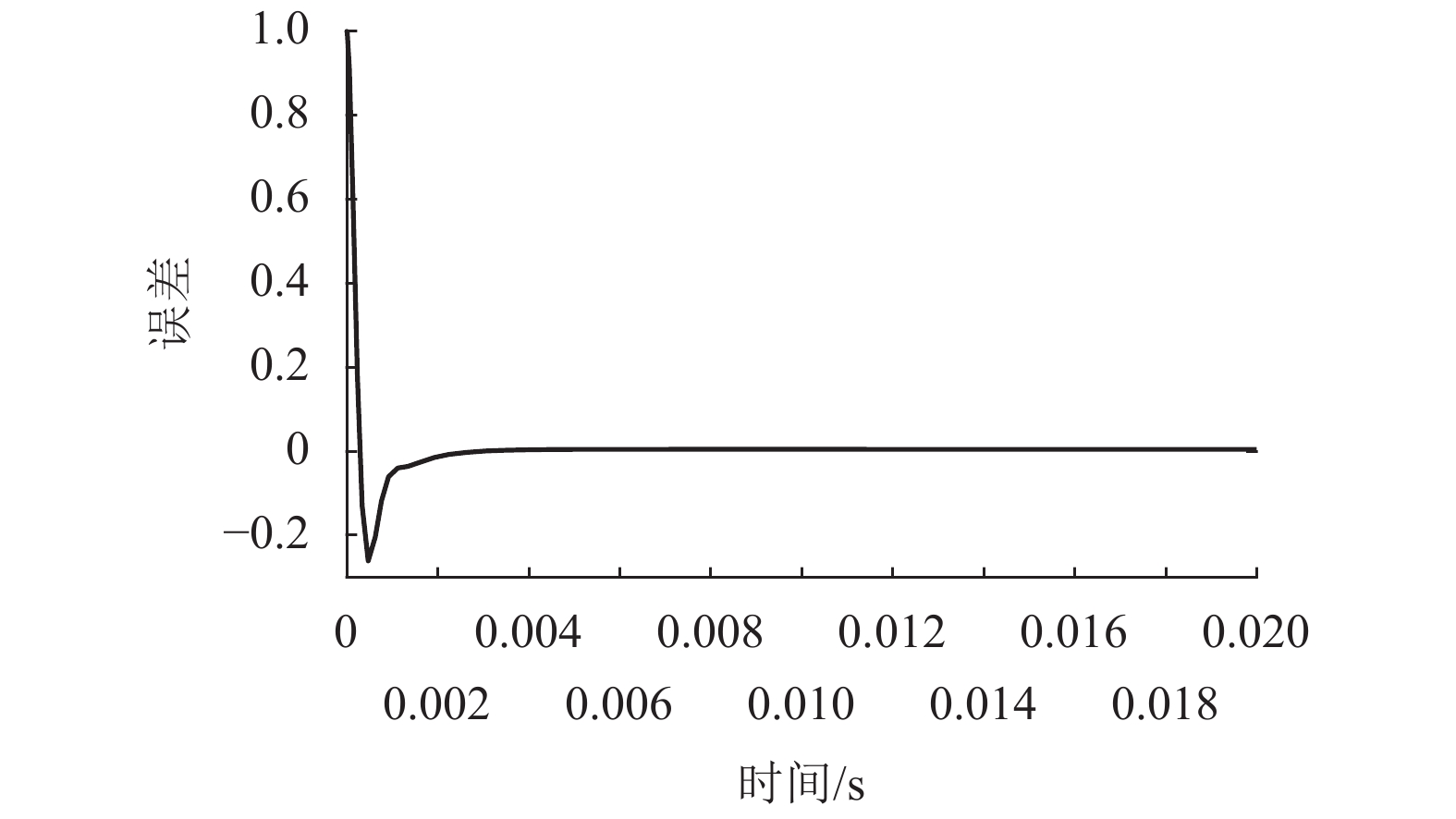
为了减小三自由度轴-径向混合磁轴承（ARHMB）的涡流损耗并增加轴向磁力，提出轴向采用软磁复合材料（SMCs）制备的推力轴承，在推力盘与转子的气隙处引入Halbach阵列以增强轴向气隙磁密，径向采用叠片结构. 首先，基于动态磁通分布及等效磁路法，建立综合考虑涡流、漏磁及交叉耦合效应的等效磁阻模型；其次，对比分析了材料类型及交叉耦合效应对等效磁阻频率响应、动态刚度的影响；最后，采用计及涡流、漏磁及交叉耦合效应不完全微分PID控制对ARHMB进行研究. 研究结果表明：SMCs制备的ARHMB相比碳钢材料可以提供更大、更稳定的磁力以及更大的工作带宽，在高频条件下具有更好的动态特性；考虑交叉耦合效应时，SMCs制备的ARHMB动态特性在高频时变化率较大，不可忽略；对于低带宽工作的碳钢轴承，交叉耦合效应不明显；电磁轴承系统响应速度很快、超调量小、稳态误差近似为0，具有良好的控制特性.
Abstract:In order to reduce the eddy current loss and increase the axial magnetic force for three degrees of freedom axial-radial hybrid magnetic bearings (ARHMB), a thrust bearing made of soft magnetic composite materials (SMCs) in the axial direction was proposed. The Halbach array was introduced at the air gap between the thrust plate and the rotor to enhance the magnetic density of the axial air gap. In the radial direction, the laminated structure was used for the radial bearing. Firstly, based on the dynamic magnetic flux distribution and the equivalent magnetic circuit method, the equivalent reluctance model considering eddy current, magnetic leakage and cross-coupling effects was established. Then, the influence of material types and cross-coupling effect on the equivalent reluctance frequency response and dynamic stiffness was analyzed. Finally, ARHMB was studied by incomplete derivative PID control considering the effect of eddy current, magnetic leakage and cross-coupling. The results show that ARHMB prepared by SMCs can provide greater and more stable magnetic force and larger bandwidth than that made of carbon steel, and has better dynamic characteristics under high-frequency conditions. When considering the cross-coupling effect, the dynamic characteristics of ARHMB made of SMCs have a large change rate at high frequency and cannot be ignored. For low-bandwidth carbon steel bearings, the cross-coupling effect is not obvious. The system of magnetic bearing has a fast response speed, small overshoot, and approximately zero steady-state error, which has good control characteristics.
-
图 16 不完全微分形式的PID控制误差变化曲线
Figure 16. Error curve of PID control in incomplete differential form
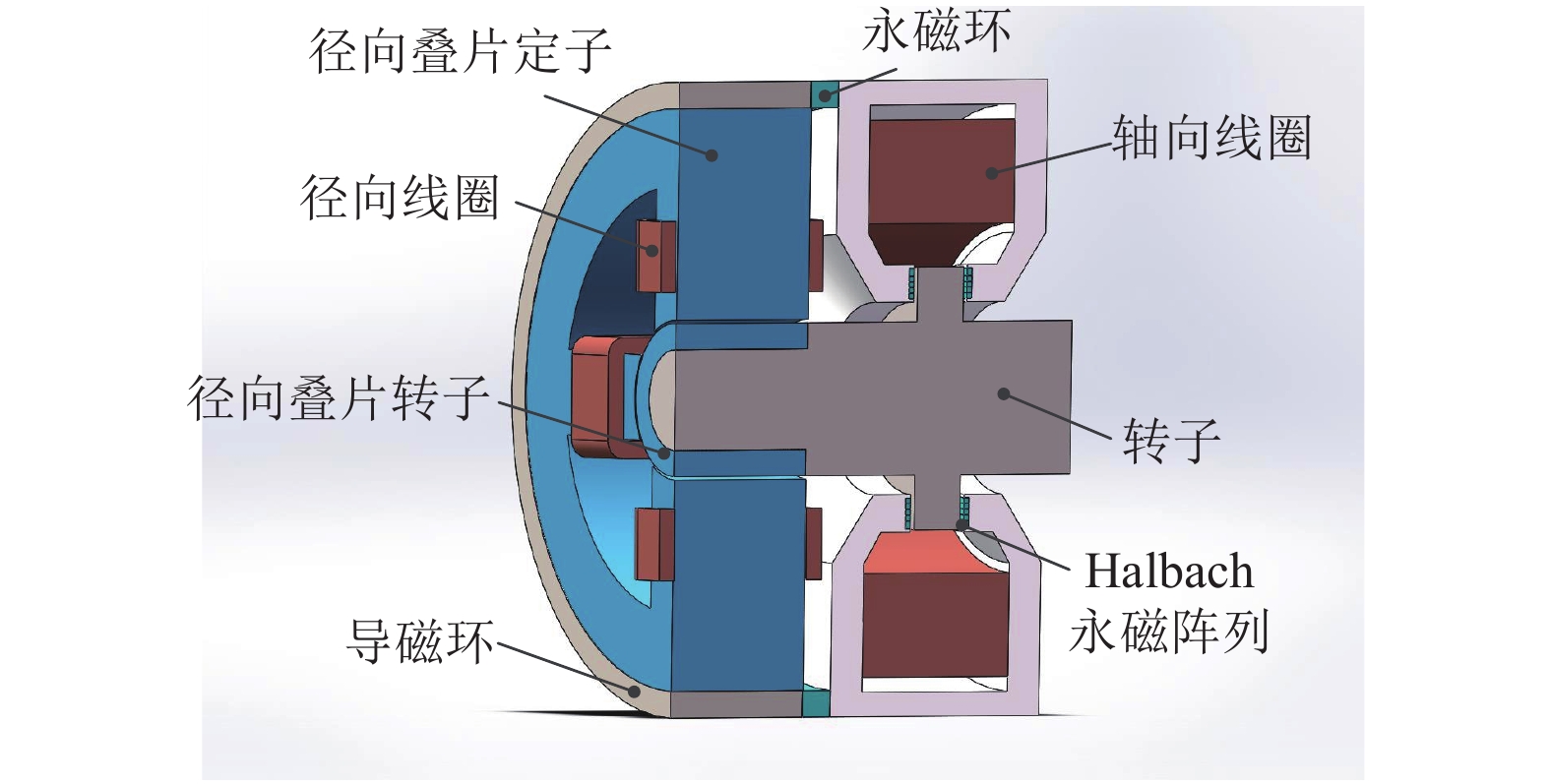
表 1 ARHMB结构参数
Table 1. ARHMB structure parameters
mm 参数 数值 参数 数值 轴向磁极
宽度 x6 转子外径
宽度 y6 轴向定子腔
宽度 b20 径向磁极轴向
宽度 c25 径向磁极径向
宽度 l9 气隙宽度 g 0.4 转子半径 d1 15 轴向磁极
内径 d218 转子外径 d3 24 径向磁极
外径 d428 轴向定子
内径 d558 轴向定子内外径
间距 d67 径向定子
外径 d758 导磁环厚度 d8 6 
下载: 导出CSV
-
[1] 崔恒斌,周瑾,董继勇,等. 磁悬浮旋转机械振动稳定性实例研究[J]. 浙江大学学报(工学版),2018,52(4): 635-640,686. doi: 10.3785/j.issn.1008-973X.2018.04.004CUI Hengbin, ZHOU Jin, DONG Jiyong, et al. Case study on vibration stability of rotating machinery equipped with active magnetic bearings[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(4): 635-640,686. doi: 10.3785/j.issn.1008-973X.2018.04.004 [2] 林子豪,胡业发,冉少林,等. 3自由度混合磁轴承支承特性及仿真分析[J]. 机械设计与研究,2019,35(5): 32-35,40.LIN Zihao, HU Yefa, RAN Shaolin, et al. Simulation study on supporting characteristics of three-DOF hybrid magnetic bearings[J]. Machine Design & Research, 2019, 35(5): 32-35,40. [3] ZHONG Y L, WU L J, HUANG X Y, et al. Modeling and design of a 3-DOF magnetic bearing with toroidal radial control coils[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-7. [4] XIAO L, HE X W, CHENG W J, et al. Structural optimization and dynamic characteristics of the new type 3-degrees of freedom axial and radial hybrid magnetic bearing[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2021: 09544062211052826.1- 09544062211052826.14. [5] LE Y, WANG K. Design and optimization method of magnetic bearing for high-speed motor considering eddy current effects[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(4): 2061-2072. doi: 10.1109/TMECH.2016.2569822 [6] REN X J, LE Y, SUN J J, et al. Magnetic flux leakage modelling and optimisation of a CRAHMB for DC motor[J]. IET Electric Power Applications, 2017, 11(2): 212-221. doi: 10.1049/iet-epa.2016.0259 [7] REN X, FENG M,CHEN S,et al. The cross-coupling problem caused by the structure of a combined radial-axial magnetic bearing for DC motors[J]. International Journal of Applied Electromagnetics and Mechanics, 2020, 62(1): 173-189. [8] ZHONG Y L, WU L J, FANG Y T, et al. Investigation of cross-coupling effect and its restraining methods of a 3-DOF hybrid magnetic bearing[J]. COMPEL:the International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2018, 37(6): 2195-2210. doi: 10.1108/COMPEL-01-2018-0037 [9] FENG S, AN Y, WANG Z X, et al. Preparation and magnetic properties of Fe@SiO2 Soft magnetic composites[J]. Materials Science Forum, 2020, 993: 638-645. doi: 10.4028/www.scientific.net/MSF.993.638 [10] XIAO L, HOU T Y, LI M, et al. Dynamic performances of a magnetic thrust bearing based on new soft magnetic composites[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(10): 3388-3399. doi: 10.1177/0954406218813587 [11] HAN B C, XU Q J, ZHENG S Q. Integrated radial/thrust magnetic bearing without thrust disk for a high-speed driving system[J]. IET Electric Power Applications, 2016, 10(4): 276-283. doi: 10.1049/iet-epa.2015.0335 [12] ZHU L. Non-laminated magnetic actuators: Modeling and performance limitations[D]. Virginia: University of Virginia, 2005 [13] 邴守东,李国林. 不完全微分PID控制算法研究与仿真实验[J]. 电子工业专用设备,2013,42(1): 46-50. doi: 10.3969/j.issn.1004-4507.2013.01.011BING Shoudong, LI Guolin. Incomplete derivative PID control algorithm and simulation experiment[J]. Equipment for Electronic Products Manufacturing, 2013, 42(1): 46-50. doi: 10.3969/j.issn.1004-4507.2013.01.011 [14] 王忠博. 主动电磁轴承-刚性转子系统振动主动控制[D]. 杭州: 浙江大学, 2018. [15] LIN F J, HUANG M S, CHEN S Y. Intelligent double integral sliding-mode control for five-degree-of-freedom active magnetic bearing system[J]. IET Control Theory & Applications, 2011, 5(11): 1287-1303. [16] LIU C, LIU G. Equivalent damping control of radial twist motion for permanent magnetic bearings based on radial position variation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6417-6427. doi: 10.1109/TIE.2015.2416681 -
下载:
点击查看大图
计量
- 文章访问数: 343
- HTML全文浏览量: 167
- PDF下载量: 39
- 被引次数: 0