基于均值-方差理论的多阶段公交走廊设计

夏亮; 江欣国; 范英飞

doi:10.3969/j.issn.0258-2724.20210874

基于均值-方差理论的多阶段公交走廊设计

doi: 10.3969/j.issn.0258-2724.20210874

夏亮^{1, 2, 3,},
江欣国^{1, 2, ,},
范英飞³

1.
西南交通大学交通运输与物流学院，四川成都 611756
2.
西南交通大学综合交通运输智能化国家地方联合工程实验室，四川成都 610031
3.
太原科技大学交通与物流学院，山西太原 030024
4.
长沙市望城区交通运输局，湖南长沙 410203

基金项目: 国家自然科学基金（71771191）

详细信息

作者简介:
夏亮（1992—），男，博士研究生，研究方向为公共交通规划设计，E-mail：lxia@my.swjtu.edu.cn

通讯作者:
江欣国（1975—），男，教授，博士，研究方向为道路交通安全，E-mail：xjiang@swjtu.edu.cn

中图分类号: U491
计量
- 文章访问数: 240
- HTML全文浏览量: 63
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-08
- 修回日期: 2022-01-25
- 网络出版日期: 2023-08-25
- 刊出日期: 2022-04-01

Phased Transit Service Design Based on Mean-Variance Theory

XIA Liang^{1, 2, 3
,},
JIANG Xinguo^{1, 2
, ,},
FAN Yingfei³

1.
School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China
2.
Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
3.
School of Transportation and Logistics Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China
4.
Wangcheng Transportation Bureau, Changsha 410203, China

摘要

摘要:
随机性是公交出行需求的重要特性. 随机需求下的公交系统中，不同风险态度（中立风险、规避风险和寻求风险）的决策者会选择不同的设计方案，这在多阶段公交系统走廊设计中更为明显. 为研究不同决策风险态度下随机特性对公交服务设计的影响，首先，基于均值-方差理论，提出不同风险态度下的决策方法，并构建对应的多阶段公交走廊设计模型，同时优化不同阶段的公交线路长度、站点选址和发车间隔；之后，利用局部分解法和最优化理论，得出模型的解析解；最后，对不同设计策略（全覆盖设计、单阶段和多阶段的公交线路非全覆盖设计）和风险决策态度下的公交走廊设计进行对比分析. 结果表明：1）公交线路多阶段设计具有比全覆盖设计和单阶段设计更低的期望系统成本，以及比单阶段设计更稳定的方案；2）在不同设计策略中，决策风险态度对公交系统的参数配置（即公交线路长度、站点分布和发车间隔）有不同的影响，例如规避风险态度决策者在全覆盖设计中追求更密集的站点分布，而在单阶段设计中则会追求相对更低的站点密度，在多阶段设计中这就更为复杂. 该研究从政府管理者和运营商的角度，提供基于需求随机增长下公交系统多阶段设计的风险投资决策方法.
- 公共交通 /
- 多阶段设计 /
- 随机需求 /
- 均值-方差理论
Abstract:
Transit travel demand has an important characteristic of being stochastic. The decision-makers with different risk attitudes (i.e., risk-neutral, risk-averse, and risk-seeking) will choose various transit service designs in response to the stochastic demand, which seems to be especially critical in the phased transit design. In order to study the impacts of stochastic travel demand on the transit service design, we firstly propose a mean-variance based decision-making approach for decision-makers with different risk attitudes. Correspondingly, the study proposes a model for phased transit corridor design, which can concurrently optimize the line length, transit station location, and headway in each phase. Then, the local decomposition method and optimization theory are adopted to find the analytical solution. Finally, the study compares the transit corridor designs with different design strategies (i.e., full-covered, once-and-done, and phased designs of the transit line) and risk decision-making attitudes. The results indicate: 1) the phased design has a lower expected system cost than the full-covered and the once-and-done designs, and a more robust scheme than the once-and-done design; and 2) risk decision- making attitudes substantially affect the parameters (i.e., the transit length, station location, and headway) of transit system under different design strategies; for example, the risk-averse decision-makers tend to seek denser station locations in the full-covered design, but relatively lower station density in the once-and-done design in phased design. The issue becomes more complex in the phased transit design. This study serves to provide a risk-based decision-making model of phased transit service under the increasing stochastic demand for the government manager and transit operators.
- transit traffic /
- phased design /
- stochastic demand /
- mean-variance theory

HTML全文

图 1 单中心公交走廊

Figure 1. Layout of monocentric corridor

下载: 全尺寸图片幻灯片

图 2 公交线路全覆盖设计的发车间隔

Figure 2. Headways of transit system with full-covered design

下载: 全尺寸图片幻灯片

图 3 公交线路单阶段设计的发车间隔

Figure 3. Headways with once-and-done design

下载: 全尺寸图片幻灯片

图 4 公交系统多阶段设计结果

Figure 4. Result of transit system under phased design

下载: 全尺寸图片幻灯片

表 1 实验中的参数值

Table 1. Value of parameters in experiment

参数	数值	参数	数值
v_w/（km·h⁻¹）	2	ζ	1
v_c/（km·h⁻¹）	60	k/（户·km⁻¹）	4600
T_d/（h·站⁻¹）	0.0125	$\bar {g} $/（户·年⁻¹）	0.03
C_V/（人·车⁻¹）	1800	σ_g/（户·年⁻¹）	0.01
π₁/（h·（km·d）⁻¹）	14256 + 475.2μ	p_g	0.7
π₂/ （h·（站·d）⁻¹）	7056 + 235.2μ	κ	0.1
π₃/（h·km⁻¹）	2.2	T_w/（d·年⁻¹）	250
π₄/（h·h⁻¹）	101 + 5 μ	N₀/ 户	30000
T_r/ （h·d⁻¹）	16	μ/ （h·h⁻¹）	20
η/ （次·（户·d）⁻¹）	4

下载: 导出CSV

表 2 公交线路全覆盖设计结果

Table 2. Result of transit system with full-covered design

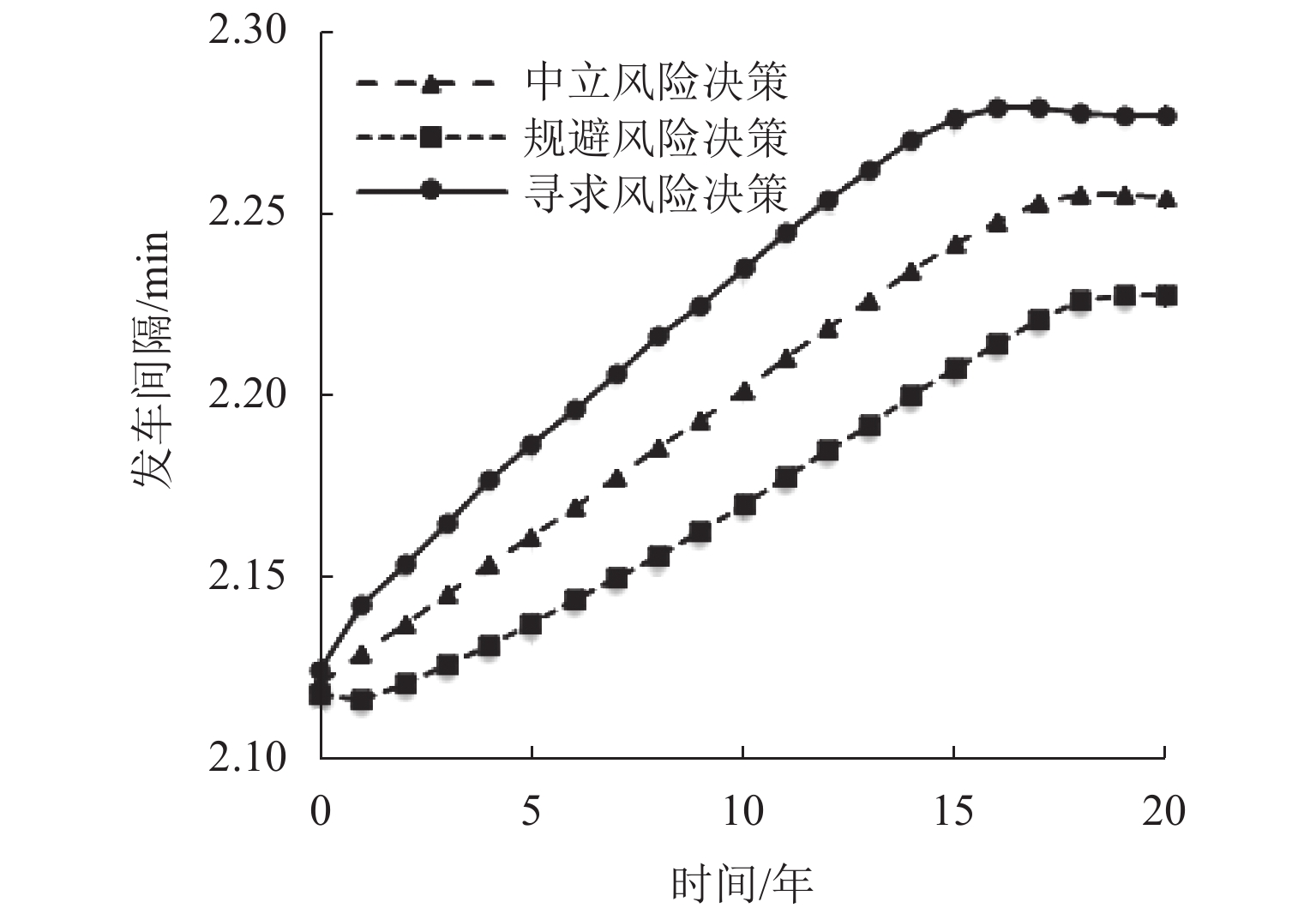
风险决策态度	公交线路/ 走廊长度/km	平均站点密度/ （站·km⁻¹）	平均发车间隔/ min	期待用户通勤成本/ （h·（户·d）⁻¹）	期待运营商成本/ （h·（户·d）⁻¹）	期待系统成本/ （h·（户·d）⁻¹）	系统成本标准差/ （h·（户·d）⁻¹）
中立风险	（6.81, 14.93）	1.0937	2.1989	1.1280	0.8123	1.9403	0.0794
规避风险	（6.81, 14.93）	1.1773	2.1721	1.1261	0.8154	1.9414	0.0761
寻求风险	（6.81, 14.93）	0.9814	2.2252	1.152	0.8076	1.9595	0.1057

下载: 导出CSV

表 3 公交线路单阶段设计结果

Table 3. Result of transit system with once-and-done design

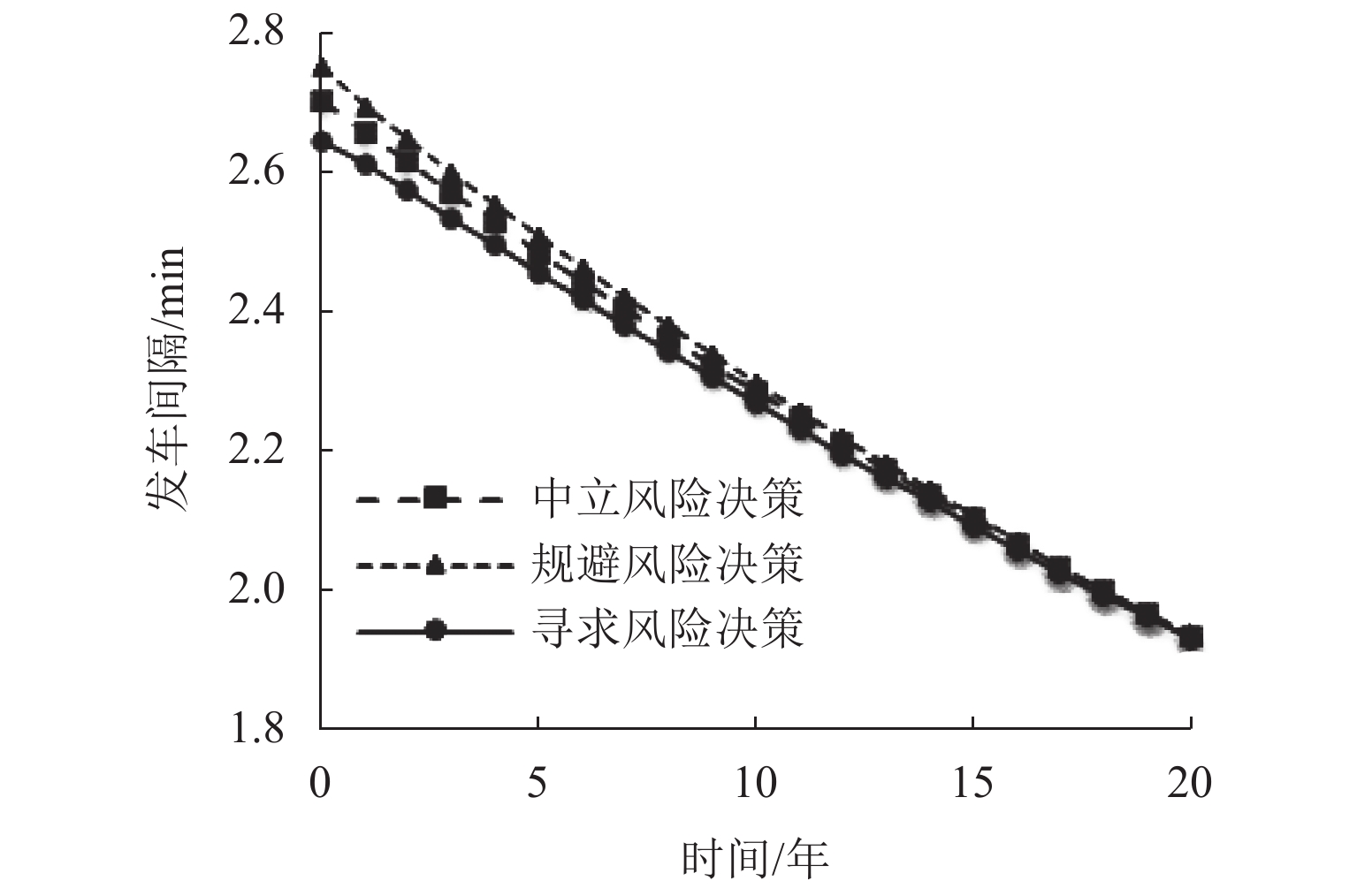
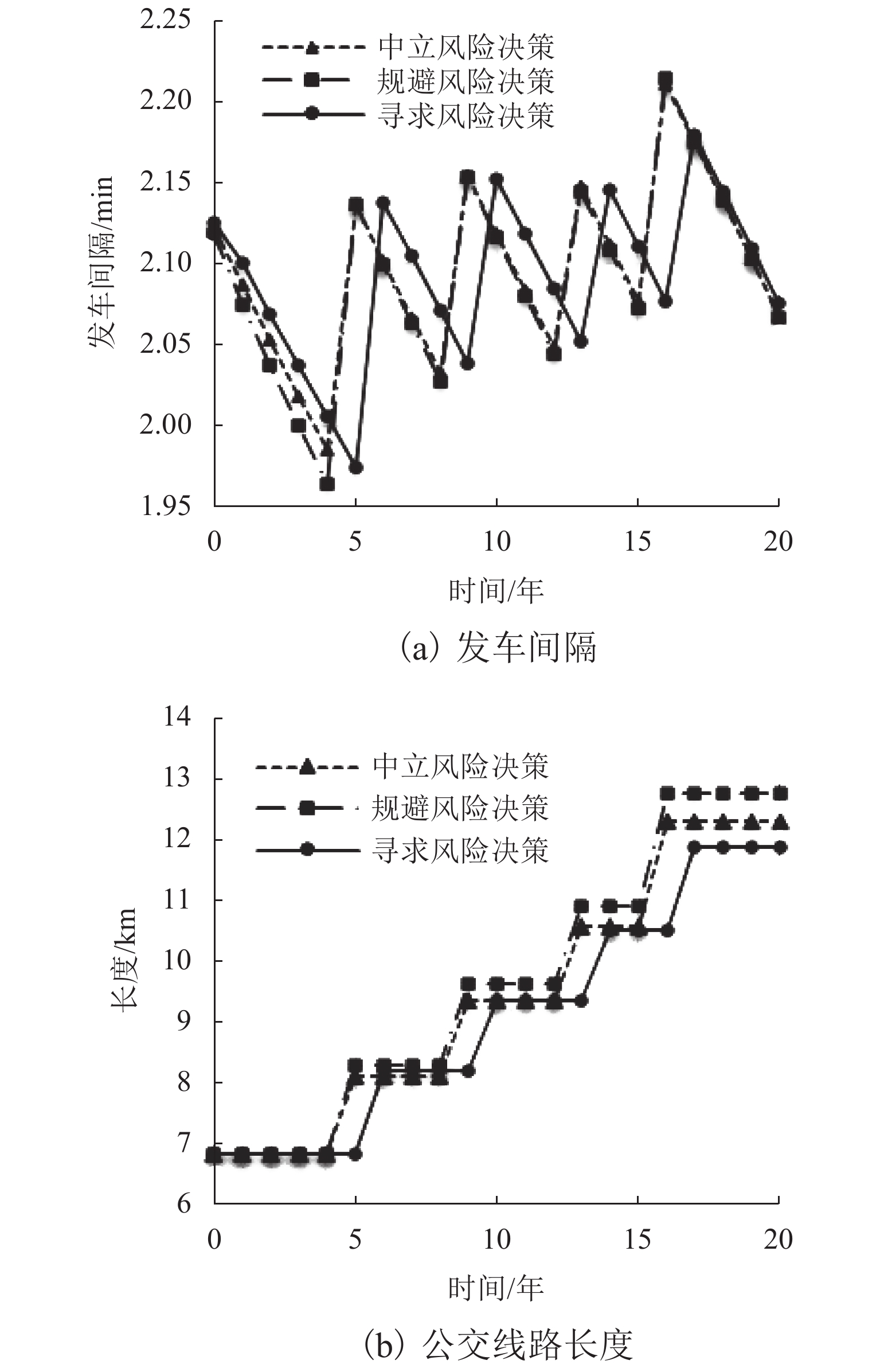
风险决策态度	线路长度/km	走廊长度/km	平均站点密度/ （站·km⁻¹）	平均发车间隔/min	期待用户通勤成本/ （h·（户·d）⁻¹）	期待运营商成本/ （h·（户·d）⁻¹）	期待系统成本/ （h·（户·d）⁻¹）	系统成本标准差/ （h·（户·d）⁻¹）
中立风险	10.97	（6.81, 14.93）	1.1011	2.2979	1.208	0.8504	2.0584	0.1334
规避风险	11.40	（6.81, 14.93）	1.0976	2.3131	1.1813	0.8827	2.064	0.1169
寻求风险	10.48	（6.81, 14.93）	1.1099	2.2766	1.2499	0.8144	2.0644	0.1546

下载: 导出CSV

表 4 公交线路多阶段设计结果

Table 4. Result of transit system with phased design

风险决策态度	线路长度/km		走廊长度/km	平均站点密度/ （站·km⁻¹）	平均发车间隔/min	阶段数/个	期待用户通勤成本/ （h· （户·d）⁻¹）	期待运营商成本/（h· （户·d）⁻¹）	期待系统成本/ （h·（户·d）⁻¹）	系统成本标准差/（h· （户·d）⁻¹）
风险决策态度	初始	最终	走廊长度/km	平均站点密度/ （站·km⁻¹）	平均发车间隔/min	阶段数/个	期待用户通勤成本/ （h· （户·d）⁻¹）	期待运营商成本/（h· （户·d）⁻¹）	期待系统成本/ （h·（户·d）⁻¹）	系统成本标准差/（h· （户·d）⁻¹）
中立风险	6.82	12.31	（6.81, 14.93）	1.2080	2.0977	5	1.1539	0.7398	1.8936	0.1095
规避风险	6.82	12.76	（6.81, 14.93）	1.2186	2.0930	5	1.1420	0.7580	1.9000	0.0947
寻求风险	6.82	11.88	（6.81, 14.93）	1.2209	2.0916	5	1.1856	0.7147	1.9003	0.1352

下载: 导出CSV

参考文献(27)

[1]	FUSCO G, ALESSANDRINI A, COLOMBARONI C, 等. A model for transit design with choice of electric charging system[J]. Procedia - Social and Behavioral Sciences, 2013, 87: 234–249. FUSCO G X,ALESSANDRINI A,COLOMBARONI C,et al. A model for transit design with choice of electric charging system[J]. Procedia-Social and Behavioral Sciences,2013,87: 234-249.
[2]	FAN W B, RAN Y. Planning skip-stop services with schedule coordination[J]. Transportation Research Part E: Logistics and Transportation Review, 2021, 145: 102119.1-102119.19. doi: 10.1016/j.tre.2020.102119
[3]	郭小乐. 高铁站接运公交线路设计与运营方案优化研究[D]. 北京: 北京交通大学, 2020.
[4]	LUO X L, FAN W B, JIANG Y S, et al. Optimal design of bus stop locations integrating continuum approximation and discrete models[J]. Journal of Advanced Transportation, 2020, 2020: 8872748.1-8872748.10.
[5]	王殿海,熊满初,章立辉,等. 基于舒适度的公交线网优化方法[J]. 西南交通大学学报,2017,52(4): 789-795. doi: 10.3969/j.issn.0258-2724.2017.04.018 WANG Dianhai, XIONG Manchu, ZHANG Lihui, et al. Optimization of public traffic network based on comfort improvement[J]. Journal of Southwest Jiaotong University, 2017, 52(4): 789-795. doi: 10.3969/j.issn.0258-2724.2017.04.018
[6]	梁东,李远富,樊敏. 基于区间数距离的铁路线路方案决策模型与方法[J]. 西南交通大学学报,2019,54(4): 823-830. doi: 10.3969/j.issn.0258-2724.20180847 LIANG Dong, LI Yuanfu, FAN Min. Decision making model and method based on distance measure between interval numbers in railway location[J]. Journal of Southwest Jiaotong University, 2019, 54(4): 823-830. doi: 10.3969/j.issn.0258-2724.20180847
[7]	MATISZIW T C, MURRAY A T, KIM C. Strategic route extension in transit networks[J]. European Journal of Operational Research, 2006, 171(2): 661-673. doi: 10.1016/j.ejor.2004.09.029
[8]	CHENG W C, SCHONFELD P. A method for optimizing the phased development of rail transit lines[J]. Urban Rail Transit, 2015, 1(4): 227-237. doi: 10.1007/s40864-015-0029-2
[9]	SUN Y S, SCHONFELD P, GUO Q W. Optimal extension of rail transit lines[J]. International Journal of Sustainable Transportation, 2018, 12(10): 753-769. doi: 10.1080/15568318.2018.1436730
[10]	XIA L, JIANG X G, FAN W B. Continuum approximation model for optimizing phased development of scalable transit corridors[C]//2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland: IEEE, 2019: 852-857.
[11]	HASSANNAYEBI E, ZEGORDI S H, AMIN-NASERI M R, 等. Train timetabling at rapid rail transit lines: A robust multi-objective stochastic programming approach[J]. Operational Research, 2017, 17(2): 435–477. HASSANNAYEBI E,ZEGORDI S H,AMIN-NASERI M R,et al. Train timetabling at rapid rail transit lines: a robust multi-objective stochastic programming approach[J]. Operational Research,2017,17(2): 435-477.
[12]	HASSANNAYEBI E, ZEGORDI S H, AMIN-NASERI M R, 等. Demand-oriented timetable design for urban rail transit under stochastic demand[J]. Journal of Industrial and Systems Engineering, 2016, 9(3): 28–56. HASSANNAYEBI E,ZEGORDI S H,AMIN-NASERI M,et al. Demand-oriented timetable design for urban rail transit under stochastic demand[J]. Journal of Industrial and Systems Engineering,2016,9(3): 28-56.
[13]	HØYEM H, ODECK J. Optimal public transit frequency under stochastic demand and fixed vehicle size: application in the Norwegian car ferry sector[J]. Research in Transportation Economics, 2020, 82: 100878.1-100878.14. doi: 10.1016/j.retrec.2020.100878
[14]	HUANG Z F, REN G, LIU H X. Optimizing bus frequencies under uncertain demand: case study of the transit network in a developing city[J]. Mathematical Problems in Engineering, 2013, 2013: 1-10.
[15]	AN K, LO H K. Robust transit network design with stochastic demand considering development density[J]. Transportation Research Part B: Methodological, 2015, 81: 737-754. doi: 10.1016/j.trb.2015.05.019
[16]	LI M, XU J, WEI L, 等. Modeling a risk-based dynamic bus schedule problem under no-notice evacuation incorporated with dynamics of disaster, supply, and demand conditions[J]. Journal of Advanced Transportation, 2019, 2019: 1–17. LI M H,XU J L,WEI L Y,et al. Modeling a risk-based dynamic bus schedule problem under no-notice evacuation incorporated with dynamics of disaster, supply, and demand conditions[J]. Journal of Advanced Transportation,2019,2019: 1-17.
[17]	HADAS Y, SHNAIDERMAN M. Public-transit frequency setting using minimum-cost approach with stochastic demand and travel time[J]. Transportation Research Part B: Methodological, 2012, 46(8): 1068-1084. doi: 10.1016/j.trb.2012.02.010
[18]	AMIRIPOUR S M M, CEDER A , MOHAYMANY A S. Designing large-scale bus network with seasonal variations of demand[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 322-338. doi: 10.1016/j.trc.2014.08.017
[19]	魏长钦,王伟智. 随机需求下定制公交站点及路径动态优化模型[J]. 福州大学学报(自然科学版),2020,48(1): 98-104. WEI Changqin, WANG Weizhi. Dynamic optimization model of customized bus stations and route under random demand[J]. Journal of Fuzhou University (Natural Science Edition), 2020, 48(1): 98-104.
[20]	YAN Y, MENG Q, WANG S, 等. Robust optimization model of schedule design for a fixed bus route[J]. Transportation Research Part C, 2012, 25: 113–121. YAN Y D,MENG Q,WANG S A,et al. Robust optimization model of schedule design for a fixed bus route[J]. Transportation Research Part C: Emerging Technologies,2012,25: 113-121.
[21]	MEDINA M, GIESEN R, MUÑOZ J C. Model for the optimal location of bus stops and its application to a public transport corridor in Santiago, Chile[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2352(1): 84-93. doi: 10.3141/2352-10
[22]	李欢. 基于连续近似法的公交线路优化及实例分析[D]. 成都: 西南交通大学, 2018.
[23]	CHOI T M, LI D, YAN H M. Mean–variance analysis for the newsvendor problem[J]. IEEE Transactions on Systems, Man, and Cybernetics−Part A: Systems and Humans, 2008, 38(5): 1169-1180. doi: 10.1109/TSMCA.2008.2001057
[24]	FAN W B, MEI Y, GU W H. Optimal design of intersecting bimodal transit networks in a grid city[J]. Transportation Research Part B: Methodological, 2018, 111: 203-226. doi: 10.1016/j.trb.2018.03.007
[25]	GU W H, AMINI Z, CASSIDY M J. Exploring alternative service schemes for busy transit corridors[J]. Transportation Research Part B: Methodological, 2016, 93: 126-145. doi: 10.1016/j.trb.2016.07.010
[26]	DAGANZO C F. Structure of competitive transit networks[J]. Transportation Research Part B: Methodological, 2010, 44(4): 434-446. doi: 10.1016/j.trb.2009.11.001
[27]	LI Z C, LAM W H K, WONG S C, 等. Modeling the effects of integrated rail and property development on the design of rail line services in a linear monocentric city[J]. Transportation Research Part B: Methodological, 2012, 46(6): 710–728. LI Z C,LAM W H K,WONG S C,et al. Modeling the effects of integrated rail and property development on the design of rail line services in a linear monocentric city[J]. Transportation Research Part B: Methodological,2012,46(6): 710-728.