Influence of Bridge Flexibility on Horizontal Curve Passing of Medium-Low-Speed Maglev Vehicles
-
摘要:
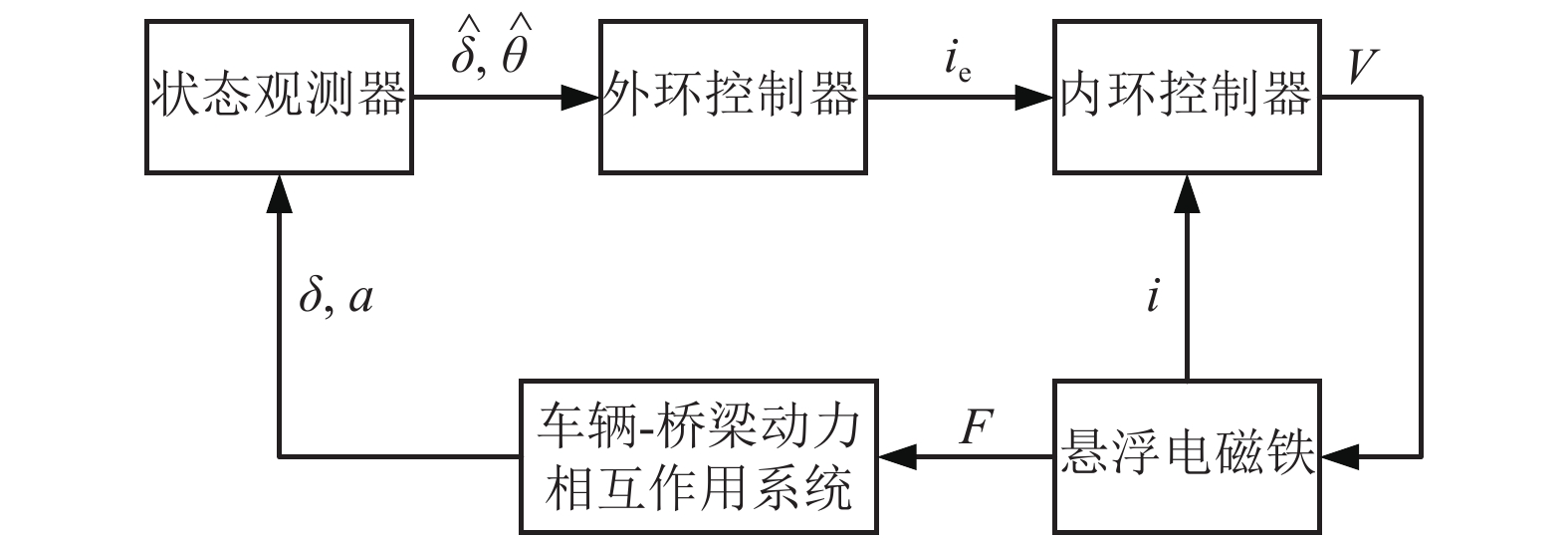
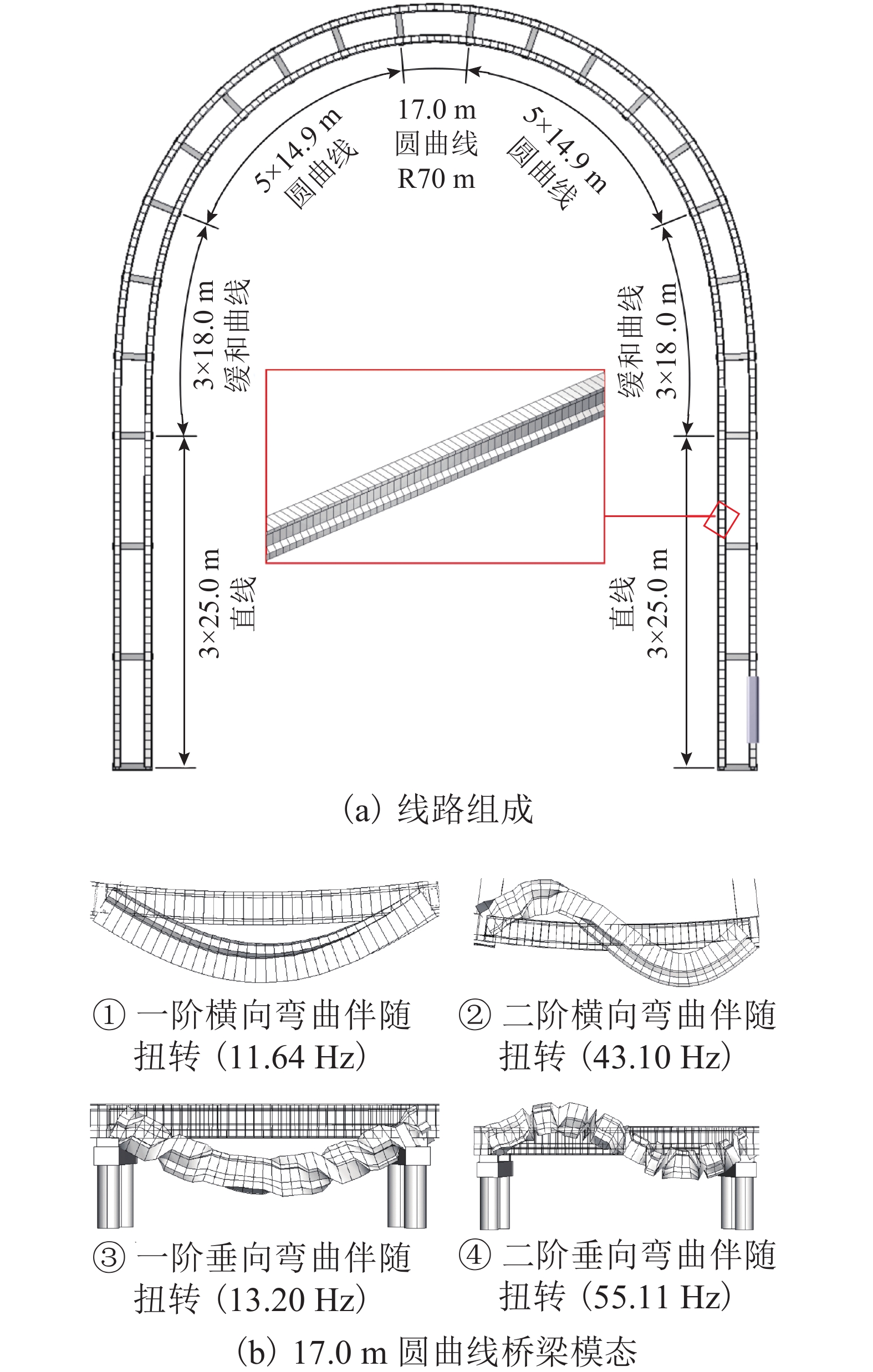
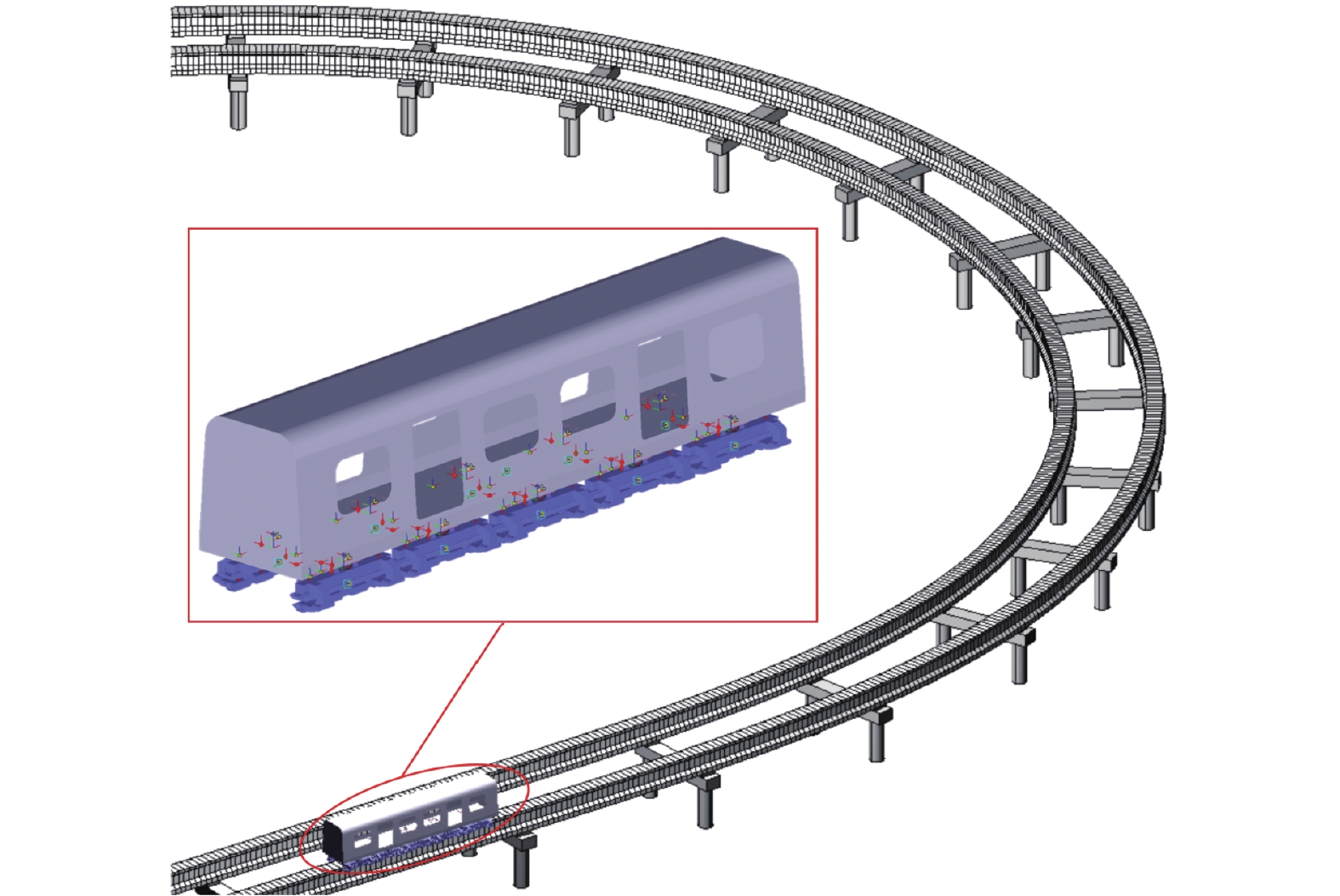
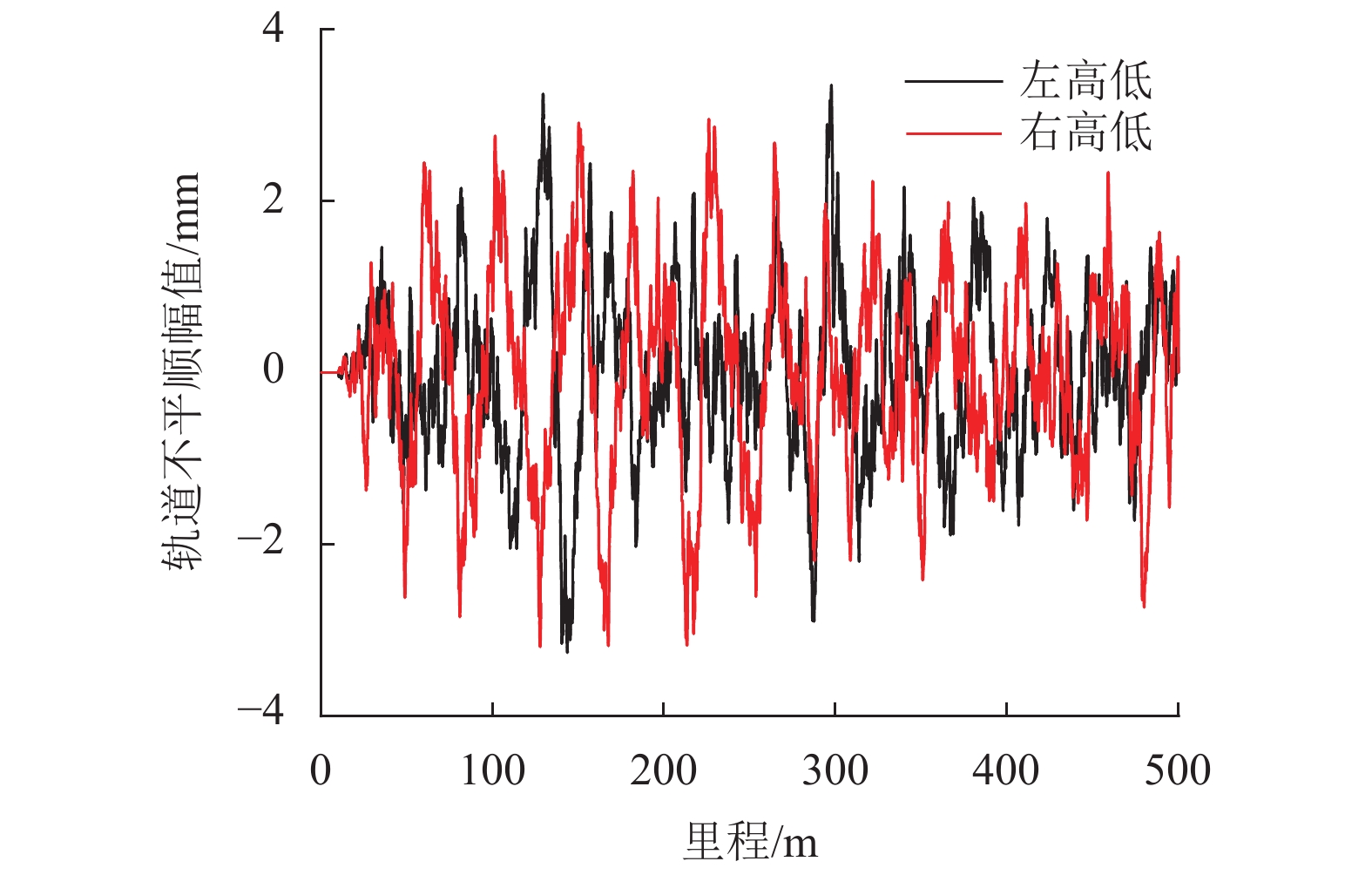
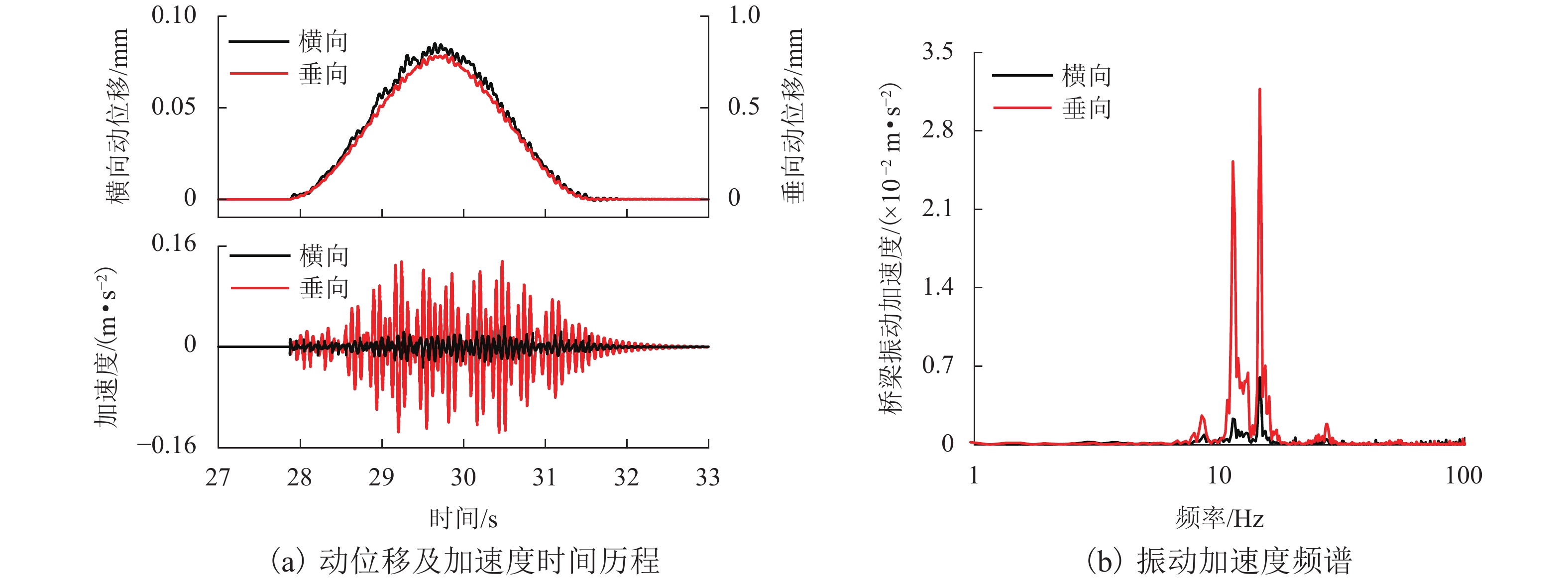
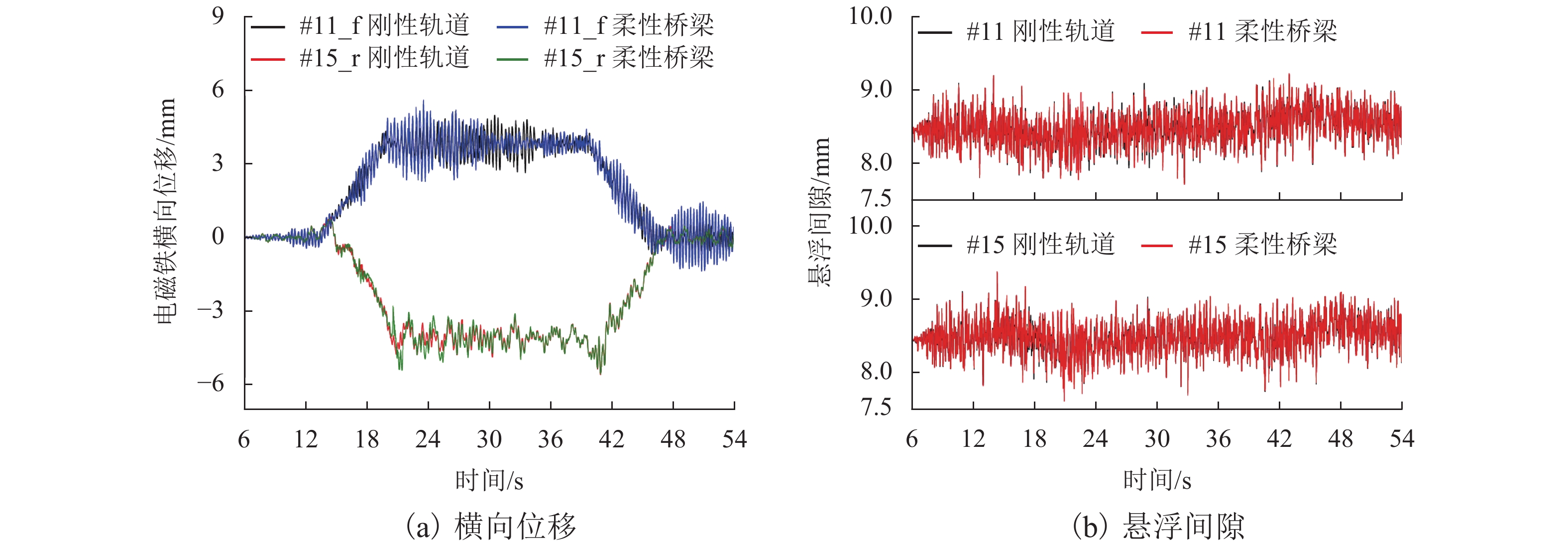
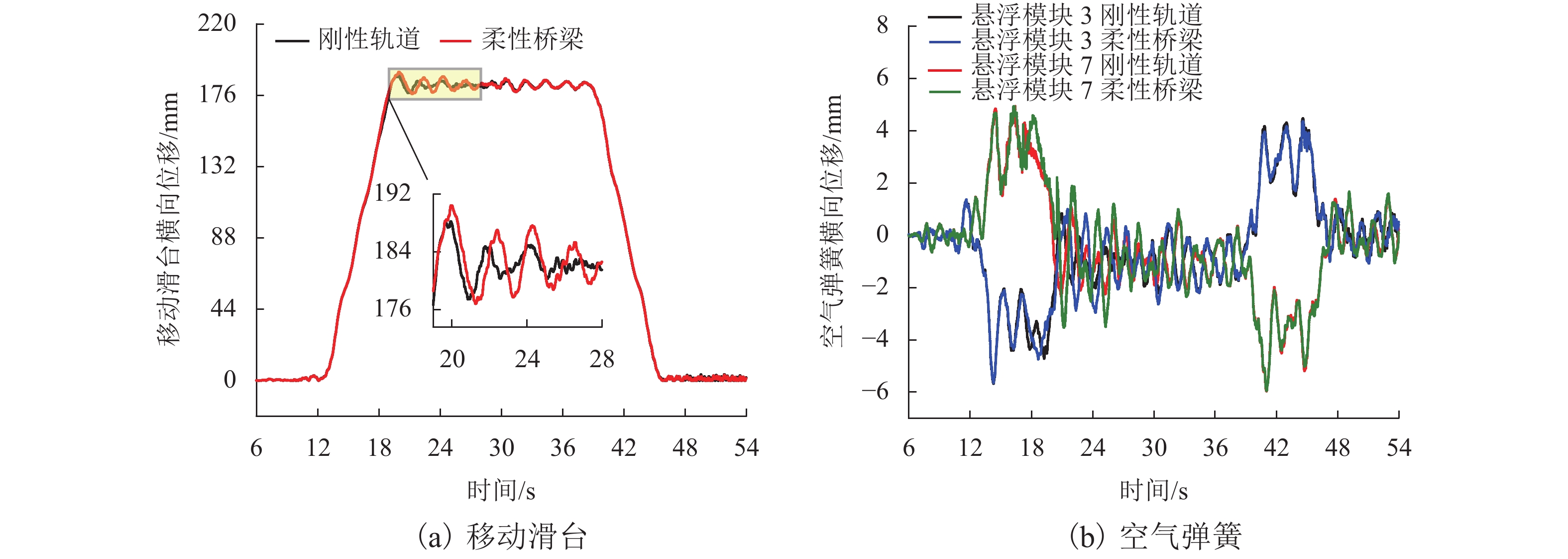
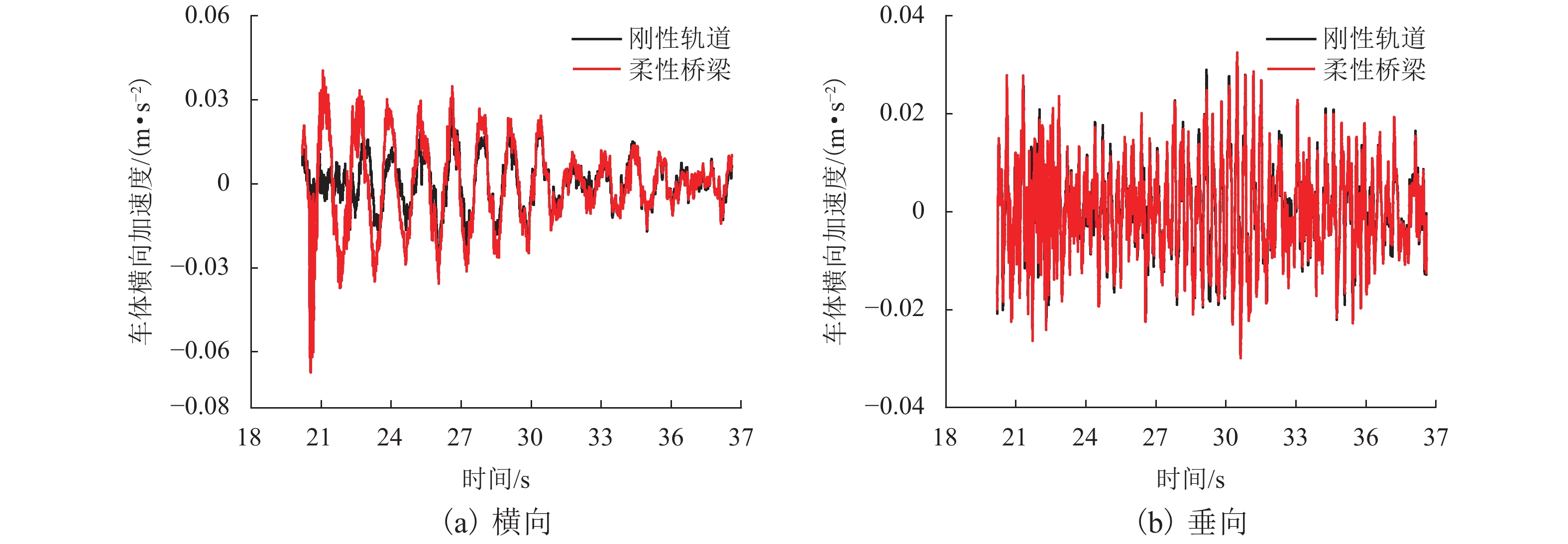
为研究桥梁柔性对中低速磁浮车辆在曲线半径为70.0 m的平曲线上运行时的动态响应影响，对通过柔性桥梁和刚性轨道时的车辆动态响应开展了对比分析. 首先，建立了122个自由度的车辆空间动力学模型，模型中考虑了具有主动悬浮与被动导向特性的二维磁轨关系；其次，利用三维铁木辛柯梁参数化建模方法，建立了由柔性桥梁组成的平曲线有限元模型；最后，通过悬浮力的联系形成了车辆-曲线桥梁系统刚柔耦合动力学模型. 研究结果表明：17.0 m跨径的圆曲线桥梁的自振特性和动位移响应满足相关标准要求；与车辆通过刚性轨道相比，柔性桥梁作用下的车辆系统动态响应更为剧烈，这种差异在车辆系统的横向动态响应上体现明显，而悬浮间隙和车体垂向加速度的响应差异较小，考虑刚性轨道时将高估车辆的曲线通过能力；柔性桥梁和刚性轨道两种模型计算得到的电磁铁最大横向位移不超过6.0 mm，悬浮间隙可在额定值的 ± 4.0 mm内波动，表明在开展对比计算的工况下车辆具有良好的曲线通过性能.
Abstract:In order to study the effect of bridge flexibility on the dynamic response of medium-low-speed maglev vehicles running on a horizontal curve with a curve radius of 70.0 m, a comparative analysis of the vehicle dynamic response through a flexible bridge and a rigid track is carried out. Firstly, a spatial dynamics vehicle model with 122 degrees of freedom is established, and the two-dimensional magnet/rail relationship with active levitation and passive guidance characteristics is considered in the model. Secondly, a horizontal curve finite element model consisting of flexible bridges is developed by using a parametric modeling method of three-dimensional Timosheko beam. Finally, the rigid-flexible coupled dynamic model of the vehicle-curve bridge system is constructed with the connection of levitation forces. The results show that, the self-oscillation characteristics and dynamic displacement response of the 17.0 m span circular-curve bridge meet the requirements of relevant standards. Compared with the case of a vehicle passing the rigid track, the dynamic response of the vehicle system under the influence of the flexible bridge is more drastic, and evident in the lateral dynamic response of the vehicle system, while the difference in the response of the levitation gap and the vertical acceleration of the car body is smaller, and the curve passing ability of the vehicle will be overestimated in the case of the rigid track. The maximum lateral displacement of the electromagnet calculated with the flexible bridge and rigid track models does not exceed 6.0 mm, and the levitation gap fluctuates within ±4.0 mm of the rated value, indicating that the vehicle has a good curve passing performance in the comparison analysis.
-
Key words:
- medium-low-speed maglev vehicles /
- curve passing /
- bridge /
- levitation control /
- dynamic response
-
为缓解由于城市化进程的提速带来的日益严重的交通拥堵问题，我国聚焦于多样化的城市轨道交通发展，并取得了显著成效[1]. 其中，中低速磁浮交通具有运行安全性高、选线灵活、对环境友好等优点，近年来在国内的发展获得了广泛关注[2]，广东清远和湖南凤凰的中低速磁浮线路也正在如火如荼地建设和试运行中. 然而，中低速磁浮车辆的导向功能主要依靠悬浮力的横向分力被动提供，这给车辆通过平曲线实现稳定悬浮、导向和保障良好的动力学性能带来了挑战.
中低速磁浮车辆的电磁力具有固有的开环不稳定特性，车辆与桥梁是一个典型的强耦合非线性系统[3-5]，悬浮控制与车辆-桥梁耦合动力学研究获得了研究人员的大量关注. 在悬浮控制方面，众多学者基于自适应控制、滑模控制、模糊控制、卡尔曼滤波器、非线性理论等方法研究了车辆的悬浮稳定性及车辆-桥梁耦合系统的分岔特征[6-10]. 此外，轮轨交通中车辆-轨道耦合动力学理论的日臻完善[11]，也促进了磁浮交通在该领域的发展和应用. 基于车辆-桥梁系统耦合振动模型，车速、轨道不平顺、轨道结构、桥梁高度、挠跨比等因素对耦合系统动态性能的影响研究取得了积极的进展[12-17]. 而在曲线通过研究方面，Yim等[18]利用车辆多体动力学模型评估了曲线通过性能，并研究了使横向偏移变化最小的悬浮架设计方向. 赵春发等[19-20]研究了低速磁浮车辆以不同速度通过不同半径曲线时的动态响应，并分析了被动、主动导向方式对悬浮模块横向动态特性的影响. Cui等[21]推导了低速磁浮车辆在直线上和曲线上时的最大承载能力公式，分析了曲线半径、横坡角、车辆重心高度等因素对车辆承载能力的影响. 曾佑文等[22]基于导向力平衡分析了三悬浮架磁浮车辆通过曲线时的运动学规律.
尽管取得了上述进展，但桥梁柔性对中低速磁浮车辆通过平曲线的影响还鲜有报道. 当前，针对车辆通过平曲线的研究通常不考虑桥梁结构的柔性变形，主要基于刚性轨道模型研究车辆系统的曲线通过能力. 鉴于此，本文建立考虑桥梁柔性影响的车辆-桥梁系统耦合动力学模型，模型中采用二维磁轨关系，将车辆视为多刚体系统，研究车辆通过小半径平曲线时桥梁的柔性变形对车辆系统动态响应的影响.
1. 耦合系统动力学模型
1.1 车辆模型
以作者所在团队提出的应用（悬挂）中置式悬浮架技术方案的中低速磁浮车辆为例（该悬浮架的结构组成见图1）[2]，考虑车体、悬浮模块、防侧滚梁、吊杆、移动滑台、固定滑台、牵引杆等部件，建立具有如下微分代数方程形式的车辆系统动力学模型[23]：
[M(q)ΦT(q,t)Φ(q,t)0][¨qλ]=[Q(q,˙q,t)+S(q,˙q)−η], (1) 式中：q为各刚体的广义坐标；M为各刚体的质量矩阵；S为广义惯量；Q为作用在各刚体上的广义力矩阵；λ为拉格朗日乘子；Ф为约束雅克比矩阵；η为约束条件的加速度矢量；t为时间.
车辆空间动力学模型的拓扑关系如图2所示，图中各刚体的自由度说明见表1，车辆系统共有122个自由度. 表2为车辆的主要计算参数，车辆总重为30 t.
表 1 车辆系统自由度Table 1. Degrees of freedom of vehicle system部件 纵向 横向 垂向 侧滚 点头 摇头 备注 悬浮模块 xlj ylj zlj αlj βlj γlj j = 1~10 防侧滚梁 γaj j = 1~10 吊杆 αhj βhj j = 1~10 车体 xc yc zc αc βc γc 移动滑台 ysj j = 1~6 牵引杆 βtj γtj j = 1~10 表 2 主要计算参数Table 2. Main calculation parameters名称 数值 车体质量/kg 17 010 车体绕 x/y/z 轴的转动
惯量/（kg•m2）19 972/349411/351664 悬浮模块质量/kg 1225 悬浮模块绕 x/y/z 轴的转动
惯量/（kg•m2）72/914/908 防侧滚梁质量/kg 27.5 防侧滚梁绕 x/y/z 轴的转动
惯量/（kg•m2）2.28/0.12/2.23 悬浮模块左右中心距/mm 1900 空气弹簧水平刚度/（N•m−1） 1.45 × 105 空气弹簧垂向刚度/（N•m−1） 1.6 × 105 1.2 悬浮控制模型
根据中低速磁浮交通系统的悬浮原理，悬浮电磁铁位于轨道下方，可在一定范围内进行垂向和横向运动，悬浮力F为线圈电流i和悬浮间隙δ的函数[10]，如式（2）.
F=μ0AN24(iδ)2, (2) 式中：μ0为真空磁导率；A为磁极正对面积；N为线圈匝数.
根据基尔霍夫定律，线圈电流i与控制电压V的关系可写为
V=2iR+μ0AN2δ˙i−μ0AN2iδ2˙δ, (3) 式中：R为线圈电阻.
在实际的工程应用中，传感器可同时获得悬浮间隙和加速度信号，但缺少速度信号，一般还需要引入状态观测器来重构速度信号[15]：
˙ˆδ=ˆθ+2ξ0ω0(δ−ˆδ), (4) ˙ˆθ=a+ω20(δ−ˆδ), (5) 式中：
$ a$ 为传感器测得的垂向加速度；$ \xi_{0} $ 和$ \omega_{0} $ 分别为观测器的阻尼比和特征频率；$ \hat{\delta} $ 和$ \hat{\theta} $ 分别为观测的间隙和速度.通过对悬浮间隙和垂向速度进行反馈得到目标悬浮电流ie，并进一步采用比例反馈控制确定控制电压V，如式（6）、（7）.
ie=i0+kp(ˆδ−δ0)+ki∫t0(δ−δ0)dτ+kdˆθ, (6) V=ke(ie−i)+2iR, (7) 式中：kp、ki、kd、ke、i0、δ0分别为间隙反馈系数、积分系数、速度反馈系数、电流反馈系数、额定悬浮电流、额定悬浮间隙. 相关参数的取值可参考文献[24].
中低速磁浮车辆的运行速度相对较低，没有像上海高速磁浮车辆那样配置专门的导向电磁铁，而是采用了U型电磁铁的设计方案，该方案可使车辆具有被动导向能力. 当悬浮电磁铁与F轨存在横向错位时，悬浮力在垂向和横向方向上的分力Fz、Fy可分别表示为[25]
Fz=F[1+2δπwm−|y|wm+2yπwmtan−1(δy)], (8) Fy=F2δπwm tan−1(yδ), (9) 式中：wm和y分别为磁极宽度和电磁铁横向偏移.
由式（2） ~ （9）可搭建出系统的控制逻辑框图，如图3所示.
1.3 桥梁模型
采用文献[26]给出的三维铁木辛柯梁参数化建立方法，搭建包含直线、缓和曲线和圆曲线的柔性桥梁（均为简支梁）有限元模型，桥梁的弹性模量和泊松比分别取36.5 GPa和0.2，其中圆曲线半径为70.0 m，最大横坡角为6°，如图4（a）所示. 跨径为17.0 m的曲线桥梁前二阶横向和垂向弯曲模态如图4（b）所示，13.20 Hz显然大于90/L （L为跨径），满足《磁浮铁路技术标准（试行）》（TB 10630—2019）[27]对桥梁垂向一阶固有频率的要求.
图 4 柔性桥梁组成及圆曲线桥梁模态Figure 4. Composition of flexible bridge and modal of circle curved bridge1.4 模型耦合及求解
通过车辆-桥梁耦合系统之间力的平衡及变形协调关系，耦合系统动力学方程可表示为
{Mv..Xv+Cv.Xv+KvXv=Fbv,Mb..Xb+Cb.Xb+KbXb=Fvb, (10) 式中：下标v、b分别表示车辆和桥梁；C、K分别为阻尼、刚度矩阵；
${\ddot{\boldsymbol{X}}{\text{、}} \dot{\boldsymbol{X}}}$ 、 X 分别为加速度、速度、位移向量；Fbv、Fvb分别为桥梁作用于车辆和车辆作用于桥梁的载荷向量.建立的车辆-曲线桥梁耦合系统可视化动力学模型如图5所示，并在UM （universal mechanism）中采用基于二阶变步长隐式求解器进行数值计算，该方法对刚柔耦合模型中包含刚性微分代数方程的求解十分有效[28].
图 5 可视化的车辆-曲线桥梁耦合系统动力学模型Figure 5. Visualized dynamic model of vehicle-curve bridge coupled system2. 仿真计算结果及讨论
2.1 工况设置
为满足车辆通过平曲线时的安全性和平稳性要求，《磁浮铁路技术标准（试行）》（TB 10630—2019）[27]还指出：车辆通过曲线时的未平衡离心加速度不超过0.59 m/s2. 综合考虑横坡角和未平衡离心加速度的影响，车辆运行速度取30 km/h，对车辆通过刚性轨道和柔性桥梁2种模型进行对比计算，并采用文献[16]提到的轨道不平顺谱（见式（11））生成本文仿真计算所需的轨道不平顺样本，如图6所示，高低不平顺幅值不超过3.5 mm.
S(Ω)=ArΩn, (11) 式中：
$\varOmega$ 、$ A_{\mathrm{r}} $ 、n 分别为空间波数、表面粗糙度系数、频率特征参数，本文中分别取为3000 rad/m、8 × 10−7 m、2. 波长范围设定为0.5~50.0 m.2.2 结果与讨论
为探究圆曲线桥梁的动态响应特性，图7给出了车辆以30 km/h的速度运行时，17.0 m跨径圆曲线桥梁跨中的动位移、加速度响应时间历程以及加速度频谱计算结果.
从图7中可知：桥梁跨中在垂向上的动位移和加速度响应幅值均比横向的更高（垂向动位移和加速度幅值分别不超过0.8 mm、0.16 m/s2），这主要是因为车辆通过圆曲线时在垂向方向上分解的载荷更大；桥梁跨中的横向、垂向加速度优势频率集中在11.00~15.00 Hz区间，且两个方向的优势频率相同，这是因为电磁铁和F轨之间的悬浮力和导向力具有强耦合关系. 由前述分析，17.0 m跨径圆曲线桥梁的动位移满足2.1节提到的标准和《中低速磁浮交通设计规范》（CJJ/T 262—2017 ）[29]中的相关要求，该柔性桥梁模型可以进一步用于与车辆通过刚性轨道（不考虑线路上弹性体的参振作用）模型的对比分析.
图8所示为车辆在刚性轨道和柔性桥梁上运行时电磁铁的横向位移和悬浮间隙响应时程曲线. 图中：#11_f 为控制点#11前端线圈对应位置（即悬浮模块5第3个线圈对应位置）；#15_r 为控制点#15后端线圈对应位置（即悬浮模块7第4个线圈对应位置）.
计算结果表明，该工况下这两处位置的横向偏移最大，为避免赘述，其余观测点的响应不再给出. 从图8（a）可以看出：车辆在通过缓和曲线和圆曲线的过程中，第3个线圈向曲线内侧偏移，第4个线圈则与之相反，且这两个位置偏移的最大幅值基本相等；观测点的横向位移最大值不超过6.0 mm，电磁铁与F轨不会发生机械碰撞；车辆处在缓和曲线及圆曲线上时，柔性桥梁下的电磁铁横向位移波动比刚性轨道下的计算结果更为剧烈，且悬浮模块 5比悬浮模块 7存在更明显的波动变化差异，这一方面与悬浮模块 5采用移动滑台（悬浮模块 7为固定滑台）多出的横向移动自由度有关，移动滑台处的空气弹簧在横向方向上的阻尼效果相对较弱；另一方面与被动导向方案下控制算法无法提供横向阻尼效果有关. 从图8（b）可以看出：柔性桥梁比刚性轨道作用下的悬浮间隙响应略大，但两者相差较小，这与悬浮控制的主动调节影响有关；悬浮间隙波动范围在 ± 4.0 mm以内，表明车辆通过刚性轨道和柔性桥梁的曲线线路时具有良好的悬浮稳定性.
图9所示为悬浮模块 1上方的移动滑台相对车体和悬浮模块 3、7上的空气弹簧横向位移响应时间历程曲线.
计算结果表明移动滑台相对车体向曲线内侧滑动，柔性桥梁和刚性轨道作用下的最大滑动量分别为190.4、188.2 mm；空气弹簧的横向位移响应在−6.0~5.0 mm之间变化，且车辆在缓和曲线上的空气弹簧横向位移比在圆曲线上更大，这是因为车辆以30.0 km/h的速度通过圆曲线时，车辆的未平衡离心加速度很小. 相比于在刚性轨道上运行，柔性桥梁作用下移动滑台和空气弹簧的横向位移波动更大，且这种差异主要体现在缓和曲线和圆曲线的交界处与前半段圆曲线上.
图10所示为车辆通过圆曲线阶段时的车体地板中心振动加速度时间历程曲线. 整体上看，车辆通过刚性轨道和柔性桥梁的圆曲线时，车体的横向、垂向振动加速度响应幅值均较小，表明车辆在圆曲线上运行时具有较好的平稳性. 此外，从图10中也可以观察出一些区别，柔性桥梁模型下计算得到的车体横向加速度响应波动比刚性轨道模型对应的结果更为剧烈，而在垂向方向上的振动加速度差异并不明显（整体上看，仍然是考虑了柔性桥梁时略大）.
进一步地，综合图8 ~ 10的结果可知：车辆通过由柔性桥梁组成的平曲线线路时，电磁铁、移动滑台和空气弹簧等的横向位移均相比刚性轨道模型对应的结果有所加剧，相对而言，悬浮间隙和车体垂向加速度的响应波动的差异较小. 造成这些结果差异的原因主要与磁轨关系和悬浮控制特性有关. 一方面，桥梁在横向和垂向两个方向上的柔性变形将使轨道不平顺相对更加恶劣，而中低速磁浮车辆的导向能力主要依靠电磁铁相对F轨的自动对中效应被动提供，因此尽管桥梁的横向动位移比垂向动位移小，但电磁铁、移动滑台和空气弹簧的横向位移响应在柔性桥梁影响下相比刚性轨道时更大，这也意味着采用刚性轨道模型将高估车辆的曲线通过性能. 另一方面，悬浮控制系统在垂向方向上有主动调节作用，对桥梁的小变形和正常的轨道不平顺具有较好的适应性，故在两种计算模型下车辆系统的垂向响应差异相对较小.
3. 结 论
1） 车辆以30 km/h的速度通过圆曲线半径为70.0 m的平曲线时，17.0 m跨径圆曲线桥梁的振动加速度优势频率集中在11.00~15.00 Hz，其自振频率和跨中动位移响应满足相关标准要求. 电磁铁相对F轨的横向位移幅值小于6.0 mm，车辆具备足够的横向安全间隙通过该曲线线路.
2） 相比于刚性轨道线路模型，考虑柔性桥梁作用时，电磁铁、移动滑台、空气弹簧的横向位移以及车体的横向加速度响应更加剧烈，而由于悬浮控制器的主动调节影响，悬浮间隙和车体垂向加速度波动仅略有增大，两种模型所得结果差异较小.
3） 在评估中低速磁浮车辆的平曲线通过能力时，建议在未来的数值计算中考虑柔性桥梁对车辆系统横向动态响应的影响，从而避免高估车辆的曲线通过能力.
致谢：感谢牵引动力国家重点实验室自主研究课题（2020TPL-T01，2020TPL-T04）、河南省轨道交通智能安全工程技术研究中心开放基金（2019KFJJ001）的资助.
-
图 4 柔性桥梁组成及圆曲线桥梁模态
Figure 4. Composition of flexible bridge and modal of circle curved bridge
图 5 可视化的车辆-曲线桥梁耦合系统动力学模型
Figure 5. Visualized dynamic model of vehicle-curve bridge coupled system
表 1 车辆系统自由度
Table 1. Degrees of freedom of vehicle system
部件 纵向 横向 垂向 侧滚 点头 摇头 备注 悬浮模块 xlj ylj zlj αlj βlj γlj j = 1~10 防侧滚梁 γaj j = 1~10 吊杆 αhj βhj j = 1~10 车体 xc yc zc αc βc γc 移动滑台 ysj j = 1~6 牵引杆 βtj γtj j = 1~10 
下载: 导出CSV
表 2 主要计算参数
Table 2. Main calculation parameters
名称 数值 车体质量/kg 17 010 车体绕 x/y/z 轴的转动
惯量/（kg•m2）19 972/349411/351664 悬浮模块质量/kg 1225 悬浮模块绕 x/y/z 轴的转动
惯量/（kg•m2）72/914/908 防侧滚梁质量/kg 27.5 防侧滚梁绕 x/y/z 轴的转动
惯量/（kg•m2）2.28/0.12/2.23 悬浮模块左右中心距/mm 1900 空气弹簧水平刚度/（N•m−1） 1.45 × 105 空气弹簧垂向刚度/（N•m−1） 1.6 × 105
下载: 导出CSV
-
[1] 翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001ZHAI Wanming, ZHAO Chunfa. Frontiers and challenges of sciences and technologies in modern railway engineering[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 209-226. doi: 10.3969/j.issn.0258-2724.2016.02.001 [2] 马卫华,罗世辉,张敏,等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报,2021,21(1): 199-216.MA Weihua, LUO Shihui, ZHANG Min, et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 199-216. [3] 翟婉明,赵春发. 磁浮车辆/轨道系统动力学(Ⅰ): 磁/轨相互作用及稳定性[J]. 机械工程学报,2005,41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001ZHAI Wanming, ZHAO Chunfa. Dynamics of maglev vehicle/guideway systems (Ⅰ): magnet/rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001 [4] DING J F, YANG X, LONG Z Q. Structure and control design of levitation electromagnet for electromagnetic suspension medium-speed maglev train[J]. Journal of Vibration and Control, 2019, 25(6): 1179-1193. doi: 10.1177/1077546318813405 [5] 龙志强,洪华杰,周晓兵. 磁浮列车的非线性控制问题研究[J]. 控制理论与应用,2003,20(3): 399-402. doi: 10.3969/j.issn.1000-8152.2003.03.016LONG Zhiqiang, HONG Huajie, ZHOU Xiaobing. Research of nonlinear control for maglev train[J]. Control Theory & Applications, 2003, 20(3): 399-402. doi: 10.3969/j.issn.1000-8152.2003.03.016 [6] 周丹峰,李杰,余佩倡,等. 磁浮交通轨排耦合自激振动分析及自适应控制方法[J]. 自动化学报,2019,45(12): 2328-2343.ZHOU Danfeng, LI Jie, YU Peichang, et al. Analysis and adaptive control of the track induced self-excited vibration for the maglev transport[J]. Acta Automatica Sinica, 2019, 45(12): 2328-2343. [7] KONG E, SONG J S, KANG B B, et al. Dynamic response and robust control of coupled maglev vehicle and guideway system[J]. Journal of Sound and Vibration, 2011, 330(25): 6237-6253. doi: 10.1016/j.jsv.2011.05.031 [8] SUN Y G, XU J Q, CHEN C, et al. Fuzzy H∞ robust control for magnetic levitation system of maglev vehicles based on T-S fuzzy model: design and experiments[J]. Journal of Intelligent & Fuzzy Systems, 2019, 36(2): 911-922. [9] WANG H, ZHONG X B, SHEN G. Analysis and experimental study on the MAGLEV vehicle-guideway interaction based on the full-state feedback theory[J]. Journal of Vibration and Control, 2015, 21(2): 408-416. doi: 10.1177/1077546313488431 [10] CHEN X H, MA W H, LUO S H. Study on stability and bifurcation of electromagnet-track beam coupling system for EMS maglev vehicle[J]. Nonlinear Dynamics, 2020, 101(4): 2181-2193. doi: 10.1007/s11071-020-05917-8 [11] ZHAI W M, HAN Z L, CHEN Z W, et al. Train-track-bridge dynamic interaction: a state-of-the-art review[J]. Vehicle System Dynamics, 2019, 57(7): 984-1027. doi: 10.1080/00423114.2019.1605085 [12] KIM K J, HAN J B, HAN H S, et al. Coupled vibration analysis of maglev vehicle-guideway while standing still or moving at low speeds[J]. Vehicle System Dynamics, 2015, 53(4): 587-601. doi: 10.1080/00423114.2015.1013039 [13] HAN J B, HAN H S, KIM S S, et al. Design and validation of a slender guideway for maglev vehicle by simulation and experiment[J]. Vehicle System Dynamics, 2016, 54(3): 370-385. doi: 10.1080/00423114.2015.1137957 [14] LEE J S, KWON S D, KIM M Y, et al. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guideway bridges[J]. Journal of Sound and Vibration, 2009, 328(3): 301-317. doi: 10.1016/j.jsv.2009.08.010 [15] WANG D X, LI X Z, LIANG L, et al. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system[J]. Advances in Structural Engineering, 2019, 22(14): 2937-2950. doi: 10.1177/1369433219854550 [16] 王党雄,李小珍,梁林. 中低速磁浮列车-桥梁系统竖向耦合振动理论分析与试验验证[J]. 土木工程学报,2019,52(8): 81-90.WANG Dangxiong, LI Xiaozhen, LIANG Lin. Theoretical analysis and experimental verification of the vertical coupling vibration of low-to-medium speed maglev train-bridge system[J]. China Civil Engineering Journal, 2019, 52(8): 81-90. [17] WANG D X, LI X Z, WANG Y W, et al. Dynamic interaction of the low-to-medium speed maglev train and bridges with different deflection ratios: experimental and numerical analyses[J]. Advances in Structural Engineering, 2020, 23(11): 2399-2413. doi: 10.1177/1369433220913367 [18] YIM B H, HAN H S, LEE J K, et al. Curving performance simulation of an EMS-type maglev vehicle[J]. Vehicle System Dynamics, 2009, 47(10): 1287-1304. doi: 10.1080/00423110802632071 [19] 赵春发,翟婉明,王其昌. 低速磁浮车辆曲线通过动态响应仿真分析[J]. 中国铁道科学,2005,26(3): 94-98. doi: 10.3321/j.issn:1001-4632.2005.03.020ZHAO Chunfa, ZHAI Wanming, WANG Qichang. Simulation analysis of the dynamic response of low-speed maglev vehicle curve negotiation[J]. China Railway Science, 2005, 26(3): 94-98. doi: 10.3321/j.issn:1001-4632.2005.03.020 [20] 赵春发,翟婉明. 低速磁浮车辆导向方式及其横向动态特性[J]. 中国铁道科学,2005,26(6): 28-32. doi: 10.3321/j.issn:1001-4632.2005.06.006ZHAO Chunfa, ZHAI Wanming. Guidance mode and dynamic lateral characteristics of low-speed maglev vehicle[J]. China Railway Science, 2005, 26(6): 28-32. doi: 10.3321/j.issn:1001-4632.2005.06.006 [21] CUI P, LI J, LIU D S. Carrying capacity for the electromagnetic suspension low-speed maglev train on the horizontal curve[J]. Science China Technological Sciences, 2010, 53(4): 1082-1087. doi: 10.1007/s11431-009-0394-8 [22] 曾佑文,王少华. 三转向架磁悬浮车几何曲线通过分析[J]. 西南交通大学学报,2003,38(3): 282-285. doi: 10.3969/j.issn.0258-2724.2003.03.009ZENG Youwen, WANG Shaohua. Research on geometrical curve negotiating of three-truck maglev vehicle[J]. Journal of Southwest Jiaotong University, 2003, 38(3): 282-285. doi: 10.3969/j.issn.0258-2724.2003.03.009 [23] POGORELO D. Differential-algebraic equations in multibody system modeling[J]. Numerical Algorithms, 1998, 19(1): 183-194. [24] CHEN X H, MA W H, LUO S H, et al. A vehicle–track beam matching index in EMS maglev transportation system[J]. Archive of Applied Mechanics, 2020, 90(4): 773-787. doi: 10.1007/s00419-019-01638-6 [25] BRZEZINA W, LANGERHOLC J. Lift and side forces on rectangular pole pieces in two dimensions[J]. Journal of Applied Physics, 1974, 45(4): 1869-1872. doi: 10.1063/1.1663505 [26] 德米特里 · 波戈列洛夫,雷强,根纳季 · 米克希夫,等. 基于UM的磁浮列车-轨道梁耦合振动仿真程序开发[J]. 计算机辅助工程,2019,28(1): 28-35.POGORELOV Dmitry, LEI Qiang, MIKHEEV Gennady, et al. Development of dynamics simulation program for coupling vibration of maglev train-track beam based on UM[J]. Computer Aided Engineering, 2019, 28(1): 28-35. [27] 中国铁路设计集团有限公司, 中铁第四勘察设计院集团有限公司, 中车同月研究院有限公司. 磁浮铁路技术标准（试行）: TB 10630—2019[S]. 北京: 中国铁道出版社有限公司, 2019. [28] PARK K C. An improved stiffly stable method for direct integration of nonlinear structural dynamic equations[J]. Journal of Applied Mechanics, 1975, 42(2): 464-470. doi: 10.1115/1.3423600 [29] 中华人民共和国住房和城乡建设部. 中低速磁浮交通设计规范: CJJ/T 262—2017[S]. 北京: 中国建筑工业出版社, 2017. 期刊类型引用(1)
1. 张一敏，胡俊雄，牟翰林，华晓连，马卫华. 采用新型悬浮架的小运量中低速磁浮车辆动力学分析. 铁道标准设计. 2024(12): 196-202+210 . 
百度学术其他类型引用(1)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 362
- HTML全文浏览量: 171
- PDF下载量: 15
- 被引次数: 2