Corrosion Detection Based on Frequency Spectrum Difference Coefficient of Higher-Order Lamb Modes
-
摘要:
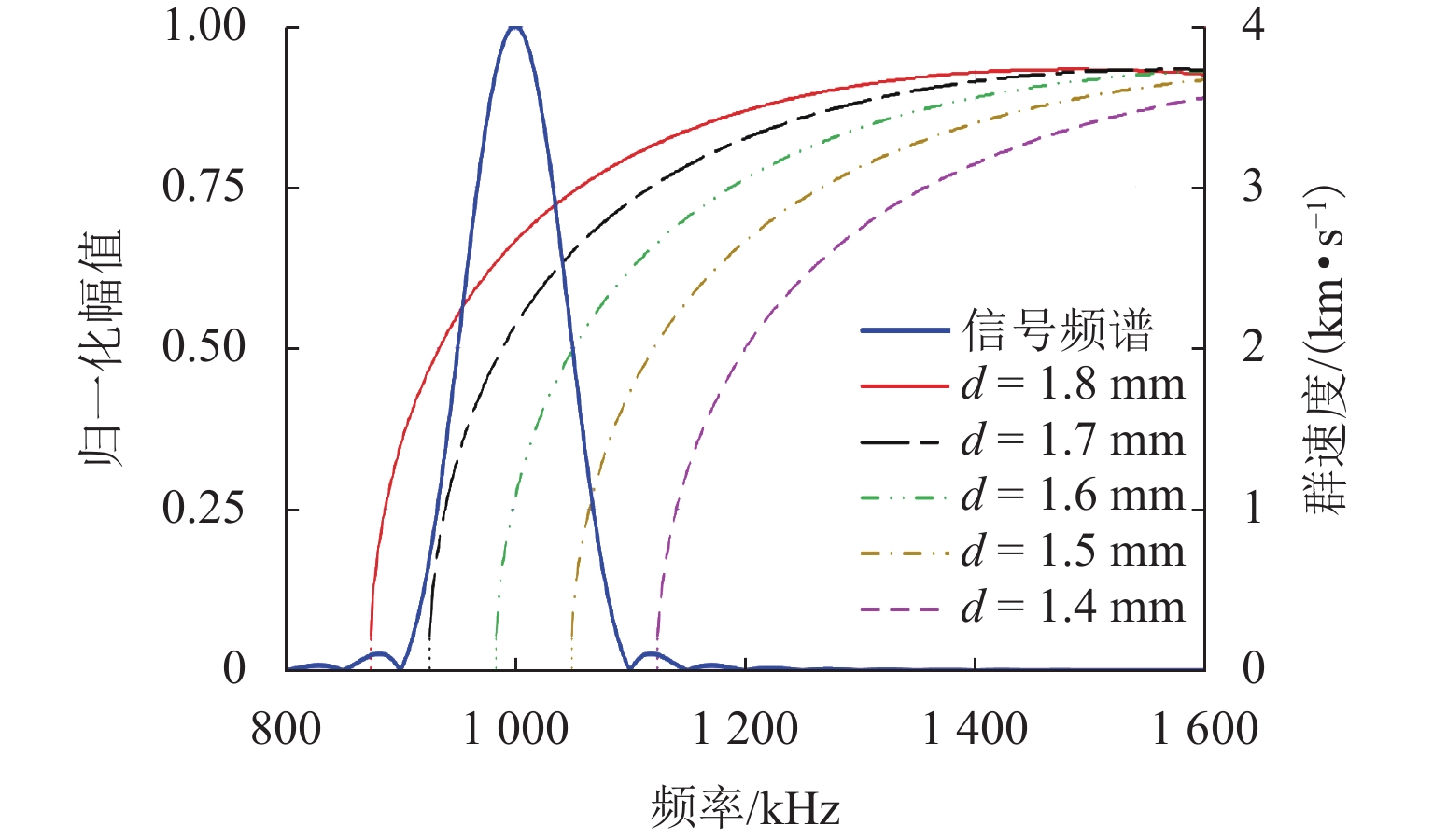
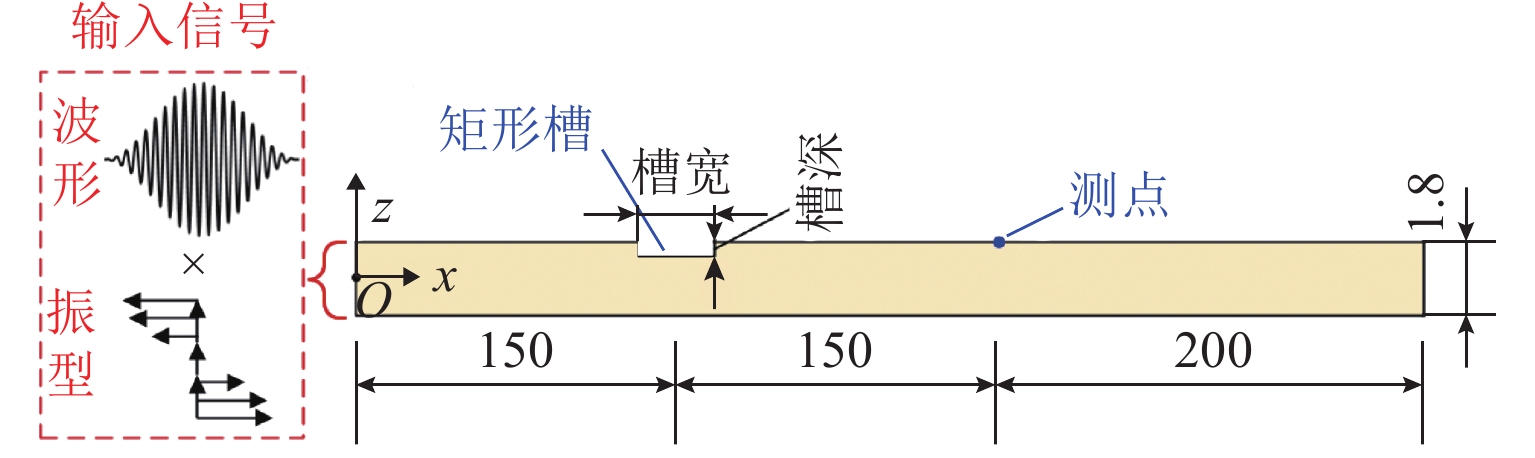
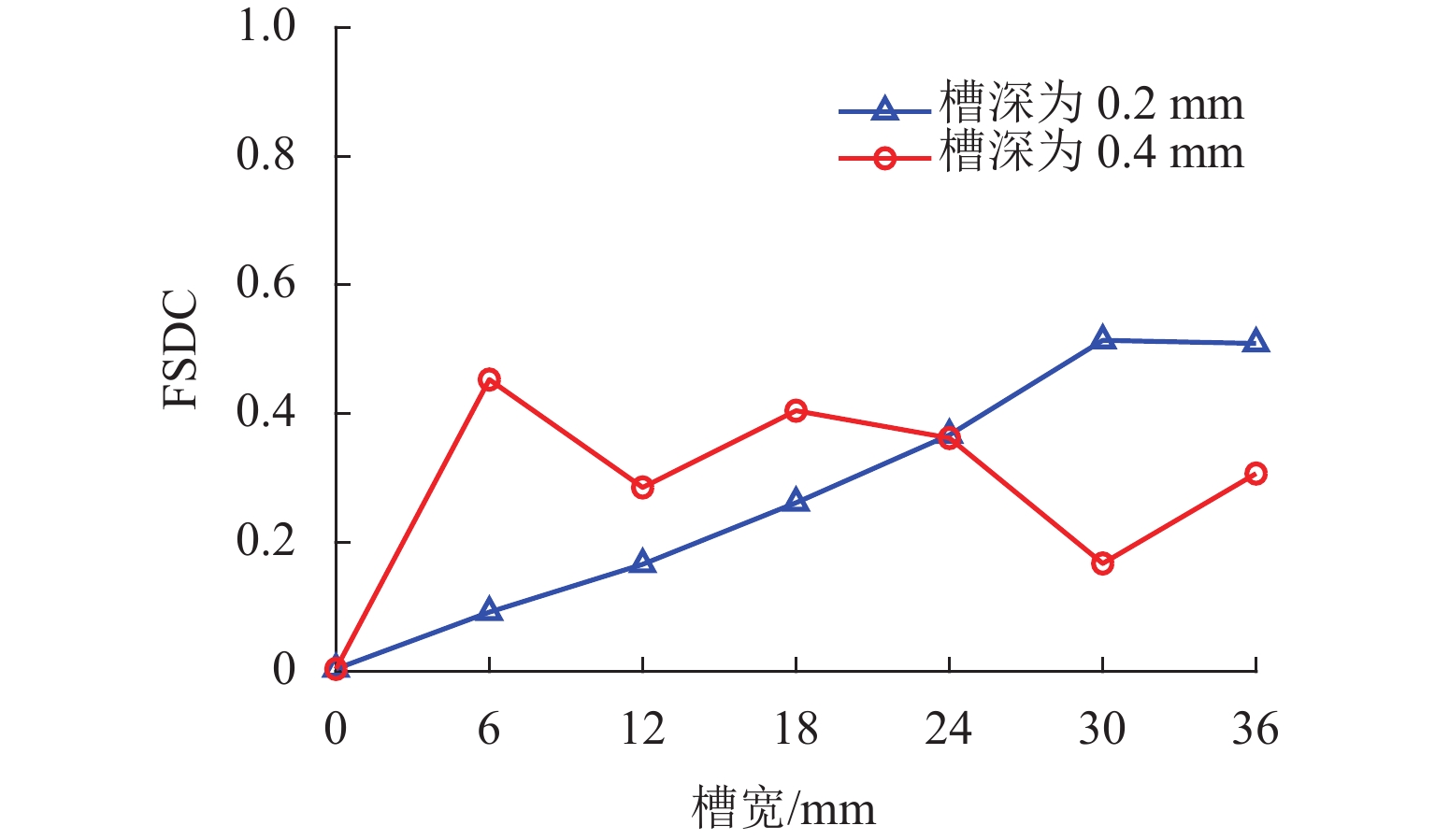
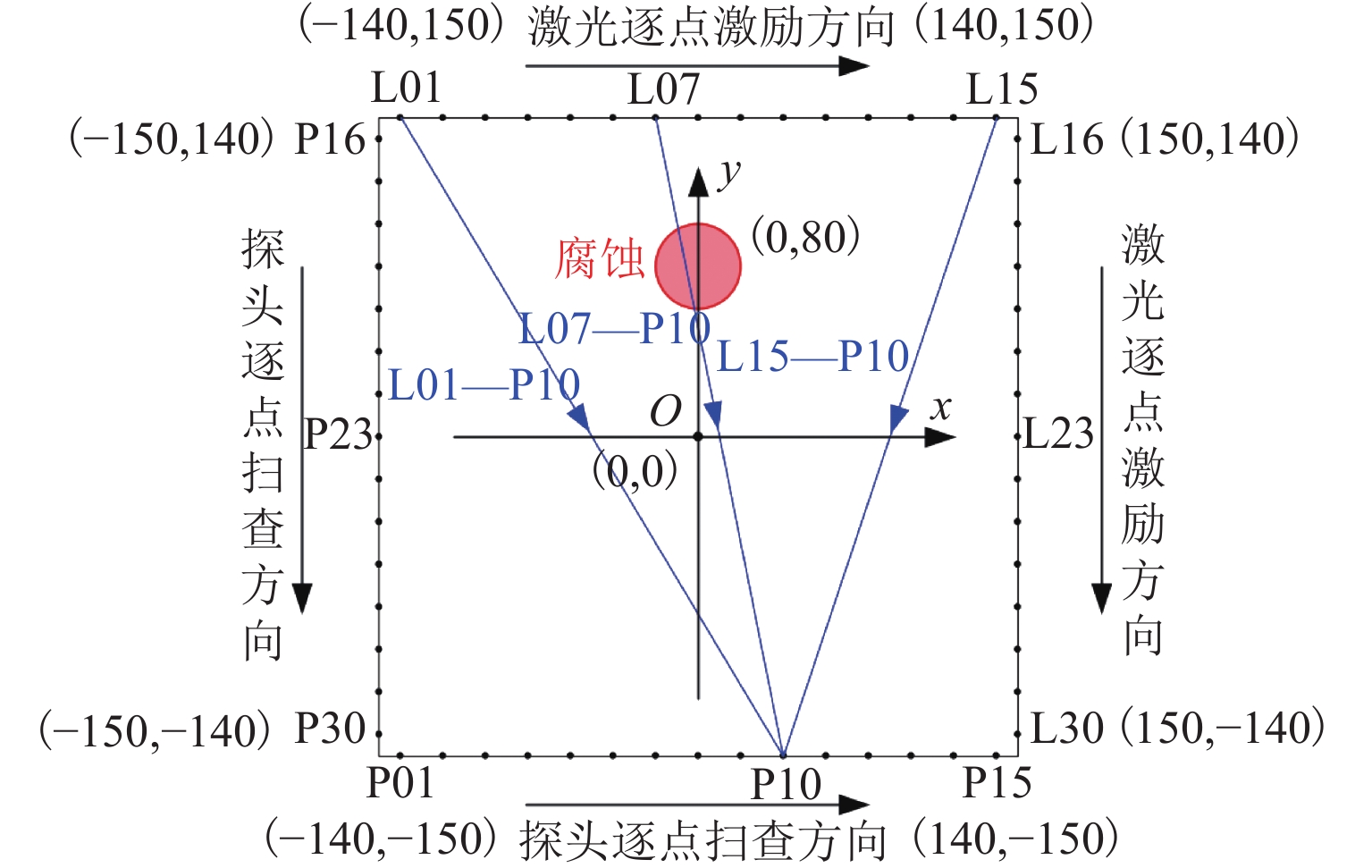
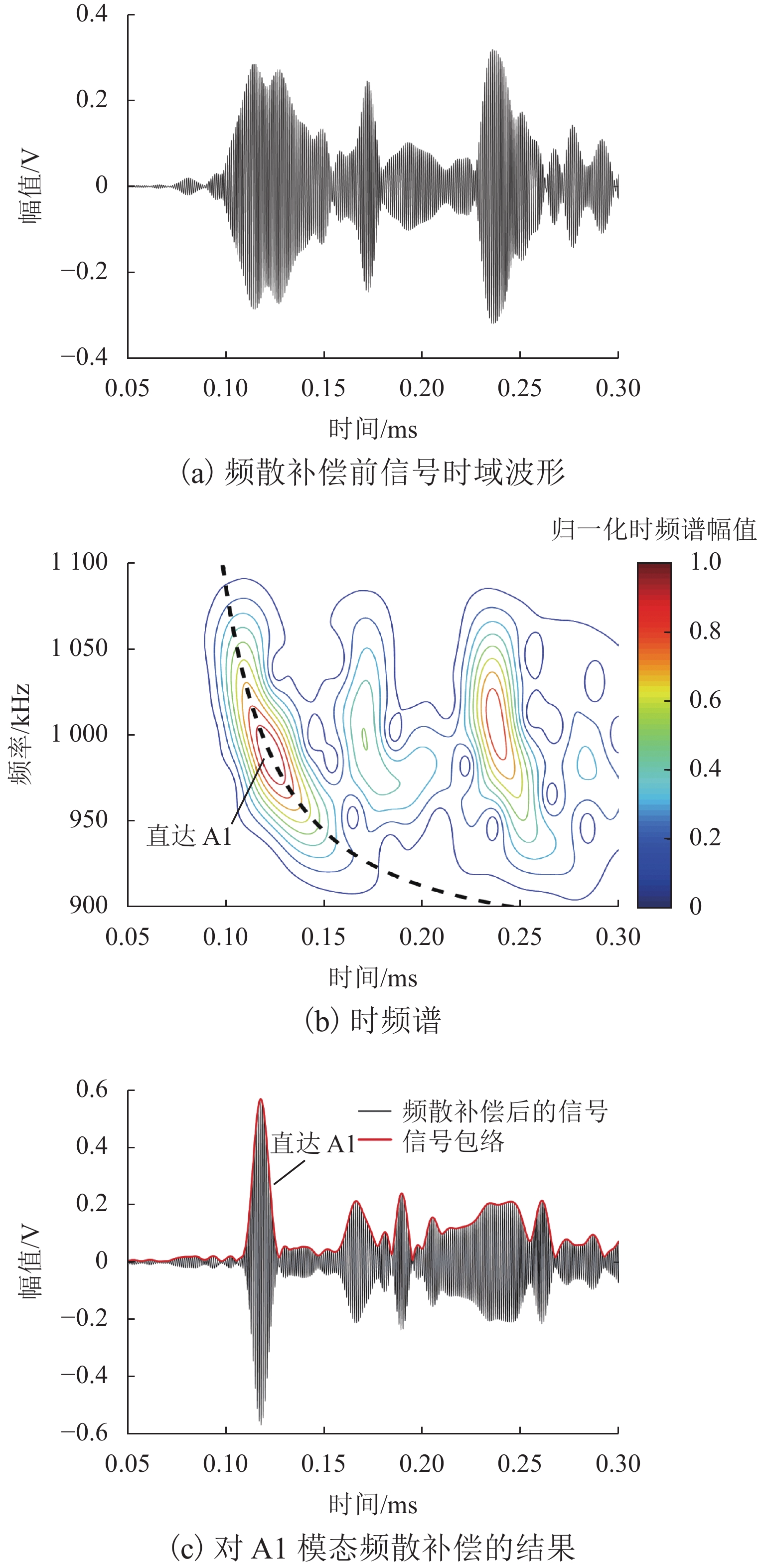
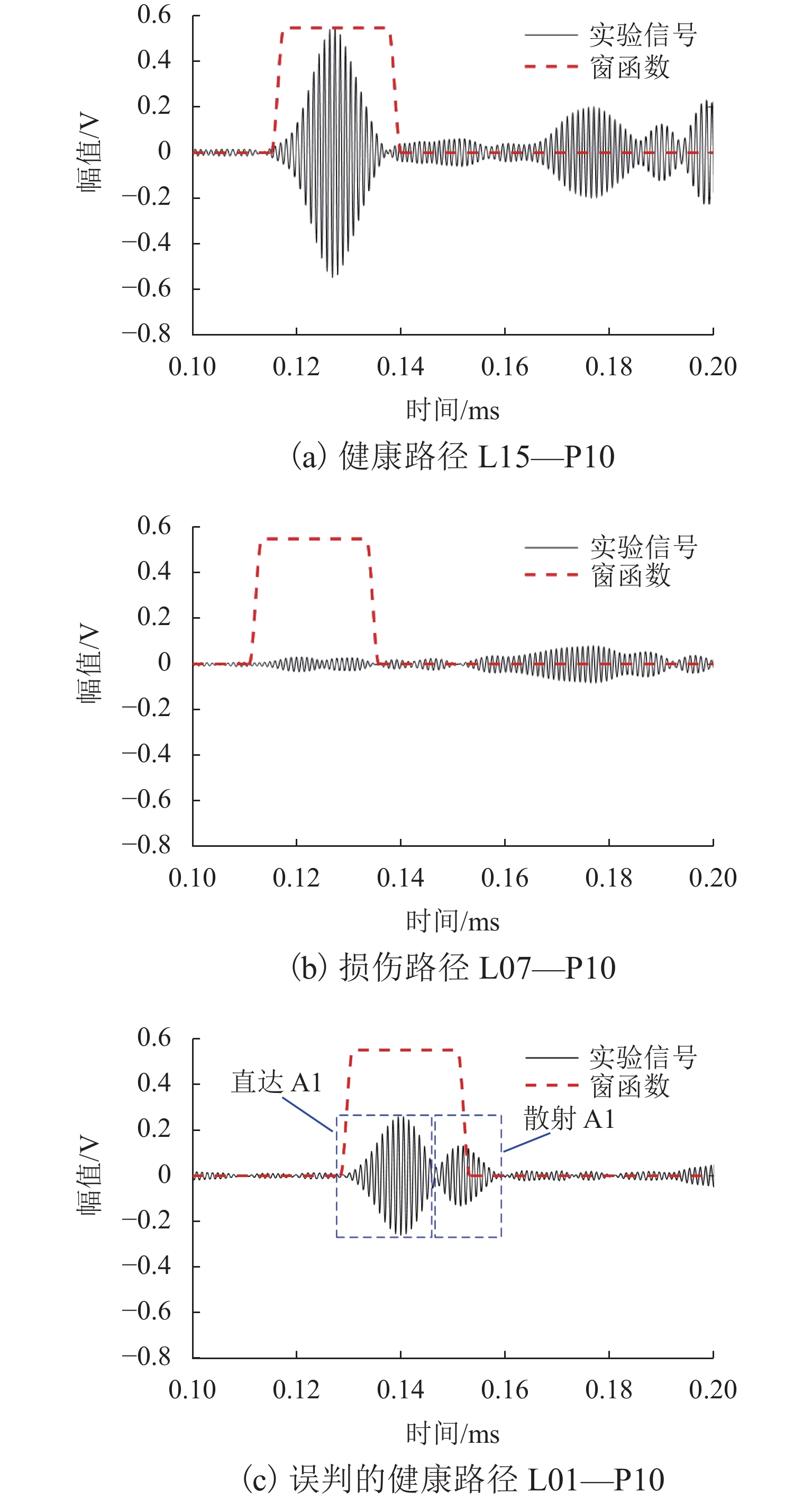
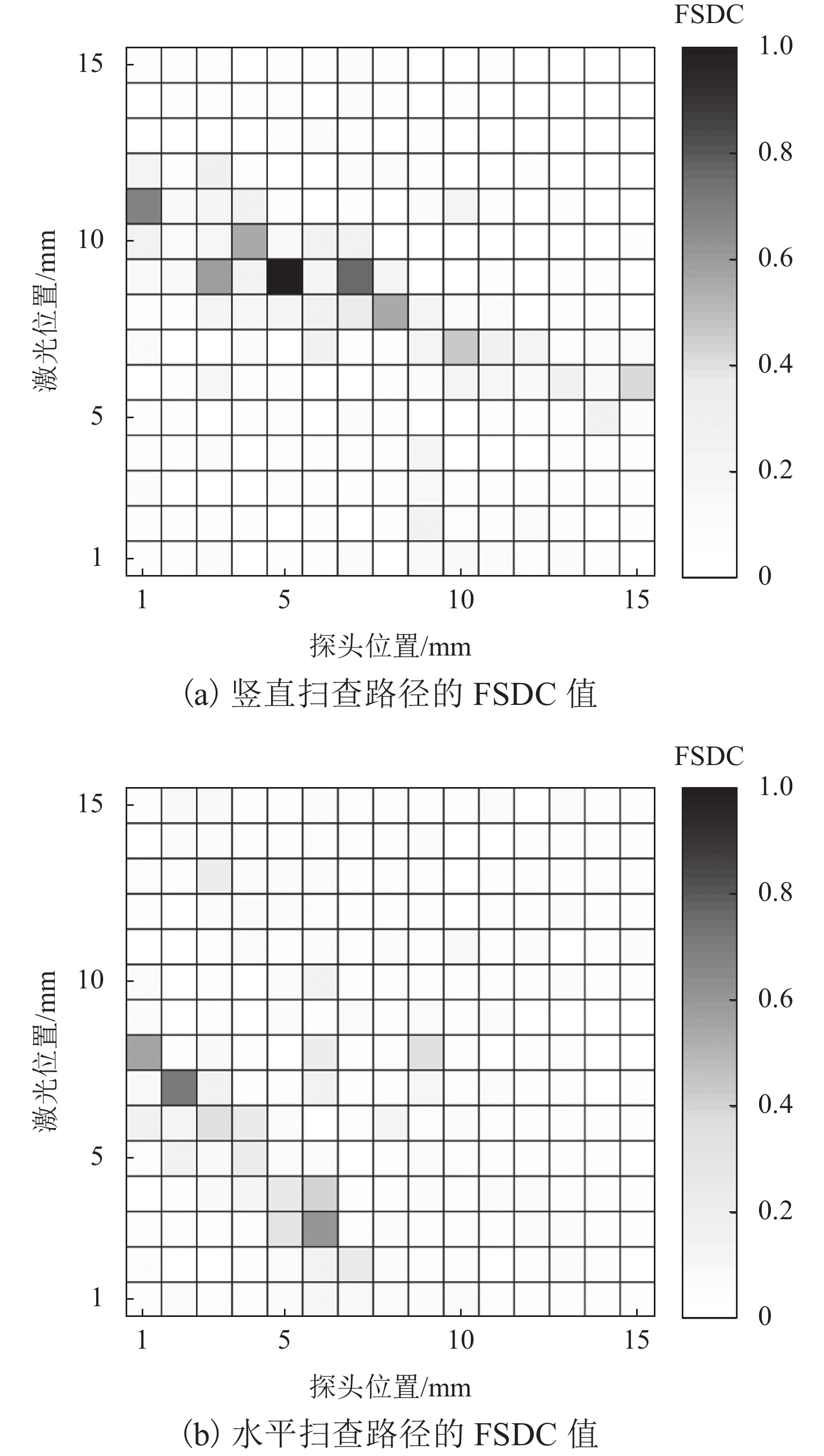
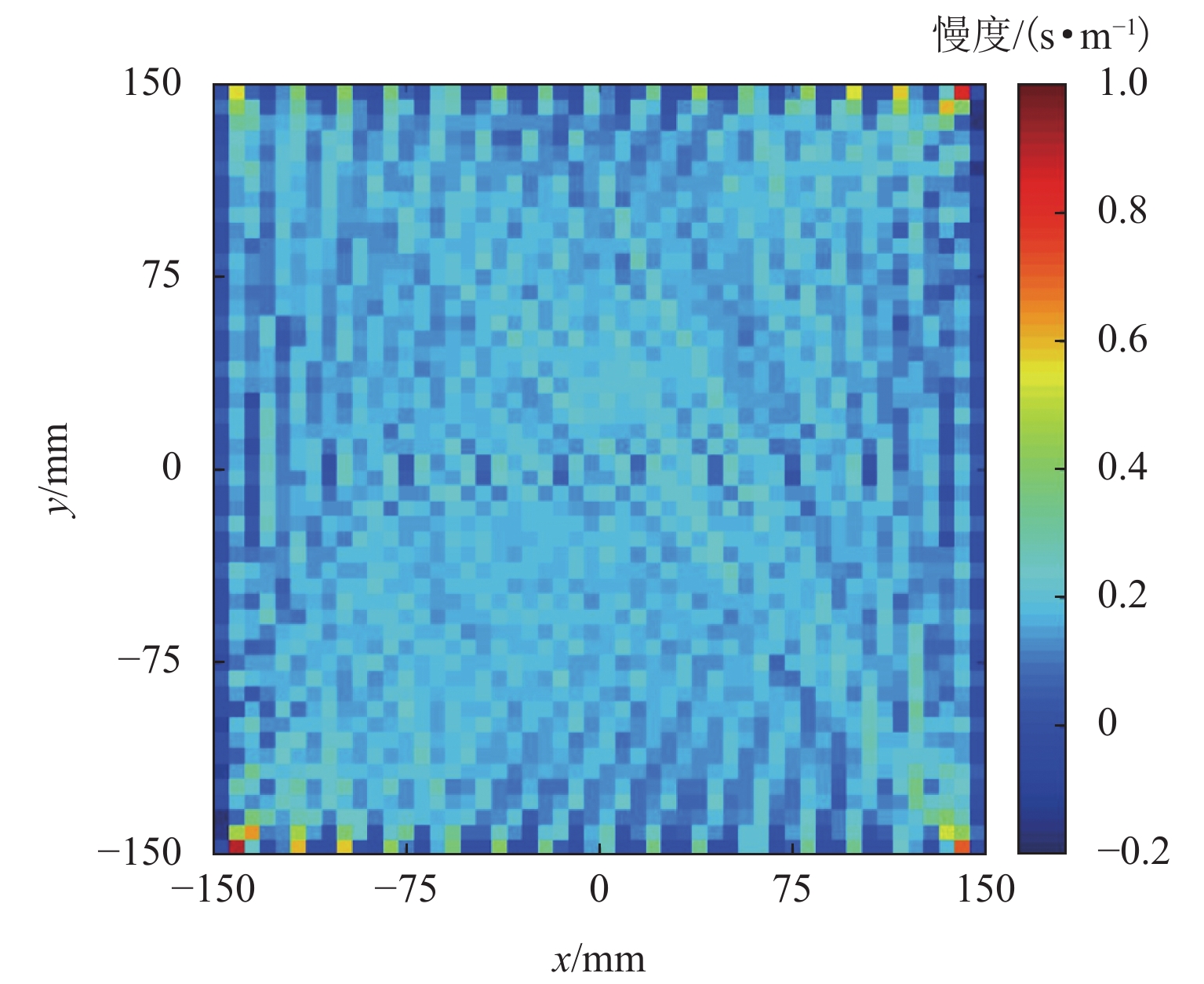
针对工业设备中大型薄壁结构件的腐蚀检测问题，提出一种基于频谱相干性分析的高阶Lamb波腐蚀损伤检测方法. 首先，利用略高于截止频率的A1模态Lamb波对含腐蚀薄壁结构的不同位置进行激励，并采集各传播路径上的响应信号；随后，采用频散补偿技术消除信号中的频散效果，通过合适的窗函数对信号中的A1模态直达波包进行分离提取，建立其与激励信号的频谱差异系数 (frequency spectrum difference coefficient, FSDC)，通过有限元仿真研究该指标对不同宽度、深度腐蚀损伤的敏感性；最后，在含腐蚀铝板上进行实验验证，结合各路径FSDC指标与概率成像算法，对检测区域的腐蚀损伤进行定位与成像. 结果表明：FSDC值在健康状态下为0，而在不同宽度、深度的腐蚀影响下FSDC在0～1；相较于传统层析成像方法，所提出方法具有更好的检测灵敏度和抗干扰能力.
Abstract:In view of the corrosion detection of large thin-walled structural parts in industrial equipment, a corrosion detection method based on spectral coherence analysis using high-order Lamb waves was proposed. Firstly, the A1 mode Lamb wave with a frequency slightly higher than the cutoff frequency was adopted and transmitted at different positions on the corroded thin-walled structure, and the response signal of each propagation path was collected; then, the dispersion compensation technique was used to eliminate the dispersion effect in the signal, so the direct wave packet of A1 mode could be separated and extracted from the signal using a suitable window function. On this basis, the frequency spectrum difference coefficient (FSDC) of the extracted wave packet and the excitation signal was established as an index, which was subsequently discussed in terms of its sensitivity to corrosion defects of different widths and depths with the help of finite element simulation; finally, an experimental validation was conducted on a corroded aluminum plate, where the FSDC index of each path was combined with the probability imaging algorithm to locate and visualize the corrosion defect in the detection area. Results show that the FSDC value keeps zero for an intact path and stays between 0 and 1 for corrosions of different widths and depths. Compared with the traditional tomography method, the proposed method has better detection sensitivity and anti-interference ability.
-
Key words:
- Lamb waves /
- higher-order modes /
- cutoff property /
- corrosion /
- defect detection
-
图 2 A1模态群速度频散随板厚变化的演化关系
Figure 2. Evolution of group velocity dispersion of A1 mode with plate thickness
图 3 1.8 mm 铝板中A1模态的频散关系及其一阶泰勒展开
Figure 3. Dispersion relationship and first-order Taylor expansion of A1 mode in aluminum plate with a thickness of 1.8 mm
图 4 包含矩形槽的二维有限元模型（左边界施加1 000 kHz A1模态的振型）
Figure 4. Two-dimensional finite element model with a rectangular notch (applying A1 mode of 1 000 kHz to the left boundary)
图 5 FSDC随矩形槽宽度、深度的演化关系
Figure 5. Evolution of FSDC with width and depth of rectangular notch
图 7 1.8 mm铝板的扫查示意
Figure 7. Layout of inspected aluminum plate with a thickness of 1.8 mm
图 8 健康路径L15—P10提取的窄带响应信号
Figure 8. Extracted narrow-band response signal from intact path L15—P10
图 9 健康、损伤路径的补偿实验信号
Figure 9. Compensated experimental signals of intact and damaged paths
图 11 基于FSDC的概率成像结果
Figure 11. Image obtained from probability reconstruction based on FSDC
-
[1] NAGATA Y, HUANG J, ACHENBACH J D, et al. Lamb wave tomography using laser-based ultrasonics[M]. Review of Progress in Quantitative Nondestructive Evaluation. Boston: Springer, 1995: 561-568. [2] PEI J, YOUSUF M I, DEGERTEKIN F L, et al. Lamb wave tomography and its application in pipe erosion/corrosion monitoring[J]. Research in Nondestructive Evaluation, 1996, 8(4): 189-197. doi: 10.1080/09349849609409599 [3] MALYARENKO E V, HINDERS M K. Fan beam and double crosshole Lamb wave tomography for mapping flaws in aging aircraft structures[J]. The Journal of the Acoustical Society of America, 2000, 108(4): 1631-1639. doi: 10.1121/1.1289663 [4] MALYARENKO E V, HINDERS M K. Ultrasonic Lamb wave diffraction tomography[J]. Ultrasonics, 2001, 39(4): 269-281. doi: 10.1016/S0041-624X(01)00055-5 [5] BELANGER P, CAWLEY P. Feasibility of low frequency straight-ray guided wave tomography[J]. NDT & E International, 2009, 42(2): 113-119. [6] BELANGER P, CAWLEY P. Lamb wave tomography to evaluate the maximum depth of corrosion patches[C]//34th Annual Review of Progress in Quantitative Nondestructive Evaluation. Colorado: American Institute of Physics, 2008, 975(1): 1290-1297. [7] HUTHWAITE P. Improving accuracy through density correction in guided wave tomography[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016, 472(2186): 20150832.1-20150832.25. [8] RAO J, RATASSEPP M, FAN Z. Guided wave tomography based on full waveform inversion[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(5): 737-745. doi: 10.1109/TUFFC.2016.2536144 [9] RAO J, RATASSEPP M, FAN Z. Investigation of the reconstruction accuracy of guided wave tomography using full waveform inversion[J]. Journal of Sound and Vibration, 2017, 400: 317-328. doi: 10.1016/j.jsv.2017.04.017 [10] ROSE J L, BARSHINGER J N. Using ultrasonic guided wave mode cutoff for corrosion detection and classification[C]//1998 IEEE Ultrasonics Symposium. Sendai: IEEE, 1998(1): 851-854. [11] LUO Z, ZENG L, LIN J. A hidden corrosion detection method based on robust multimodal Lamb waves[J]. Measurement Science and Technology, 2020, 31(4): 044002.1-044002.12. [12] CAO X, ZENG L, LIN J, et al. A correlation-based approach to corrosion detection with Lamb wave mode cutoff[J]. Journal of Nondestructive Evaluation, 2019, 38(87): 1-16. [13] ROSE J L. Ultrasonic guided waves in solid media[M]. New York: Cambridge University Press, 2014: 104-106 [14] ZENG L, LIN J, BAO J, et al. Spatial resolution improvement for Lamb wave-based damage detection using frequency dependency compensation[J]. Journal of Sound and Vibration, 2017, 394: 130-145. [15] AULD B A. Acoustic fields and waves in solids: volume 2[M]. Florida: [s.n.], 1973: 75-94. [16] PAVLAKOVIC B N. Leaky guided ultrasonic waves in NDT[D]. London, UK: Imperial College London, 1998. [17] MICHAELS J E, LEE S J, CROXFORD A J, et al. Chirp excitation of ultrasonic guided waves[J]. Ultrasonics, 2013, 53(1): 265-270. doi: 10.1016/j.ultras.2012.06.010 [18] ZHOU C, SU Z, CHENG L. Probability-based diagnostic imaging using hybrid features extracted from ultrasonic Lamb wave signals[J]. Smart Materials and Structures, 2011, 20(12): 125005.1-125005.14. [19] SUBBARAO P M V, MUNSHI P, MURALIDHAR K. Performance of iterative tomographic algorithms applied to non-destructive evaluation with limited data[J]. NDT & E International, 1997, 30(6): 359-370. [20] HANSEN P C, JØRGENSEN J S. AIR tools II: algebraic iterative reconstruction methods, improved implementation[J]. Numerical Algorithms, 2018, 79(1): 107-137. doi: 10.1007/s11075-017-0430-x -
下载:
点击查看大图
计量
- 文章访问数: 309
- HTML全文浏览量: 112
- PDF下载量: 24
- 被引次数: 0