Optimization of Vehicle–Cargo Matching Regarding Interests of Three Parties
-
摘要:
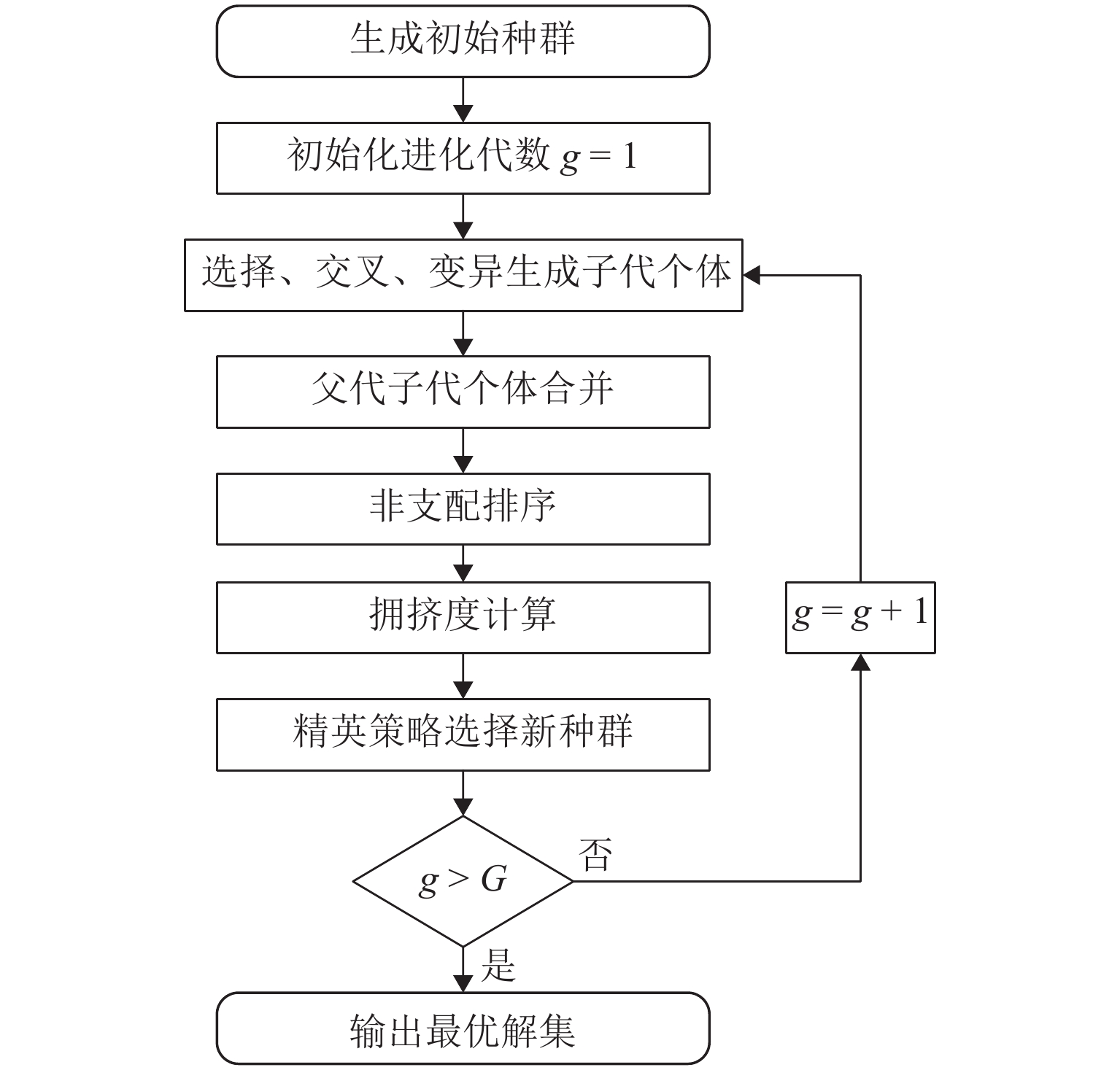
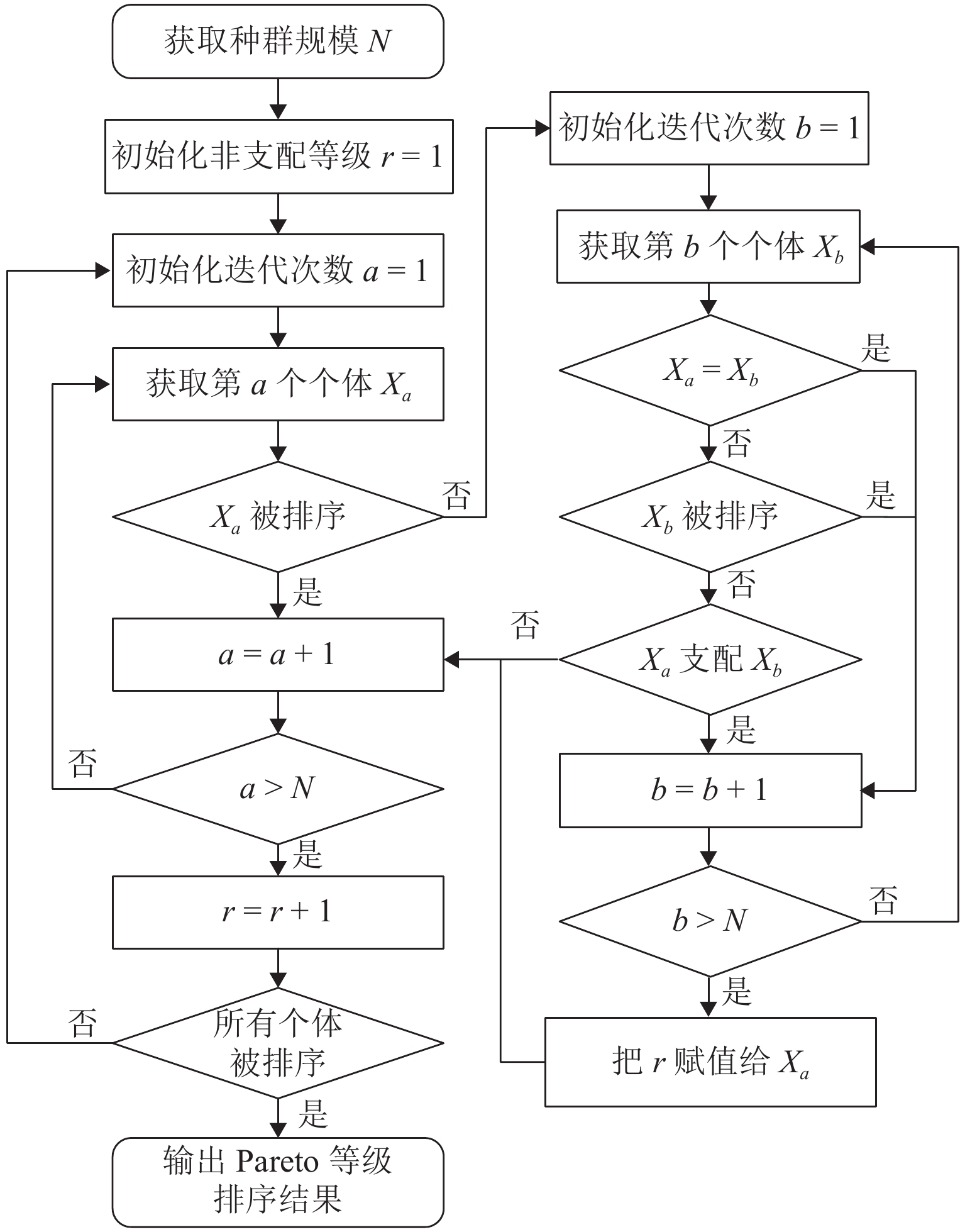
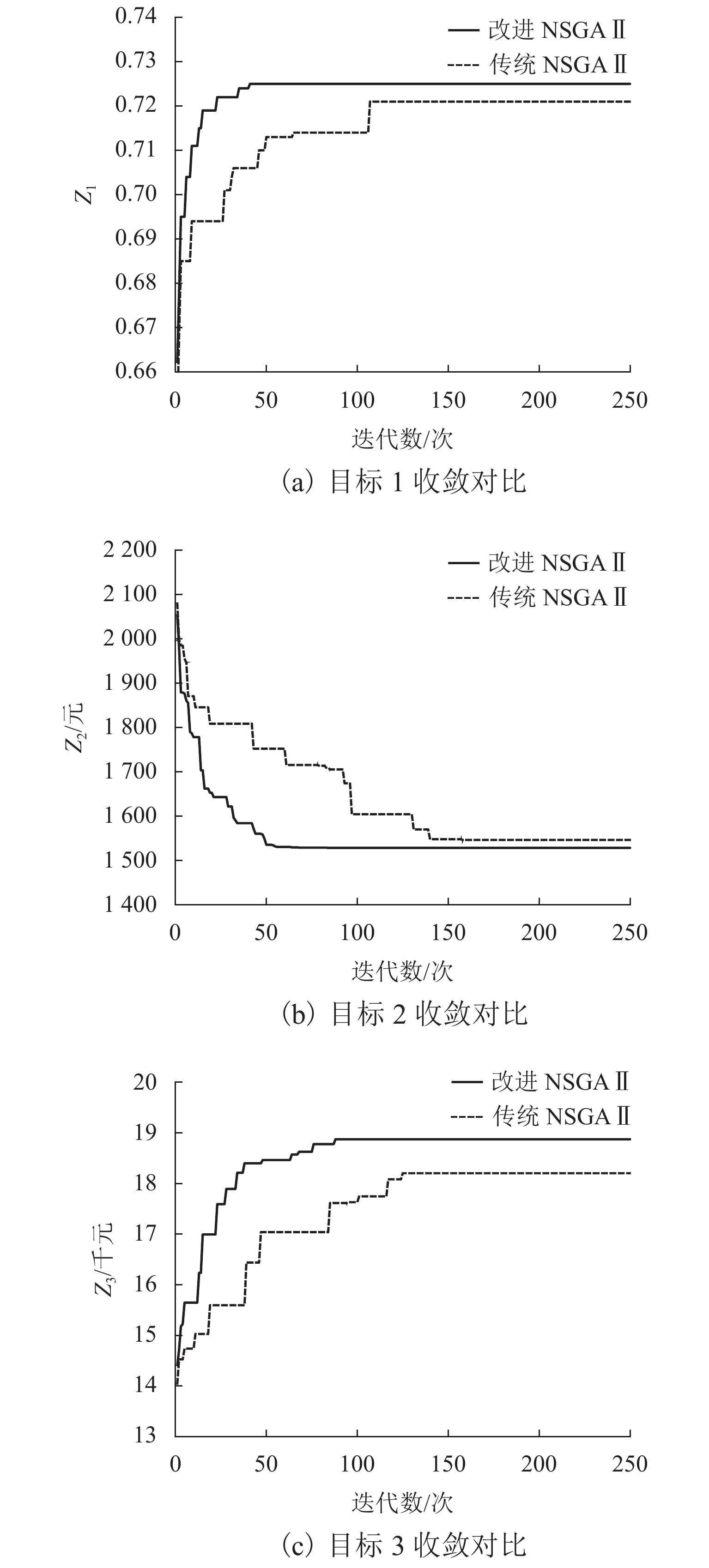
为研究平台模式下考虑车主、货主及平台三方异质化需求的车货匹配问题,在既往研究考虑车货双方利益的基础上,引入了平台方需求. 首先,在分析车货匹配活动参与方需求的基础上,构建了最大化送达时效满意度、最小化货运成本和最大化平台收益的多目标优化模型;其次,在模型求解方面,改进了带精英保留策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ,NSGA Ⅱ),一方面在子代种群更新过程中引入精英选择系数,提升种群的多样性,另一方面结合自适应的思想,在算法迭代过程中调整交叉变异的概率;最后,利用成渝区域间的车源和货源数据进行仿真实验. 结果表明:改进的NSGAⅡ在中小型算例上的准确率均超过91%,与传统的NSGAⅡ相比,平均收敛速度提升了45%左右;在算法稳定性方面,所提出的算法受随机初始化影响较低,多次实验的相对标准偏差值小于1%.
Abstract:To study the vehicle–cargo matching problem regarding the heterogeneous needs of the vehicle owner, cargo owner and platform under the platform mode, the platform demand is introduced given that the previous studies only consider the interests of both vehicle and cargo parties. Firstly, based on the analysis of the participant needs in the vehicle−cargo matching activity, a multi-objective optimization model is built to maximize the satisfaction of the delivery timeliness, minimize the freight cost and maximize the platform revenue. Secondly, in terms of model solution, the non-dominated sorting genetic algorithm Ⅱ (NSGA Ⅱ) with elite retention strategy is improved. On the one hand, elite selection coefficient is introduced in the process of updating the offspring population to improve the diversity of the population, and on the other hand, the adaptive idea is combined to adjust the probability of cross mutation in the algorithm iterations. Finally, the simulation experiments are carried out using the data of vehicles and freights in the areas of Chengdu and Chongqing. The results show that the accuracy of the improved algorithm proposed is more than 91% on small and medium-sized examples, and the average convergence speed is increased by about 45%, compared with the conventional NSGA Ⅱ algorithm. In terms of algorithm stability, the proposed algorithm is less affected by random initialization, and the relative standard deviation of multiple experiments is less than 1%.
-
表 1 符号说明
Table 1. Symbol descriptions
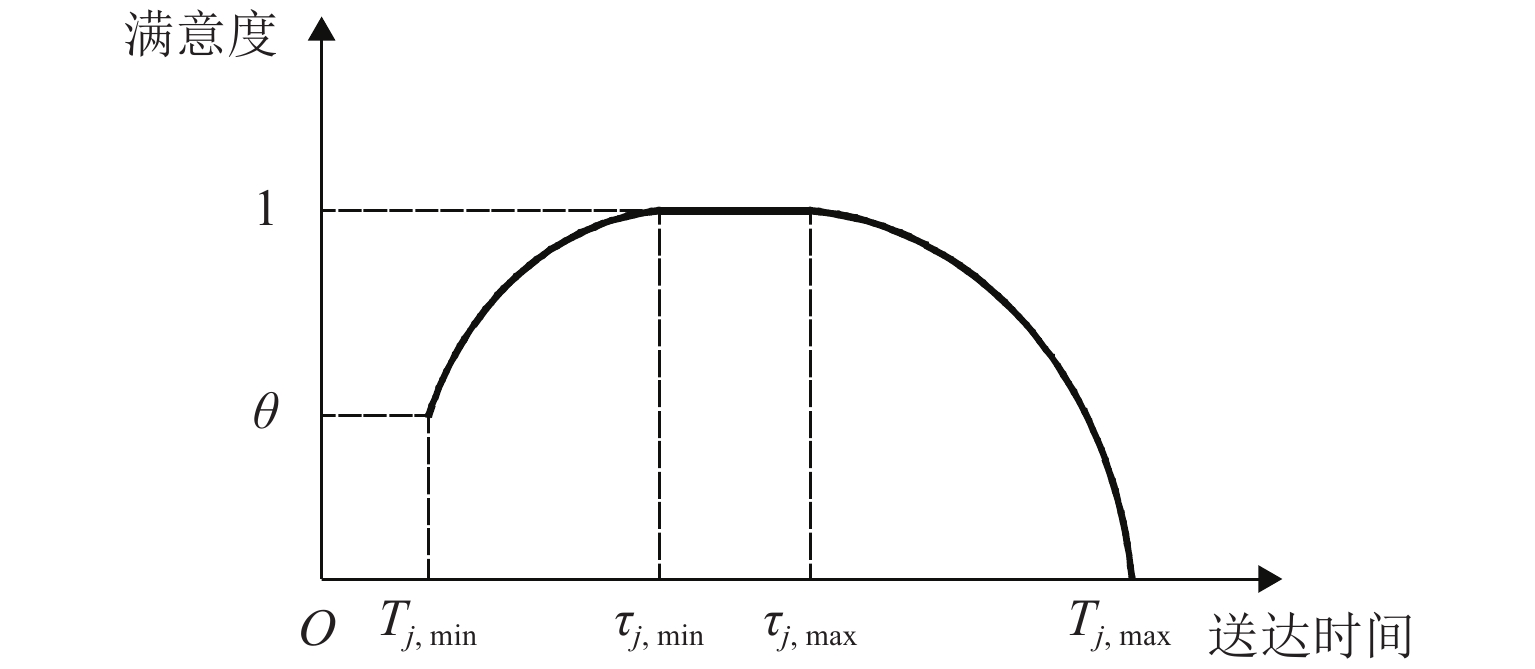
符号 说明 符号 说明 m 车辆总数 PijH 针对客户 j 的目的地,车主 i 对重货的单位质量报价 n 货主(货物)总数 Ic 成功匹配平台向货主收取的信息服务费 dij 车辆 i 与货主 j 之间的距离,i=1, 2, …, m, j=1, 2, …, n Ir 平台在达成匹配后对车主收益进行抽成的比例 dj 货物 j 起始地与目的地之间的距离 si 车辆 i 的接货半径 tij 车辆 i 送达货物 j 的时间 Pr 促成一组车货匹配带来的平台收益 Yi 车辆 i 的类型编号 Lk 第 k 类货物发生货物损耗的可能性 Yj 可用于承运货主 j 货物的车辆类型编号集合 Lp 货损的货物质量占承运总质量的百分比 Qi 车辆 i 的额定载重 Fj 货物 j 的送达时间满意度 Qj 货主 j 的货物总重 Tj,min,Tj,max 货物 j 的最早收货时间和最迟收货时间 Vi 车辆 i 的可用容积 τj,min,τj,max 客户期望的货物 j 的最早送达时间和最迟送达时间 Vj 货主 j 的货物总体积 Hj 货主 j 的最高出价 ci 车辆 i 单位距离行驶成本 cz 单次服务的车辆折旧费 cw 单位时间等待成本 ce 单次服务过程中的花销 cj 货主 j 单位质量的货损赔偿费用 θ 货物最早送达的基本满意度 cL 单位装卸费用 决策变量 cFi 车辆 i 单位距离通行费 xij 0-1 变量,表示车辆 i 与货主 j 是否匹配,
0 代表不匹配,1 代表匹配PijL 针对客户 j 的目的地,车主 i 对轻货的单位体积报价 Bj 0-1 变量,表示货物 j 是否购买保险,
0 代表未购买,1 代表购买表 2 不同载重车辆单位运输费用
Table 2. Transport costs per unit distance for different trucks
Qi/t ci/(元·km−1) Qi/t ci/(元·km−1) (0,2] 0.6 (15,20] 2.5 (2,5] 0.9 (20,30] 3.3 (5,10] 1.4 > 30 4.5 (10,15] 1.8 表 3 不同品类货物货损概率
Table 3. Probability of cargo damage of different categories
品类 Lk/% 品类 Lk/% 蔬菜 15 药品 2 水果 15 其他品类 1 畜产品 10 表 4 不同载重车辆通行收费标准
Table 4. Tolls for different loaded vehicles
Qi/t 通行费/(元·km−1) Qi/t 通行费/(元·km−1) (0,2] 0.45 (10,15] 1.80 (2,5] 0.90 > 15 2.25 (5,10] 1.35 表 5 车辆百公里折旧额
Table 5. Vehicle depreciation per 100 km
Qi/t 百公里折旧/元 Qi/t 百公里折旧/元 (0,5] 19.00 (15,30] 97.83 (5,10] 45.92 > 30 126.67 (10,15] 69.67 表 6 改进NSGAⅡ最优解集
Table 6. Optimal solution set of improved NSGAⅡ
方案 ${Z_1}$ ${Z_2}$/元 ${Z_3}$/元 1 0.709 1715.06 18872.94 2 0.694 1528.43 16518.98 3 0.725 1815.83 16216.22 4 0.724 1803.64 15829.95 5 0.722 1796.48 16556.88 6 0.703 1626.84 17168.01 7 0.712 1728.16 17565.18 8 0.721 1790.38 16881.49 9 0.714 1762.58 17205.61 10 0.706 1688.28 17427.67 注: 下划线数值表示各目标的最优值. 表 7 改进NSGAⅡ与穷举法对比情况
Table 7. Comparison of exhaustive search algorithm and improved NSGAⅡ
车辆数/辆 货物数/组 穷举法Pareto
解数量/个平均正确率/% 20 20 8 100.00 30 30 6 100.00 40 40 14 91.67 50 50 17 92.94 60 60 12 96.00 表 8 传统NSGAⅡ最优解集
Table 8. Optimal solution set of conventional NSGAⅡ
方案 ${Z_1}$ ${Z_2}$/元 ${Z_3}$/元 1 0.721 1790.38 16881.49 2 0.701 1546.28 17634.89 3 0.699 1602.94 18202.03 4 0.697 1571.87 17981.85 5 0.716 1784.61 16781.28 6 0.715 1781.21 17116.88 7 0.712 1728.16 17565.18 8 0.708 1707.22 17973.12 9 0.706 1688.28 17427.67 10 0.703 1626.84 17168.01 注:下划线数值表示各目标的最优值. 表 9 改进前后算法结果对比
Table 9. Comparison of algorithm results before and after improvement
车辆数/
辆货物数/
组改进 NSGAⅡ 传统 NSGAⅡ Z1 最
优值Z2 最优
值/元Z3 最优
值/元解集数
量/个平均收敛
代数/次Z1 最
优值Z2 最优
值/元Z3 最优
值/元解集数
量/个平均收敛
代数/次289 221 0.746 1514.36 42587.26 28 75 0.739 1525.04 40527.84 30 135 389 321 0.761 1496.68 60153.58 36 79 0.756 1502.49 59744.65 37 147 489 421 0.782 1488.31 78308.62 39 86 0.774 1492.77 78005.91 41 155 589 521 0.797 1470.62 93927.17 47 95 0.792 1472.36 91683.47 46 166 表 10 多次运行各目标相对标准偏差
Table 10. Relative standard deviation of each target after multiple operations
重复数/次 Z1/% Z2/% Z3/% 20 0.52 0.61 0.74 30 0.55 0.62 0.72 40 0.54 0.62 0.73 50 0.52 0.63 0.71 -
[1] DENG J X, ZHANG H P, WEI S F. Prediction of vehicle-cargo matching probability based on dynamic Bayesian network[J]. International Journal of Production Research, 2021, 59(17): 5164-5178. doi: 10.1080/00207543.2020.1774677 [2] WANG Z H, LI Y Y, GU F, et al. Two-sided matching and strategic selection on freight resource sharing platforms[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 559: 125014. doi: 10.1016/j.physa.2020.125014 [3] FENG M, CHENG Y R. Solving truck-cargo matching for drop-and-pull transport with genetic algorithm based on demand-capacity fitness[J]. Alexandria Engineering Journal, 2021, 60(1): 61-72. doi: 10.1016/j.aej.2020.05.015 [4] XIE K W, XU H Y, LV H X. Two-sided matching on comprehensive transportation network emergency vehicles’ allocation[J]. Journal of Advanced Transportation, 2021, 2021: 6817013.1-6817013.13. [5] 李建斌,周泰,徐礼平,等. 货运O2O平台有时间窗同城零担集货匹配优化决策[J]. 系统工程理论与实践,2020,40(4): 978-988. doi: 10.12011/1000-6788-2018-2300-11LI Jianbin, ZHOU Tai, XU Liping, et al. Matching optimization decision of city LTL carpool based on time windows on the freight O2O platform[J]. Systems Engineering—Theory & Practice, 2020, 40(4): 978-988. doi: 10.12011/1000-6788-2018-2300-11 [6] 牟向伟,陈燕,高书娟,等. 基于改进量子进化算法的车货供需匹配方法研究[J]. 中国管理科学,2016,24(12): 166-176. doi: 10.16381/j.cnki.issn1003-207x.2016.12.019MU Xiangwei, CHEN Yan, GAO Shujuan, et al. Vehicleand cargo matching method based on improved quantum evolutionary algorithm[J]. Chinese Journal of Management Science, 2016, 24(12): 166-176. doi: 10.16381/j.cnki.issn1003-207x.2016.12.019 [7] 杨滨舟, 叶欣扬, 王睿, 等. 基于直觉模糊优化的车货双边公平匹配方法[J/OL]. 计算机集成制造系统: 1-14. (2021-01-06) [2021-09-15]. http://kns.cnki.net/kcms/detail/11.5946.tp.20210105.1654.051.html.YANG Binzhou, YE Xinyang, WANG Rui, et al. Method for vehicle-cargo two-sided fair matching based on intuitionistic fuzzy optimization[J/OL]. Computer Integrated Manufacturing Systems: 1-14. (2021-01-06)[2021-09-15]. http://kns.cnki.net/kcms/detail/11.5946.tp.20210105.1654.051.html. [8] 余以胜,刘鑫艳. 基于改进Balance算法的车货匹配研究[J]. 武汉理工大学学报,2016,38(10): 47-54. doi: 10.3963/j.issn.1671-4431.2016.10.009YU Yisheng, LIU Xinyan. Research on vehicles and cargos matching based on improved balance algorithm[J]. Journal of Wuhan University of Technology, 2016, 38(10): 47-54. doi: 10.3963/j.issn.1671-4431.2016.10.009 [9] 陆慧娟,安春霖,程倬,等. 基于SaaS和CSCW的车货匹配系统研究与应用[J]. 华中科技大学学报(自然科学版),2012,40(增1): 324-327.LU Huijuan, AN Chunlin, CHENG Zhuo, et al. Research and application of goods vehicles matching system based on SaaS and CSCW[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(S1): 324-327. [10] 张菲,张锦. 基于多目标优化的物流服务组合研究[J]. 西南交通大学学报,2018,53(6): 1278-1285,1307. doi: 10.3969/j.issn.0258-2724.2018.06.025ZHANG Fei, ZHANG Jin. Logistics service composition based on multi-objective optimization[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1278-1285,1307. doi: 10.3969/j.issn.0258-2724.2018.06.025 [11] 王娜,李引珍,柴获. 考虑匹配均衡性的供需双方多对多双边匹配决策方法[J]. 西南交通大学学报,2022,57(2): 425-433. doi: 10.3969/j.issn.0258-2724.20200567WANG Na, LI Yinzhen, CHAI Huo. Decision-making approach of two-sided many-to-many matching of supply and demand for logistics service based on matching balance[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 425-433. doi: 10.3969/j.issn.0258-2724.20200567 [12] TVERSKY A, KAHNEMAN D. Advances in prospect theory: cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323. doi: 10.1007/BF00122574 [13] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 [14] AHMADI A. Memory-based adaptive partitioning (MAP) of search space for the enhancement of convergence in pareto-based multi-objective evolutionary algorithms[J]. Applied Soft Computing, 2016, 41: 400-417. doi: 10.1016/j.asoc.2016.01.029 -




 下载:
下载: