干寒大温差下早龄期混凝土收缩特性及防裂技术

李福海; 文涛; 唐慧琪; 李继芸; 李瑞; 陈昭; 李学友; 李超

doi:10.3969/j.issn.0258-2724.20210839

干寒大温差下早龄期混凝土收缩特性及防裂技术

doi: 10.3969/j.issn.0258-2724.20210839

1.
西南交通大学土木工程学院，四川成都 610031
2.
中铁二局集团有限公司中国建筑第四工程有限公司，四川成都 610031

基金项目: 四川省科技厅中央引导地方科技发展专项（2020ZYD011）；四川省应用基础研究项目（2021YJ0545）；四川省交通运输科技项目（2021-B-01）

详细信息

作者简介:
李福海（1979—），男，高级工程师，博士，研究方向为混凝土耐久性、高性能混凝土等，E-mail：lifuhai2007@swjtu.edu.cn

中图分类号: TU501
计量
- 文章访问数: 395
- HTML全文浏览量: 247
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-27
- 修回日期: 2022-03-14
- 网络出版日期: 2023-06-21
- 刊出日期: 2022-12-01

Shrinkage Characteristics and Anti-Crack Technology of Early-Age Concrete under Large Dry-Cold Temperature Difference

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
China Construction Fouth Engineering Division Corp., Ltd., China Railway No.2 Engineering Group Co., Ltd., Chengdu 610031, China

摘要

摘要:
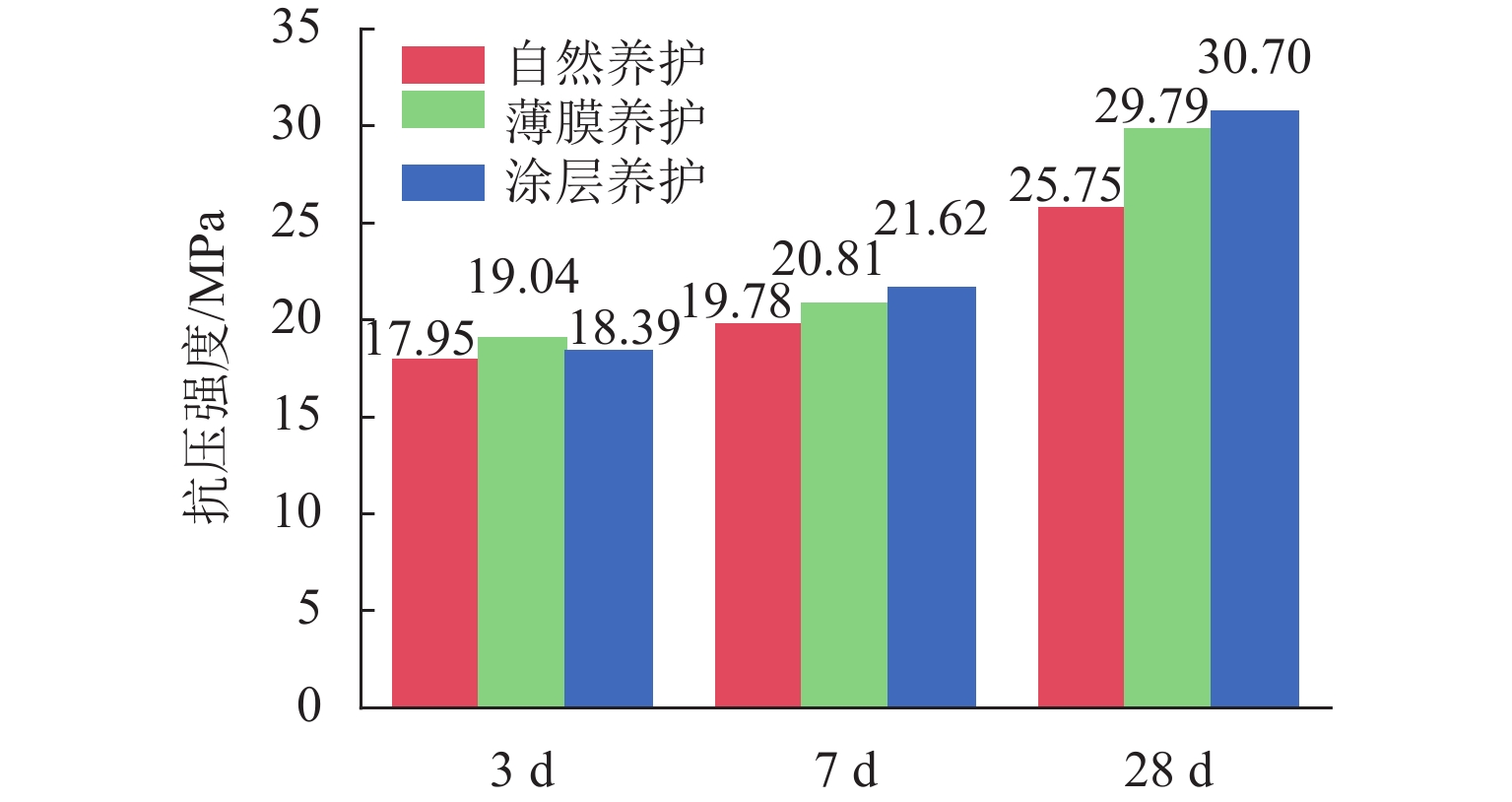
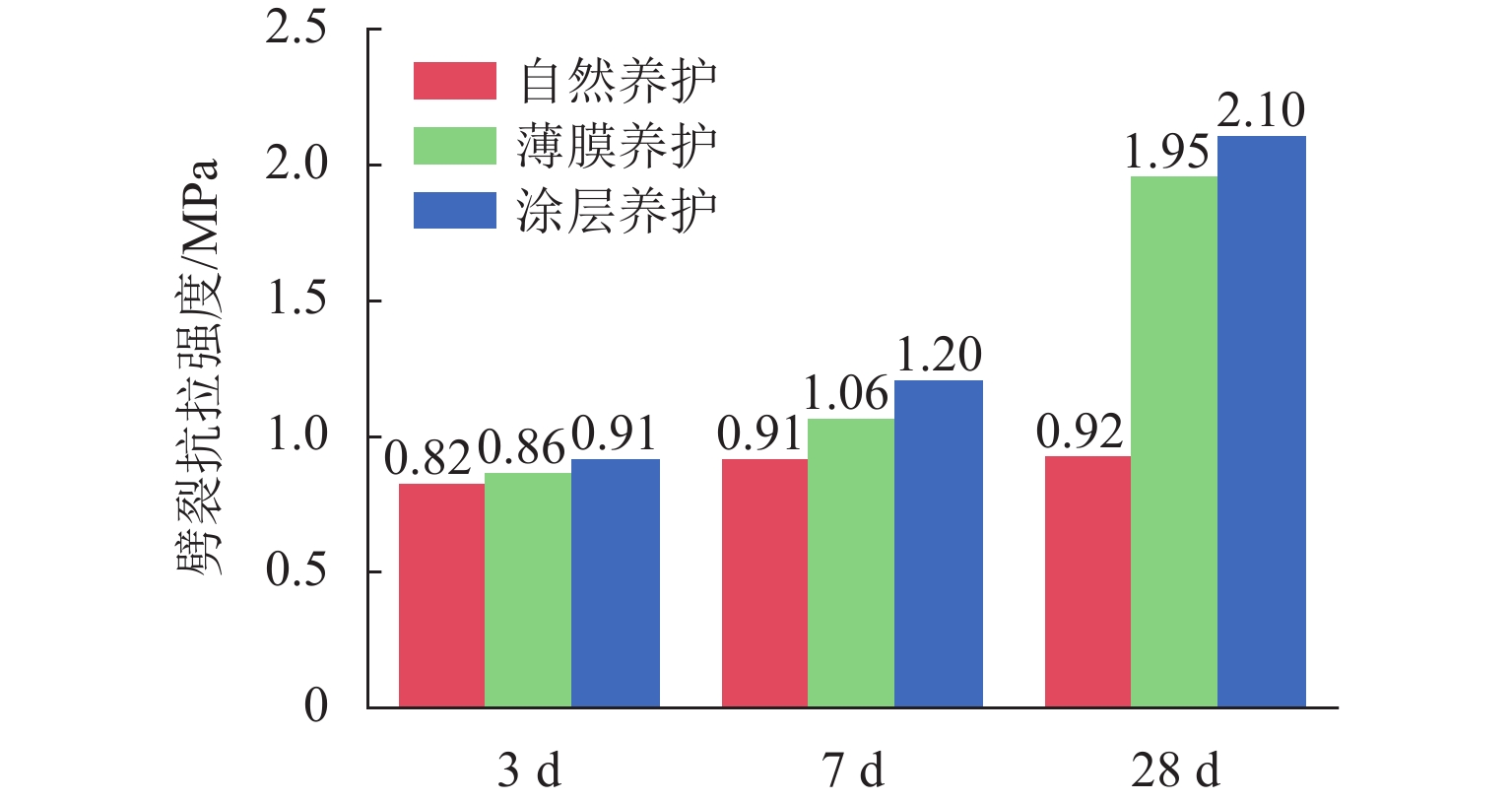
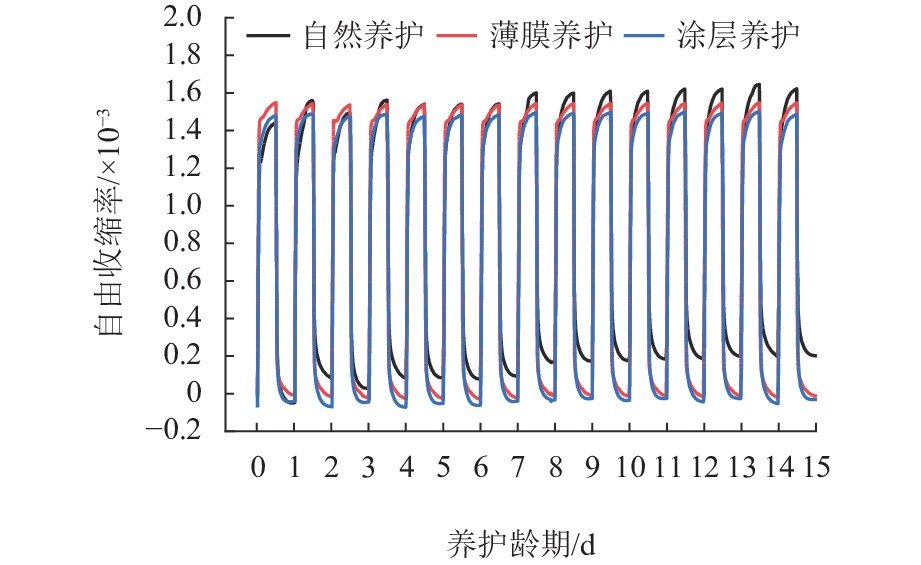
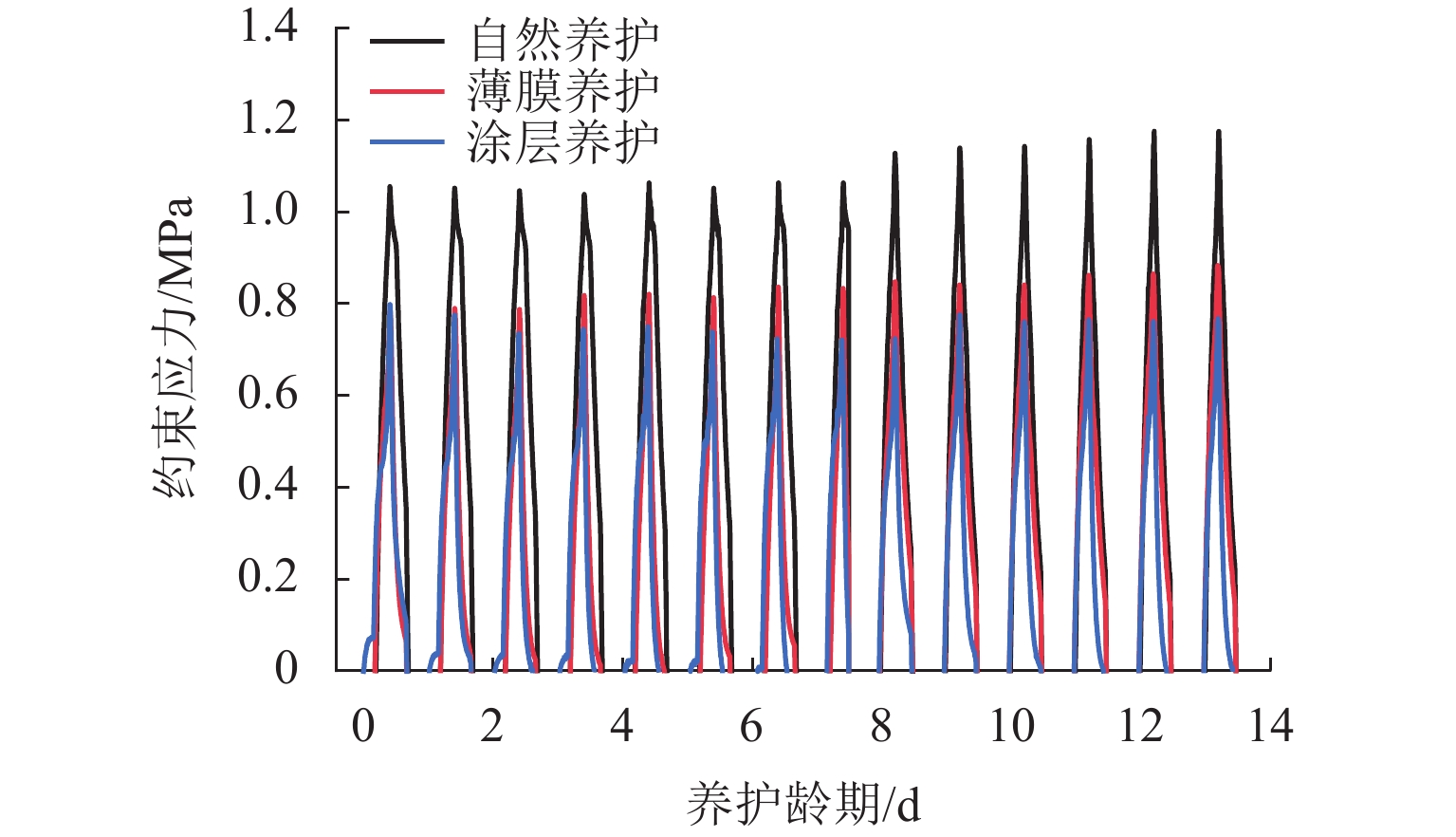
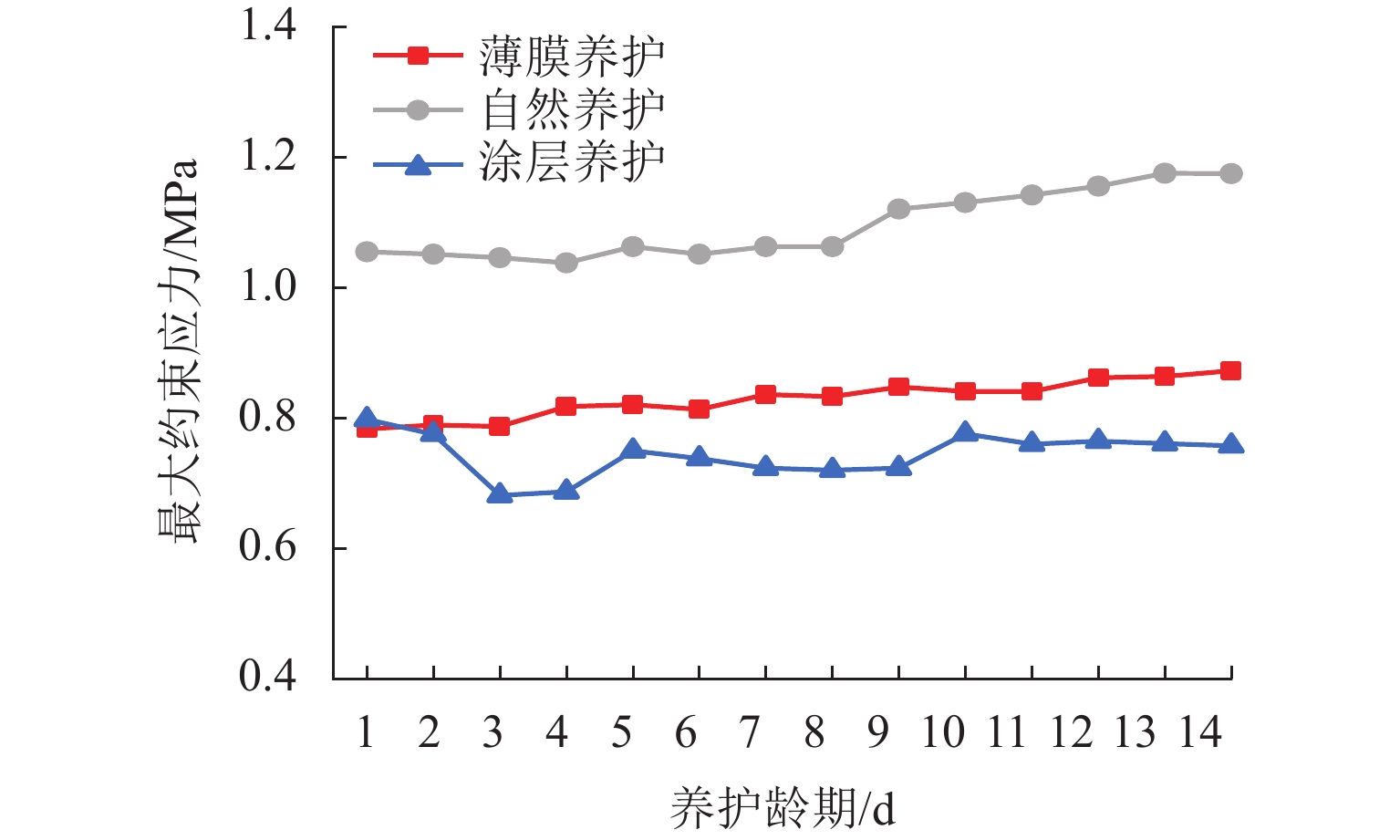
为探究干寒大温差下早龄期混凝土收缩变形规律，降低开裂风险，采用3种养护方法对混凝土进行早龄期养护，以抗压强度、劈裂抗拉强度、自由收缩率及最大约束应力为表征手段，设置了基本力学性能试验、自由收缩试验与约束收缩试验，并采用综合型多指标的灰色关联法分析了不同养护方式下混凝土的抗裂性能. 同时，设计了纳米涂层保温性能试验，探究其对混凝土的保温隔热性能. 试验结果表明：在−20.0～15.0 ℃的循环温度中，采用纳米涂层使得圆柱体混凝土试件内部平均温差降低2.95 ℃；相比于标准养护，3种养护方式下混凝土抗压及劈裂抗拉强度均有显著降低，干寒大温差不利于混凝土的强度发展；自由收缩率随温度变化明显，呈现出温度降低，自由收缩率增大，反之，温度升高自由收缩率减小，并在−20.0 ℃与15.0 ℃时出现极值；最大约束应力受到养护方式影响，自然养护下最大约束应力发展最快，终值最大，薄膜养护次之，涂层养护最大约束应力发展最慢，终值最小；涂层养护下灰色关联度高达0.9149，明显高于自然养护与薄膜养护，表现出优异的抗裂性能.
- 早龄期混凝土 /
- 养护方式 /
- 强度 /
- 收缩 /
- 抗裂性能
Abstract:
In order to explore the shrinkage and deformation laws of early-age concrete under large dry-cold temperature differences and reduce the risk of cracking, three curing methods were used for early-age curing of concrete. The compressive strength, splitting tensile strength, free shrinkage rate, and maximum restraint stress were used as the characterization methods. Basic mechanical performance test, free shrinkage test, and restraint shrinkage test were designed. The comprehensive multi-index grey correlation method was adopted to analyze the anti-cracking performance of concrete under different curing methods. In addition, a nano-coating thermal insulation performance test was designed to explore its thermal insulation performance on concrete. The test results show that the use of nano-coating reduces the average temperature difference inside the cylindrical concrete specimen by 2.95 ℃ in the circulating temperature of ‒20.0–15.0 ℃; compared with those under standard curing, the compressive and splitting tensile strengths of concrete under the three curing methods are significantly reduced, and the large dry-cold temperature difference is not conducive to the strength development of concrete. The free shrinkage rate changes significantly with temperature. Specifically, as the temperature decreases, the free shrinkage rate increases, and as the temperature rises, the free shrinkage rate decreases. In addition, extreme values appear at ‒20.0 ℃ and 15.0 ℃; the maximum restraint stress is affected by the curing method. Under natural curing, the maximum restraint stress develops the fastest, with the largest final value, followed by that under film curing. Under coating curing, the maximum restraint stress develops the slowest, with the smallest final value. The gray correlation degree under coating curing is as high as 0.9149, which is significantly higher than that under natural curing and film curing, showing excellent anti-cracking performance.
- early-age concrete /
- curing method /
- strength /
- shrinkage /
- anti-cracking performance

HTML全文

市域铁路是都市圈内客运轨道交通的组成部分，随着我国城市化水平不断提高，大城市空间结构逐渐由单中心向多中心演化，中心城与外围新城间交通需求也日益增长，市域铁路成为解决该交通需求的有效途径.

市域铁路兼具干线铁路和城市轨道交通的特征. 针对其运输需求，借助干线铁路已经发展起来的同相供电技术^[1-2]，市域铁路的单相交流牵引供电可采用双边供电，取消分区所处电分相环节，提升牵引供电系统供电能力及供电可靠性.综合分析单边和双边供电的技术经济指标^[3]，双边供电最大的优点是提高牵引网电压水平，且在稳态情况下，实施双边供电能够满足电力系统的要求^[4]. 采用双边供电技术会增加既有继电保护对牵引网故障的识别难度，因此，可采用牵引网分段供电与测控技术^[5-7]，将供电臂适当分段，运用同步测量技术，更准确、及时地判别故障类型与部位，将故障限制在最小范围内，最大限度地保证牵引网的可靠性和可用性. 可通过建立双边供电等值电路，得到均衡电流的计算模型^[3]；或在分区所测量两侧牵引网的电压，利用两侧牵引网均为空载时，两侧牵引母线的电压差除以折算至牵引侧的系统总阻抗预估均衡电流^[8]. 可在变电所馈线串接电抗器或将牵引变压器制成高漏抗牵引变压器^[2]，或通过适用于交流电气化铁路牵引供电的移相器减小均衡电流^[9]，也可以通过选择合适的外部电源构成树形双边供电，达到没有均衡电流的目的^[10]. 目前，市域铁路的研究主要集中于牵引电缆贯通供电方案，并对该方案进行了建模和潮流计算^[11]. 本文主要分析市域铁路在牵引侧双边供电运行，改变城市电网在配电网侧辐射状的电网结构，双边供电可能跨越较多的电压等级，构成电磁环网结构，需分析双边供电系统中“电磁环网”的潮流分布和对电力系统的影响，给出不同外部电源均衡电流的计算模型，并得到其影响及其相应的控制措施. 结合工程案例，推导多个牵引变电所双边供电时均衡电流的计算模型，对市域铁路单相交流牵引供电采用双边供电时的潮流、均衡电流进行计算，分析双边供电的可行性.

1. 电磁环网分析

1.1 电磁环网形成的原因

电磁环网是由2组不同电压等级的输电线路通过变压器T1、T2磁回路的联结并列运行而形成的环形电力网^[12]，一般形成于相邻的2个电压等级间，典型的电磁环网如所示，图中： ${{\dot U}}_{\rm{S}}$ 、Z_S分别为环网中的电压和等值电阻，S为环网中的潮流.

图 1 典型的电磁环网

Figure 1. Typical electromagnetic loop network

下载: 全尺寸图片幻灯片

1.2 双边供电系统中“电磁环网”分析

在双边供电系统中，牵引变电所间牵引网联通成为电力系统的并联支路，类似于电力系统中的电磁环网，然而二者也有显著的不同，电力系统中存在三相电压（电流） ${{\dot U}}_{\rm{A}}$ 、 ${{\dot U}}_{\rm{B}}$ 、 ${{\dot U}}_{\rm{C}}$ （ ${{\dot I}}_{\rm{A}}$ 、 ${{\dot I}}_{\rm{B}}$ 、 ${{\dot I}}_{\rm{C}}$ ），但电气化铁路双边供电仅是某一相连通而不是三相连通，如图2所示^[13]，T为接触线，R为钢轨.

图 2 潮流转移

Figure 2. Flow transfer

下载: 全尺寸图片幻灯片

双边供电系统中“电磁环网”存在潮流转移和穿越功率的问题.

1）潮流转移：当相邻两牵引变电所SS₁、SS₂间三相输电线发生故障时，根据选择性，仅断开K₁及K₂，由于双边供电分区所（SP）两侧供电臂被联通，三相输电线A相及B相功率可经牵引网继续传导，牵引变电所连接到高压侧的公共连接点P_CC,_K、P_CC,K+1之间的电气距离大大增加，系统稳定性水平可能下降，其中，K为牵引变电所序号.

2）穿越功率：牵引网作为电力系统的一个支路，会在电力系统中形成许多环网，电力系统中负荷潮流流过时，产生的穿越功率同时会在牵引网上造成分流，即均衡电流.

2. 均衡电流分析

2.1 均衡电流影响分析

均衡电流的影响主要体现在：1）电压损失，均衡电流会在牵引网上产生额外的电压降. 2）电能损失，均衡电流通过牵引网会产生额外电能损失. 3）影响牵引变压器，穿越功率是牵引供电系统实行双边供电时额外增加的功率，会额外占用牵引变压器部分容量；4）对电度计量的影响，若电度表可以反转，牵引变电所Q1只多计量均衡电流 ${{{\dot I}}_{\rm{q}}}$ 引起的牵引网损耗；若电度表不能反转，则从点a、b流入的穿越功率都将被计量表所计量，如所示^[3]， ${{{\dot I}}_{\rm{S}}}$ 为环网中的电流，k为牵引变压器统一变比，V、X对应V型和X型接线方式.

图 3 双边供电系统电能计量

Figure 3. Energy metering in bilateral power supply system

下载: 全尺寸图片幻灯片

2.2 均衡电流计算

双边供电根据外部电源供电方式的差异可分为平行双边供电和树形双边供电，有不同的等值电路模型，计算均衡电流时需分开讨论. 平行双边供电的外部电源供电方式包括双侧单回路、双侧双回路等，即牵引供电系统两侧均有三相电源的供电方式以及非终端情形的单侧双回路供电方式，此时，牵引网作为电力系统的一个支路，会在电力系统中形成许多个环网，产生均衡电流；树形双边供电的外部电源供电方式为包括牵引供电系统作为终端的单侧双回路供电方式、辐射型供电方式或树形结构供电方式，2个牵引变电所的电源进线接在变电站同一分段母线的不同分段上，两牵引变电所一次侧进线电压相等，不会产生均衡电流.

2.2.1 平行双边供电均衡电流计算

空载的平行双边供电系统等值电路如所示. 图中： ${{{\dot U}}_{{\text{A1}}}}$ 、 ${{{\dot U}}_{{\text{B1}}}}$ 、 ${{{\dot U}}_{{\text{C1}}}}$ 和 ${{{\dot U}}_{{\text{A2}}}}$ 、 ${{{\dot U}}_{{\text{B2}}}}$ 、 ${{{\dot U}}_{{\text{C2}}}}$ 分别为两侧三相电力系统电压， ${L_1}$ 为左侧三相电源到P_CC,₁的距离， ${L_2}$ 为P_CC,₁和P_CC,₂之间的距离， ${L_3}$ 为右侧三相电源到P_CC,₂的距离， ${Z_{\text{D}}}$ 为三相电力输电线的单位阻抗， $L$ 为构成双边供电的2个牵引变电所之间的距离， ${{{\dot U}}_{{\text{S1}}}}$ 、 ${{{\dot U}}_{{\text{S11}}}}$ 和 ${{{\dot U}}_{{\text{S2}}}}$ 、 ${{{\dot U}}_{{\text{S22}}}}$ 分别为2个牵引变压器原、次边电压，Z_J11、Z_J12、Z_J21、Z_J22、Z_TT1、Z_TT2为牵引变压器等效阻抗， ${{{\dot I}}_{\text{f}}}$ 为均衡电流，T1为接触线1，R1为钢轨1，T2为接触线2，R2为钢轨2，Z₁为接触线等效阻抗，Z₂为钢轨等效阻抗.

图 4 平行双边供电系统等值电路

Figure 4. Equivalent circuit diagram of parallel bilateral power supply system

下载: 全尺寸图片幻灯片

根据图4中三相电力输电线的电压差，可以得到

$\left\{ \begin{gathered} {{{\dot U}}_{{\text{A1}}}} - {{{\dot U}}_{{\text{A2}}}} = {Z_{\text{D}}}\left( {{L_1} + {L_2} + {L_3}} \right){{{\dot I}}_{\text{A}}}, \\ {{{\dot U}}_{{\text{B1}}}} - {{{\dot U}}_{{\text{B2}}}} = {Z_{\text{D}}}\left( {{L_1} + {L_2} + {L_3}} \right){{{\dot I}}_{\text{B}}} - {Z_{\text{D}}}{L_2}{{{\dot I}}_{\text{f}}}, \\ {{{\dot U}}_{{\text{C1}}}} - {{{\dot U}}_{{\text{C2}}}} = {Z_{\text{D}}}\left( {{L_1} + {L_2} + {L_3}} \right){{{\dot I}}_{\text{C}}} + {Z_{\text{D}}}{L_2}{{{\dot I}}_{\text{f}}}. \end{gathered} \right.$

(1)

通过2台牵引变压器原边和次边的节点电压电流关系，可以得到

$\left\{ \begin{gathered} {{{\dot U}}_{{\text{S1}}}} - {{{\dot U}}_{{\text{S2}}}} = \left[ {\left( {{{{\dot I}}_{\text{B}}} - {{{\dot I}}_{\text{f}}}} \right) - \left( {{{{\dot I}}_{\text{C}}} + {{{\dot I}}_{\text{f}}}} \right)} \right]{Z_{\text{D}}}{L_2} - \\ \quad {{{\dot I}}_{\text{f}}}{Z_{{\text{JS}}}} = k\left( {{{{\dot U}}_{{\text{S11}}}} - {{{\dot U}}_{{\text{S22}}}}} \right), \\ {{{\dot U}}_{{\text{S11}}}} - {{{\dot U}}_{{\text{S22}}}} = k{{{\dot I}}_{\text{f}}}\left( {\bar ZL + {Z_{{\text{TT1}}}} + {Z_{{\text{TT2}}}}} \right), \\ \end{gathered} \right.$

(2)

式中： ${Z_{{\text{JS}}}} = {Z_{{\text{J11}}}} + {Z_{{\text{J12}}}} + {Z_{{\text{J21}}}} + {Z_{{\text{J22}}}}$ ， $\bar Z = \left( {{Z_1} + {Z_2}} \right)/2$ .

根据式（1）和式（2），解得

$\left\{\begin{array}{l} \dot{I}_{\mathrm{f}}=\dfrac{k_{\mathrm{f}}\left(\Delta {{\dot U}}_{\mathrm{B}}-\Delta {{\dot U}}_{\mathrm{c}}\right)}{Z_{\mathrm{D}}\left(L_{1} + L_{2} + L_{3}\right)-2 k_{\mathrm{f}} Z_{\mathrm{D}} L_{2}}, \\ k_{\mathrm{f}}=\dfrac{Z_{\mathrm{D}} L_{2}}{2 Z_{\mathrm{D}} L_{2} + Z_{\mathrm{JS}} + k^{2}\left(\bar{Z} L + Z_{\mathrm{TT1}} + Z_{\mathrm{TT2}}\right)}, \end{array}\right.$

(3)

式中：k_f为阻抗系数；Z_JS为进线阻抗； $\Delta {{{\dot U}}_{\text{B}}} = {{{\dot U}}_{{\text{B1}}}} - {{{\dot U}}_{{\text{B2}}}}$ ， $\Delta {{{\dot U}}_{\text{C}}} = {{{\dot U}}_{{\text{C1}}}} -{{{\dot U}}_{{\text{C2}}}}$ .

2.2.2 树形双边供电均衡电流计算

空载的树形双边供电系统等值电路如所示. 图中： ${{{{\dot I}}}_{{\text{f}}1}}$ 和 ${{{\dot I}}_{{\text{f}}2}}$ 分别为2个牵引变压器原边测量的实际均衡电流， ${k_1}$ 和 ${k_2}$ 分别为2个牵引变压器的实际变比.

图 5 树形双边供电系统等值电路

Figure 5. Equivalent circuit diagram of tree bilateral power supply system

下载: 全尺寸图片幻灯片

2台牵引变压器原边和次边的节点电压方程为

$\left\{ \begin{gathered} {{{\dot U}}_{{\text{S}}1}} = {k_1}{{{\dot U}}_{{\text{S}}11}} = {{{\dot U}}_{\text{B}}} - {{{\dot U}}_{\text{C}}} - \left( {{Z_{{\text{J11}}}} + {Z_{{\text{J12}}}}} \right){{{\dot I}}_{{\text{f}}1}}, \\ {{{\dot U}}_{{\text{S}}2}} = {k_2}{{{\dot U}}_{{\text{S22}}}} = {{{\dot U}}_{\text{B}}} - {{{\dot U}}_{\text{C}}} - \left( {{Z_{{\text{J21}}}} + {Z_{{\text{J22}}}}} \right){{{\dot I}}_{{\text{f2}}}}, \\ {{{\dot U}}_{{\text{S}}11}} - {{{\dot U}}_{{\text{S22}}}} = {k_1}{{{\dot I}}_{{\text{f}}1}}\left( {{Z_{{\text{TT1}}}} + {Z_{{\text{TT2}}}} + \frac{{{Z_1} + {Z_2}}}{2}L} \right), \\ {k_1}{{{\dot I}}_{{\text{f}}1}} + {k_2}{{{\dot I}}_{{\text{f2}}}} = 0. \\ \end{gathered} \right.$

(4)

解式得（4），均衡电流 ${{{\dot I}}_{{\text{f}}1}}{\text{ = }}{{{\dot I}}_{{\text{f2}}}}{\text{ = }}0$ ，即线路中不存在均衡电流. 双边供电的两牵引变电所进线处存在电压差时均可等值为平行双边供电系统，而树形双边供电的外部电源呈树形结构，牵引变电所的电源进线来自电力变电站同一分段母线的不同分段，因此平行双边供电模型相较于树形双边供电适用性更强.

3. 实例分析

以某市域线路为例，其牵引供电系统由110 kV牵引变电所Q1、Q2、Q3、Q4（预留）分段供电. 为保证市域铁路的持续可靠供电，考虑运行时将3个变比为110 kV/27.5 kV的牵引变压器在低压27.5 kV侧合环运行，实现列车运行的不间断供电. 该方案改变了目前城市电网在配电网侧辐射状的电网结构，合环时跨越了较多的电压等级，构成电磁环网结构，因此需要考虑在正常运行时合环线路的潮流情况，防止合环线路潮流穿越功率太大，超过线路的载流能力. 牵引变压器可以短时（2 h）承受的最大功率为100 MV·A；110 kV线路采用的是截面积为1600 mm²的电缆，能承受的最大电流为1000 A；27.5 kV刚性接触网型号为CTA150 + HL2213，能承受的最大电流为3500 A. 合环示意如图6所示.

图 6 低压27.5 kV侧合环运行方案

Figure 6. Closing ring operation scheme at low voltage 27.5 kV side

下载: 全尺寸图片幻灯片

对电网的网架结构初步分析，4个牵引变电所位于3个500 kV供电区，3个500 kV变电站之间有潮流分布，如图7所示.

图 7 电网架构

Figure 7. Power grid architecture

下载: 全尺寸图片幻灯片

3.1 合环线路均衡电流分析

3.1.1 合环线路均衡电流计算

市域线路在27.5 kV侧合环运行，即两两牵引变电所双边供电，可能会产生均衡电流，根据线路的网架结构，结合2.2节，推导出均衡电流的计算模型，如所示. 图中： ${{{\dot U}}_{{\rm{{Q1}A}}}}$ 、 ${{{\dot U}}_{{\rm{{Q1}B}}}}$ 、 ${{{\dot U}}_{{\rm{{Q1}C}}}}$ （ ${{{\dot U}}_{{\rm{{Q2}A}}}}$ 、 ${{{\dot U}}_{{\rm{{Q2}B}}}}$ 、 ${{{\dot U}}_{{\rm{{Q2}C}}}}$ 、 ${{{\dot U}}_{{\rm{{Q3}A}}}}$ 、 ${{{\dot U}}_{{\rm{{Q3}B}}}}$ 、 ${{{\dot U}}_{{\rm{{Q3}C}}}}$ ）分别为牵引变电所Q1（Q2、Q3）的三相电源电压； ${{{\dot I}}_{{\rm{{Q{1}}q}}}}$ 、 ${{{\dot I}}_{{\rm{{Q{2}}q}}}}$ 、 ${{{\dot I}}_{{\rm{{Q{3}}q}}}}$ 分别为牵引变电所Q1、Q2、Q3到合环点的均衡电流； ${{{\dot I}}_{{\rm{{Q{12}}A}}}}$ 、 ${{{\dot I}}_{{\rm{{Q{12}}B}}}}$ 、 ${{{\dot I}}_{{\rm{{Q{12}}C}}}}$ 为牵引变电所Q1流向Q2的三相电流； ${{{\dot I}}_{{\rm{{Q{23}}A}}}}$ 、 ${{{\dot I}}_{\rm{{Q{23}}B}}}$ 、 ${{{\dot I}}_{\rm{{Q{23}}C}}}$ 为牵引变电所Q2流向Q3的三相电流； ${{{\dot I}}_{\rm{{Q{13}}A}}}$ 、 ${{{\dot I}}_{\rm{{Q{13}}B}}}$ 、 ${{{\dot I}}_{\rm{{Q{13}}C}}}$ 为牵引变电所Q1流向Q3的三相电流； ${Z_{{\rm{S{Q1}}}}}$ 、 ${Z_{{\rm{SQ2}}}}$ 、 ${Z_{{\rm{SQ3}}}}$ 为电力系统的短路阻抗； ${Z_{{\rm{jQ1}}}}$ 、 ${Z_{{\rm{jQ2}}}}$ 、 ${Z_{{\rm{jQ3}}}}$ 电力系统到变电站的进线阻抗； ${Z_{{\rm{TQ1}}}}$ 、 ${Z_{{\rm{TQ2}}}}$ 、 ${Z_{{\rm{TQ3}}}}$ 为牵引变压器归算到牵引侧的漏抗； ${Z_{{\rm{dQ12}}}}$ 、 ${Z_{{\rm{dQ13}}}}$ 、 ${Z_{{\rm{dQ23}}}}$ 分别为牵引变电所Q1到Q2、Q1到Q3、Q2到Q3之间的传输线阻抗； ${L_{\rm{{Q1}}}}$ 、 ${L_{\rm{Q2}}}$ 、 ${L_{{\rm{Q3}}}}$ 分别为牵引变电所Q1、Q2、Q3到合环点的距离； ${Z_{\text{q}}}$ 为牵引网单位阻抗. 各牵引变电所带的负荷见表1，牵引网阻抗值为0.0440 + 0.371 0i Ω/km.

图 8 市域线路均衡电流的计算模型

Figure 8. Calculation model of equilibrium current for suburban lines

下载: 全尺寸图片幻灯片

表 1 变电所正常运行时牵引负荷

Table 1. Traction loads at substations

主变电所	牵引负荷/ (MV·A)	牵引变压器接线形式	牵引变压器容量/ (MV·A)	同相供电容量配置/ (MV·A)
Q1	44.7	单相	2 × （40 + 10）	5
Q2	64.0	单相	2 × （40 + 10）	5
Q3	62.9	单相	2 × （40 + 10）	5
Q4	20.0	单相	2 × （40 + 10）	5

下载: 导出CSV

| 显示表格

可利用叠加原理计算3个牵引变电所合环的均衡电流，先计算每2个牵引变电所之间的均衡电流，再进行叠加. 结合2.2节均衡电流的计算公式得到Q1与Q2之间的均衡电流 ${{{\dot I}}_{{\rm{Q{12}q}}}}$ 、Q2与Q3之间的均衡电流 ${{{\dot I}}_{{\rm{Q{23}q}}}}$ 、Q1与Q3之间的均衡电流 ${{{\dot I}}_{{\rm{Q{13}q}}}}$ 分别为

$\qquad\qquad\qquad{{{\dot I}}}_{\rm{Q{12}q}}=\dfrac{{{\dot U}}_{\rm{Q1A}}-{{\dot U}}_{\rm{Q1B}}-{{\dot U}}_{\rm{Q2A}} + {{\dot U}}_{\rm{Q2B}} + ({{\dot I}}_{\rm{Q{12}B}}-{{\dot I}}_{\rm{Q{12}A}}){Z}_{\rm{SQ1}}-({{\dot I}}_{\rm{Q{12}A}}-{{\dot I}}_{\rm{Q12B}}){Z}_{\rm{SQ2}}}{k[{Z}_{\rm{TQ1}} + {Z}_{\rm{TQ2}} + ({L}_{\rm{Q1}} + {L}_{\rm{Q2}}){{\textit{z}}}_{\rm{q}}] + \dfrac{2}{k}({Z}_{\rm{jQ1}} + {Z}_{\rm{jQ2}} + {Z}_{\rm{SQ1}} + {Z}_{\rm{SQ2}})},$

(5)

$\qquad\qquad\qquad {{{\dot I}}_{{\rm{Q{23}q}}}} = \dfrac{{{{{\dot U}}_{{\rm{Q2A}}}} - {{{\dot U}}_{{\rm{Q2B}}}} - {{{\dot U}}_{{\rm{Q3A}}}} + {{{\dot U}}_{{\rm{Q3B}}}} + ({{{\dot I}}_{{\rm{Q{23}B}}}} - {{{\dot I}}_{{\rm{Q{23}A}}}}){Z_{{\rm{SQ2}}}} - ({{{\dot I}}_{{\rm{Q{23}A}}}} - {{{\dot I}}_{{\rm{Q{23}B}}}}){Z_{{\rm{SQ3}}}}}}{{k[{Z_{{\rm{TQ2}}}} + {Z_{{\rm{TQ3}}}} + ({L_{{\rm{Q2}}}} + {L_{{\rm{Q3}}}}){{\textit{z}}_{\rm{q}}}] + \dfrac{2}{k}({Z_{{\rm{jQ2}}}} + {Z_{{\rm{jQ3}}}} + {Z_{{\rm{SQ2}}}} + {Z_{{\rm{SQ3}}}})}},$

(6)

$\qquad\qquad\qquad{{{\dot I}}_{{\rm{Q{13}q}}}} = \dfrac{{{{{\dot U}}_{{\rm{Q1A}}}} - {{{\dot U}}_{{\rm{Q1B}}}} - {{{\dot U}}_{{\rm{Q3A}}}} + {{{\dot U}}_{{\rm{Q3B}}}} + ({{{\dot I}}_{{\rm{Q{13}B}}}} - {{{\dot I}}_{{\rm{Q{13}A}}}}){Z_{{\rm{SQ1}}}} - ({{{\dot I}}_{{\rm{Q{13}A}}}} - {{{\dot I}}_{{\rm{Q{13}B}}}}){Z_{{\rm{SQ2}}}}}}{{k[{Z_{{\rm{TQ1}}}} + {Z_{{\rm{TQ3}}}} + ({L_{\rm{Q1}}} + {L_{{\rm{Q3}}}}){{\textit{z}}_{\rm{q}}}] + \dfrac{2}{k}({Z_{{\rm{jQ1}}}} + {Z_{{\rm{jQ3}}}} + {Z_{{\rm{SQ1}}}} + {Z_{{\rm{SQ3}}}})}}.$

(7)

利用叠加原理，得到牵引变电所Q1、Q2、Q3到合环点的均衡电流分别为

$\begin{split} \\ {{{\dot I}}_{{\rm{Q1q}}}} = {{{\dot I}}_{{\rm{Q{12}q}}}} + {{{\dot I}}_{{\rm{Q{13}q}}}}, \end{split}$

(8)

${{{\dot I}}_{{\rm{Q2q}}}} = - {{{\dot I}}_{{\rm{Q{12}q}}}} + {{{\dot I}}_{{\rm{Q{23}q}}}},$

(9)

${{{\dot I}}_{{\rm{Q3q}}}} = - {{{\dot I}}_{{\rm{Q{23}q}}}} - {{{\dot I}}_{{\rm{Q{13}q}}}}.$

(10)

根据电网架构和线路的参数，测得电网正常运行和出现各类故障（110、220 kV电网侧环网故障解环）时各牵引变电所110 kV高压侧电压的变化范围，Q1高压侧的电压为110∠−26.052°～110∠−26.881° kV，Q2高压侧的电压为110∠−29.409°～110∠−29.513° kV，Q3高压侧的电压为110∠−32.897°～110∠−33.236° kV，可计算Q1与Q2高压侧的电压相角差α₁₂变化范围约为0～4°，Q1与Q3高压侧的电压相角差α₁₃变化范围约为0～8°，Q2与Q3高压侧的电压相角差α₂₃变化范围约为0～4° 时合环线路上的均衡电流大小，如图9所示.

图 9 牵引变电所Q1、Q2、Q3到合环点的均衡电流计算值

Figure 9. Calculation values of equilibrium currents from traction substation Q1, Q2, Q3 to loop closing point

下载: 全尺寸图片幻灯片

由图9可知：3个牵引变电所的电压相角差为0时，均衡电流也为0；牵引变电所到合环点的均衡电流随着该牵引变电所与其余牵引变电所的电压相角差增大而增大；3个牵引变电所的穿越功率最大值为1.500、1.375、1.125 MV·A，穿越功率占牵引变压器容量比最大为3%.

3.1.2 合环线路均衡电流仿真

在MATLAB/simulink软件中建立合环线路均衡电流的仿真模型，如所示，并进行仿真计算，得到牵引变电所Q1、Q2、Q3到合环点的均衡电流仿真值 ${\dot I}_{{\rm{fQ1q}}}$ 、 ${\dot I}_{{\rm{fQ2q}}}$ 、 ${\dot I}_{{\rm{fQ3q}}}$ ，如图11所示.

图 10 合环线路均衡电流的计算模型

Figure 10. Calculation model of equilibrium currents in closed-loop lines

下载: 全尺寸图片幻灯片

图 11 牵引变电所Q1、Q2、Q3到合环点的均衡电流仿真值

Figure 11. Simulation values of equilibrium currents from traction substation Q1、Q2、Q3 to loop closing point

下载: 全尺寸图片幻灯片

使用合环线路均衡电流的仿真结果验证均衡电流计算模型的正确性，得出均衡电流的最大值为 60.264 A，占比为2.322%.

3.2 合环线路潮流仿真

使用MATLAB/simulink软件搭建牵引变电所Q1、Q2、Q3、Q4在27.5 kV侧合环运行的市域铁路牵引供电系统模型，如图12所示，仿真模型中E、F、G、H、I、J、K为系统侧电力变压器，L1～L10为系统侧输电线路阻抗，仿真考虑市域铁路供电在夜间停运和高峰时段运行2种工况.

图 12 市域铁路牵引供电系统仿真模型

Figure 12. Simulation model of traction power supply system for suburban railways

下载: 全尺寸图片幻灯片

夜间解环、夜间合环、高峰时段合环、牵引供电所解列时电网的潮流分布，如图13所示，牵引变压器承受的最大功率为70.36 MV·A，电压波动最大为0.7025%，在牵引变压器承受范围内；110 kV线路承受的最大电流为833.418 A，27.5 kV接触网承受的最大电流为2595.789 A，均未超过线路载流能力.

图 13 合环线路潮流仿真（MV·A）

Figure 13. Power flow simulation for loop closing line (MV·A)

下载: 全尺寸图片幻灯片

4. 结　论

市域铁路单相交流牵引供电系统采用双边供电方式时，可能存在电磁环网和均衡电流的问题.

1）电磁环网：双边供电系统中“电磁环网”主要存在潮流转移和穿越功率的问题，潮流转移可能会影响系统稳定性，穿越功率会在牵引网上造成均衡电流.

2）均衡电流：双边供电系统的均衡电流与外部电源供电方式有关，若施行双边供电的两牵引变电所进线处存在电压差，则会导致在牵引网上产生分流，即均衡电流. 外部电源呈树形结构时，牵引变电所的电源进线来自一个电力变电站同一分段母线的不同分段，电压差为0，因此树形双边供电不产生均衡电流. 国家标准中并没有明确给出均衡电流的取值范围，只能通过减小电力系统变电所间等值阻抗或增大牵引供电系统阻抗达到减小均衡电流的目的.

3）以某市域线路为例进行仿真计算可以发现，双边供电系统中“电磁环网”对电网的潮流分布的影响均在牵引变压器、线路的承受范围内，即双边供电在稳态情况下不会对电网的安全运行造成影响；合环线路中均衡电流占比为2.322%，侧面反映均衡电流对系统影响较小. 但这些结论只针对目前分析的市域线路，其余的市域线路如果要采用双边供电还需根据实际情况分析.

致谢：广州地铁设计研究院股份有限公司科技项目（R110421H01090）.

图 1 循环温度机制示意

Figure 1. Schematic diagram of circulating temperature mechanism

下载: 全尺寸图片幻灯片

图 2 保温性能试验试件及仪器照片

Figure 2. Thermal insulation performance test specimens and instrument photo

下载: 全尺寸图片幻灯片

图 3 养护方式示意

Figure 3. Schematic of curing methods

下载: 全尺寸图片幻灯片

图 4 约束收缩处理方式示意

Figure 4. Schematic of restraint shrinkage processing

下载: 全尺寸图片幻灯片

图 5 涂层保温性能试验结果

Figure 5. Test results of coating thermal insulation performance

下载: 全尺寸图片幻灯片

图 6 不同龄期3种养护方式下混凝土抗压强度

Figure 6. Compressive strength of concrete under three curing methods at different ages

下载: 全尺寸图片幻灯片

图 7 不同龄期3种养护方式下混凝土劈裂抗拉强度

Figure 7. Splitting tensile strength of concrete under three curing methods at different ages

下载: 全尺寸图片幻灯片

图 8 不同龄期3种不同养护方式下混凝土收缩率

Figure 8. Shrinkage rate of concrete under three curing methods at different ages

下载: 全尺寸图片幻灯片

图 9 3种养护方式下约束应力随龄期的变化曲线

Figure 9. Curves of restraint stress with age under three curing methods

下载: 全尺寸图片幻灯片

图 10 3种养护方式下最大约束应力随龄期的变化曲线

Figure 10. Curves of maximum restraint stress with age under three curing methods

下载: 全尺寸图片幻灯片

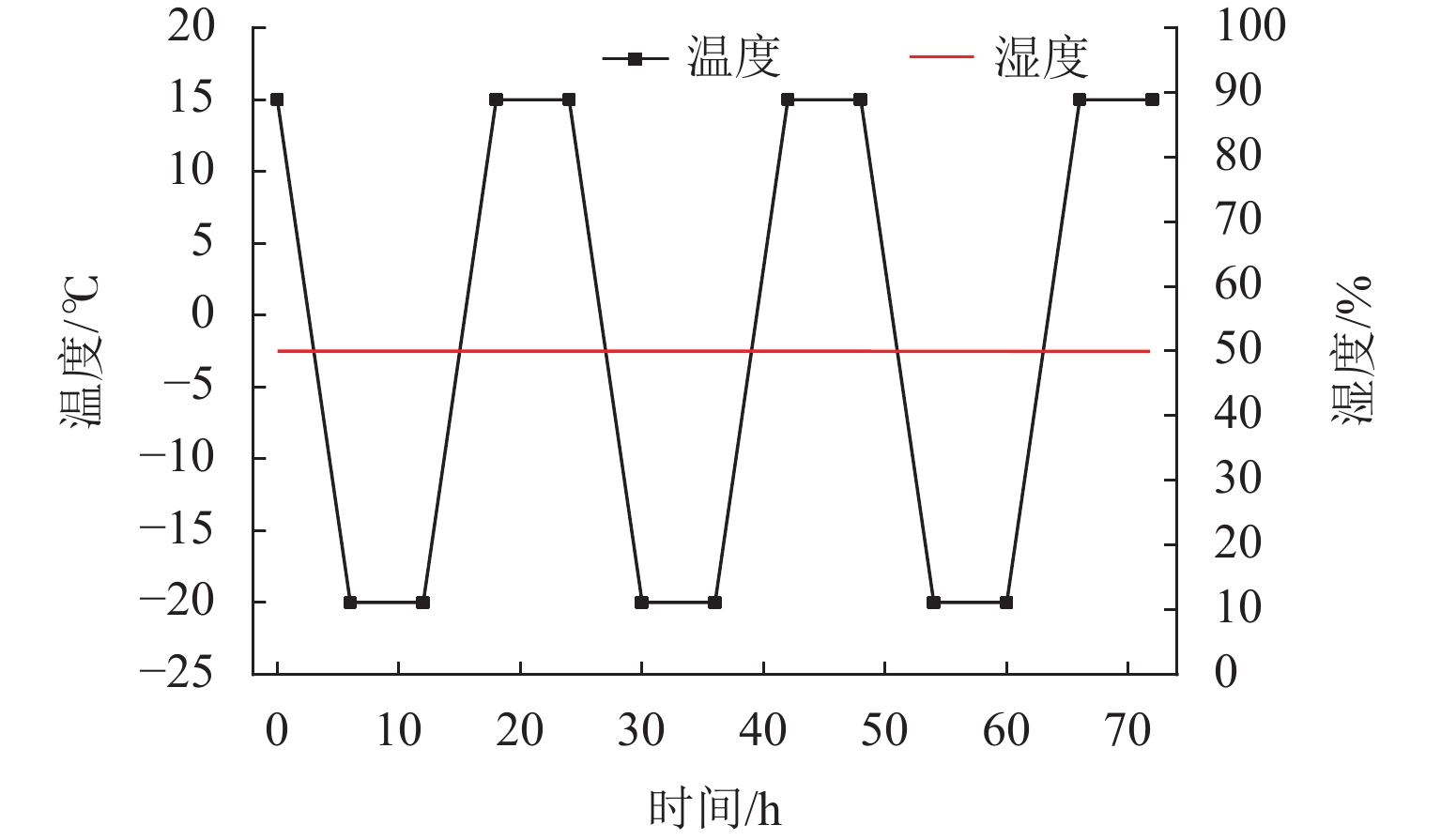
表 1 涂层保温性能试验设计表

Table 1. Test design table of coating thermal insulation performance

试件编号	循环温度/℃	保温隔热涂层厚度/mm				测试时长/d	试件个数/个
试件编号	循环温度/℃	底涂层	中涂层	面涂层	总厚度	测试时长/d	试件个数/个
1	−20.0～15.0	0.1	1.0	0.1	1.2	7	2
2	−20.0～15.0					7	2

下载: 导出CSV

表 2 混凝土各项性能测试结果汇总

Table 2. Summary of concrete performance test results

养护方式	劈裂抗拉强度/MPa	抗压强度/MPa	最大自由收缩率/ × 10⁻³	最大约束应力/MPa
自然养护	0.91	19.78	1.601	1.06
薄膜养护	1.06	20.81	1.544	0.84
涂层养护	1.20	21.62	1.494	0.72

下载: 导出CSV

表 3 矩阵判断各元素选取标准^[24]

Table 3. Judgement matrix criteria for selecting each element

标度值	意义
1	X_ai 与 X_jb 重要性相同
3	X_ai 比 X_jb 稍重要
5	X_ai 比 X_jb 明显重要
2、4	X_ai 比 X_jb 重要性介于相邻标度值之间
上面各行标度值的倒数	相比于 X_ai、X_jb 的重要性

下载: 导出CSV

参考文献(24)

[1]	赵文斌,刘建勋,张戎令,等. 强风、干寒、大温差地区混凝土箱梁早期抗裂性分析[J]. 硅酸盐通报,2016,35(10): 3253-3257,3273. ZHAO Wenbin, LIU Jianxun, ZHANG Rongling, et al. Strongly windy and dry cold large temperature difference analysis on early cracking of concrete box girder[J]. Bulletin of the Chinese Ceramic Society, 2016, 35(10): 3253-3257,3273.
[2]	陈华鑫,王铜,何锐,等. 高原复杂气候环境对混凝土气孔结构与力学性能的影响[J]. 长安大学学报(自然科学版),2020,40(2): 30-37. CHEN Huaxin, WANG Tong, HE Rui, et al. Effect of complex climatic environment on pore structure and mechanical properties of concrete[J]. Journal of Chang’an University (Natural Science Edition), 2020, 40(2): 30-37.
[3]	胡玉兵,曹瑞普. 高原地区混凝土内外部结构性能的差异性研究[J]. 硅酸盐通报,2017,36(增1): 213-218. HU Yubing, CAO Ruipu. Differences of internal and external structural properties of concrete in the plateau area[J]. Bulletin of the Chinese Ceramic Society, 2017, 36(S1): 213-218.
[4]	AL-SALEH S A, AL-ZAID R Z. Effects of drying conditions, admixtures and specimen size on shrinkage strains[J]. Cement and Concrete Research, 2006, 36(10): 1985-1991. doi: 10.1016/j.cemconres.2004.11.005
[5]	TORRENTI J M, GRANGER L, DIRUY M, et al. Modeling concrete shrinkage under variable ambient conditions[J]. ACI Materials Journal, 1999, 96(1): 35-39.
[6]	EMBORG M, BERNANDER S. Assessment of risk of thermal cracking in hardening concrete[J]. Journal of Structural Engineering, 1994, 120(10): 2893-2912. doi: 10.1061/(ASCE)0733-9445(1994)120:10(2893)
[7]	TENG L W, HUANG R, CHEN J, et al. A study of crystalline mechanism of penetration sealer materials[J]. Materials, 2014, 7(1): 399-412. doi: 10.3390/ma7010399
[8]	SALAZAR-HERNÁNDEZ C, ALQUIZA M J P, SALGADO P, et al. TEOS-colloidal silica-PDMS-OH hybrid formulation used for stone consolidation[J]. Applied Organometallic Chemistry, 2010, 24(6): 481-488.
[9]	CERVANTES J, ZARRAGA R, SALAZAR-HERNANDEZ C. ChemInform abstract: organotin catalysts in organosilicon chemistry[J]. ChemInform, 2012, 43(39): 157-163.
[10]	张戎令,王起才,刘树红,等. 极端大温差、干旱戈壁地区桥墩养护方法研究[J]. 兰州交通大学学报,2014,33(4): 49-55. ZHANG Rongling, WANG Qicai, LIU Shuhong, et al. Research on method of pier maintenance in gobi region of extreme large temperature difference and drought[J]. Journal of Lanzhou Jiaotong University, 2014, 33(4): 49-55.
[11]	高鹏,陈阳,黄浩良,等. 干燥环境下混凝土内部损伤的量化[J]. 硅酸盐学报,2021,49(2): 312-322. GAO Peng, CHEN Yang, HUANG Haoliang, et al. Quantification of damage in concrete under drying condition[J]. Journal of the Chinese Ceramic Society, 2021, 49(2): 312-322.
[12]	魏亚,郑小波,郭为强. 干燥环境下内养护混凝土收缩、强度及开裂性能[J]. 建筑材料学报,2016,19(5): 902-908. WEI Ya, ZHENG Xiaobo, GUO Weiqiang. Shrinkage, strength development and cracking of internally cured concrete exposed to dry conditions[J]. Journal of Building Materials, 2016, 19(5): 902-908.
[13]	中国建筑科学研究院有限公司. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019.
[14]	中国建筑科学研究院. 普通混凝土长期性能和耐久性能试验方法标准: GB/T 50082—2009[S]. 北京: 中国建筑工业出版社, 2009.
[15]	QIN Y, YI Z J, WANG W N, et al. Time-dependent behavior of shrinkage strain for early age concrete affected by temperature variation[J]. Advances in Materials Science and Engineering, 2017, 2017: 1-7.
[16]	曾启. 温度循环作用后混凝土力学性能试验研究及破坏机理分析[D]. 广州: 华南理工大学, 2018.
[17]	邵爽爽. 蒸养混凝土超早龄期性能与开裂分析[D]. 青岛: 青岛理工大学, 2019.
[18]	苏安双. 高性能混凝土早期收缩性能及开裂趋势研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
[19]	CORTAS R, ROZIÈRE E, STAQUET S, et al. Effect of the water saturation of aggregates on the shrinkage induced cracking risk of concrete at early age[J]. Cement and Concrete Composites, 2014, 50: 1-9. doi: 10.1016/j.cemconcomp.2014.02.006
[20]	LI H, LIU J P, WANG Y J, et al. Deformation and cracking modeling for early-age sidewall concrete based on the multi-field coupling mechanism[J]. Construction and Building Materials, 2015, 88: 84-93. doi: 10.1016/j.conbuildmat.2015.03.005
[21]	王树和,水中和,玄东兴. 大温差环境条件下混凝土表面裂缝损伤[J]. 东南大学学报(自然科学版),2006,36(增2): 122-125. WANG Shuhe, SHUI Zhonghe, XUAN Dongxing. Investigation on surface cracking damage of concrete under big temperature difference[J]. Journal of Southeast University (Natural Science Edition), 2006, 36(S2): 122-125.
[22]	ALY T, SANJAYAN J G. Mechanism of early age shrinkage of concretes[J]. Materials and Structures, 2009, 42(4): 461-468. doi: 10.1617/s11527-008-9394-6
[23]	张强勇,王保群,向文. 盐岩地下储气库风险评价层次分析模型及应用[J]. 岩土力学,2014,35(8): 2299-2306. ZHANG Qiangyong, WANG Baoqun, XIANG Wen. Hierarchical analytical model of risk evaluation for underground salt rock gas storage and its application[J]. Rock and Soil Mechanics, 2014, 35(8): 2299-2306.
[24]	王卓甫. 工程项目风险管——理论、方法与应用[M]. 北京: 中国水利水电出版社, 2003.

施引文献

附加材料(0)

访问统计

点击查看大图

图(10) / 表(3)

计量

文章访问数: 395
HTML全文浏览量: 247
PDF下载量: 57
被引次数: 0

1. 电磁环网分析
1.1 电磁环网形成的原因
1.2 双边供电系统中“电磁环网”分析
2. 均衡电流分析
2.1 均衡电流影响分析
2.2 均衡电流计算
3. 实例分析
3.1 合环线路均衡电流分析
3.2 合环线路潮流仿真
4. 结　论

干寒大温差下早龄期混凝土收缩特性及防裂技术

doi: 10.3969/j.issn.0258-2724.20210839

作者简介: 李福海（1979—），男，高级工程师，博士，研究方向为混凝土耐久性、高性能混凝土等，E-mail：lifuhai2007@swjtu.edu.cn

计量

出版历程