Coupled Vibration Between Low-Medium Speed Maglev Vehicle and Turnout
-
摘要:
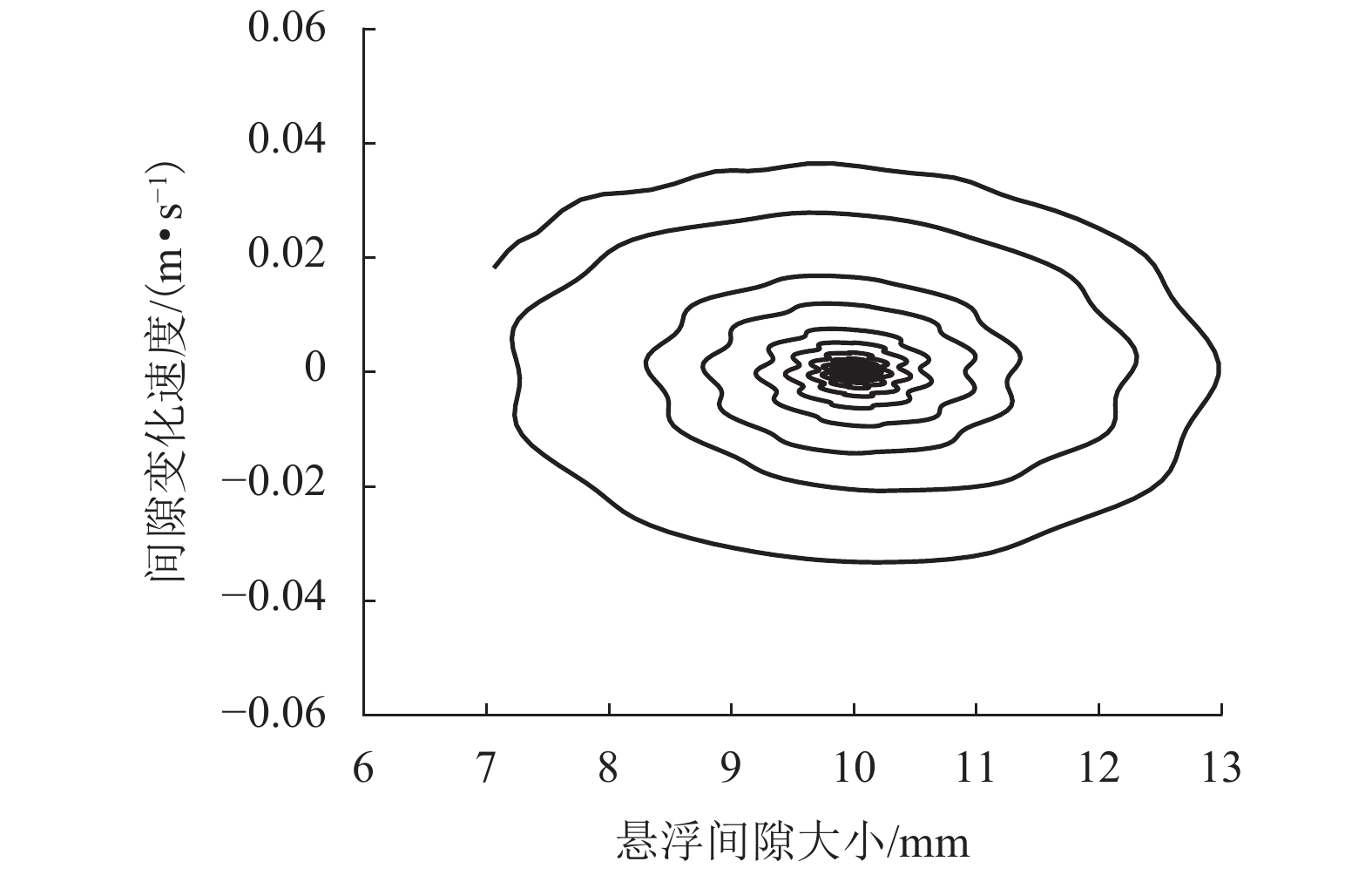
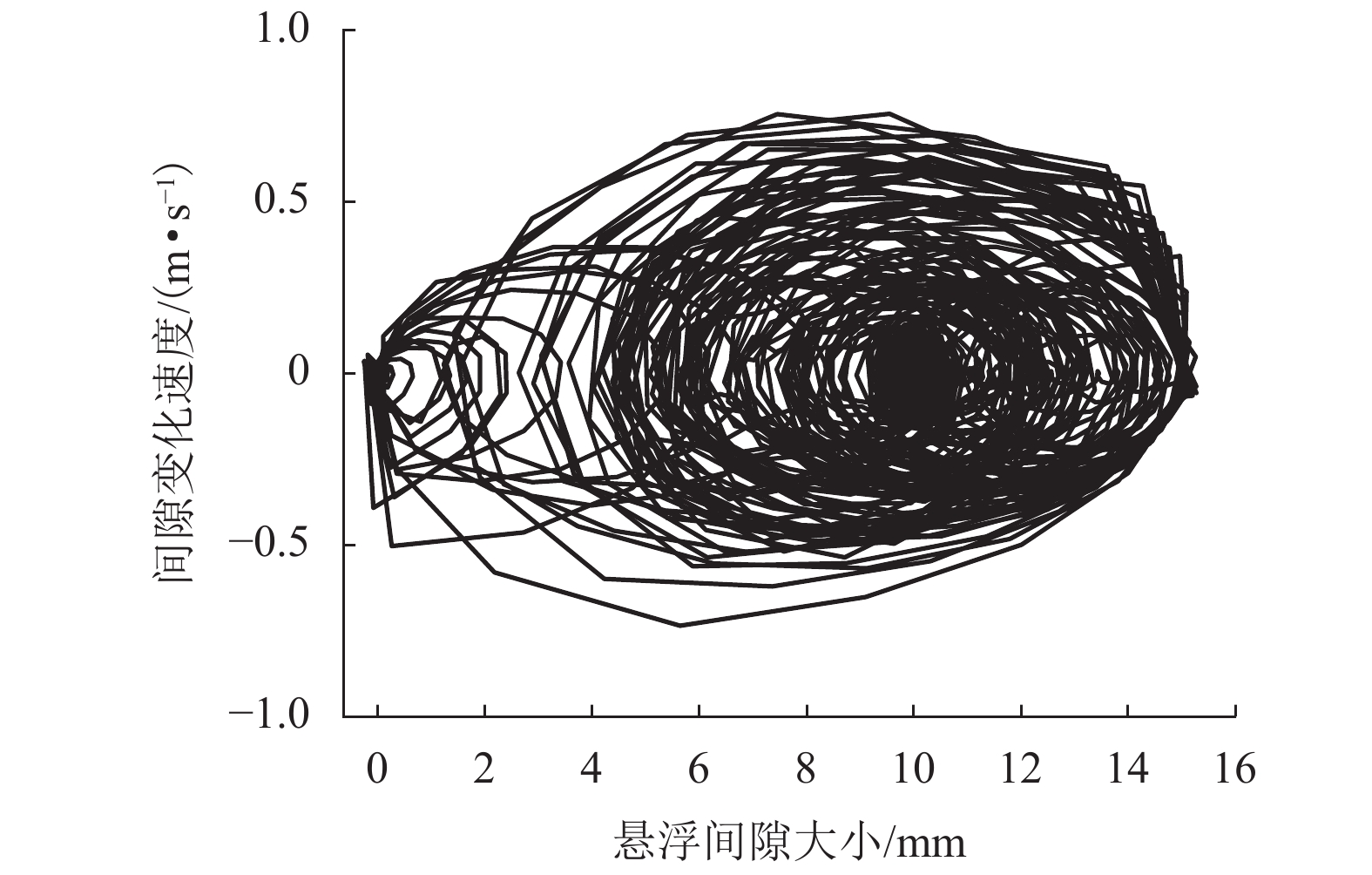
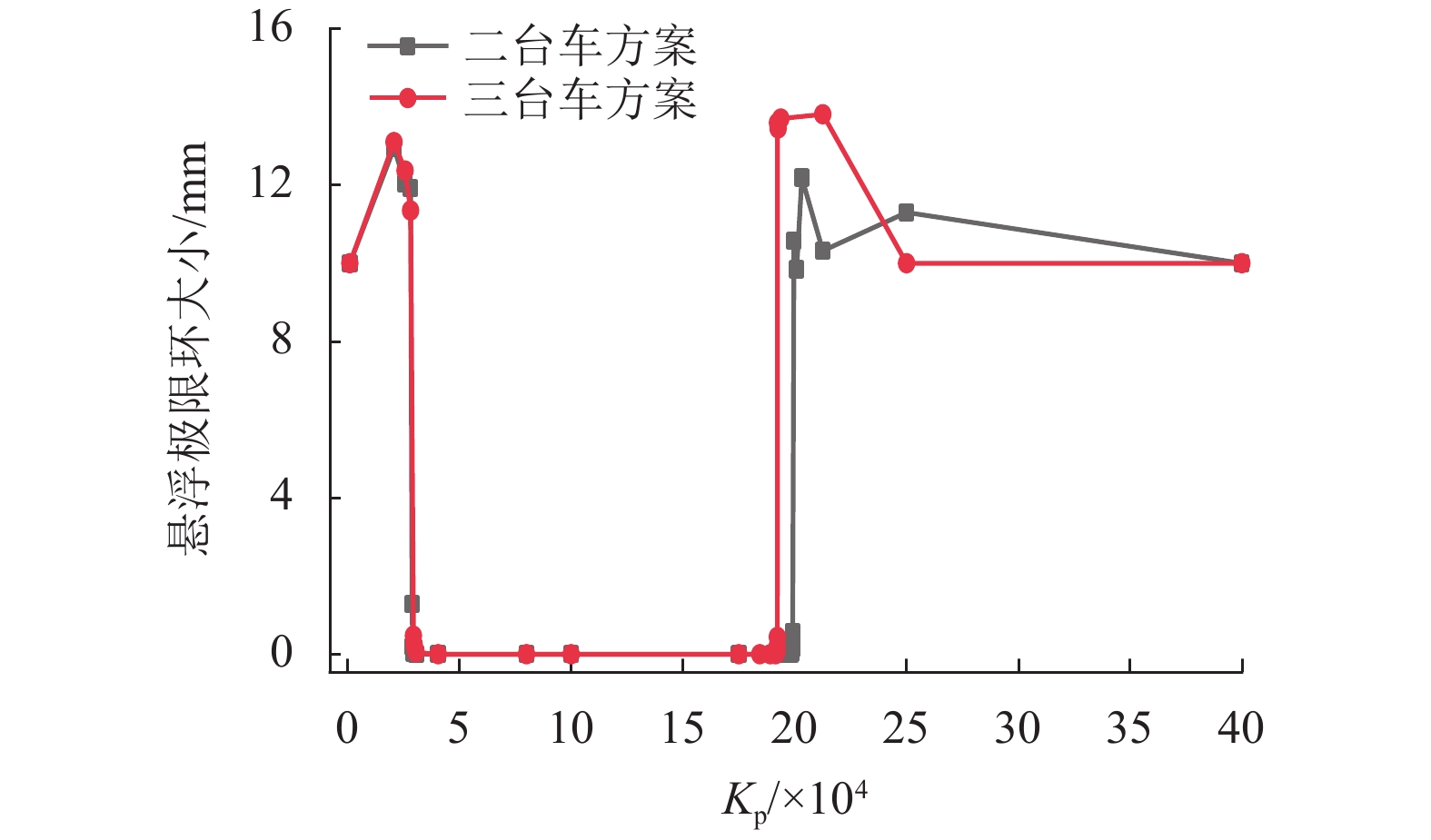
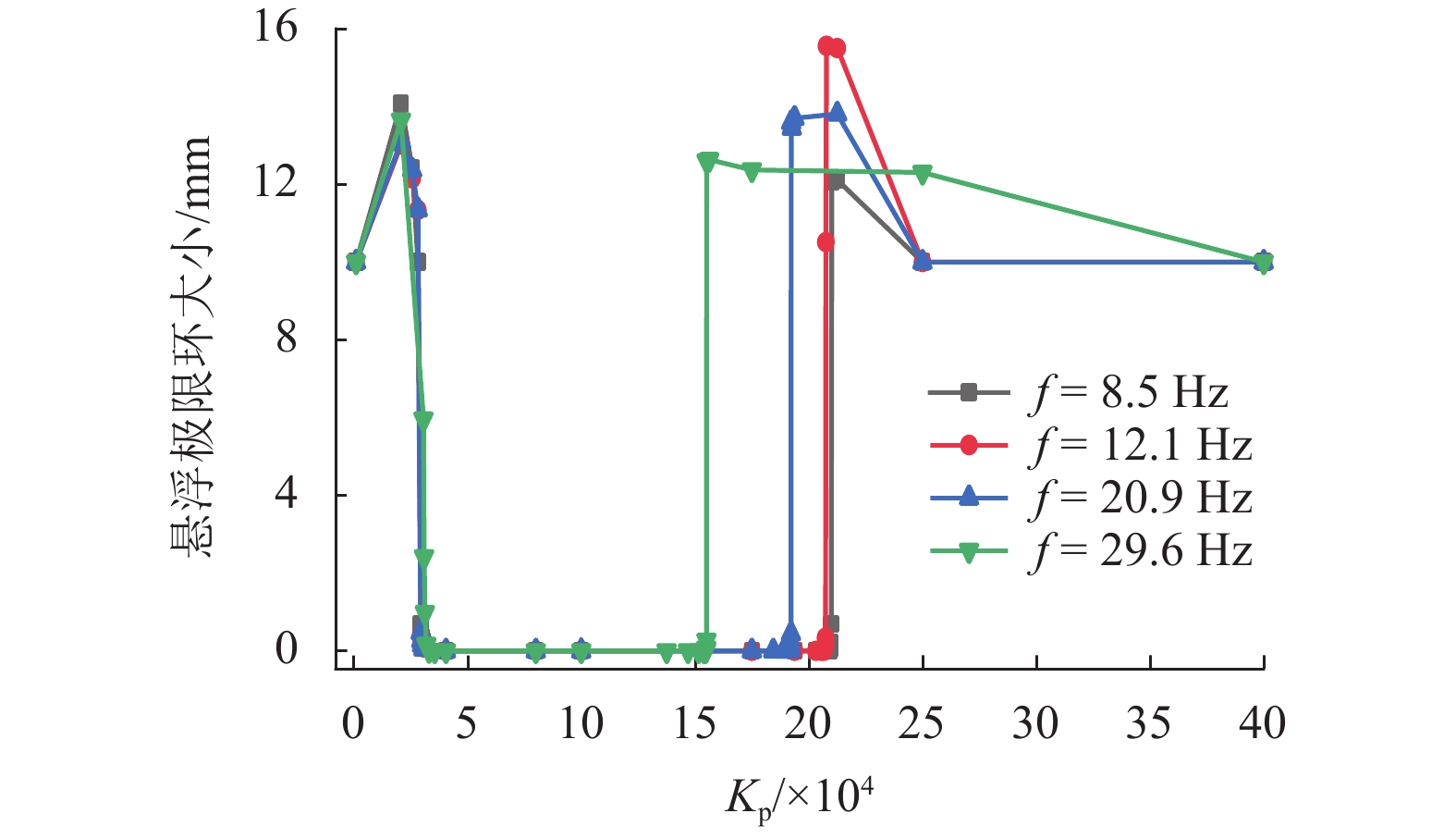
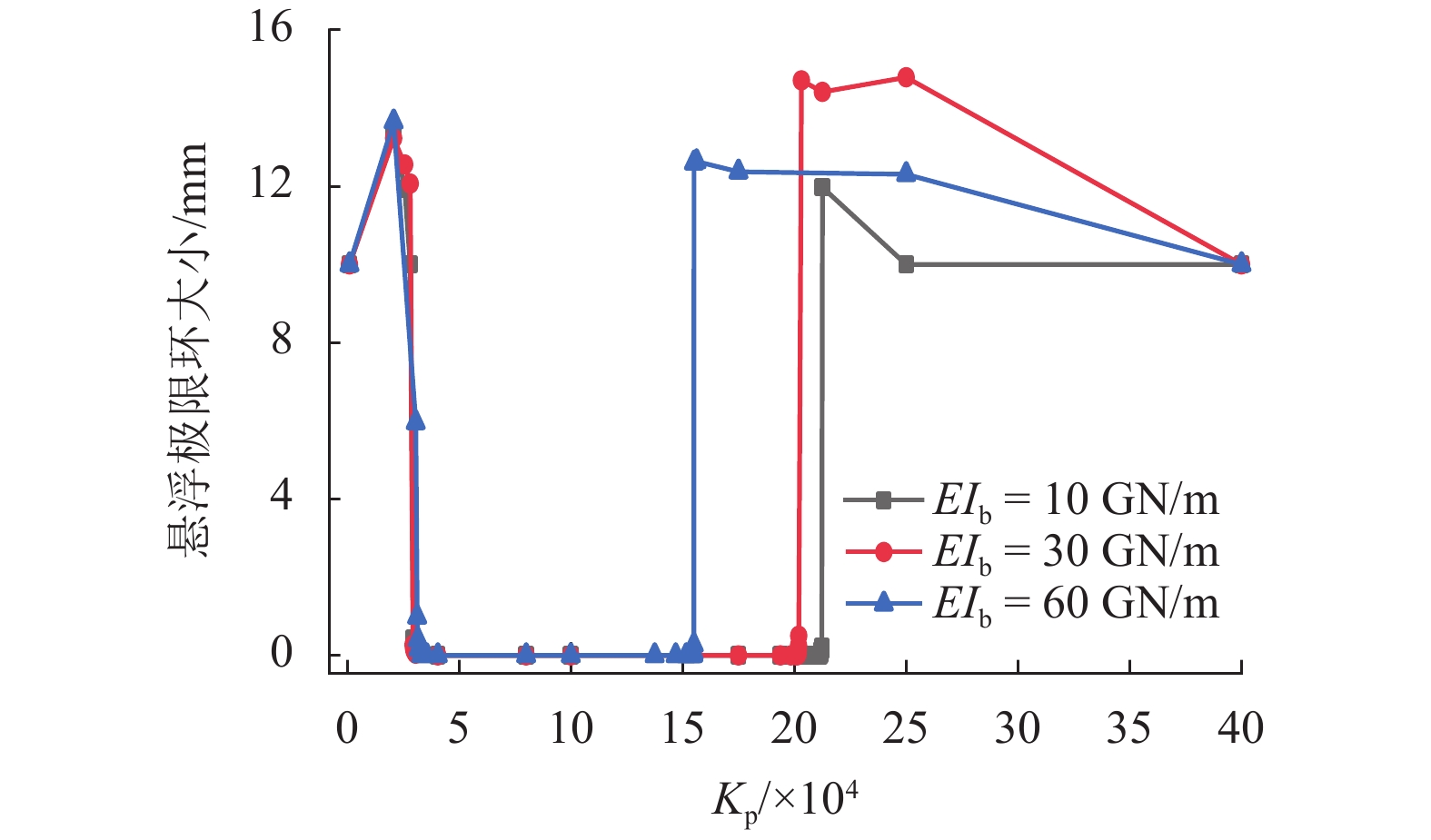
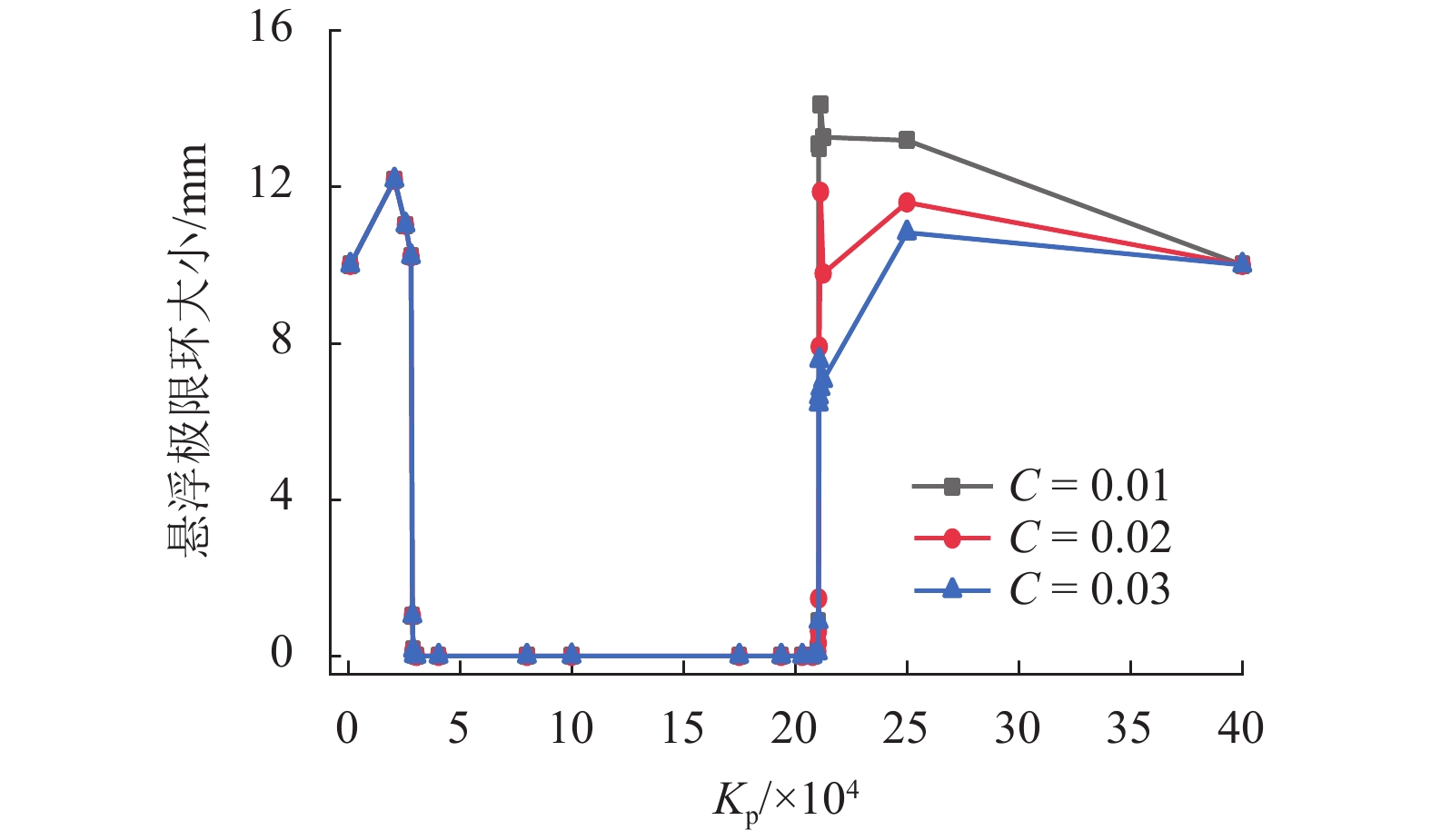
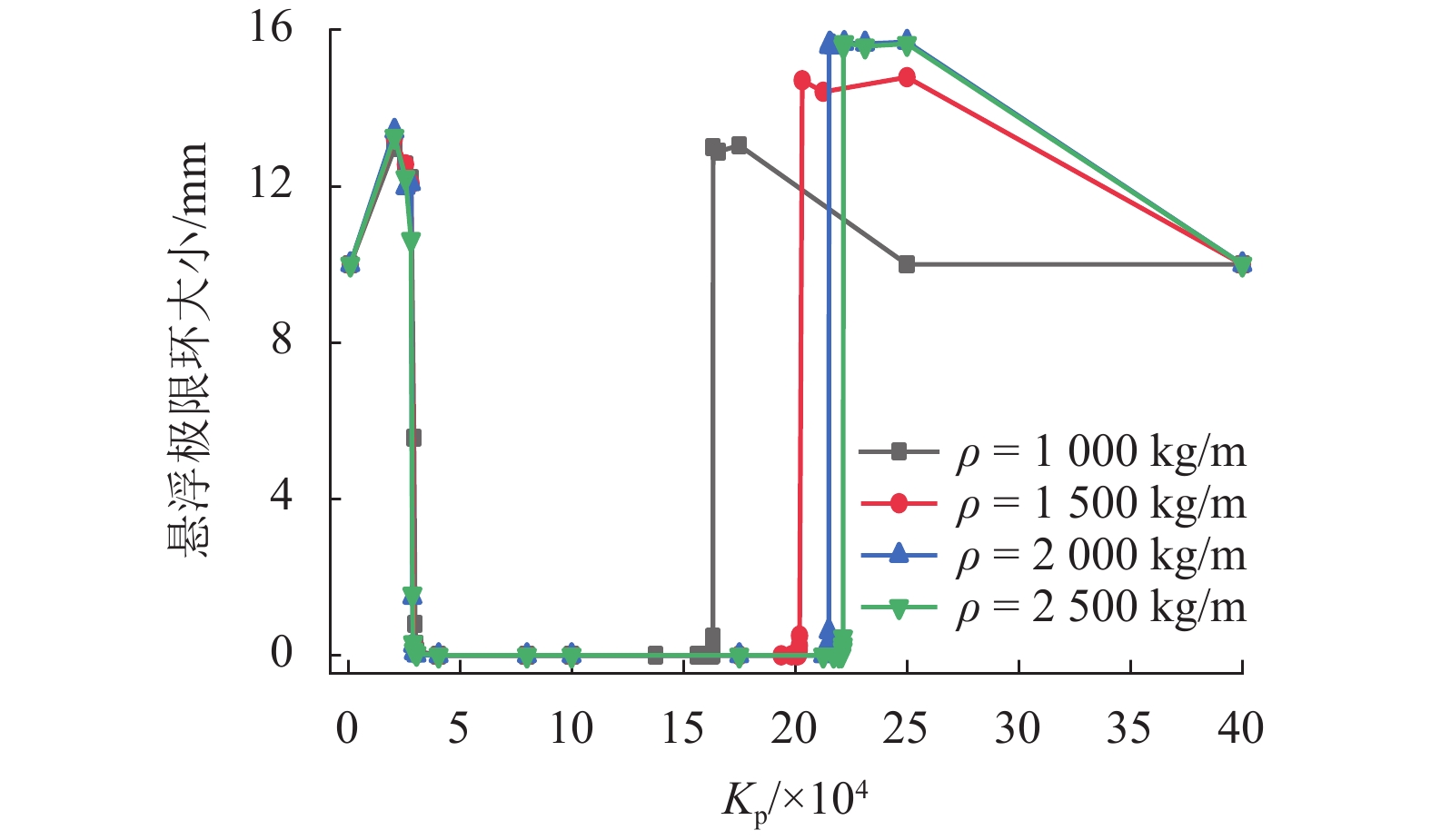
为研究中低速磁浮道岔主动梁关键参数对车岔耦合振动的影响，进行了各工况下磁浮道岔主动梁的模态测试，并建立了考虑道岔主动梁弹性振动的车岔耦合动力学模型，对悬浮稳定性进行了分析. 通过仿真与试验对比，对道岔主动梁的模态特征进行了修正，并基于修正后的车岔耦合动力学模型，研究了磁浮道岔主动梁不同设计参数对悬浮稳定性的影响规律. 研究结果表明：中间台车采用50 MN/m的弹性约束进行等效，能够达到比较理想的误差要求；二台车支撑方案相比三台车支撑方案，更容易避开磁浮车岔耦合的共振频率；随着主动梁一阶垂向弯曲频率的不断增大，悬浮控制参数的稳定区间越小，当道岔主动梁垂向弯曲频率大于12 Hz时，更容易出现车岔耦合振动现象；随着道岔主动梁刚度的增加，悬浮控制参数的稳定范围越小；增加道岔主动梁结构阻尼比不能解决车岔耦合共振问题，只能降低振动幅值大小；随着道岔主动梁线密度的增大，越不容易出现车岔共振现象，当线密度低于1 500 kg/m时，悬浮稳定区间将急剧下降；中间台车的等效支撑刚度越大，控制参数的稳定区间越小，但影响幅度不大.
Abstract:In order to study the influence of key parameters of the main beam of a low-medium speed maglev turnout on the coupled vibration of the vehicle-turnout system, modal tests of the main beam of maglev turnout are carried out in various conditions, and a vehicle-turnout coupling dynamic model considering the elastic vibration of the main beam of turnout is established for numerical simulation analysis of the levitating stability. First, the modal characteristics of the turnout main beam are modified through comparisons between simulation and experiment. Based on the modified vehicle-turnout coupling dynamic model, the influence of different design parameters of the maglev turnout main beam on levitating stability is then studied. The results obtained are as follows: The intermediate bogie can be equivalent to a 50 MN/m elastic constraint to meet the ideal error requirements, and the two-bogie support scheme is easier to avoid the resonance frequency between vehicle and turnout than the three-bogie support scheme. With the increasing of the first-order vertical bending frequency of the main beam, the stability range of the levitating control parameters becomes smaller; when the first-order vertical bending frequency of the main beam of turnout is greater than 12 Hz, the phenomenon of vehicle-turnout coupled vibration is more likely to occur. As the stiffness of the turnout main beam increases, the stability range of the levitating control parameters becomes smaller. Besides, increasing the structural damping ratio of the turnout active beam can only reduce the vibration amplitude but cannot solve the coupling resonance problem between vehicle and turnout. It is also found that the higher the linear density of the turnout main beam, the less likely the vehicle-turnout resonance is to occur; when the linear density is lower than 1500 kg/m, the levitating stability range drops sharply. In addition, a greater equivalent support stiffness of the intermediate bogie leads to a smaller stability range of the control parameters, but the influence range is small.
-
Key words:
- low-medium speed maglev /
- levitating stability /
- turnout /
- coupling vibration.
-
图 5 两台车与三台车对悬浮稳定性的影响
Figure 5. Influence of two-bogie and three-bogie schemes on levitating stability
图 7 道岔梁刚度对悬浮稳定性的影响
Figure 7. Influence of turnout beam stiffness on levitating stability
图 8 道岔梁阻尼比对悬浮稳定性的影响
Figure 8. Influence of the damping ratio of turnout beam on levitating stability
图 9 道岔梁线密度对悬浮稳定性的影响
Figure 9. Influence of the linear density of turnout beam on levitating stability
图 10 控制参数与悬浮稳定性关系
Figure 10. Relationships between control parameters and levitating stability
表 1 模态测试结果
Table 1. Results of modal tests
试验工况 模态振型 频率/Hz 阻尼比 1 一阶垂向弯曲 11.56 0.012 2 一阶垂向弯曲 16.25 0.059 3 一阶垂向弯曲 10.00 0.030 
下载: 导出CSV
表 2 模态仿真结果
Table 2. Results of modal simulations
仿真工况 模态振型 频率/Hz 自由状态 一阶垂向弯曲 23.65 两台车方案 一阶垂向弯曲 11.48 三台车方案 一阶垂向弯曲 15.40
下载: 导出CSV
表 3 模态仿真结果
Table 3. Results of modal simulations
试验结果/Hz 仿真结果/Hz 误差/% 11.56 11.48 0.7 16.25 15.40 5.0
下载: 导出CSV
表 4 模型参数
Table 4. Parameters of model
符号 数值 符号 数值 ${M_{\rm{c}}}$ 24000 kg ${C_{\rm{s}}}$ 6 kN·s/m ${I_{\rm{c}}}$ 84 620 kg·m2 ${L_{\rm{s}}}$ 2.46 m ${M_{\rm{e}}}$ 1 774 kg ${L_{\rm{e}}}$ 1.39 m ${I_{\rm{e}}}$ 1 312 kg·m2 ${K_{\rm{b}}}$ 50 MN/m ${K_{\rm{s}}}$ 0.08 MN/m ${C_{\rm{b}}}$ 2 kN·s/m
下载: 导出CSV
-
[1] 翟婉明,赵春发. 磁浮车辆/轨道系统动力学(Ⅰ): 磁/轨相互作用及稳定性[J]. 机械工程学报,2005,41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001ZHAI Wanming, ZHAO Chunfa. Dynamics of maglev vehicle/guideway systems (Ⅰ)−magnet /rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001 [2] 李小珍,王党雄,耿杰,等. F轨对中低速磁浮列车-桥梁系统竖向耦合振动的影响研究[J]. 土木工程学报,2017,50(4): 97-106.LI Xiaozhen, WANG Dangxiong, GENG Jie, et al. Study on the influence of F-rail in vertical coupling vibration of low-medium speed maglev train-bridge system[J]. China Civil Engineering Journal, 2017, 50(4): 97-106. [3] 王连春,李金辉,周丹峰,等. 磁浮列车-桥梁耦合自激振动机理分析与仿真验证[J]. 振动与冲击,2017,36(18): 13-19,55.WANG Lianchun, LI Jinhui, ZHOU Danfeng, et al. Principle analysis and simulation verification on the vehicle-bridge coupled self-excited vibration of maglevs[J]. Journal of Vibration And Shock, 2017, 36(18): 13-19,55. [4] 赵春发,翟婉明. 常导电磁悬浮动态特性研究[J]. 西南交通大学学报,2004,39(4): 464-468.ZHAO Chunfa, ZHAI Wanming. Dynamic characteristics of electromagnetic levitation systems[J]. Journal of Southwest Jiaotong University, 2004, 39(4): 464-468. [5] 罗华军,吴志会,佟来生,等. 中低速磁浮交通车岔耦合振动研究[J]. 电力机车与城轨车辆,2018,41(1): 5-8.LUO Huajun, WU Zhihui, TONG Laisheng, et al. Research on vehicle and turnout coupling vibration for mid-low speed maglev[J]. Electric Locomotives & Mass Transit Vehicles, 2018, 41(1): 5-8. [6] 姜卫利,高芒芒. 轨道梁参数对磁浮车-高架桥垂向耦合动力响应的影响研究[J]. 中国铁道科学,2004,25(3): 71-75. doi: 10.3321/j.issn:1001-4632.2004.03.015JIANG Weili, GAO Mangmang. Study of the effect of track beam parameters on vertical coupled dynamic response of maglev vehicle-viaduct[J]. China Railway Science, 2004, 25(3): 71-75. doi: 10.3321/j.issn:1001-4632.2004.03.015 [7] 汪科任,罗世辉,马卫华,等. 磁浮列车静悬浮车轨耦合振动对比分析[J]. 西南交通大学学报,2020,55(2): 282-289. doi: 10.3969/j.issn.0258-2724.20170891WANG Keren, LUO Shihui, MA Weihua, et al. Vehicle-guideway coupling vibration comparative analysis for maglev vehicles while standing still[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 282-289. doi: 10.3969/j.issn.0258-2724.20170891 [8] KIM, K J, HAN J B, HAN H S, et al. Coupled vibration analysis of maglev vehicle-guideway while standing still or moving at low speeds[J]. Vehicle System Dynamics, 2015, 53(4): 587-601. doi: 10.1080/00423114.2015.1013039 [9] MIN D J, JUNG M R, KIM M Y, et al. Dynamic interaction analysis of maglev-guideway system based on a 3D full vehicle model[J]. International Journal of Structural Stability and Dynamics, 2017, 17(1): 1750006.1-1750006.39. [10] HAN J B, HAN H S, LEE J M, et al. Dynamic modeling and simulation of EMS maglev vehicle to evaluate the levitation stability and operational safety over an elastic segmented switch track[J]. Journal of Mechanical Science and Technology, 2018, 32(7): 2987-2998. doi: 10.1007/s12206-018-0602-1 [11] LI J H, LI J, ZHOU D F, et al. The active control of maglev stationary self-excited vibration with a virtual energy harvester[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2942-2951. doi: 10.1109/TIE.2014.2364788 [12] LI J H, LI J, ZHOU D F, et al. The modeling and analysis for the self-excited vibration of the maglev vehicle-bridge interaction system[J]. Mathematical Problems in Engineering, 2015, 2015: 709583.1-709583.10. [13] 翟婉明,赵春发,蔡成标. 磁浮列车与轮轨高速列车对线桥动力作用的比较研究[J]. 交通运输工程学报,2001,1(1): 7-12. doi: 10.3321/j.issn:1671-1637.2001.01.002ZHAI Wanming, ZHAO Chunfa, CAI Chengbiao. On the comparison of dynamic effects on bridges of maglev trains with high-speed wheel/rail trains[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 7-12. doi: 10.3321/j.issn:1671-1637.2001.01.002 [14] 施晓红,佘龙华,常文森. EMS磁浮列车车/轨耦合系统的分岔现象研究[J]. 中国铁道科学,2004,36(5): 634-640.SHI Xiaohong, SHE Longhua, CHANG Wensen. The bifurcation analysis of the EMS maglev vehicle-coupled-guideway system[J]. Acta Mechanica Sinica, 2004, 36(5): 634-640. -
下载:
点击查看大图
计量
- 文章访问数: 368
- HTML全文浏览量: 158
- PDF下载量: 27
- 被引次数: 0