Data-Driven Parameter Tuning for Maglev Train Levitation System
-
摘要:
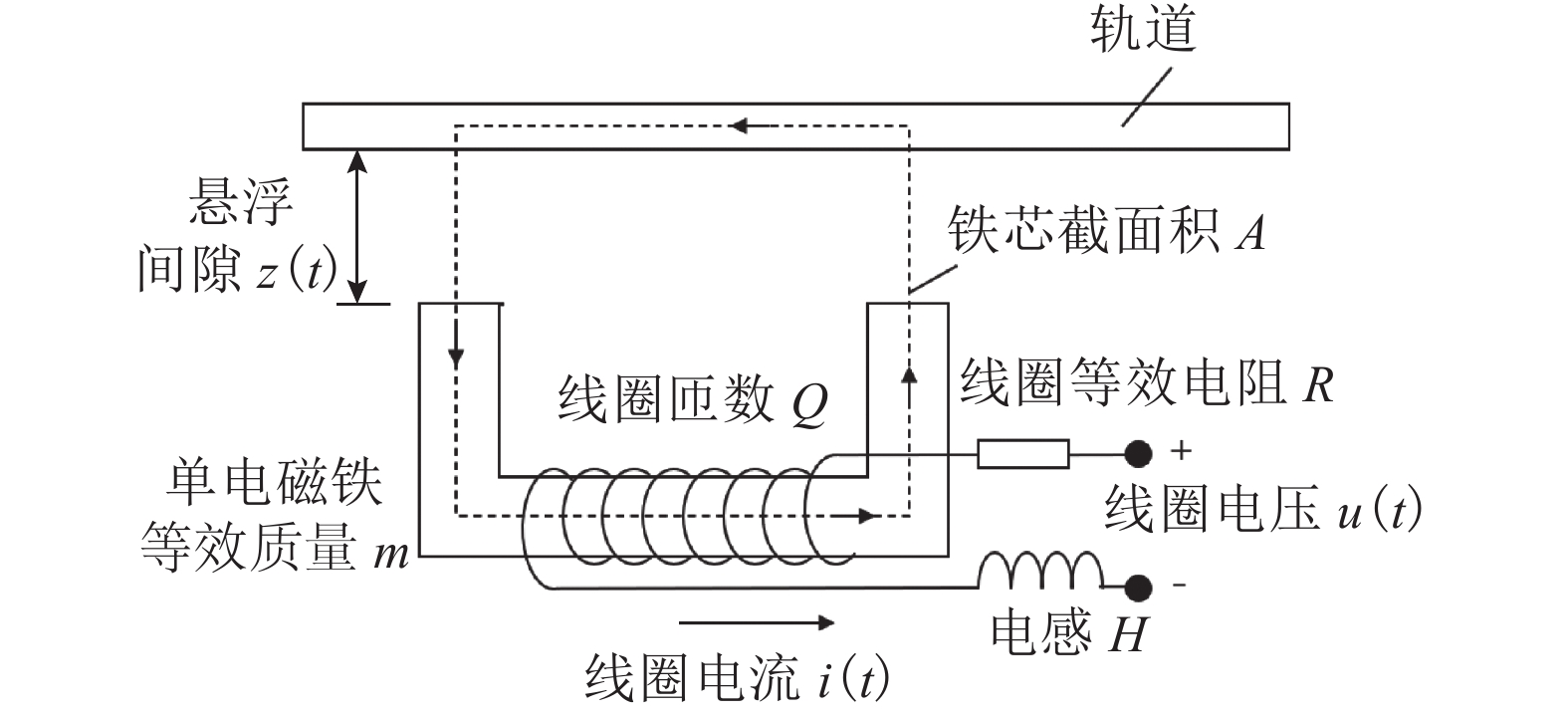
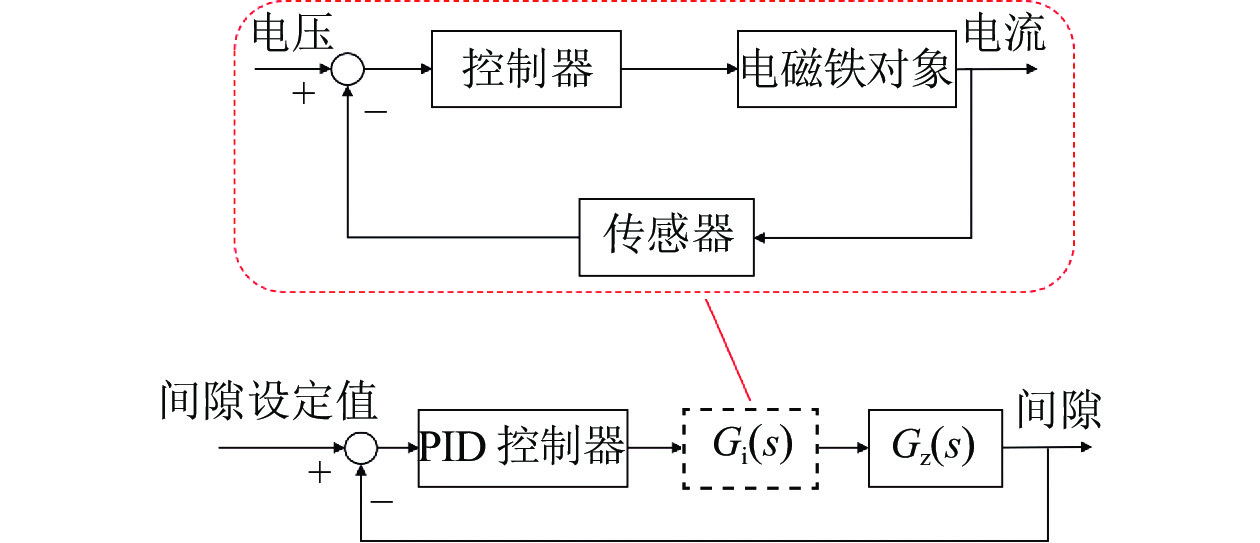
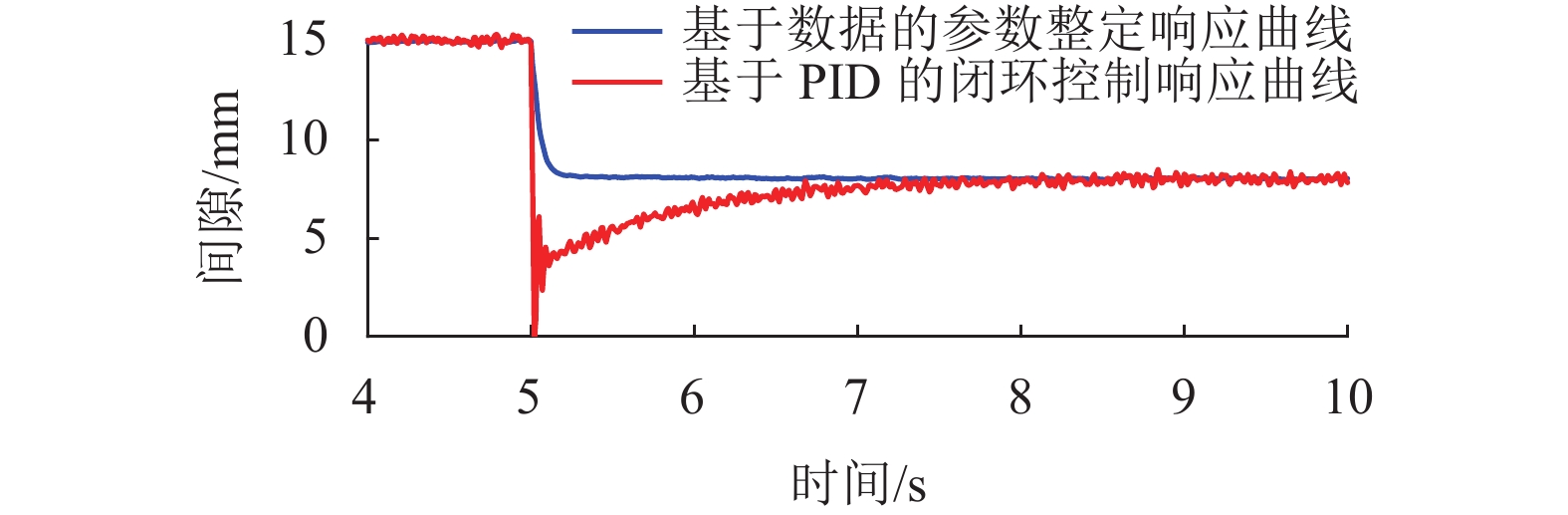
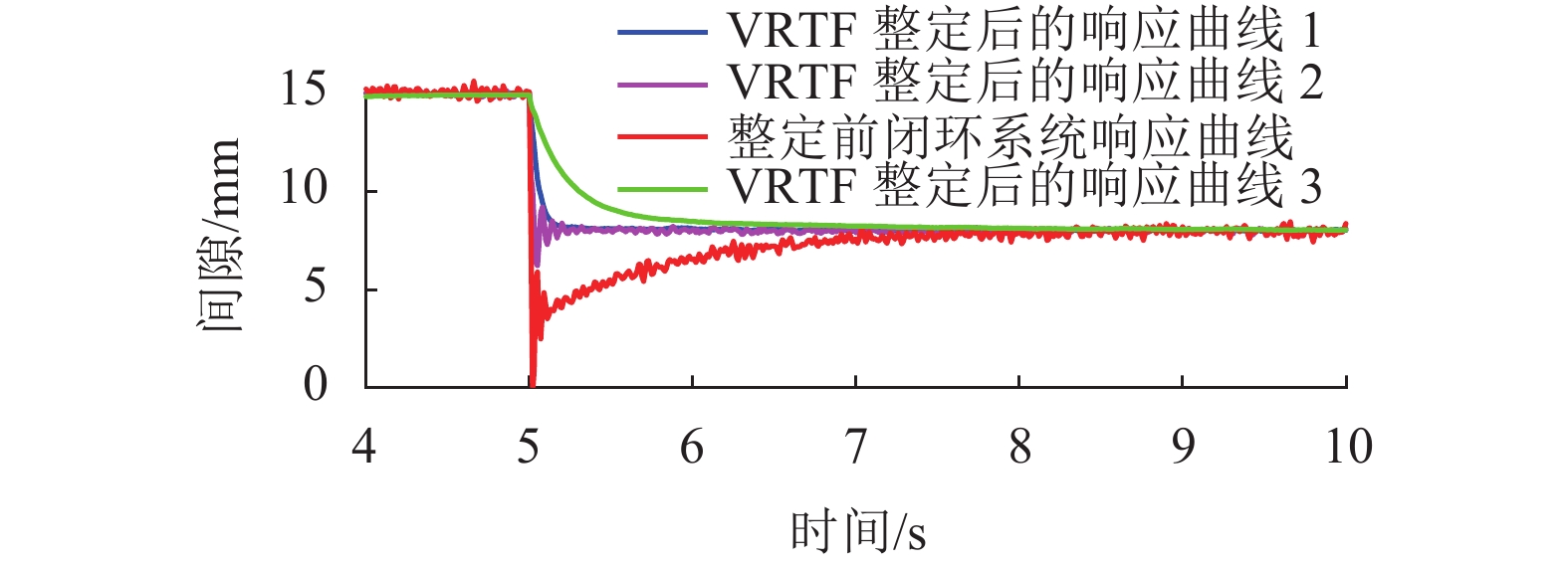
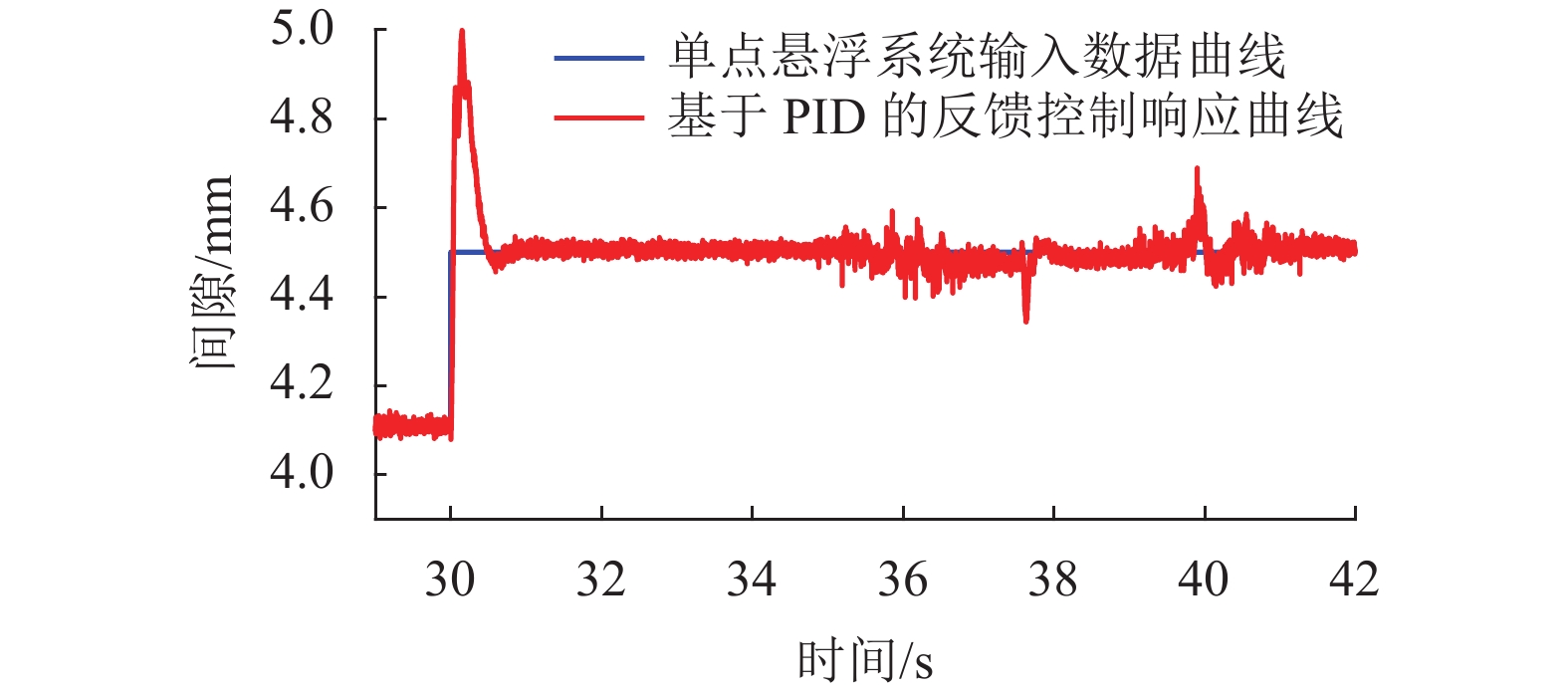
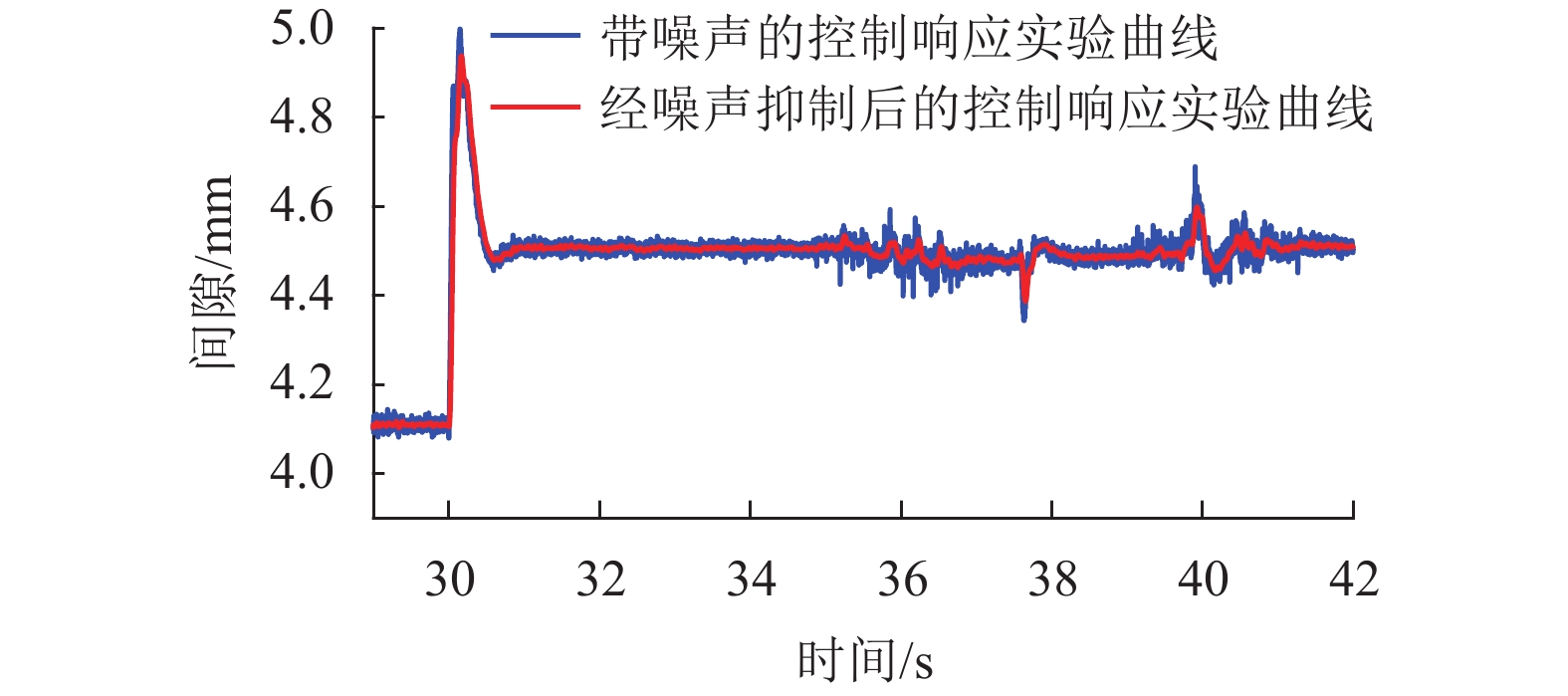
为了解决由于磁浮列车悬浮系统模型存在复杂非线性所带来的控制器参数整定难题，考虑仅依靠悬浮系统单次悬浮调试的输入输出数据来实现控制器参数整定，研究了基于数据驱动的磁浮列车悬浮系统快速参数整定方法. 首先，通过磁浮列车悬浮系统的建模分析了悬浮系统的开环不稳定性和复杂非线性；其次，针对虚拟参考反馈参数整定方法存在的参考模型确定问题，利用估计闭环响应方法来实现数据驱动的控制器参数整定；并且考虑到数据中存在的干扰噪声会影响控制器参数整定，提出了基于信号投影的磁悬浮系统数据噪声抑制方法；最后，以单铁磁悬浮系统为研究对象，通过单铁悬浮实验验证了本文提出的基于数据驱动的磁浮列车悬浮系统参数整定方法的有效性. 研究结果表明：悬浮系统的开环不稳定性和复杂非线性会给参数的快速整定带来较大困难；基于信号投影的噪声抑制方法能够将带噪声数据的方差降低54.1%；基于数据驱动的参数整定方法能够快速地整定好悬浮系统控制器参数，经参数整定后的系统相较于初始条件下只粗调好的PID反馈控制系统的阶跃响应超调量下降72.0%，平方误差积分 （ISE）下降79.8%，绝对误差积分 （IAE）下降54.5%.
Abstract:In order to solve the controller parameter tuning problem caused by the complex nonlinearity of the maglev train levitation system model, a data-driven fast parameter tuning method for the maglev train levitation system is proposed, which is based on only the input and output data of a single levitation tuning of the levitation system. First, the open-loop instability and complex nonlinearity of the levitation system are analyzed by modeling of the maglev train levitation system. Aiming at the problem of determining the reference model in the virtual reference feedback tuning method, estimation of the closed-loop response is then used to realize the data-driven controller parameter tuning. Considering that the interference noise in the data will affect the tuning of controller parameters, a data noise suppression method of maglev system based on signal projection is proposed. Finally, taking a single-rail levitation system for example, the effectiveness of this data-driven parameter tuning method for maglev train levitation system was verified through the single-rail levitation experiment. The results show that the open-loop instability and complex nonlinearity of the suspension system will bring great difficulties to the rapid adjustment of parameters; the noise suppression method based on signal projection can reduce the variance of noise data by 54.1%; and the parameter tuning method based on data driven technique can quickly set the controller parameters of the suspension system. Compared with the PID feedback control system with only coarse tuning under the initial conditions, the step response overshoot of the system after parameter tuning is reduced by 72.0%, the square error integral (ISE) is reduced by 79.8%, and the absolute error integral (IAE) is reduced by 54.5%.
-
Key words:
- levitation system /
- data driven /
- parameter tuning /
- virtual reference feedback /
- signal projection
-
近年来，传感器有限的能量遏制着无线传感器网络（wireless sensor networks, WSN）的永续发展. 且当传感器节点的电池寿命即将结束时，常常会发生传感错误和链路故障. 因此，延长传感器节点的生命周期并维持其感知性能是WSN中的一个主要问题[1-2].
随着射频能量收集（radio frequency energy harvesting, RF-EH）技术[3]的不断发展，使得受限于能量的WSN可以实现自持作业. 然而，传感器节点与目的节点之间常常由于地形地貌、建筑物、距离等原因以及受路径衰落的影响，导致无线链路被阻塞或不存在直达路径，影响系统覆盖范围[4].于是，基于无线携能通信（simultaneous wireless information and powertransfer, SWIPT）的中继协作系统备受关注. 文献[5]随机地在蜂窝网络中部署能量站（power beacon, PB），建立随机几何模型，并研究数据链路中断约束下的混合网络部署问题. 文献[6]研究了双向能量收集（energy harvesting, EH）中继网络中联合波束赋形设计与时隙切换（time switching, TS）策略问题. 文献[7]将解码转发全双工中继网络中的中继能量建模为二级马尔可夫链，获得贪婪切换策略下的最优功率分配（power splitting, PS）因子，并以精确积分的形式推导相应的中断概率. 文献[8]研究了多径瑞利衰落信道下基于缓冲器辅助差分混沌移位键控的SWIPT中继系统，通过采用Meijer G函数和Gauss-Hermite算法，得到误码率和平均延迟的闭式表达式. 文献[9]针对基于SWIPT的全双工中继网络的最优中继选择问题，利用Karush-Kuhn-Tucker （KKT）条件和拉格朗日函数分别对最优中继选择及发射功率控制进行优化. 文献[10]考虑一种联合直连链路与中继链路的数据传输系统，推导选择式合并（selection combining, SC）策略下的系统中断概率表达式. 文献[11]针对多天线目的节点的中继通信网络提出4种协议，即静态TS因子下的SC、静态TS因子下的最大比合并（maximal ratio- combining, MRC）、最佳动态TS因子下的SC和最佳动态TS因子下的MRC，较为全面地研究系统的中断性能.
值得注意的是，以上文献研究的场景较为理想化，假设所有节点均能获得足够的初始能量，从而保持系统始终处于激活状态；在SWIPT多中继协作系统中[12-13]，并未对目的节点采用多天线时的吞吐量（throughput, TH）性能进行优化分析. 鉴于此，本文针对EH-WSN系统提出基于PS策略的SWIPT多中继通信模型，研究联合优化TS因子与PS因子的吞吐量最大化中继选择算法，评估系统的中断性能.
1. 系统模型
本文考虑一种基于PS-SWIPT的EH-WSN系统模型，如图1所示. 该系统包括1个射频PB、N个传感器节点（1,2,$\cdots $,j,$\cdots $,N）、K个中继节点Ri （i = 1,2,$\cdots $,K）和1个目的节点D. 每个传感器节点安设单天线，中继节点安设2根天线、目的节点安设M根天线. 假设传感器节点在半双工（half-duplex, HD）模式下工作，中继节点在全双工模式下工作[14]. 图中：hj为PB与传感器节点j之间的链路信道系数，$h_{{{S}},{{R}}_i} $、$h_{{{R}}_i,{{D}}_m} $分别为源节点S到中继节点Ri、Ri到目的节点D第m根天线的链路信道系数.
PB周期性地广播射频（radio frequency，RF）波，系统模型所有传感器节点和中继节点都从该RF信号中获取能量. 传感器节点j作为源节点S，经由中继节点Ri将传感信息传输到目的节点D. 假设无线信道为多径独立的Rayleigh衰落信道，且令信道系数在一个通信周期T内保持不变，而在不同时隙间独立变化[15]. $ |{h_j}{|^2} $、$ |{h_{{{S}},{{{R}}_i}}}{|^2} $、$ |{h_{{{{R}}_i},{{{D}}_m}}}{|^2} $服从均值分别为λj、$ {\lambda _{{{S}},{{{R}}_i}}} $、$ {\lambda _{{{{R}}_i},{{{D}}_m}}} $的指数分布，例如$ {\lambda _j} = {d_j}^{ - \xi } $. 其中，$ {d_j} $为PB与传感器节点j之间的距离，$ \xi $为路径损耗指数.
基于PS-SWIPT的EH-WSN系统模型采用时分广播（time division broadcasting, TDBC）协议. 1个通信周期T分为2个时隙. 第1个时隙(1−θ)T内 (0<θ<1)，传感器节点和中继节点同时从PB发出的RF信号中收集能量；第2个时隙θT为传感器节点的协作传输阶段，传感器节点j作为源节点S以SWIPT方式将信息和能量同时传输至中继节点，中继节点再以解码转发方式将信息传输至目的节点D.TS因子θ控制着能量接收时隙长度和信息接收时隙长度，是重要的动态优化参数.
第1个时隙(1−θ)T：单天线传感器节点j 收集到的能量为[16]
Eharj=η|hj|2P(1−θ)T, (1) 式中：η为能量转化效率（0<η<1），P为PB的发射功率.
第2个时隙θT：传感器节点j作为源节点S的发射功率为
PS=EharjθT=η|hj|2P(1−θ)θ=k|hj|2P， (2) 式中：$k = \displaystyle{{\eta (1 - \theta )}}/{\theta }$.
中继节点Ri接收来自源节点S的信号为
yRi=√PShS,RixS+√PRihRi,RixRi+nRi,a， (3) 式中：$ {x_{{S}}} \in C $，C为满足$ {{E}}\left\{ {|{x_{{S}}}{|^2}} \right\} = 1 $的源节点S发送信号；$ {P_{{{{R}}_i}}} $是Ri的发射功率；$ {x_{{{{R}}_i}}} \in C $，为Ri发送的信号；$ {n_{{{{R}}_i},{\rm{a}}}} $为Ri处的加性高斯白噪声，服从独立同分布的复高斯随机变量，$ {n_{{{{R}}_i},{\rm{a}}}} $ ～ $CN(0,\sigma _{{n_{{{{R}}_i},{\rm{a}}}}}^2) $；$h_{{{R}}_i,{{R}}_i} $为中继节点Ri的环回链路信道系数；$ \sqrt {{P_{{{{R}}_i}}}} {h_{{{{R}}_i},{{{R}}_i}}}{x_{{{{R}}_i}}} $为Ri的环回自干扰信号.
基于PS因子$ {\rho _i} \in (0,1) $，Ri的接收信号$ {y_{{{{R}}_i}}} $分为两部分：$ {\rho _i} $部分用于信息传输，1−$ {\rho _i} $部分用于能量收集. 信息传输信号$y_{{{R}}_i}^{{\rm{ID}}} $和能量收集信号$y_{{{R}}_i}^{{\rm{EH}}} $分别为
yIDRi=√ρiyRi+nRi,P=√ρi(√PShS,RixS+√PRihRi,RixRi+nRi,a)+nRi,P, (4) yEHRi=√1−ρiyRi=√1−ρi(√PShS,RixS+√PRihRi,RixRi+nRi,a), (5) 式中：$ {n_{{{{R}}_i},{\rm{P}}}} $为Ri发射产生的人为噪声，且${n_{{{{R}}_i},{\rm{P}}}}$ ～$ CN(0,\sigma _{{n_{{{{R}}_i},{\rm{P}}}}}^2) $.
自干扰消除后[17]，Ri的接收信号更替为
yID−SICRi=√ρi(√PShS,RixS+nRi,a)+nRi,P. (6) 由式（2）、（6），Ri的接收信噪比（signal-to-noise ratio, SNR）为
γRi=ρiPS|hS,Ri|2ρiσ2nRi,a+σ2nRi,P=ρik|hj|2P|hS,Ri|2ρiN0+N0=ρik|hj|2|hS,Ri|2Φρi+1, (7) 式中：$\sigma ^2_{{n_{{{\rm{R}}_i},{\rm{a}}}}} = \sigma ^2_{{n_{{{\rm{R}}_i},{\rm{P}}}}} = {N_0}$（常数），$\varPhi \triangleq \displaystyle{P}/{{{N_0}}}$.
因能量部署站PB和中继节点的位置是固定的，单位发射功率下，假设每个中继节点在T内接收到的平均能量是Qavg，则在PB发射功率为P且能量收集时间为(1−θ)T时，中继节点Ri收集到的能量为QavgP(1−θ)T. 忽略中继节点Ri收集过程中噪声产生的微弱能量[8]，则Ri收集了PB的能量，接收了源节点S发射信号的能量，并对自干扰信号进行能量自回收，最终收集的总能量为
ERi=ESWIPTRi+ηQavgP(1−θ)T， (8) 式中：$E_{{{{R}}_i}}^{{\text{SWIPT}}} = \eta \left( {1 - {\rho _i}} \right)\left( {k|{h_j}{|^2}P|{h_{{{S}},{{{R}}_i}}}{|^2} + {P_{{{{R}}_i}}}|{h_{{{{R}}_i},{{{R}}_i}}}{|^2}} \right)\theta T$，为从源节点处收集到的能量.
当中继节点Ri将最终收集的能量$E_{R_i} $均用于发射，发射功率$ {P_{{{{R}}_i}}} = \dfrac{{{E_{{{{R}}_i}}}}}{{\theta T}} $. 假设T = 1，化简得到
PRi=η(1−ρi)k|hj|2P|hS,Ri|2θ+ηQavgP(1−θ)θ−η(1−ρi)|hRi,Ri|2θ. (9) 1.1 目的节点D采用SC策略
目的节点D采用SC策略时，节点D处第m根天线的接收信号为
ySCRi,Dm=√PRihRi,DmxRi+nDm， (10) 式中：$ {n_{{{{D}}_m}}} $为加性高斯白噪声，且$n _{{{{{D}}_m}}}～N(0,{\sigma _{{n_{{{{D}}_m}}}}^2})$.
令$ \sigma _{{n_{{{{D}}_m}}}}^2 = {N_0} $，则节点D第m根天线处的SNR为
γSCDm=PRimax|hRi,Dm|2σ2nDm=[η(1−ρi)k|hj|2P|hS,Ri|2θ+ηQavgP(1−θ)]max|hRi,Dm|2N0θ[1−η(1−ρi)|hRi,Ri|2]. (11) 目的节点D采用SC策略时，选取最佳天线数为
m∗=argmax1⩽m⩽M|hRi,Dm|2. (12) 设变量Z的累积分布函数（cumulative distribution function, CDF）函数和概率密度函数（probability density function, PDF）分别为FZ(z)和fZ(z) ，令$ Z = \mathop {\max }\limits_{m = 1,2, \cdots ,M} {\text{\{ }}|{h_{{{{R}}_i},{{{D}}_m}}}{|^2}{\text{\} }} $，则
FZ(z)=1+M∑m=1(−1)mCmMe−mzλRi,Dm， (13) fZ(z)=λRi,DmM−1∑m=1(−1)mCmM−1e−(m+1)zλRi,Dm, (14) 式中：$ {\text{C}}_M^m = \displaystyle\frac{{M!}}{{m!(M - m)!}} $.
1.2 目的节点D采用MRC策略
目的节点D采用MRC策略时，可合并来自M根天线的信号，其接收信号为
yMRCRi,D=M∑m=1√PRihRi,DmxRi+nD, (15) 式中：${n_{{D}}}$为加性高斯白噪声，且${n_{{D}}}～N(0,{\sigma _{{n_{{D}}}}^2}) $.
根据式（9）、（15），并令$\sigma _{{n_{{D}}}}^2 = {N_0}$，得到节点D的SNR为
γMRCD=M∑m=1PRi|hRi,Dm|2σ2nD=[η(1−ρi)k|hj|2P|hS,Ri|2θ+ηQavgP(1−θ)]M∑m=1|hRi,Dm|2N0[θ−η(1−ρi)|hRi,Ri|2θ]. (16) 令$ W = \displaystyle\sum\limits_{m = 1}^M {|{h_{{R_i},{D_m}}}{|^2}} $，其PDF为
fW(w)=λMRi,D(M−1)!wM−1e−wλRi,D. (17) 2. 中断概率与吞吐量分析
2.1 目的节点D采用SC策略
在基于PS-SWIPT的EH-WSN系统中，目的节点D采用SC策略的中断概率可表示为[18]
Pout,SC≜ (18) 式中：Pr(·)为概率，$ \gamma _{{\rm{e2e}}}^{{\text{SC}}} \triangleq \min \{{\gamma _{{{{R}}_i}}},\gamma _{{{{D}}_m}}^{{\text{SC}}}\} $，$ {\gamma _{{\rm{th}}}} $为预设SNR阈值.
令$ X=\left|h_{j}\right|^{2}\left|h_{{{S}},{{R}}_{i}}\right|^{2} $，则其CDF为
\begin{split} & {F_X}(x) = {P_{\rm{r}}}\left( {X < x} \right) = {P_{\rm{r}}}\left( {|{h_j}{|^2} < \frac{x}{{|{h_{{{S}},{{{R}}_i}}}{|^2}}}} \right) =\\ &\quad\displaystyle\int_0^\infty {{F_{|{h_j}{|^2}}}} \left( {\frac{x}{{|{h_{{{S}},{{{R}}_i}}}{|^2}}}} \right) {f_{|{h_{{{S}},{{{R}}_i}}}{|^2}}}(|{h_{{{S}},{{{R}}_i}}}{|^2}){\rm{d}}|{h_{{{S}},{{{R}}_i}}}{|^2} =\\ & \quad1 - 2\sqrt {{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}x} {K_1}\left( {2\sqrt {{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}x} } \right) \text{，} \end{split} (19) 式中：$ {K_v} $(·)为第二类v阶修正贝塞尔函数.
令$ t = {\rho _i} + 1 $，$ d = {\rho _i}k\varPhi $，$ a = \eta (1 - {\rho _i})k\theta $， $ b = \eta {Q_{{\rm{avg}}}}\times (1 - \theta ) $，$ c = \theta - \eta (1 - {\rho _i})|{h_{{R_i},{R_i}}}{|^2}\theta $，则式（18）可以等价转化为
\begin{split} &{P}_{{\rm{out}}\text{,SC}}=1-{P_{\rm{r}}}\left(\frac{d\left|{h}_{j}{|}^{2}\right|{h}_{{{S}},{{{R}}}_{i}}{|}^{2}}{t}\geqslant {\gamma }_{{\rm{th}}}\text{，}\right.\\ &\quad\left.\frac{ \left(a\left|{h}_{j}{|}^{2}\right|{h}_{{{S}},{{{R}}}_{i}}{|}^{2} + b\right) \varPhi\;\mathrm{max}\;|{h}_{{{{R}}}_{i},{{{D}}}_{m}}{|}^{2} }{c}\geqslant {\gamma }_{{\rm{th}}}\right) =\\ &\quad 1-{P_{\rm{r}}}\left(X\geqslant \frac{{t\gamma }_{{\rm{th}}} }{d}\text{，}Z\geqslant \frac{{\gamma }_{{\rm{th}}} c}{(ax + b)\varPhi }\right)=\\ &\quad1-{\displaystyle {\int }_{\frac{{t\gamma }_{{\rm{th}}} }{d}}^{\infty }\left({\displaystyle {\int }_{\frac{{c\gamma }_{{\rm{th}}} }{(ax + b)\varPhi }}^{\infty }{f}_{Z}({\textit{z}})}{\rm{d}}{\textit{z}}\right)} {f}_{X}(x){\rm{d}}x =\\ &\quad1 - \int_{\frac{{{t\gamma _{{\rm{th}}}} }}{d}}^\infty {\left( {\sum\limits_{m = 1}^M {{{\left( { - 1} \right)}^{m + 1}}{\rm{C}}_M^m} {{\rm{e}}^{ - {\lambda _{{{{R}}_{i,}}{{D}}_m}}\frac{{{\gamma _{{\rm{th}}}} cm}}{{(ax + b) \varPhi}}}}} \right)} {f_X}(x){\rm{d}}x{\text{ }} . \end{split} (20) 通过使用文献[19]中的等式(8.486,18)，可以计算得
{f_X}(x) = \frac{{{\rm{d}} {{F_X}(x)} }}{{{\rm{d}}x}} = 2{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}{K_0}\left( {2\sqrt {{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}x} } \right) . (21) 将式（21）代入式（20），得到
\begin{split} & {P_{{\rm{out}}{\text{,SC}}}} = 1 - \displaystyle\int_{\frac{{{t\gamma _{{\rm{th}}}} }}{d}}^\infty {\left( {\sum\limits_{m = 1}^M {{{\left( { - 1} \right)}^{m + 1}}{\rm{C}}_M^m} {{\rm{e}}^{ - {\lambda _{{{{R}}_{i,}}{{D}}_m}}\frac{{{\gamma _{{\rm{th}}}} cm }}{{(ax + b)\varPhi }}}}} \right)} \times \\ &\quad \left[ {2{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}{K_0}\left( {2\sqrt {{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}x} } \right)} \right]{\rm{d}}x . \end{split} (22) 根据解码转发协议，目的节点采取SC接收策略下的吞吐量为
T_{{{\text{H,SC}}}} = \theta {\log _2}(1 + \min \{{\gamma _{{{{R}}_i}}},\gamma _{D_m}^{{\text{SC}}}\}) \text{.} (23) 2.2 目的节点D采用MRC策略
目的节点D采用MRC策略的中断概率为
\begin{split} & {P_{{\rm{out}}{\text{,MRC}}}} \triangleq P_{\rm{r}} (\gamma _{{\rm{e2e}}}^{{\text{MRC}}} < {\gamma _{{\rm{th}}}}) =1 - \displaystyle\int_{\frac{{{t\gamma _{{\rm{th}}}} }}{d}}^\infty 2{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}\times \\ &{K_0}\left( {2 \sqrt {{\lambda _j}{\lambda _{{{S}},{{{R}}_i}}}x} } \right) \Biggl({30} \frac{{ \Gamma (M)}}{{(M - 1)!}} -\frac{1}{{(M - 1)!}} \times \Biggl.{30}\\ & \left.{{\rm{e}}^{ - \tfrac{{{\gamma _{{\rm{th}}}} c {\lambda _{{{{R}}_i},{{D}}}}}}{{(ax + b)\varPhi }}}}\sum\limits_{q = 0}^N {\frac{{{{\left( {\dfrac{{{\gamma _{{\rm{th}}}} c {\lambda _{{{{R}}_i},{{D}}}}}}{{(ax + b)\varPhi }}} \right)}^{M + q}}}}{{M(M + 1) \cdots (M + q)}}} \right){\rm{d}}x{\text{ }} , \end{split} (24) 式中：$\gamma _{{\rm{e2e}}}^{{\text{MRC}}} \triangleq \min \{{\gamma _{{{{R}}_i}}},\gamma _{{D}}^{{\text{MRC}}}\}$，Γ(M)为伽马函数.
目的节点D采用MRC策略时系统吞吐量为
T_{{{\text{H,MRC}}}} = \theta {\log _2}(1 + \min \{{\gamma _{{{{R}}_i}}},\gamma _{{D}}^{{\text{MRC}}}\}) \text{.} (25) 3. 问题描述与优化求解
在保证通信服务质量（quality of service, QoS）和PB发射功率P、能量转化效率η等约束条件下，本文提出一种以吞吐量最大化为优化目标的最优中继选择算法. 通过联合优化TS因子θ与PS因子$ {\rho _i} $，使得吞吐量TH最大，然后选择最佳中继，实现基于SWIPT的EH-WSN中继系统的吞吐量最大化.
TH性能优化问题（P1）建模为式（26）～（31）（以目的节点D采用SC策略为例）.
\mathop {\max }\limits_{i ,{\rho _{i}},\theta } \;T_{{{\text{H,SC}}}} = \theta {\log _2}(1 + \min \{{\gamma _{{{{R}}_i}}},\gamma _{{{{D}}_m}}^{{\text{SC}}}\}), (26) {{\rm{s}}} .{\rm{t}}：\mathop {\min\limits_{i,{\rho _{i}},\theta } \{{\gamma _{{{{R}}_i}}},\gamma _{{{{D}}_m}}^{{\text{SC}}}\} \geqslant {\gamma _{{\rm{th}}}}} , (27) \quad\;\; {Q_{{\rm{avg}}}} \geqslant e , (28) \quad\;\;\; {\text{0 < }}P \leqslant {P_{\rm{m}}} , (29) \quad\;\;\; 0 < \theta < 1 , (30) \quad\;\;\; 0 < {\rho _i} < 1, (31) 式中：e为中继节点捕获的平均能量阈值，Pm为PB发射功率限制.
P1是一个复杂的0-1 NP-hard问题， 涉及中继选择以及参数θ与$ {\rho _i} $的优化. 因此，本文将P1优化重新定义为一对耦合优化问题，分解为关于θ与$ {\rho _i} $的内部优化问题（P2）以及选择最优中继节点的外部优化问题2个子问题.
内部优化问题P2的解决方案是：在假定中继节点Ri活跃状态的情况下，针对EH-WSN中的每个中继节点，搜寻最佳的θ与$ {\rho _i} $，使其对应的系统TH值最大. 内部优化问题P2表示为式（27）～（32）.
\mathop {\max }\limits_{{\rho _{i}},\theta } T{_{{\text{H,SC}}}} = \theta {\text{lo}}{{\text{g}}_2}(1 + \min \{{\gamma _{{{{R}}_i}}},\gamma _{{{{D}}_m}}^{{\text{SC}}}\}) \text{.} (32) 通过分析函数TH,SC与θ、$ {\rho _i} $的关系，可以得知这是一个拟凸函数，在区间（0,1）上具有最优值θ*、$\rho _{i}^{*} $使系统TH值最大，可采用斐波那契（黄金分割法）查找算法[20]搜索到θ*与$\rho _{i}^{*} $。
然而，本文考虑基于θ与$ {\rho _i} $联合优化下的中继选择算法，通过参数的动态调整，使系统的TH值最大，提高系统的整体性能. 根据式（7），计算中继节点Ri的接收信噪比$ {\gamma _{{{{R}}_i}}} $对$ {\rho _i} $的一阶偏导数，其值大于0，说明$ {\gamma _{{{{R}}_i}}} $沿着$ {\rho _i} $方向为单调递增函数；同理，由式（11）知，目的节点D的接收信噪比$ \gamma _{{{{D}}_m}}^{{\text{SC}}} $对$ {\rho _i} $的一阶偏导数小于0，说明$ \gamma _{{{{D}}_m}}^{{\rm{SC}}} $沿着$ {\rho _i} $方向为单调递减函数. 由此得出，当$ {\gamma _{{{{R}}_i}}}(\rho_i ) = \gamma _{{{{D}}_m}}^{{\text{SC}}}(\rho_i ) $时，存在唯一的$\rho _{i}^{*} $使系统TH值最大. 进而，将$\rho _{i}^{*} $代入式（23），通过设置不同的θ值提升系统性能. 当每个中继节点对应最优值θ*与$ \rho _i^* $获得最大TH值后，即可进行最佳中继节点的一维搜索. 最佳中继节点索引为
{i^*} = \arg {\max } \; T_{{\text{H,SC}}}({\rho _i^*},{\theta ^*}) . (33) 基于以上分析，在优化问题P1时，首先通过求解内部优化问题P2，提出一种动态联合优化方案，得到内层优化式的最优目标值；然后，根据θ*和$ \rho _i^* $搜寻最佳中继节点，即可获得整体问题的最优解. 联合优化最优中继选择算法如图2所示. 其中：$ \gamma _{{{{D}}_m},i}^{{\text{SC}}} $为SC策略下信息经第i个中继节点传输到目的节点D处的信噪比；$ \gamma _{{\rm{e2e}},i}^{{\text{SC}}} $为SC策略下选取第i个中继节点时，中继节点Ri处和目的节点D处的信噪比最小值； $ {T_{{\text{H,SC}},i}} $为选取第i个中继节点后，在SC策略下的系统吞吐量； $ \mathop T\nolimits_{{\text{H,SC,}}i}^ * $为信息经最佳中继节点i* 传输时，SC策略下的系统吞吐量.
最优中继选择算法的计算复杂度为O(K2 + K)，最优中继节点的选取是在联合优化θ和ρi的方案下提出的，相比在固定TS因子以及静态PS因子下的最优中继节点的选取[21-22]，此算法可使系统变量间相互调节，提高EH-WSN系统性能.
4. 仿真结果与性能分析
为验证本文提出的基于PS-SWIPT的EH-WSN系统模型及中继选择算法的有效性，评估PB功率、时隙切换因子等参数对系统中断概率、吞吐量性能的影响，通过Monte Carlo仿真分析. 假设系统模型中有K = 6个可实现全双工的中继节点，η = 0.8，Qavg =0.5 J. 令所有Ri的自干扰信道增益均相等，$ |{h_{{{{R}}_i},{{{R}}_i}}}{|^2} = 0.1 $；所有噪声的方差相等，$ \sigma _{{n_{{{{R}}_{{i}}},{\rm{a}}}}}^2 = \sigma _{{n_{{{{R}}_{{i}}},{\rm{P}}}}}^2 = \sigma _{{n_{{{{D}}_m}}}}^2 = {N_0} = 1 $；所有中继具有相同的PS因子、TS因子. 进行约106次独立实验，使用瑞利衰落模型[23]，采用正交幅度调制（QAM）.
理论上，式（24）中的N取无穷大，但经过数次仿真实验发现，N取到一定数值后，结果会趋于稳定. 图3显示了遍历总次数对MRC接收策略下中断概率的影响，可以看出，当N>7时，Pout,MRC已趋于收敛，因此，N = 50.
图 3 MRC接收策略下循环次数对中断概率的影响Figure 3. Effect of loop number on outage probability under MRC strategy图4为SC、MRC接收策略下PS因子ρi对系统中断概率和吞吐量的影响. 其中，$ {\gamma _{{\rm{th}}}} $=1 dB，M =3根，θ = 0.8. 由图4可以看出：当ρi = 0时，源节点RF信号的所有功率都用于能量收集，此时，不论目的节点D采取何种接收策略，系统中断概率均为1.00，吞吐量为0；随ρi的增大，中断概率先减小后增大，吞吐量先增大后减小. SC接收策略在ρi =0.58时，对应中断概率最小，吞吐量最大；MRC接收策略在ρi = 0.71时，对应中断概率最小，吞吐量最大. 当P = 3 dBW时，SC、MRC策略下的最小中断概率分别为0.52、0.49；当P = 5 dBW时，SC、MRC策略下的最小中断概率分别为0.42、0.39. 当P = 3 dBW时，SC、MRC策略下的最大吞吐量分别为0.12、0.15 bit/（s·Hz）；当P = 5 dBW时，SC、MRC策略下的最大吞吐量分别为0.18、0.23 bit/（s·Hz）.
图 4 不同PS因子的中断概率与吞吐量Figure 4. Outage probability and throughput under different PS factors图5和图6分别为不同接收策略下PB发射功率以及天线数目对系统中断概率的影响. 其中，$ {\gamma _{{\rm{th}}}} $=1 dB，θ = 0.8. 从图5可得，当PS因子ρi取值相同时，相同发射功率下，基于MRC策略的中断性能优于SC策略的性能. 这是因为，MRC策略可合并所有天线的接收信号，而SC策略仅选择了最佳通道接收信号. 从图6看出，当给定P值时，SC策略下的系统中断概率在M≥9根时基本保持不变，而MRC策略下的中断概率在M≥5根时趋于稳定. 在相同天线数目下，发射功率P对系统中断性能的影响远远大于接收策略对中断性能的影响.
图7为不同接收策略下TS因子θ对系统中断概率和吞吐量的影响. 其中，$ {\gamma _{{\rm{th}}}} $= 1 dB，M = 3根，ρi =0.8. 图7（a）表明：当给定P、θ值时，MRC策略的中断性能始终优于SC策略的中断性能；若给定θ值，增大P，系统中断概率减小；此外，当θ逐渐增大，MRC策略在P = 3 dBW时的中断概率大于SC策略在P = 5 dBW时的中断概率. 这是由于当节点收集能量时间相同时，相比于发射功率，接收策略对中断概率的影响更小. 图7（b）表明：当θ取值逼近0时，因系统无法进行有效的信息传输，吞吐量较低；当θ持续增大，接近1.0时，传感器节点和中继节点因无法收集到足够能量，从而导致吞吐量趋于0.
图 7 不同TS因子下的中断概率与吞吐量Figure 7. Outage probability and throughput for different TS factors图8对比了采用随机中继选择算法（Random）、最大最小中继选择算法（Max-Min）和本文提出的联合优化最优中继选择算法在不同TS因子时的系统最优吞吐量. 假设P = 5 dBW，M = 3根，Random和Max-Min在采取SC接收策略时，ρi = 0.58，MRC接收策略时ρi = 0.71，而本文算法ρi在（0,1.00）内动态变化. 由图8 可以看出：随着θ的变化，3种中继选择算法均可达到最大吞吐量；在相同接收策略下，Random的吞吐量最小，Max-Min次之，本文算法的吞吐量最大. 以MRC策略为例：当θ*= 0.21时，Random的最大吞吐量为0.54 bit/（s·Hz）；当θ* = 0.23时，Max-Min的最大吞吐量为0.68 bit/（s·Hz）；当θ* = 0.28时，本文算法的最大吞吐量为0.82 bit/（s·Hz）. 由此可知，本文提出的算法通过联合优化θ和ρi，较好地实现了系统吞吐量性能的整体提升.
图 8 不同TS因子时各算法的吞吐量对比Figure 8. Throughput comparison of different algorithms with different TS factorsM=3根，3种算法下系统最大吞吐量与PB发射功率P之间的关系如图9所示. 可以看出，当P = 6 dBW，采取SC策略时，相比Random、Max-Min，本文算法的系统吞吐量增益分别为0.29、0.15 bit/（s·Hz）；采取MRC策略时，相比Random、Max-Min，本文算法的系统吞吐量增益分别为0.32、0.16 bit/（s·Hz）. 由此可知，本文所提方案能达到更大的系统吞吐量.
图 9 不同PB发射功率时各算法的吞吐量对比Figure 9. Throughput comparison of different algorithms with different PB transmit powers5. 结 论
本文基于PS-SWIPT技术，在PB辅助下构建了EH-WSN系统模型. 与其他WSN系统不同的是，所有节点先进行一段时间的能量收集，然后再用收集到的能量发射信息，且中继节点应用SWIPT技术还可得到源节点能量和自干扰信号自回收的能量补充. 在考虑目的节点D采用多天线的情况下，分别推导了SC和MRC接收策略下的中断概率、吞吐量的表达式. 在保证通信QoS等多约束条件下构建数学模型，将复杂的0-1 NP-hard问题拆分成2个子问题，并提出TS和PS因子联合优化下的最优中继选择算法. 仿真结果表明，各参数对EH-WSN中断性能影响明显，联合优化最优中继选择算法可使系统吞吐量性能得到优化. 未来可通过考虑非线性EH，将这项研究扩展到更广义的模型.
-
图 1 磁浮列车悬浮系统单转向架机械解耦结构示意
Figure 1. Schematic diagram of mechanical decoupling structure of single bogie of maglev train levitation system
图 2 磁浮列车单点悬浮系统模型示意
Figure 2. Schematic diagram of single-point levitation system model of maglev train
图 3 带有电流负反馈内环的悬浮系统闭环反馈示意
Figure 3. Closed loop feedback diagram of levitation system with negative current feedback inner loop
图 5 基于悬浮系统输入输出数据的控制器参数整定原理示意
Figure 5. Schematic diagram of controller parameter tuning based on input and output data of levitation system
图 7 悬浮控制器参数整定后单点悬浮系统闭环响应仿真曲线
Figure 7. Simulation curves of closed-loop response of single-point levitation system before and after levitation controller parameter tuning
图 8 单点悬浮系统闭环响应仿真曲线
Figure 8. Simulation curves of closed-loop response of single point levitation system
图 9 单铁磁悬浮系统悬浮控制实验装置
Figure 9. Experimental device for levitation control of single-iron magnetic levitation system
图 10 基于PID的单点悬浮系统闭环反馈控制响应实验曲线
Figure 10. Experimental response curves of closed loop feedback control of single-point levitation system based on PID
图 11 经噪声抑制处理后的单点悬浮系统闭环反馈控制响应实验曲线
Figure 11. Experimental response curves of closed-loop feedback control of single-point levitation system after noise suppression
图 12 悬浮控制器参数整定前、后单点悬浮系统闭环响应实验曲线
Figure 12. Experimental curves of closed-loop response of single-point levitation system before and after parameter tuning of levitation controller
表 1 悬浮控制性能指标
Table 1. Levitation control performance indexes
参数整定状态 ISE IAE 前 10.104 6 5.302 9 后 1.712 4 1.442 7 
下载: 导出CSV
表 2 参数整定前、后单点悬浮系统的悬浮控制性能指标
Table 2. Levitation control performance indexes of single-point levitation system before and after parameter tuning
参数整定状态 ISE IAE 前 0.0810 0.2585 后 0.0164 0.1176
下载: 导出CSV
-
[1] FORMENTIN S, VAN HEUSDEN K, KARIMI A. A comparison of model-based and data-driven controller tuning[J]. International Journal of Adaptive Control and Signal Processing, 2014, 28(10): 882-897. doi: 10.1002/acs.2415 [2] HJALMARSSON H, GEVERS M, GUNNARSSON S, et al. Iterative feedback tuning: theory and applications[J]. IEEE Control Systems Magazine, 1998, 18(4): 26-41. doi: 10.1109/37.710876 [3] RADAC M B, PRECUP R E, PETRIU E M, et al. Iterative data-driven controller tuning with actuator constraints and reduced sensitivity[J]. Journal of Aerospace Information Systems, 2014, 11(9): 551-564. doi: 10.2514/1.I010154 [4] CAMPI M C, LECCHINI A, SAVARESI S M. Virtual reference feedback tuning:a direct method for the design of feedback controllers[J]. Automatica, 2002, 38(8): 1337-1346. doi: 10.1016/S0005-1098(02)00032-8 [5] CAMPESTRINI L, ECKHARD D, GEVERS M, et al. Virtual reference feedback tuning for non-minimum phase plants[J]. Automatica, 2011, 47(8): 1778-1784. doi: 10.1016/j.automatica.2011.04.002 [6] SOMA S, KANEKO O, FUJII T. A new approach to parameter tuning of controllers by using one-shot experimental data-a proposal of fictitious reference iterative tuning[J]. Transactions of the Institute of Systems, Control and Information Engineers, 2004, 17(12): 528-536. doi: 10.5687/iscie.17.528 [7] VAN HEUSDEN K, KARIMI A, BONVIN D. Data-driven model reference control with asymptotically guaranteed stability[J]. International Journal of Adaptive Control and Signal Processing, 2011, 25(4): 331-351. doi: 10.1002/acs.1212 [8] SAKATOKU T, YUBAI K, YASHIRO D, et al. Proposal of Estimation of Closed-loop Response Using Input and Output Data[C]//2020 International Automatic Control Conference (CACS). Taiwan: IEEE, 2020: 1-5 [9] CHILUKA S K, AMBATI S R, SEEPANA M M, et al. A novel robust Virtual Reference Feedback Tuning approach for minimum and non-minimum phase systems[J]. ISA Transactions, 2021, 115: 163-191. doi: 10.1016/j.isatra.2021.01.018 [10] HORI T, YUBAI K, YASHIRO D, et al. Data-driven controller tuning for sensitivity minimization[C]//2016 International Conference on Advanced Mechatronic Systems (ICAMechS). Melbourne: IEEE, 2016: 132-137. [11] MATSUI Y, AYANO H, MASUDA S, et al. A controller tuning method based on finite impulse response estimation using closed-loop response data[J]. IEEJ Transactions on Electronics, Information and Systems, 2019, 139(8): 858-865. doi: 10.1541/ieejeiss.139.858 [12] KOSAKA M, KOSAKA A, KOSAKA M. Virtual time-response based iterative gain evaluation and redesign[J]. IFAC-PapersOnLine, 2020, 53(2): 3946-3952. [13] 龙志强,郝阿明,常文森. 考虑轨道周期性不平顺的磁浮列车悬浮控制系统设计[J]. 国防科技大学学报,2003,25(2): 84-89.LONG Zhiqiang, HAO Aming, CHANG Wensen. Suspension controller design of maglev train considering the rail track periodical irregularity[J]. Journal of National University of Defense Technology, 2003, 25(2): 84-89. [14] 李云钢,常文森. 磁浮列车悬浮系统的串级控制[J]. 自动化学报,1999,25(2): 247-251.LI Yungang, CHANG Wensen. Cascade control of an Ems maglev vehicle's levitation control system[J]. Acta Automatica Sinica, 1999, 25(2): 247-251. [15] 哀微,朱学峰. 在线VRFT数据驱动控制方法及其仿真研究[J]. 计算机应用研究,2011,28(4): 1254-1256,1265. doi: 10.3969/j.issn.1001-3695.2011.04.014AI Wei, ZHU Xuefeng. Research on online VRFT data-driven control method and simulation[J]. Application Research of Computers, 2011, 28(4): 1254-1256,1265. doi: 10.3969/j.issn.1001-3695.2011.04.014 [16] CHUPIN T J E. Data-driven attitude control design for multirotor UAVs[D]. Milan: Polytechnic University of Milan, 2017. [17] FORMENTIN S, COLOGNI A, BELLOLI D, et al. Fast tuning of cascade control systems[J]. IFAC Proceedings Volumes, 2011, 44(1): 10243-10248. doi: 10.3182/20110828-6-IT-1002.02761 [18] SAKATOKU T, YUBAI K, YASHIRO D, et al. Data-driven controller tuning with closed-loop response estimation[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2021, 16(10): 1397-1406. doi: 10.1002/tee.23436 [19] CARE A, TORRICELLI F, CAMPI M C, et al. A toolbox for virtual reference feedback tuning (VRFT)[C]//2019 18th European Control Conference (ECC). Naples: IEEE, 2019: 4252-4257 [20] FUJIMOTO Y. Estimated response iterative tuning with signal projection[J]. IFAC Journal of Systems and Control, 2022, 19: 100179.1-100179.8. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 293
- HTML全文浏览量: 415
- PDF下载量: 38
- 被引次数: 0