CPS-SPWM级联H桥激励的变压器铁耗快速计算方法

张新生; 王瑞田; 肖飞; 任强; 谢沁园

doi:10.3969/j.issn.0258-2724.20210789

CPS-SPWM级联H桥激励的变压器铁耗快速计算方法

doi: 10.3969/j.issn.0258-2724.20210789

海军工程大学舰船综合电力技术国防科技重点实验室，湖北武汉 430033

详细信息

作者简介:
张新生（1992—），男，讲师，研究方向为磁性元件建模与设计，E-mail：marvinzxs@163.com

通讯作者:
王瑞田（1987—），男，副研究员，研究方向为大容量电能变换，E-mail：wangrt4321@163.com

中图分类号: TM275
计量
- 文章访问数: 152
- HTML全文浏览量: 118
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-12
- 修回日期: 2022-03-09
- 网络出版日期: 2024-03-20
- 刊出日期: 2022-05-20

Fast Calculation Method for Iron Loss of Transformer Fed by Cascaded H-Bridges with CPS-SPWM

National Key Laboratory of Science and Technology on Vessel Integrated Power System, Naval University of Engineering, Wuhan 430033, China

摘要

摘要:
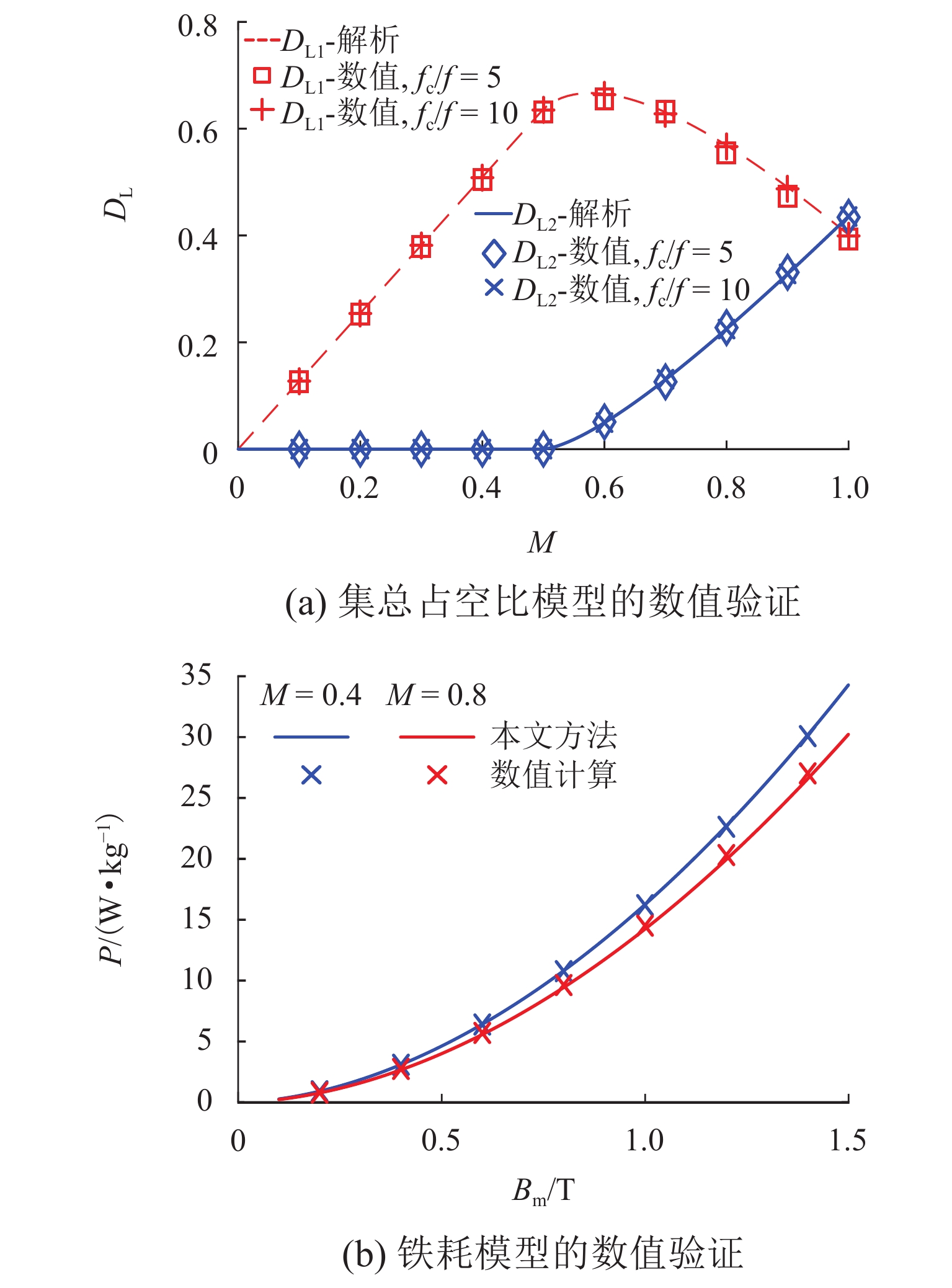
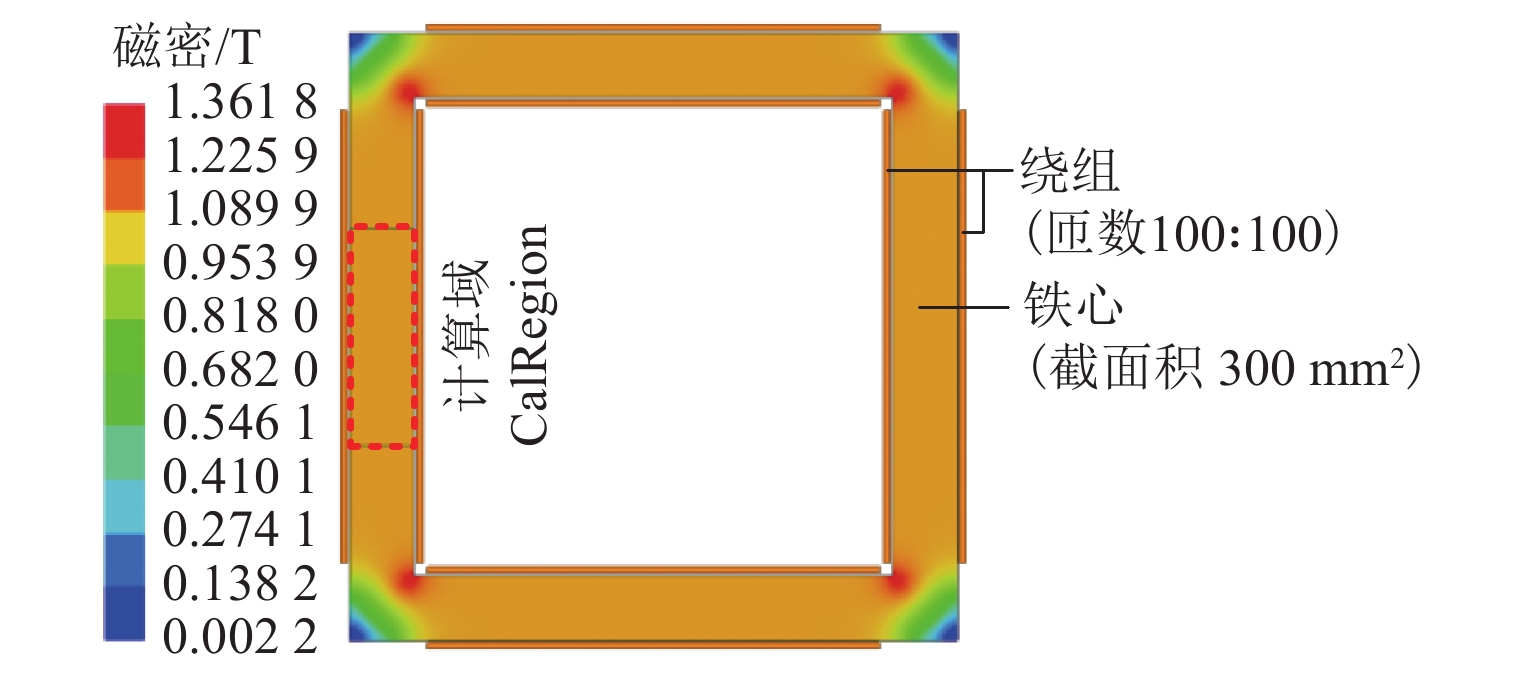
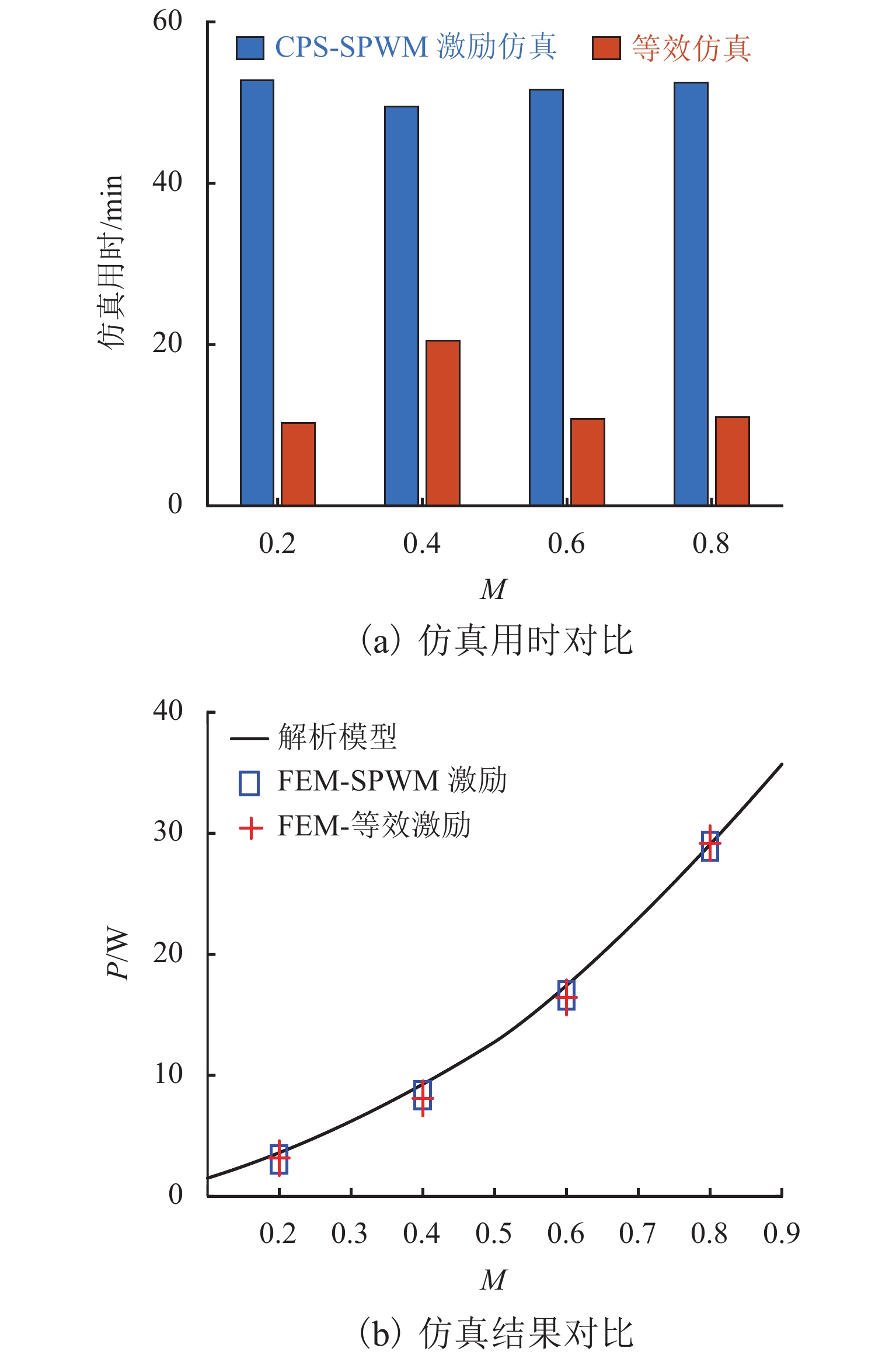
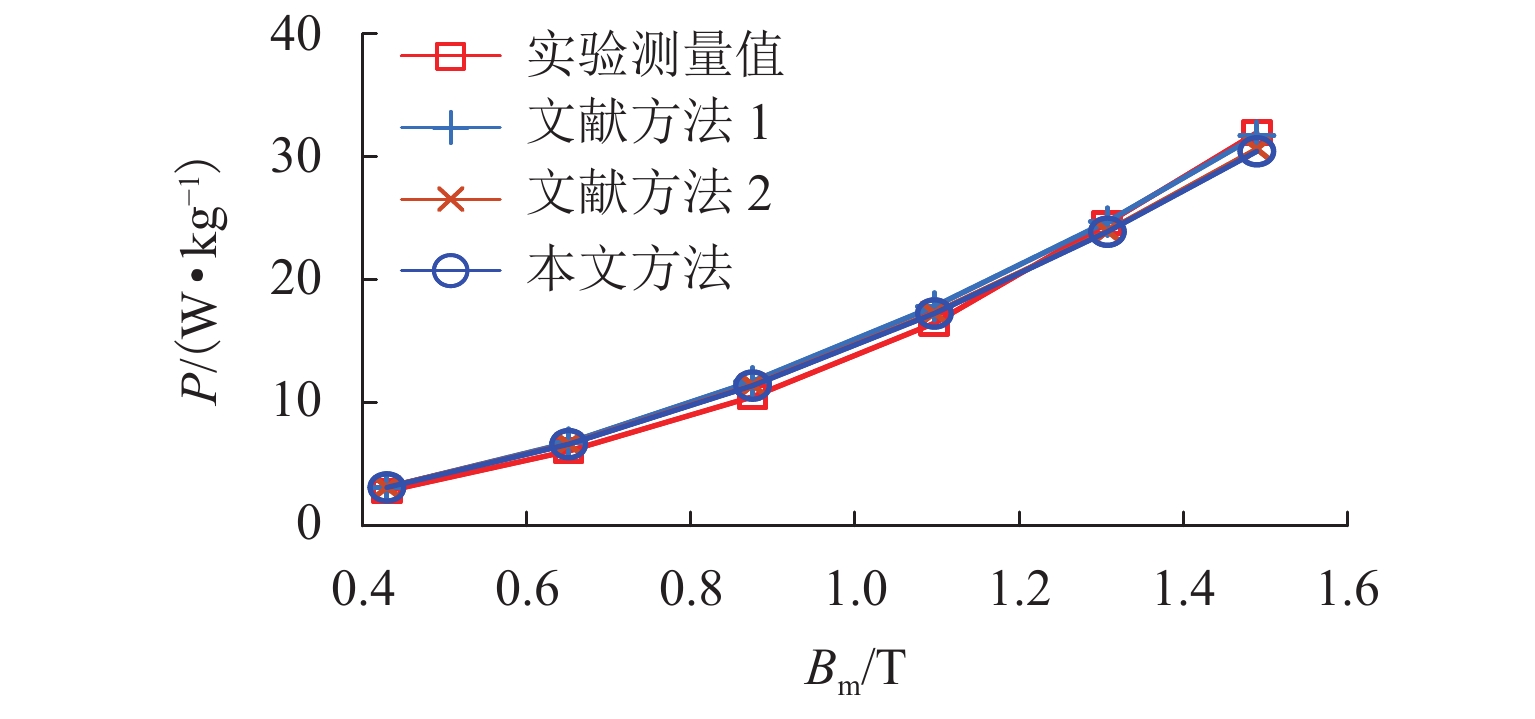
针对载波移相（CPS）正弦脉宽调制（SPWM）级联H桥激励的变压器，提出一种基于经典损耗分离模型的铁耗快速计算方法. 首先，结合SPWM电压波形特征定义集总占空比，并推导其关于调制比的解析模型；其次，基于经典损耗分离模型和集总占空比，构建CPS-SPWM级联H桥的铁耗计算模型，该方法可以直接使用调制比、直流母线电压等参数对铁耗进行计算，从而避免传统方法中的谐波分析或者数值积分过程；再次，基于本文铁耗计算模型，提出了一种针对SPWM电压激励的有限元（FEM）仿真等效方法，最后，通过实验验证了本文计算方法的有效性. 研究结果表明：等效仿真铁耗误差小于3.6%、仿真用时减少74.5%；最大铁耗计算误差为7.6%.
- 载波移相正弦脉宽调制 /
- 级联H桥 /
- 变压器 /
- 硅钢片 /
- 铁耗
Abstract:
Aiming at the transformer fed by cascaded H-bridges with carrier phase-shifted (CPS) sinusoidal pulse-width modulation (SPWM), a fast method is proposed to calculate the iron loss on the basis of the classical loss separation model. Firstly, the lumped duty cycle of the SPWM voltage waveform is defined, and the analytical model for modulation ratio is derived. Secondly, based on the classical loss separation model and the lumped duty cycle, the iron loss calculation model is built for CPS-SPWM cascaded H-bridge. The method can directly use the modulation ratio, DC bus voltage, and other parameters to calculate the iron loss, thus avoiding the harmonic analysis or numerical integration process in conventional methods. Then, based on the proposed iron loss model, an equivalent simulation method is proposed for the iron loss under the SPWM voltage excitation. With this method, the relative error of iron loss is less than 3.6% and the used time is reduced by 74.5%. Finally, the proposed method is verified by experiments and the maximum calculation error of iron loss is less than 7.6%.
- CPS-SPWM /
- cascaded H-bridge /
- power transformers /
- silicon steel sheet /
- iron loss

HTML全文

图 2 两级级联H桥逆变器拓扑

Figure 2. Topology of two-stage cascaded H-bridge convertor

下载: 全尺寸图片幻灯片

图 1 铁耗测量数据与回归曲线

Figure 1. Iron loss measurement data and regression curves

下载: 全尺寸图片幻灯片

图 3 两级级联H桥工作模式示意

Figure 3. Operating modes of two-stage cascaded H-bridges

下载: 全尺寸图片幻灯片

图 4 三电平SPWM电压和磁密波形示意

Figure 4. Waveforms of 3-level SPWM voltage and flux density

下载: 全尺寸图片幻灯片

图 5 五电平SPWM电压和磁密波形示意

Figure 5. Waveforms of 5-level SPWM voltage and flux density

下载: 全尺寸图片幻灯片

图 6 载波周期内脉冲电压

Figure 6. Voltage pulses in carrier period

下载: 全尺寸图片幻灯片

图 7 集总占空比和铁耗模型的数值验证

Figure 7. Numerical verification of lumped duty cycle and iron loss model

下载: 全尺寸图片幻灯片

图 8 FEM仿真模型

Figure 8. FEM simulation model

下载: 全尺寸图片幻灯片

图 9 仿真与解析模型结果对比

Figure 9. Comparison between simulation and analytical results

下载: 全尺寸图片幻灯片

图 10 三电平SPWM电压和等效电压

Figure 10. Three-level SPWM voltage and equivalent voltage

下载: 全尺寸图片幻灯片

图 11 仿真电压和损耗波形对比（第4组，M=0.8）

Figure 11. Comparison between simulated voltage and loss waveforms （the 4^th group, M=0.8）

下载: 全尺寸图片幻灯片

图 12 SPWM激励和等效激励仿真结果对比

Figure 12. Comparison of simulation results under SPWM voltage excitation and under equivalent voltage excitation

下载: 全尺寸图片幻灯片

图 13 实验平台

Figure 13. Experimental platform

下载: 全尺寸图片幻灯片

图 14 实验电压和电流波形

Figure 14. Waveforms of experimental voltage and current

下载: 全尺寸图片幻灯片

图 15 SPWM铁耗计算值与实验值对比

Figure 15. Comparison between calculated and simulated results of iron loss under SPWM voltage excitation

下载: 全尺寸图片幻灯片

图 16 不同调制比下的铁耗对比

Figure 16. Comparison between iron losses under different modulation ratios

下载: 全尺寸图片幻灯片

图 17 不同载波频率下的铁耗

Figure 17. Iron losses under different carrier frequencies

下载: 全尺寸图片幻灯片

表 1 损耗分离模型系数

Table 1. Coefficients of iron loss models

公式 a b/×10⁻⁵ c/×10⁻⁴ x MRE/%

式（1） 0.0203 1.223 4.894 1.972 4.8

式（2） 0.0233 2.964 1.796 5.6

下载: 导出CSV

参考文献(16)

[1]	孙兴法,聂子玲,朱俊杰,等. 交直流共用主电路及其控制方法在双输出航空静变电源中的应用[J]. 电机与控制应用,2017,44(12):6-11. doi: 10.3969/j.issn.1673-6540.2017.12.002 SUN Xingfa, NIE Ziling, ZHU Junjie, et al. Application of AC/DC electrical source sharing the same main circuit and its control method in double-output aeronautical power supply[J]. Electric Machines & Control Application,2017,44(12):6-11. doi: 10.3969/j.issn.1673-6540.2017.12.002
[2]	MAHESWARI K T, BHARANIKUMAR R, ARJUN V, et al. A comprehensive review on cascaded H-bridge multilevel inverter for medium voltage high power applications[J]. Materials Today: Proceedings,2021,45(2):2666-2670.
[3]	CHANG L , JAHNS T M , BLISSENBACH R . Characterization and modeling of soft magnetic materials for improved estimation of PWM-induced iron loss[J]. IEEE Transactions on Industry Applications, 2020, 56(1):287-300.
[4]	ZHU S, SHI B. Modeling of PWM-induced iron losses with frequency-domain methods and low-frequency parameters[J]. IEEE Transactions on Industrial Electronics,2022,69(3):2402-2413. doi: 10.1109/TIE.2021.3065626
[5]	KAUDER T, BELGRAND T, LEMAÎTRE R, et al. Medium-frequency power transformer using GOES for a three-phase dual active bridge[J]. Journal of Magnetism and Magnetic Materials,2020,504:166672.1-166672.13. doi: 10.1016/j.jmmm.2020.166672
[6]	BERTOTTI G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics,1988,24(1):621-630. doi: 10.1109/20.43994
[7]	张冬冬,郭新志,安睿驰,等. 基于DFT的感应电机转子谐波磁通密度高效分离方法及负载条件下变频电机转子铁耗特性[J]. 电工技术学报,2019,34(1):75-83. ZHANG Dongdong, GUO Xinzhi, AN Ruichi, et al. A separation method of rotor flux density harmonics based on DFT and fine analysis rotor iron losses in inverter-fed induction motors[J]. Transactions of China Electrotechnical Society,2019,34(1):75-83.
[8]	刘刚,孙立鹏,王雪刚,等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报,2018,33(21):4909-4918. LIU Gang, SUN Lipeng, WANG Xuegang, et al. Improvement of core loss calculation method and simulation application under sinusoidal and harmonic excitations[J]. Transactions of China Electrotechnical Society,2018,33(21):4909-4918.
[9]	BOGLIETTI A, CAVAGNINO A, LAZZARI M, et al. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: an engineering approach[J]. IEEE Transactions on Magnetics,2003,39(2):981-989. doi: 10.1109/TMAG.2003.808599
[10]	ZHANG Z Q, JULEN C, ARNE N, et al. Comparison of core loss models considering the impact of PWM switching[C]//2023 IEEE 6^th Student Conference on Electric Machines and Systems (SCEMS). Huzhou: IEEE, 2023: 1-7.
[11]	BARBISIO E, FIORILLO F, RAGUSA C. Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops[J]. IEEE Transactions on Magnetics,2004,40(4):1810-1819. doi: 10.1109/TMAG.2004.830510
[12]	ZHANG X S, WANG R T, XIAO F, et al. Design of an inductor-integrated transformer applied to inverter power supply[C]//2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE). Wuhan: IEEE, 2020: 1-7.
[13]	赵志刚,赵瑞,张学增. 考虑脉冲宽度调制激励特征及松弛过程影响的铁磁材料损耗分离模型研究[J]. 中国电机工程学报,2021,41(18):6431-6440. ZHAO Zhigang, ZHAO Rui, ZHANG Xuezeng. Loss separation model of ferromagnetic materials under pulse width modulation excitation characteristics and magnetic relaxation processes[J]. Proceedings of the CSEE,2021,41(18):6431-6440.
[14]	刘任,李琳. 基于损耗分离理论的非正弦激励磁心损耗计算方法研究[J]. 电工电能新技术,2018,37(9):1-9. doi: 10.12067/ATEEE1801040 LIU Ren, LI Lin. Research on calculation methods for core losses under nonsinusoidal excitation based on loss separation theory[J]. Advanced Technology of Electrical Engineering and Energy,2018,37(9):1-9. doi: 10.12067/ATEEE1801040
[15]	CHEN J Q, WANG D, CHENG S W, et al. Influence of DC-biased magnetic induction on magnetic property of silicon steel[J]. IEEE Transactions on Magnetics,2019,55(5):2002007.1-2002007.7.
[16]	国家市场监督管理总局,国家标准化管理委员会. 电工钢带(片)中频磁性能测量方法:GB/T 10129—2019[S]. 北京: 中国标准出版社,2019.