考虑梁弯扭耦合对钢轨横向振动特性的影响

豆银玲; 韦凯; 曹勇; 王绍华; 亓伟; 王平

doi:10.3969/j.issn.0258-2724.20210774

考虑梁弯扭耦合对钢轨横向振动特性的影响

doi: 10.3969/j.issn.0258-2724.20210774

豆银玲^{1, 2, 3,},
韦凯^{1, 3},
曹勇²,
王绍华⁴,
亓伟²,
王平^{1, 3, ,}

1.
西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031
2.
成都工业职业技术学院，四川成都 610031
3.
西南交通大学土木工程学院，四川成都 610031
4.
奥克兰大学机械学院，奥克兰 1010

基金项目: 国家自然科学基金（U1734207, 51978583）

详细信息

作者简介:
豆银玲（1993—），女，博士研究生，研究方向为道路与铁道工程，E-mail：douyinling@my.swjtu.edu.cn

通讯作者:
王平（1969—），男，教授，博士，研究方向为道路与铁道工程，E-mail：wping@home.swjtu.edu.cn

中图分类号: U211.3
计量
- 文章访问数: 264
- HTML全文浏览量: 57
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-07
- 修回日期: 2022-01-05
- 网络出版日期: 2023-04-26
- 刊出日期: 2022-01-14

Effect of Bending-Torsional Coupling of Beams on Lateral Vibration Characteristics of Rails

DOU Yinling^{1, 2, 3
,},
WEI Kai^{1, 3},
CAO Yong²,
WANG Shaohua⁴,
QI Wei²,
WANG Ping^{1, 3
, ,}

1.
MOE Key Laboratory of High-Speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
Chengdu Vocational & Technical College of Industry, Chengdu 610031, China
3.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
4.
Department of Mechanical Engineering, The University of Auckland, Auckland 1010, New Zealand

摘要

摘要:
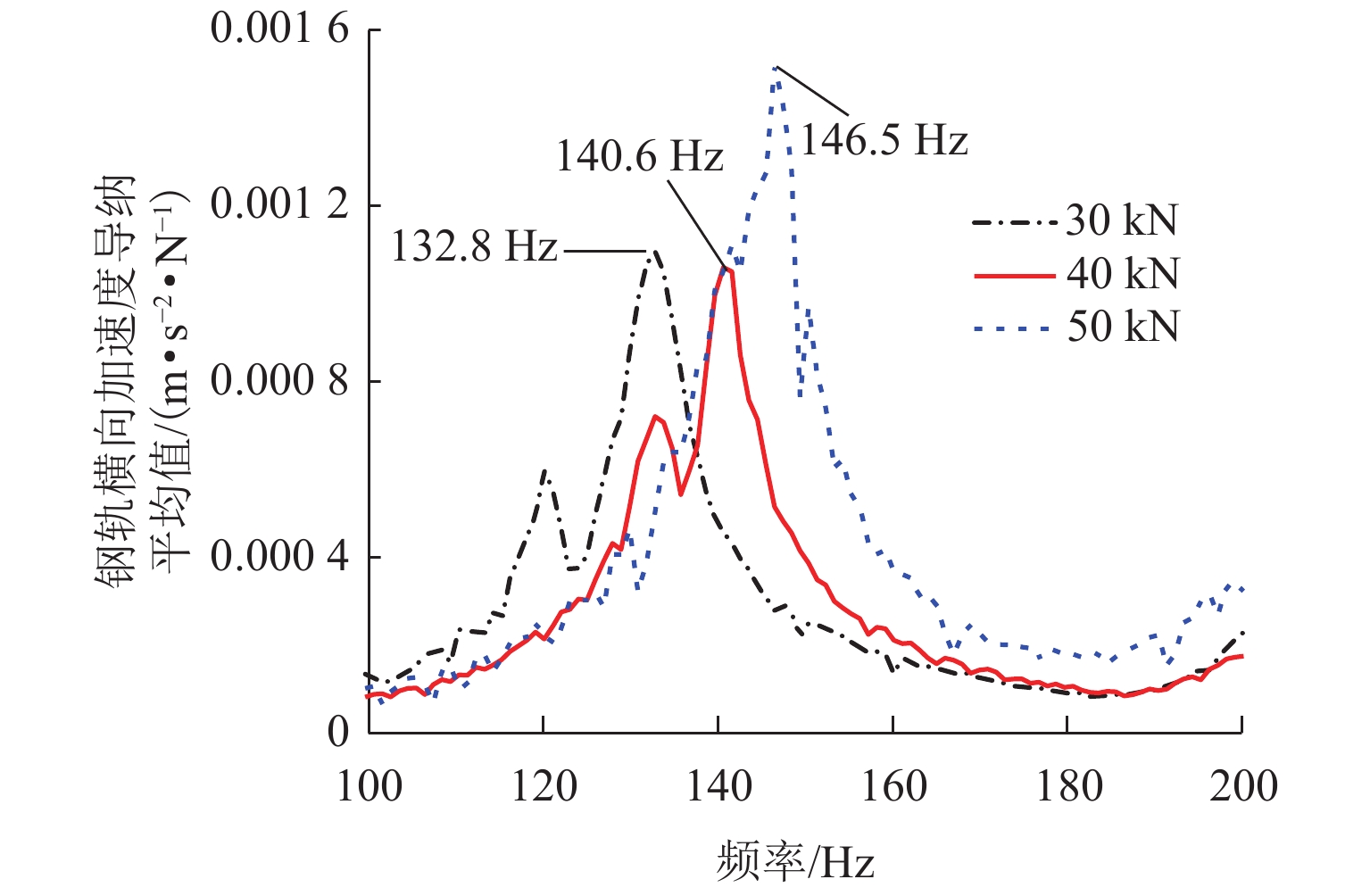
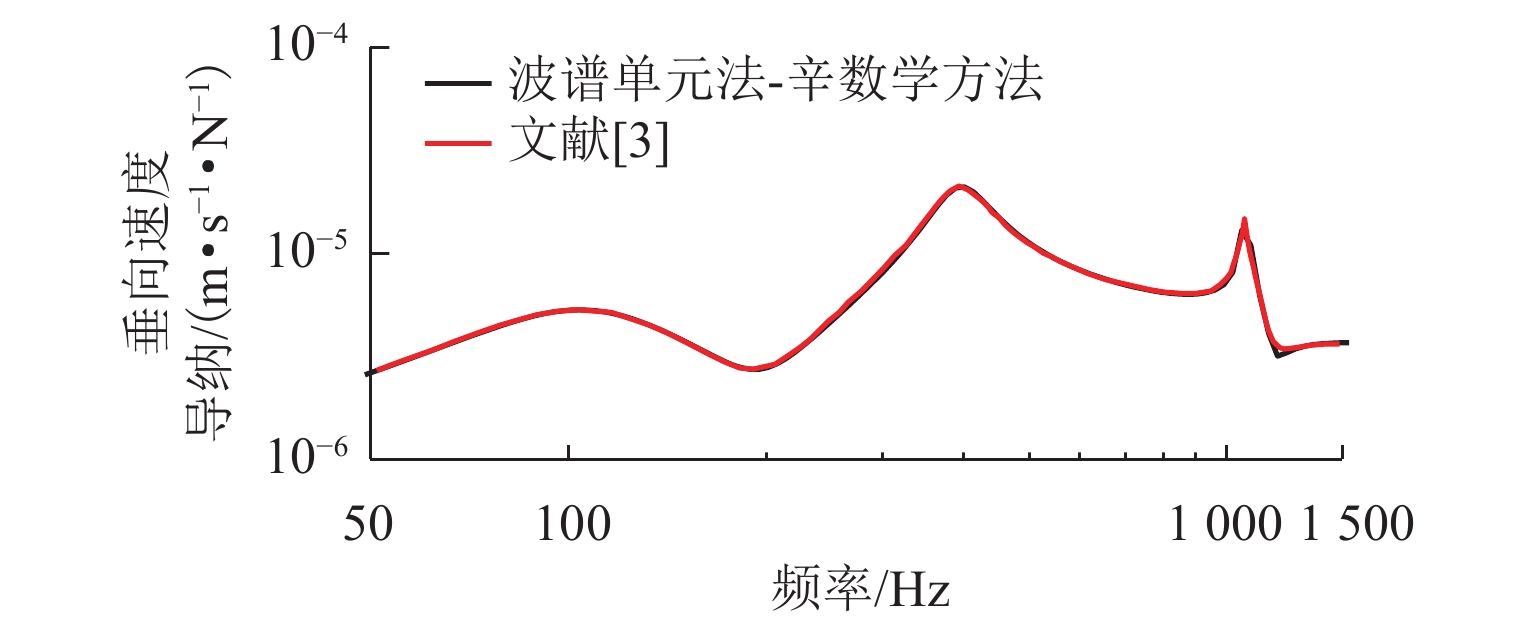
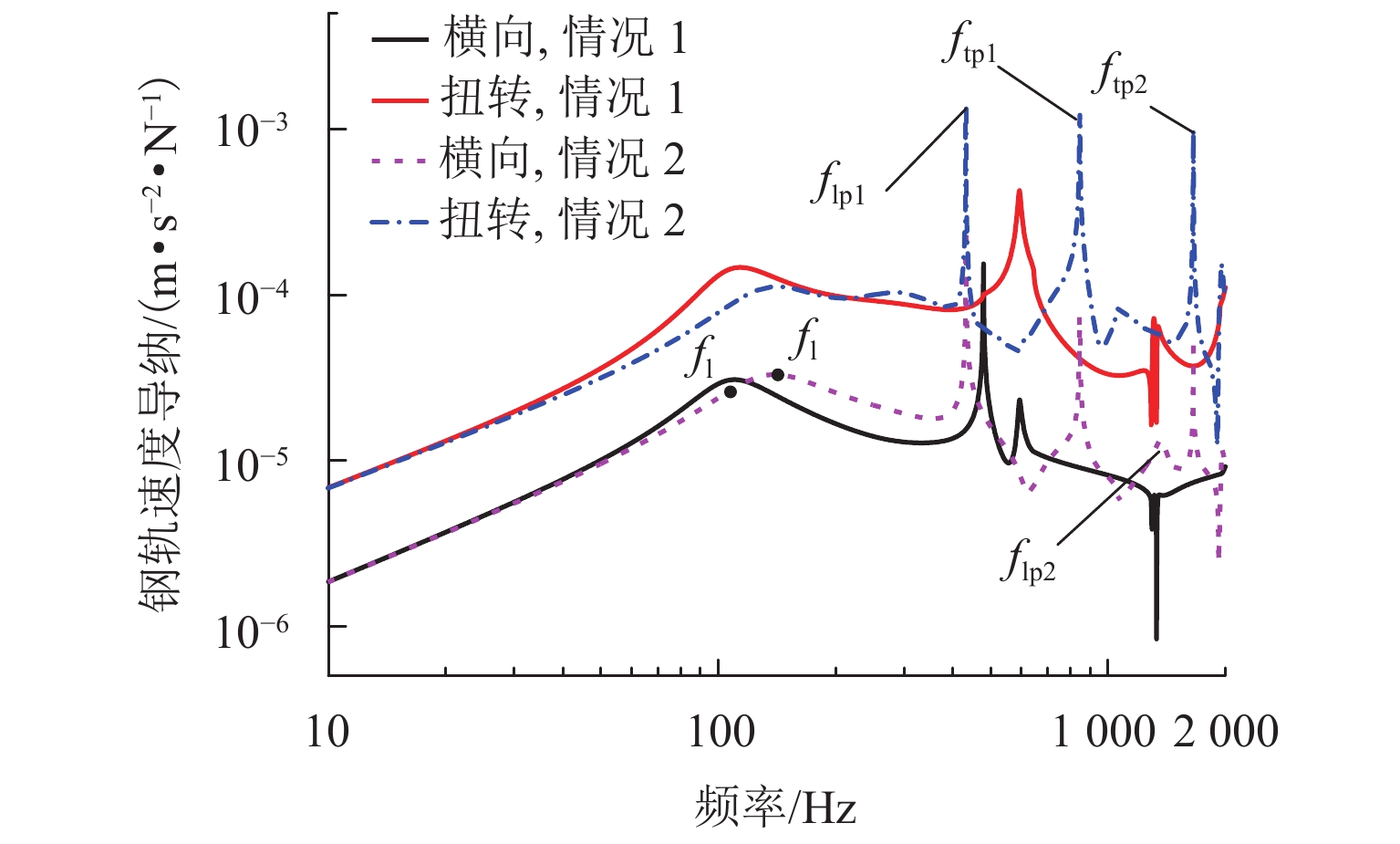
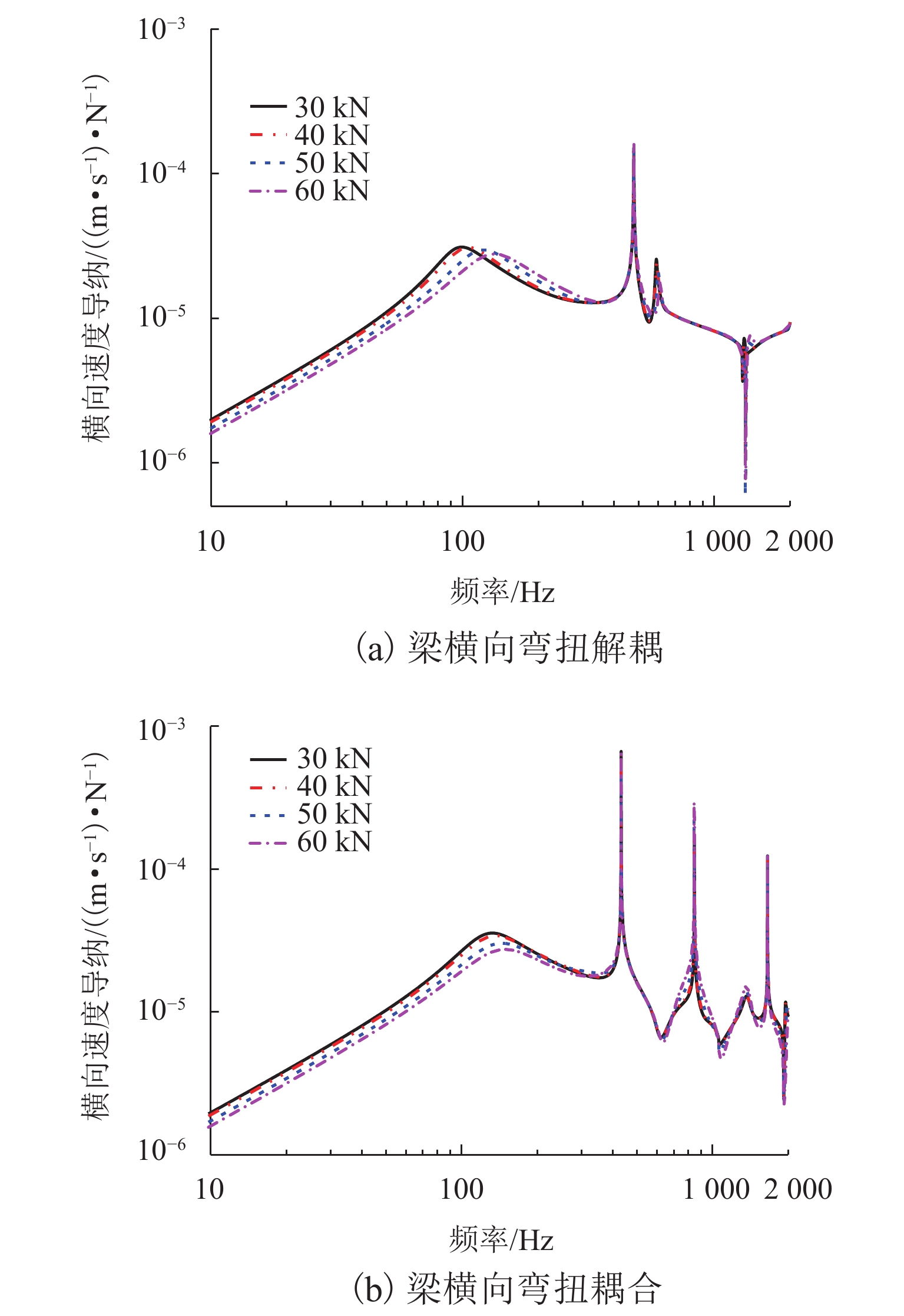
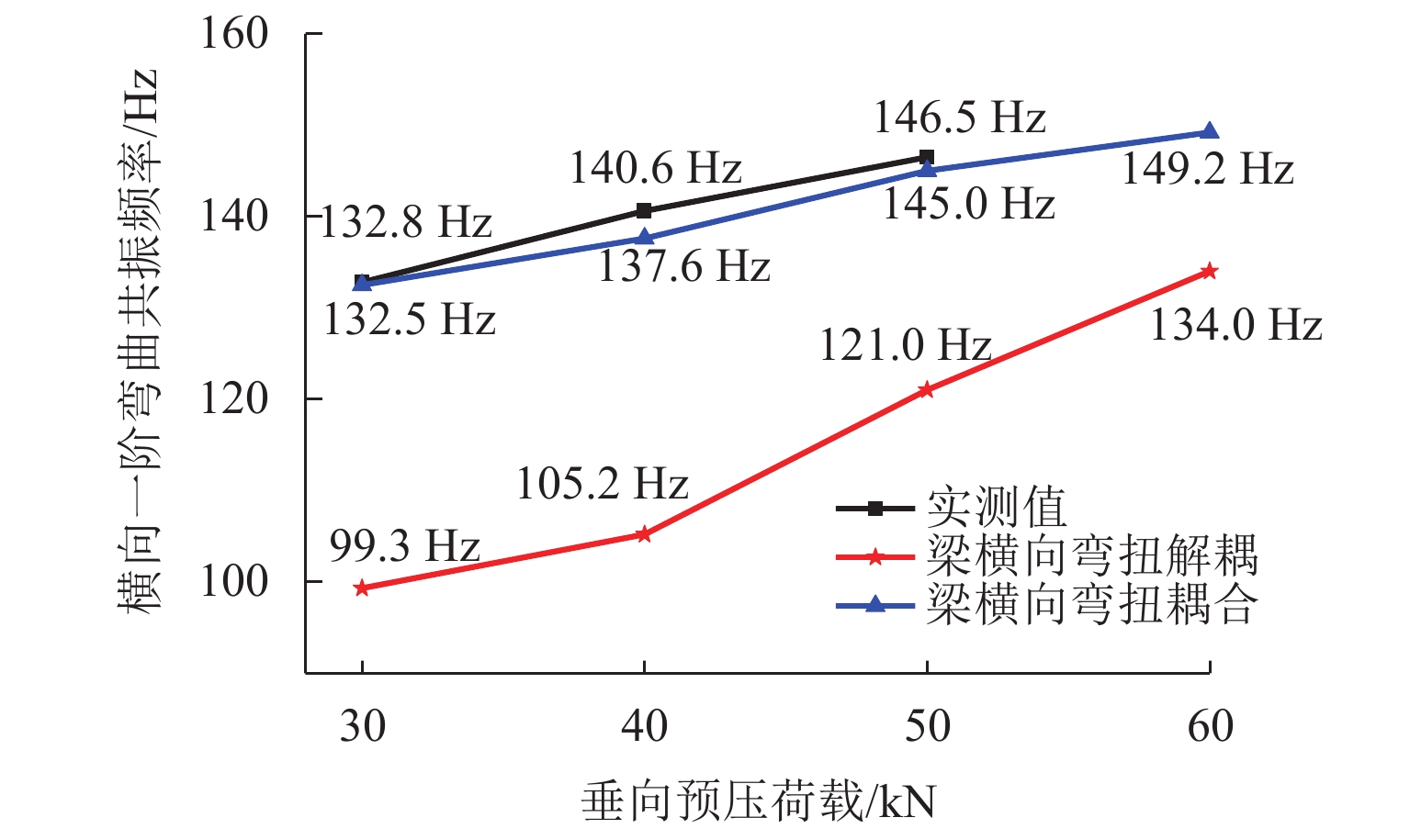
为准确预测弹性波在钢轨中的传播，且探究考虑Timoshenko梁弯扭耦合的必要性，基于波谱‒辛混合法建立了考虑梁弯扭耦合的钢轨-扣件空间无限长模型. 在模型验证的基础上，分析考虑Timoshenko梁弯扭耦合对钢轨横向固有频率与速度导纳的影响，进一步从理论和试验方面分析了扣件胶垫垂向预压特性对钢轨横向弯曲振动特性的影响. 研究结果表明：考虑梁弯扭耦合使得钢轨横向弯曲共振频率增大了约29.6 Hz，且在钢轨横向弯曲振动中同时出现弯曲和扭转pinned-pinned模态；扣件胶垫垂向预压特性主要影响钢轨横向中低频振动，随着预压的增大，钢轨横向弯曲共振频率增大；当预压从30 kN增加到50 kN时，实测的横向弯曲共振频率增加了13.7 Hz，考虑和不考虑梁弯扭耦合时其分别增加了12.5 Hz和21.7 Hz；不同预压下考虑梁弯扭耦合的钢轨横向弯曲共振频率变化规律与实测的结果更为接近.
- 弯扭耦合 /
- 预压特性 /
- 波谱-辛混合法 /
- 固有频率 /
- 速度导纳
Abstract:
To accurately predict the propagation of elastic waves in rails and explore the necessity of considering the bending-torsional coupling (BTC) of Timoshenko beam, a rail-fastener spatial infinite model considering the BTC of the beam was developed based on the spectral element method (SEM) and the symplectic method (SM). Based on model verification, the BTC effect of Timoshenko beam on the lateral natural frequency and velocity admittance of the rail was analyzed, and the effect of vertical preload dependence of fastener pads on the lateral bending vibration characteristics of the rail was analyzed theoretically and experimentally. The research results show that because of the BTC effect of the beam, the lateral bending resonance frequency (BRF) of the rail increases by about 29.6 Hz, and the bending and torsional pinned-pinned modes appear simultaneously in the lateral bending vibration of the rail. The vertical preload dependence of fastener pads mainly affects the lateral low- and mid-frequency vibrations of the rail. As the preload increases, the lateral BRF of the rail increases. When the preload is increased from 30 kN to 50 kN, the measured lateral BRF increases by about 13.7 Hz, while the increase is about 12.5 Hz and 21.7 Hz by considering the BTC effect of the beam or not. The variation law of lateral BRF of the rail considering the BTC of the beam under different preloads is closer to the measured results.
- bending-torsion coupled /
- preload dependence /
- spectral element method and symplectic method /
- natural frequency /
- velocity admittance

HTML全文

图 1 钢轨横向加速度导纳测试装置

Figure 1. Schematic of testing device of lateral acceleration admittance of rail

下载: 全尺寸图片幻灯片

图 2 垂向30 kN预压下钢轨横向加速度导纳

Figure 2. Lateral acceleration admittance of rail under vertical preload of 30 kN

下载: 全尺寸图片幻灯片

图 3 不同预压下钢轨横向加速度导纳测试结果平均值

Figure 3. Average test results of lateral acceleration admittance of rail under different preloads

下载: 全尺寸图片幻灯片

图 4 钢轨-扣件系统的整体结构与周期子结构示意

Figure 4. Overall structure and periodic substructure of a rail-fastener system

下载: 全尺寸图片幻灯片

图 5 钢轨横截面示意

Figure 5. Schematic of rail cross section

下载: 全尺寸图片幻灯片

图 6 钢轨跨中垂向速度导纳

Figure 6. Vertical velocity admittance of a rail at the mid-span

下载: 全尺寸图片幻灯片

图 7 考虑梁弯扭耦合对钢轨横向和扭转速度导纳的影响

Figure 7. Influence of vertical preload dependence of fastener pads on lateral velocity admittance of rail

下载: 全尺寸图片幻灯片

图 8 扣件胶垫垂向预压特性对钢轨横向速度导纳的影响

Figure 8. Influence of the vertical preload dependence of rail pads on the lateral mobility of rail

下载: 全尺寸图片幻灯片

图 9 不同预压下钢轨横向弯曲共振频率的实测与仿真值

Figure 9. Measured and simulated results of lateral BRF of rail under different preloads

下载: 全尺寸图片幻灯片

表 1 轨道结构参数

Table 1. Structural parameters of rail

轨道结构	参数	数值
钢轨	I₀ /m⁴	3.714 × 10⁻⁵
	扭转常数 I_d/m⁴	0.215 × 10⁻⁵
	y₀/m	0.037
	K_y	0.4
	K_z	0.09
	h_r2/mm	81.47
	b_r2/mm	75
扣件胶垫	l/m	0.592
	K_zp/（ N·m⁻¹）	3.2 × 10⁷
	C_zp/ （N·s·m⁻¹）	2.78 × 10⁴

下载: 导出CSV

表 2 Timoshenko简支梁横向弯曲和扭转固有频率

Table 2. Lateral bending and torsional natural frequencies of a simply-supported Timoshenko beam Hz

模态阶数	SEM		FEM
模态阶数	弯扭解耦	弯扭耦合	n=20	n=100	n=1000
1	5.9	6.8	6.0	5.9	5.9
2	23.8	23.5	24.0	23.8	23.8
3	52.6	52.6	54.3	52.6	52.6
4	64.5	71.0	68.5	64.5	64.4
5	92.8	94.8	97.0	93.1	92.9
10	257.4	244.2	265.7	257.6	257.1
15	418.2	443.1	477.1	420.6	418.7
20	581.8	605.3	679.8	585.0	581.7

下载: 导出CSV

参考文献(17)

[1]	THOMPSON D J. Wheel-rail noise generation, part Ⅲ: rail vibration[J]. Journal of Sound and Vibration, 1993, 16: 421-446.
[2]	翟婉明. 车辆-轨道耦合动力学·上册[M]. 4版. 北京: 科学出版社, 2015.
[3]	THOMPSON D. Railway noise and vibration: mechanisms, modelling and means of control[M]. Amsterdam: Elsevier Science, 2009.
[4]	BANERJEE J R, WILLIAMS F W. Coupled bending– torsional dynamic stiffness matrix for Timoshenko beam elements[J]. Computers & Structures, 1992, 42(3): 301-310.
[5]	VINCENT N, BOUVET P, THOMPSON D J, et al. Theoretical optimization of track components to reduce rolling noise[J]. Journal of Sound and Vibration, 1996, 193(1): 161-171. doi: 10.1006/jsvi.1996.0255
[6]	KOSTOVASILIS D, THOMPSON D J, HUSSEIN MFM. A semi-analytical beam model for the vibration of railway tracks[J]. Journal of Sound and Vibration, 2017, 393: 321-337. doi: 10.1016/j.jsv.2016.12.033
[7]	TIMOSHENKO S, YOUNG D H. Vibration problems in engineering[M]. 3rd ed. New York: Van Nostrand, 1955.
[8]	LI J, SHI C X, KONG X S, et al. Stochastic response of an axially loaded composite Timoshenko beam exhibiting bending-torsion coupling[J]. Archive of Applied Mechanics, 2013, 84(1): 109-122.
[9]	易强. 周期性铁路轨道结构弹性波传播特性及调控方法研究[D]. 成都: 西南交通大学, 2020.
[10]	农兴中,魏晓,李祥,等. 地铁常用减振轨道钢轨横向振动特性测试分析[J]. 铁道工程学报,2019,36(1): 43-47. NONG Xingzhong, WEI Xiao, LI Xiang, et al. Test and analysis of transverse vibration characteristics of commonly used vibration-damping rails in metro[J]. Journal of Railway Engineering Society, 2019, 36(1): 43-47.
[11]	WEI K, YANG Q L, DOU Y L, et al. Experimental investigation into temperature-and frequency-dependent dynamic properties of high-speed rail pads[J]. Construction and Building Materials, 2017, 151: 848-858. doi: 10.1016/j.conbuildmat.2017.06.044
[12]	THOMPSON D J, VAN VLIET W J, WERHEIJ J W. Developments of the indirect method for measuring the high frequency dynamic stiffness of resilient elements[J]. Journal of Sound and Vibration, 1998, 213(1): 169-188. doi: 10.1006/jsvi.1998.1492
[13]	中华人民共和国铁道行业标准. 高速铁路扣件, 第一部分, 通用技术条件: TB/T 3395.1—2015[S]. 北京: 国家铁路局, 2015.
[14]	范盛金. 一元三次方程的新求根公式与新判别法[J]. 海南师范学院学报(自然科学版),1989(2): 91-98.
[15]	WEI K, DOU Y L, WANG F, et al. High-frequency random vibration analysis of a high-speed vehicle-track system with the frequency-dependent dynamic properties of rail pads using a hybrid SEM-SM method[J]. Vehicle System Dynamics, 2018, 56(12): 1838-1863. doi: 10.1080/00423114.2018.1439977
[16]	韦凯,王丰,牛澎波,等. 钢轨扣件弹性垫板的动态黏弹塑性力学试验及理论表征研究[J]. 铁道学报,2018,40(12): 115-122. WEI Kai, WANG Feng, NIU Pengbo, et al. Experimental investigation and theoretical model of viscoelastic and plastic dynamic properties of rail pads[J]. Journal of the China Railway Society, 2018, 40(12): 115-122.
[17]	HOWSON W P, JEMAH A K. Exact out-of-plane natural frequencies of curved Timoshenko beams[J]. Journal of Engineering Mechanics, 1999, 125(1): 19-25. doi: 10.1061/(ASCE)0733-9399(1999)125:1(19)