考虑碳排放的两阶段选址-路径问题及其算法

汤希峰; 何杰; 张浩

doi:10.3969/j.issn.0258-2724.20210773

考虑碳排放的两阶段选址-路径问题及其算法

doi: 10.3969/j.issn.0258-2724.20210773

汤希峰^1,,
何杰^2, ,,
张浩²

1.
河海大学土木与交通学院，江苏南京 210098
2.
东南大学交通学院，江苏南京 211189

基金项目: 国家自然科学基金（71874067，52072069）；江苏省农业科技自主创新资金（CX(20)3074）

详细信息

作者简介:
汤希峰（1980—），男，讲师，博士，研究方向为运输与物流工程， E-mail：20110029@hhu.edu.cn

通讯作者:
何杰（1973—），男，教授，博士生导师，研究方向为载运工具运用工程，E-mail：hejie@seu.edu.cn

中图分类号: F252
计量
- 文章访问数: 453
- HTML全文浏览量: 254
- PDF下载量: 71
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-01
- 修回日期: 2022-01-08
- 网络出版日期: 2023-04-13
- 刊出日期: 2022-01-14

Two-Echelon Location Routing Problem Considering Carbon Emissions and Its Algorithm

TANG Xifeng^1
,,
HE Jie^{2
, ,},
ZHANG Hao²

1.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China
2.
School of Transportation, Southeast University, Nanjing 211189, China

摘要

摘要:
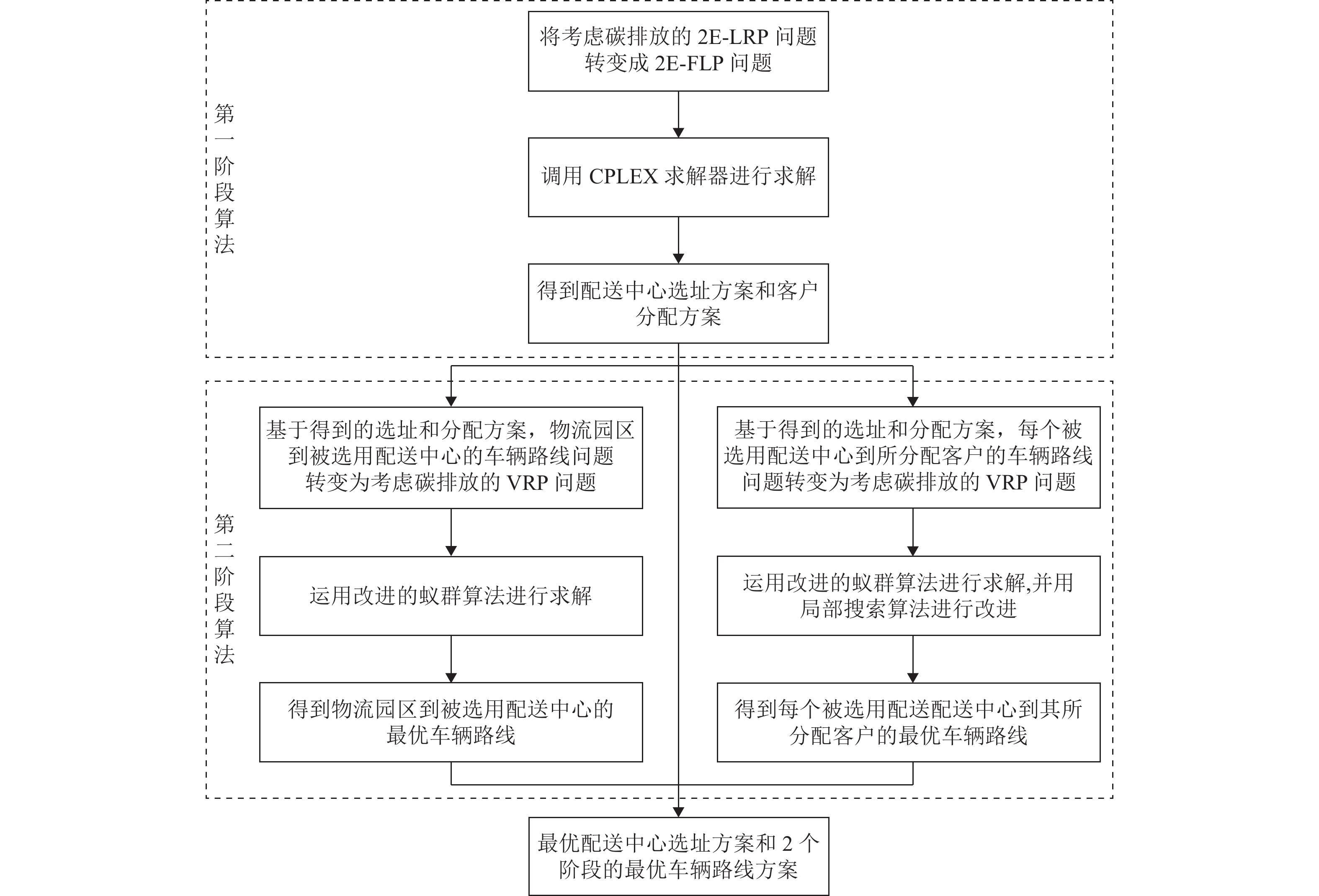
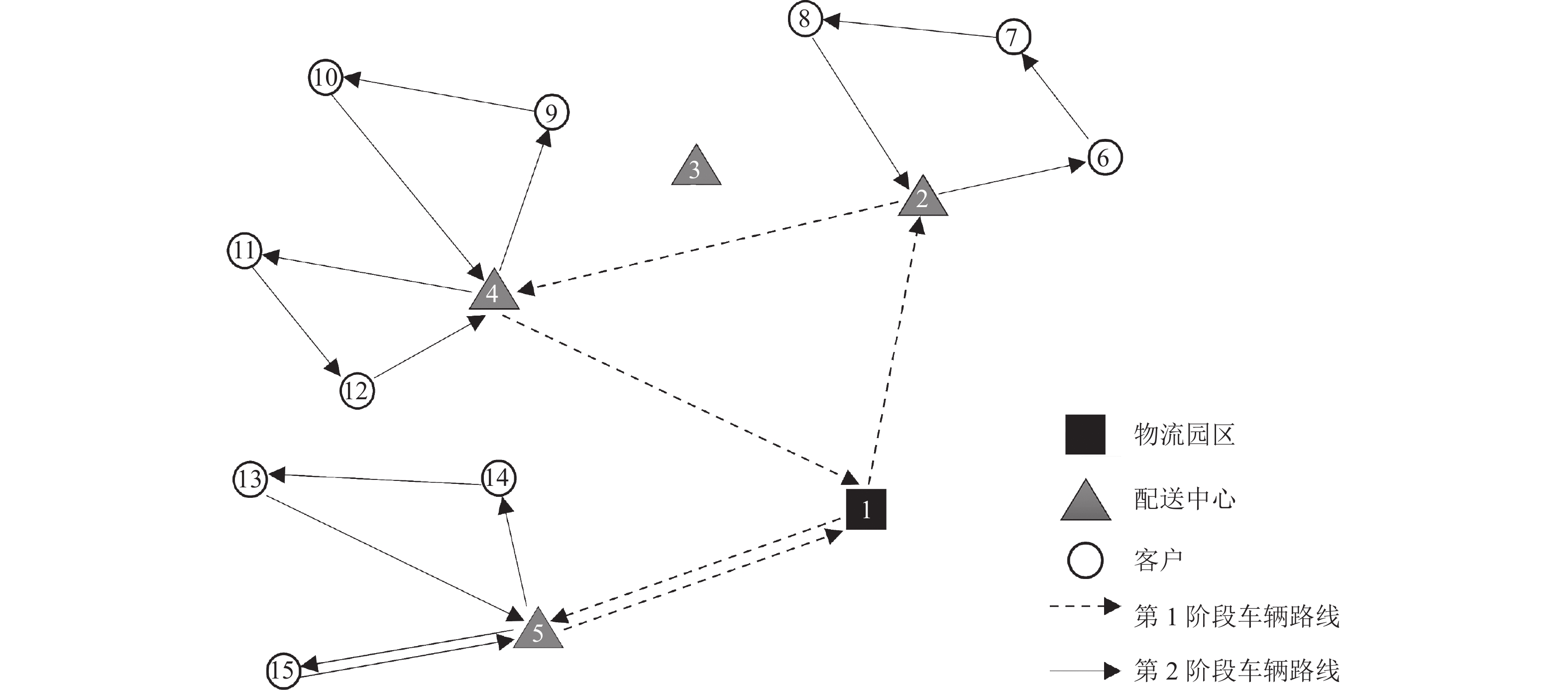
为减少物流车辆的碳排放，基于以排放因子为主要参数的碳排放计算方法，建立以碳排放最小化为目标的两阶段选址-路线问题（2E-LRP）模型，并设计了一种可用于快速求解大规模问题的两阶段混合算法（TSHA）. 算法第一阶段将2E-LRP转化成不考虑车辆路径的两阶段设施选址问题，调用Cplex直接求解得到配送中心选址和客户分配方案；在此基础上，算法第二阶段中，物流园区到被选用的配送中心以及配送中心到所分配客户的车辆路径问题被进一步转化成若干个独立的VRP （vehicle routing problem）问题，再运用改进的蚁群算法进行求解；最后，对Prodhon标准算例集中全部6个最大规模的算例进行测试. 研究结果表明：与TSHA具有相同算法思想的TSHA-Ⅱ算法能够在求解质量下降2.3%的情况下将计算时长大大缩短至25 s左右；TSHA算法在求解考虑碳排放的2E-LRP算例时表现非常稳定，可以作为一种求解考虑碳排放2E-LRP的有效算法.
- 城市物流 /
- 两阶段选址-路径问题 /
- 碳排放 /
- 两阶段混合算法 /
- 蚁群算法
Abstract:
To reduce the carbon emissions from logistics vehicles, this paper presented a two-echelon location routing problem (2E-LRP) model aiming at minimizing carbon emissions based on a carbon emission calculation method employing emission factors as the key parameter. The paper also designed a two-stage hybrid algorithm (TSHA) capable of rapidly solving a large-scale problem. The algorithm first simplified the 2E-LRP into the two-echelon facility location problem without taking vehicle routes into account and called Cplex to solve it to obtain the location solution of distribution centers and the assignment solution of customers. Based on the above solutions, the 2E-LRP was transformed into independent vehicle route problems, and then an improved ant colony algorithm was employed for a solution. All six largest-sized instances from the standard Prodhon benchmark were tested. The test results show that the TSHA-Ⅱ, with the same algorithm ideas as TSHA, can reduce the computation time to about 25 seconds with a decrease of 2.3% in solution quality. The TSHA is stable in solving 2E-LRP considering carbon emissions and can be used as an effective algorithm to solve the 2E-LRP considering carbon emissions.
- city logistics /
- two-echelon location routing problem /
- carbon emissions /
- two-stage hybrid algorithm /
- ant colony algorithm

HTML全文

图 1 2E-LRP示意

Figure 1. An illustration of the 2E-LRP

下载: 全尺寸图片幻灯片

图 2 两阶段混合算法的算法流程

Figure 2. Flowchart of the TSHA

下载: 全尺寸图片幻灯片

图 3 改进蚁群算法的伪代码

Figure 3. Pseudocode of the improved ant colony algorithm

下载: 全尺寸图片幻灯片

表 1 TSHA-II算法与LNS-2E、Two-stage算法求解2E-LRP原算例的结果对比

Table 1. Comparison of the results obtained by LNS-2E, two-stage algorithm, and TSHA-II in solving original 2E-LRP instances

算例	B	LNS-2E 算法			Two-stage 算法			TSHA-II 算法
算例	B	C_min	T_min/s	G/%	C_min	T_min/s	G/%	C_min	T_min/s	G/%
200-10-1	548 703	550 672	725	0.36	561 840	8.15	2.39	557 751	25.179	1.65
200-10-1b	445 301	447 113	692	0.41	466 288	7.51	4.71	462 251	26.014	3.81
200-10-2	497 451	498 397	656	0.19	505 700	7.52	1.66	498 770	23.125	0.27
200-10-2b	422 668	422 877	601	0.05	428 749	7.67	1.44	424 170	24.794	0.36
200-10-3	527 162	533 174	668	1.14	546 708	7.31	3.71	541 628	23.366	2.74
200-10-3b	401 672	417 429	700	3.92	451 278	7.07	12.35	421 728	25.364	4.99
平均值			674	1.01		7.54	4.38		24.640	2.30

下载: 导出CSV

表 2 TSHA算法求解考虑碳排放的2E-LRP算例的结果

Table 2. Results obtained by TSHA in solving 2E-LRP instances considering carbon emissions

算例	E_avg/kg	E_max/kg	E_min/kg	T_avg/s	T_min/s
200-10-1	1860.3	1896.3	1818.9	23.195	23.087
200-10-1b	1341.9	1390.5	1275.6	27.905	24.598
200-10-2	1562.9	1579.4	1548.1	22.291	22.627
200-10-2b	1098.5	1110.3	1085.0	25.492	24.560
200-10-3	1968.5	1984.8	1947.6	26.037	26.508
200-10-3b	1357.4	1375.5	1342.5	26.570	27.128

下载: 导出CSV

参考文献(17)

[1]	CRAINIC T G, RICCIARDI N, STORCHI G. Advanced freight transportation systems for congested urban areas[J]. Transportation Research Part C: Emerging Technologies, 2004, 12(2): 119-137. doi: 10.1016/j.trc.2004.07.002
[2]	CRAINIC T G, RICCIARDI N, STORCHI G. Models for evaluating and planning city logistics systems[J]. Transportation Science, 2009, 43(4): 432-454. doi: 10.1287/trsc.1090.0279
[3]	CATTARUZZA D, ABSI N, FEILLET D, et al. Vehicle routing problems for city logistics[J]. EURO Journal on Transportation and Logistics, 2017, 6(1): 51-79. doi: 10.1007/s13676-014-0074-0
[4]	胡大伟,陈希琼,高扬. 定位-路径问题综述[J]. 交通运输工程学报,2018,18(1): 111-129. doi: 10.3969/j.issn.1671-1637.2018.01.011 HU Dawei, CHEN Xiqiong, GAO Yang. Review on location-routing problem[J]. Journal of Traffic and Transportation Engineering, 2018, 18(1): 111-129. doi: 10.3969/j.issn.1671-1637.2018.01.011
[5]	CUDA R, GUASTAROBA G, SPERANZA M G. A survey on two-echelon routing problems[J]. Computers & Operations Research, 2015, 55: 185-199. doi: 10.1016/j.cor.2014.06.008
[6]	中华人民共和国生态环境部. 中国移动源环境管理年报(2020)[EB/OL]. (2020-08-10)[2021-02-17]. https://www.mee.gov.cn/xxgk2018/xxgk/xxgk15/202008/t20200810_793252.html.
[7]	GOVINDAN K, JAFARIAN A, KHODAVERDI R, et al. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food[J]. International Journal of Production Economics, 2014, 152: 9-28. doi: 10.1016/j.ijpe.2013.12.028
[8]	胡大伟,刘成清,胡卉,等. 基于低碳视角的两阶段开放式选址路径问题——燃油车与电动车对比[J]. 系统工程理论与实践,2020,40(12): 3230-3242. doi: 10.12011/SETP2019-0533 HU Dawei, LIU Chengqing, HU Hui, et al. The two-echelon open location routing problem based on low carbon perspective–fuel vehicles vs. electric vehicles[J]. Systems Engineering−Theory & Practice, 2020, 40(12): 3230-3242. doi: 10.12011/SETP2019-0533
[9]	刘成清,胡大伟,黄榕. 基于路径灵活性的两阶段开放式低碳选址-路径问题[J]. 科学技术与工程,2020,20(17): 7080-7087. doi: 10.3969/j.issn.1671-1815.2020.17.055 LIU Chengqing, HU Dawei, HUANG Rong. Two-echelon open low carbon location-routing problem based on path flexibility[J]. Science Technology and Engineering, 2020, 20(17): 7080-7087. doi: 10.3969/j.issn.1671-1815.2020.17.055
[10]	PITAKASO R, SETHANAN K, THEERAVIRIYA C. Variable neighborhood strategy adaptive search for solving green 2-echelon location routing problem[J]. Computers and Electronics in Agriculture, 2020, 173: 105406. doi: 10.1016/j.compag.2020.105406
[11]	DEMIR E, BEKTAS T, LAPORTE G. A review of recent research on green road freight transportation[J]. European Journal of Operational Research, 2014, 237(3): 775-793. doi: 10.1016/j.ejor.2013.12.033
[12]	蒋海青,赵燕伟,张景玲,等. 基于碳排放的开放选址-路径问题及算法[J]. 系统工程理论与实践,2020,40(1): 182-194. doi: 10.12011/1000-6788-2017-1375-13 JIANG Haiqing, ZHAO Yanwei, ZHANG Jingling, et al. Minimizing the carbon emission for the open location-routing problem and algorithm[J]. Systems Engineering−Theory & Practice, 2020, 40(1): 182-194. doi: 10.12011/1000-6788-2017-1375-13
[13]	DORIGO M, BIRATTARI M, STUTZLE T. Ant colony optimization: Artificial ants as a computational intelligence technique[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39.
[14]	TING C J, CHEN C H. A multiple ant colony optimization algorithm for the capacitated location routing problem[J]. International Journal of Production Economics, 2013, 141(1): 34-44. doi: 10.1016/j.ijpe.2012.06.011
[15]	PRODHON C. Classical instances for LRP[DB/OL]. Villetaneuse, Ile-de-France: Université Paris-Nord, (2010-02-25)[2021-02-17]. http://prodhonc.free.fr/Instances/instances_us.htm.
[16]	BREUNIG U, SCHMID V, HARTL R F, et al. A large neighbourhood based heuristic for two-echelon routing problems[J]. Computers & Operations Research, 2016, 76: 208-225.
[17]	DAI Z, AQLAN F, ZHOU Y. A two-phase method for multi-echelon location-routing problems in supply chains[J]. Expert Systems with Applications, 2019, 115: 618-634. doi: 10.1016/j.eswa.2018.06.050