Modeling and Evaluation of Aggregate Based on Influence of Geometry Morphology
-
摘要:
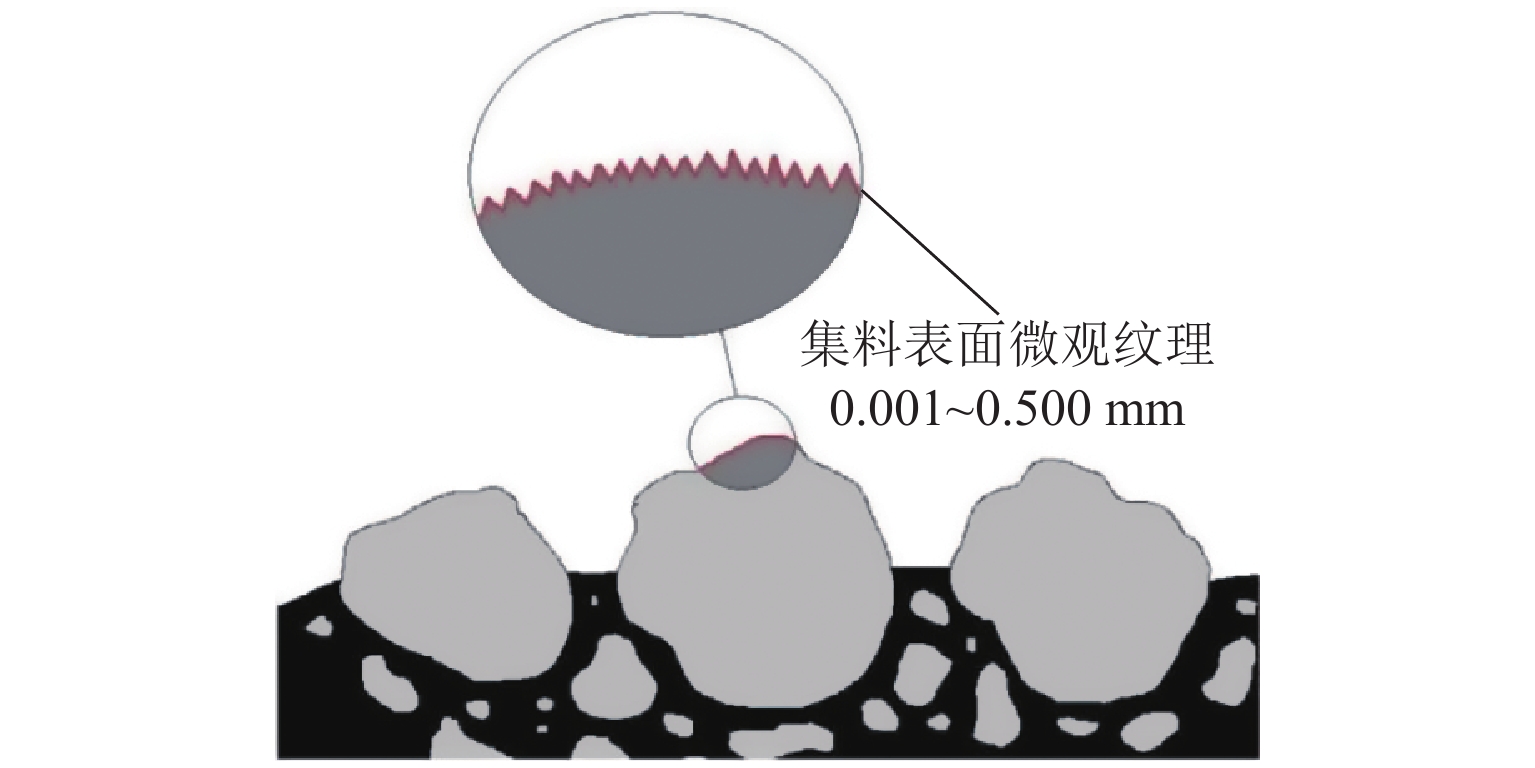
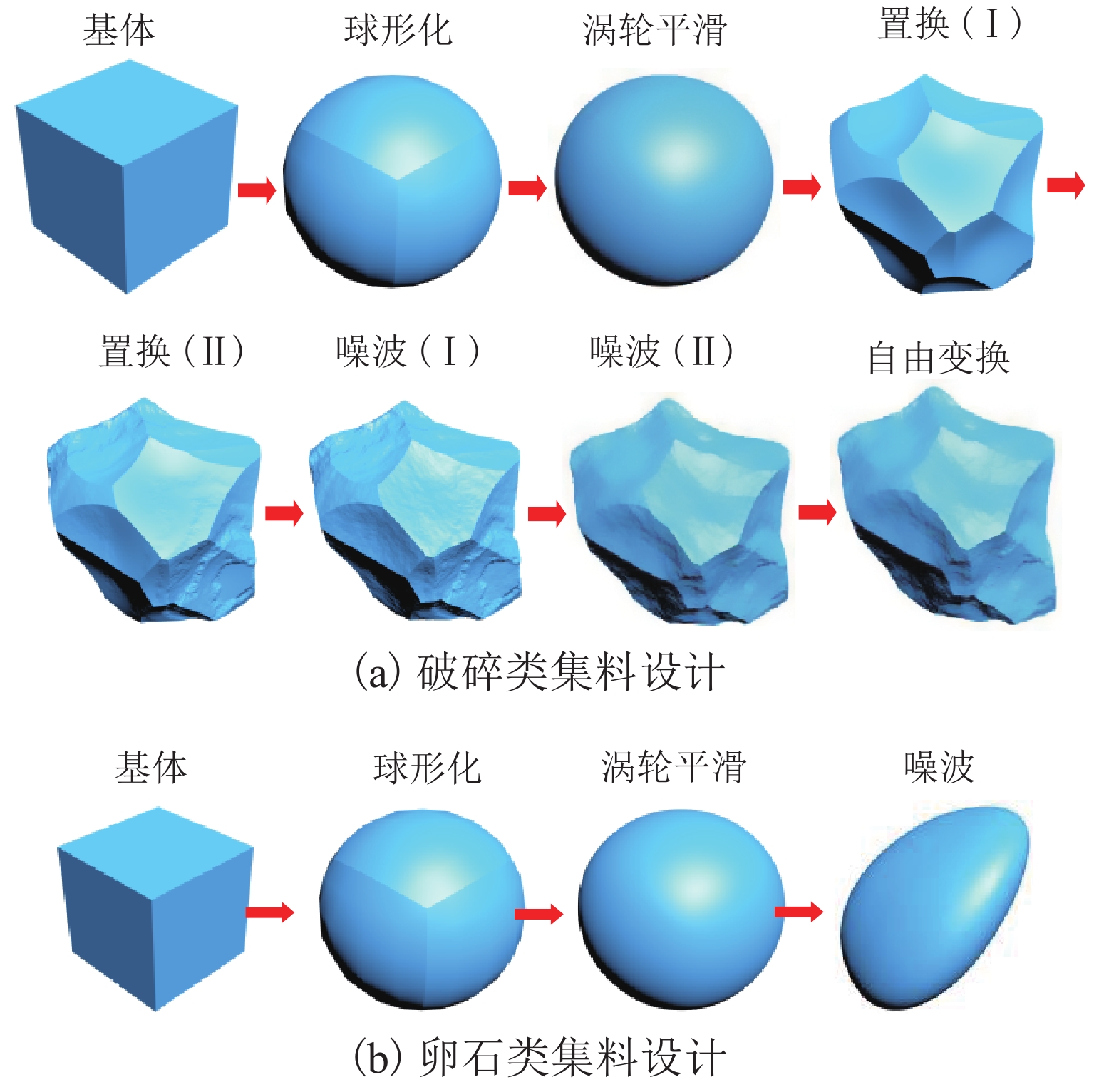
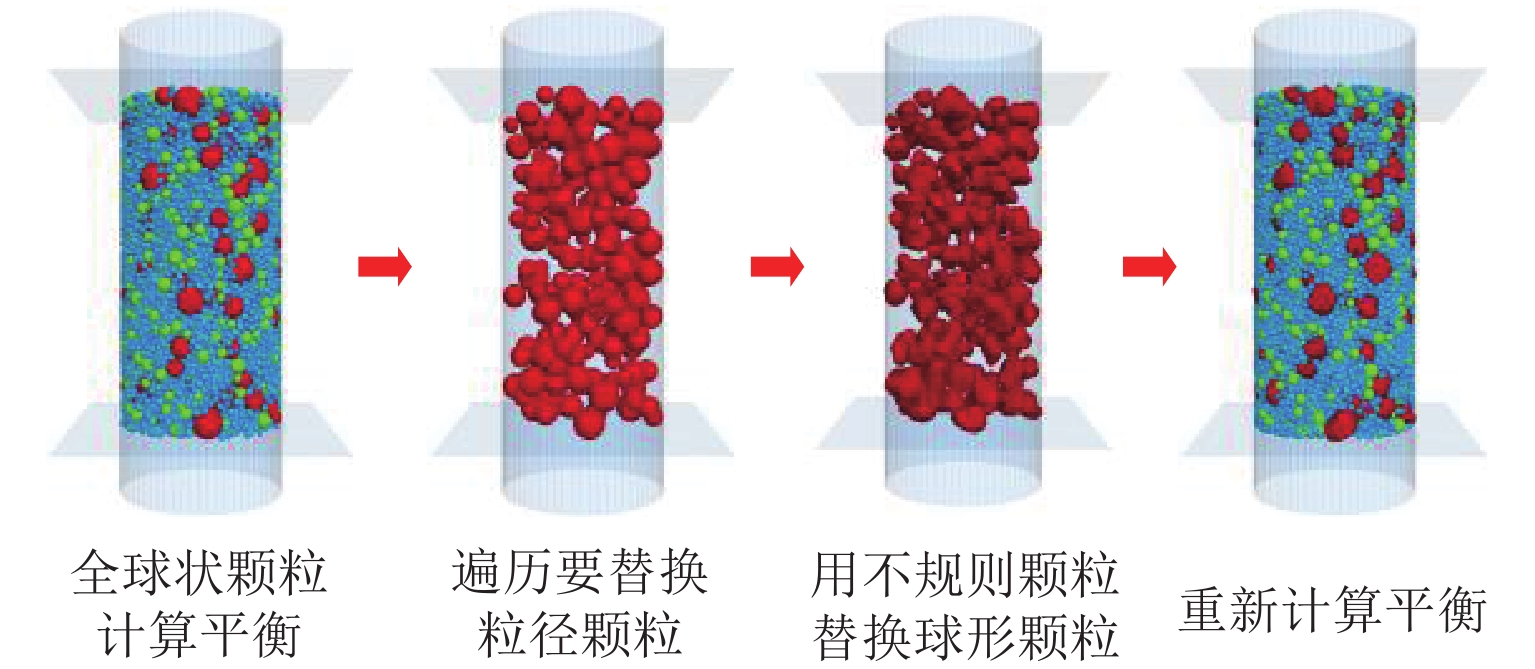
目前流行的数字集料建模技术效率和质量低，参数不可控且不能兼顾集料的形状、棱角、纹理等多个几何形态参数，导致难以有效在细观层面研究集料几何形态参数对颗粒复合材料综合性能的影响. 针对上述问题，首先，研究了单一集料几何形态特征评价，并给出一种评价集料表面微观纹理和集料系统的数学方法；其次，基于3D Max提出一种新颖的单一集料数字模型设计技术，创建了带有不规则形状、无序棱角和精细表面纹理的集料数字模型；最后，基于PFC 3D并采用“颗粒替换法”创建颗粒复合材料数字模型，进而分析了实物模型和数字模型空隙率差异，并给出解决空隙率差异的数学方法. 在此基础上，通过单轴压缩试验研究了集料几何学特性对颗粒复合材料峰值抗压强度的影响. 研究结果表明：1） 给出的集料纹理评价数学方法能量化集料微观结构，而集料系统评价数学模型拓展了集料几何形态学评价指标；2） 颗粒复合材料实物模型和数字模型空隙率存在较大差异；3） 集料的几何学特征能提高集料之间的咬合互锁效应，用不规则颗粒替换粒径 ≥ 2.36 mm的球形颗粒可使复合材料的峰值抗压强度提高20.7%.
Abstract:The popular digital aggregate modeling technology has low efficiency and quality, with the parameters uncontrollable and not involving the shape, edges, texture and other geometric morphological parameters of the aggregate. Thus it is difficult to effectively study the effects of geometric-morphology parameters on the comprehensive performance of particle composites at a micro level. In view of this shortcoming, firstly, the evaluation method of the geometric morphology characteristics of a single aggregate is explored and a mathematical method is presented to evaluate the micro-texture of the aggregate surface, as well as the aggregate system. Secondly, with 3D Max, a novel digital model design method for a single aggregate is proposed to create a digital model with irregular shapes, disordered edges and corners, and fine surface textures. Finally, the particle-replacement method is used to create a digital model of particle composites with PFC 3D. Then the porosity difference between the physical and the digital models is analyzed and the method to solve the porosity difference is provided. On this basis, the influence of aggregate geometry on the peak compressive strength of particle composites is studied through uniaxial compression experiments. The results show that, 1) the mathematical evaluation method of aggregate texture can quantify the microstructure of the aggregate, and the mathematical model of aggregate system evaluation expands the geometric morphology evaluation indexes of the aggregate; 2) there is a big difference in the porosity between the physical and digital models of particle composites; 3) the geometric characteristics of the aggregate can improve the occlusal interlocking effect between aggregates, and the replacement of spherical particles with particle size ≥ 2.36 mm by irregular particles can increase the peak compressive strength of the composite by 20.7%.
-
Key words:
- aggregate /
- modeling /
- geometrical morphology /
- composite /
- porosity
-
图 3 3D Max中集料几何特征的实现
Figure 3. Realization of geometric characteristics of aggregate in 3D Max
图 5 3D Max优化工具对集料控制网格的影响
Figure 5. Influence of 3D Max optimization tool on aggregate wrap mesh
图 7 基体分段数和涡轮平滑迭代次数对颗粒簇包络网格节点的影响
Figure 7. Influence of numbers of segments and turbo smooth iterations on wrap mesh nodes
图 8 不同试验方案下的集料精度和数值分析效率
Figure 8. Aggregate accuracy and numerical analysis efficiency under different test schemes
图 9 建模参数对集料表面积和体积的影响
Figure 9. Influence of modeling parameters on aggregate surface area and volume
图 10 纹理构造参数对纹理评价指标的影响
Figure 10. Influence of texture construction parameters on texture index
图 11 集料几何学特性对RMC抗压强度的影响
Figure 11. Influence of aggregate geometric properties on RMC compressive strength
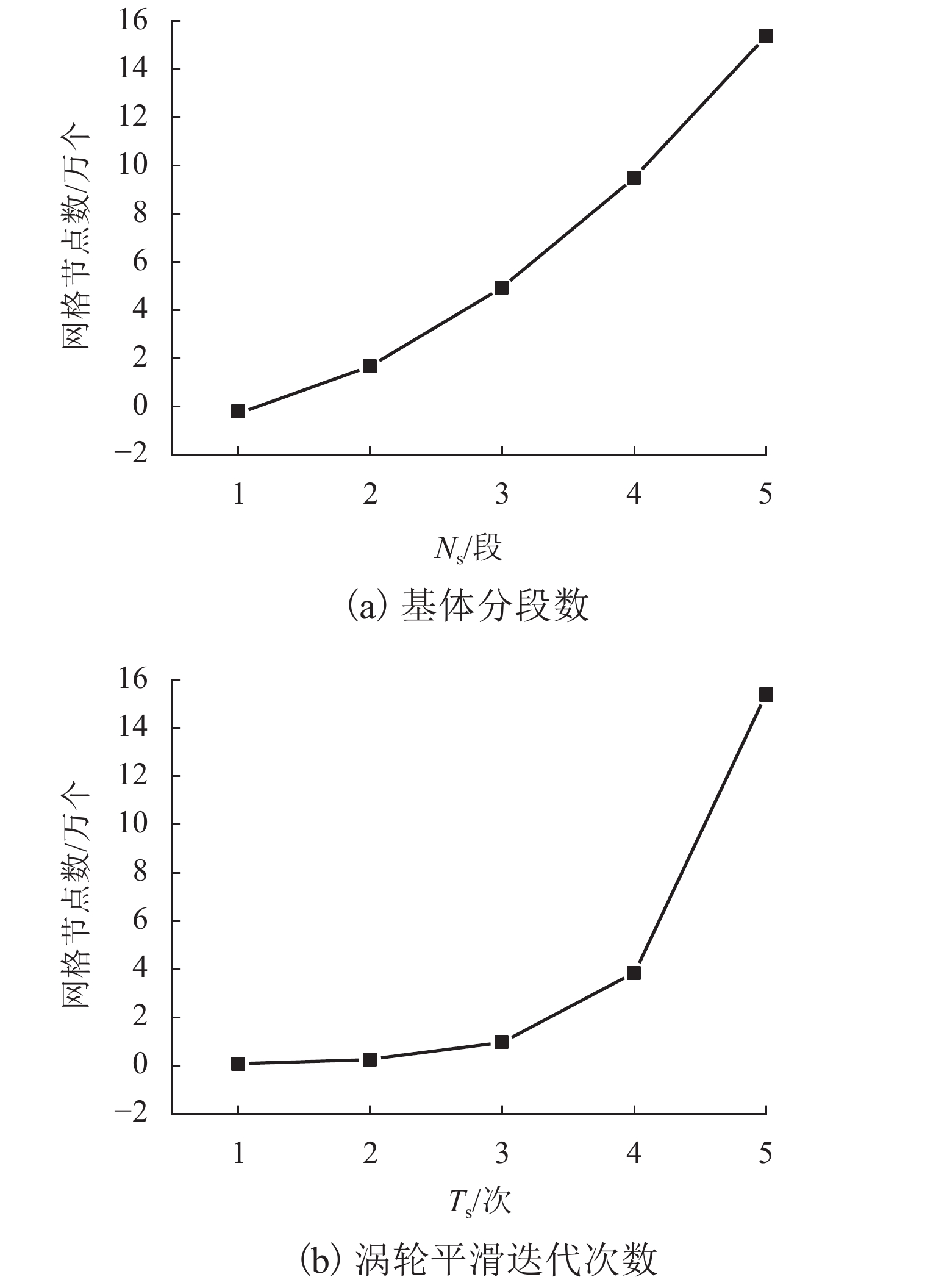
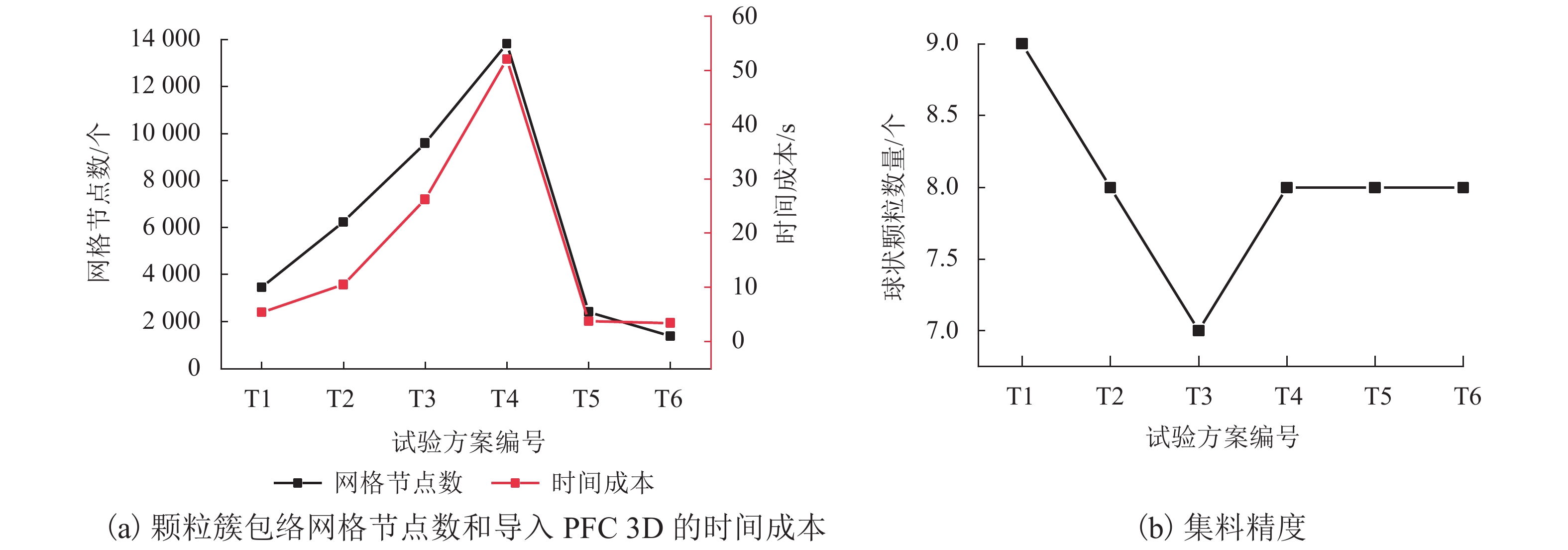
表 1 集料建模精度试验方案
Table 1. Accuracy test schemes of aggregate modeling
试验方案
编号Ns/段 Ts/次 优化量/% T1 3 3 0 T2 4 3 0 T3 5 3 0 T4 3 4 0 T5 3 4 70 T6 3 4 40 
下载: 导出CSV
-
[1] LUCAS JUNIOR L O, BABADOPULOS L F A L, SOARES J B. Effect of aggregate shape properties and binder’s adhesiveness to aggregate on results of compression and tension/compression tests on hot mix asphalt[J]. Materials and Structures, 2020, 53(2): 43.1-43.15. [2] VALDES-VIDAL G, CALABI-FLOODY A, SANCHEZ-ALONSO E, et al. Effect of aggregate type on the fatigue durability of asphalt mixtures[J]. Construction and Building Materials, 2019, 224: 124-131. doi: 10.1016/j.conbuildmat.2019.07.064 [3] ZHOU S, ZHU H H, YAN Z G, et al. A micromechanical study of the breakage mechanism of microcapsules in concrete using PFC2D[J]. Construction and Building Materials, 2016, 115: 452-463. doi: 10.1016/j.conbuildmat.2016.04.067 [4] LIU H. Fractal dimension analysis of the fine aggregate gradation of interlocking skeleton asphalt mixture[J]. Journal of Wuhan University of Technology (Materials Science), 2011, 26(3): 567-572. doi: 10.1007/s11595-011-0269-2 [5] WANG Y P. Physical stochastic damage model for concrete subjected to fatigue loading[J]. International Journal of Fatigue, 2019, 121: 191-196. doi: 10.1016/j.ijfatigue.2018.12.023 [6] 尹纪财. 机床用树脂矿物复合材料力学性能及其湿热老化机理研究[D]. 济南: 山东大学, 2016. [7] JI S Y, WANG S Q, ZHOU Z Y. Influence of particle shape on mixing rate in rotating drums based on super-quadric DEM simulations[J]. Advanced Powder Technology, 2020, 31(8): 3540-3550. doi: 10.1016/j.apt.2020.06.040 [8] 季顺迎. 计算颗粒力学及工程应用[M]. 北京: 科学出版社, 2018. [9] LIU Y, YOU Z P. Visualization and simulation of asphalt concrete with randomly generated three-dimensional models[J]. Journal of Computing in Civil Engineering, 2009, 23(6): 340-347. doi: 10.1061/(ASCE)0887-3801(2009)23:6(340) [10] QIU W J, FU S J, YE J Q. Auto-generation methodology of complex-shaped coarse aggregate set of 3D concrete numerical test specimen[J]. Construction and Building Materials, 2019, 217: 612-625. doi: 10.1016/j.conbuildmat.2019.05.109 [11] MA T, ZHANG D Y, ZHANG Y, et al. Microstructure modeling and virtual test of asphalt mixture based on three-dimensional discrete element method[J]. Journal of Central South University, 2016, 23(6): 1525-1534. doi: 10.1007/s11771-016-3204-z [12] DANDAPAT R, GHOSH S, DEB A. A discrete element implementation for concrete:particle generation, contact calculations, packing under gravity and modeling material response[J]. Granular Matter, 2018, 20(2): 1-37. [13] 李智,王子硕,吴文亮,等. 离散元法中的集料三维数字模型构建[J]. 湖南大学学报(自然科学版),2019,46(11): 106-113. doi: 10.16339/j.cnki.hdxbzkb.2019.11.012LI Zhi, WANG Zishuo, WU Wenliang, et al. Construction of 3D digital model of aggregate in discrete element method[J]. Journal of Hunan University (Natural Sciences), 2019, 46(11): 106-113. doi: 10.16339/j.cnki.hdxbzkb.2019.11.012 [14] MARKAUSKAS D, KAČIANAUSKAS R, DŽIUGYS A, et al. Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations[J]. Granular Matter, 2010, 12(1): 107-123. doi: 10.1007/s10035-009-0158-y [15] 张徐,赵春发,翟婉明,等. 铁路有砟道床振动和变形的离散元模拟与试验验证[J]. 岩土力学,2017,38(5): 1481-1488. doi: 10.16285/j.rsm.2017.05.031ZHANG Xu, ZHAO Chunfa, ZHAI Wanming, et al. Discrete element simulation and its validation on vibration and deformation of railway ballast[J]. Rock and Soil Mechanics, 2017, 38(5): 1481-1488. doi: 10.16285/j.rsm.2017.05.031 [16] FLORKOVÁ Z, JAMBOR M. Quantification of aggregate surface texture based on three dimensional microscope measurement[J]. Procedia Engineering, 2017, 192: 195-200. doi: 10.1016/j.proeng.2017.06.034 [17] FLORKOVÁ Z, KOMAČKA J. Usage of microscope method for detection of aggregate microtexture[J]. Procedia Engineering, 2015, 111: 209-214. doi: 10.1016/j.proeng.2015.07.078 [18] 崔喆,张生瑞. 基于CT图像的集料三维棱角性计算方法[J]. 交通运输工程学报,2017,17(5): 39-49. doi: 10.3969/j.issn.1671-1637.2017.05.004CUI Zhe, ZHANG Shengrui. Computational method of 3D aggregate angularity based on CT images[J]. Journal of Traffic and Transportation Engineering, 2017, 17(5): 39-49. doi: 10.3969/j.issn.1671-1637.2017.05.004 [19] 秦雪. 基于图像分析的集料形状特征与分布特征研究[D]. 青岛: 青岛理工大学, 2016. [20] 裴建中. 沥青路面细观结构特性与衰变行为[M]. 北京: 科学出版社, 2010. [21] KOUCHAKI S, ROSHANI H, PROZZI J A, et al. Evaluation of aggregates surface micro-texture using spectral analysis[J]. Construction and Building Materials, 2017, 156: 944-955. doi: 10.1016/j.conbuildmat.2017.08.174 [22] 全书海. 基于表面灰度图像的加工表面形貌分形特征研究[D]. 武汉: 武汉理工大学, 2003. [23] 杨金玲,李德成,张甘霖,等. 土壤颗粒粒径分布质量分形维数和体积分形维数的对比[J]. 土壤学报,2008,45(3): 413-419. doi: 10.3321/j.issn:0564-3929.2008.03.005YANG Jinling, LI Decheng, ZHANG Ganlin, et al. Comparison of mass and volume fractal dimensions of soil particle size distributions[J]. Acta Pedologica Sinica, 2008, 45(3): 413-419. doi: 10.3321/j.issn:0564-3929.2008.03.005 [24] 夏春,刘浩吾. 混凝土细骨料级配的分形特征研究[J]. 西南交通大学学报,2002,37(2): 186-189. doi: 10.3969/j.issn.0258-2724.2002.02.018XIA Chun, LIU Haowu. Research on fractal characteristics of the size-distribution of concrete aggregates[J]. Journal of Southwest Jiaotong University, 2002, 37(2): 186-189. doi: 10.3969/j.issn.0258-2724.2002.02.018 -
下载:
点击查看大图
计量
- 文章访问数: 299
- HTML全文浏览量: 88
- PDF下载量: 31
- 被引次数: 0