基于自适应非奇异终端滑模的悬浮控制策略

靖永志; 冯伟; 王森; 马先超; 郝建华; 董金文

doi:10.3969/j.issn.0258-2724.20210743

基于自适应非奇异终端滑模的悬浮控制策略

doi: 10.3969/j.issn.0258-2724.20210743

靖永志^{1, 2,},
冯伟^{1, 2},
王森^{1, 2},
马先超^{1, 2},
郝建华^{1, 2},
董金文^{1, 2}

1.
西南交通大学电气工程学院，四川成都 611756
2.
西南交通大学磁浮技术与磁浮列车教育部重点实验室，四川成都 611756

基金项目: 国家自然科学基金（52077183）

详细信息

作者简介:
靖永志（1979—），男，副研究员，研究方向为磁浮列车与磁浮技术、电力电子技术及其应用等，E-mail： jingyongzhi@swjtu.edu.cn

中图分类号: TP273
计量
- 文章访问数: 454
- HTML全文浏览量: 208
- PDF下载量: 30
- 被引次数: 12
出版历程
- 收稿日期: 2021-08-31
- 录用日期: 2022-03-24
- 修回日期: 2022-03-16
- 刊出日期: 2022-03-24

Levitation Control Strategy Based on Adaptive Non-singular Terminal Sliding Mode

JING Yongzhi^{1, 2
,},
FENG Wei^{1, 2},
WANG Sen^{1, 2},
MA Xianchao^{1, 2},
HAO Jianhua^{1, 2},
DONG Jinwen^{1, 2}

1.
School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
Key Laboratory of maglev technology and maglev train, Ministry of Education, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要:
针对采用传统线性滑模控制的电磁悬浮系统存在响应速度慢以及抗干扰能力差的问题，提出了一种基于自适应非奇异终端滑模的悬浮控制方法，该方法将自适应控制引入到终端滑模控制，结合滑模控制对扰动不敏感的优点，利用自适应控制对滑模趋近律系数进行在线自适应调节，改善悬浮系统的动态性能. 首先，建立了电磁悬浮系统数学模型；然后，利用李雅普诺夫稳定理论证明了所设计控制器的稳定性；最后，进行了仿真和实验验证. 实验结果表明：自适应非奇异终端滑模对信号跟踪具有更快的响应速度和更小的稳态误差，对峰峰值为2 N的正弦或锯齿干扰力气隙波动可限定在0.2 mm以内，进行0.1 kg加减载实验时气隙波动为0.6 mm，各项性能均优于终端滑模和线性滑模.
- 磁悬浮 /
- 终端滑模 /
- 自适应控制 /
- 李雅普诺夫函数
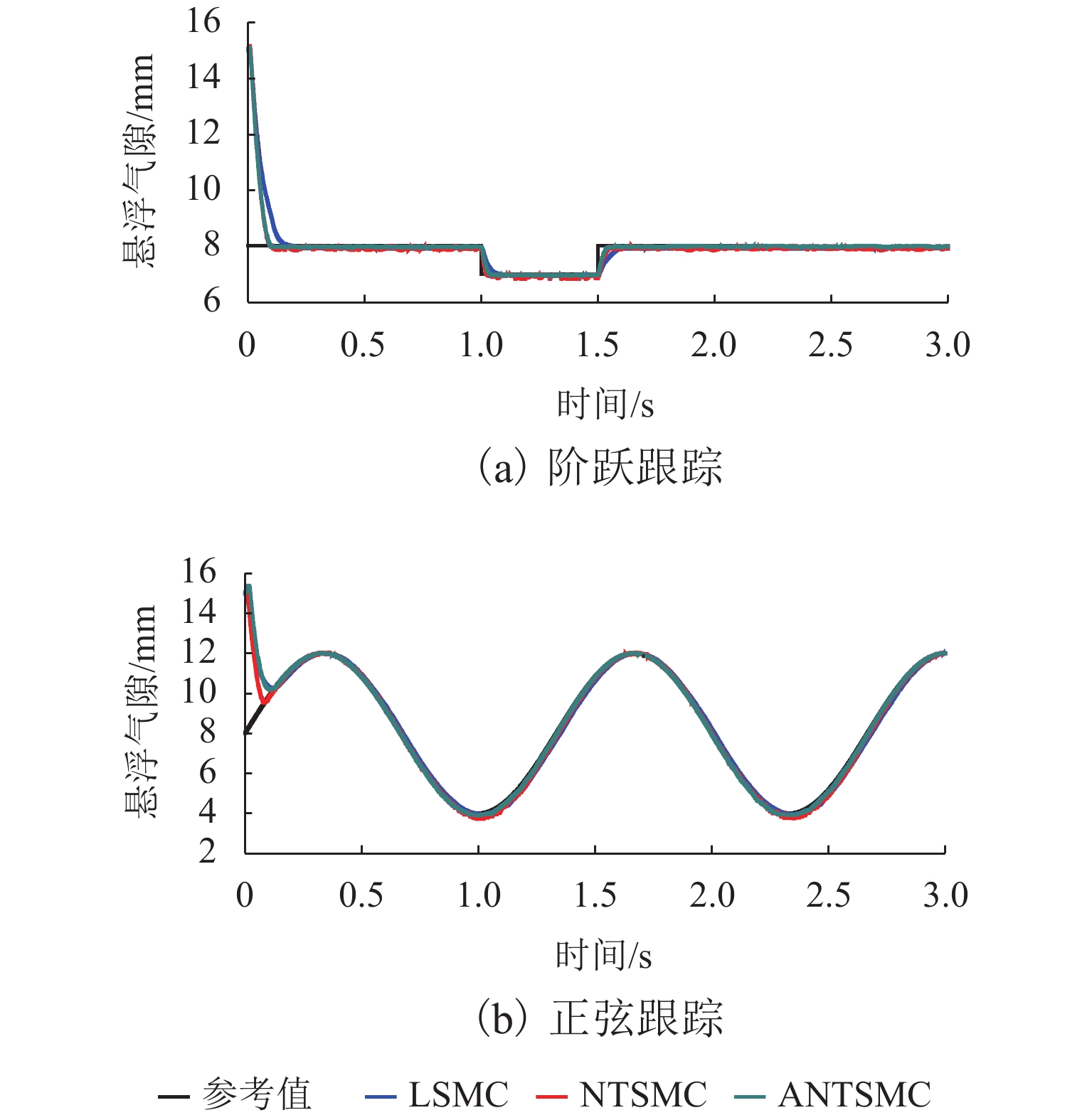
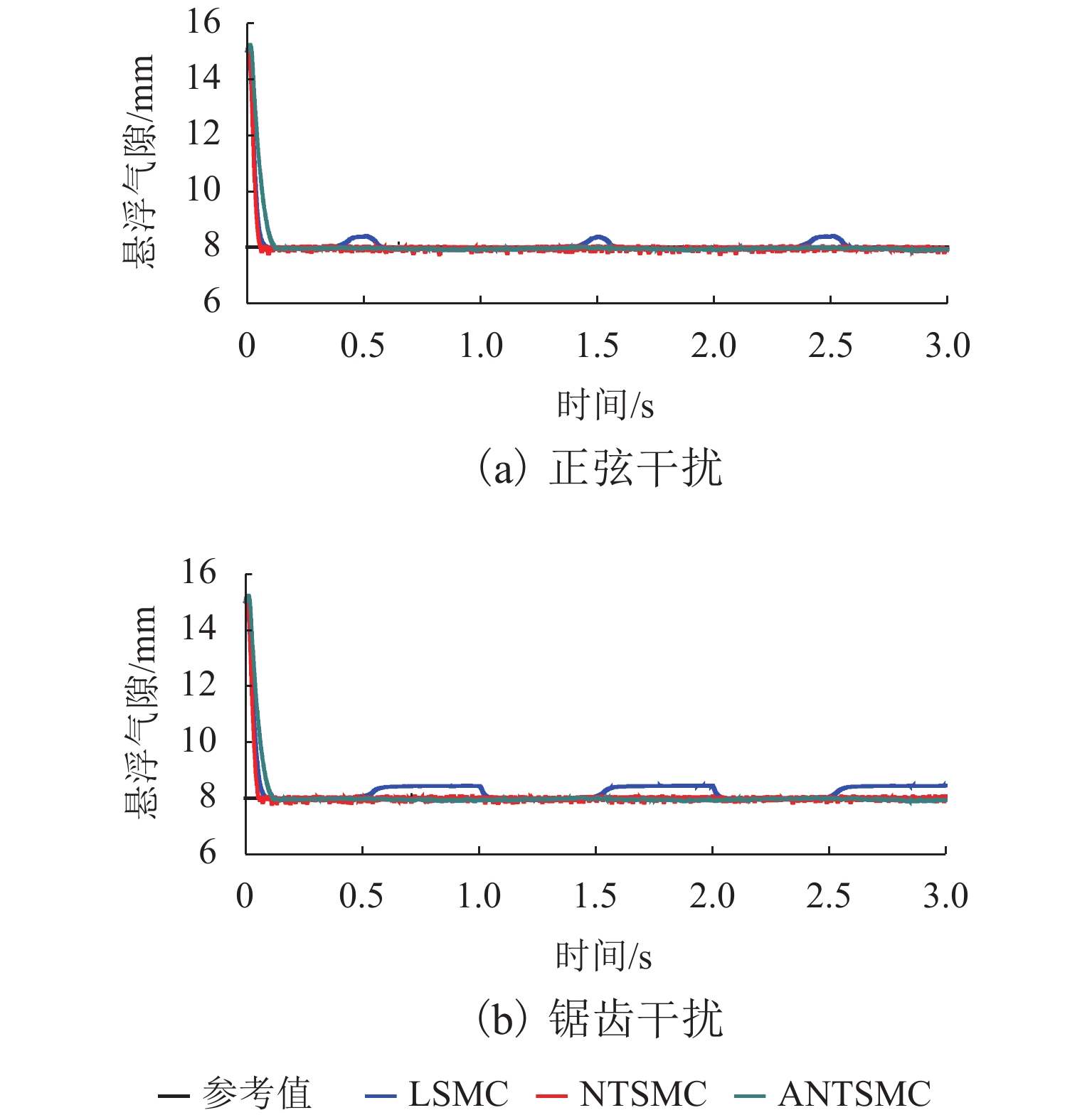
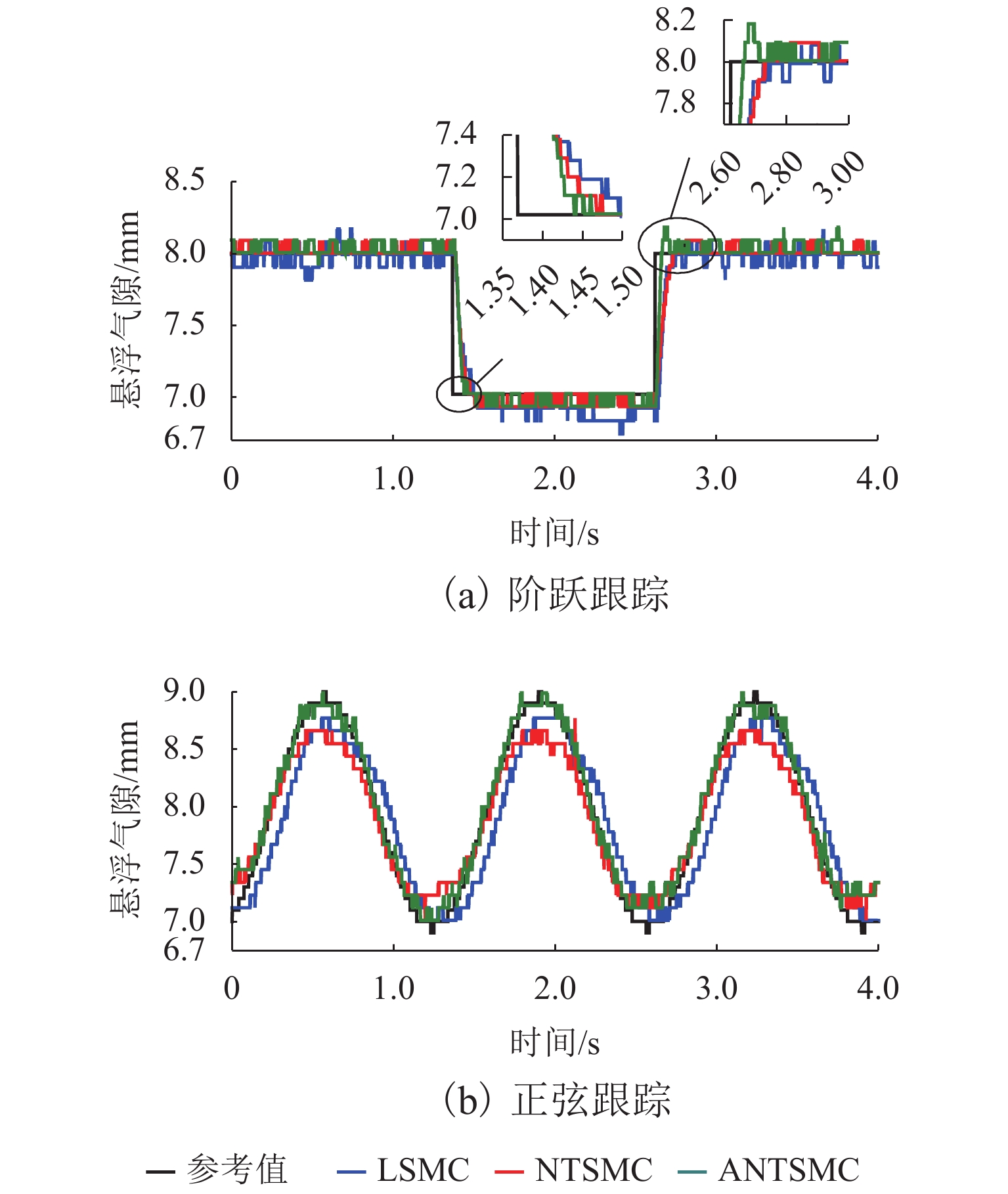
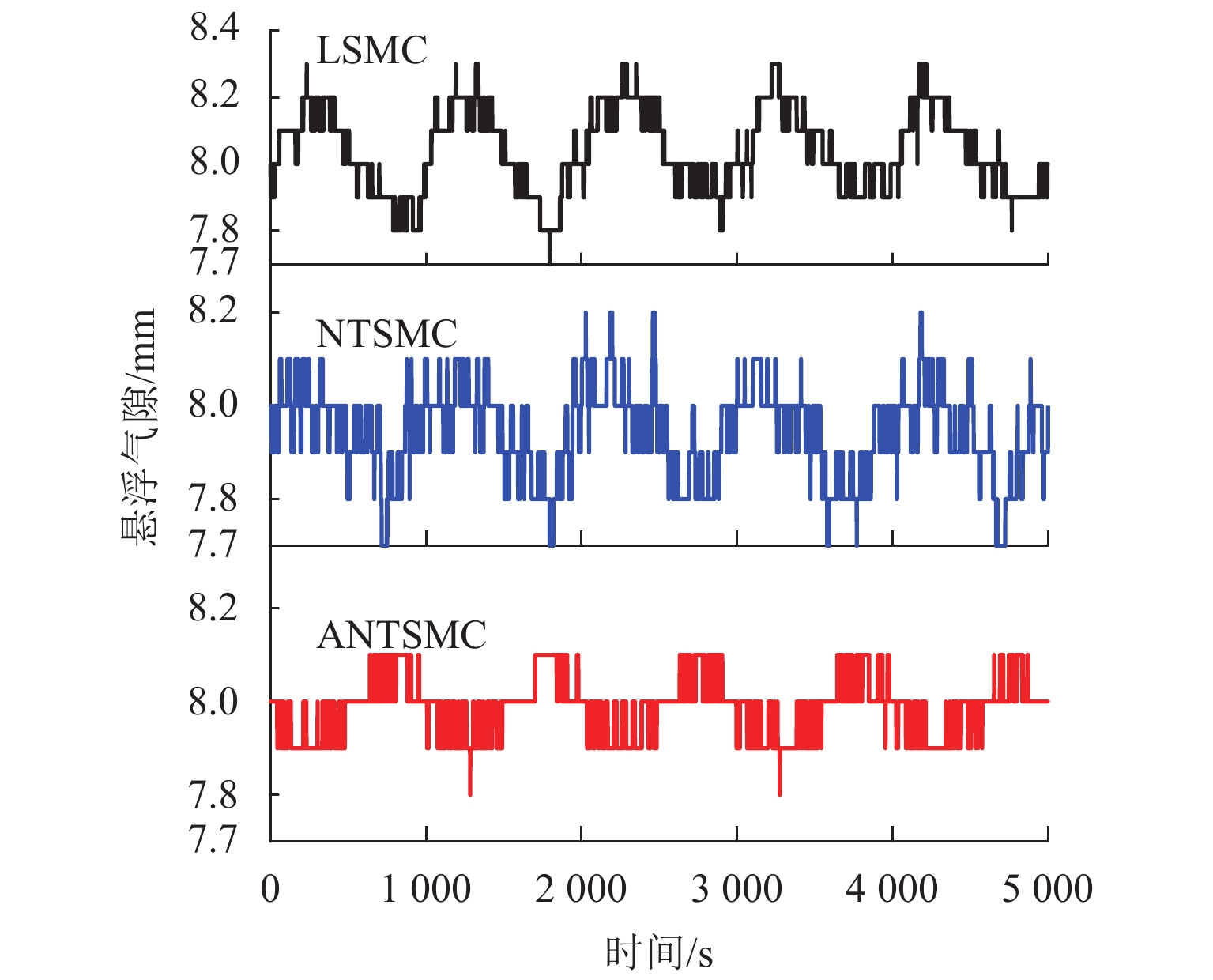
Abstract:
Aiming at the problems of slow response speed and poor anti-interference ability of the traditional linear sliding mode control (LSMC) for electromagnetic levitation systems, a levitation control method based on adaptive non-singular terminal sliding mode control (ANTSMC) is proposed. The proposed method introduces an adaptive controller into the terminal sliding mode control (TSMC) to take its advantage of insensitivity to disturbance in sliding mode control. The convergence law coefficients in the sliding mode control are adjusted on line by adaptive control to improve the dynamic performance of the levitation system. First, a mathematical model of the electromagnetic levitation system is established. Then the stability of the designed controller is proved by Lyapunov stability theory. Finally, simulation and experimental verification are carried out. Experimental results show that the system with ANTSMC has a faster response speed and a smaller steady-state error in signal tracking. For sinusoidal or sawtooth interference with peak to peak value of 2 N, air gap fluctuations can be limited to 0.2 mm. The air gap fluctuates 0.6 mm during the 0.1 kg loading and unloading experiments. Generally the proposed levitation controller based on ANTSMC has better performance than those based on TSMC and LSMC.
- maglev /
- terminal sliding mode /
- adaptive control /
- Lyapunov function

HTML全文

磁悬浮技术因其无接触、低噪声及摩擦小等优点在磁悬浮列车、磁悬浮轴承等工程领域具有广泛应用^[1-2]. 磁悬浮球系统是一个典型的非线性、开环不稳定系统^[3]，常作为研究悬浮控制方法的实验平台. 近年来，对磁悬浮装置的控制研究已取得了很多成果，如将非线性模型进行线性化处理后对磁悬浮系统采用线性控制方法，应用反馈线性化或前馈线性化技术设计非线性控制器^[4-5]. 自适应控制、滑模变结构控制、神经网络控制、模糊控制等非线性控制方法也被广泛应用于磁悬浮控制系统.

文献[6]设计了一种基于磁通观测器的磁悬浮列车系统自适应滑模控制，提升了系统的鲁棒性；文献[7]提出了一种自适应鲁棒输出反馈控制器，跟踪误差通过自适应律得以降低；文献[8]基于径向基函数（RBF）网络逼近原理，设计了一种磁悬浮系统的滑模自适应状态反馈控制器，能有效抑制外界干扰. 在实际工业过程中，滑模控制因其具有响应快速、鲁棒性强以及不确定扰动不敏感等优点而被广泛应用^[9].

文献[10]针对飞行机器人设计了一种鲁棒自适应控制策略，有效减弱机械臂扰动和转动惯量变化的影响；文献[11]提出了一种带有观测器的复合自适应神经网络控制，提高了系统的抗干扰能力；文献[12]提出一种自适应非奇异快速终端滑模控制方法，提升了永磁直线同步电机伺服系统的鲁棒性能，可有效削弱抖振现象.

文献[13]表明终端滑模控制器可以提供更快的收敛速度和更高的精度控制；文献[14]提出一种基于改进指数趋近率的滑模观测器，可有效削弱感应电机矢量控制系统的抖振，实现对系统状态的自适应控制；文献[15]在连续快速终端滑模控制基础上提出了一种新的自适应终端滑模趋近律，可以在有限时间内收敛，并能提高跟踪精度；文献[16]提出的离散时间分数阶终端滑模，在直线电机跟踪控制中具有更高的跟踪精度；文献[17]提出一种新型的滑模观测器并将其应用于永磁同步电机无传感器矢量控制系统，提高了系统的稳定性.

与常规线性滑模（linear sliding mode control, LSMC）相比，非奇异终端滑模（non-singular terminal sliding mode control, NTSMC）是一种能够提升系统响应速度和抗干扰能力的滑模控制方法，常规的终端滑模控制虽然提升了系统响应速度，但其动态性能较差. 针对常规线性滑模控制响应速度较慢、抗干扰能力不强以及终端滑模动态性能差的问题，本文提出了一种基于自适应非奇异终端滑模（ANTSMC）的控制器，并将其应用于电磁悬浮控制系统，用自适应控制对滑模控制器的趋近律增益进行自校正调节，并通过李雅普诺夫稳定理论证明了所设计控制器的稳定性. 然后通过仿真和实验验证所设计的控制器具有良好的动态性能和稳态特性.

1. 电磁悬浮球系统

1.1 电磁悬浮球系统组成

电磁悬浮球系统结构如图1所示. 该系统由悬浮球、电磁铁、斩波器、气隙传感器、电流传感器、A/D转换模块和数字信号处理器（DSP）等部分组成. 间隙传感器和电流传感器分别采集悬浮气隙信号和电磁铁的电流信号，并通过A/D转换模块传输至DSP控制器，DSP控制器将悬浮气隙值与给定值比较得到电流控制量，然后将电磁铁电流与电流控制量比较后输出脉冲宽度调制（PWM）至斩波器，进而调节电磁铁电流，使悬浮球在给定气隙处稳定悬浮.

图 1 电磁悬浮球系统结构

Figure 1. Structure of electromagnetic levitation ball system

下载: 全尺寸图片幻灯片

1.2 电磁悬浮球系统数学模型

电磁悬浮系统的悬浮气隙给定值一般设在8 mm左右，远小于悬浮球的直径，因此可以忽略漏磁通，认为磁通全部通过小球. 为了简化推导过程，通常作以下假定^[3]：

1）忽略悬浮球和电磁铁中的磁阻，即认为电磁铁与悬浮球组成磁路的磁阻全部集中在悬浮气隙处；

2）忽略铁芯的磁化强度μ_r，使μ_r ≈ 1；

3）忽略剩磁、磁滞及磁饱和现象.

基于以上假定，得到电磁悬浮球系统数学模型^[18]为

$\left\{ \begin{array}{l} m\ddot x = mg - F\left( {i,x} \right) + f, \\ F\left( {i,x} \right) = \dfrac{{{\mu _0}{N^2}{i^2}A}}{{4{x^2}}} , \\ mg - F\left( {{i_0},{x_0}} \right) = 0 , \end{array} \right.$

(1)

式中：m为悬浮球的质量；x为悬浮球悬浮气隙；i为电磁铁电流；F（i，x）为悬浮球所受电磁吸力大小；f为外界施加干扰力；μ₀=4π×10⁻⁷ H/m为真空磁导率；A为铁芯面积；N为电磁铁线圈匝数；i₀、x₀分别为平衡点处的电磁铁电流和悬浮气隙.

将系统进行线性化处理，对F（i，x）在平衡点处进行泰勒展开并舍去高次项，可得

$\begin{split} & F\left( {i，x} \right) = F\left( {{i_0},{x_0}} \right) + \frac{{\partial F}}{{\partial i}}\left| \begin{array}{l} i = {i_0}\\ x = {x_0} \end{array} \right.\left( {i - {i_0}} \right) + \\&\quad \frac{{\partial F}}{{\partial x}}\left| \begin{array}{l} i = {i_0}\\ x = {x_0} \end{array} \right.\left( {x - {x_0}} \right). \end{split}$

(2)

忽略干扰力f，将式（2）代入（1），得

$\begin{array}{*{20}{c}} {m\ddot x = {k_1}x + {k_2}i} \end{array}\text{，}$

(3)

式中： ${k}_{1}=\dfrac{{\mu }_{0}{N}^{2}{i}_{0}A}{2{x}_{0}^{3}}，{k}_{2}=-\dfrac{{\mu }_{0}{N}^{2}{i}_{0}{}^{2}A}{2{x}_{0}^{2}}$ ，分别为气隙刚度系数和电流刚度系数.

取x和悬浮球运动速度 $\dot x$ 为状态变量，即 ${\boldsymbol{X}} = {\left[ {x{\text{ }}\dot x} \right]^{\rm{T}}}$ ，i为系统输入，x为系统输出，则系统状态方程为

$\left\{ \begin{array}{l}\begin{array}{l}\dot{{\boldsymbol{X}}}=\left[\begin{array}{cc}0& 1\\ {k}_{1}/m& 0\end{array}\right]{\boldsymbol{X}} + \left[\begin{array}{c}0\\ {k}_{2}/m\end{array}\right]i, \\ Y\text{ }=\left[1\text{ }0\right]{\boldsymbol{X}}.\hfill \end{array}\end{array}\right.$

(4)

由式（3）可得系统开环特征方程为

$\begin{array}{*{20}{c}} {m{a^2} - {k_1} = 0}, \end{array}$

(5)

式中：a为开环极点.

解得 $a = \pm \sqrt {{k_1}/m}$ ，可知系统有一个极点位于复平面中虚轴的右侧，说明系统是开环不稳定系统，因此必须引入状态反馈构成闭环控制使系统达到稳定状态.

2. 自适应非奇异终端滑模控制器

令 $x = {x_1}$ ， $\dot x = {x_2}$ ， ${k_1}/m = {a_0}$ ， ${k_2}/m = {b_0}$ ，则电磁悬浮系统的状态空间方程可写为

$\begin{array}{l} {\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}}, \\ {{{\dot x}_2} = {a_0}{x_1} + {b_0}i}, \\ {Y = {x_1}}. \end{array}} \right.} \end{array}$

(6)

本节在研究了非奇异终端滑模悬浮控制器基础上设计了一种自适应非奇异终端滑模悬浮控制器，并验证所设计控制器闭环稳定性.

2.1 非奇异终端滑模控制器

令 ${e_1} = {x_{\rm{r}}} - {x_1}$ ， ${e_2} = {\dot x_{\rm{r}}} - {x_2}$ ，其中，x_r为悬浮气隙的参考值，则终端滑模函数定义^[9]为

$\begin{array}{*{20}{c}} s = {e_1}{\text{ + }}\left( {{1 \mathord{\left/ {\vphantom {1 \beta }} \right. } \beta }} \right){e}_2^{p / q} , \end{array}$

(7)

式中：β>0， $1 < p/q < 2$ ，且p和q都为正奇数.

对式（7）求导得

$\begin{array}{*{20}{c}} \dot{s}={{e}_{2}}\text{ + }\dfrac{1}{\beta }\dfrac{p}{q}e_{2}^{p/q-1}, \end{array}$

(8)

滑模趋近率采用等速趋近率，如式（9）.

$\begin{array}{*{20}{c}} {\dot s = - \xi {\rm{sgn}}\;s } , \end{array}$

(9)

式中：ξ为趋近律的系数.

联立式（6）、（8）和式（9）可得基于终端滑模的电磁铁控制电流为

$\begin{split} &{i_{\rm{c}}} = - {b_0^{ - 1}}( - \beta \frac{q}{p}{e_2^{2 - {p}/{q}}} -\\ &\quad \xi \beta \frac{p}{q}{e_2^{1 - {p}/{q}}}{\rm{sgn}}\;s { { - {{\ddot x}_{\rm{r}}} + {a_0}{x_1}} )}. \end{split}$

(10)

为避免 $\beta \dfrac{p}{q}{e_2}^{1 - {p/q}}$ 导致控制电流奇异的问题，参照文献[9]将控制电流改为

$\begin{array}{*{20}{c}} {{i_c} = - {b_0}^{ - 1}\left( { - \beta \dfrac{q}{p}{e_2^{2 - {p}/{q}}} - \xi {\rm{sgn}}\;s- {{\ddot x}_{\rm{r}}} + {a_0}{x_1}} \right)}. \\[-15pt] \end{array}$

(11)

由式（11）可知：控制电流不存在负数次幂，所以避免了奇异问题，下面给出稳定性证明.

证：选取李雅普诺夫函数： $\begin{array}{*{20}{c}} {{V_1} = {s^2}/2} \end{array}$

可知V₁>0，V₁对时间求导可得

$\begin{split} &{{\dot V}_1} = s\dot s = \\ &\quad s\left( {{e_2} + \frac{1}{\beta }\frac{p}{q}e_2^{p/q - 1}({{\ddot x}_{\rm{r}}} - {a_0}{x_1} - {b_0}i)} \right){\rm{ = }}\\ &\quad s\left( {{e_2} + \frac{1}{\beta }\frac{p}{q}e_2^{p/q - 1}\left( { - \beta q/pe_2^{2 - p/q} - \xi {\rm{sgn}}\;s} \right)} \right) = \\ &\quad - \frac{1}{\beta }\frac{p}{q}e_2^{p/q - 1}\xi \left| s \right|. \\[-10pt] \end{split}$

(12)

已知 $\beta$ ， $\varepsilon$ ， $\xi$ >0，因此可得

$\begin{array}{*{20}{c}} {{{\dot V}_1} = - \dfrac{1}{\beta } \dfrac{p}{q}{e_2^{{p}/{q} - 1}} \xi \left| s \right| < 0}, \end{array}$

(13)

即该系统是稳定的.

2.2 自适应非奇异终端滑模控制器设计

在实际控制中，通常选择较大的 $\xi$ 以确保系统稳定性. 为了进一步降低 $\xi$ 的调节复杂度，在改善系统动态响应的同时保证系统稳态性能和抗干扰能力，设计了以下自适应律：

$\begin{array}{*{20}{c}} {\dot{\hat{\xi}} = \left\{ {\begin{array}{*{20}{l}} {\varphi {\gamma ^{ - \theta }}\left( {\left| s \right| + \eta {e^{ - \left| s \right|}}} \right)\theta ,\;\;\;\hat \xi > 0}, \\ {\varphi {\gamma ^{ - 1}}\left( {\left| s \right| + \eta {e^{ - \left| s \right|}}} \right),\;\;\; \hat \xi = 0}, \end{array}} \right.} \end{array}$

(14)

式中： $\theta = {\rm{sgn}}\left( {{{\left\| s \right\|}_\infty } - \varepsilon } \right)$ ； $\hat \xi$ 为 $\xi$ 的观测值；φ、γ和η均为调节自适应律的增益且都为正值，φ和γ影响自适应律调节速度，φ越大γ越小，调节速度越快，但会增大稳态时气隙波动，ε影响滑模函数s的最终界^[19].

基于自适应非奇异终端滑模的电磁铁控制电流可表示为

$\begin{split} {i_{\rm{c}}} = - b_{0}^{- 1}\Bigg( - \beta \frac{q}{p}{e_2^{2 - {p}/{q}}} -\hat \xi {\rm{sgn}}\;s -{{\ddot x}_{\rm{r}}} + {a_0}{x_1} \Bigg). \end{split}$

(15)

由式（14）可以看出：在参数 $\xi$ 的自适应调节过程中，|s| 和 $\eta {e^{ - \left| s \right|}}$ 两个增益项根据 |s| 的大小交替占主导地位，当 |s| 趋于0时， $\eta {e^{ - \left| s \right|}}$ 较大，可以保证较快的调节速度，同时 $\eta {e^{ - \left| s \right|}}$ 有上限η可以保证不会出现过度调节，下面给出稳定性证明.

证：选取李雅普诺夫函数：

$\begin{array}{*{20}{c}} {{V_2} = \dfrac{1}{2}{s^2} + \dfrac{1}{2}\dfrac{\gamma }{\varphi }{{\tilde \xi }^2}} , \end{array}$

(16)

式中： $\tilde \xi = \hat \xi - {\xi ^*}$ ， ${\xi ^*}$ 为 $\hat \xi$ 的上界，即 $\tilde \xi$ <0.

对式（16）求关于时间t的导数，并将式（7）和式（8）代入式（16）得

$\begin{split} & {{\dot V}_2} = s\dot s + \dfrac{\gamma }{\varphi }\tilde \xi \dot{\hat{\xi}} =\\&\quad { - \dfrac{1}{\beta } \frac{p}{q}e_{2}^{{p}/{q} - 1} \xi \left| s \right| + \frac{\gamma }{\varphi }\tilde \xi \dot{\hat{\xi}} }. \end{split}$

(17)

考虑 |s|>ε和 |s|<ε这两种情况，当 |s|>ε时，将式（14）代入（16）得

$\begin{split} {{\dot V}_2} = - \frac{1}{\beta } \frac{p}{q}{e_2^{{p}/{q} - 1}} \xi \left| s \right| +\tilde \xi \left( {\left| s \right| + \eta {e^{ - \left| s \right|}}} \right) < 0. \end{split}$

(18)

这说明当 |s|>ε时， ${V_2}$ 是不断减小的，且在有限时间内s能达到 |s|<ε区域.

当滑模函数s进入 |s|<ε的区域时，由于不能保证 ${\dot V_2}$ 是非正的，s可能会不断地在该区域进出. 当s离开该区域时 |s|>ε，根据式（18）可知 ${\dot V_2}$ 的极性变为负，则将使s进入滑模面使系统趋于稳定.

3. 仿真结果与分析

为验证所设计悬浮控制器的有效性，在基于Matlab/Simulink环境中搭建电磁悬浮球系统仿真模型，分别使用LSMC、NTSMC和ANTSMC 3种不同的控制器对悬浮性能进行仿真验证，并对控制器参数进行优化，表1是电磁悬浮球系统的参数值.

将表1中的参数值代入式（4），电磁悬浮球系统的状态方程可表示为

$\left\{ \begin{array}{c} \begin{array}{l}\dot{{\boldsymbol{X}}}=\left[\begin{array}{cc}0& 1\\ 2\;483& 0\end{array}\right]{\boldsymbol{X}} + \left[\begin{array}{c}0\\ -7.36\end{array}\right]i, \\ Y\text{ }=\left[\begin{array}{cc}1& 0\end{array}\right]{\boldsymbol{X}}. \end{array}\end{array}\right.$

(19)

表 1 电磁悬浮球系统参数

Table 1. Parameters of the electromagnetic levitation ball system

参数	数值	参数	数值
m/kg	0.318	x₀/m	0.008
N/匝	530	i₀/A	2.7
A/m²	π × 10⁻⁴

下载: 导出CSV

| 显示表格

悬浮球的初始悬浮气隙值设为15 mm，然后分别验证LSMC、NTSMC和ANTSMC的信号跟踪性能、抗干扰能力以及加减载性能，并将仿真结果进行对比. 各悬浮控制器优化后的仿真参数如表2所示.

表 2 悬浮控制器仿真参数

Table 2. Simulation parameters of levitation controllers

控制器	β	ξ	φ	γ	ε	η
LSMC	50	40
NTSMC	20	40
ANTSMC	10		1000	0.5	0.03	1

下载: 导出CSV

| 显示表格

3.1 信号跟踪性能

悬浮气隙的参考值分别设定为阶跃信号和正弦信号时，LSMC、NTSMC和ANTSMC 3种控制器的跟踪性能曲线如图2所示. 在图2（a）中设定给定悬浮气隙的初始值为8.0 mm，在1.0 s时，悬浮气隙给定值变为7.0 mm，在1.5 s时，悬浮气隙给定值变回8.0 mm；在图2（b）中，设置悬浮气隙给定值为幅值4.0 mm、频率0.75 Hz、偏置8 mm的正弦信号.

图 2 跟踪曲线

Figure 2. Tracking curves

下载: 全尺寸图片幻灯片

从图2可知：3种控制方法都能较好地跟踪悬浮气隙的参考值，但是与LSMC相比，NTSMC和ANTSMC具有更快的响应速度；ANTSMC的稳态误差最小，而LSMC和NTSMC的稳态误差都较大；使用NTSMC的悬浮系统稳定后响应曲线有较明显的波动，图2（a）中稳定悬浮后NTSMC方法的气隙波动范围为0.165 mm，而ANTSMC方法的气隙波动范围为0.071 mm，说明ANTSMC对这种波动抑制效果较好.

3.2 抗干扰性能

为了验证所设计悬浮控制器的抗干扰性能，在控制器中分别加入正弦波和锯齿波干扰力，图3（a）和图3（b）分别为加入幅值为1、频率为2 Hz的正弦干扰力之后和幅值为2、频率为1 Hz的锯齿波干扰力之后，分别使用3种控制方法的悬浮气隙响应曲线.

图 3 正弦干扰和锯齿干扰响应曲线

Figure 3. Response curves of sinusoidal disturbance and sawtooth disturbance

下载: 全尺寸图片幻灯片

从图3的可知：在给定气隙不变的情况下，LSMC的悬浮气隙受干扰力影响较大，由于受电流环跟随性能的影响，气隙曲线并不完全跟随干扰信号呈正弦波或者锯齿波； NTSMC和ANTSMC受干扰影响并不明显，说明NTSMC和ANTSMC控制方法具有更好的抗干扰性能，而ANTSMC相比于NTSMC在稳态时抖动更小.

3.3 加、减载性能

为进一步验证所设计控制器的抗干扰性能，本小节模拟悬浮系统的加减载过程，在第1 s时分别加入质量为0.2m和0.4m的负载，然后在第2 s时去除负载. 3种控制器的悬浮气隙响应曲线如图4所示.

由图4（a）可知：在1 s时加入了0.2m的负载时，由于悬浮系统质量突然增大，LSMC控制器的悬浮气隙也随之有较小的变化，而NTSMC和ANTSMC控制器的悬浮气隙并无明显变化，但是NTSMC控制器的悬浮气隙抖动现象较严重. 由图4（b）可知：负载增加至0.4m后，LSMC控制器的悬浮气隙输出受负载变化影响很大，由8.0 mm增加至8.4 mm，而NTSMC和ANTSMC两种控制器的输出仍无较大变化，但是NTSMC控制器的悬浮气隙抖动现象较严重.

图 4 悬浮气隙响应曲线

Figure 4. Suspension air gap response curves

下载: 全尺寸图片幻灯片

因此，从仿真波形可知：相较于LSMC，所设计的NTSMC和ANTSMC控制器具有更快的响应速度和更强的抗干扰性能，且ANTSMC比NTSMC的悬浮气隙抖动小，具有更好的静态特性.

4. 实验结果与分析

为进一步验证所设计悬浮控制器的性能，分别进行动态跟踪、抗干扰能力和加减载实验，搭建了电磁悬浮球系统硬件实验平台如图5所示. 该实验平台使用气隙传感器和霍尔电流传感器分别采集悬浮气隙信号和电磁铁电流信号，并通过14位高分辨率ADC芯片转换为数字量传输至DSP控制器，经悬浮控制器输出不同占空比PWM，以实现电磁铁的电流调节. 各悬浮控制器优化后的实验参数如表3. 由于仿真建模时对系统进行了一定简化，因此，仿真模型和实际对象有一定差异，实验时在仿真参数基础上针对实际系统对参数进行优化，导致仿真和实验时的控制器参数不完全一致.

图 5 电磁悬浮系统实验平台

Figure 5. Eletromagnetic levitation system experimental platform

下载: 全尺寸图片幻灯片

表 3 悬浮控制器实验参数

Table 3. Parameters of levitation controllers

控制器	β	ξ	φ	γ	ε	η
LSMC	40	1
NTSMC	20	1
ANTSMC	20		100	0.5	0.03	1

下载: 导出CSV

| 显示表格

4.1 信号跟踪性能

设置初始时刻的悬浮气隙给定值为8.0 mm，在悬浮球稳定悬浮后先加入幅值为 −1 mm的阶跃信号，1 s后加入幅值为1 mm的阶跃信号，3种悬浮控制器的响应曲线如图6（a）所示；设置给定悬浮气隙为幅值1 mm、频率0.75 Hz、偏置8 mm的正弦信号，LSMC、NTSMC、ANTSMC 3种控制器的悬浮气隙响应曲线如图6（b）所示.

从图6（a）可以看出：在给定气隙由8.0 mm变为7.0 mm时，ANTSMC的响应速度最快，能在更短的时间内收敛至给定悬浮气隙处，而LSMC和NTSMC的响应速度较慢，且LSMC的稳态误差较大；在给定气隙由7.0 mm变为8.0 mm时，ANTSMC的响应速度也明显比LSMC和NTSMC快. 从图6（b）中可以看出：在跟踪相同的正弦信号时，LSMC的输出气隙稳态误差较大且响应速度较慢，NTSMC的跟踪速度比LSMC更快，但也有较大的跟踪误差；而与前两者相比，ANTSMC的输出悬浮气隙稳态误差最小，响应速度最快，其跟踪效果比LSMC和NTSMC更好.

4.2 抗干扰能力

设给定悬浮气隙为8.0 mm，在控制器中模拟加入幅值为1 N，频率为1 Hz的正弦干扰力，则3种控制器的输出悬浮气隙实验曲线如图7所示. 加入幅值为2 N，频率为1 Hz的锯齿干扰力，3种控制器的悬浮气隙实验曲线如图8所示.

图 6 跟踪实验曲线

Figure 6. Tracking curves

下载: 全尺寸图片幻灯片

图 7 正弦干扰实验曲线

Figure 7. Sinusoidal disturbance experiment curves

下载: 全尺寸图片幻灯片

由图7和图8可知：在加入同样的正弦干扰力或锯齿干扰力时，LSMC、NTSMC、ANTSMC的悬浮气隙波动峰峰值分别为0.4、0.3、0.2 mm，LSMC的悬浮气隙峰峰值最大，且气隙曲线近似为正弦曲线，而ANTSMC的悬浮气隙峰峰值最小，其悬浮气隙曲线在（8.0 ± 0.1） mm范围内变化，这说明3种控制器中，ANTSMC的抗干扰性能最好，LSMC的抗干扰性能较弱，而NTSMC的抗干扰性比LSMC好，但不如ANTSMC. 由于控制器的仿真参数和实验参数有差异，且悬浮控制性能还受电流环跟随效果、开关器件工作效率等因素的影响，实验波形与仿真波形也会有一定的差异.

图 8 锯齿干扰实验曲线

Figure 8. Sawtooth disturbance experiment curves

下载: 全尺寸图片幻灯片

4.3 加、减载性能

设给定悬浮气隙为8.0 mm，使用质量为0.1 kg的砝码作为负载进行加减载实验，在悬浮球稳定悬浮后进行加载实验，然后在悬浮系统稳定后分别验证3种控制器的抗干扰性能，得到的悬浮气隙响应曲线如图9所示.

图 9 负载质量为0.1 kg时悬浮气隙响应曲线

Figure 9. Suspension air gap response curves withload mass of 0.1 kg

下载: 全尺寸图片幻灯片

本文重点研究控制器的抗干扰性能，控制器中没有引入积分环节，因此在加减载实验中悬浮气隙存在一定的稳态误差. 由图9可以看出：当加入质量为0.1 kg的负载时，LSMC和NTSMC的悬浮气隙在加载后变化较大，分别从8.0 mm增大到9.5 mm和9.4 mm，且LSMC有一定的超调，响应曲线最大值达10.4 mm；ANTSMC的悬浮气隙相对来说变化较小，从8.0 mm变化到8.6 mm左右. 在悬浮系统稳定后减去负载，这时3种控制器都能使系统恢复至平衡位置. 根据3种控制器的加减载实验结果可以看出：ANTSMC比LSMC和NTSMC具有更好的抗干扰性能.

5. 结　论

本文提出了一种基于自适应终端滑模的电磁悬浮系统悬浮控制方法. 首先建立了电磁悬浮系统的数学模型，并分析了系统的稳定性；然后在非奇异终端滑模悬浮控制器的基础上提出一种自适应非奇异终端滑模悬浮控制器，对趋近增益进行在线自适应校正，并根据李雅普诺夫稳定性理论证明了所提出悬浮控制器的稳定性；最后通过仿真和实验对所提出控制器的信号跟踪性能、抗干扰能力、加减载性能等进行验证. 仿真与实验结果表明：与传统滑模悬浮控制器和非奇异终端滑模悬浮控制器相比，所设计的非奇异终端滑模悬浮控制器在保证静态性能和动态响应速度的同时具有更好的抗干扰能力.

图 1 电磁悬浮球系统结构

Figure 1. Structure of electromagnetic levitation ball system

下载: 全尺寸图片幻灯片

图 2 跟踪曲线

Figure 2. Tracking curves

下载: 全尺寸图片幻灯片

图 3 正弦干扰和锯齿干扰响应曲线

Figure 3. Response curves of sinusoidal disturbance and sawtooth disturbance

下载: 全尺寸图片幻灯片

图 4 悬浮气隙响应曲线

Figure 4. Suspension air gap response curves

下载: 全尺寸图片幻灯片

图 5 电磁悬浮系统实验平台

Figure 5. Eletromagnetic levitation system experimental platform

下载: 全尺寸图片幻灯片

图 6 跟踪实验曲线

Figure 6. Tracking curves

下载: 全尺寸图片幻灯片

图 7 正弦干扰实验曲线

Figure 7. Sinusoidal disturbance experiment curves

下载: 全尺寸图片幻灯片

图 8 锯齿干扰实验曲线

Figure 8. Sawtooth disturbance experiment curves

下载: 全尺寸图片幻灯片

图 9 负载质量为0.1 kg时悬浮气隙响应曲线

Figure 9. Suspension air gap response curves withload mass of 0.1 kg

下载: 全尺寸图片幻灯片

表 1 电磁悬浮球系统参数

Table 1. Parameters of the electromagnetic levitation ball system

参数数值参数数值

m/kg 0.318 x₀/m 0.008
N/匝 530 i₀/A 2.7
A/m² π × 10⁻⁴

下载: 导出CSV

表 2 悬浮控制器仿真参数

Table 2. Simulation parameters of levitation controllers

控制器 β ξ φ γ ε η

LSMC 50 40
NTSMC 20 40
ANTSMC 10 1000 0.5 0.03 1

下载: 导出CSV

表 3 悬浮控制器实验参数

Table 3. Parameters of levitation controllers

控制器 β ξ φ γ ε η

LSMC 40 1
NTSMC 20 1
ANTSMC 20 100 0.5 0.03 1

下载: 导出CSV

参考文献(19)

[1]	LIN G B, SHENG X W. Application and further development of maglev transportation in China[J]. Transportation Systems and Technology, 2018, 4(3): 36-43. doi: 10.17816/transsyst20184336-43
[2]	靖永志,何飞,廖海军,等. 基于PSO优化RBF-NN的磁浮车间隙传感器温度补偿[J]. 西南交通大学学报,2018,53(2): 367-373,384. doi: 10.3969/j.issn.0258-2724.2018.02.020 JING Yongzhi, HE Fei, LIAO Haijun, et al. Temperature compensation of maglev vehicle gap sensor based on RBF-NN optimized by PSO[J]. Journal of Southwest Jiaotong University, 2018, 53(2): 367-373,384. doi: 10.3969/j.issn.0258-2724.2018.02.020
[3]	吕治国,龙志强. 磁悬浮球系统的非线性自适应控制方法[J]. 控制工程,2020,27(1): 127-133. LV Zhiguo, LONG Zhiqiang. Method on nonlinear adaptive controller for maglev levitation ball system[J]. Control Engineering, 2020, 27(1): 127-133.
[4]	曹广忠, 潘剑飞, 黄苏丹, 等. 磁悬浮系统控制算法及实现[M]. 北京: 清华大学出版社, 2013.
[5]	ZHANG X Y, CHEN X K, ZHU G Q, et al. Output feedback adaptive motion control and its experimental verification for time-delay nonlinear systems with asymmetric hysteresis[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6824-6834. doi: 10.1109/TIE.2019.2938460
[6]	XU J Q, SUN Y G, GAO D G, et al. Dynamic modeling and adaptive sliding mode control for a maglev train system based on a magnetic flux observer[J]. IEEE Access, 2018, 6: 31571-31579. doi: 10.1109/ACCESS.2018.2836348
[7]	YANG Z J, KUNITOSHI K, KANAE S, et al. Adaptive robust output-feedback control of a magnetic levitation system by K-filter approach[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 390-399. doi: 10.1109/TIE.2007.896488
[8]	CHEN C, XU J Q, JI W, et al. Sliding mode robust adaptive control of maglev vehicle ’s nonlinear suspension system based on flexible track:design and experiment[J]. IEEE Access, 2019, 7: 41874-41884. doi: 10.1109/ACCESS.2019.2906245
[9]	WANG J X, ZHAO L, YU L. Adaptive terminal sliding mode control for magnetic levitation systems with enhanced disturbance compensation[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 756-766. doi: 10.1109/TIE.2020.2975487
[10]	张振国,陈彦杰,占巍巍,等. 作业型飞行机器人动态滑翔抓取的鲁棒自适应控制[J]. 控制理论与应用,2021,38(6): 775-783. doi: 10.7641/CTA.2020.00326 ZHANG Zhenguo, CHEN Yanjie, ZHAN Weiwei, et al. Robust adaptive control for unmanned aerial manipulator in dynamic gliding grasping[J]. Control Theory & Applications, 2021, 38(6): 775-783. doi: 10.7641/CTA.2020.00326
[11]	王云龙,王泽政,王永富,等. 带有干扰观测器的线控转向系统复合自适应神经网络控制[J]. 控制理论与应用,2021,38(4): 433-443. doi: 10.7641/CTA.2020.00340 WANG Yunlong, WANG Zezheng, WANG Yongfu, et al. Composite adaptive neural network control for steer-by-wire systems with disturbance observer[J]. Control Theory & Applications, 2021, 38(4): 433-443. doi: 10.7641/CTA.2020.00340
[12]	付东学,赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报,2020,35(4): 717-723. FU Dongxue, ZHAO Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[13]	LIN C K. Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks[J]. IEEE Transactions on Fuzzy Systems, 2006, 14(6): 849-859. doi: 10.1109/TFUZZ.2006.879982
[14]	陈闯,王勃,于泳,等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报,2020,35(增刊1): 155-163. CHEN Chuang, WANG Bo, YU Yong, et al. An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[15]	JUNEJO A K, XU W, MU C X, et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12110-12121. doi: 10.1109/TPEL.2020.2986893
[16]	SUN G H, MA Z Q, YU J Y. Discrete-time fractional order terminal sliding mode tracking control for linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3386-3394. doi: 10.1109/TIE.2017.2748045
[17]	张立伟,李行,宋佩佩,等. 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统[J]. 电工技术学报,2019,34(增刊1): 70-78. ZHANG Liwei, LI Hang, SONG Peipei, et al. Sensorless vector control using a new sliding mode observer for permanent magnet synchronous motor speed control system[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 70-78.
[18]	朱坚民,沈正强,李孝茹,等. 基于神经网络反馈补偿控制的磁悬浮球位置控制[J]. 仪器仪表学报,2014,35(5): 976-986. ZHU Jianmin, SHEN Zhengqiang, LI Xiaoru, et al. Magnetic levitation ball position control based on neural network feedback compensation control[J]. Chinese Journal of Scientific Instrument, 2014, 35(5): 976-986.
[19]	BAEK S, BAEK J, HAN S. An adaptive sliding mode control with effective switching gain tuning near the sliding surface[J]. IEEE Access, 2019, 7: 15563-15572. doi: 10.1109/ACCESS.2019.2894911

施引文献

期刊类型引用(5)

1.	李至勇，杨杰，周发助，胡海林. 电磁悬浮系统的改进滑模控制方法. 电子测量技术. 2024(04): 87-94 . 百度学术
2.	柯炎，王胜虎. 基于火电机组的协同线性自抗扰协调控制策略. 电子设计工程. 2024(14): 100-104+109 . 百度学术
3.	胡轲珽，徐俊起，刘志刚，林国斌. 基于强化学习的电磁悬浮型磁浮列车悬浮控制. 同济大学学报(自然科学版). 2023(03): 332-340 . 百度学术
4.	杨杰，秦耀，汪永壮，张振利. 永磁电磁混合型磁浮球的改进滑模控制方法. 湖南大学学报(自然科学版). 2023(04): 200-209 . 百度学术
5.	陈萍，史天成，于明月，单磊. 基于模型参考自适应的自学习悬浮控制策略. 西南交通大学学报. 2023(04): 799-807 . 本站查看