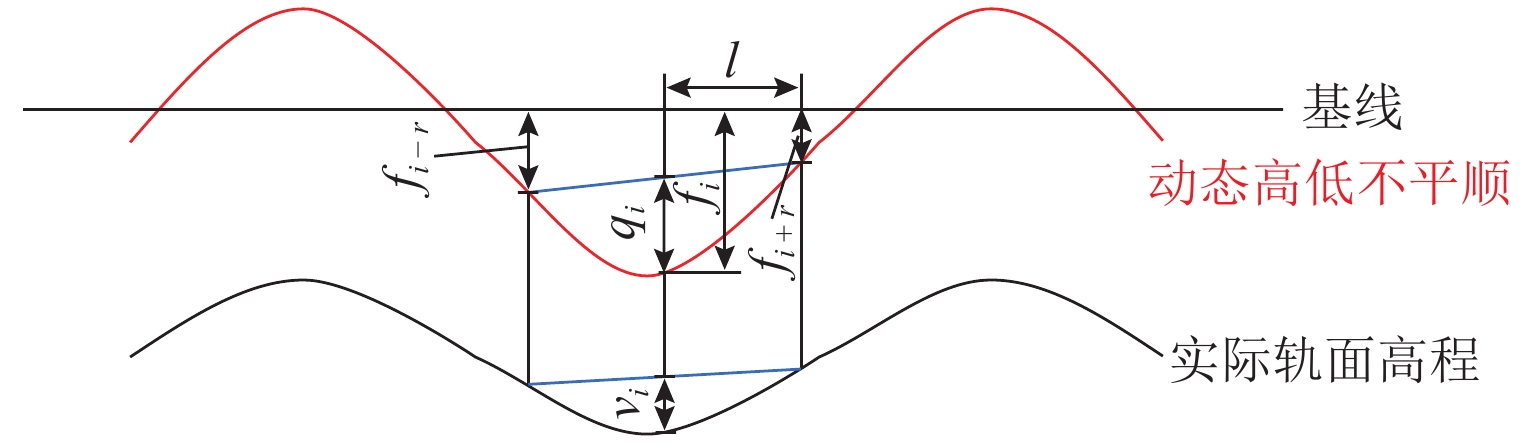
Evaluation Difference of Dynamic and Static Track Irregularity and Characteristics of Dynamic Chord Measurement Method
-
摘要:
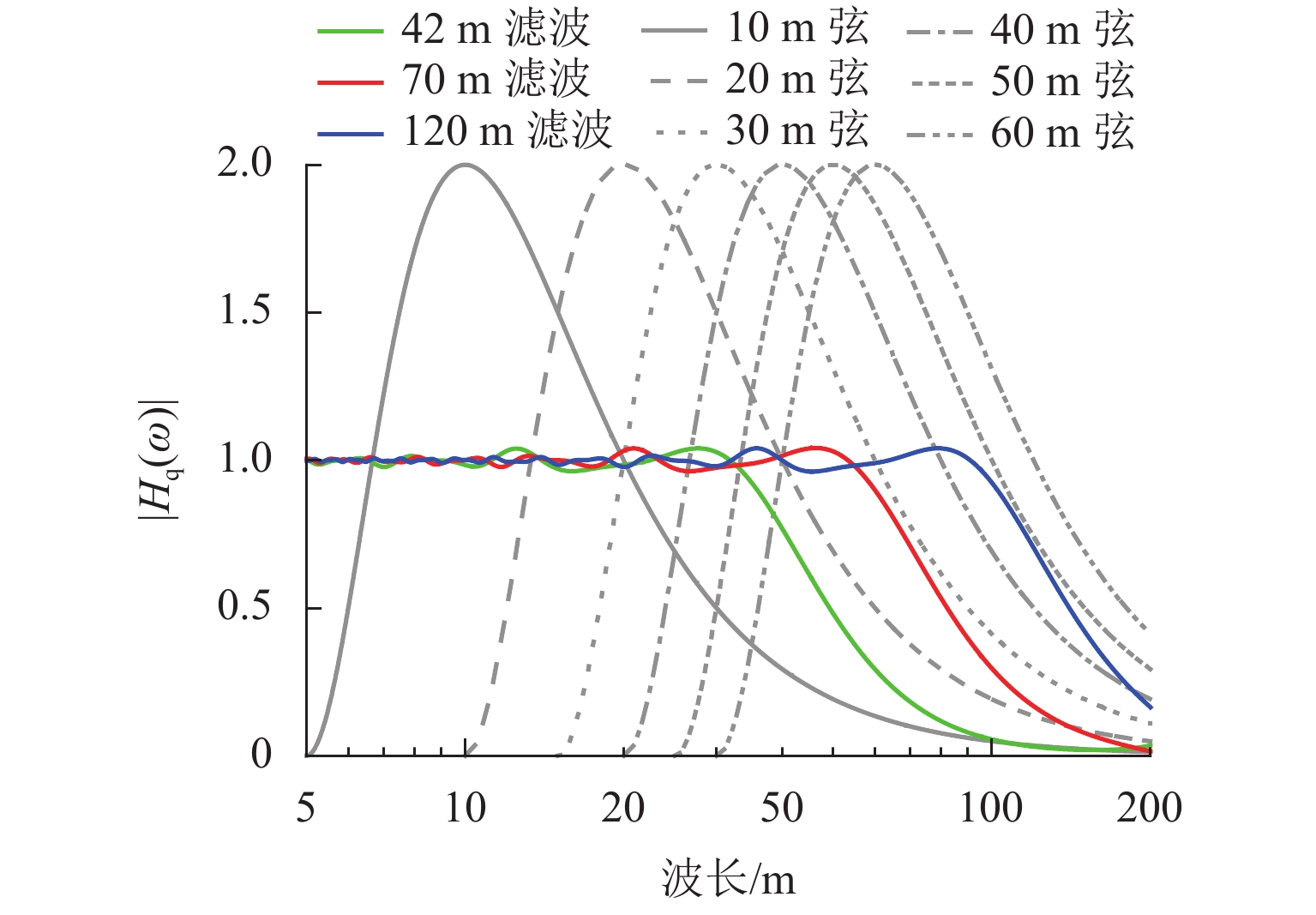
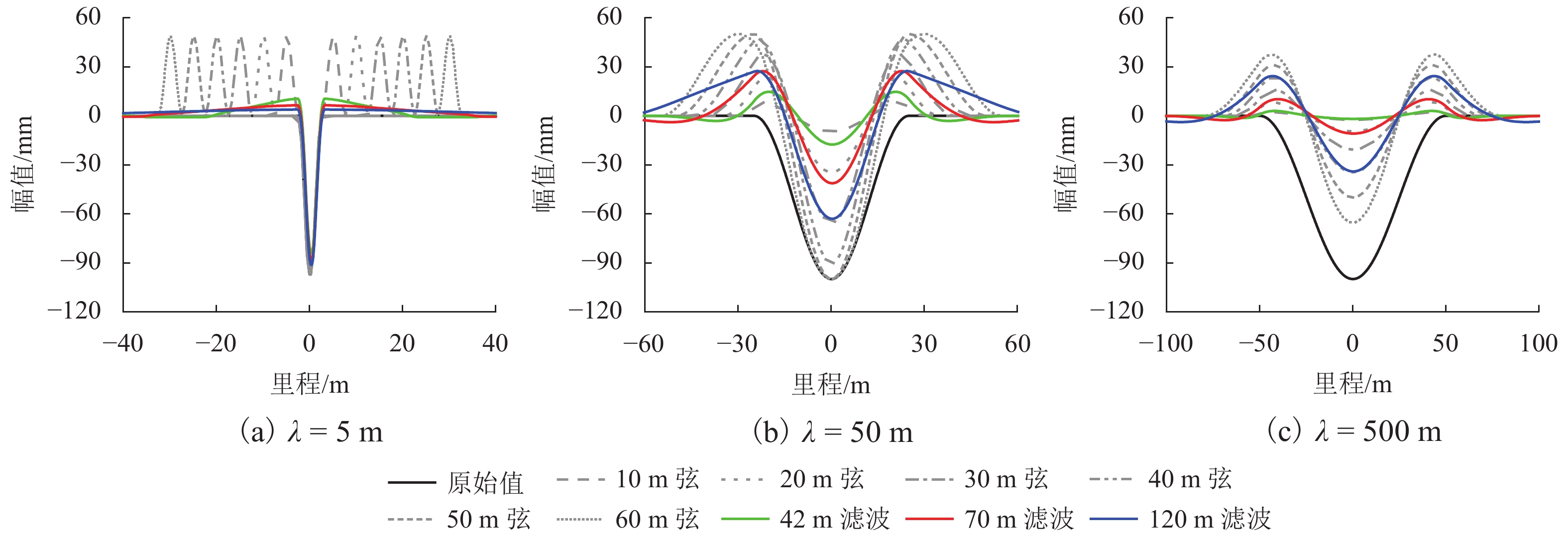
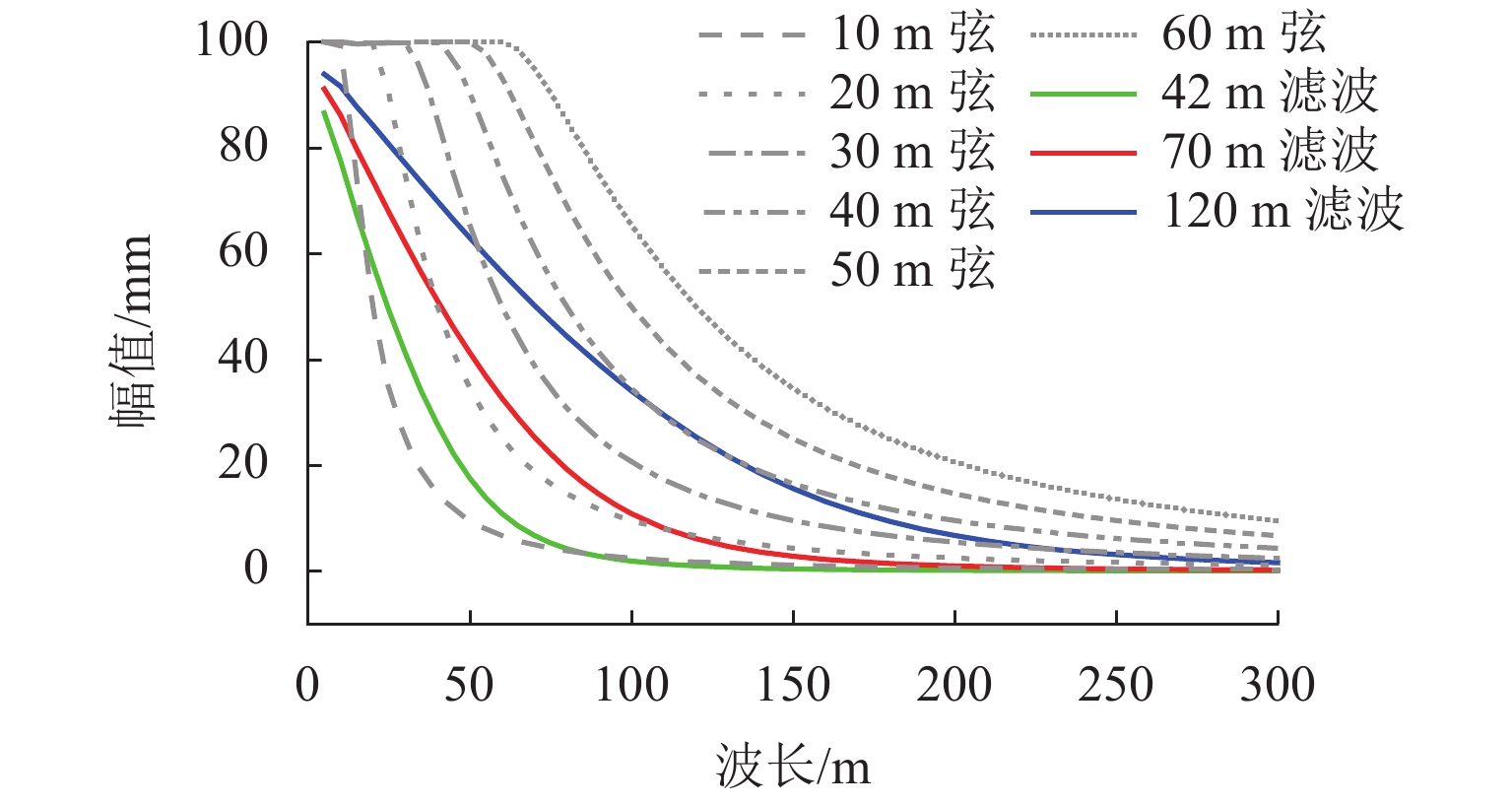
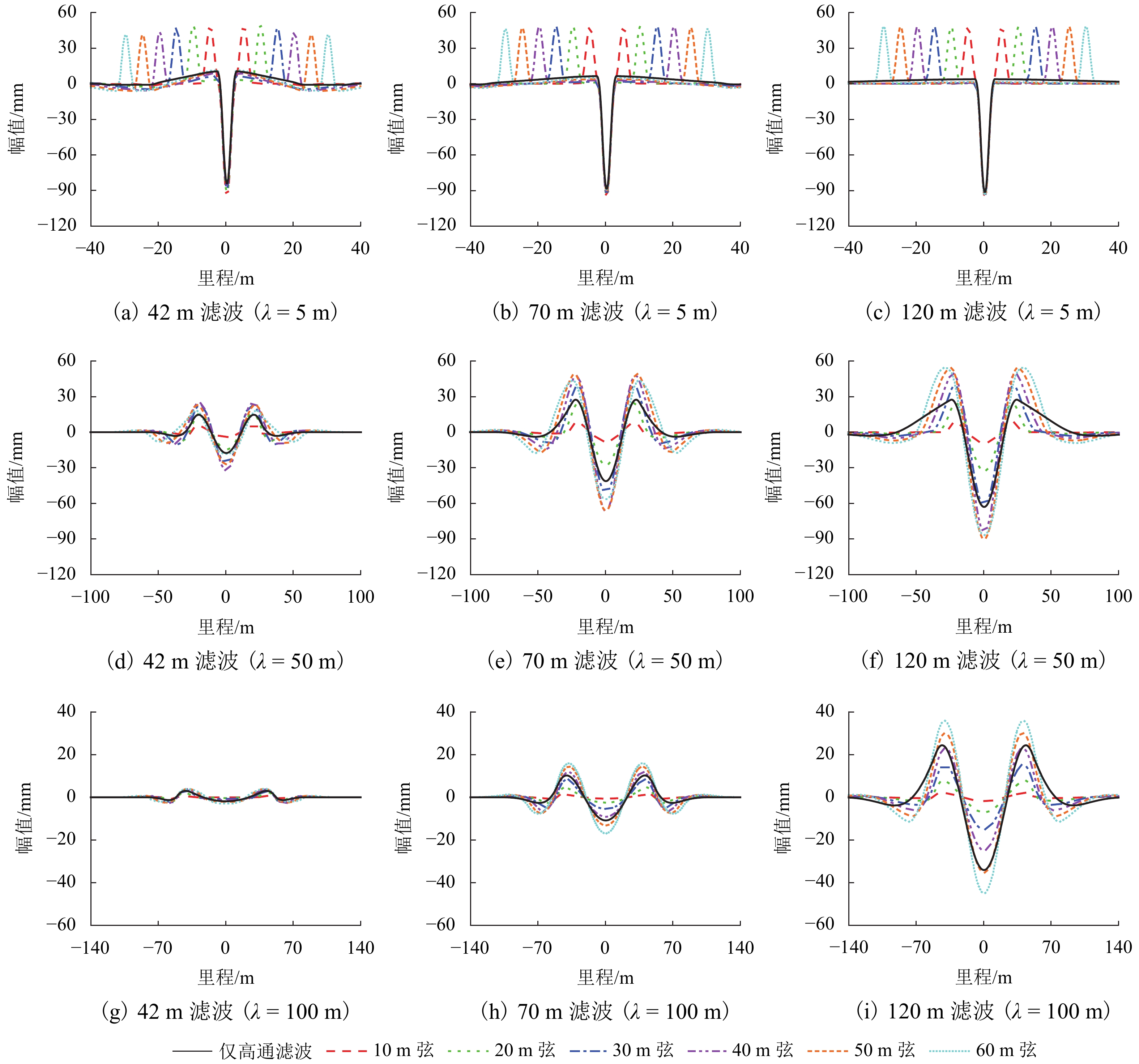
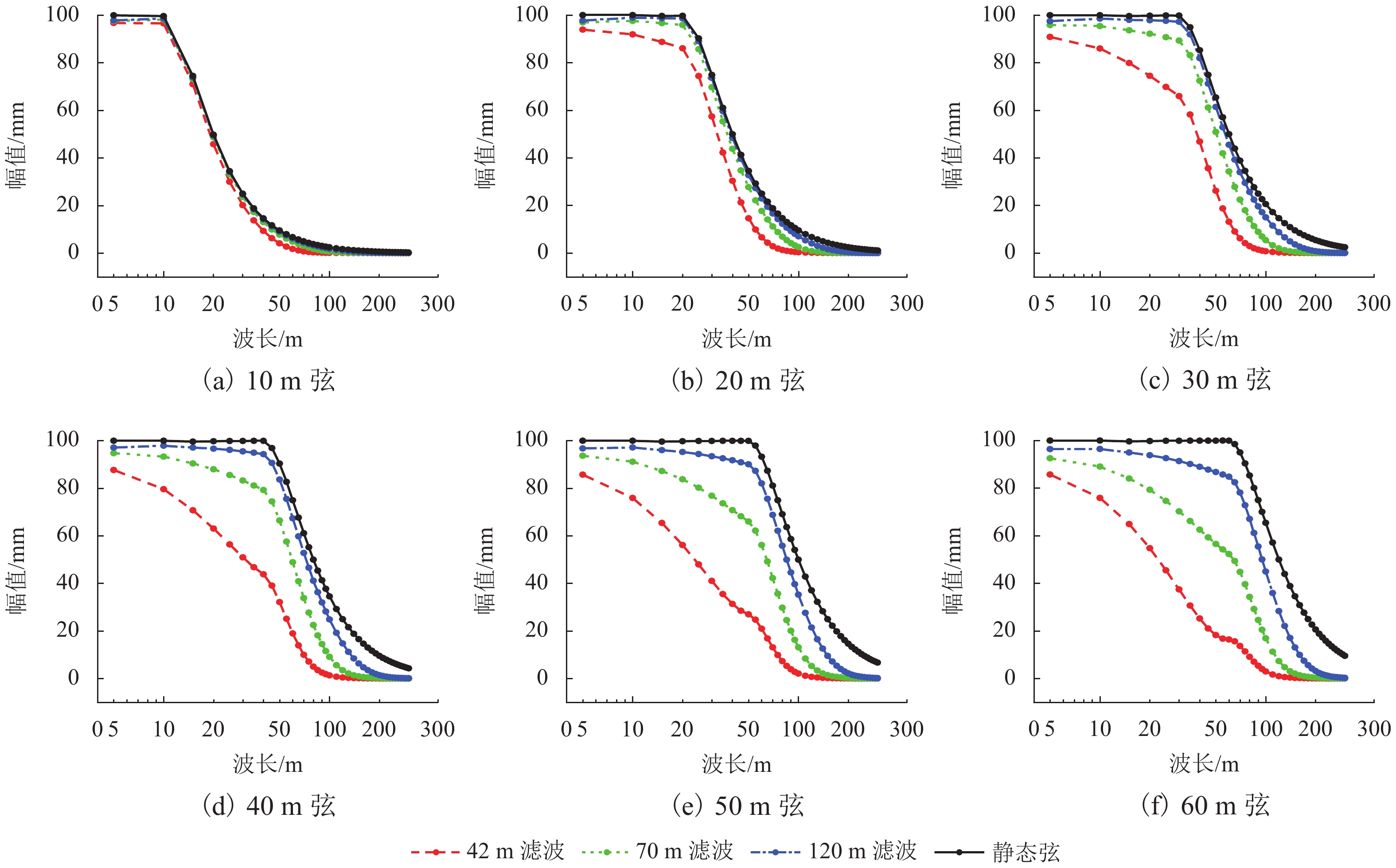
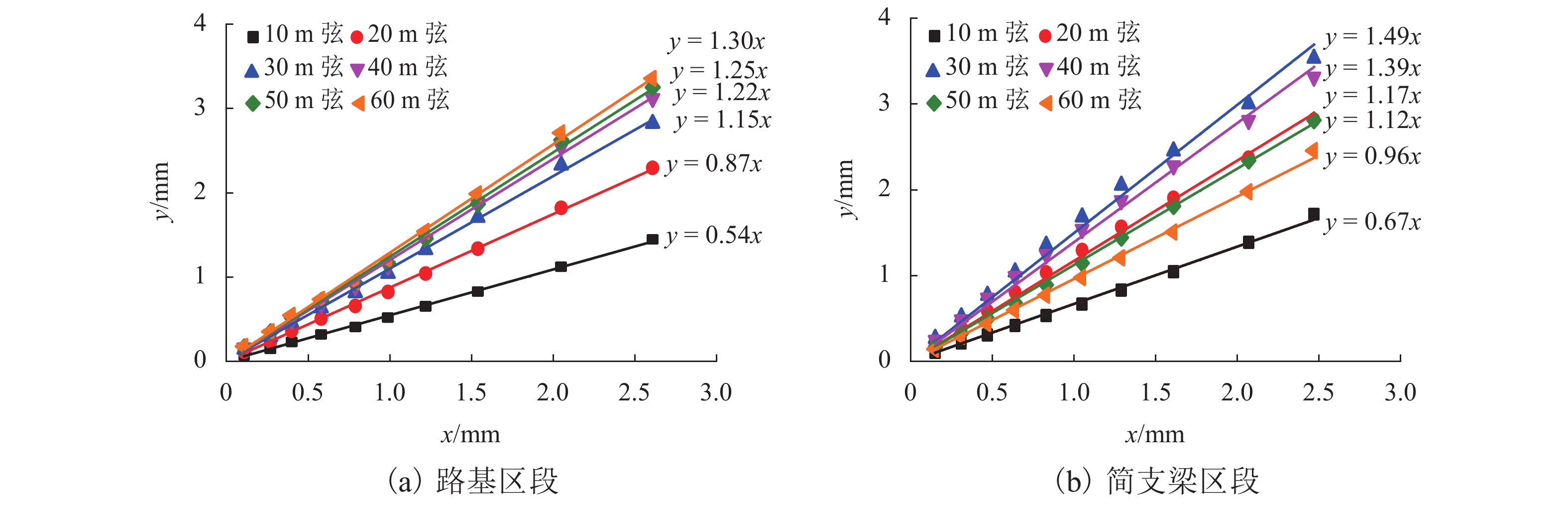
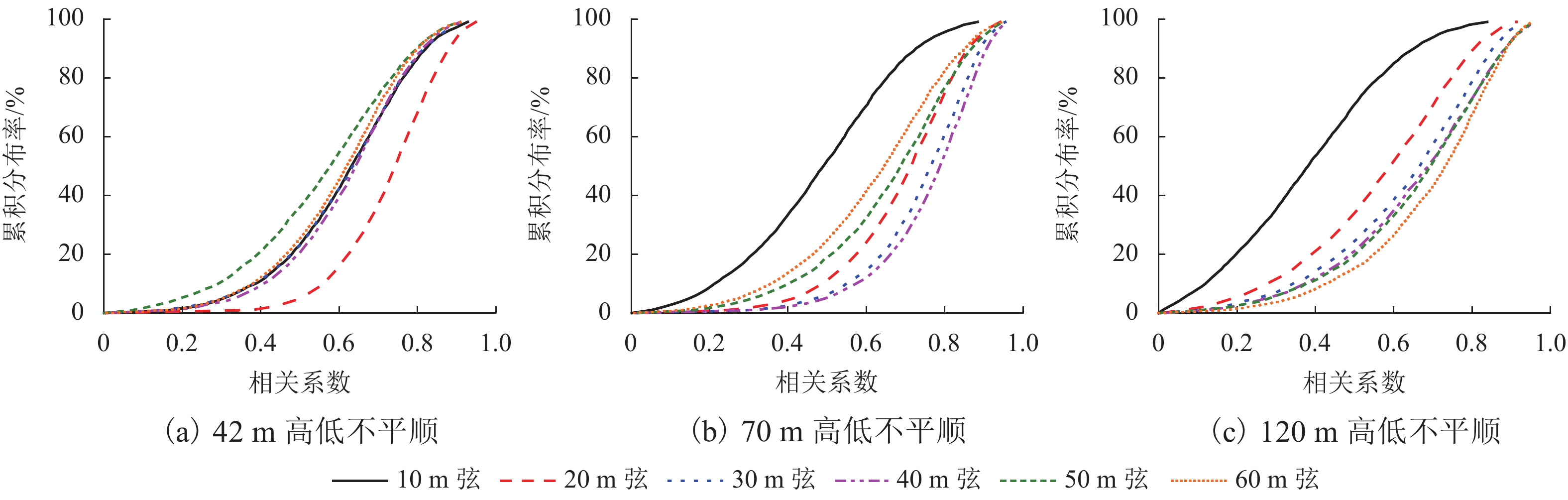
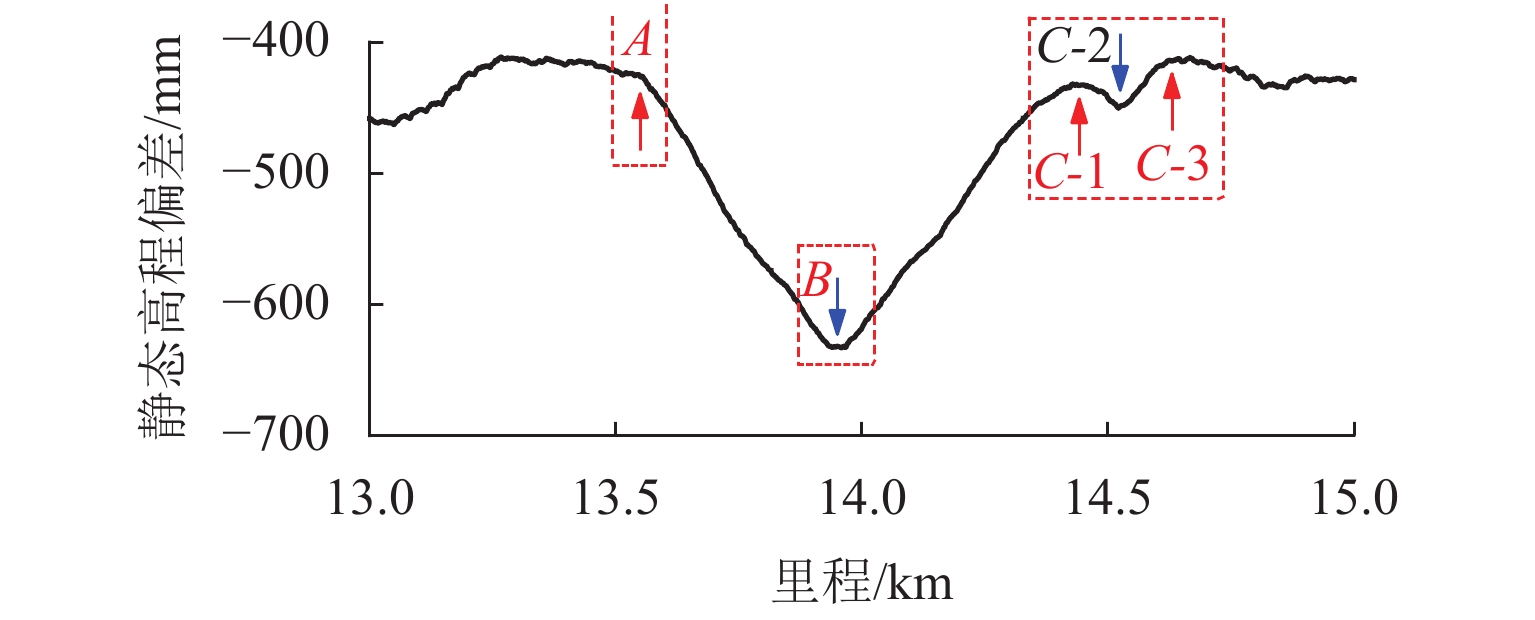
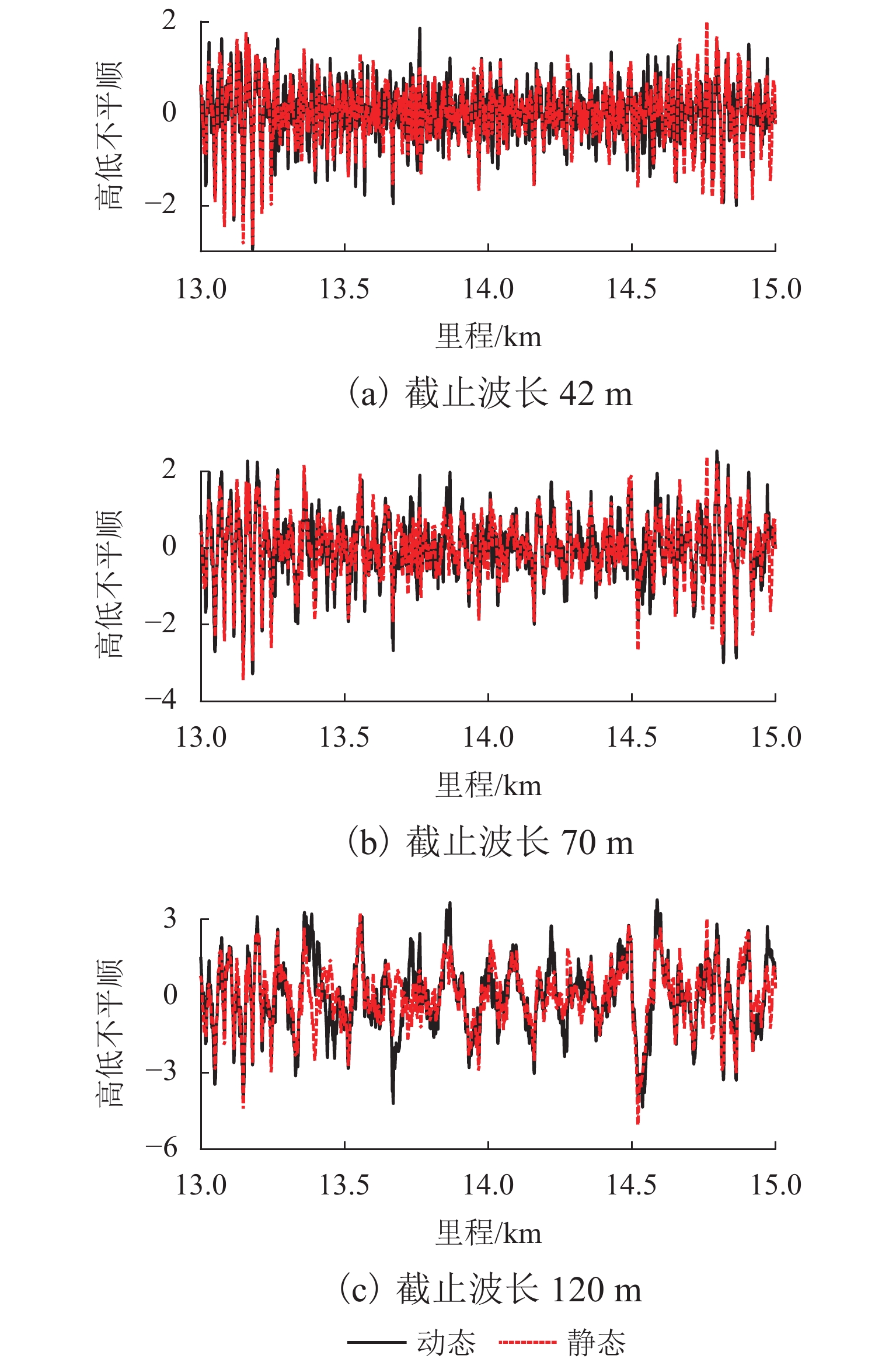
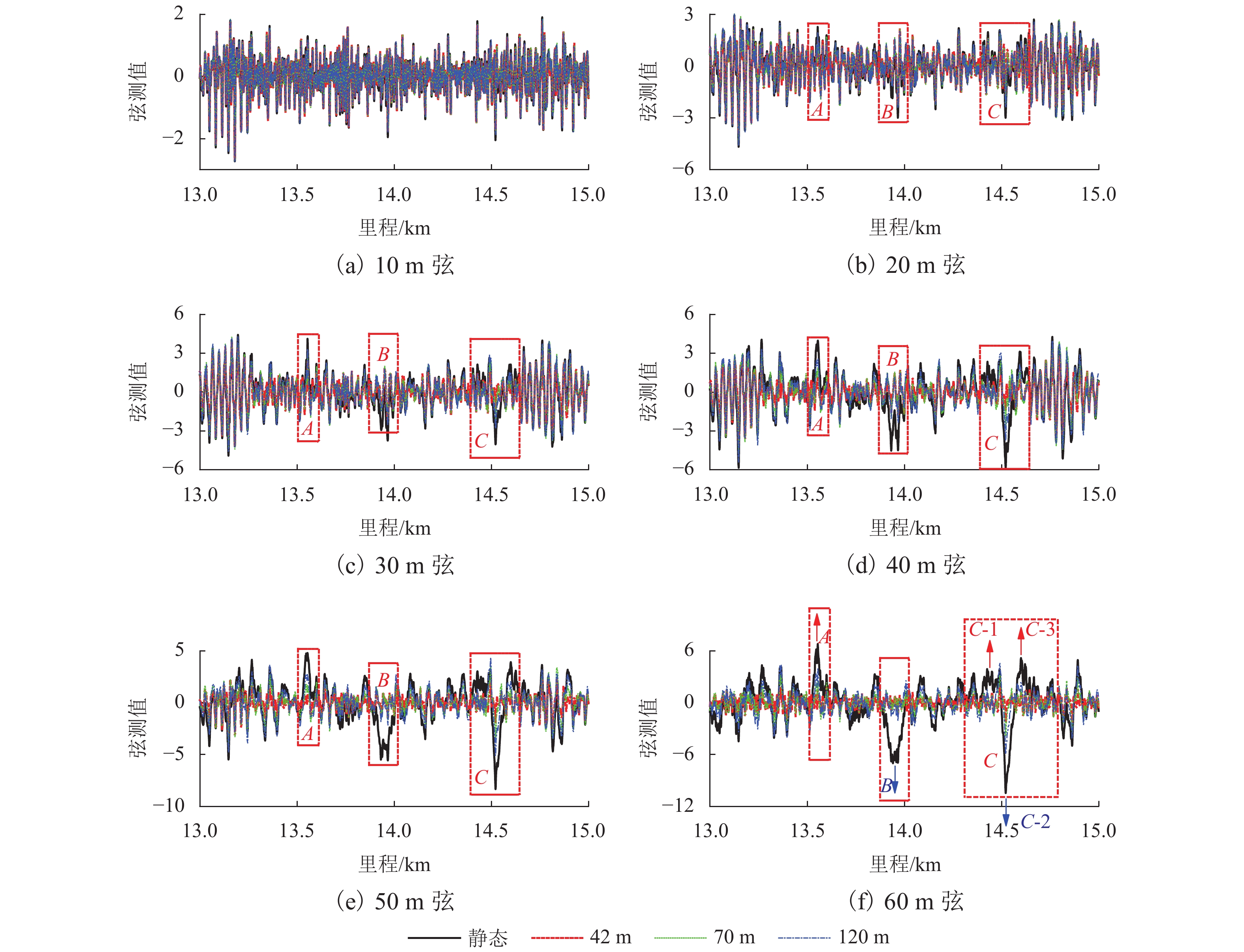
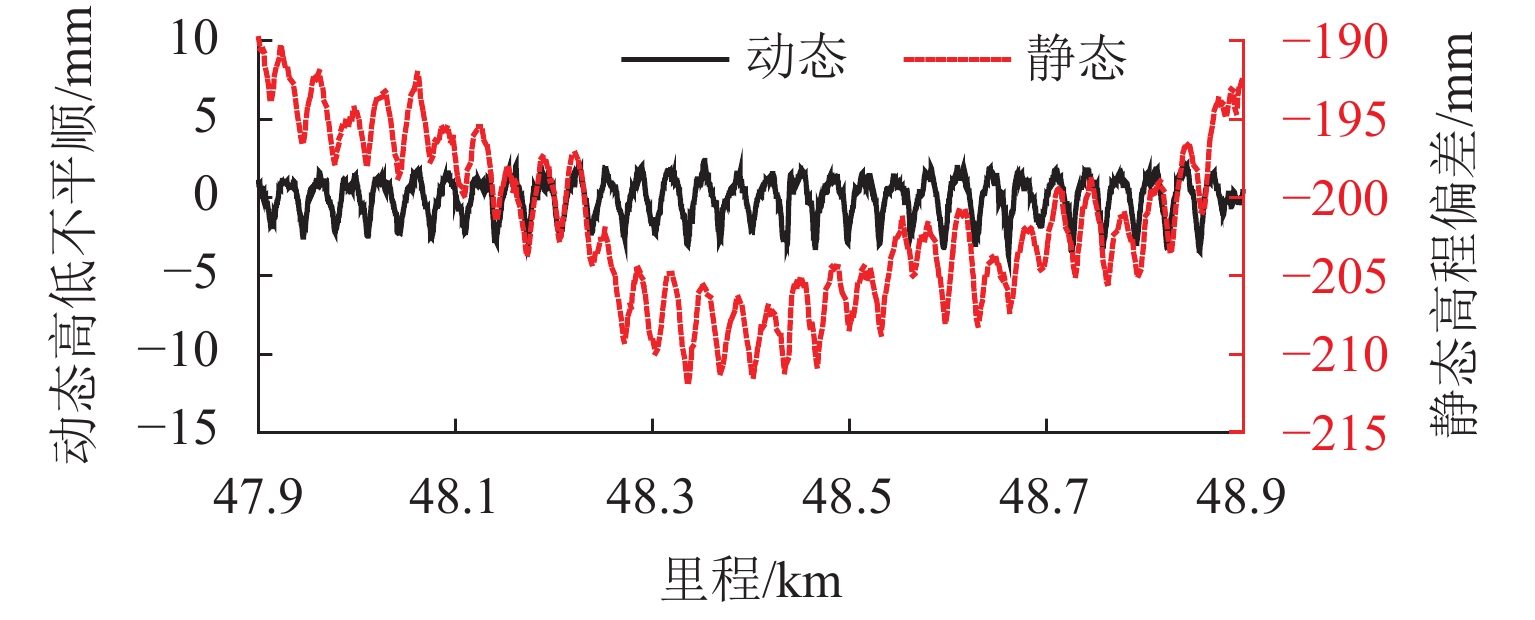
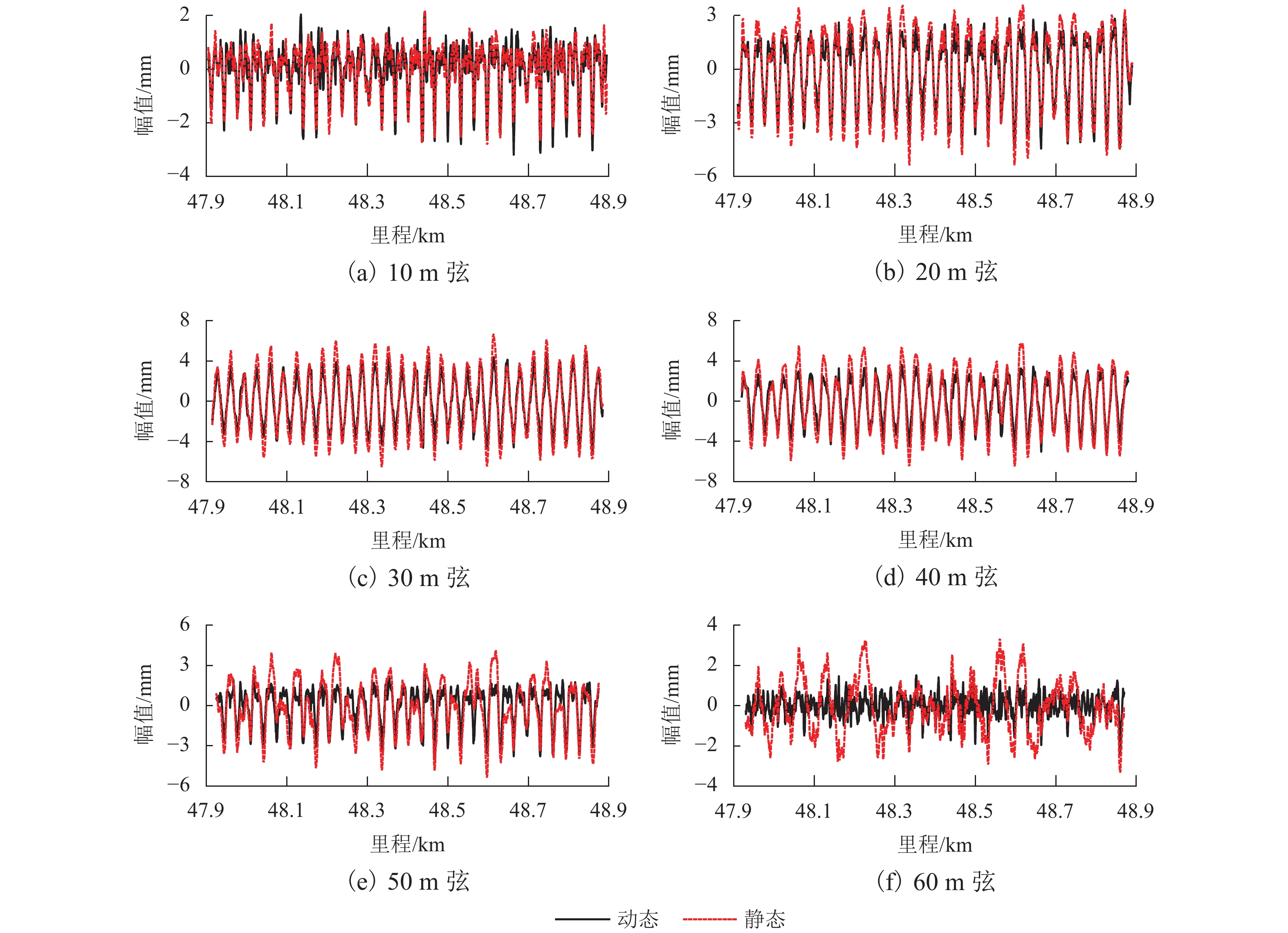
中点弦测法能够有效控制影响行车安全性和舒适性的指定波段轨道不平顺，主要用于测量轨道静态不平顺，但其较低的测量效率制约着轨道“状态修”的发展. 针对上述问题，将轨道动态不平顺按中点弦测输出，分析动静态弦测值差异与弦长和不平顺波长的关联关系，提出能够评价轨道动态平顺性的动态弦测法，研究动态不平顺与静态不平顺间的映射关系. 研究结果表明：42 m和70 m动态高通滤波幅值分别与10 m弦和20 m弦测值变化规律相当；当不平顺波长大于70 m时，120 m动态高通滤波幅值与40 m弦测值变化规律基本对应；截止波长为42、70、120 m的轨道动态不平顺，分别与弦长为20、30 ~ 40、30 ~ 60 m的动态弦测波形相关性最优，对应的动态弦测法最大合理弦长分别为20、30、40 m，通过路基和简支梁区段实测数据验证了动态弦测法的适应性；在路基沉降区段，弦长为60 m时，静态弦测值明显朝负方向偏离动态弦测值的处所为沉降点，相邻两侧朝正方向偏离动态弦测值的处所为沉降区段起终点.
Abstract:The midpoint chord method can effectively control the track irregularity of the designated band that affects the driving safety and comfort. It is mainly used to measure the track static irregularity. However, its low measurement efficiency restricts the development of track ‘state-maintenance’. To solve the above problems, the track dynamic irregularity is output according to the midpoint chord. The correlation between the dynamic and static chord measured values with the chord length and the irregularity wavelength is analyzed. The dynamic track irregularity is outputed according to the midpoint chord measurement. A dynamic chord measurement method is proposed, that can evaluate the dynamic smoothness of the track, and studies the mapping relationship between dynamic irregularity and static irregularity. The results show that, the dynamic high-pass filter amplitudes of 42 m and 70 m are equivalent to the measured values of 10 m chord and 20 m chord respectively. When the irregularity wavelength is greater than 70 m, the 120 m dynamic high-pass filter amplitude basically corresponds to the variation law of 40 m chord measured value. The track dynamic irregularities with cut-off wavelengths of 42, 70 m and 120 m have the best correlation with the dynamic chord measurement waveforms with chord lengths of 20, 30–40 m and 30–60 m respectively. The maximum reasonable chord lengths of the dynamic chord measurement method are 20, 30 m and 40 m respectively. The adaptability of the dynamic chord measurement method has been verified by the measured data of subgrade and simply supported beam sections. In the subgrade settlement section, when the chord length is 60 m, the place where the static chord measurement value deviates significantly from the dynamic chord measurement value in the negative direction is the settlement point, and the places where the adjacent two sides deviate from the dynamic chord measurement value in the positive direction are the beginning and end of the settlement section.
-
轮轨式轨道交通通过数平方毫米大小的接触斑传递摩擦力. 当轮轨界面出现较大的滑动量时，接触斑内温度因摩擦温升而迅速升高，并在车轮通过后迅速降低，剧烈的温度变化会导致钢轨表面生成脆硬的马氏体，诱发轮轨扁疤、材料剥离等问题的出现并加剧磨耗[1]，对列车运行的安全性造成严重的威胁. 因此，轮轨摩擦热问题一直是业界的研究热点.
在以往研究中，轮轨摩擦热问题的研究主要分为数值模拟和解析法2类. 有限元方法是研究轮轨摩擦热问题的主要手段. 赵鑫等[2]采用有限元和有限差分混合算法建立轮轨温升模型模拟轮轨滚动、滑动接触温升过程，结果表明滑动工况的温升较滚动工况更大. 李伟等[3]基于热弹塑性有限元理论，对滚滑状态下钢轨进行二维热力耦合分析，研究发现钢轨表面温升很高时，热载荷在钢轨表层产生的残余拉应力会对钢轨材料产生破坏性的影响. 肖乾等[4]建立了考虑函数型摩擦系数的热机耦合有限元模型，分析了轮轨滚动、滑动条件下的热机耦合特性，结果表明轮轨滑动条件下的摩擦温升足以改变材料性能，影响轮轨接触性能. 刘洋等[5]对滑动条件下的轮轨进行了二维热弹塑性有限元分析发现，变摩擦系数条件下计算的轮轨温升比常摩擦系数条件下大幅降低. Vo等[6]建立了轮轨三维弹塑性有限元模型，讨论了多轮经过的温度场叠加现象发现，6轮通过后在钢轨上引起的摩擦温度达723 ℃，高于马氏体层形成的临界温度.
数值模拟研究能够很准确地模拟轮轨摩擦温升，然而值得关注的一个问题是有限元模拟需要对轮轨接触界面进行精细的网格划分，极大地限制了模型的计算效率，不适于工程计算，而解析和半解析方法在这方面具有显著的优势. Knothe等[7]利用拉普拉斯变换和格林函数法，提出了二维滚滑条件下摩擦温度场的计算方法，研究了热通量分布形式和表面粗糙度对摩擦温升有较大影响. Ertz等[8]应用半解析方法提出了一种滑动条件下的摩擦温升简化计算方法，与Knothe等的结果十分吻合. Fischer等[9]提出了一种考虑热分配因子的轮轨摩擦温升计算模型，能够考虑轮轨表面粗糙度和局部塑性变形的影响. 杨新文等[10]在赫兹接触理论的基础上应用移动热源法编制了摩擦温升计算程序，研究发现，轮轨滑动接触条件下摩擦温升十分明显，摩擦温升足以引起钢轨热相变并形成脆硬的马氏体. 徐培娟等[11]借助半无限空间热传导理论建立轮轨热力耦合模型，研究了大轴重荷载作用下的摩擦温升，研究结果表明，大轴重车辆低速滑动时钢轨表面不可避免地会因摩擦温升而产生材质硬化现象.
上述研究侧重于描述温度场分布，忽略了摩擦温升对轮轨材料特性及轮轨接触状态的影响. 伏培林等[12]基于弹塑性接触理论，通过基尔霍夫变换方法提出了一种不限制材料温度相关性的摩擦温升求解方法，其结果表明，当轮轨温升处于较高水平时，考虑材料属性的温度相关性能更准确地预测摩擦温升，且摩擦温升与蠕滑率、行车速度和法向载荷成正相关. 伏培林所建模型的前提假设是二维接触，仅能考虑纵向蠕滑率，忽略了横向蠕滑和自旋的影响，与实际的轮轨接触状态存在一定的差异，如列车与轨道在小半径曲线处的动态相互作用.
为了更为准确地描述任意蠕滑状态下的三维轮轨摩擦温升现象，本文采用基于Kalker简化理论的FASTSIM算法模拟轮轨切向接触，借助Knothe的方法模拟轮轨摩擦温升，并通过考虑材料属性的温度相关性实现轮轨热力耦合. 据此调查了材料温度相关性对摩擦温升的影响，进一步将此模型应用到车辆-轨道耦合动力学计算，研究地铁车辆通在小半径曲线时的轮轨摩擦温升现象.
1. 三维轮轨接触热力耦合计算模型
1.1 三维轮轨接触模型
本节利用赫兹接触理论和Kalker的简化理论建立轮轨接触模型. 假定轮轨材料相同，轮轨接触为弹性接触，其接触区域为椭圆形状，接触区域点（x, y）法向压力分布可表示为
p(x,y)=p0√1−(xa)2−(yb)2, (1) 式中：p0为最大法向接触应力，如式（2）；a、b分别为接触斑的长、短半轴，如式（3）.
p0 = 3P2πab， (2) {a=m[3G∗P4(A+B)]1/3,b=n[3G∗P4(A+B)]1/3, (3) G∗=1−υG=2(1−υ2)E, (4) 式（2）～（4）中：G*为轮轨材料特性参数，P为轮载， m、n为与椭圆积分有关的参数，A、B为取决于车轮和钢轨曲面的主曲率大小的常数，υ、G和E 分别为轮轨材料的泊松比、剪切模量和弹性模量[13].
以往的摩擦温升解析/半解析模型一般只关注纵向蠕滑，为了更为真实地模拟轮轨接触状态，需要考虑三向蠕滑率对轮轨接触应力的影响，本文采用Kalker的简化理论及其数值算法FASTSIM获取轮轨接触切向解，具体方法见文献[14].
1.2 摩擦温升计算模型
车轮在钢轨表面滚动时，不可避免会与钢轨发生相对滑动，即$ {v_{\text{w}}} \ne {v_{\text{r}}} $，$ {v_{\text{w}}} $为车轮速度，$ {v_{\text{r}}} $为钢轨速度，如图1所示. 图中：$ {v_{\text{s}}} $为轮轨间绝对滑动速度，v0为车辆运行速度. 轮轨材料摩擦生热，接触区域温度升高，在列车牵引加速或制动时轮轨摩擦升温尤为显著. 以往的摩擦温升解析模型大多基于轮轨滑动接触状态建立，而Knothe提出的差分模型不限制滚滑状态，所以本文采用Knothe差分方法计算摩擦温升.
忽略纵向和横向导热[8]，轮轨导热微分方程为
ρc∂T∂t−λ∂2T∂z2=0, (5) 式中：$ \rho $为轮轨材料的密度，c为轮轨材料的比热容，$ \lambda $为轮轨材料的导热系数，T为轮轨材料的温度，t为时间.
接触斑摩擦生热可以视为位于轮轨接触表面的热源，可表示为
−λ∂T∂z(x,y,z=0)=q(x,y), (6) 式中：$ q(x,y) $为接触斑表面$(x,y) $处的热流密度，与该点处的切向应力呈线性关系.
当轮轨间摩擦系数和相对滑动速度的值恒定时，接触斑上任一点流入钢轨或车轮上的热通量与该点处的切向应力呈线性关系，如式（7）.
q(x,y)=εqt(x,y)vs, (7) 式中：$ \varepsilon $为热量分配因子；${q_{\rm{t}}}({x},{y})$为点（x、y）处的切向应力，由1.1节求得.
研究表明，热流密度的最大值和最高接触温度都是在平行于滚动方向的主轴上发生的[15]，所以将接触椭圆划分为若干沿着滚动方向的条带，独立地计算每一条带的接触温度. 引入无量纲坐标$ \xi {\text{ = }}x/a $、 $\zeta = {\textit{z}}/\delta$（$ \delta $为热渗透深度，与接触斑长轴和佩克莱数有关的常量），代入Carslaw和Jaeger的摩擦温升解析公式[16]，并应用差分方法可得钢轨接触区域每一条带的接触温度为
Ta(ξk,ζ)=1β√2avrk∑i=1qi×(G(ξk−ξi−1,ζ)−G(ξk−ξi,ζ)), (8) G(ξ,ζ) = √2ξπexp(−ζ22ξ)−ζerfc(ζ√2ξ). (9) 当$ \zeta = 0 $，钢轨表面的温度为
Tb(ξk)=2β√aπvrk∑i=1qi(√ξk−ξi−1−√ξk−ξi), (10) 式（8）～（10）中：k为沿滚动方向的差分网格编号；$ \beta $为热穿透系数，其值为$ \sqrt {\lambda \rho c} $；qi为差分计算时第i个网格处的热流密度；$ {\xi _k} $为沿滚动方向差分网格k对应的无量纲坐标.
由于忽略了横向热传导，各个条带的温度场互不影响，由此可得三维接触区域的温度分布.
1.3 热力耦合过程实现
由1.1节和1.2节的描述可知，计算摩擦温升的前提是获得轮轨接触应力和滑动速度，然而当轮轨界面温度较高时，弹性模量和泊松比会出现明显的变化，轮轨接触应力和滑动速度会因此而改变，因而有必要引入与温度相关的材料参数以实现热力耦合. 其实现过程如下：
首先，给定法向荷载、三向蠕滑率、接触几何、车辆运行速度以及初始温度下的材料参数，通过1.1节的接触模型获得轮轨接触应力和滑动速度，确定轮轨界面的热通量.
其次，利用1.2节描述的方法计算轮轨摩擦温升Tj−1. 假设轮轨材料属性取决于接触界面的最大温升，基于表1和表2中随温度变化的实测数据，利用线性插值获得此温度下的材料参数.
表 1 随温度变化的比热容和导热系数Table 1. Specific heat capacity and thermal conductivity at different temperatures温度/℃ 比热容/（J·kg−1·℃−1） 导热系数/（W·m−1·℃−1） 0 419.5 59.71 350 629.5 40.88 703 744.5 30.21 710 652.9 30.00 800 657.7 25.00 950 665.2 27.05 1200 677.3 30.46 表 2 随温度变化的材料参数Table 2. Material parameters at different temperatures温度/℃ 弹性模量/GPa 泊松比 24 213 0.295 230 201 0.307 358 193 0.314 452 178 0.320 567 102 0.326 900 43 0.345 相应地，弹性模量和泊松比不再是给定值，接触斑尺寸以及接触应力随之发生变化，会得到一个新的温度场Tj. 因而，需要不断迭代计算，将差异缩小到允许的误差范围内，即
Tj−Tj−1<10−4℃. (11) 为了加速迭代收敛过程，采用二阶收敛的斯特芬森迭代法[17]，如式（12）.
{T′j=f(Tj),Tj″=f(T′j),Tj+1=Tj−(T′j−Tj)2Tj″−2T′j+Tj, (12) 式中：j为迭代次数，j = 1,2，…；$ f $(·)为迭代函数.
2. 热力耦合建模方式对轮轨接触行为及摩擦温升的影响分析
为了调查热力耦合效应对轮轨接触行为的影响，以一个典型的轮轨接触算例为例，应用上述所建模型进行分析. 下文计算中，采用我国地铁车辆常用的LM型踏面与CHN60钢轨，在列车运行速度为100 km/h，纵向蠕滑率为0.08的条件下，取模型参数环境温度为20 ℃，摩擦系数为0.337，静轮载为100 kN，轮轨材料密度为7 790 kg/m3，车轮半径为430 mm，轨底坡为1/40，轨距为1 435 mm.
图2和图3分别显示了2种建模方式获得的轮轨界面及钢轨体内的摩擦温升分布. 由图2、3可以发现：非热力耦合条件下模型计算的摩擦温升明显较大，钢轨摩擦温升最大值为655 ℃，出现在钢轨表面接触斑后半轴接近边缘的位置；考虑热力耦合后，钢轨表面最大温升则从655 ℃下降到401 ℃，幅度变化达到39%；摩擦温升主要影响接触区域（−1≤x/a≤1），对于非接触区（x/a>1）的影响则较小；由于轮轨接触区相对于钢轨来说体量很小，接触斑的温升范围有限，降温速率较大.
图 2 2种模拟方式条件下轮轨界面摩擦温升对比Figure 2. Comparison of frictional temperature rise of wheel–rail interface under two simulation conditions为进一步研究各向蠕滑率对摩擦温升的影响，图4展示了轮轨界面温升随纵向蠕滑率和自旋蠕滑率的变化情况，并对比了热力耦合的影响. 从图4可以看出：钢轨表面温升峰值随各向蠕滑率的增大而上升，这是因为蠕滑率的增大会提高轮轨接触点对间的相对滑动速度，摩擦热流密度随之增大，进而引起钢轨表面温度的上升；不考虑热力耦合时，钢轨表面最大温升与蠕滑率或自旋呈线性相关，而考虑热力耦合时钢轨表面最大温升曲线则体现出明显的非线性特征；当蠕滑率较低（<0.01）时，轮轨摩擦温升不足以显著改变材料属性，因而2种建模方式计算得到的温升曲线基本重合；随着蠕滑率的进一步增大，两者的差异随蠕滑率的增加而增大，即蠕滑率较高时需要考虑热力耦合建模；不考虑热力耦合时，当纵、横向蠕滑率达到0.08时，钢轨表面最大温升超过钢轨钢的奥氏体临界温度723 ℃[6]，钢轨表面会形成马氏体，容易引起钢轨擦伤；考虑热力耦合后，其预测的摩擦温升小于该相变温度，与实际运行情况是相符的. 因为列车通常以15%～20%蠕滑率控制列车滑行，而现场较少发现钢轨擦伤现象. 这表明热力耦合建模方式更为合理，可以避免过高估计轮轨摩擦温升.
图 3 2种模拟方式条件下钢轨内部的温度场分布对比Figure 3. Comparison of temperature field distribution inside the rail under two simulation methods
图 4 钢轨表面最大温升随蠕滑率变化Figure 4. Variation of maximum temperature rise of rail surface with creepage rate图4中显示的规律可以从轮轨接触解得到解释. 图5对比了2种建模方式下接触斑面积与最大法向接触应力随纵向蠕滑率的变化，由图5可以看出：2种方式下最大法向接触应力和接触斑面积存在着显著的差异；热力耦合条件下接触斑面积随纵向蠕滑率的增大而增大，最大法向应力则相应地随纵向蠕滑率的增大而减小. 这是材料属性随温度变化的结果，即轮轨弹性模量随温度增加而减小，接触斑面积增大，接触应力和摩擦热流密度减小. 而在不考虑热力耦合时，材料属性和接触应力都不发生变化，所以2种模型计算的温升曲线逐渐偏离.
图 5 接触斑面积与最大法向应力随纵向蠕滑率变化Figure 5. Variation of contact spot area and maximum normal stress with longitudinal creepage rate3. 地铁车辆曲线通过时的轮轨接触-热分析
通过上述分析可以发现，较大的蠕滑率和自旋对轮轨摩擦温升和轮轨接触的计算有着显著的影响，本节进一步将其结合车辆-轨道耦合动力学模型研究地铁车辆通过小半径曲线时的轮轨接触行为，通过参数变化调查热力耦合建模方式对分析此类问题的必要性.
3.1 工况介绍
运用SIMPACK建立车辆-轨道耦合动力学模型，如图6所示. 采用我国地铁车辆常用的LM型踏面与CHN60钢轨，轨距取为1435 mm，内外轨轨底坡均设置为1/40. 车辆过曲线速度设为60 km/h，线路设置为圆曲线段长100 m，其半径为150 m，圆曲线两端均设50 m 的缓和曲线，超高120 mm，曲线出入口设置100 m的直线. 轮轨表面摩擦系数一般为0.2～0.6[18-19]，此处小曲线线路摩擦系数取为0.5.
3.2 摩擦温升与接触行为
图7展示了曲线线路上外轨侧轮轨蠕滑率和自旋随运行里程的变化. 由图可以看出：在仿真线路的直线段（0～100 m），各向蠕滑率均较小，当车辆进入缓和曲线（100～150 m）时，各向蠕滑率迅速增大，其中横向和自旋蠕滑率的增加尤为显著；车辆运行在圆曲线（150～250 m）时，蠕滑率和自旋达到最大值；随着车辆离开圆曲线段，蠕滑率逐渐降低并恢复初始状态. 由此可以看出，在列车通过曲线时，横向蠕滑率和自旋均处于较高的水平，在分析热力耦合方式下的轮轨接触行为时有必要考虑三向蠕滑率，这是本文引入FASTSIM计算模型的初衷.
图 7 线路内外侧轮轨蠕滑率变化Figure 7. Variation of wheel–rail creepage rate inside and outside the line图8展示了列车通过过程中2种建模方式下钢轨表面最大温升的时程变化. 由图8可以看出：摩擦温升的时程变化与线路蠕滑率变化趋势相同，热力耦合建模方式对直线段的轮轨摩擦温升影响几乎可以忽略，而在曲线段其影响是显著的；具体而言，非热力耦合条件下摩擦温升最大值为709 ℃，而热力耦合条件下其计算结果为420 ℃. 这表明列车通过曲线时考虑热力耦合建模对于预测轮轨摩擦温升是十分必要的.
对应于图8，图9展示了2种建模方式下轮轨最大接触应力的变化. 由图可以看出：列车进入曲线段时，由于轮轨接触点向轮缘与轨距角转移，轮轨最大法向接触应力显著增大；在圆曲线段处（150～250 m），热力耦合条件下计算得到的轮轨最大法向接触应力与最大切向接触应力明显小于非热力耦合工况，其降低幅值分别达到17.4%和14.7%.
为定量描述轮轨损伤，本文采用Dirks等[20]提出的摩擦能量指数E. 该指数越高，表明轮轨界面越易发生损伤，如式（13）.
E = τx(vx−φy)+τy(vy+φx), (13) 式中：vx、vy、φ分别为轮轨纵向、横向和自旋蠕滑率；τx、τy分别为轮轨切向应力在纵向和横向的大小.
线路里程200 m处2种建模方式下外轨接触斑的摩擦能量指数分布见图10. 此处接触斑极为狭长，经调查此处为左侧轮缘与外轨的轨角接触. 由于轮轨接触斑处于全滑动状态，因而切向应力与法向应力分布相同，摩擦能量指数最大值出现在接触斑中心区域. 通过对比可以发现，热力耦合条件下接触斑能量指数明显小于非热力耦合工况，其变化可达25%. 这说明考虑热力耦合建模方式在轮轨热损伤分析中是必要的.
3.3 曲线半径与行车速度对轮轨摩擦温升的影响
以小半径曲线线路为例，进一步分析曲线半径（200～600 m）与列车通过速度（30～80 km/h）对轮轨摩擦温升的影响（所设置工况仅用于参数分析，实际运行中列车通过200 m半径曲线速度不会达到80 km/h）. 图11展示了2种建模方式下轮轨最大摩擦温升随曲线半径和行车速度的变化. 可以看出，随着运行速度的增大和曲线半径的减小，轮轨界面最大温升逐渐增大. 2种建模方式的差异展示于图11（b）和11（c），结果表明：当行车速度超过40 km/h，两者的温升误差超过10%，需要考虑热力耦合建模；当行车速度超过50 km/h，两者的法向接触应力温升误差超过10%.
图 11 工况摩擦温升及误差分布Figure 11. Frictional temperature rise and error distribution under working conditions4. 结 论
通过所建的三维热力耦合温升计算模型，考虑横向蠕滑和自旋，详细分析一般的温升计算模型和热力耦合温升计算模型计算的温度场差异，探究小半径曲线工况下的热力耦合效应，基于本文的计算结果，可以获得以下结论：
1） 摩擦温升随着各向蠕滑率的增大而增大，较大的横向和自旋蠕滑率也会引起剧烈的摩擦温升，在计算摩擦温升时尤其是在横向蠕滑和自旋主导的小半径曲线工况下有必要考虑横向和自旋蠕滑率的影响.
2） 在计算摩擦温升或估计热损伤作用时，考虑热力耦合效应可有效避免对温升和热损伤作用的过分高估，计算温升越高，热力耦合效应对温升的抑制越显著.
3） 车辆在小半径曲线线路上运行时，会引起较大的轮轨摩擦温升，温升与运行速度成正比，与曲线半径成反比，而受曲线超高和缓和曲线长度的影响较小.
4） 本文建立的三维热力耦合摩擦温升模型可以较为准确地计算摩擦温升，在横向蠕滑和自旋主导的小半径曲线工况下更具优越性. 本文模型基于弹性理论并假设摩擦系数恒定，在后续研究中会进一步考虑变摩擦系数和材料塑性，并将结合轮轨接触温升试验进一步完善本文模型.
-
图 2 基于动态弦测法的轨道高低不平顺测量
Figure 2. Track longitudinal level measurements with the dynamic chord method
图 5 部分典型余弦型不平顺动、静态波形
Figure 5. Dynamic and static waveforms of some typical cosine irregularities
图 6 动、静态不平顺峰值随波长的变化规律
Figure 6. Variation of peak values of dynamic and static irregularity with wavelength
图 7 部分典型余弦型不平顺动态弦对比
Figure 7. Comparison of dynamic chords with some typical cosine irregularities
图 9 动态弦与原始动态高低不平顺峰值的关系
Figure 9. Relationship between dynamic chord and original dynamic longitudinal level peak
图 10 动态弦与实测动态高低不平顺相关性
Figure 10. Correlation between dynamic chord and measured dynamic longitudinal level
图 13 路基区段动态弦测与静态弦测对比
Figure 13. Comparison between dynamic and static chord measurements in subgrade section
图 15 简支梁区段动态弦测与静态弦测对比
Figure 15. Comparison between dynamic and static chord measurements in simply supported beam section
表 1 动态弦测误差
Table 1. Dynamic chord measurement error
% 截止波长/m 弦长/m 10 20 30 40 50 60 42 5.4 20.0 39.3 58.2 73.2 83.6 70 2.4 7.7 16.6 27.5 39.3 51.0 120 2.2 2.7 6.0 10.4 15.7 21.8 
下载: 导出CSV
表 2 动态弦测值与静态弦测值峰值差
Table 2. Peak value difference between dynamic chord measurement and static chord measurement mm
弦长/m 截止波长/m 动、静态弦测值峰值差 A B C-1 C-2 C-3 10 42 0.2 0.3 0.1 0.4 0.1 70 0.2 0.2 0.1 0.3 0.1 120 0.1 0.2 0.1 0.2 0.1 20 42 0.8 0.8 0.4 1.3 0.6 70 0.6 0.7 0.4 0.9 0.5 120 0.4 0.6 0.3 0.6 0.3 30 42 1.7 1.5 0.5 2.7 1.3 70 1.2 1.4 0.4 1.9 0.9 120 0.8 1.2 0.3 1.2 0.6 40 42 2.8 2.7 1.4 4.5 0.9 70 2.1 2.6 1.4 3.3 0.7 120 1.4 2.2 1.2 2.2 0.5 50 42 4.0 4.1 2.0 6.4 3.0 70 3.1 4 1.9 4.8 2.6 120 2.0 3.4 1.7 3.2 1.8 60 42 5.2 5.6 2.9 7.7 4.0 70 4.3 5.6 2.7 6.1 3.6 120 2.9 4.8 2.4 4.0 2.5
下载: 导出CSV
-
[1] 罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态的控制[M]. 北京: 中国铁道出版社, 2006: 62-65 [2] 刘学文,杨怀志,杨飞,等. 基于动静态检测数据的轨道精测精调评价技术[J]. 铁道建筑,2019,59(9): 111-115. doi: 10.3969/j.issn.1003-1995.2019.09.27LIU Xuewen, YANG Huaizhi, YANG Fei, et al. Evaluation technology of track precision measurement and fine adjustment based on dynamic and static detection data[J]. Railway Engineering, 2019, 59(9): 111-115. doi: 10.3969/j.issn.1003-1995.2019.09.27 [3] 杨飞,刘丙强,谭社会,等. 高速铁路轨道静态几何不平顺弦测评价标准体系研究[J]. 铁道建筑,2021,61(6): 107-111,120. doi: 10.3969/j.issn.1003-1995.2021.06.24YANG Fei, LIU Bingqiang, TAN Shehui, et al. Research on evaluation standard system of chord measurement for track static geometric irregularity of high speed railway[J]. Railway Engineering, 2021, 61(6): 107-111,120. doi: 10.3969/j.issn.1003-1995.2021.06.24 [4] 田新宇,高亮,杨飞,等. 基于动态短弦的无砟轨道板周期性不平顺管理标准[J]. 中国铁道科学,2020,41(6): 30-38. doi: 10.3969/j.issn.1001-4632.2020.06.04TIAN Xinyu, GAO Liang, YANG Fei, et al. Management standard for cyclic irregularity of ballastless track slab based on dynamic short chord[J]. China Railway Science, 2020, 41(6): 30-38. doi: 10.3969/j.issn.1001-4632.2020.06.04 [5] 张国锋,高晓蓉,王黎,等. 数字逆滤波技术在轨道不平顺检测中的应用[J]. 信号处理,2004,20(6): 667-670. doi: 10.3969/j.issn.1003-0530.2004.06.030ZHANG Guofeng, GAO Xiaorong, WANG Li, et al. The applying of digital- inverse filtering technology in track irregularity inspection[J]. Signal Processing, 2004, 20(6): 667-670. doi: 10.3969/j.issn.1003-0530.2004.06.030 [6] 程樱,许玉德,周宇,等. 三点偏弦法复原轨面不平顺波形的理论及研究[J]. 华东交通大学学报,2011,28(1): 42-46. doi: 10.3969/j.issn.1005-0523.2011.01.009CHENG Ying, XU Yude, ZHOU Yu, et al. Theory and research of asymmetrical chord offset method of restoring a waveform of track irregularity[J]. Journal of East China Jiaotong University, 2011, 28(1): 42-46. doi: 10.3969/j.issn.1005-0523.2011.01.009 [7] 王源,徐金辉,陈嵘,等. 基于中点弦测法的轨道不平顺精确值数学模型研究[J]. 铁道建筑,2015,55(5): 139-143. doi: 10.3969/j.issn.1003-1995.2015.05.35WANG Yuan, XU Jinhui, CHEN Rong, et al. Research on mathematical model of accurate value of track irregularity based on midpoint chord measurement method[J]. Railway Engineering, 2015, 55(5): 139-143. doi: 10.3969/j.issn.1003-1995.2015.05.35 [8] 魏晖,朱洪涛,殷华,等. 高铁轨道平顺性的150 m/300 m校验及其快速测量[J]. 铁道工程学报,2015,32(1): 44-48,54. doi: 10.3969/j.issn.1006-2106.2015.01.009WEI Hui, ZHU Hongtao, YIN Hua, et al. 150 m/300 m check for the irregularities of HSR and its rapid survey[J]. Journal of Railway Engineering Society, 2015, 32(1): 44-48,54. doi: 10.3969/j.issn.1006-2106.2015.01.009 [9] 杨飞,赵文博,高芒芒,等. 运营期高速铁路轨道长波不平顺静态测量方法及控制标准[J]. 中国铁道科学,2020,41(3): 41-49. doi: 10.3969/j.issn.1001-4632.2020.03.05YANG Fei, ZHAO Wenbo, GAO Mangmang, et al. Static measurement method and control standard for long-wave irregularity of high-speed railway track during operation period[J]. China Railway Science, 2020, 41(3): 41-49. doi: 10.3969/j.issn.1001-4632.2020.03.05 [10] 赵文博,杨飞,李国龙,等. 高速铁路轨道平顺性静态长弦测量矢距差法数学模型推导及特性分析[J]. 铁道建筑,2020,60(2): 105-109.ZHAO Wenbo, YANG Fei, LI Guolong, et al. Mathematical model derivation and characteristics analysis of vector distance difference method for static long chord measurement of high speed railway[J]. Railway Engineering, 2020, 60(2): 105-109. [11] 魏世斌,李颖,赵延峰,等. GJ-6型轨道检测系统的设计与研制[J]. 铁道建筑,2012,52(2): 97-100. doi: 10.3969/j.issn.1003-1995.2012.02.030 [12] 魏晖,朱洪涛,吴维军,等. 高速铁路长波不平顺的相对测量整道[J]. 铁道建筑,2014,54(8): 95-98. doi: 10.3969/j.issn.1003-1995.2014.08.29 [13] 魏晖,朱洪涛,赵国堂,等. 基于中点弦测模型的无砟轨道精调量迭代求解[J]. 西南交通大学学报,2015,50(1): 131-136. doi: 10.3969/j.issn.0258-2724.2015.01.019WEI Hui, ZHU Hongtao, ZHAO Guotang, et al. Iterative algorithm of HSR ballastless track realignment calculation based on MCO model[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 131-136. doi: 10.3969/j.issn.0258-2724.2015.01.019 [14] 中华人民共和国铁道部. 高速铁路无砟轨道线路维修规则（试行）: TG/GW 115—2012 [S]. 北京: 中国铁道出版社, 2012. [15] 杨飞,吴细水,孙宪夫,等. 钢轨轧制不平顺激扰下的动车组动力响应特性[J]. 西南交通大学学报,2022,57(2): 267-276,294.YANG Fei, WU Xishui, SUN Xianfu, et al. Dynamic response characteristics of EMU under excitation of rail straightening irregularity[J]. Journal of Southwest Jiaotong University, 2022, 57(2): 267-276,294. [16] NAGANUMA Y, KOBAYASHI M, OKUMURA T. Inertial measurement processing techniques for track condition monitoring on Shinkansen commercial trains[J]. Journal of Mechanical Systems for Transportation and Logistics, 2010, 3(1): 315-325. doi: 10.1299/jmtl.3.315 [17] 魏世斌,刘伶萍,刘维桢,等. 提速线路轨道长波不平顺检测技术[J]. 中国铁道科学,2010,31(2): 141-144.WEI Shibin, LIU Lingping, LIU Weizhen, et al. Technology for the measurement of long-wavelength track irregularity of speed-up railway[J]. China Railway Science, 2010, 31(2): 141-144. [18] HAIGERMOSER A, LUBER B, RAUH J, et al. Road and track irregularities: measurement, assessment and simulation[J]. Vehicle System Dynamics, 2015, 53(7): 878-957. doi: 10.1080/00423114.2015.1037312 [19] 中国国家铁路集团有限公司. 铁路基础设施动态检测——轨道几何检测系统: Q/CR 751—2020[S]. 北京: 中国铁道出版社, 2020 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 800
- HTML全文浏览量: 466
- PDF下载量: 112
- 被引次数: 0