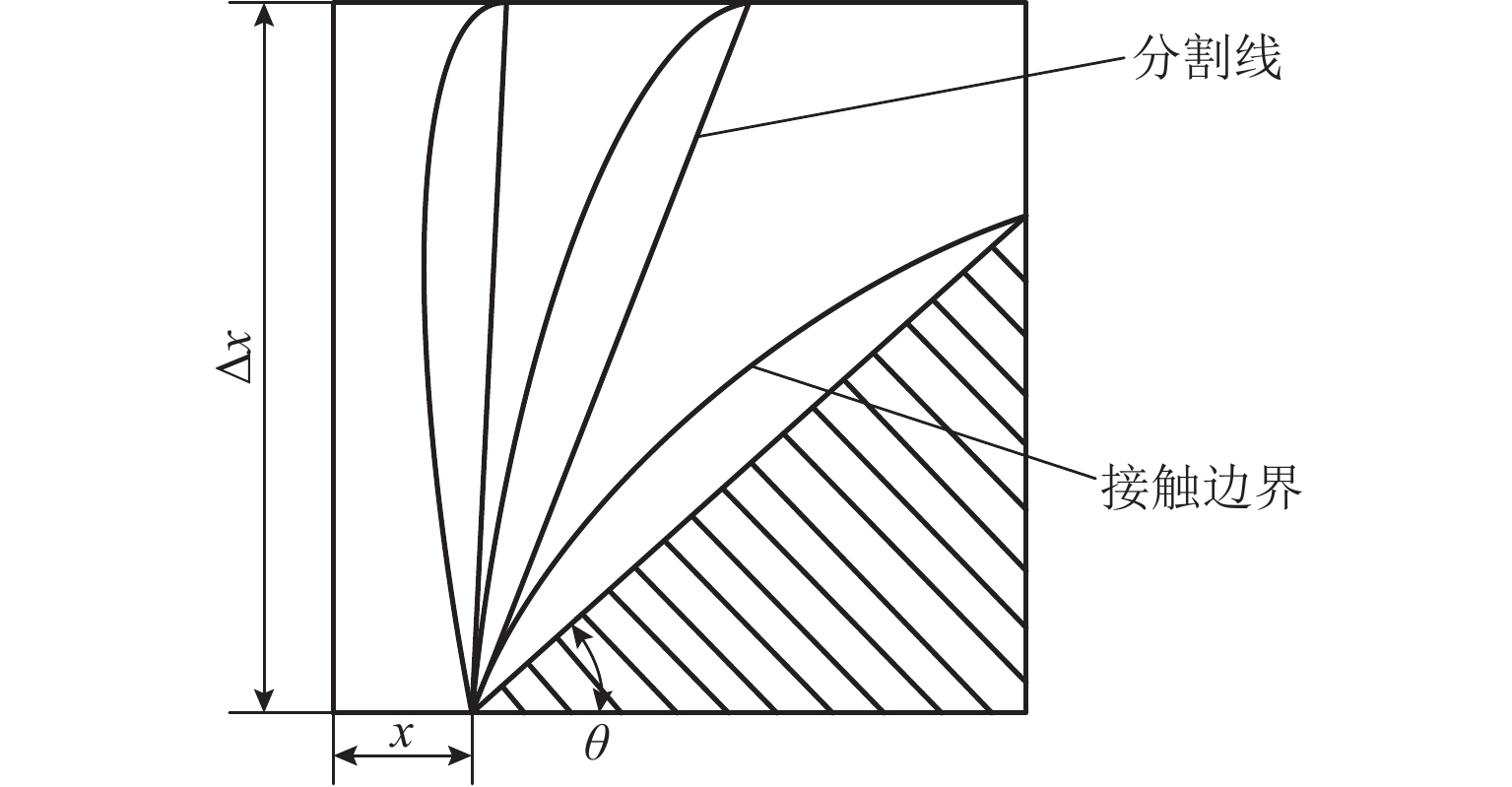
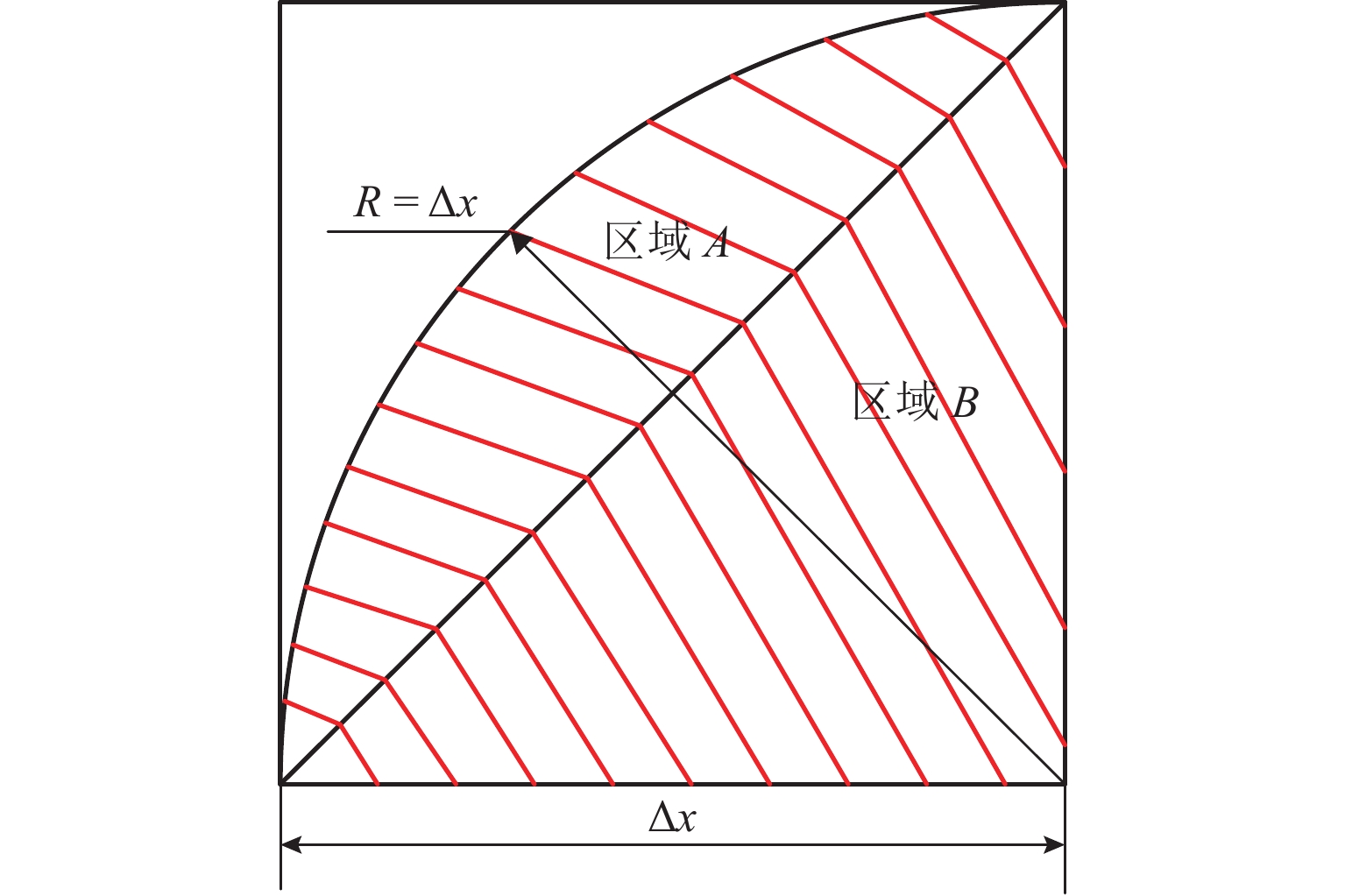
Thermal Characteristics of Steel-BFPC Interface Under Oil Medium
-
摘要:
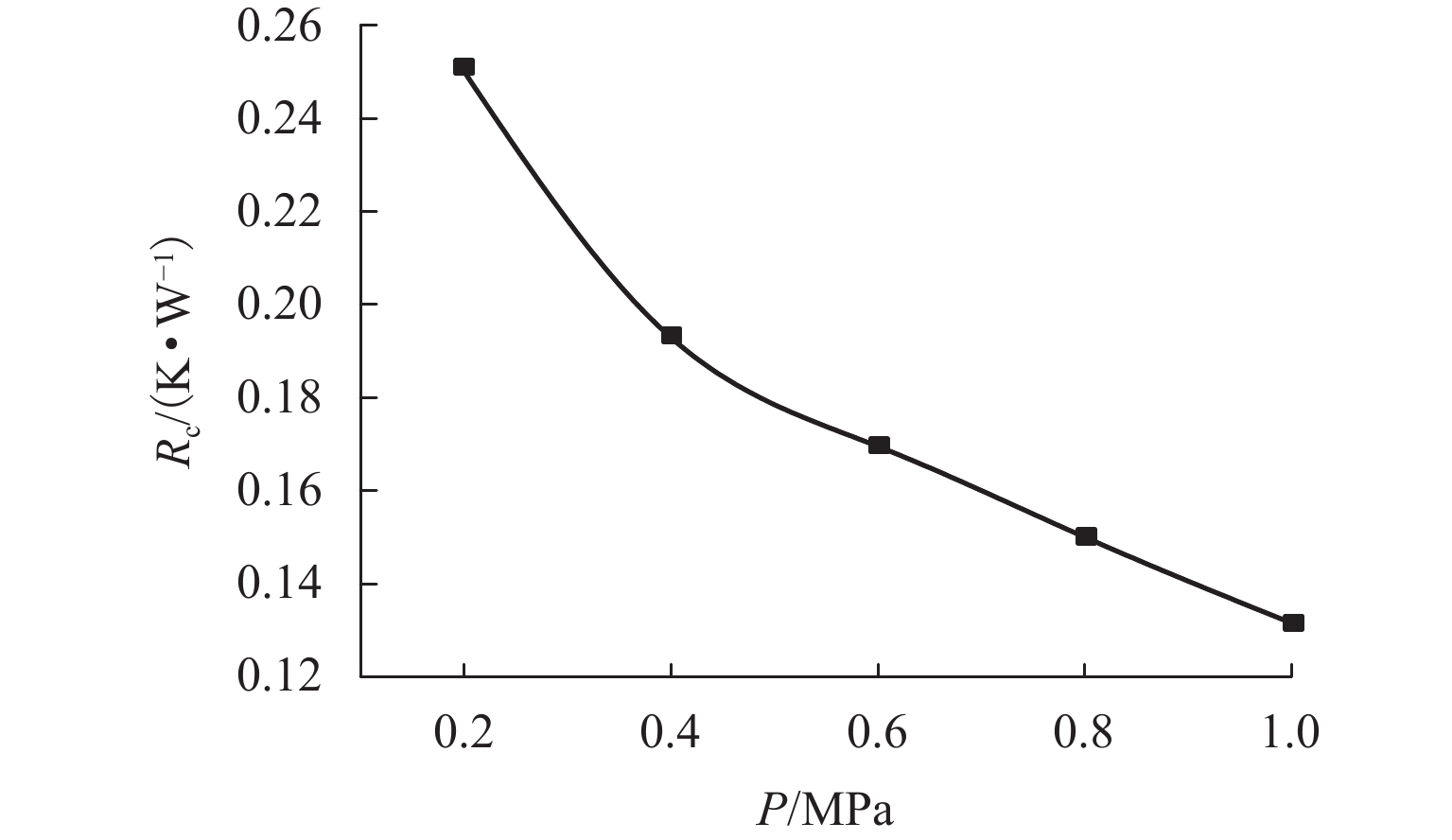
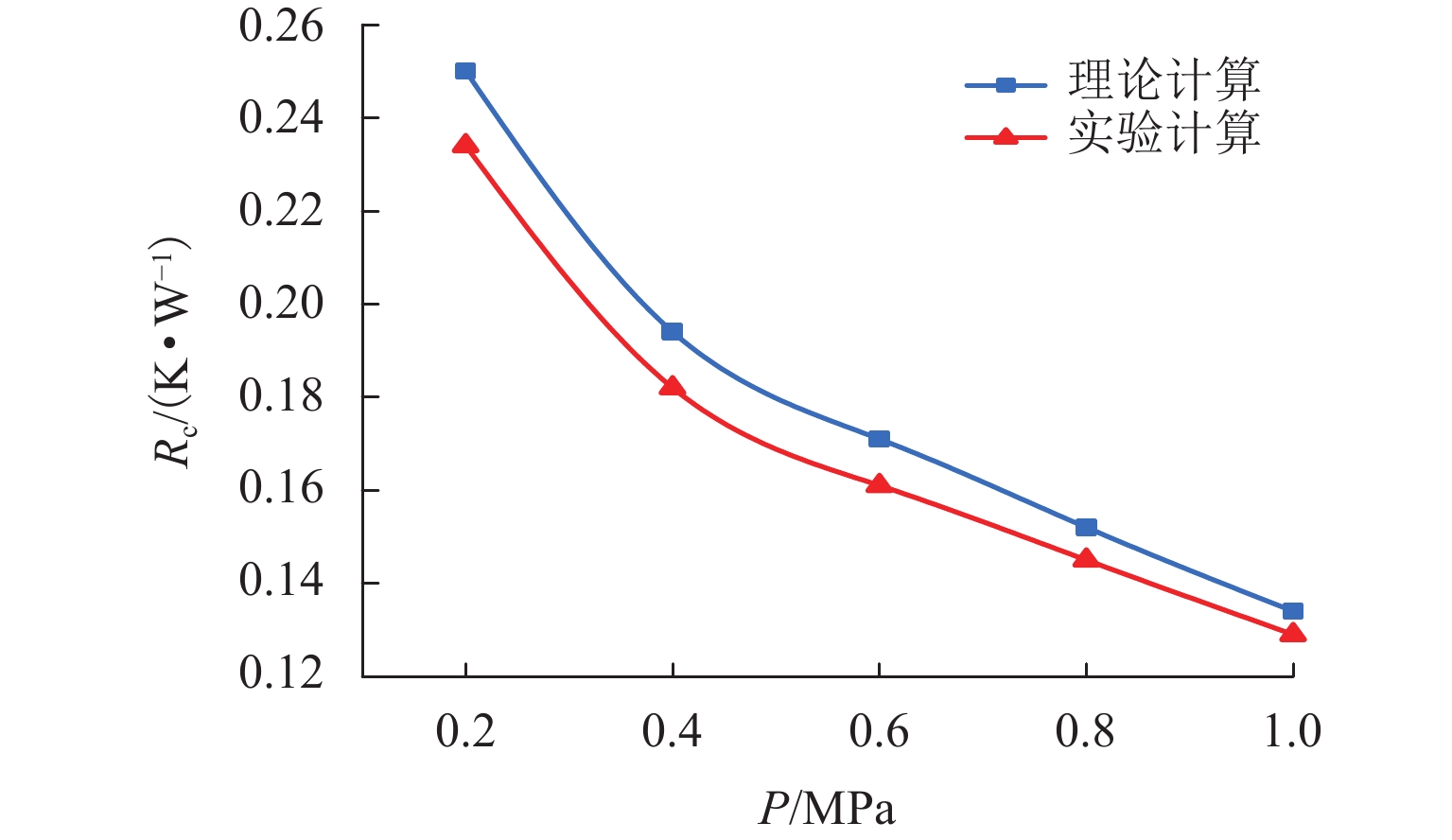
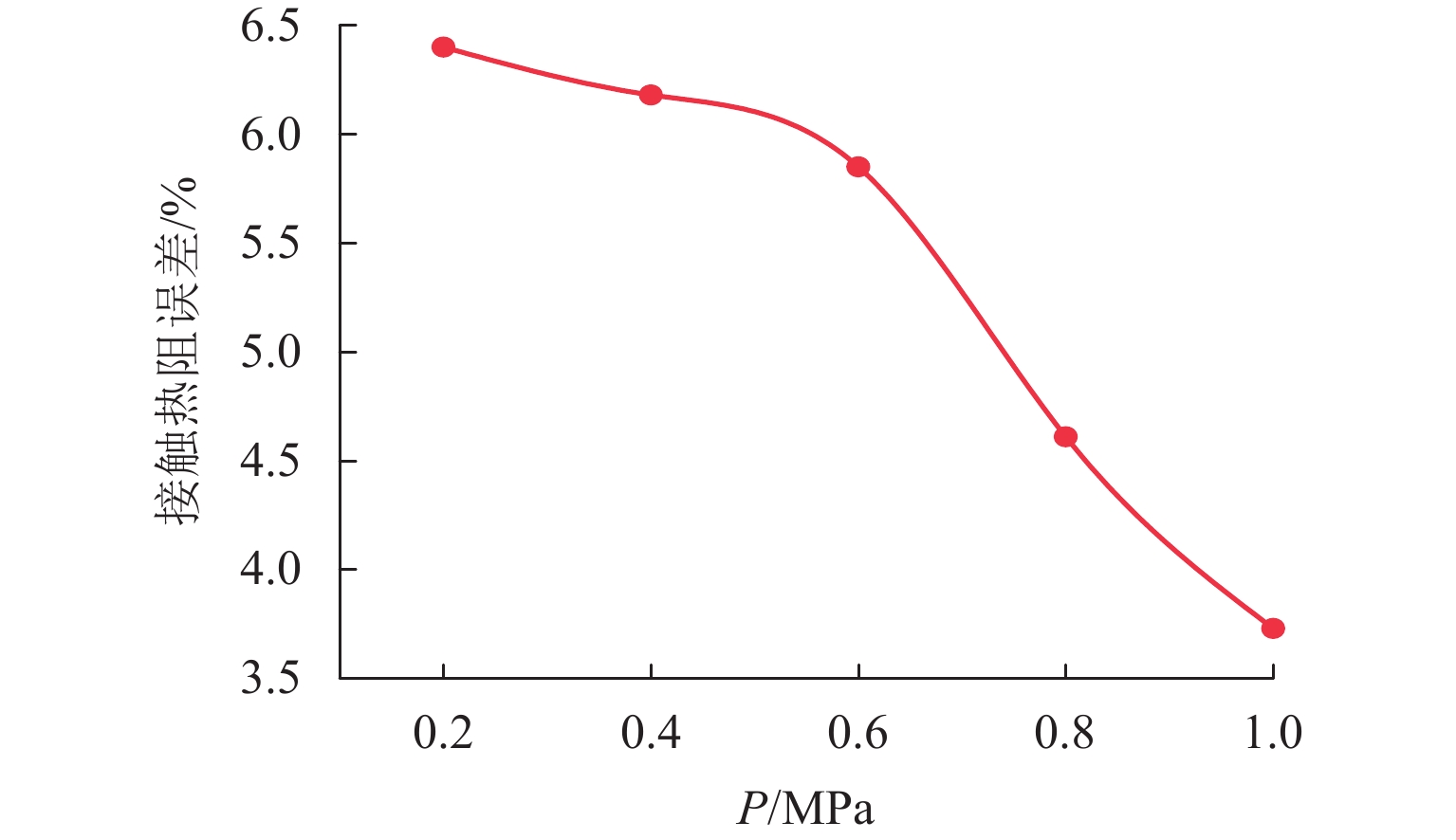
为了研究钢和玄武岩纤维树脂混凝土（BFPC）组成的结合面在油介质条件下的热特性，首先，利用离散原理来计算钢-BFPC结合面的实际接触面积，由于结合面接触时本质上是微凸体接触，微凸体会受到挤压形成挤压应力不同的面积区域，故进一步考虑接触比重，提高实际接触面积结果的精确性；然后，根据结合面的形貌特征，结合傅里叶定律分析油介质条件下钢-BFPC结合面的传热机理；最后，分别通过理论计算和实验研究分析不同载荷（0.2、0.4、0.6、0.8、1.0 MPa）对结合面热特性参数的影响. 研究结果表明：接触热阻随着载荷增大而减小，传热系数和导热系数随着载荷增大而增大，不同载荷下，理论计算与实验计算的接触热阻误差分别为6.40%、6.18%、5.85%、4.61%、3.73%，接触热阻的误差随着载荷增大而减小.
Abstract:In order to study the thermal characteristics of the interface composed of steel and basalt fiber polymer concrete (BFPC) under oil medium conditions, the discrete principle was first used to calculate the actual contact area of the steel-BFPC interface. Since the contact surface is essentially a micro convex contact, the micro convex body is subjected to certain extrusion, forming an area with different extrusion stresses. Therefore, the accuracy of the actual contact area was further improved while considering the specific gravity of contact. Then, based on the morphology characteristics of the interface and Fourier’s law, the heat transfer mechanism of the steel-BFPC interface under oil medium conditions was analyzed. Finally, the influence of different loads (0.2, 0.4, 0.6, 0.8, and 1.0 MPa) on the thermal characteristic parameters of the interface was analyzed through theoretical calculation and experimental research. The results show that with the increase in load, the contact thermal resistance decreases, and the heat transfer coefficient and thermal conductivity coefficient increase. Under different loads, the error of contact thermal resistance between theoretical calculation and experimental calculation is 6.40%, 6.18%, 5.85%, 4.61%, and 3.73%, respectively. The error of contact thermal resistance decreases with increasing load.
-
图 4 考虑接触比重的离散单元
Figure 4. Discrete element diagram considering specific gravity of contact
图 7 载荷对结合面接触热阻影响
Figure 7. Influence of load on contact thermal resistance of interface
图 9 理论计算与实验计算的接触热阻结果对比
Figure 9. Comparison of contact thermal resistance results between theoretical calculation and experimental calculation
图 10 理论计算与实验计算的接触热阻误差
Figure 10. Contact thermal resistance error of theoretical calculation and experimental calculation
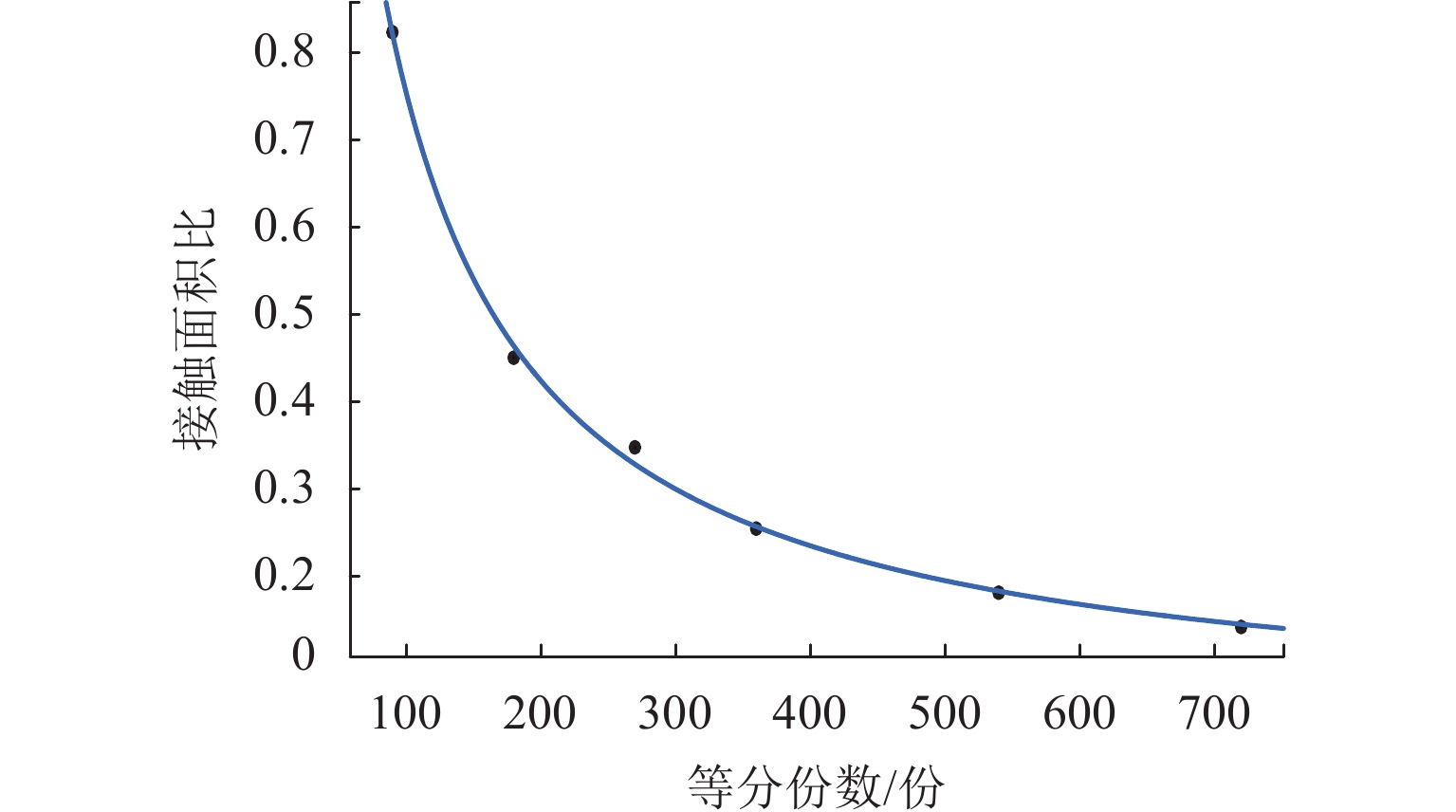
表 1 不同等分份数的计算结果
Table 1. Calculation results for different aliquots
等分
份数/份内接触
单元数/个边界接触
单元数/个接触
面积比90 6236 722 0.8235 180 10726 7427 0.4502 270 15032 17615 0.3474 360 21738 27822 0.2542 540 36158 49821 0.1807 720 63545 63358 0.1413 
下载: 导出CSV
表 2 不同载荷下计算得到的热特性参数
Table 2. Thermal characteristic parameters calculated under different loads
载荷P/
MPa单位面积法向刚度/
（N·（m·mm2）−1）传热厚Lc/
μm实际接触面积之比
Ac/A导热系数λc/（W·（m·K）−1） 传热系数hc/（W·（m2·K）−1） 接触热阻Rc/
(K·W−1)0.2 7769.34 1474.26 0.0502 0.262 177.716 0.250 0.4 13093.29 1469.49 0.0767 0.337 229.331 0.194 0.6 17326.02 1465.37 0.0918 0.380 259.320 0.171 0.8 21029.01 1461.96 0.1103 0.427 292.398 0.152 1.0 23105.36 1456.72 0.1349 0.483 331.675 0.134
下载: 导出CSV
表 3 不同载荷下实验计算得到的结合面热特性参数
Table 3. Thermal characteristic parameters of interface calculated by experiments under different loads
载荷P/MPa T1/
℃T2/
℃温差ΔT/
℃导热系数
λc/（W·（m·K）−1）传热系数
hc/（W·（m2·K）−1）接触热阻
Rc/（K·W−1）接触热阻
误差/%0.2 114.5 82.3 32.2 0.281 189.933 0.234 6.40 0.4 115.3 85.2 30.1 0.359 244.204 0.182 6.18 0.6 115.7 85.4 29.3 0.405 276.052 0.161 5.85 0.8 114.9 86.2 28.7 0.448 306.513 0.145 4.61 1.0 115.6 87.4 28.2 0.487 344.531 0.129 3.73
下载: 导出CSV
-
[1] 于英华,曹茂林,徐平,等. 玄武岩纤维树脂混凝土填充结构机床横梁优化及性能分析[J]. 辽宁工程技术大学学报(自然科学版),2021,40(1): 22-31.YU Yinghua, CAO Maolin, XU Ping, et al. Optimization and performance analysis structure of machine tool beam filled with basalt fiber polymer concrete[J]. Journal of Liaoning Technical University (Natural Science Edition), 2021, 40(1): 22-31. [2] 沈佳兴,徐平,于英华,等. BFPC机床龙门框架组件优化设计及综合性能分析[J]. 机械工程学报,2019,55(9): 127-135. doi: 10.3901/JME.2019.09.127SHEN Jiaxing, XU Ping, YU Yinghua, et al. Optimization design and comprehensive performance analysis of BFPC gantry machine framework components[J]. Journal of Mechanical Engineering, 2019, 55(9): 127-135. doi: 10.3901/JME.2019.09.127 [3] 屈重年,伍良生,马建峰,等. 铁基多孔含油固定结合面法向动态特性研究[J]. 振动与冲击,2013,32(13): 56-61.QU Chongnian, WU Liangsheng, MA Jianfeng, et al. Normal dynamic characteristics of a fixed joint interface with oily Fe-based porous-media[J]. Journal of Vibration and Shock, 2013, 32(13): 56-61. [4] 顾慰兰,杨燕生. 温度对接触热阻的影响[J]. 南京航空航天大学学报,1994,26(3): 342-350.GU Weilan, YANG Yansheng. The influence of temperature on contact resistance of metallic surfaces temperature[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 1994, 26(3): 342-350. [5] 钟明. 接触热阻及双层组合介质温度场的研究[D]. 合肥: 中国科学技术大学, 2001. [6] 许敏. 机床固定结合面动态与热态特性分析[D]. 南京: 东南大学, 2006. [7] ZOU M Q, YU B M, CAI J C, et al. Fractal model for thermal contact conductance[J]. Journal of Heat Transfer, 2008, 130(10): 101301.1-10130.9. [8] 祁宁. 固—固界面接触热阻的实验研究及数据库查询系统的开发[D]. 南京: 南京理工大学, 2014. [9] ABDULLAH M Z, YAU Y C, ZAINAL ALAUDDIN A Z A, et al. Effects of pressure on thermal contact resistance for rough mating surfaces[J]. ASEAN Journal on Science and Technology for Development, 2017, 18(2): 29-35. [10] 袁超. 热界面材料热阻模型和导热强化研究[D]. 武汉: 华中科技大学, 2017. [11] 王佳. 机床固定结合面接触热阻的研究[D]. 天津: 天津大学, 2018. [12] 李俊南,张锁怀,吕超颖,等. 分布式拉杆转子轮盘结合面接触热阻建模与分析[J]. 汽轮机技术,2018,60(4): 267-270,302.LI Junnan, ZHANG Suohuai, LV Chaoying, et al. Modeling and analysis of thermal contact resistance on joint interfaces of distributed rod fastening rotor[J]. Turbine Technology, 2018, 60(4): 267-270,302. [13] 田小龙,王雯,傅卫平,等. 考虑微凸体相互作用的机械结合面接触刚度模型[J]. 机械工程学报,2017,53(17): 149-159. doi: 10.3901/JME.2017.17.149TIAN Xiaolong, WANG Wen, FU Weiping, et al. Contact stiffness model of mechanical joint surfaces considering the asperity interactions[J]. Journal of Mechanical Engineering, 2017, 53(17): 149-159. doi: 10.3901/JME.2017.17.149 [14] YASTREBOV V A, ANCIAUX G, MOLINARI J F. On the accurate computation of the true contact-area in mechanical contact of random rough surfaces[J]. Tribology International, 2017, 114(4): 161-171. [15] XU M, JIANG S Y, CAI Y. An improved thermal model for machine tool bearings[J]. International Journal of Machine Tools and Manufacture, 2007, 47(1): 53-62. doi: 10.1016/j.ijmachtools.2006.02.018 [16] HOLMAN J P. Heat transfer[M]. 9 ed. [S.l.]: McGraw-Hill, 2002: 53-55. [17] FENECH H, ROHSENOW W. Prediction of thermal conductance of metallic surfaces in contact[J]. Journal of Heat Transfer, 1963, 85(1): 15-24. doi: 10.1115/1.3686003 [18] 张学良,范世荣,温淑花,等. 基于等效横观各向同性虚拟材料的固定结合部建模方法[J]. 机械工程学报,2017,53(15): 141-147. doi: 10.3901/JME.2017.15.141ZHANG Xueliang, FAN Shirong, WEN Shuhua, et al. Modeling method of fixed joint interfaces based on equivalent transversely isotropic virtual material[J]. Journal of Mechanical Engineering, 2017, 53(15): 141-147. doi: 10.3901/JME.2017.15.141 [19] 田红亮,刘芙蓉,方子帆,等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报,2013,26(4): 561-573.TIAN Hongliang, LIU Furong, FANG Zifan, et al. Immovable joint surface’s model using isotropic virtual material[J]. Journal of Vibration Engineering, 2013, 26(4): 561-573. [20] SHEN J X, XU P, YU Y H. Dynamic characteristics analysis and finite element simulation of steel-BFPC machine tool joint surface[J]. Journal of Manufacturing Science and Engineering, 2019, 142(1): 1-14. [21] 徐平,曹泉,于英华,等. BFPC固定结合面虚拟材料参数识别[J]. 机械科学与技术,2021,40(8): 1305-1312.XU Ping, CAO Quan, YU Yinghua, et al. Parameter identification of virtual material in fixed joint interface of BFPC[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(8): 1305-1312. [22] 龚钊,杨春信. 接触热阻理论模型的简化[J]. 工程热物理学报,2007,28(5): 850-852.GONG Zhao, YANG Chunxin. The simplification of the thermal contact conductance model[J]. Journal of Engineering Thermophysics, 2007, 28(5): 850-852. -
下载:
点击查看大图
计量
- 文章访问数: 191
- HTML全文浏览量: 85
- PDF下载量: 8
- 被引次数: 0