考虑整体效应的盒状压型钢板受弯性能试验研究

李永振; 曾晗; 刘豪; 潘毅

doi:10.3969/j.issn.0258-2724.20210670

考虑整体效应的盒状压型钢板受弯性能试验研究

doi: 10.3969/j.issn.0258-2724.20210670

李永振^1,,
曾晗²,
刘豪²,
潘毅^{1, 2, ,}

1.
成都大学建筑与土木工程学院，四川成都 610106
2.
西南交通大学土木工程学院，四川成都 610031

基金项目: 四川省自然科学基金（2022NSFSC0423）；成都大学科研启动项目经费（2081921008）

详细信息

作者简介:
李永振（1984—），男，副研究员，博士，研究方向为钢结构及组合结构，E-mail：liyongzhen@cdu.edu.cn

通讯作者:
潘毅（1977—），男，教授，博士，博士生导师，研究方向为结构工程抗震与加固，E-mail：panyi@swjtu.edu.cn，

中图分类号: TU392.4；TU317
计量
- 文章访问数: 303
- HTML全文浏览量: 95
- PDF下载量: 32
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-16
- 修回日期: 2021-12-29
- 网络出版日期: 2023-03-20
- 刊出日期: 2022-03-28

Experimental Study on Flexural Behavior of Box-Shape Profiled Steel Sheet Integrating with System Effect

LI Yongzhen^1
,,
ZENG Han²,
LIU Hao²,
PAN Yi^{1, 2
, ,}

1.
School of Architecture and Civil Engineering, Chengdu University, Chengdu 610106, China
2.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
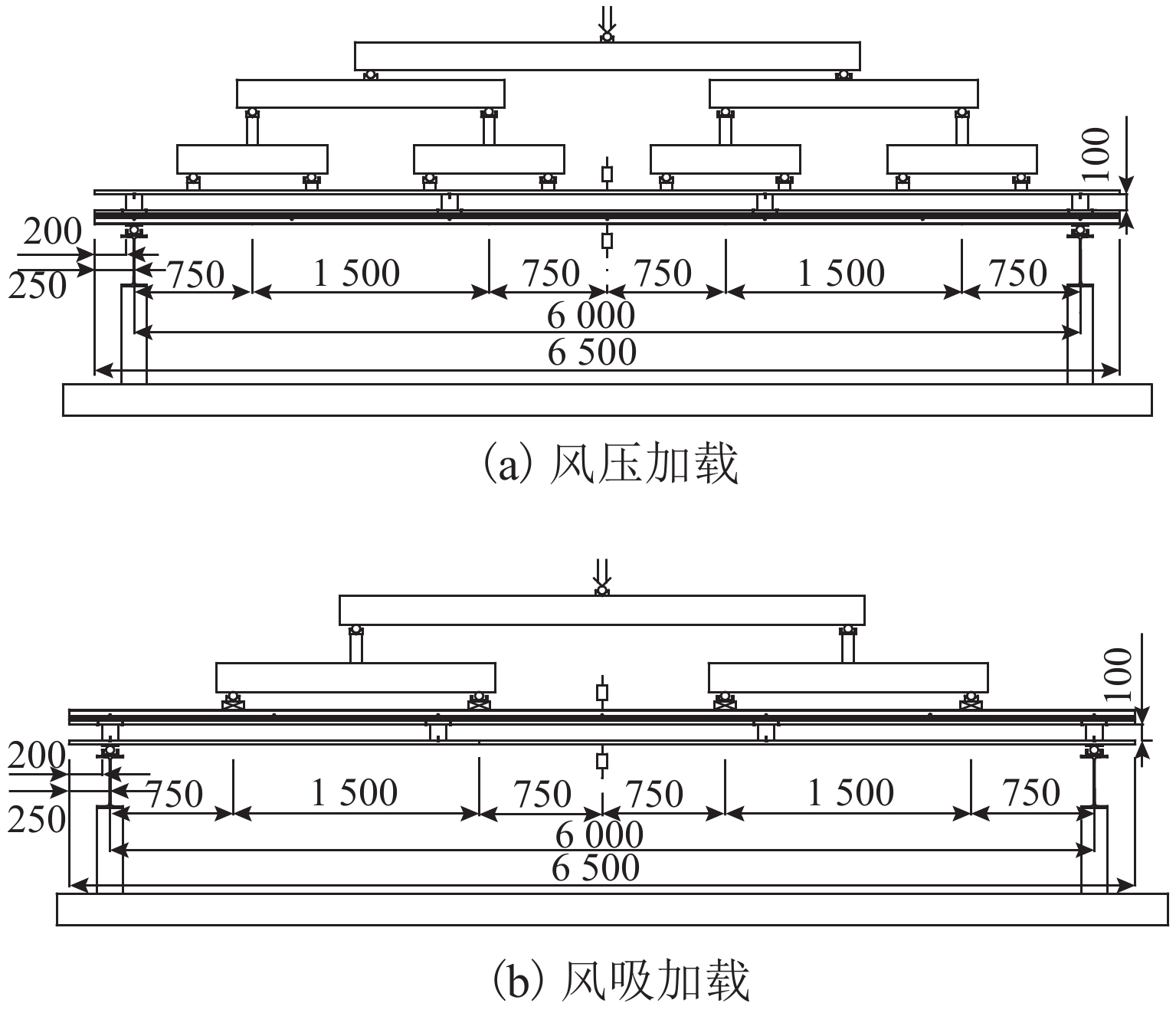
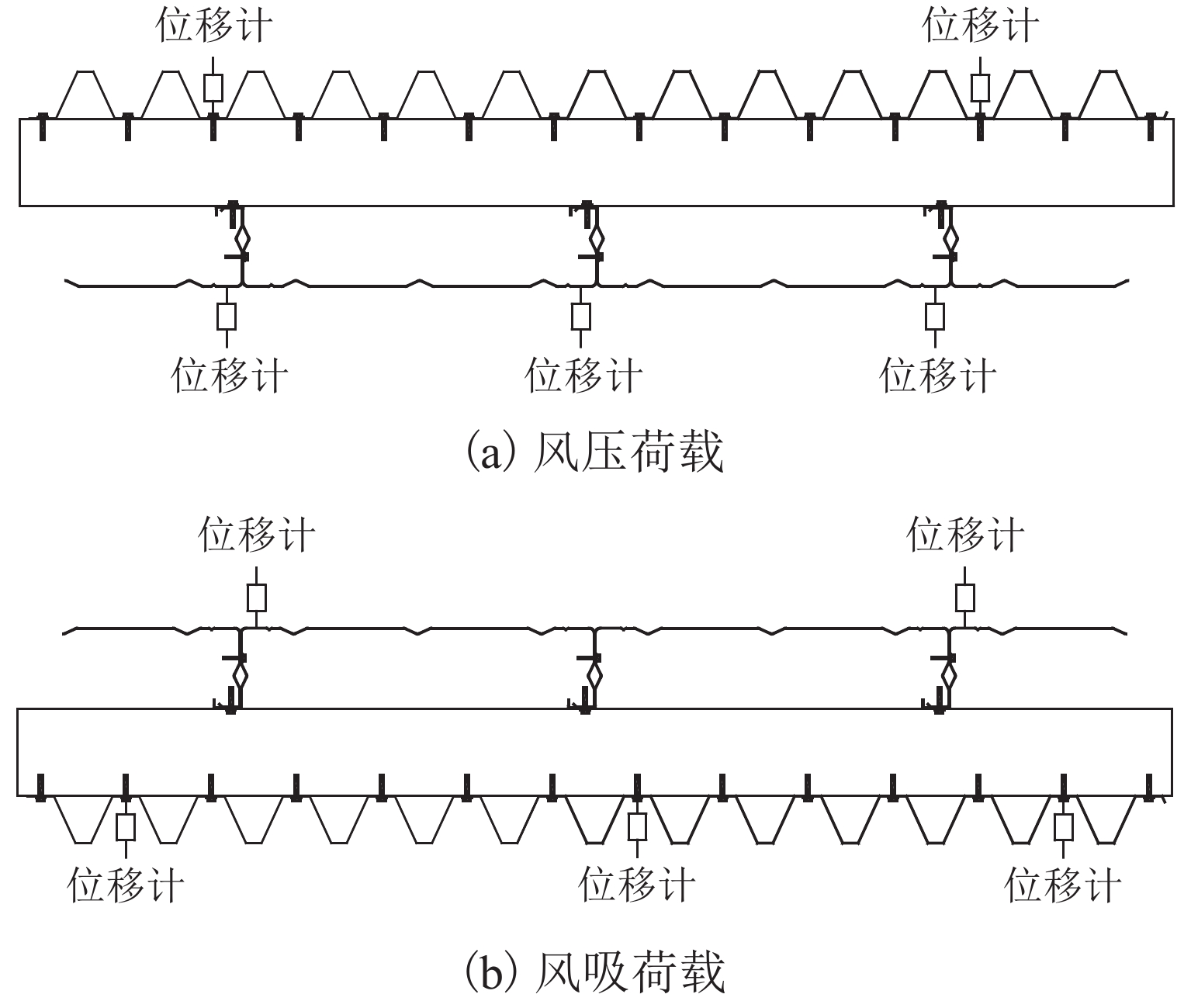
为研究外层钢板及衬檩对盒状压型钢板受弯性能的影响，考虑风压和风吸两种荷载，对8个双层压型钢板的组合试件和2个盒状压型钢板的标准试件进行了受弯加载试验，分析了外层钢板刚度、衬檩高度对盒状压型钢板的受弯承载力、受弯刚度的影响. 试验结果表明：1）当衬檩高度为100 mm时，外层钢板为Ⅰ型和Ⅱ型的组合试件相对于标准试件，在风压荷载下的受弯承载力分别提高27.6%和111.3%，受弯刚度提高17.3%和56.7%；在风吸荷载下的受弯承载力分别提高32.1%和77.6%，受弯刚度提高29.4%和48.1%. 2）当外层钢板为Ⅱ型时，衬檩高度为200 mm和100 mm的组合试件相对于标准试件，在风压荷载下的受弯承载力分别提高66.9%和111.3%，受弯刚度提高39.9%和56.7%；在风吸荷载下的受弯承载力分别提高59.1%和77.6%，受弯刚度提高33.5%和48.1%. 3）考虑外层钢板及衬檩的整体效应可提高盒状压型钢板的受弯承载力和受弯刚度，且外层钢板的刚度越大，衬檩高度越低，提高幅度越明显. 4）提出的考虑整体效应的盒状压型钢板受弯计算式其计算结果与试验结果吻合良好.
- 盒状压型钢板 /
- 整体效应 /
- 受弯承载力 /
- 受弯刚度 /
- 双层压型钢板
Abstract:
Box-shape profiled steel sheet is usually used as the bearing element, with external claddings and spacers together, they constitute a double-layer profiled steel sheet wall system. In order to study the influence of external cladding and spacers on the flexural behavior of box-shape profiled steel sheet, 8 double-layer profiled steel sheet composite specimens and 2 box-shape profiled steel sheet standard specimens were tested for both pressure and suction loading conditions. The influences of the stiffness of external cladding and the height of spacers on the bending capacity and flexural stiffness of the double-layer profiled steel sheet were analyzed. The test results showed that when the spacer height is 100 mm, compared with the standard specimen, the bending capacity can be increased by 27.6% and 111.3%, and the flexural stiffness by 17.3% and 56.7% for the composite specimens with external cladding type I and Ⅱ, respectively, under wind pressure loading condition; and the bending capacity can be increased by 32.1% and 77.6%, and the flexural stiffness can be increased by 29.4% and 48.1% respectively for wind suction case. When the external cladding is type Ⅱ, compared with the standard specimen, the bending capacity can be increased by 66.9% and 111.3%, and the flexural stiffness by 39.9% and 56.7% for the composite specimens with spacer height 200 mm and 100 mm, respectively, under wind pressure loading condition; and the bending capacity can be increased by 59.1% and 77.6%, and the flexural stiffness can be increased by 33.5% and 48.1% respectively for wind suction case. Thus considering the system effect of the external cladding and spacers, the bending capacity and flexural stiffness of the inner box-shape profiled steel sheet can be significantly improved, and greater stiffness of the external cladding can bring better performance. Based on theoretical analysis and Eurocode, combining with the influence of the stiffness of external cladding and the height of spacers, the global design formula of the box-shape profiled steel sheet is proposed, including system effect. The analytical results obtained using this formula coincide well with the experimental ones.
- box-shape profiled steel sheet /
- system effect /
- bending capacity /
- flexural stiffness /
- double-layer profiled steel sheet

HTML全文

图 1 截面几何信息

Figure 1. Geometrical dimensions of cross-sections

下载: 全尺寸图片幻灯片

图 2 试验加载装置

Figure 2. Test loading equipment

下载: 全尺寸图片幻灯片

图 3 模拟风荷载的加载方案

Figure 3. Loading scheme for simulated wind pressure and suction

下载: 全尺寸图片幻灯片

图 4 位移计布置

Figure 4. Disposition of displacement meters

下载: 全尺寸图片幻灯片

图 5 盒状压型钢板的试验现象

Figure 5. Experimental phenomena of box-shape profiled steel sheet

下载: 全尺寸图片幻灯片

图 6 盒状压型钢板的破坏特征

Figure 6. Failure modes of box-shape profiled steel sheet

下载: 全尺寸图片幻灯片

图 7 试件荷载-挠度曲线

Figure 7. Load-displacement curves of specimens

下载: 全尺寸图片幻灯片

图 8 不同外层钢板的荷载-挠度曲线

Figure 8. Load-displacement curves of specimens with different external claddings

下载: 全尺寸图片幻灯片

图 9 不同衬檩高度的荷载-挠度曲线

Figure 9. Load-displacement curves of specimens with different spacer heights

下载: 全尺寸图片幻灯片

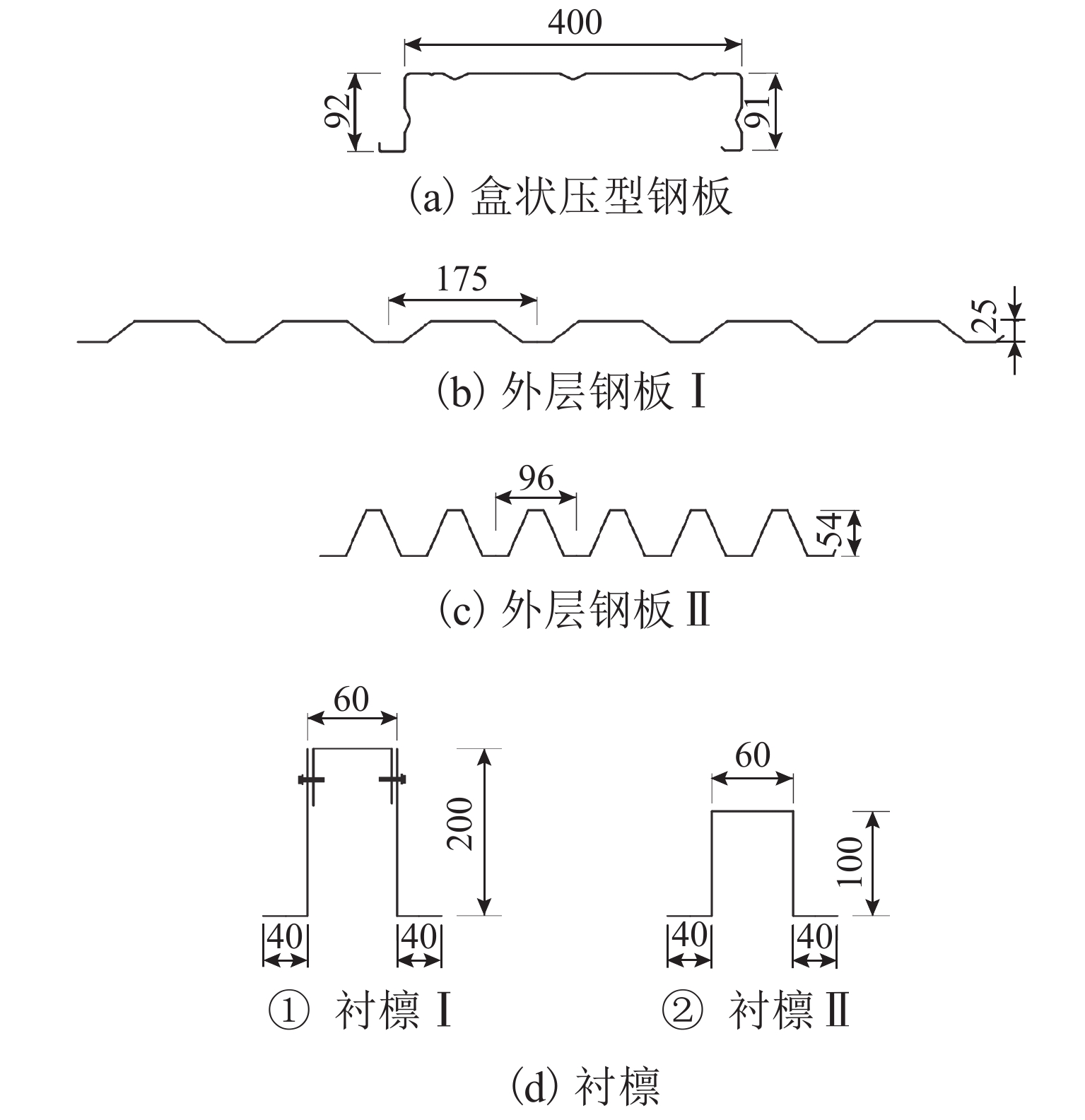
表 1 试件参数

Table 1. Parameters of specimens

编号	工况	组成
TS1	风压	盒状压型钢板
TS2		盒状压型钢板+衬檩Ⅰ+外层钢板Ⅰ
TS3		盒状压型钢板+衬檩Ⅱ+外层钢板Ⅰ
TS4		盒状压型钢板+衬檩Ⅰ+外层钢板Ⅱ
TS5		盒状压型钢板+衬檩Ⅱ+外层钢板Ⅱ
TS6	风吸	盒状压型钢板
TS7		盒状压型钢板+衬檩Ⅰ+外层钢板Ⅰ
TS8		盒状压型钢板+衬檩Ⅱ+外层钢板Ⅰ
TS9		盒状压型钢板+衬檩Ⅰ+外层钢板Ⅱ
TS10		盒状压型钢板+衬檩Ⅱ+外层钢板Ⅱ

下载: 导出CSV

表 2 钢材材性参数

Table 2. Mechanical properties of steel

构件类型	钢板厚度 t/mm	ε_y/× 10⁻⁶	σ_y/MPa	σ_u/MPa
盒状压型钢板	0.707	1825	377	418
衬檩Ⅰ	1.465	1768	365	432
衬檩Ⅱ	1.454	1739	359	427
外层钢板Ⅰ	0.691	1744	360	405
外层钢板Ⅱ	0.693	1758	363	395

下载: 导出CSV

表 3 正常使用状态下荷载极值、承载力极值和最大挠度值

Table 3. Maximum SLS (serviceability limit state) load, ULS (ultimate limit state) load and maximum deflection

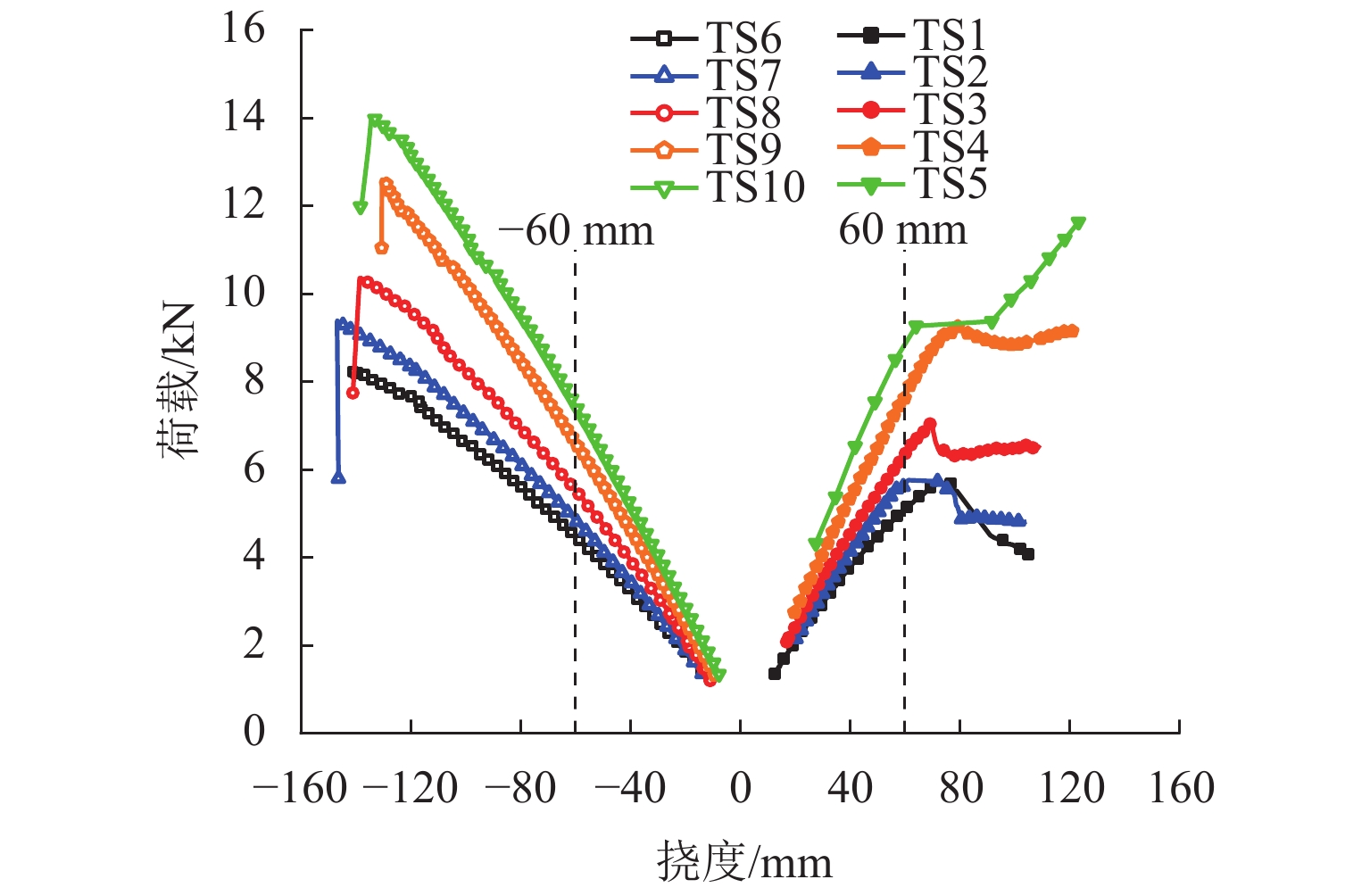
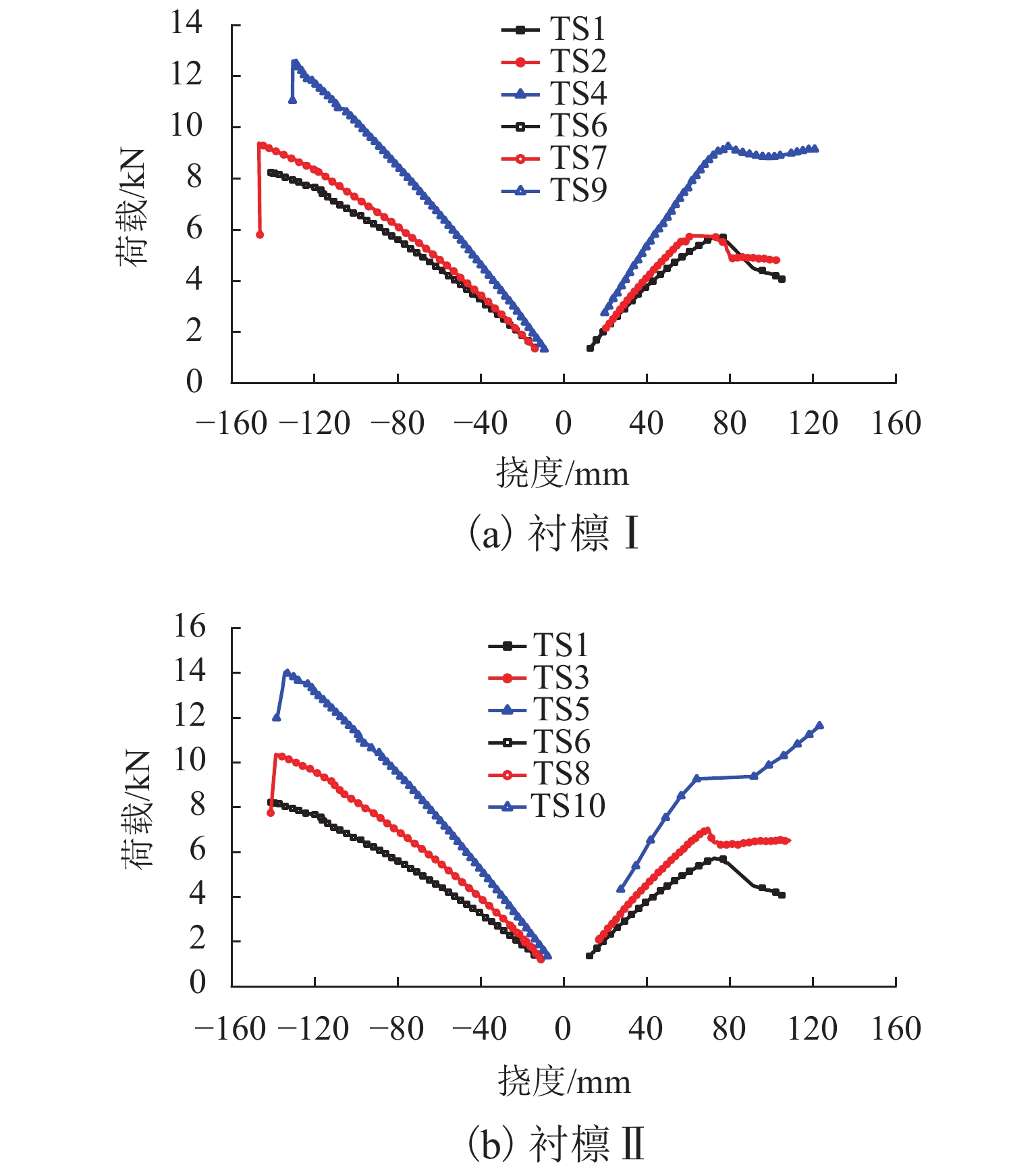
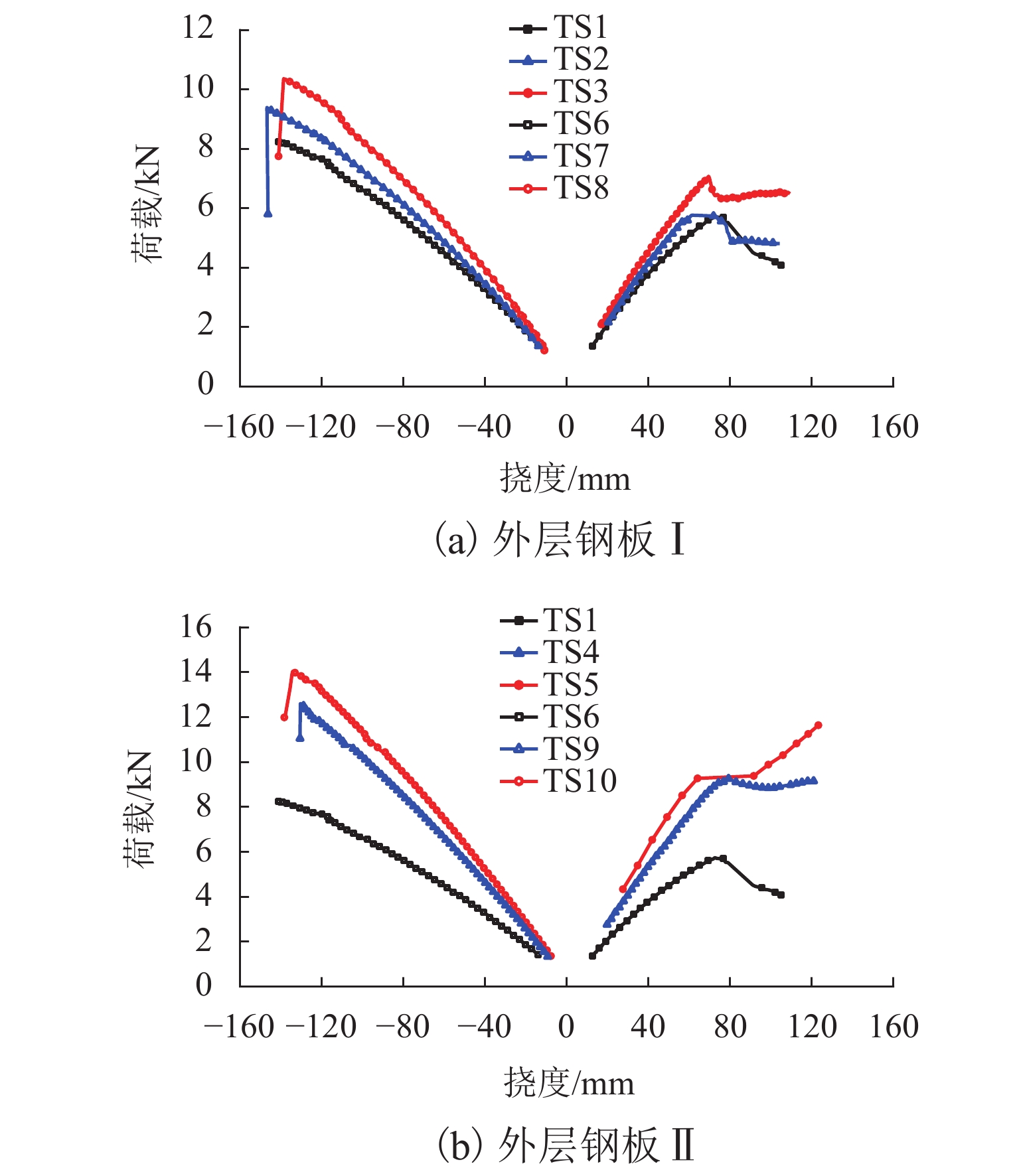
试件编号	F_SLS/kN	F_max/kN	ω_max/mm
TS1	5.07	5.72	72.7
TS2	5.66	5.76	61.3
TS3	6.34	7.06	69.5
TS4	7.62	9.25	79.3
TS5	8.88	11.63	123.3
TS6	4.51	8.23	140.7
TS7	4.85	9.38	146.7
TS8	5.53	10.36	138.5
TS9	6.62	12.59	130.4
TS10	7.46	14.03	134.2

下载: 导出CSV

表 4 组合试件与标准试件受弯性能的比较

Table 4. Comparison of flexural behavior between the composite specimens and the standard ones

试件编号	M /（kN·m）	Δ₁/%	I /cm⁴	Δ₂/%
TS1	3.62	0	116.6	0
TS2	3.89	7.5	111.8	2.3
TS3	4.62	27.6	136.7	17.3
TS4	6.04	66.9	163.1	39.9
TS5	7.65	111.3	182.6	56.7
TS6	4.91	0	100.4	0
TS7	5.96	21.2	105.4	5.0
TS8	6.49	32.1	129.9	29.4
TS9	7.82	59.1	134.1	33.5
TS10	8.73	77.6	148.7	48.1

下载: 导出CSV

表 5 标准试件受弯性能试验值与欧洲规范值的比较

Table 5. Comparison of flexural performance （test vs Eurocode）

工况	M_test/ （kN·m）	M_EC/ （kN·m）	I_test/cm⁴	I_EC/cm⁴
风压（TS1）	3.62	2.13	116.6	121.2
风吸（TS6）	4.91	2.61	100.4	95.6

下载: 导出CSV

表 6 本文公式计算值、欧洲规范值与试验值比较

Table 6. Comparison of global design formula, Eurocode and experimental values

试件编号	M_test/（kN·m）	M_GDA/（kN·m）	M_GDA/M_test	M_EC/M_test	I_test/cm⁴	I_GDA/cm⁴	I_GDA/I_test	I_EC/I_test
TS1	3.62	2.66	0.73	0.59	116.6	121.2	1.04	1.04
TS2	3.89	3.23	0.83	0.55	111.8	124.2	1.04	1.02
TS3	4.62	3.52	0.76	0.46	136.7	127.2	0.93	0.89
TS4	6.04	5.12	0.85	0.35	163.1	143.3	0.88	0.74
TS5	7.65	6.36	0.83	0.28	182.6	165.4	0.91	0.66
TS6	4.91	3.27	0.67	0.53	100.4	95.6	0.95	0.95
TS8	5.96	4.00	0.67	0.44	105.4	97.9	0.93	0.91
TS7	6.49	4.36	0.67	0.40	129.9	100.3	0.77	0.74
TS9	7.82	5.69	0.73	0.33	134.1	113.0	0.84	0.71
TS10	8.73	6.89	0.79	0.30	148.7	130.4	0.88	0.64
平均值			0.753	0.423			0.917	0.830
标准差			0.070	0.109			0.083	0.149
变异系数			0.093	0.258			0.091	0.180

下载: 导出CSV

参考文献(15)

[1]	王戈,马建昌. 压型金属板围护结构的设计与应用[J]. 工业建筑,1994,30(增1): 37-43. doi: 10.3321/j.issn:1000-8993.1994.z1.003 WANG Ge, MA Jianchang. Design and application of profiled metal plate enclosure structure[J]. Industrial Construction, 1994, 30(S1): 37-43. doi: 10.3321/j.issn:1000-8993.1994.z1.003
[2]	肖庆,孙晓勇,杜晶,等. 压型金属板在钢结构冷却塔围护结构中的应用[J]. 钢结构,2017,32(12): 72-75,96. doi: 10.13206/j.gjg201712014 XIAO Qing, SUN Xiaoyong, DU Jing, et al. Application of profiled metal plate in steel cooling tower enclosure structure[J]. Steel Construction, 2017, 32(12): 72-75,96. doi: 10.13206/j.gjg201712014
[3]	中华人民共和国住房和城乡建设部. 压型金属板工程应用技术规范: GB 50896—2013[S]. 北京: 中国计划出版社, 2014.
[4]	葛连福. 新编《压型金属板应用技术规范》若干问题的商榷(1)[J]. 钢结构,2012,27(10): 53-59. GE Lianfu. Discussion on some problems in the newly compiled technical standard for application of profiled metal sheet[J]. Steel Construction, 2012, 27(10): 53-59.
[5]	葛连福. 新编《压型金属板应用技术规范》若干问题的商榷(2)[J]. 钢结构,2012,27(11): 41-47. GE Lianfu. Discussion on some problems in the new technical standard for application of profiled metal sheet (Ⅱ)[J]. Steel Construction, 2012, 27(11): 41-47.
[6]	VOUTAY P A, DAVIES J M. Analysis of cassette sections in compression[C]//Proceedings of International Conference on Advances in Steel Structures. Hongkong: ICASS, 2002: 401-408.
[7]	DAVIES J M, FRAGOS A S. Shear strength of empty and infilled cassettes[J]. Thin-Walled Structures, 2003, 41(2/3): 109-125.
[8]	MICHAEL DAVIES J, ATHANASIOS S F. The local shear buckling of thin-walled cassettes infilled by rigid insulation[J]. Journal of Constructional Steel Research, 2004, 60(3/4/5): 581-599.
[9]	DAVIES J M. Light gauge steel cassette wall construction–theory and practice[J]. Journal of Constructional Steel Research, 2006, 62(11): 1077-1086. doi: 10.1016/j.jcsr.2006.06.028
[10]	李玉顺,张王丽,沈煌莹,等. 复合胶结型压型钢板-竹胶板组合楼板受弯性能试验研究[J]. 建筑结构学报,2009,30(增2): 176-181. doi: 10.14006/j.jzjgxb.2009.s2.032 LI Yushun, ZHANG Wangli, SHEN Huangying, et al. Experimental study on flexural behavior of multiple-interlink profiled steel sheet-bamboo plywood composite slabs[J]. Journal of Building Structures, 2009, 30(S2): 176-181. doi: 10.14006/j.jzjgxb.2009.s2.032
[11]	李玉顺,沈煌莹,张王丽,等. 压型钢板-竹胶板组合墙体抗震性能试验研究[J]. 工程力学,2010,27(增1): 108-112,126. LI Yushun, SHEN Huangying, ZHANG Wangli, et al. Experimental study on aseismic behavior of profiled steel sheet-bamboo plywood composite walls[J]. Engineering Mechanics, 2010, 27(S1): 108-112,126.
[12]	张建伟,刘方方,卡卓乍,等. 钢-压型钢板再生粗骨料混凝土组合梁受弯性能[J]. 哈尔滨工业大学学报,2015,47(12): 86-92. doi: 10.11918/j.issn.0367-6234.2015.12.015 ZHANG Jianwei, LIU Fangfang, KAZOZA Emery, et al. Experimental study on flexural behavior of recycled coarse aggregate concrete composite beams with closed-section steel deck[J]. Journal of Harbin Institute of Technology, 2015, 47(12): 86-92. doi: 10.11918/j.issn.0367-6234.2015.12.015
[13]	张秀华,张义卓,裴骏,等. 压型钢板-稻草板组合楼板力学性能[J]. 建筑材料学报,2018,21(6): 943-949. doi: 10.3969/j.issn.1007-9629.2018.06.014 ZHANG Xiuhua, ZHANG Yizhuo, PEI Jun, et al. Mechanical behavior of profiled steel sheet-strawboard composite slabs[J]. Journal of Building Materials, 2018, 21(6): 943-949. doi: 10.3969/j.issn.1007-9629.2018.06.014
[14]	中华人民共和国住房和城乡建设部. 建筑金属围护系统工程技术标准: JGJ/T 473—2019[S]. 北京: 中国建筑工业出版社, 2019.
[15]	Comité européen de Normalisation. Eurocode 3-Design of steel structures-part 1−3, general rules-supplementary rules for cold-formed members and sheeting: NF P22-313—2007[S]. Brussels: [s.n.], 2007.