Feature Matching Method of Oblique Images Based on Geometric Constraints
-
摘要:
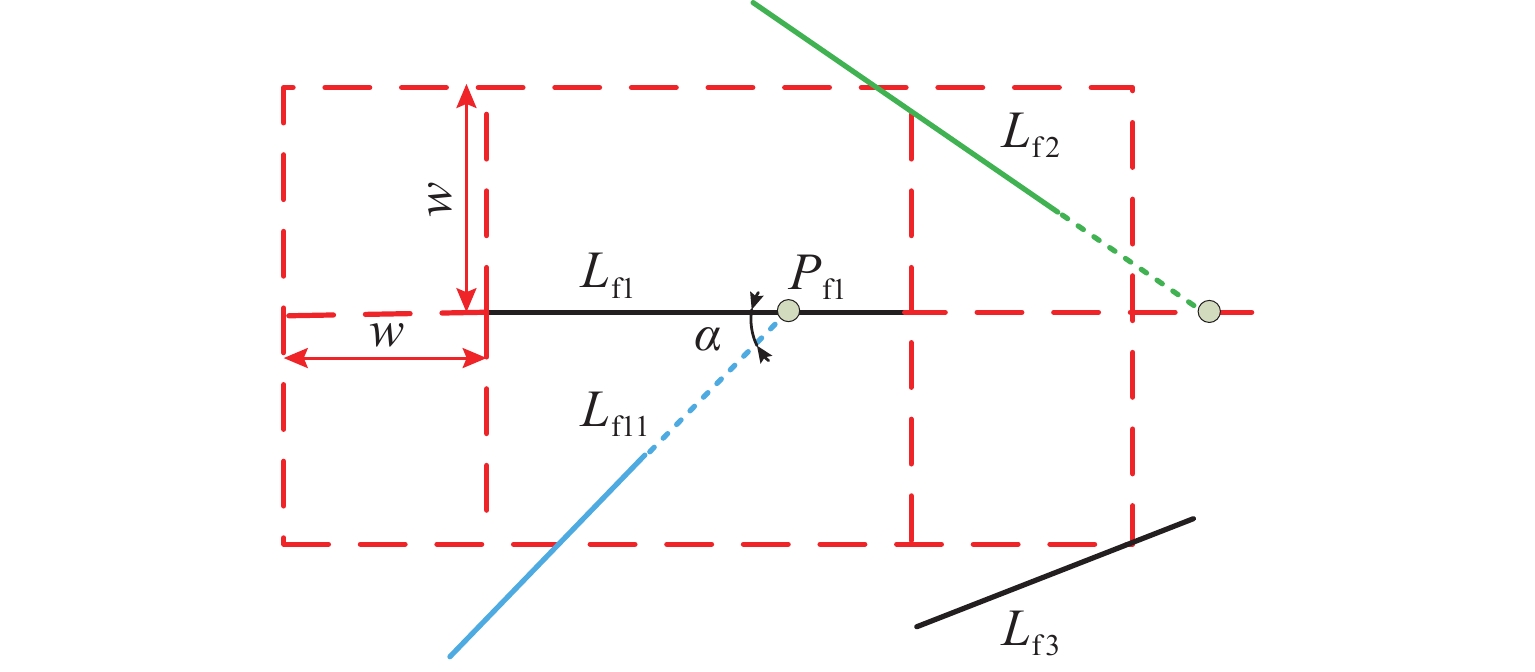
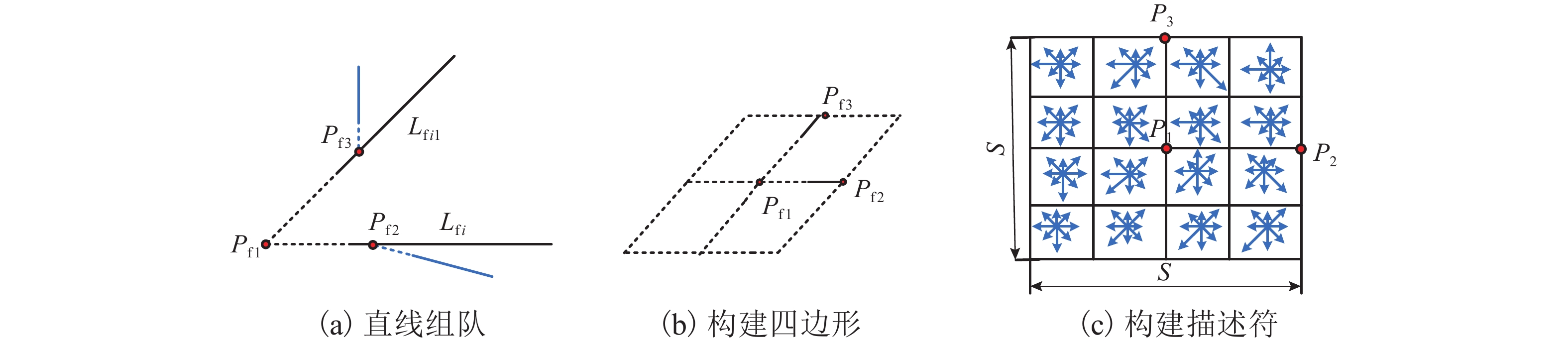
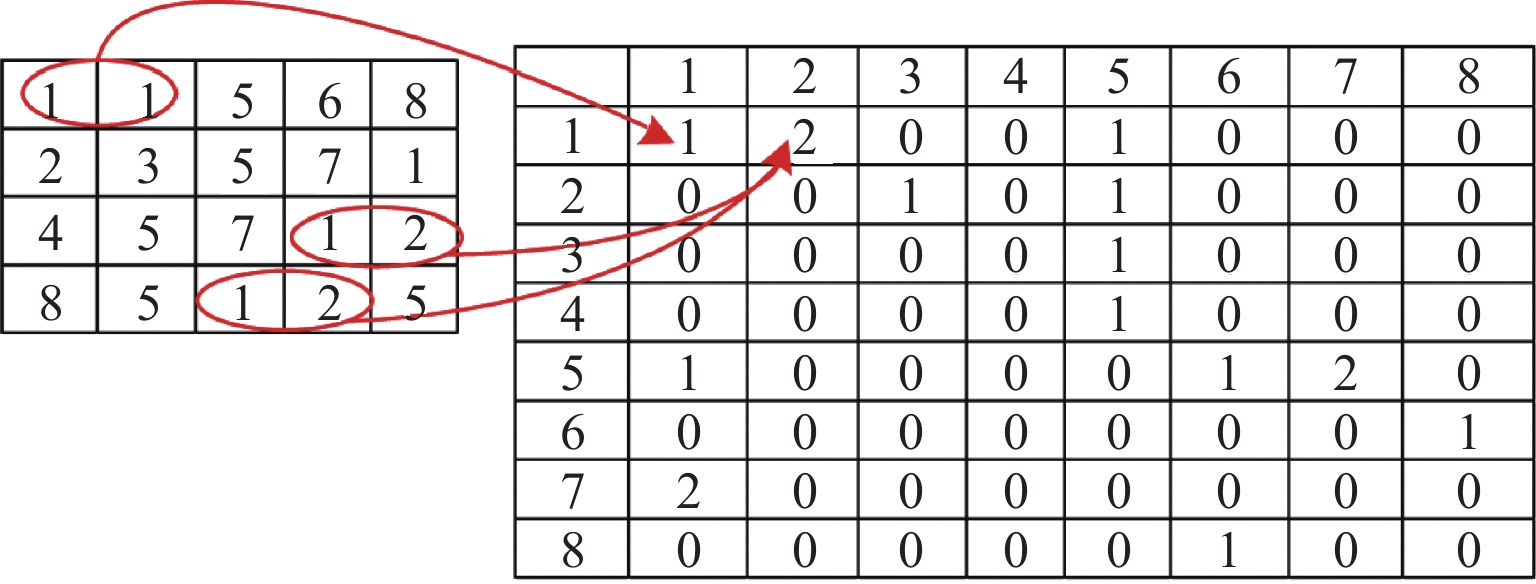
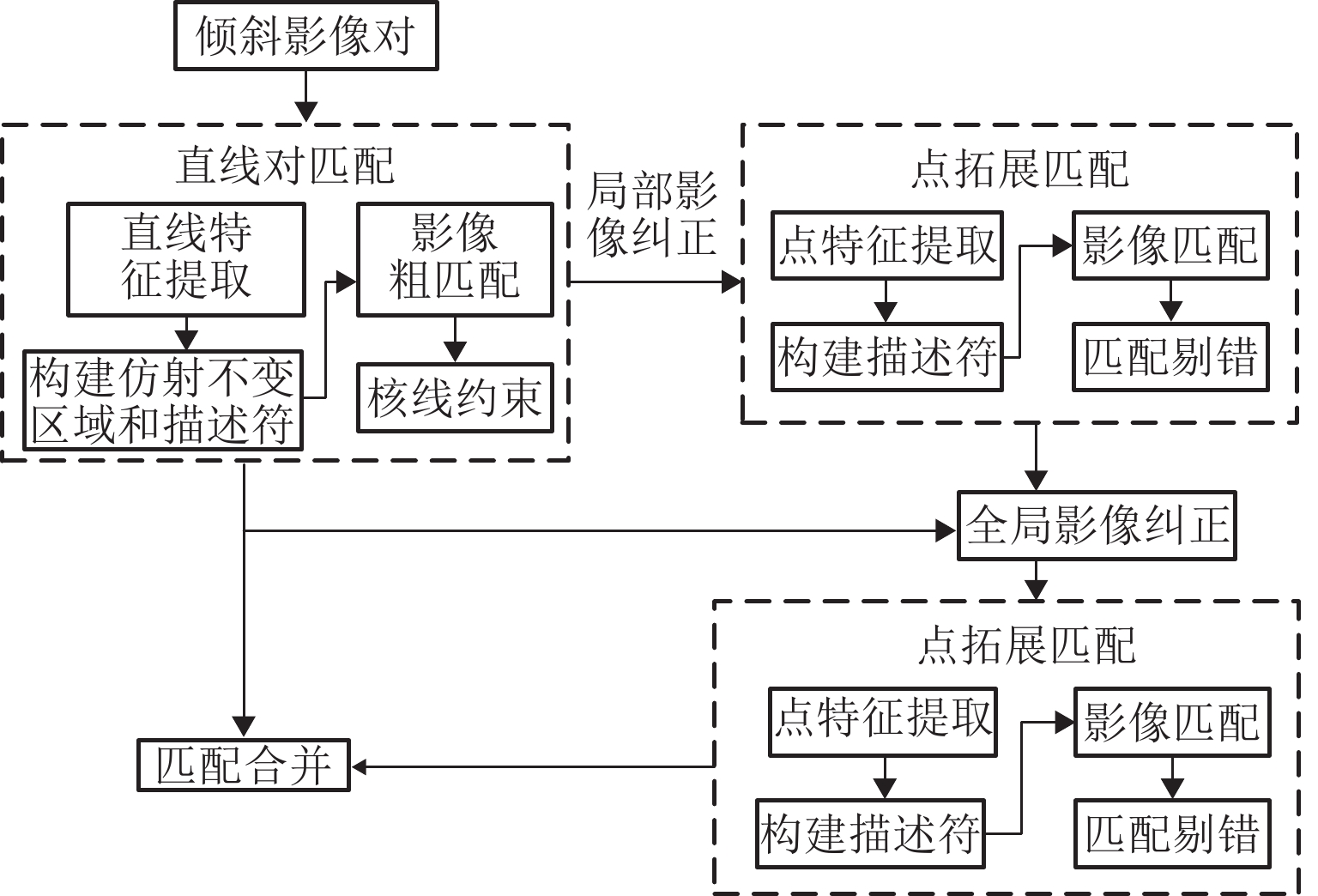
针对倾斜影像视角变换较大、重复纹理导致匹配数量少、匹配精度不高的问题，提出一种适用于倾斜影像的特征点、线分级匹配方法. 首先，用直线提取（检测）算法（LSD）获取影像直线特征，并将直线特征以一定约束进行直线组对，构建直线对区域与改进的SIFT （scale-invariant feature transform）特征描述符进行匹配，使用RANSAC算法剔除误匹配，获得初始匹配结果后再进行核线约束；然后，利用已获得直线对区域进行影像局部纠正，在纠正后的局部影像上采用SIFT匹配并反算回原始影像，利用得到的同名点全局纠正倾斜影像，并进行特征点匹配与采用基于方格的运动统计算法（GMS）剔除误匹配，仍将匹配结果反算回原始影像上；最后，将仿射尺度不变特征变化结果与点拓展匹配结果进行合并，得到最终匹配结果. 试验结果表明：本文方法匹配正确率与经典的仿射不变匹算法（ASIFT）的正确率相差不大，但匹配数量却是ASIFT算法的1倍～3倍.
Abstract:A feature point and line hierarchical matching method is proposed, suitable for oblique images to solve the challenges of large angle in view transformation, a few matches due to repeated texture, and low matching accuracy. Firstly, the line features of images derive from the line extraction (detection) algorithm (LineSegmentDector), follow constraints to pair, and construct line pair regions to match the improved SIFT feature descriptor. Secondly, after RANSAC algorithm eliminates mismatches, the epipolar constraint acts upon the initial matching results. Then, the obtained lines correct the local image, and the corrected local image uses SIFT matching, which contributes to calculating the original image reversely. The obtained matching points are used to globally correct the oblique image, and the feature points are matched; the grid-based motion statistics (GMS) algorithm eliminates the mismatches; the matching results go through reverse calculation and return to the original image. The line matching results and the point expanding matching results combine into final results, showing that the matching accuracy of the proposed method is close to that of ASIFT, but the number of matching is 1-3 times it.
-
Key words:
- oblique image /
- line feature /
- epipolar constraint /
- point expanding matching /
- global correction
-
近年来，振动半主动控制系统在各工程领域受到广泛关注，其能提供接近主动控制装置的减振效果，且能耗低，同时还能提供如同被动装置的可靠性. 在众多半主动控制系统中，磁流变（MR）阻尼器在应用的简单性、可靠性和鲁棒性方面具有显著优势，应用磁流变阻尼器的半主动控制悬架系统受到车辆振动舒适性研究人员的重视.
对磁流变半主动悬架系统的研究内容主要包括磁流变阻尼器动力学建模[1-2]、悬架系统建模及振动传递特性研究[3]、半主动悬架控制系统仿真分析及试验验证[4-5]等. 磁流变阻尼器作为半主动悬架的执行元件，其力学特性分析及正逆模型建立一直是半主动悬架的研究热点问题. MR阻尼器的阻尼力表现出明显的非线性及滞回特性，且具有显著的场强依赖性及激励特性（振幅及频率）依赖性[6]. 阻尼力具有多值特性，不仅取决于阻尼器活塞速度，同时受活塞运动历史状态及控制电流的影响.
用于描述磁流变阻尼力的模型众多，如：包含微分环节的Bouc-Wen模型、Duhem模型、LuGre模型等；包含代数模型的sigmoid模型、双曲正切模型、魔术公式模型等；由非参数模型表示的多项式模型、神经网络模型等[7-9]. 上述模型各自具有准确性、复杂性等方面的优缺点，目前还没有一种通用的应用于半主动悬架的磁流变阻尼器力学模型.
建立准确的控制电流逆模型是使阻尼器产生期望阻尼力的重要基础，传统的逆模型建立方法包括不基于阻尼力正模型的闭环控制逆模型（如阶梯函数逆模型、Sigmoid函数逆模型、状态连续反馈逆模型等）、基于阻尼力正向模型直接逆推的逆动力学模型（如基于Bingham模型、Bouc-Wen模型、魔术公式模型模型等）[10-12]. 基于正向模型直接逆推逆动力学模型的主要难点在于容易产生难以直接计算解析解的超越方程，不可避免地需要对正向模型进行简化处理，影响建模精度. 上述建模方法无法准确描述不同工况下控制电流与阻尼器运动状态及期望阻尼力的关系，因此，基于神经网络及模糊推理系统的逆模型建模方法受到研究者们的关注.
本文在试验获取磁流变阻尼器力学性能的基础上，对磁流变阻尼器正逆动力学模型进行建模及参数识别，并将建立的正逆模型引入半主动座椅悬架控制系统模型中进行分析，对所提出正逆模型的效果进行验证.
1. 磁流变阻尼器建模及参数识别
1.1 磁流变阻尼器滞回分离模型
建立结构简单、拟合精度高且通用的磁流变阻尼器模型是研究磁流变阻尼器力学特性及半主动悬架控制系统的重点和基础. 基于魔术公式的磁流变阻尼器力学模型[13]与Bouc-Wen模型等包含微分方程的模型相比，计算复杂度明显降低，进而能够有效提高模型的参数辨识效率，如式（1）所示.
{Fd=Fk+Fc+Fm+Fb+f,Fk=k(x−x0),Fc=c˙x,Fm=m¨x,Ff=f0sign˙x,Fb=Dsin[Carctan(B˙x−E(B˙x−arctanB˙x))], (1) 式中：
$ {F}_{{\rm{d}}} $ 、$ {F}_{{\rm{k}}} $ 、$ {F}_{{\rm{c}}} $ 、$ {F}_{{\rm{m}}} $ 、$ {F}_{{\rm{f}}} $ 及$ {F}_{{\rm{b}}} $ 分别为模型输出阻尼力、弹性项、黏性项、惯性项、摩擦项及剪切项，该模型滞回特性主要由$ {F}_{{\rm{k}}} $ 及$ {F}_{{\rm{m}}} $ 表征；B、C、D、E为调整$ {F}_{{\rm{b}}} $ 曲线形状的参数，$ B={b}_{1}I + {b}_{2} $ ，$ D={d}_{1}I + {d}_{2} $ ，I为电流，b1、b2、d1、d2为与电流相关的参数;$ x $ 和$ \dot{x} $ 分别为阻尼器活塞位移及速度；$ k $ 、$ c $ 、$ {f}_{0} $ 分别为弹性项、黏性项、摩擦项系数；$ {x}_{0} $ 为弹性项初始位移；f为频率.在建立模型参数与电流的关系中，魔术公式内部参数B包含与电流相关参数，无法直接逆向推导出控制电流与期望力的关系式，对控制电流的计算精度产生影响.
本文在魔术公式模型的基础上，参考于建强等[14-15]建立的基于骨架曲线与滞回分离的建模方法，建立基于正弦、余弦型魔术公式的磁流变阻尼器滞回分离模型,如式（2）. 滞回分离模型建立的原理如图1所示.
{Fd=FmaxFnorm +f0,Fnorm =Fpf+Fhyssignx+c˙x,Fpf=Dpsin[Cparctan(Bp˙x−Ep(Bp˙x−arctanBp˙x))],Fhys=Dhcos[Charctan(Bh˙x−Eh(Bh˙x−arctanBh˙x))], (2) 式中：
$ {F}_{{\rm{max}}} $ 和$ {F}_{{\rm{norm}}} $ 分别为最大阻尼力及归一化后的阻尼力；$ {F}_{{\rm{pf}}} $ 和$ {F}_{{\rm{hys}}} $ 分别对应骨架曲线与滞回分离曲线；Bp、Cp、Dp、Ep及Bh、Ch、Dh、Eh分别为影响Fpf及Fhys曲线形状的参数.1.2 滞回模型参数辨识
本文采用德国SCHENCK公司液压作动器及Lord RD-8040-1磁流变阻尼器（图2），试验工况包括振幅5～20 mm、频率0.5～9.0 Hz的正弦位移激励，阻尼器输入电流为0～1 A.
磁流变减振器力学模型参数识别问题本质上是寻找模型计算结果和减振器实际力学特性误差最小值的数学优化问题，如式（3）所示.
Fobj=min{RMS(Fcalcu−Ftest)}, (3) 式中：
$ {F}_{{\rm{obj}}} $ 、$ {F}_{{\rm{test}}} $ 和$ {F}_{{\rm{calcu}}} $ 分别为目标函数、试验值及模型计算值.为考虑磁流变阻尼力动态力不对称性，通过处理试验数据，得到不同工况下滞回环速度中心，其随电流及激励的变化规律如图3所示. 由图3可知：滞回环速度中心随施加电流增加而逐渐增加；随激励幅值及频率增加均呈现出增加趋势，当频率大于2 Hz时，该趋势更加明显.
因此，可建立滞回环速度中心
$ {\dot{x}}_{{\rm{center}}} $ 与电流及激励特性的关系，如式（4）所示.˙xcenter=(v1I+v2)(v3lnvm+v4), (4) 式中：
$ {v}_{{\rm{m}}}\mathrm{为} $ 最大速度，对于正弦激励信号，${v}_{{\rm{m}}}= 2{\text{π}} Af=\sqrt{{\dot{x}}^{2}-x\ddot{x}}$ ，$\ddot{x} $ 为阻尼器加速度，A 为激励幅值；$ {v}_{1} $ 、$ {v}_{2} $ 、$ {v}_{3} $ 及$ {v}_{4} $ 为拟合公式系数.将阻尼力非对称特性考虑进模型中，式（2）中所有速度项
$ \dot{x} $ 变为$ \dot{x}-{\dot{x}}_{{\rm{center}}} $ .图4为不同激励及电流条件下最大阻尼力变化曲线，本文试验所得阻尼力随施加电流增加而逐渐增加，并未达到完全磁饱和状态. 在相同电流条件下，最大阻尼力均随阻尼器最大活塞速度增加而增加，利用式（5）形式函数可以较准确地描述最大阻尼力和电流及激励特性的关系.
Fmax(I,vm)=(k1I2+k2I+k3)(k4vk5m), (5) 式中：
$ {k}_{1} $ ～$ {k}_{5} $ 为拟合公式系数.为对考虑阻尼力非对称性及最大阻尼力与激励特性及电流变化关系后的模型参数进行辨识，本文采用一种新型的混合优化算法——基于Sobol 序列的差分-禁忌混合算法（SS-DTHA），该算法基于差分进化算法较强的全局搜索能力，引入禁忌搜索增强算法局部搜索能力，并通过调节算法对全局搜索和局部搜索的侧重比例，进一步改进算法的探索和挖掘能力，对解决非线性系统参数辨识问题具有积极作用，如图5所示.
图6为本文提出的改进魔术公式模型与tanh模型及双Sigmod模型计算阻尼力的辨识结果对比（激励工况为15 mm-4.0 Hz-1.0 A）. 由图可知：本文提出的模型在滞回环过渡区及屈服后区域均具有更好的拟合精度；3种模型与试验数据的误差均方根值分别为41.07、96.83、90.26 N.
图 6 不同模型计算值与试验数据对比Figure 6. Comparison of damping forces calculated by different models图7为不同输入电流及激励频率条件下，模型计算阻尼力的辨识结果，并与试验测试值进行对比，图中实线和虚线分别代表试验值及模型计算值. 由图可知，在不同激励频率及电流条件下，本文提出的阻尼力模型均能准确地表征磁流变阻尼器动态阻尼力的非线性及滞回特性.
图 7 不同工况下模型计算值与试验数据对比Figure 7. Comparison of damping forces calculated by the model under different working conditions表1为不同激励幅值、频率及输入电流条件下平均百分比误差
$ {E}_{{\rm{average}}} $ 的计算结果，如式（6）. 可以看出，本文提出的模型在不同工况下均能得到较低的误差，模型精度较高. 各工况平均百分比误差在3.4%附近，误差变化范围为2.7%～4.8%. 模型对试验阻尼力拟合效果较好，满足半主动控制系统建模要求.表 1 不同工况模型平均百分比误差Table 1. Comparison of average percentage error of models under different working conditions电流/A 幅值 5 mm 幅值 15 mm 3 Hz 4 Hz 3 Hz 4 Hz 0 0.0447 0.0355 0.0457 0.0452 0.2 0.0474 0.0355 0.0289 0.0396 0.4 0.0316 0.0321 0.0302 0.0319 0.6 0.0310 0.0322 0.0269 0.0284 0.8 0.0344 0.0349 0.0305 0.0315 1.0 0.0308 0.0359 0.0282 0.0273 Eaverage=RMS(Fcalcu−Ftest)/RMS(Ftest). (6) 为建立适用于阻尼器工作范围的通用模型，通过分析模型各参数的识别结果可以发现：参数Bp、Bh、c随电流及激励特性变化具有明显的规律，其他参数与电流、激励无明显变化关系，设置为常数. 参数Bp、Bh、c随电流及激励特性变化关系如图8所示. 由图可知：参数Bp、Bh随激励频率增加逐渐降低,在相同激励工况下，电流变化对参数Bp、Bh影响不大；参数c随电流变化无明显增降规律，随频率增加而逐渐降低.
图 8 参数Bp、Bh、c随激励及电流的变化规律Figure 8. Variation of parameter Bp，Bh，c with excitation and current conditions上述参数与激励和电流的关系拟合为
{Bp=p1vp2m,Bh=h1vh2m,c=c1vc2m, (7) 式中：
$ {p}_{1} $ 、$ {p}_{2} $ 、$ {h}_{1} $ 、$ {h}_{2} $ 、$ {c}_{1} $ 及$ {c}_{2} $ 分别为各参数的拟合系数.基于以上参数的变化规律，对幅值为5 mm正弦激励下1.0～9.0 Hz及0～1.0 A电流共47个工况模型参数进行重新辨识，可得到不同工况通用模型的辨识结果，如表2所示.
表 2 滞回模型参数辨识结果Table 2. Parameter identification of hysteretic model变量 辨识结果 ${F}_{{\rm{max}}}$ $\left(-9.36{I}^{2} + 123.97I + 23.05\right)\left(4.29{ {v}^{0.19}_{{\rm{m}}} }\right)$ ${\dot{x} }_{{\rm{center}}}$ $\left(-3.47I + 1.91\right)(-2.35{\rm{ln} }\;{v}_{ {\rm{m} } } + 9.21)$ ${B}_{{\rm{p}}}$ $1.97{v}^{-1.09}_{{\rm{m}}}$ ${B}_{{\rm{h}}}$ $1.01{v}_{{\rm{m}}}^{-0.86}$ $ c $ $0.32{ {v}_{ {\rm{m} } } ^{-1.01}}$ Cp 1.32 Dp 0.70 Ep −7.64 Ch 1.10 Dh 0.42 Eh −11.50 f0 −80.34 图9为所建立的通用模型对10 mm正弦激励下1.0～5.0 Hz、0.2～1.0 A电流不同工况的拟合结果与试验数据对比曲线，图中实线代表试验数据，虚线代表模型计算结果. 本文所建通用模型对不同工况下的阻尼器动态力学特性均具有较好的拟合能力.
图 9 通用模型辨识结果与试验数据对比Figure 9. Comparison of damping forces between generalized model and test data2. 基于ANFIS建立阻尼器逆模型
半主动悬架控制系统需要根据座椅运动状态及控制策略计算期望阻尼力，需建立控制电流逆模型计算获得期望阻尼力所需的电流. 本文选用自适应神经模糊系统（ANFIS）建立磁流变逆动力学模型.
为构建准确的ANFIS逆模型，建立准确全面的训练数据集是建模的重点和基础. 本文将阻尼器动态力学特性试验中所有工况案例中均匀抽取数据点整合在起，包含激励幅值5、10、15、20 mm，激励频率0.5～9.0 Hz，输入电流0～1.0 A工况，形成16400个数据点的总集合. 为避免阻尼器运动状态突变对模型的影响，选取每组数据开始及结束速度均接近0，并在每组数据后加10个全零数组，以避免先前数据集合对下一集合的输出预测的影响.
为增加ANFIS模型对变电流工况的推理能力，本文在试验获取的测试数据的基础上，根据磁流变减振器工作范围，建立激励幅值范围为2～14 mm、频率范围为0.5～10.0 Hz的扫频激励. 通过对位移信号进行微分来获得速度信号，时间步长为0.01 s，通过30 s模拟生成总共3000个数据集. 输出电流训练数据由幅值 0～1.0 A 的随机信号产生. 在激励数据不变的基础上，生成5组随机电流数组共15 000个数据点.
本文逆模型训练数据在试验恒定电流数据集及通过正向模型计算得到的随机电流数据集中各抽取7500组数据组成15000个数据点的训练集合，其余数据作为验证数据. 选取
$x\left(t\right)、\dot{x}\left(t\right)、\ddot{x}\left(t\right)、F\left(t\right)、 F\left(t-1\right)$ 作为模型输入，建立包含32 个“if-then”模糊规则的五输入单输出ANFIS模型.图10（a）为训练后逆模型的预测电流与验证目标恒定电流对比，由图可知，预测电流在目标电流值附近波动，两者之间误差均方根值为0.0869 A，电流在0附近误差较大. 图10（b）为随机电流序列模型验证结果，预测电流能够跟随目标电流的变化趋势，两者之间误差均方根值为0.1171 A.
将阻尼器逆向动力学模型与阻尼力模型结合，使该系统根据期望阻尼力产生预测电流进而产生预测阻尼力，模型验证流程如图11所示. 预测阻尼力与目标阻尼力对比结果见图12（a）. 结果表明，由 ANFIS 逆模型得到的预测电流以及产生的预测阻尼力能够较好地跟随目标阻尼力. 图12（b）为一组在阻尼力活塞运动速度范围内的验证数据，可以发现，在阻尼器运动范围内，预测阻尼力与目标阻尼力变化范围基本一致. 阻尼器全工况范围内预测阻尼力误差均方根值为135.79 N，为阻尼器最大阻尼力的5.6%.
3. 半主动座椅悬架控制系统仿真
建立包含上述建立的阻尼器正逆模型的单自由度半主动座椅悬架系统，簧上质量、刚度及被动阻尼系数分为75 kg、47.37 kN/m及1200 Ns/m. 控制策略采用on-off控制、连续天棚控制及LMS控制算法进行对比分析，on-off控制根据座椅运动状态在电流为最小值（0）和最大值（1.0 A）之间切换，天棚阻尼系数设置为2000 Ns/m，LMS算法步长因子设置为0.005，除控制算法外的半主动座椅悬架模型剩余部分均设置相同. 激励信号选取幅值5 mm、频率1.0～9.0 Hz正弦扫频激励. 图13为半主动座椅悬架控制系统示意.
图14为被动和半主动座椅悬架位移传递率. 可以发现：被动座椅悬架在共振频段将座椅下地板振动激励放大；与被动座椅悬架相比，3种控制算法在低频共振频段均能够有效地衰减振动. 通过计算，在4.0 Hz处3种算法的座椅悬架位移传递率较原被动座椅分别降低了47.62%、48.72%、42.09%. 天棚控制算法及最小均方算法（least mean square, LMS）在共振频率以上仍能保持较好的振动传递特性，on-off控制对高频激励的振动衰减性能较差.
图 14 半主动与被动座椅悬架位移传递率对比Figure 14. Comparison of transmissibility between semi-active and passive seat suspension半主动控制系统的实时性对控制效果具有显著影响. 基于磁流变阻尼器的半主动座椅悬架系统各环节时间延迟如图15所示，包括传感器信号采集时延
$ \Delta {t}_{3} $ 、 控制器时延$ \Delta {t}_{2} $ （数据处理、计算期望阻尼力、输出驱动电流时延）及磁流变阻尼器响应时延$ \Delta {t}_{1} $ .
图 15 包含时滞特性的半主动座椅悬架系统框图Figure 15. Application of time delay of the whole semi-active control system本文用经典控制算法（on-off控制、天棚控制）对磁流变阻尼器响应时滞的鲁棒性进行分析，计算结果如图16所示. 可以发现：对于两种算法，增加阻尼器响应时滞均会降低振动控制的改善效果；对于采用连续控制模型的天棚控制算法，对于阻尼器响应时滞具有一定鲁棒性，时延18 ms时在仿真频域范围内仍可以实现优于被动座椅悬架的减振效果；on-off控制算法对阻尼器响应时滞较敏感，特别是超过
$ \sqrt{2} $ 倍固有频率后的高频段，当阻尼器时延18 ms时，on-off控制座椅悬架振动传递特性变差. 因此，尽可能减小半主动座椅悬架系统各个环节的时滞，对于改善半主动控制系统减振效果具有积极作用.
图 16 不同时间延迟对座椅悬架位移传递率影响对比Figure 16. Comparison of the time delay effect to seat transmissibility通过上述分析可知，本文建立的阻尼力模型及控制电流逆模型能够产生满足控制策略需求的期望阻尼力，有效地衰减座椅下底板振动，对改善车辆乘坐舒适性具有积极作用.
4. 结 论
针对半主动座椅悬架控制系统，分析磁流变阻尼器非线性滞回特性，提出了一种改进魔术公式模型，并用改进差分进化算法进行模型辨识；利用自适应神经模糊系统建立磁流变阻尼器控制电流逆模型，并对包含阻尼器正逆模型的半主动座椅悬架进行验证计算. 结果表明，本文建立的正逆模性能够较好地表征磁流变阻尼器非线性滞回特性，满足座椅悬架的半主动控制需求.
1） Magic Formula 模型作为一种经典的轮胎模型，具有广泛的应用，对于非线性系统具有良好的拟合能力. 本文探索正弦型及余弦型魔术公式在磁流变减振器力学模型中的应用.
2） 在不同激励特性及电流条件下，本文建立的阻尼力模型均能较好地描述磁流变阻尼器的非线性滞回特性，对应于5 mm、3 Hz激励条件下，电流0～1.0 A变化范围内的模型平均百分比误差分别为0.0447、0.0474、0.0316、0.0310、 0.0344及0.0308.
3） 选取
$ x\left(t\right),\dot{x}\left(t\right),\ddot{x}\left(t\right),F\left(t\right),F\left(t-1\right) $ 作为模型输入，建立包含32 个“if-then”模糊规则的五输入单输出ANFIS磁流变逆动力学模型. 本文建立的逆模型对恒定电流工况及随机电流工况均可以得到较好的拟合效果，误差均方根值分别为0.0869 A及0.1171 A.4） 阻尼器逆向动力学模型与阻尼力模型串联模型对期望阻尼力的预测能力较好，阻尼器全工况范围内预测阻尼力误差均方根值与阻尼器最大阻尼力的百分比可达到5.6%.
5） 与被动座椅悬架相比，磁流变半主动座椅悬架在共振频率范围内均能够有效地衰减振动. on-off控制、连续天棚控制及LMS控制算法在4 Hz处的座椅悬架位移传递率较原被动座椅分别降低了47.62%、48.72%、42.09%. 阻尼器响应时滞增加会降低半主动控制的减振效果. 因此，应尽可能减小半主动座椅悬架系统各个环节的时滞.
-
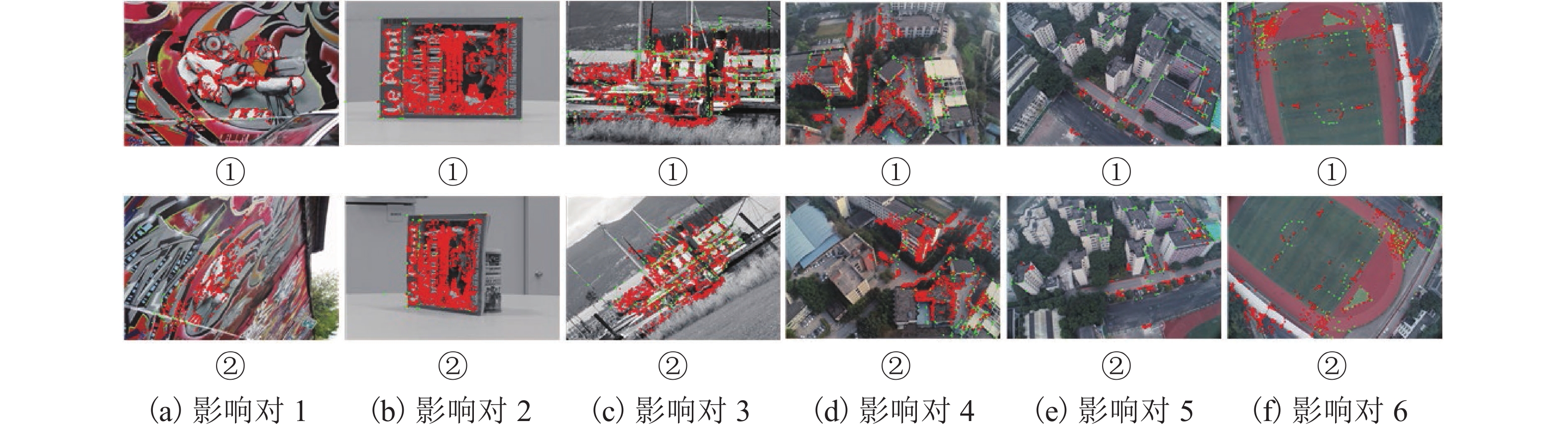
表 1 实验统计结果
Table 1. Statistic results of experiments
对 SIFT Harris-Affine Hessian-Affine ASIFT SuperGlue 本文方法 项目 影像对 RANSAC GMS RANSAC GMS RANSAC GMS RANSAC GMS GMS 匹配总数 1 41 0 20 0 38 0 708 502 0 943 2 235 69 36 0 407 294 2392 2353 168 2228 3 2081 218 79 0 79 0 2437 2181 216 8417 4 227 24 16 0 46 0 1789 1231 208 2235 5 55 0 19 0 40 0 232 56 207 443 6 167 0 13 0 16 0 259 28 2 1086 正确数 1 — 0 — 0 1 0 686 488 0 880 2 84 60 22 0 380 270 2266 2243 160 2163 3 1870 209 — 0 32 0 2383 2095 209 8302 4 198 20 — 0 1 0 1760 1207 199 2175 5 21 0 1 0 4 0 230 53 193 330 6 142 0 — 0 — 0 258 25 — 974 
下载: 导出CSV
-
[1] 余美. 倾斜立体影像匹配若干问题研究[D]. 徐州: 中国矿业大学, 2018. [2] LOWE D G. Distinctive image feature from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. doi: 10.1023/B:VISI.0000029664.99615.94 [3] MA J, CHAN C W, CANTERS F. Fully automatic subpixel image registration of multiangle CHRIS/Proba data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2829-2839. [4] MOREL J M, YU G. ASIFT: a new framework for fully affine invariant image comparison[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 438-469. doi: 10.1137/080732730 [5] YU G, MOREL J M. ASIFT: an algorithm for fully affine invariant comparison[J]. Image Processing on Line, 2011, 1: 11-38. doi: 10.5201/ipol.2011.my-asift [6] LI K, YAO J. Line segment matching and reconstruction via exploiting coplanar cues[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 125: 33-49. doi: 10.1016/j.isprsjprs.2017.01.006 [7] GIOIR RAFAEL G V, JAKUBOWICZ J , MOREL J M, et al. LSD: a fast line segment detector with a false detection control[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(4): 722-732. [8] FAN B, WU F, HU Z. Robust line matching through line-point invariants[J]. Pattern Recognition, 2012, 45(2): 794-805. doi: 10.1016/j.patcog.2011.08.004 [9] MIKOLAJCZYK K, SCHMID C. Scale & affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63-86. doi: 10.1023/B:VISI.0000027790.02288.f2 [10] MIKOLAJCZYK K, TUYTEIAARS T, SCHMID C, et al. A comparison of affine region detectors[J]. International Journal of Computor Vision, 2005, 65: 43-72. doi: 10.1007/s11263-005-3848-x [11] 姚国标,邓喀中,艾海滨,等. 倾斜立体影像自动准稠密匹配与三维重建算法[J]. 武汉大学学报(信息科学版),2014,39(7): 843-849.YAO Guobiao, DENG Kazhong, AI Haibin, et al. An algorithm of automatic quasi-dense matching and three-dimensional reconstruction for oblique stereo images[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 843-849. [12] 余美,邓喀中,杨化超,等. 基于WαSH局部特征的立体影像匹配[J]. 中国矿业大学学报,2018,47(3): 685-690.YU Mei, DENG Kazhong, YANG Huachao, et al. Stereo images matching based on WαSH local features[J]. Journal of China University of Mining & Technology, 2018, 47(3): 685-690. [13] 肖雄武,郭丙轩,李德仁,等. 一种具有仿射不变性的倾斜影像快速匹配方法[J]. 测绘学报,2015,44(4): 414-421.XIAO Xiongwu, GUO Bingxuan, LI Deren, et al. A quick and affine invariance matching method for oblique images[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 414-421. [14] YU Yinian, HUANG Kaiqi, CHEN Wei, et al. A novel algorithm for view and illumination invariant image matching[J]. IEEE Transactions on Image Processing, 2011, 21(1): 229-240. [15] XIAO X W, GUO B X, SHI Y R, et al. Robust and rapid matching of oblique UAV images of urban area[C]//Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. Wuhan: SPIE, 2013: 223-230. [16] LI K, YAO J , XIA M H, et al. Joint point and line segment matching on wide-baseline stereo images[C]//2016 IEEE Winter Conference on Applications of Computer Vision (WACV). New York: IEEE, 2016: 1-9. [17] 陈敏,朱庆,何海清,等. 面向城区宽基线立体像对视角变化的结构自适应特征点匹配[J]. 测绘学报,2019,48(9): 1129-1140.CHEN Min, ZHU Qing, HE Haiqing, et al. Structureadaptive feature point matching for urban area wide-baseline images with viewpoint variation[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(9): 1129-1140. [18] 张平,王竞雪. 直线对几何特征约束的近景影像特征匹配[J]. 遥感信息,2020,35(4): 124-132.ZHANG Ping, WANG Jingxue. Line matching for close-range images with geometry features of line pairs[J]. Remote Sensing Information, 2020, 35(4): 124-132. [19] RAGURAM R, CHUM O, POLLEFEYS M, et al. USAC: a universal framework for random sample consensus[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 2022-2038. [20] 王竞雪,朱庆,王伟玺. 顾及拓扑关系的立体影像直线特征可靠匹配算法[J]. 测绘学报,2017,46(11): 1850-1858.WANG Jingxue, ZHU Qing, WANG Weixi. Reliable line matching algorithm for stereo images with topological relationship[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1850-1858. [21] RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: an efficient alternative to SIFT or SURF[C]//2011 International Conference on Computer Vision. Barcelona: IEEE, 2011: 2564-2571. [22] LEVI G, HASSNER T. LATCH: learned arrangements of three patch codes[C]//2016 IEEE Winter Conference on Applications of Computer Vision (WACV). NewYork: IEEE, 2016: 1-9. [23] 李卓,刘洁瑜,李辉,等. 基于ORB-LATCH的特征检测与描述算法[J]. 计算机应用,2017,37(6): 1759-1762.LI Zhuo, LIU Jieyu, LI Hui, et al. Feature detection and description algorithm based on ORB-LATCH[J]. Journal of Computer Applications, 2017, 37(6): 1759-1762. [24] BIAN J W, LIN W Y, MATSUSHITA Y, et al. GMS: grid-based motion statistics for fast, ultra-robust feature correspondence[J]. International Journal of Computer Vision, 2020, 128(6): 1580-1593. doi: 10.1007/s11263-019-01280-3 [25] MIKOLAJCZYK K, SCHMID C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630. [26] SONG W H, JUNG H G, GWAK I Y, et al. Oblique aerial image matching based on iterative simulation and homography evaluation[J]. Pattern Recognition, 2019, 87: 317-331. [27] 杨蒙蒙,张爱华. 基于灰度共生矩阵和同步正交匹配追踪的分形图像压缩[J]. 计算机应用,2021,41(5): 1445-1449.YANG Mengmeng, ZHANG Aihua. Fractal image compression based on gray-level co-occurrence matrix and simultaneous orthogonal matching pursuit[J]. Journal of Computer Applications, 2021, 41(5): 1445-1449. [28] SARLIN P E, DETONE D, MALISIEWICZ T, et al. Superglue: Learning feature matching with graph neural networks[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 4938-4947. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 419
- HTML全文浏览量: 462
- PDF下载量: 65
- 被引次数: 0