DEM中砂土制样方法对浅基础承载力计算的影响

崔凯; 慈伟; 杨尚川

doi:10.3969/j.issn.0258-2724.20210620

DEM中砂土制样方法对浅基础承载力计算的影响

doi: 10.3969/j.issn.0258-2724.20210620

西南交通大学高速铁路路线工程教育部重点实验室，四川成都 610031

基金项目: 国家自然科学基金（42177128，51808456）

详细信息

作者简介:
崔凯（1979—），男，教授，研究方向为特殊土力学，E-mail：cuikai@swjtu.edu.cn

通讯作者:
杨尚川（1987—），男，助理教授，研究方向为岩土与地下工程，E-mail：shangchuan.yang@swjtu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 350
- HTML全文浏览量: 180
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-03
- 修回日期: 2021-11-16
- 网络出版日期: 2022-10-25
- 刊出日期: 2021-11-18

Influence of Sand Sampling Method on Bearing Capacity Calculation of Shallow Foundation in Discrete Element Method

Key Laboratory of High-Speed Railway Engineering of the Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
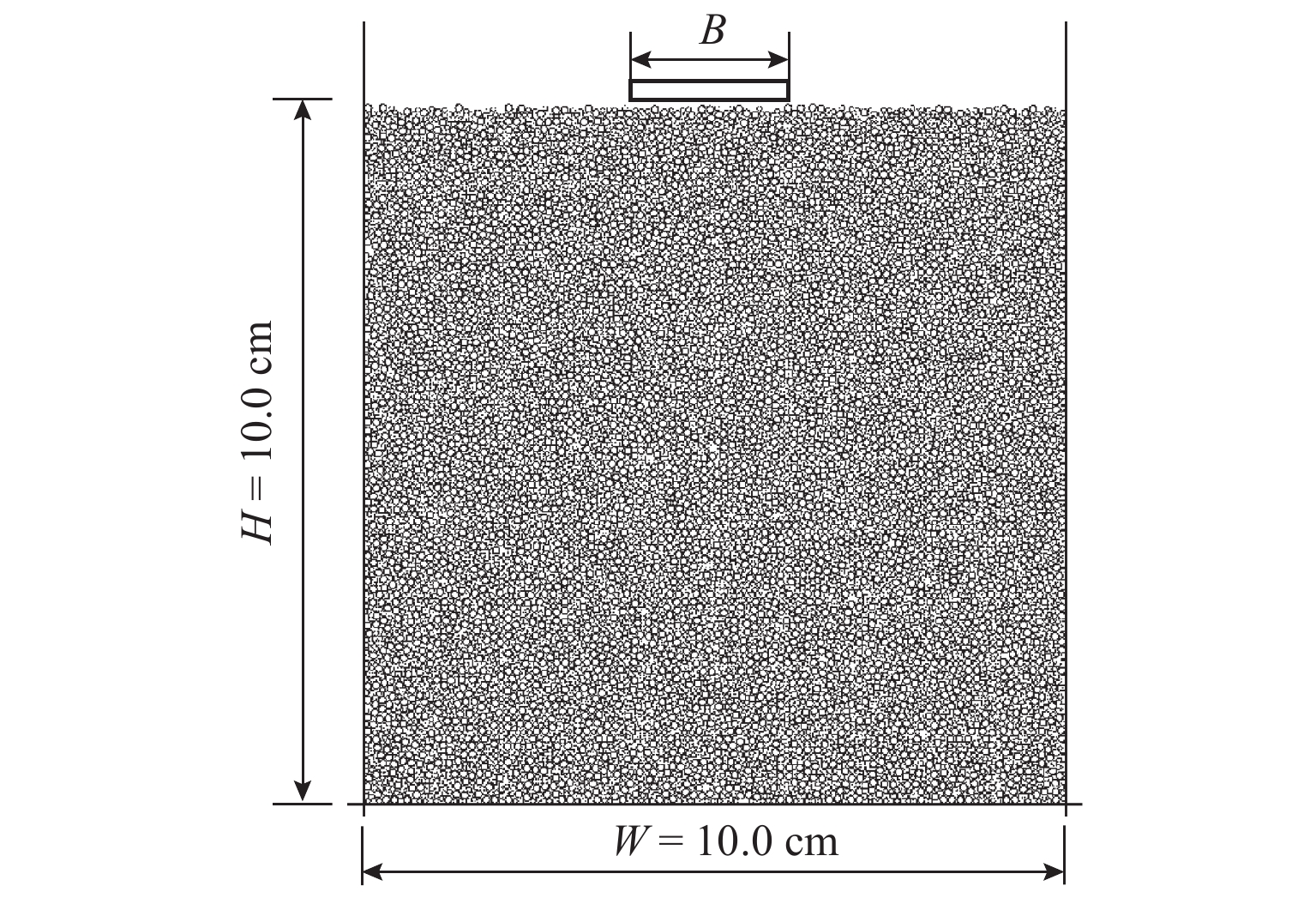
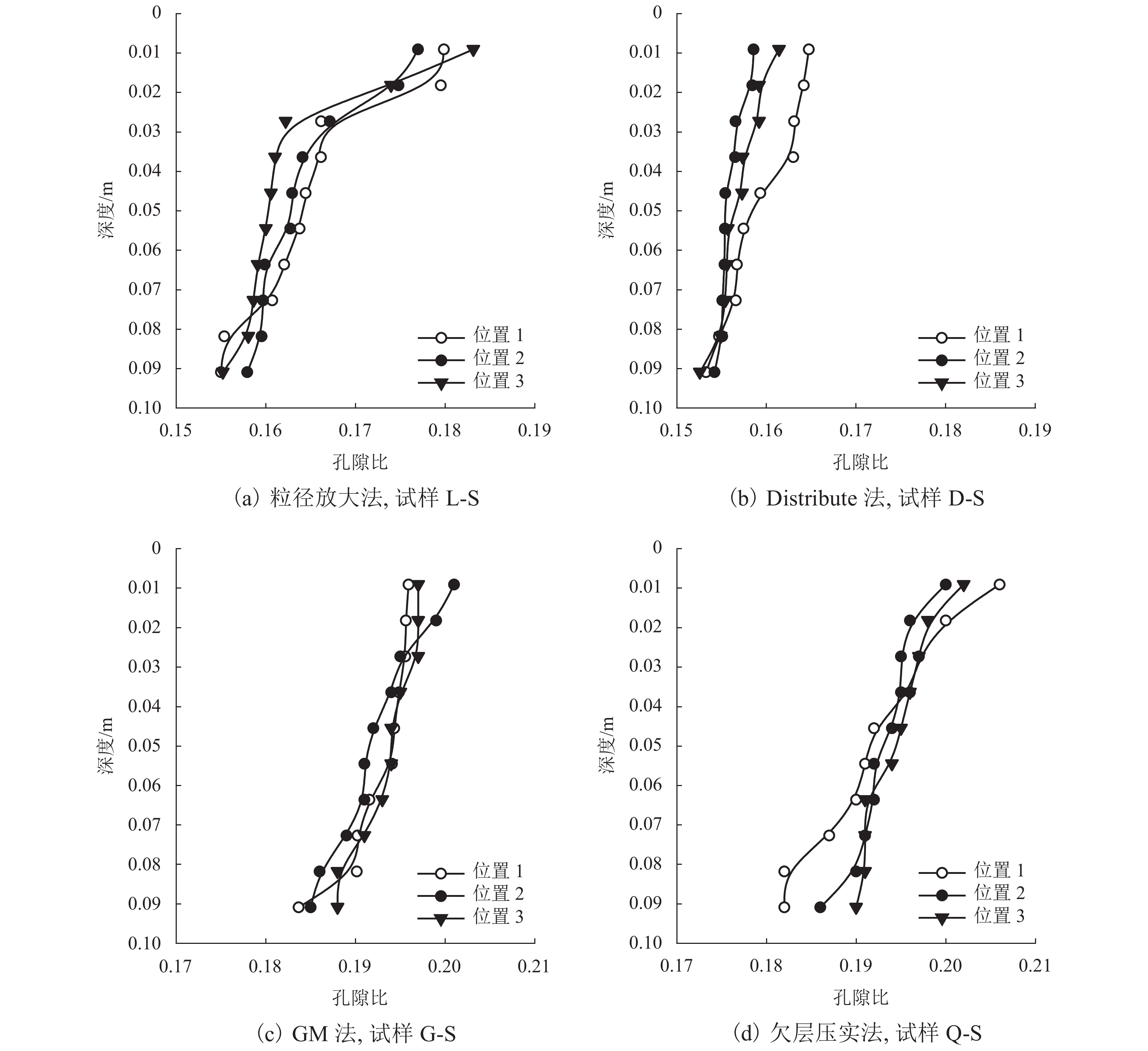
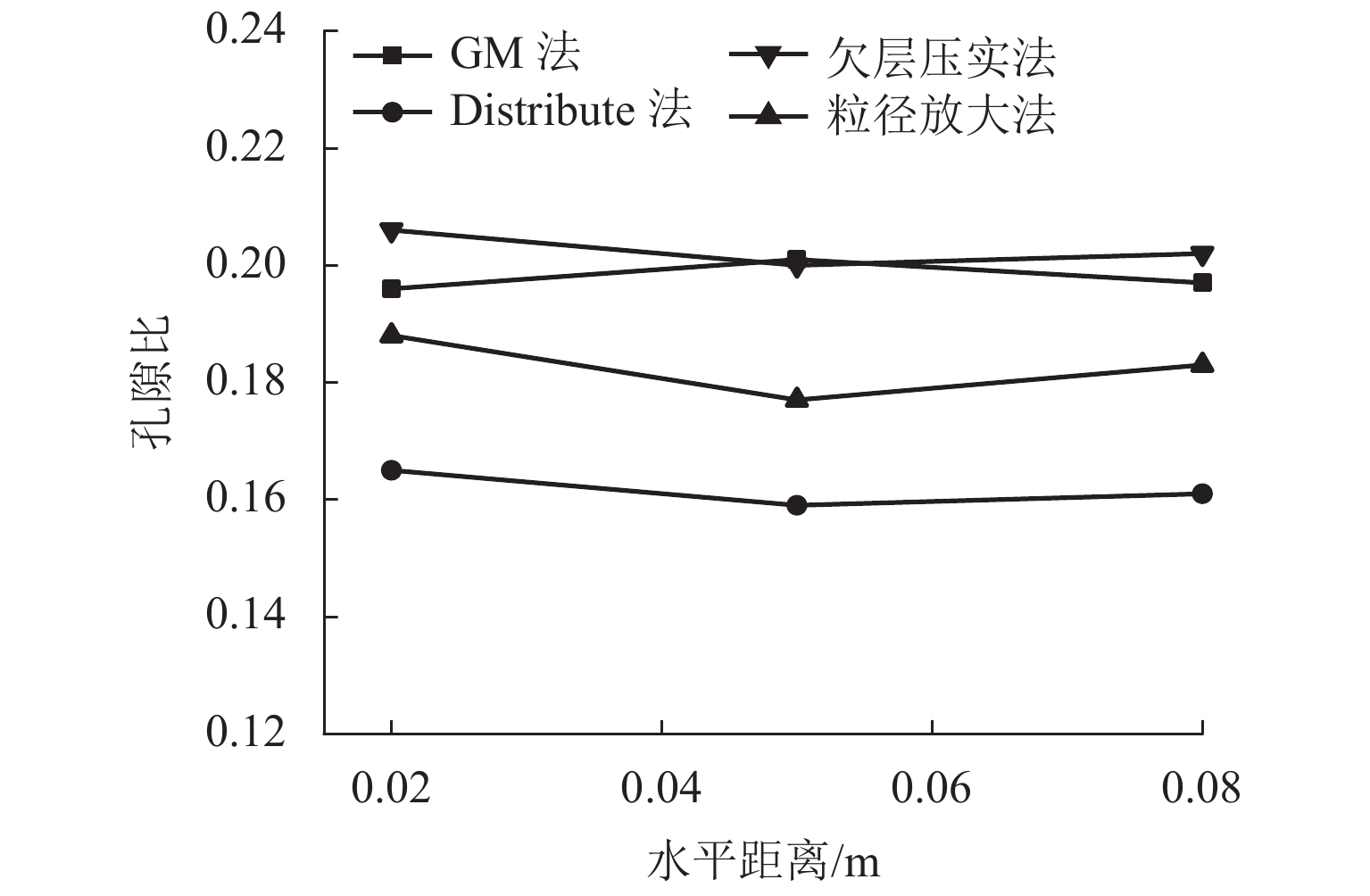
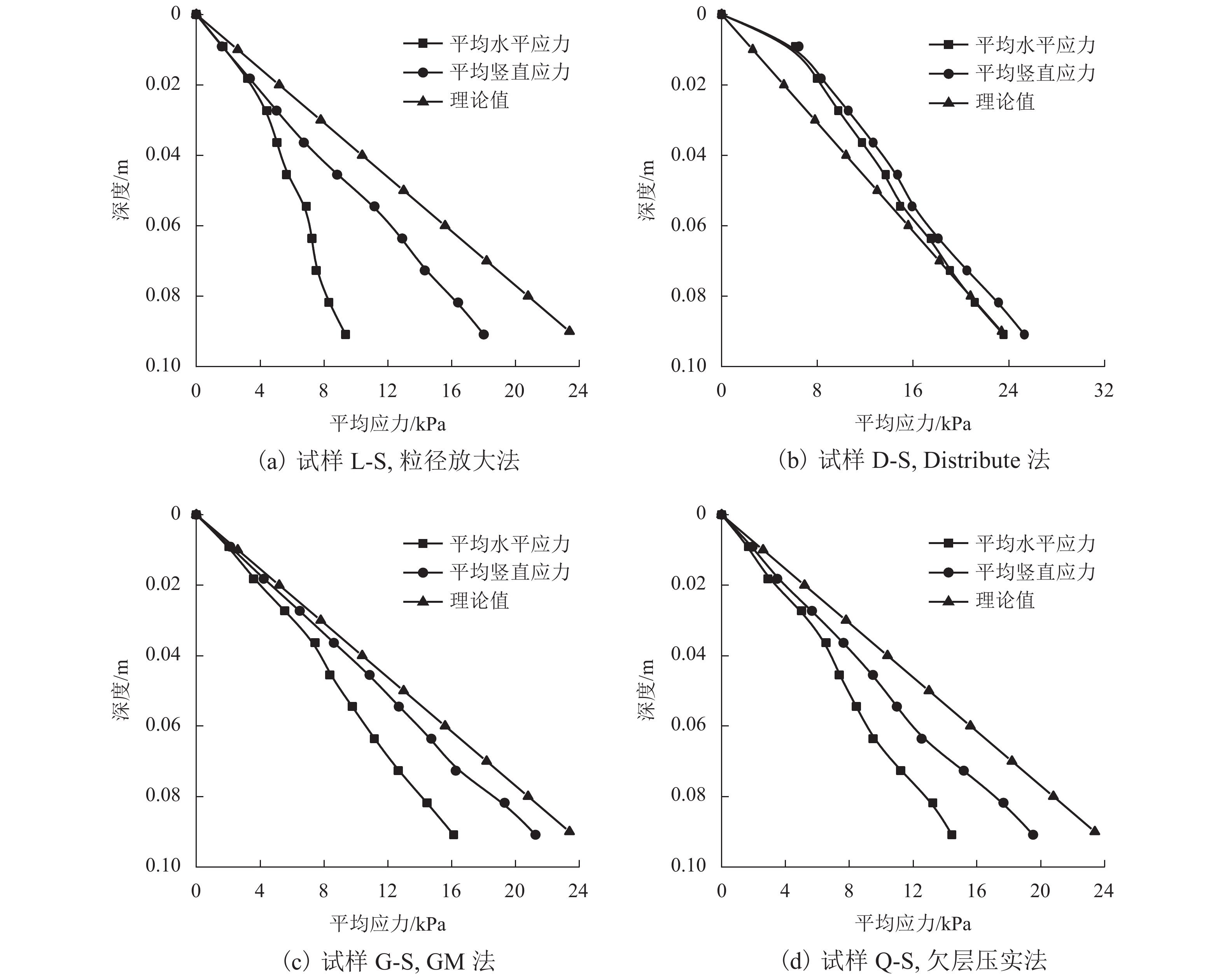
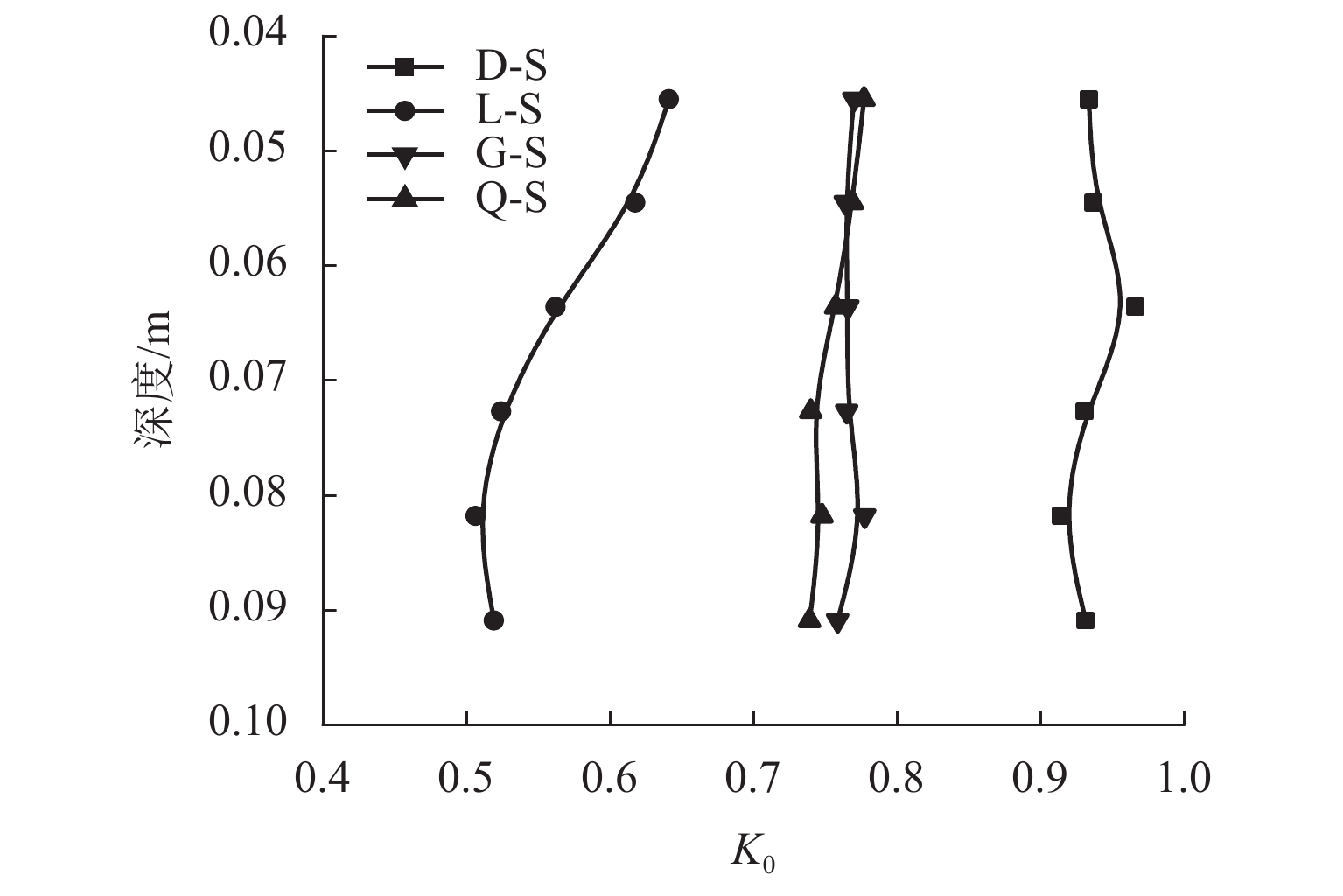
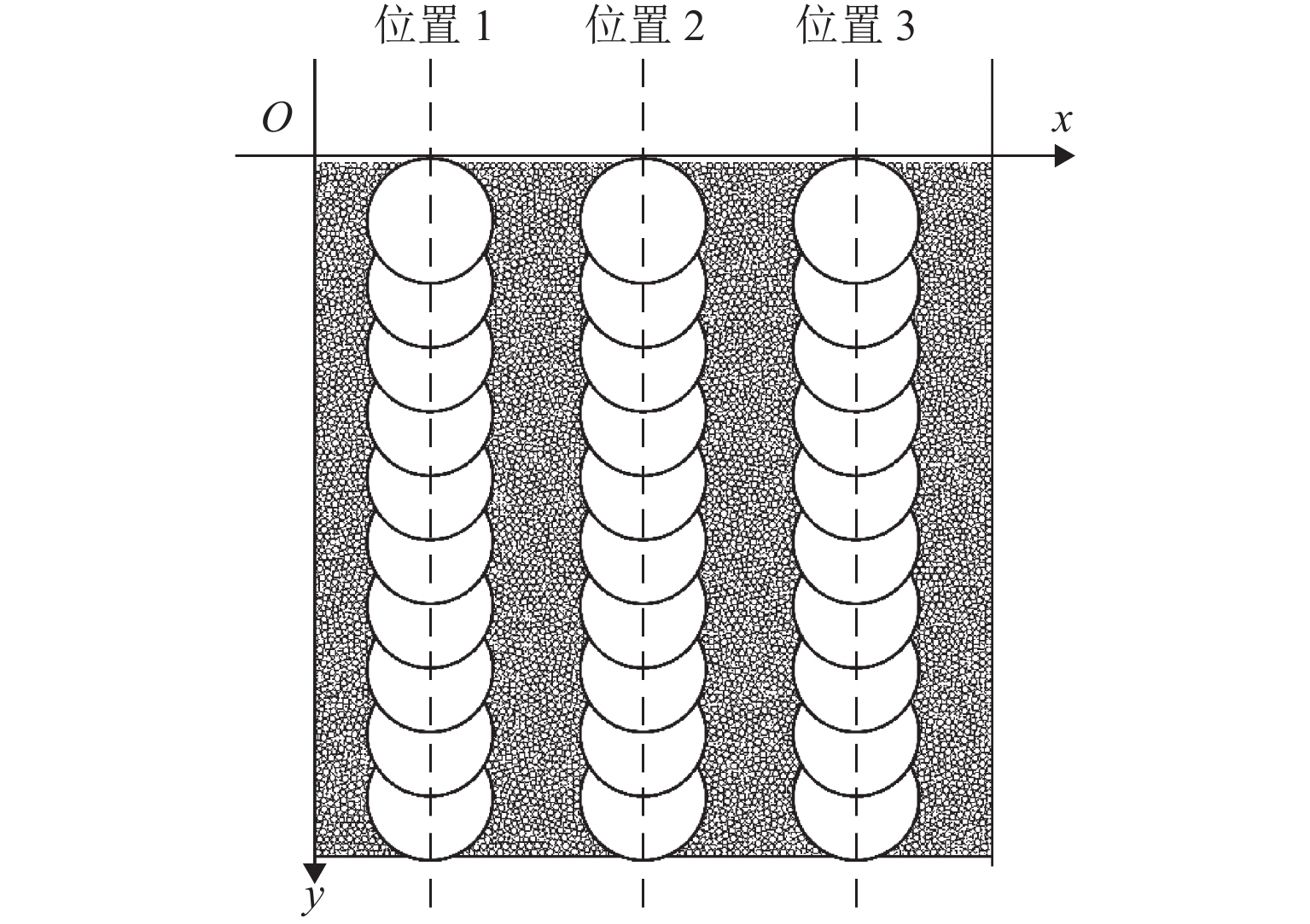
离散元数值模拟中，不同的制样方法会导致土体孔隙比和均匀性存在差异，进而对浅基础承载力的模拟计算结果产生影响，因此需要分析不同制样对浅基础承载力影响的问题. 本文分别使用粒径放大法、Distribute法、GM （grid method）法和欠层压实法对无黏性砂土进行制样，且试样在10g的重力场下进行地应力平衡；利用测量圆对不同位置土体孔隙比、水平应力和竖直应力进行监测，得到试样平均孔隙比e和小于1的侧向土压力系数K₀值；通过在试样表面放置刚性墙体并以相同的速度加载来模拟浅基础承载力试验，研究不同制样方法对浅基础承载力的影响. 研究结果表明：GM法与欠层压实法生成的试样，其孔隙比接近最初设置的目标孔隙比，误差约为3.5%；而粒径放大法与Distribute法生成的试样，其孔隙比会小于目标孔隙比，误差为20.0%左右；在试样整体均匀性方面，GM法得到的试样均匀性最好，随后依次是欠层压实法、Distribute法和粒径放大法；由于不同制样方法所得的试样孔隙比和K₀不同，在浅基础承载力模拟计算中不同制样方法得到的承载力关系为：GM法 < 欠层压实法 < 粒径放大法 < Distribute法.
- 离散元法 /
- 承载力 /
- 孔隙比 /
- 侧向土压力系数 /
- 浅基础
Abstract:
In the discrete element numerical simulation, different sample preparation methods will lead to differences in soil void ratio and uniformity, which will affect the simulation results of bearing capacity of shallow foundation. Therefore, it is necessary to analyze the influence of different sample preparation on bearing capacity of shallow foundation. Four methods (e.g., particle amplification method, distribute method, grid method, and under compaction method) were used to prepare the samples of cohesionless sand, and the samples were balanced under the gravity field of 10g. The void ratio, horizontal stress and vertical stress of soil at different positions were monitored by measuring circle, and the average void ratio e and the lateral earth pressure coefficient K₀ value less than 1 were obtained. The influence of different sample preparation methods on the bearing capacity of shallow foundation was studied by placing rigid wall on the surface of the sample and loading at the same speed to simulate the bearing capacity test of shallow foundation. The results show that the porosity ratios of samples generated by the GM and under compaction method are closer to the original target porosity ratio with an error of about 3.5%. In comparison, the porosity ratios generated by particle amplification method and distribute method are smaller than the target porosity ratio, with an error of about 20.0%. Additionally, GM presents the most homogeneous sand samples, followed by the under compaction method, distribute method and particle amplification method, respectively. Due to the varying porosity ratios and K₀ of samples, the obtained bearing capacity of shallow foundation also changes. The relationship of bearing capacity obtained by different sample preparation methods in the simulation of bearing capacity of shallow foundation is : GM < underlayer compaction method < particle size amplification method < distribute method.
- discrete element method (DEM) /
- bearing capacity /
- porosity ratio /
- lateral earth pressure coefficient /
- shallow foundation

HTML全文

图 1 DEM模型

Figure 1. Model of DEM

下载: 全尺寸图片幻灯片

图 2 位置1～3土体孔隙比随深度变化

Figure 2. Variation of soil void ratio with depth in location 1−3

下载: 全尺寸图片幻灯片

图 3 深度0.01 m时水平方向孔隙比

Figure 3. Horizontal porosity ratios at 0.01 m depth

下载: 全尺寸图片幻灯片

图 4 位置1～3土体平均水平应力与竖向应力分布

Figure 4. Distribution of average horizontal and vertical stresses of soil in location 1−3

下载: 全尺寸图片幻灯片

图 5 不同深度下试样K₀分布

Figure 5. Distribution of K₀ at different depths

下载: 全尺寸图片幻灯片

图 6 浅基础离散元模型

Figure 6. DEM model of shallow foundation

下载: 全尺寸图片幻灯片

图 7 荷载-位移曲线

Figure 7. Load-displacement curves

下载: 全尺寸图片幻灯片

图 8 加载过程中力链分布

Figure 8. Distribution of force chain during loading

下载: 全尺寸图片幻灯片

表 1 模型细观参数

Table 1. Microscopic parameters of the model

参数	值
粒径/mm	0.8～1.2
颗粒密度/（kg•m⁻³）	2650
初始孔隙比	0.2
颗粒法向刚度 k_n/ （N•m⁻¹）	5 × 10⁷
颗粒切向刚度 k_s/ （N•m⁻¹）	2.5 × 10⁷
墙体法向刚 k_nw/ （N·m⁻¹）	1 × 10⁹
墙体切向刚 k_sw/ （N•m⁻¹）	1 × 10⁹
初始摩擦系数 μ₁	8.7 × 10⁻⁴
最终摩擦系数 μ₂	0.839
墙体与颗粒摩擦系数 μ₃	0

下载: 导出CSV

表 2 试样的极限承载力

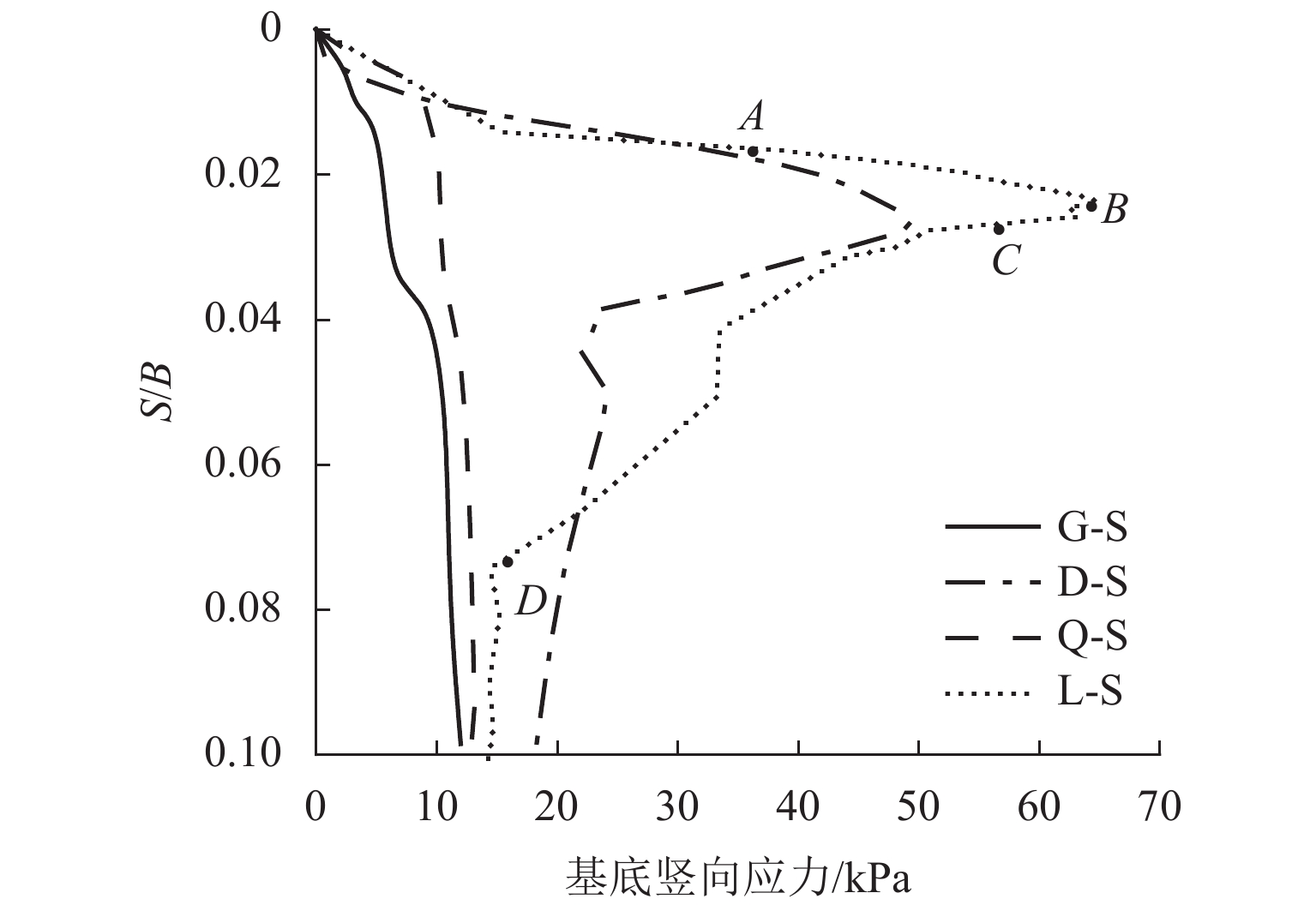
Table 2. Ultimate bearing capacity of samples

制样方法	试样	e	均匀性	极限承载力/kPa
GM 法	G-S	0.194	1	12.00
欠层压实法	Q-S	0.193	2	12.50
Distribute 法	D-S	0.157	3	18.19
粒径放大法	L-S	0.164	4	14.30

下载: 导出CSV

参考文献(39)

[1]	CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65.
[2]	JIANG M J, JIANG T, CROSTA G B, et al. Modeling failure of jointed rock slope with two main joint sets using a novel DEM bond contact model[J]. Engineering Geology, 2015, 193: 79-96. doi: 10.1016/j.enggeo.2015.04.013
[3]	BYM T, MARKETOS G, BURLAND J B, et al. Use of a two-dimensional discrete-element line-sink model to gain insight into tunnelling-induced deformations[J]. Géotechnique, 2013, 63(9): 791-795.
[4]	ZHENG G, YANG X Y, ZHOU H Z, et al. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations[J]. Computers and Geotechnics, 2018, 95: 119-128. doi: 10.1016/j.compgeo.2017.10.006
[5]	LIU Z N, KOYI H A. Kinematics and internal deformation of granular slopes: insights from discrete element modeling[J]. Landslides, 2013, 10(2): 139-160. doi: 10.1007/s10346-012-0318-8
[6]	XU W J, DONG X Y. Simulation and verification of landslide tsunamis using a 3D SPH-DEM coupling method[J]. Computers and Geotechnics, 2021, 129: 103803.1-103803.16.
[7]	CHANG C S, CHAO S J. Discrete element method for bearing capacity analysis[J]. Computers and Geotechnics, 1991, 12(4): 273-288. doi: 10.1016/0266-352X(91)90026-C
[8]	Itasca. Particle flow code in two dimensions[M]. Minnesota: Itasca Consulting Group, Inc. 2004.
[9]	戴轩,郑刚,程雪松,等. 基于DEM-CFD方法的基坑工程漏水漏砂引发地层运移规律的数值模拟[J]. 岩石力学与工程学报,2019,38(2): 396-408. DAI Xuan, ZHENG Gang, CHENG Xuesong, et al. Numerical simulation of ground movement induced by leakage of groundwater and sand in excavations based on the DEM-CFD method[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(2): 396-408.
[10]	徐琨,周伟,马刚,等. 基于离散元法的颗粒破碎模拟研究进展[J]. 岩土工程学报,2018,40(5): 880-889. doi: 10.11779/CJGE201805013 XU Kun, ZHOU Wei, MA Gang, et al. Review of particle breakage simulation based on DEM[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 880-889. doi: 10.11779/CJGE201805013
[11]	金磊,曾亚武. 土石混合体宏细观力学特性和变形破坏机制的三维离散元精细模拟[J]. 岩石力学与工程学报,2018,37(6): 1540-1550. JIN Lei, ZENG Yawu. Refined simulation for macro-and meso-mechanical properties and failure mechanism of soil-rock mixture by 3D DEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1540-1550.
[12]	景路,郭颂怡,赵涛. 基于流体动力学-离散单元耦合算法的海底滑坡动力学分析[J]. 岩土力学,2019,40(1): 388-394. JING Lu, GUO Songyi, ZHAO Tao. Understanding dynamics of submarine landslide with coupled CFD-DEM[J]. Rock and Soil Mechanics, 2019, 40(1): 388-394.
[13]	徐文杰. 滑坡涌浪流-固耦合分析方法与应用[J]. 岩石力学与工程学报,2020,39(7): 1420-1433. XU Wenjie. Fluid-solid coupling method of landslide tsunamis and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(7): 1420-1433.
[14]	马华庆,赵永志. 喷动流化床中杆状颗粒混合特性的CFD-DEM模拟[J]. 浙江大学学报(工学版),2020,54(7): 1347-1354. doi: 10.3785/j.issn.1008-973X.2020.07.013 MA Huaqing, ZHAO Yongzhi. CFD-DEM investigation on mixing of rod-like particles in spout-fluid bed[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(7): 1347-1354. doi: 10.3785/j.issn.1008-973X.2020.07.013
[15]	CHO S E, LEE S R. Instability of unsaturated soil slopes due to infiltration[J]. Computers and Geotechnics, 2001, 28(3): 185-208. doi: 10.1016/S0266-352X(00)00027-6
[16]	CHEN X Y, ZHANG L L, ZHANG L M, et al. Modelling rainfall-induced landslides from initiation of instability to post-failure[J]. Computers and Geotechnics, 2021, 129: 103877.1-103877.16.
[17]	YANG S C, CI W, LESHCHINSKY B, et al. Scale effects on the ultimate bearing capacity of rectangular footings placed on slopes[J]. Computers and Geotechnics, 2021, 137: 104254.1-104254.7.
[18]	YANG S C, LESHCHINSKY B, CUI K, et al. Influence of failure mechanism on seismic bearing capacity factors for shallow foundations near slopes[J]. Géotechnique, 2021, 71(7): 594-607.
[19]	YANG S C, LESHCHINSKY B, CUI K, et al. Unified approach toward evaluating bearing capacity of shallow foundations near slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(12): 04019110.1-04019110.16.
[20]	NG T T, MEYERS R. Side resistance of drilled shafts in granular soils investigated by DEM[J]. Computers and Geotechnics, 2015, 68: 161-168. doi: 10.1016/j.compgeo.2015.04.009
[21]	WANG Z J, JACOBS F, ZIEGLER M, et al. Visualisation and quantification of geogrid reinforcing effects under strip footing loads using discrete element method[J]. Geotextiles and Geomembranes, 2020, 48(1): 62-70. doi: 10.1016/j.geotexmem.2019.103505
[22]	FU Z Z, CHEN S S, LIU S H. Discrete element simulations of shallow plate-load tests[J]. International Journal of Geomechanics, 2016, 16(3): 1-12.
[23]	XU R, LIU E L, JIANG X Q, et al. Analysis on evolution of mesostructure of cohesionless soil ground upon loading[J]. Powder Technology, 2020, 368: 1-17. doi: 10.1016/j.powtec.2020.04.048
[24]	CHA M S, SANTAMARINA J C. Effect of dissolution on the load-settlement behavior of shallow foundations[J]. Canadian Geotechnical Journal, 2016, 53(8): 1353-1357. doi: 10.1139/cgj-2014-0370
[25]	蒋明镜,李磊,孙超. 地基承载力尺寸效应离散元分析[J]. 同济大学学报(自然科学版),2015,43(5): 649-656. JIANG Mingjing, LI Lei, SUN Chao. Analysis on scale effect of bearing capacity of foundation by discrete element method[J]. Journal of Tongji University (Natural Science), 2015, 43(5): 649-656.
[26]	ZHONG W H, LIU H L, WANG Q, et al. Investigation of the penetration characteristics of snake skin-inspired pile using DEM[J]. Acta Geotechnica, 2021, 16(6): 1849-1865. doi: 10.1007/s11440-020-01132-2
[27]	DUAN N, CHENG Y P. A modified method of generating specimens for a 2D DEM centrifuge model[C]//Geo-Chicago 2016: Sustainability, Energy, and the Geoenvironment. Chicago: American Society of Civil Engineers, 2016: 610-620.
[28]	JIANG M J, KONRAD J M, LEROUEIL S. An efficient technique for generating homogeneous specimens for DEM studies[J]. Computers and Geotechnics, 2003, 30(7): 579-597. doi: 10.1016/S0266-352X(03)00064-8
[29]	GOURVENEC S M, MANA D S K. Undrained vertical bearing capacity factors for shallow foundations[J]. Géotechnique Letters, 2011, 1(4): 101-108.
[30]	KUSAKABE O. Geotechnical centrifuge technology[M]. London: Blackie Academic & Professional. 1995: 118-167.
[31]	LAU C K, BOLTON M D. The bearing capacity of footings on granular soils Ⅱ: experimental evidence[J]. Géotechnique, 2011, 61(8): 639-650.
[32]	CERATO A B, LUTENEGGER A J. Bearing capacity of square and circular footings on a finite layer of granular soil underlain by a rigid base[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1496-1501. doi: 10.1061/(ASCE)1090-0241(2006)132:11(1496)
[33]	DAVIS R O, SELVADURAI A P S. Plasticity and Geomechanics[M]. Cambridge: Cambridge University Press, 2002.
[34]	申志福,蒋明镜,朱方园,等. 离散元微观参数对砂土宏观参数的影响[J]. 西北地震学报,2011,33(增1): 160-165. SHEN Zhifu, JIANG Mingjing, ZHU Fangyuan, et al. Influence of the micro parameters of discrete element on the macro parameters of sands[J]. Northwestern Seismological Journal, 2011, 33(S1): 160-165.
[35]	TRAN V D H, MEGUID M A, CHOUINARD L E. A finite-discrete element framework for the 3D modeling of geogrid-soil interaction under pullout loading conditions[J]. Geotextiles and Geomembranes, 2013, 37: 1-9. doi: 10.1016/j.geotexmem.2013.01.003
[36]	KIM B S, PARK S W, KATO S. DEM simulation of collapse behaviours of unsaturated granular materials under general stress states[J]. Computers and Geotechnics, 2012, 42: 52-61. doi: 10.1016/j.compgeo.2011.12.010
[37]	NGO N T, INDRARATNA B, RUJIKIATKAMJORN C. DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal[J]. Computers and Geotechnics, 2014, 55: 224-231. doi: 10.1016/j.compgeo.2013.09.008
[38]	BHANDARI A, HAN J. DEM study of a shallow foundation under vertical loading[C]//2009 International Foundation Congress and Equipment. Florida: American Society of Civil Engineers, 2009: 465-472.
[39]	LI L, JIANG M J, LI T, et al. DEM analyses of the whole failure process of shallow foundation in plate load test on dense sand[C]//IOP Conference Series: Earth and Environmental Science. Warwick: Earth and Environmental Science, 2015: 012039.1-012039.6.