GPS非差精密解算软件PLAOD及其性能分析

徐韶光; 熊永良; 张文皓; 王德军

doi:10.3969/j.issn.0258-2724.20210596

GPS非差精密解算软件PLAOD及其性能分析

doi: 10.3969/j.issn.0258-2724.20210596

1.
西南交通大学地球科学与环境工程环学院，四川成都 611756
2.
新南威尔士大学土木与环境工程学院，新南威尔士悉尼 2052
3.
河北工业大学土木与交通学院，天津 300401

基金项目: 国家自然科学基金（41274044）；四川省科技计划（2021YFG0339）

详细信息

作者简介:
徐韶光（1983—），男，讲师，研究方向为GNSS数据处理，E-mail：shaoguangxu@swjtu.edu.cn

通讯作者:
熊永良（1964—），男，教授，研究方向为GNSS理论与应用，E-mail：ylxiong@sina.com

中图分类号: P228
计量
- 文章访问数: 346
- HTML全文浏览量: 169
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-22
- 修回日期: 2021-10-09
- 网络出版日期: 2022-10-19
- 刊出日期: 2021-11-15

Undifferenced Precise GPS Processing Software PLAOD and Its Performance Analysis

1.
School of Geoscience and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China
2.
School of Civil and Environmental Engineering, The University of New South Wales, Sydney 2052, Australia
3.
School of Civil and Transportation Engineering, Hebei University of Technology, Tianjin 300401, China

摘要

摘要:
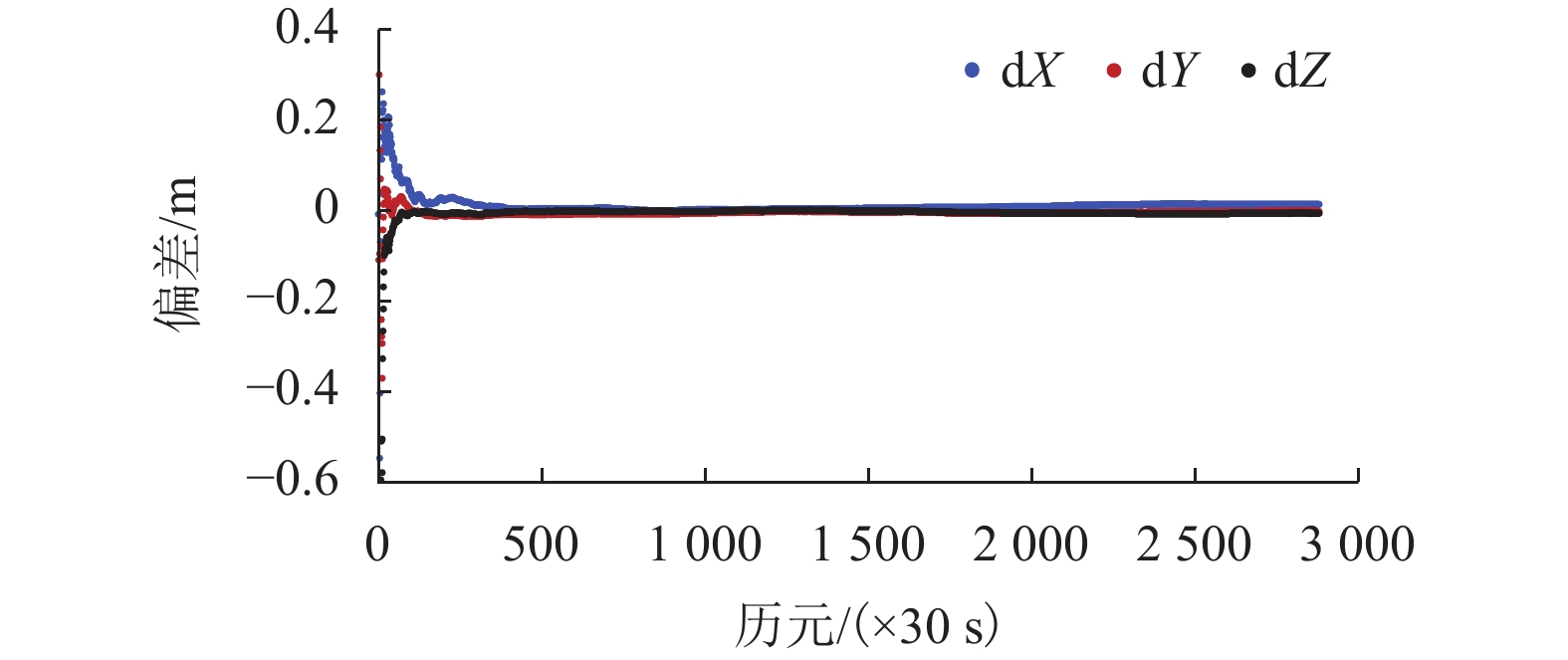
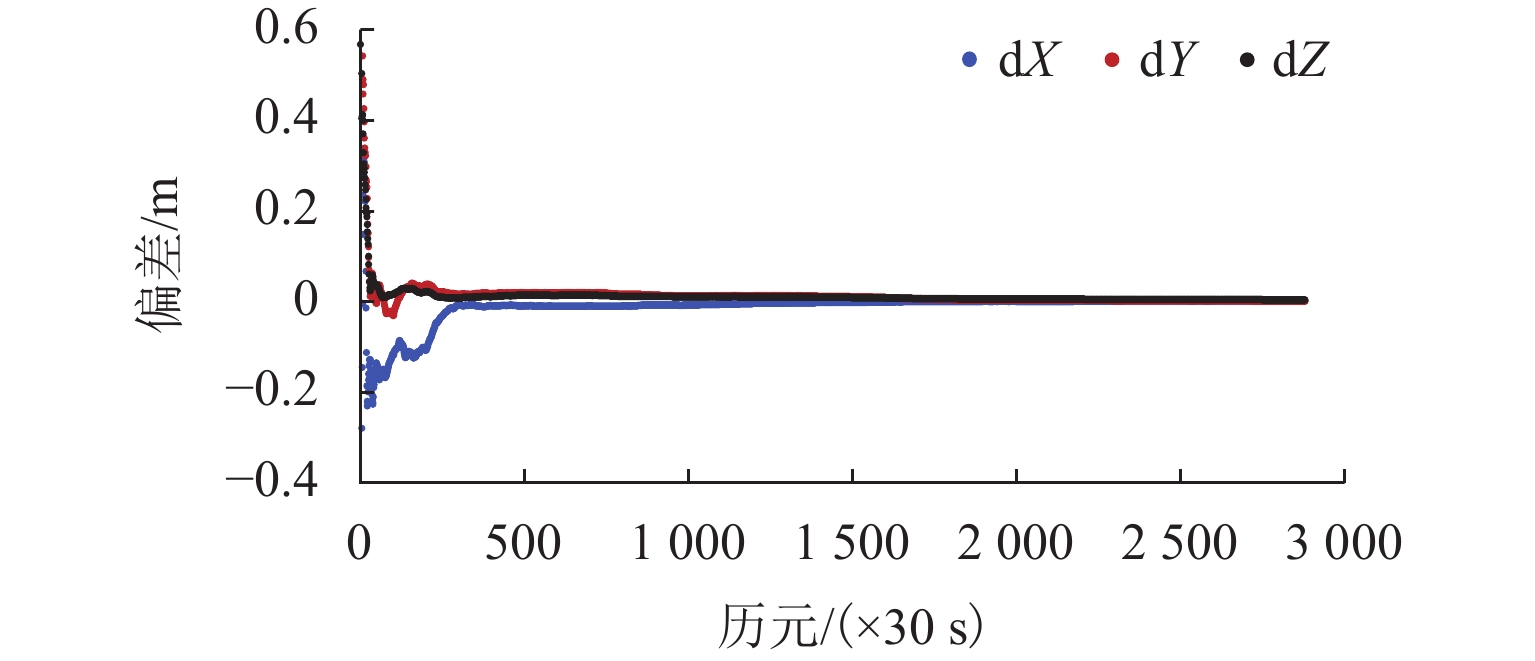
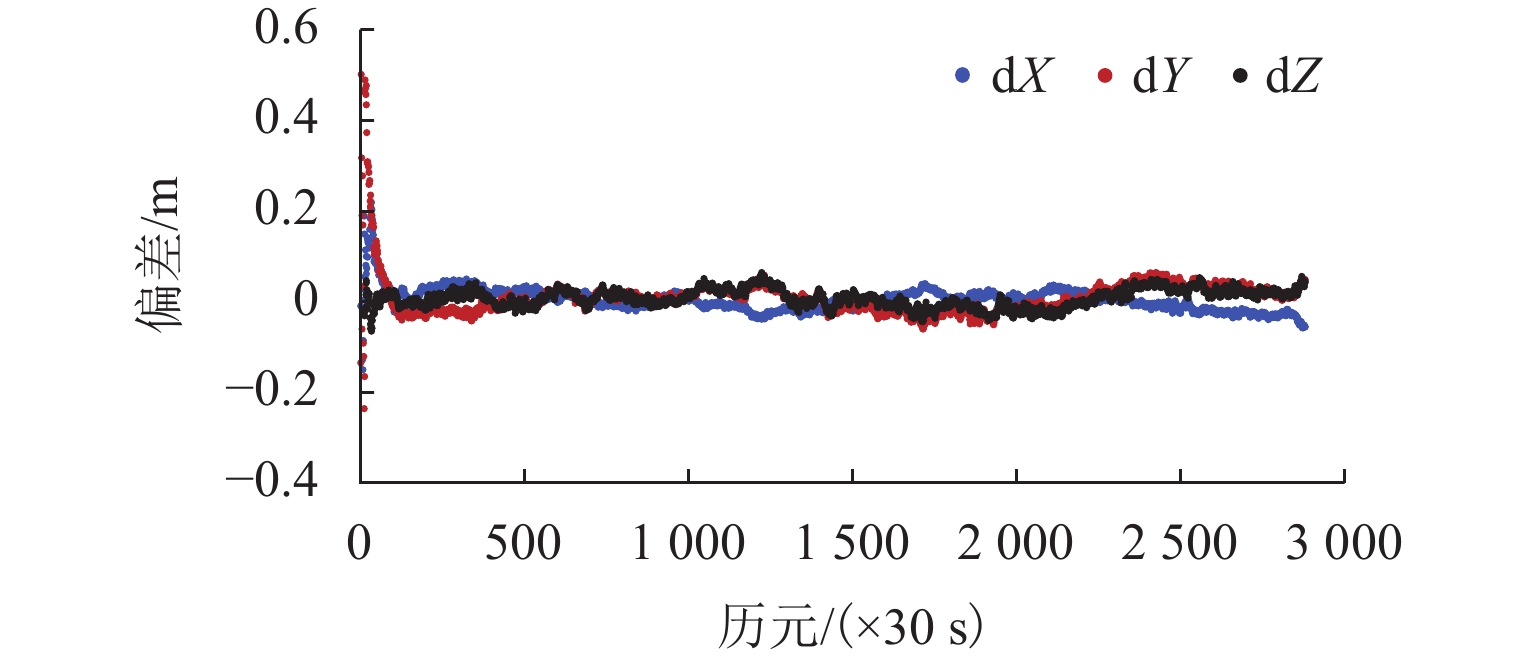
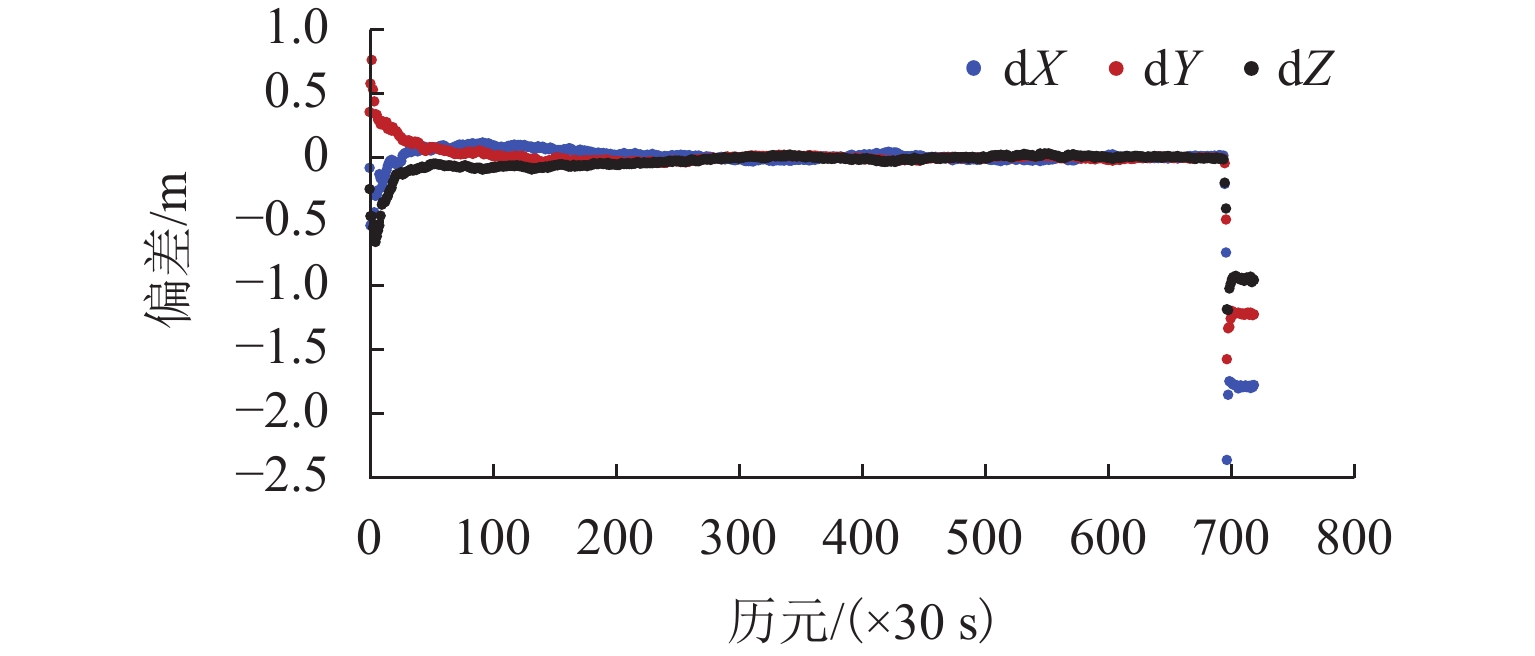
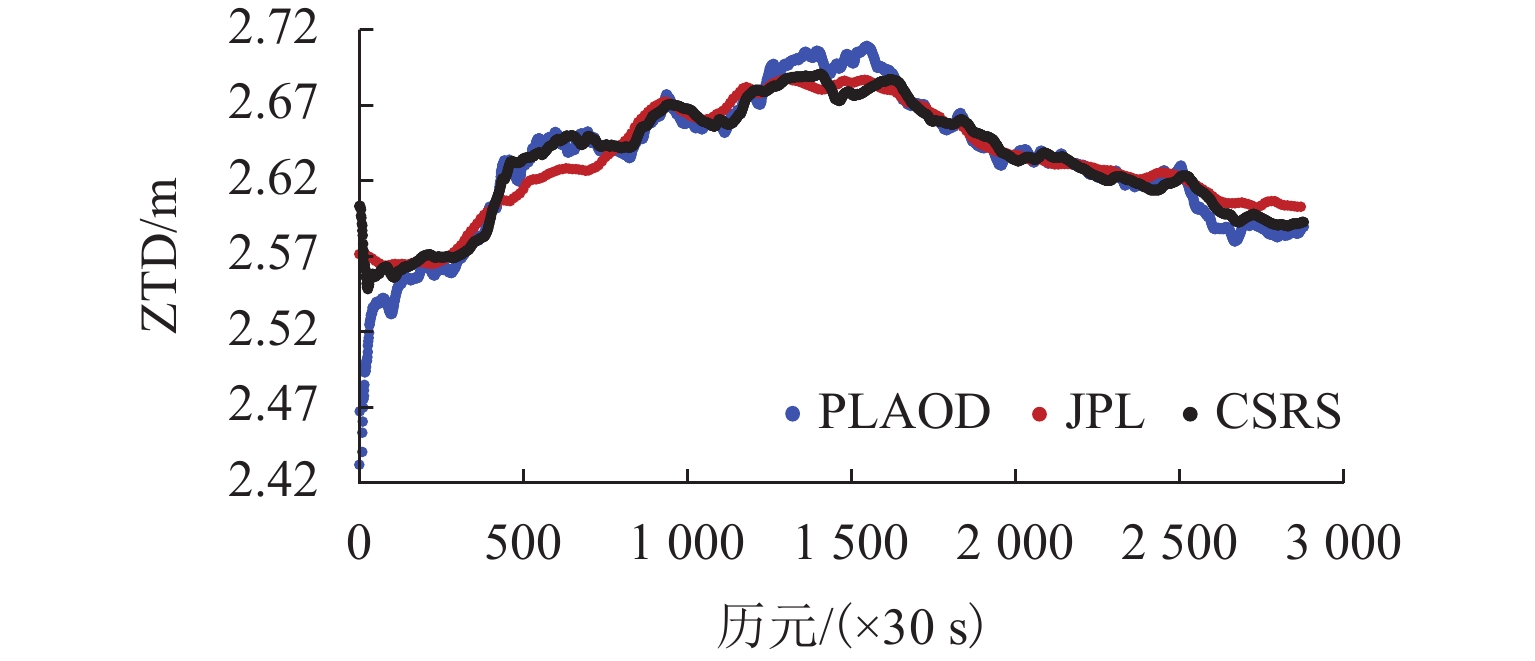
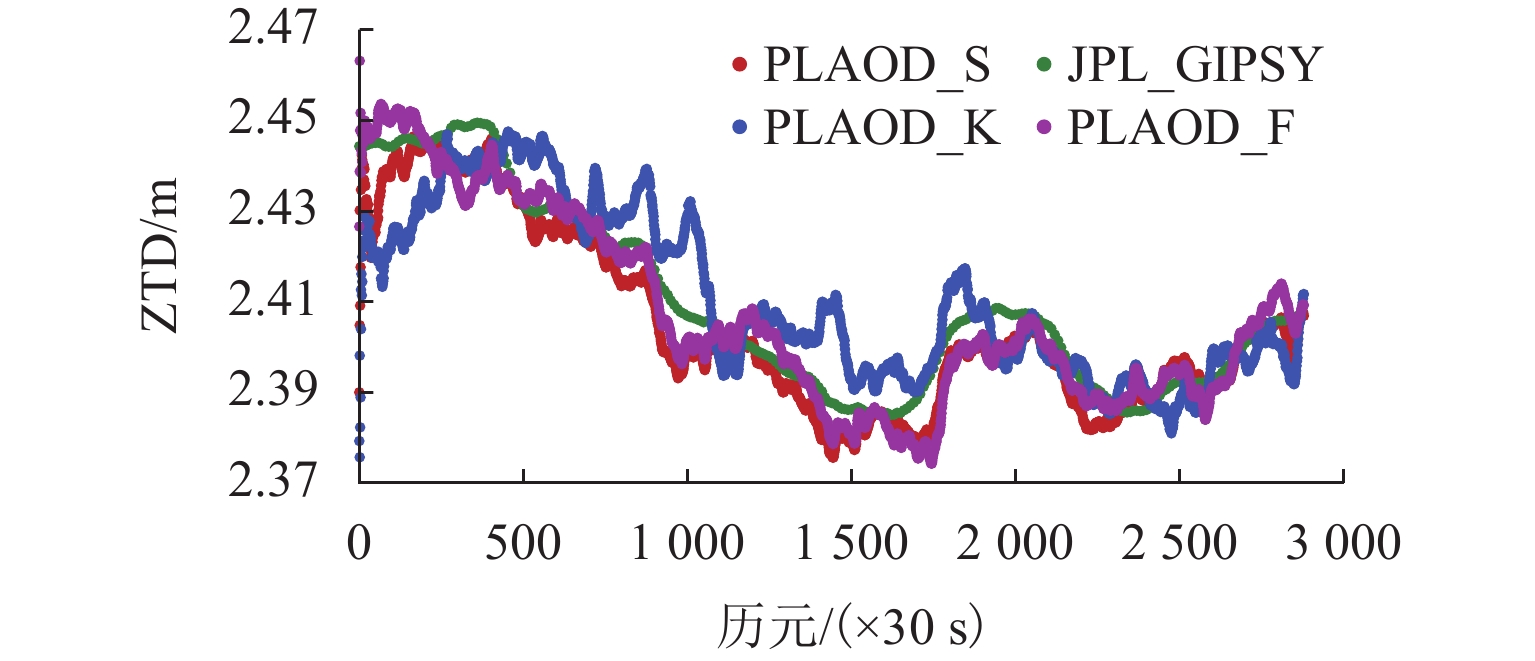
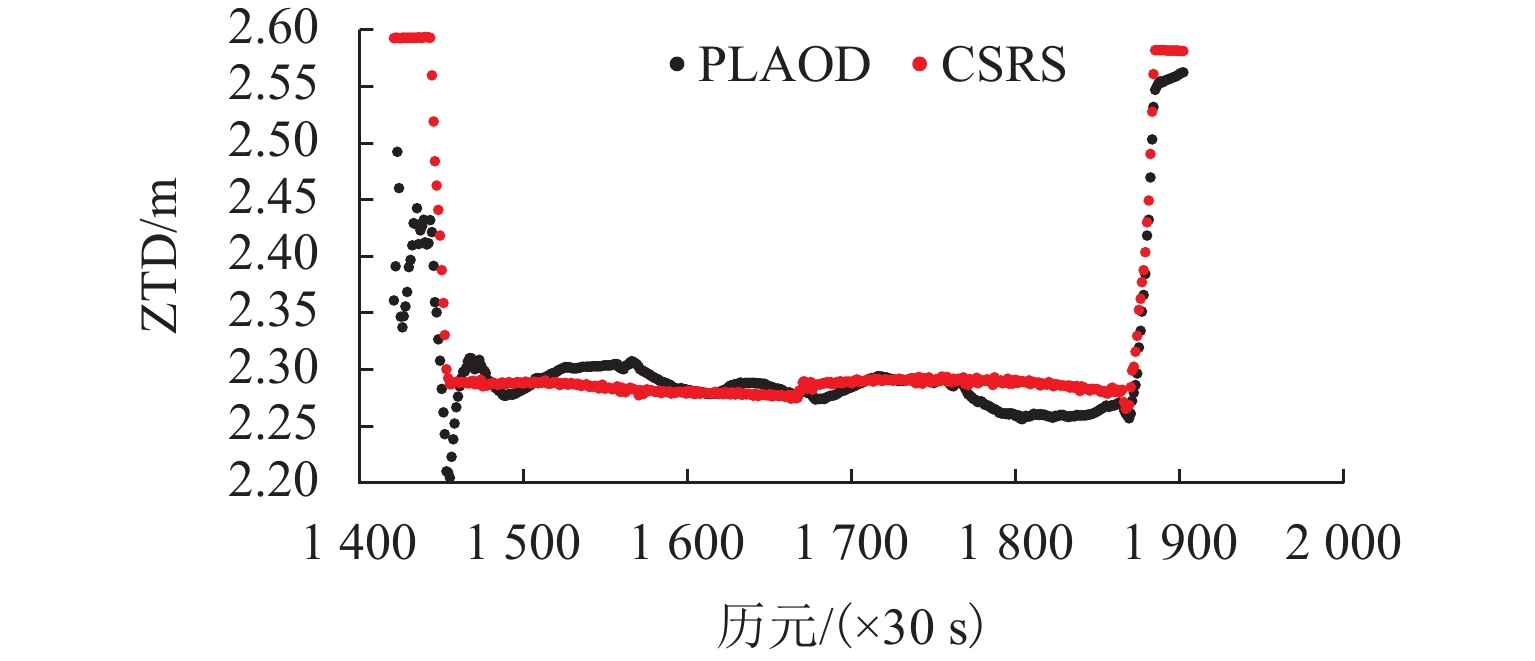
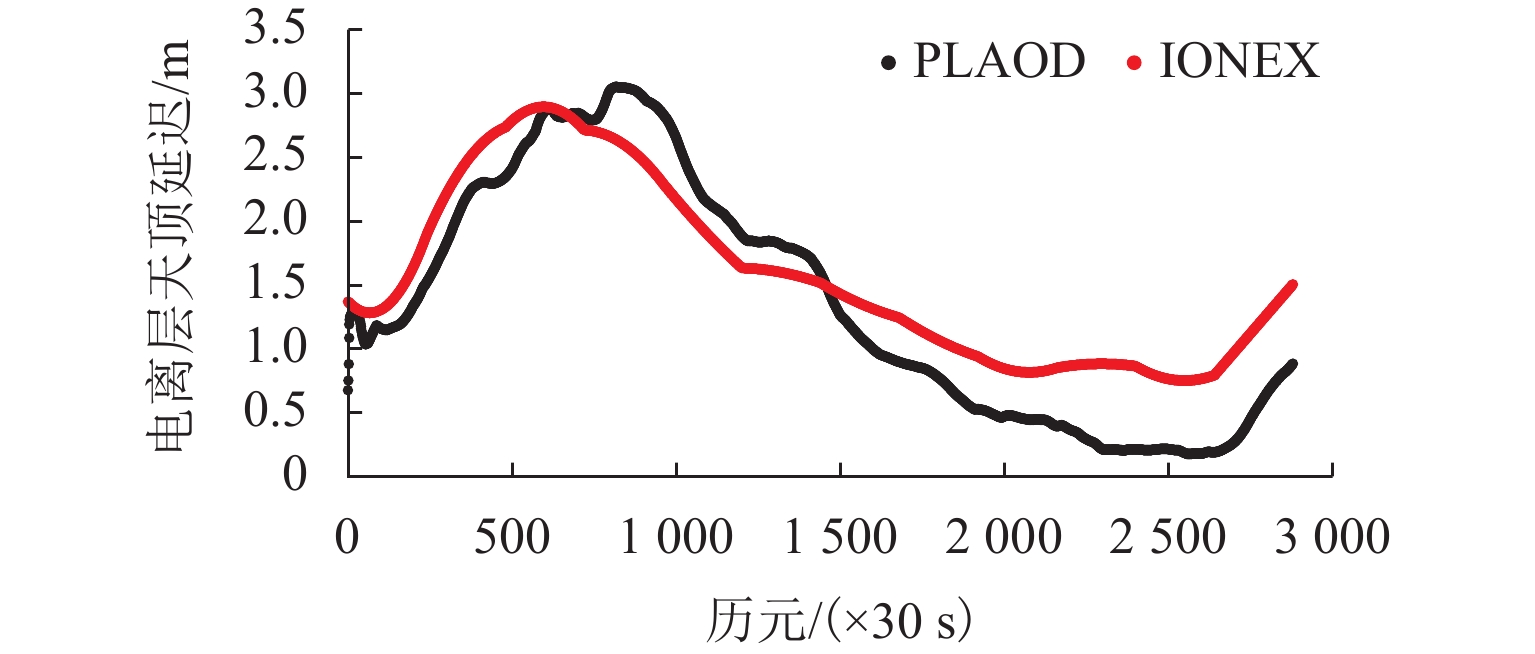
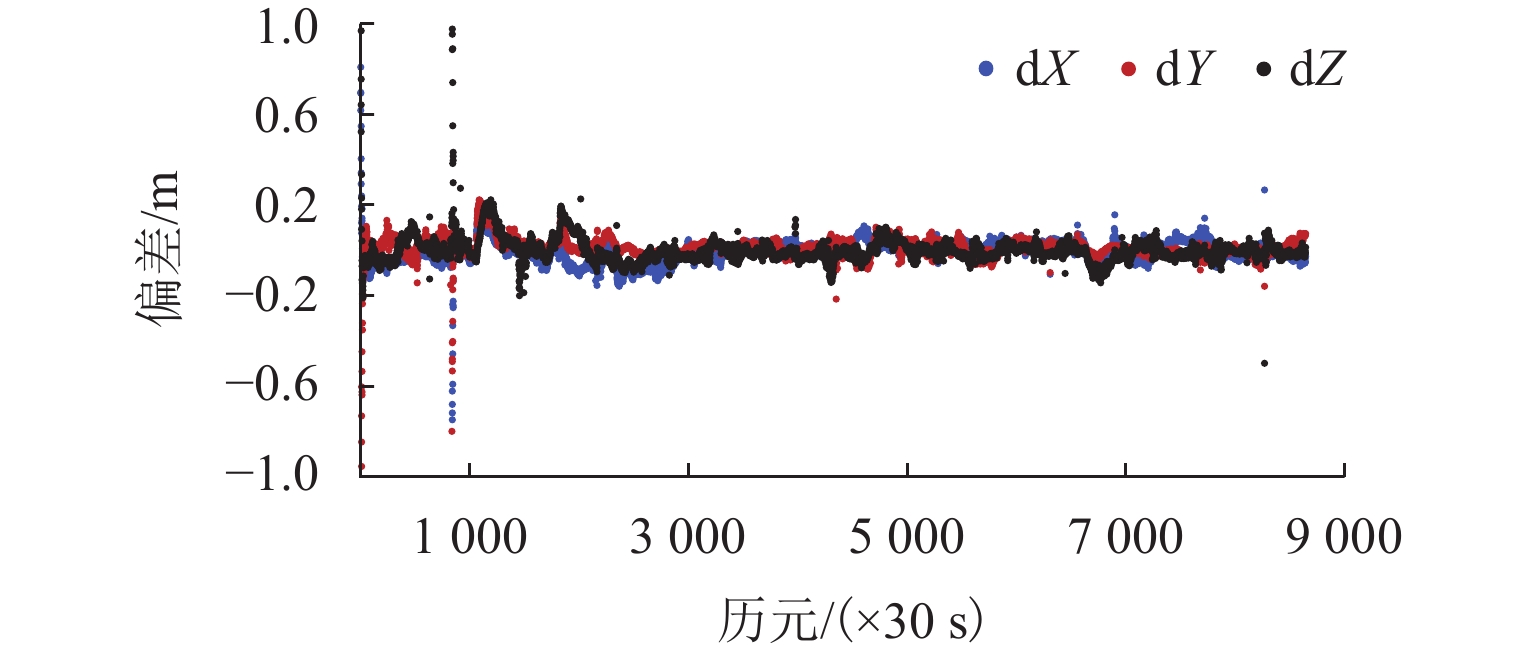
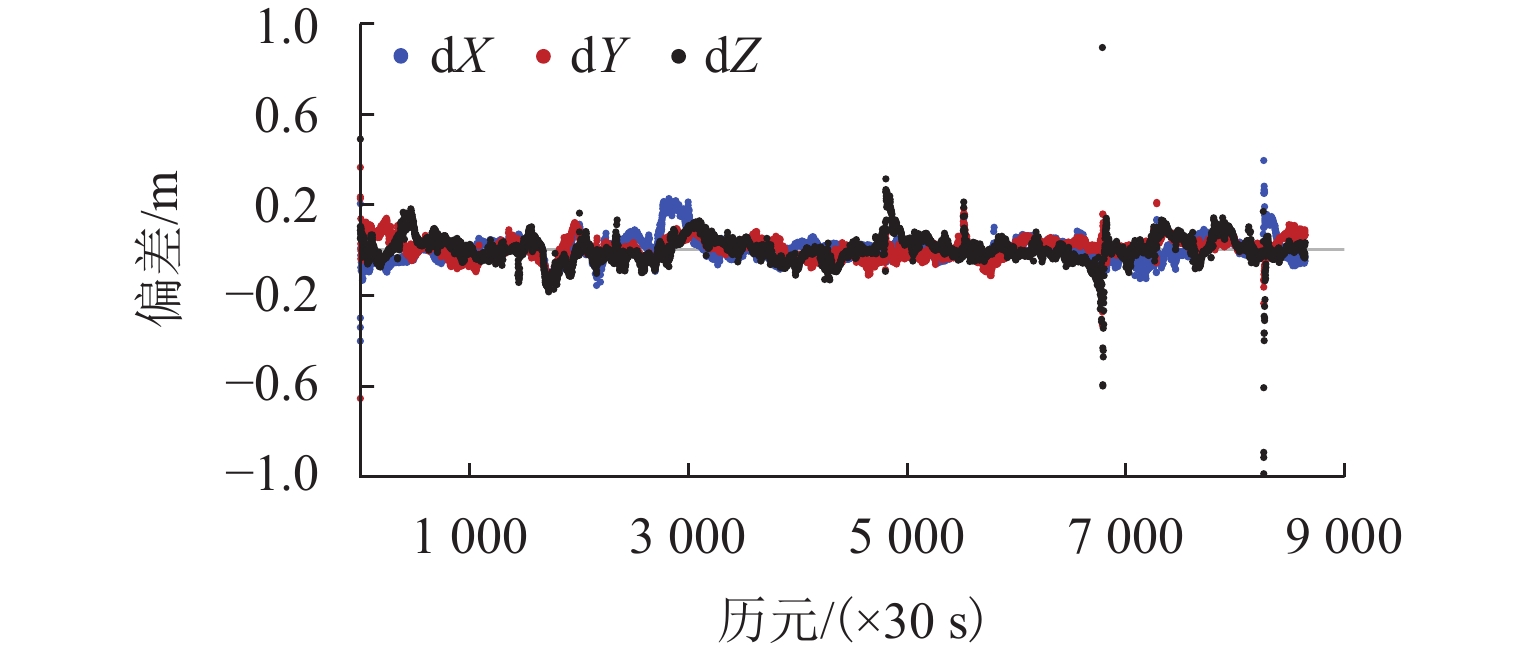
PLAOD （precise location and orbit determination）是西南交通大学自主研发的GPS非差精密定位定轨软件. 该软件目前能够处理GPS观测数据，具有高精度定位、大气反演和低轨卫星轨道确定功能. 本文在介绍PLAOD相关理论的基础之上对其性能进行了分析. 利用多组GPS观测数据进行测试，通过与IGS （international GNSS service）等相关机构精密产品对比，PLAOD具备如下性能：静态定位精度可达毫米级；动态定位精度可达厘米级；静态对流层天顶延迟的估计精度通常优于1 cm，动态对流层天顶延迟的估计精度在2 cm以内；电离层天顶延迟估计结果与IGS的IONEX （ionosphere exchange）产品具有较高的吻合度；与JPL （jet propulsion laboratory）提供的简化动力学低轨卫星轨道相比，几何法确定轨道的准确度可达厘米级.
- PLAOD /
- 精密单点定位 /
- 对流层天顶延迟 /
- 电离层天顶延迟 /
- 精密轨道确定
Abstract:
PLAOD (precise location and orbit determination) is an undifferenced precise GPS data processing software for positioning and orbit determination fully developed by Southwest Jiaotong University. Currently, the software can process GPS observation data, and has the functions of precise positioning, atmospheric inversion and orbit determination for low earth obiter. Following the introduction to basic theory of PLAOD, its performance is focused. Multiple sets of GPS observation data were tested. Compared with the precise product provided by IGS (international GNSS service) and other institutes, PLAOD has shown following features. The static positioning accuracy can reach millimeter level, the kinematic positioning accuracy can reach centimeter level, the estimation precision of the tropospheric zenith delay in static mode is usually better than 1 cm, and the one in kinematic mode is better than 2 cm. There is a high consistence between the ionospheric zenith delay results from PLAOD and the IONEX (ionosphere exchange) product of IGS. In comparison with the reduced dynamic orbit of low earth orbiter provided by JPL (jet propulsion laboratory), the accuracy of orbit determined by geometry method is usually at the centimeter level.
- precise location and orbit determination /
- precise point positioning /
- tropospheric zenith delay /
- ionospheric zenith delay /
- precise orbit determination

HTML全文

图 1 PLAOD数据处理流程

Figure 1. Data processing flowchart of PLAOD

下载: 全尺寸图片幻灯片

图 2 CHAN站2020年1月1日静态坐标偏差序列

Figure 2. Coordinate bias series of CHAN station on 1st Jan, 2020 in static mode

下载: 全尺寸图片幻灯片

图 3 HKWS站2020年1月3日静态坐标偏差序列

Figure 3. Coordinate bias series of HKWS station on 3rd Jan, 2020 in static mode

下载: 全尺寸图片幻灯片

图 4 CHAN站2020年1月1日动态坐标偏差序列

Figure 4. Coordinate bias series of CHAN station on 1st Jan, 2020 in kinematic mode

下载: 全尺寸图片幻灯片

图 5 2011年3月11日MIZU站动态坐标偏差序列

Figure 5. Coordinate bias series of MIZU station in kinematic mode on 11th Mar, 2011

下载: 全尺寸图片幻灯片

图 6 2020年8月12日BJFS 站ZTD序列

Figure 6. ZTD series of BJFS station on 12th Aug, 2020

下载: 全尺寸图片幻灯片

图 7 2020年1月1日TWTF站ZTD序列

Figure 7. ZTD series of TWTF station on 1st Jan, 2020

下载: 全尺寸图片幻灯片

图 8 2008年8月1日机载GPS ZTD序列

Figure 8. ZTD series of airborne GPS on 1st Aug, 2008

下载: 全尺寸图片幻灯片

图 9 TWTF站2020年1月1日电离层天顶延迟序列

Figure 9. Ionospheric zenith delay series of TWTF station on 1st Jan, 2020

下载: 全尺寸图片幻灯片

图 10 2016年1月3日GRACE （A）卫星轨道偏差序列

Figure 10. Orbit bias series of satellite GRACE (A) on 3rd Jan, 2016

下载: 全尺寸图片幻灯片

图 11 2016年1月3日GRACE （B）卫星轨道偏差序列

Figure 11. Orbit bias series of satellite GRACE (B) on 3rd Jan, 2016

下载: 全尺寸图片幻灯片

表 1 误差改正

Table 1. Error correction

误差来源	改正参考	误差来源	改正参考
相对论效应	Neil Ashby^[11]	DCB （需要时）	CODE
卫星天线相位中心	igs_yy.atx	重力延迟	Neil Ashby^[11]
接收机天线相位中心	igs_yy.atx	海潮	IERS2010^[12]
固体潮汐	IERS2010^[12]	极潮	IERS2010^[12]
天线相位转绕	Wu 等, 1993^[13]

下载: 导出CSV

表 2 PLAOD参数处理方案

Table 2. Parameter processing strategy of PLAOD

参数	处理方案
测站坐标	静态时过程噪声为 0，动态时先验值源自伪距单点定位
模糊度	过程噪声为 0
对流层	随机游走，过程噪声默认为 4 cm²/h，动态时顾及历元间高差引起的影响
对流层梯度	随机游走
电离层	随机游走
电离层梯度	随机游走
接收机钟差	先验值源自伪距单点定位
卫星钟差	20 min弧段二阶多项式拟合
卫星坐标	10 阶滑动拉格朗日插值

下载: 导出CSV

表 3 测试站地理点位置

Table 3. Geographic location of testing stations

站点	经度/（°）	纬度/（°）
CHAN（长春）	125.443	43.790
BJFS（北京房山）	115.892	39.609
BJNM（北京）	116.224	40.245
HKSL（香港小冷水）	113.928	22.372
HKWS（香港黄石）	114.335	22.434
JFNG（九峰）	114.491	30.516
LHAZ（拉萨）	91.104	29.657
TWTF（桃园）	121.164	24.954

下载: 导出CSV

表 4 站点解算坐标偏差

Table 4. Coordinate bias of solved stations

站点	年积日	d_N /mm	d_E /mm	d_U /mm	收敛时间 /min
CHAN	001	1.9	−9.2	−11.3	32.0
	002	2.4	−5.7	−7.5	19.0
	003	2.0	−7.1	−9.2	43.0
BJFS	001	2.0	1.2	−1.8	30.0
	002	2.5	0.7	−0.5	21.0
	003	2.5	−0.2	2.8	23.0
BJNM	001	2.6	−3.6	−0.8	29.0
	002	4.5	0.4	1.4	50.0
	003	4.0	−4.5	4.3	46.5
HKSL	001	2.0	0.5	−3.9	30.5
	002	3.8	0.1	1.7	25.0
	003	4.4	−2.5	2.0	20.5
HKWS	001	1.0	1.5	2.2	30.0
	002	3.3	1.9	−0.1	52.5
	003	3.5	−0.3	1.9	104.5
JFNG	001	2.0	3.2	0.6	20.0
	002	2.8	4.4	9.0	13.0
	003	3.1	3.4	8.1	19.0
LHAZ	001	3.6	−1.5	−3.8	42.0
	002	4.1	1.5	−0.3	57.0
	003	3.5	−1.5	−4.4	44.0
TWTF	001	0.8	3.9	−9.3	26.5
	002	4.4	1.0	−5.4	21.5
	003	4.0	0.1	−6.3	19.0

下载: 导出CSV

参考文献(18)

[1]	ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. doi: 10.1029/96JB03860
[2]	KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28. doi: 10.1007/PL00012883
[3]	GAO, Y, SHEN, X. A new method for carrier phase based precise point positioning[J]. Navigation, 2002, 49(2): 109-116. doi: 10.1002/j.2161-4296.2002.tb00260.x
[4]	张小红,李星星,李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报,2017,46(10): 1399-1407. doi: 10.11947/j.AGCS.2017.20170327 ZHANG Xiaohong, LI Xingxing, LI Pan. Review of GNSS PPP and its application[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1399-1407. doi: 10.11947/j.AGCS.2017.20170327
[5]	GENG Jianghui. Rapid integer ambiguity resolution in GPS precise point positioning[D]. Nottingham: University of Nottingham, 2010.
[6]	SIMON B, RICHARD B. L, MARCELO C. S. The precise point positioning software centre: an insight into online PPP services[R]. Buenos Aires: IAG, 2009.
[7]	IBANEZ D, ROVIRA G A, SANZ J, et al. The GNSS laboratory tool suite (gLAB) updates: SBAS, DGNSS and global monitoring system[C]//9th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing. Noordwijk: IEEE, 2018: 1-11.
[8]	TAKASU T. RTKLIB: open source program Package for RTK-GPS[R]. Tokyo: Tokyo University of Marine Science and Technology, 2009.
[9]	GENG J H, CHEN X Y, PAN Y X, et al. PRIDE PPP-AR: an open-source software for GPS PPP ambiguity resolution[J]. GPS Solutions, 2019, 23(4): 1-10.
[10]	BANVILLE S, GENG J H, LOYER S, et al. On the interoperability of IGS products for precise point positioning with ambiguity resolution[J]. Journal of Geodesy, 2020, 94(1): 1-15. doi: 10.1007/s00190-019-01332-z
[11]	ASHBY N. Relativity in the global positioning system[J]. Living Reviews in Relativity, 2003, 6(1): 1-42. doi: 10.12942/lrr-2003-1
[12]	PETIT G, LUZUM B. IERS Conventions (2010) [EB/OL]. [2021-7-26]. https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html.
[13]	WU J T, WU S C, HAJJ G A, et al. Effects of antenna orientation on GPS carrier phase[J]. Manuscripta Geodaetica, 1993, 18(2): 91-98.
[14]	WELCH G, BISHOP G. An introduction to the Kalman filter[EB/OL]. [2021-07-26]. https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf
[15]	GUO J Y, YUAN Y D, KONG Q L, et al. Deformation caused by the 2011 eastern Japan great earthquake monitored using the GPS single-epoch precise point positioning technique[J]. Applied Geophysics, 2012, 9(4): 483-493. doi: 10.1007/s11770-012-0360-2
[16]	KOUBA J. Implementation and testing of the gridded Vienna mapping function 1 (VMF1)[J]. Journal of Geodesy, 2008, 82(4/5): 193-205.
[17]	BOEHM J, NIELL A, TREGONING P, et al. Global mapping function: a new empirical mapping function based on numerical weather model data[J]. Geophysical Research Letters, 2006, 33(7): 304-317.
[18]	BOEHM J, HEINKELMANN R, SCHUH H. Short note: a global model of pressure and temperature for geodetic applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. doi: 10.1007/s00190-007-0135-3