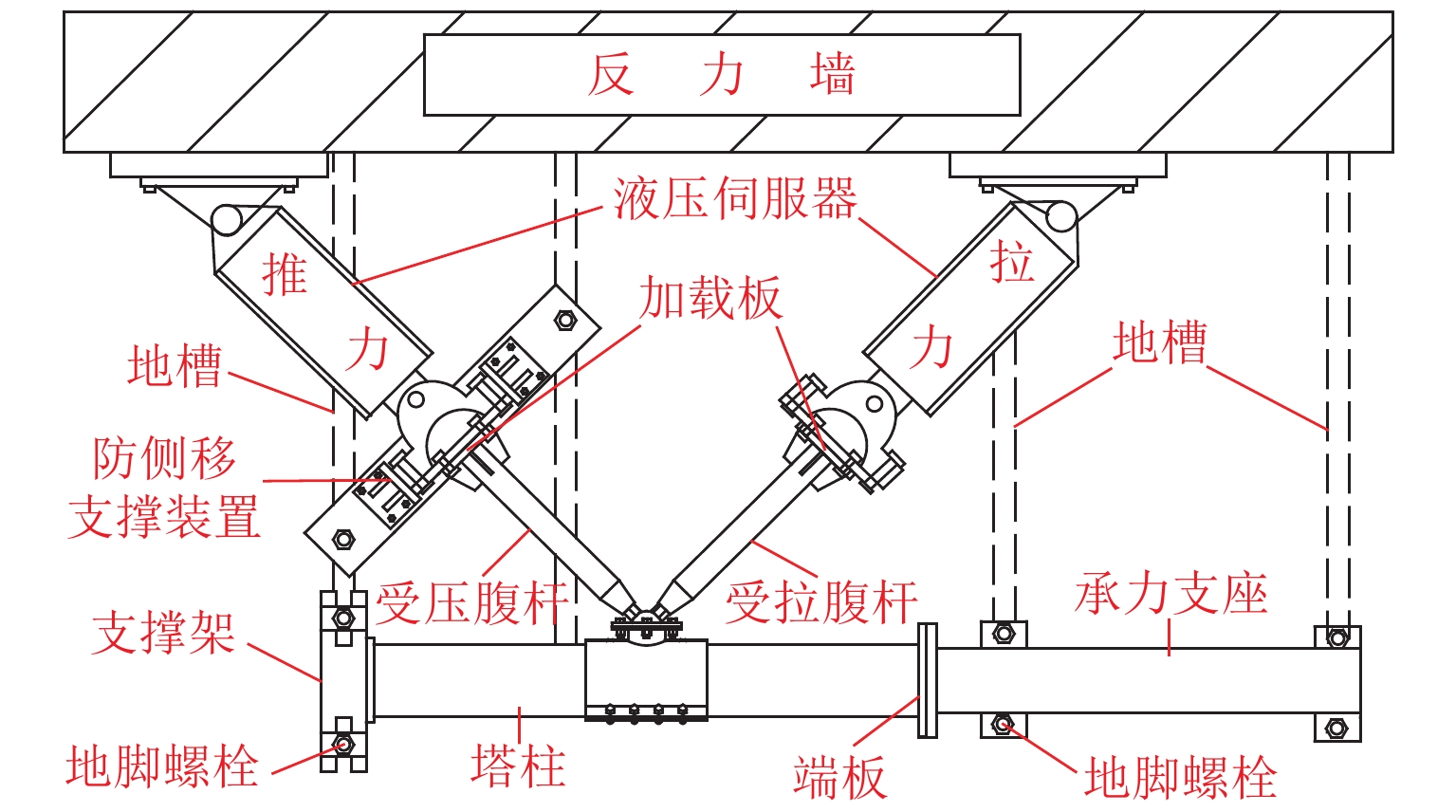
Mechanical Property Analysis of Spherical Joints of Concrete-Filled Steel Tubular Wind Power Towers
-
摘要:
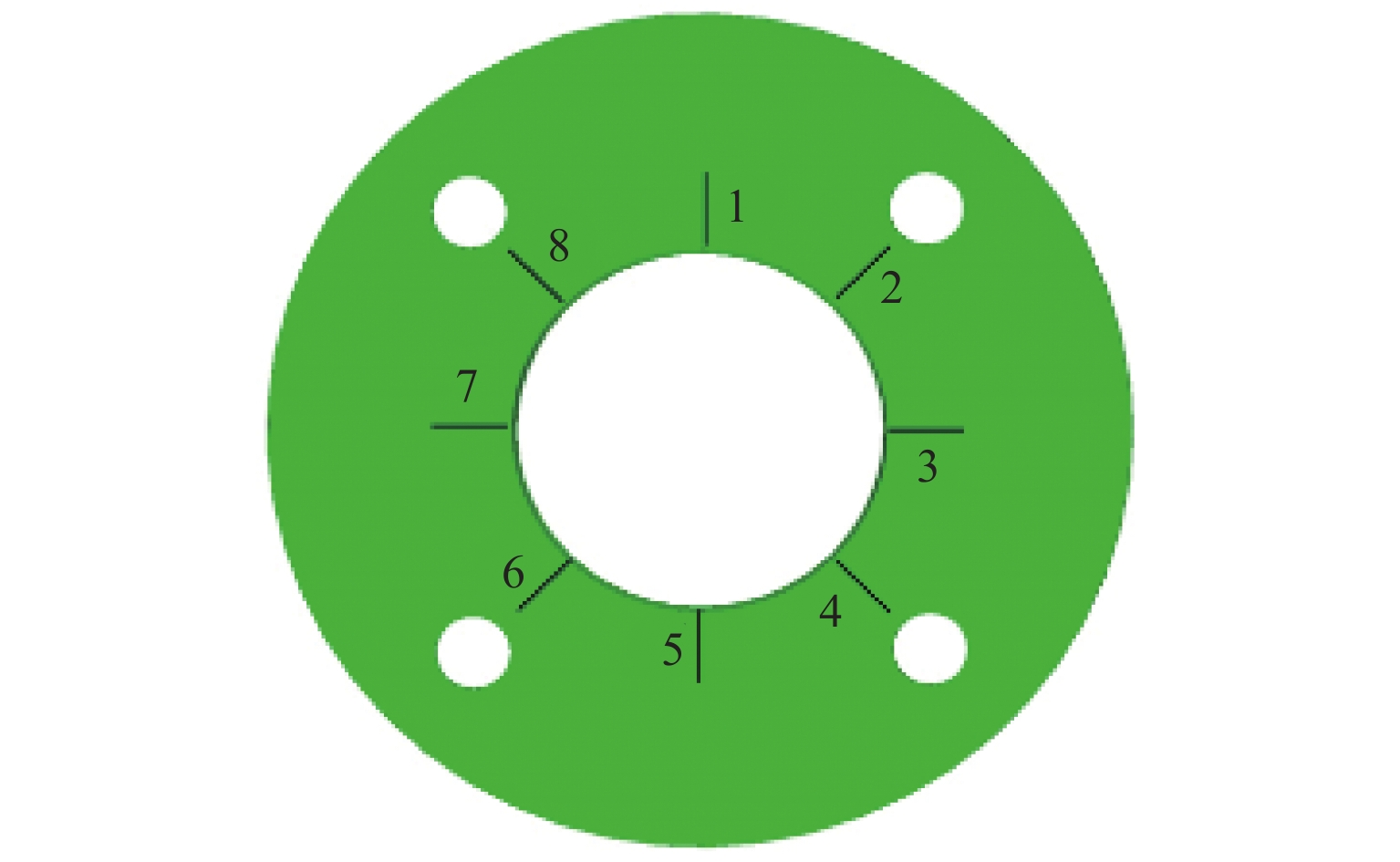
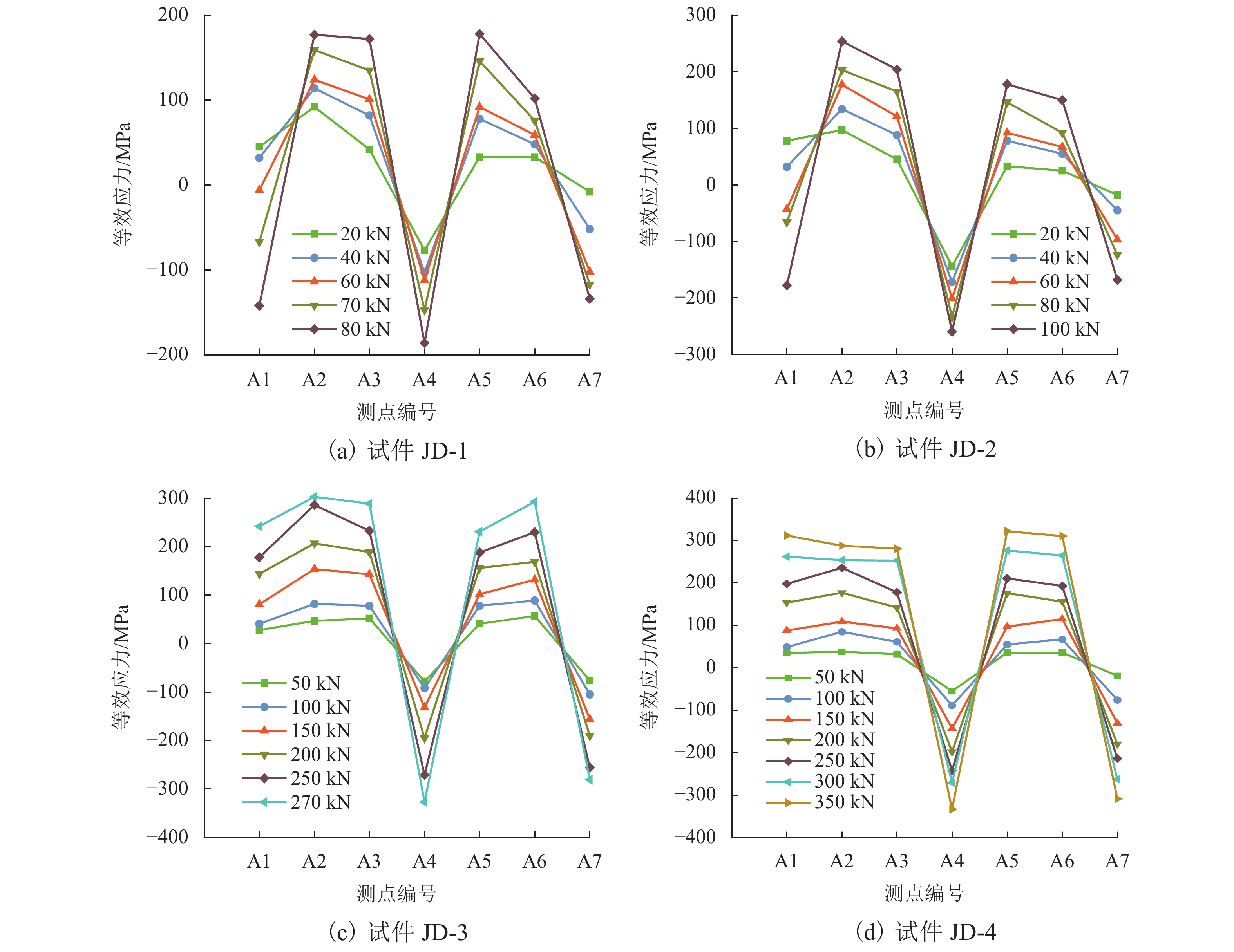
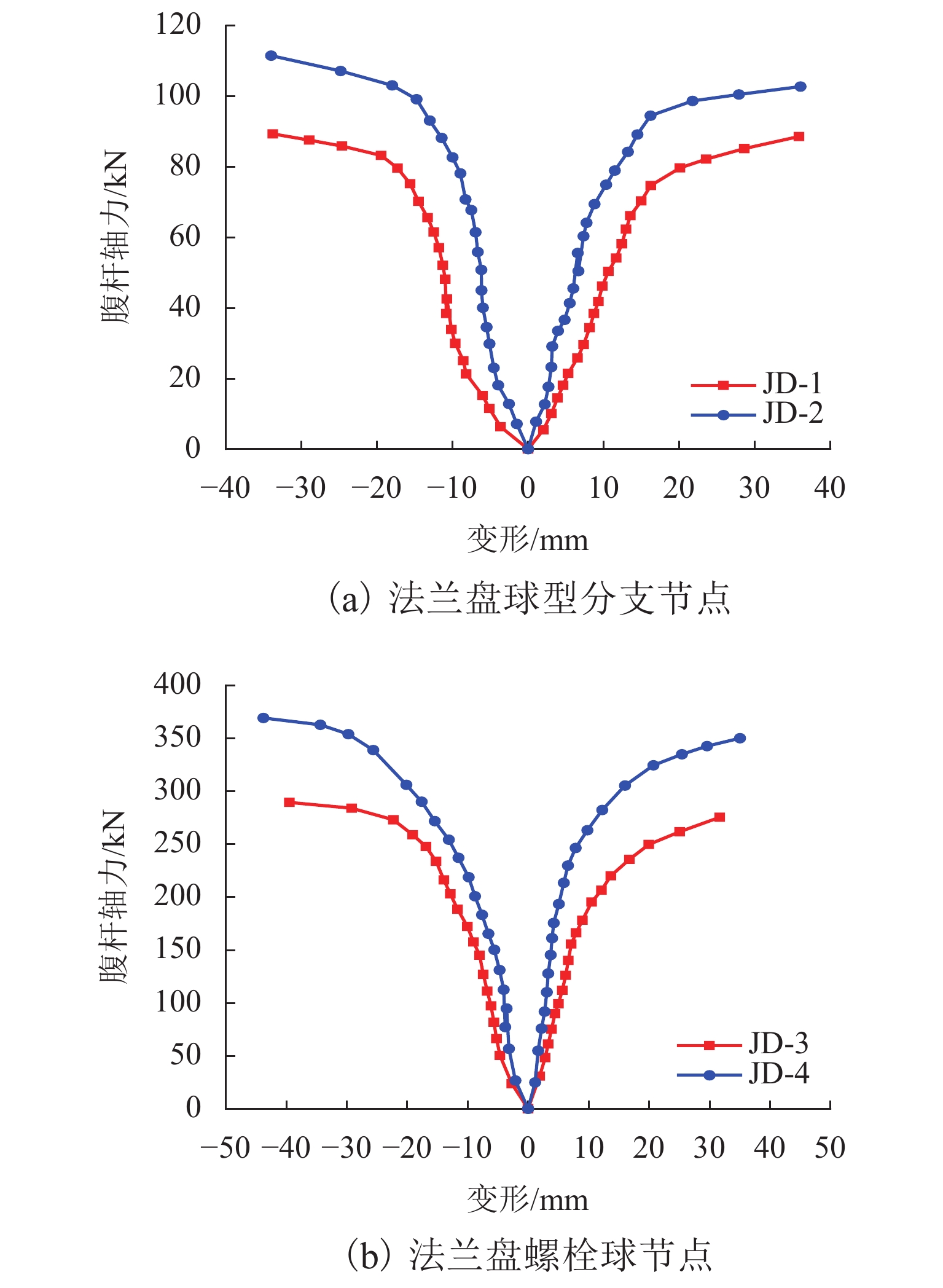
为寻找更适合钢管混凝土格构式风电塔架的节点形式,开展了2个法兰盘球型分支节点和2个法兰盘螺栓球节点模型的静力试验,并对其进行有限元分析,以球台高度和厚度为变化参数,分别对比了2种节点的破坏模式、法兰盘等效应力分布、腹杆轴力-变形曲线等. 研究结果表明:法兰盘球型分支节点的破坏模式为高强螺栓剪切破坏,法兰盘螺栓球节点的破坏模式为球台焊缝撕裂破坏和屈曲-撕裂破坏;与法兰盘球型分支节点相比,法兰盘螺栓球节点的法兰盘和球台的等效应力分布均匀,材料利用率较高,其最大应力绝对值分别提高了19%、52%,承载能力较强;腹杆轴力-变形曲线的塑性阶段长,延性较好;对球台高度或厚度的变化反映在节点极限承载力上更敏感,有更高的极限承载力;法兰盘螺栓球节点有进一步推广应用的价值.
Abstract:In order to find a more suitable joint form for the concrete-filled steel tubular (CFST) lattice wind power tower, static tests of models for two flanged spherical branch joints and two flanged bolted spherical joints were carried out, and the finite element analysis was performed. By taking the height and thickness of the table as the changing parameters, the failure modes of the two kinds of joints, the equivalent stress distribution of the flange, and the axial force-deformation curve of the web rod were compared. The research results show that the failure modes of flanged spherical branch joints are shear failure of high-strength bolts, and those of flanged bolted spherical joints are table weld tear failure and buckling-tear failure. Compared with that of the flanged spherical branch joint, the equivalent stress distribution of the flange and the table of the flanged bolted spherical joint is uniform, and the material utilization rate is higher; the absolute values of the maximum stress are increased by 19% and 52%, respectively, and the bearing capacity is strong. The plastic stage of the axial force-deformation curve of the web rod is long, and the ductility is excellent. The change in the height or thickness of the table is more sensitive to the ultimate bearing capacity of the joint, and a higher ultimate bearing capacity is observed. The flanged bolted spherical joint can be promoted and widely applied.
-
表 1 试件参数
Table 1. Specimen parameters
类型 试件
编号包裹体尺寸/
mm球台外径/
mmb/mm h/mm 腹杆尺寸/
mm螺纹外径/
mm法兰盘球形
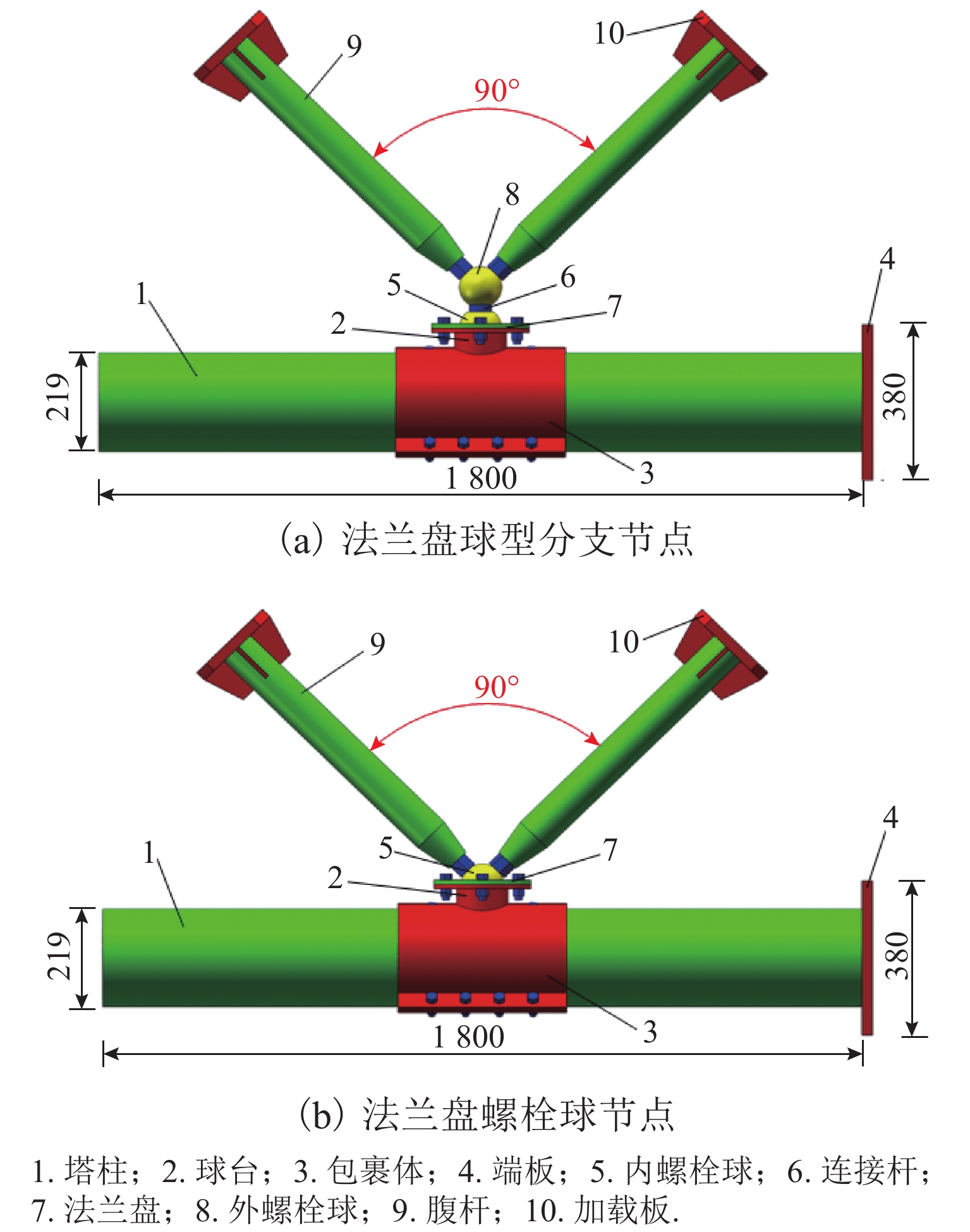
分支节点JD-1 ϕ241 × 11 ϕ122 11 50 ϕ89 × 3.5 × 700 M52 JD-2 ϕ241 × 11 ϕ114 7 60 ϕ89 × 3.5 × 700 M52 法兰盘
螺栓球节点JD-3 ϕ241 × 11 ϕ122 11 50 ϕ89 × 3.5 × 700 JD-4 ϕ241 × 11 ϕ114 7 60 ϕ89 × 3.5 × 700 表 2 钢材力学性能指标
Table 2. Mechanical property indexes of steels
部件 fy /MPa fu /MPa E/GPa 腹杆 300 479 204 塔柱 324 485 202 球台 302 464 199 法兰盘 316 479 201 表 3 节点承载力
Table 3. Joint bearing capacity
试件编号 试验值/kN 模拟值/kN 误差/% JD-1 89.0 94.1 5.7 JD-2 112.0 118.5 5.8 JD-3 289.0 281.3 2.7 JD-4 369.0 351.4 4.8 表 4 参数拓展结果
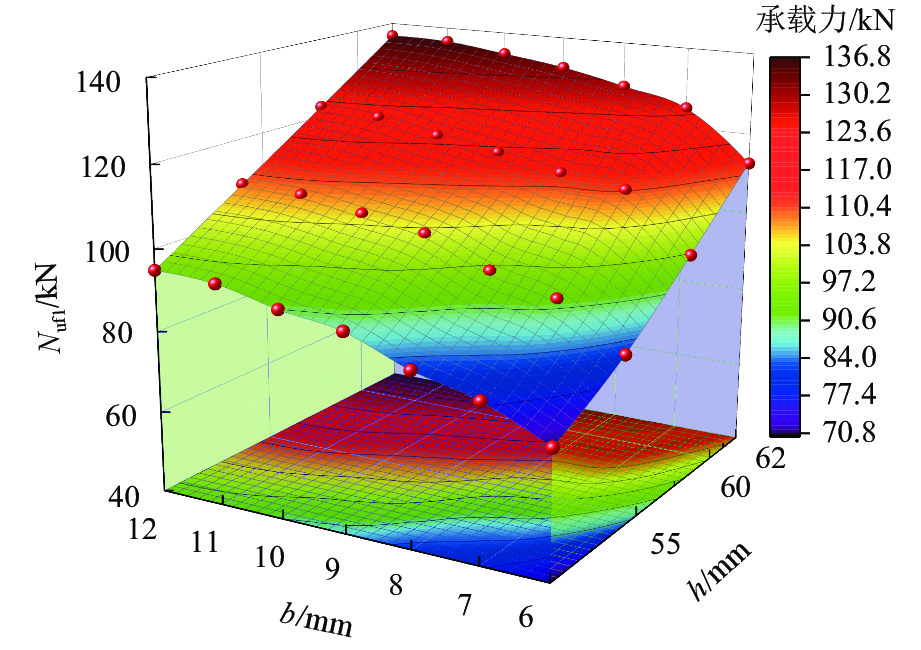
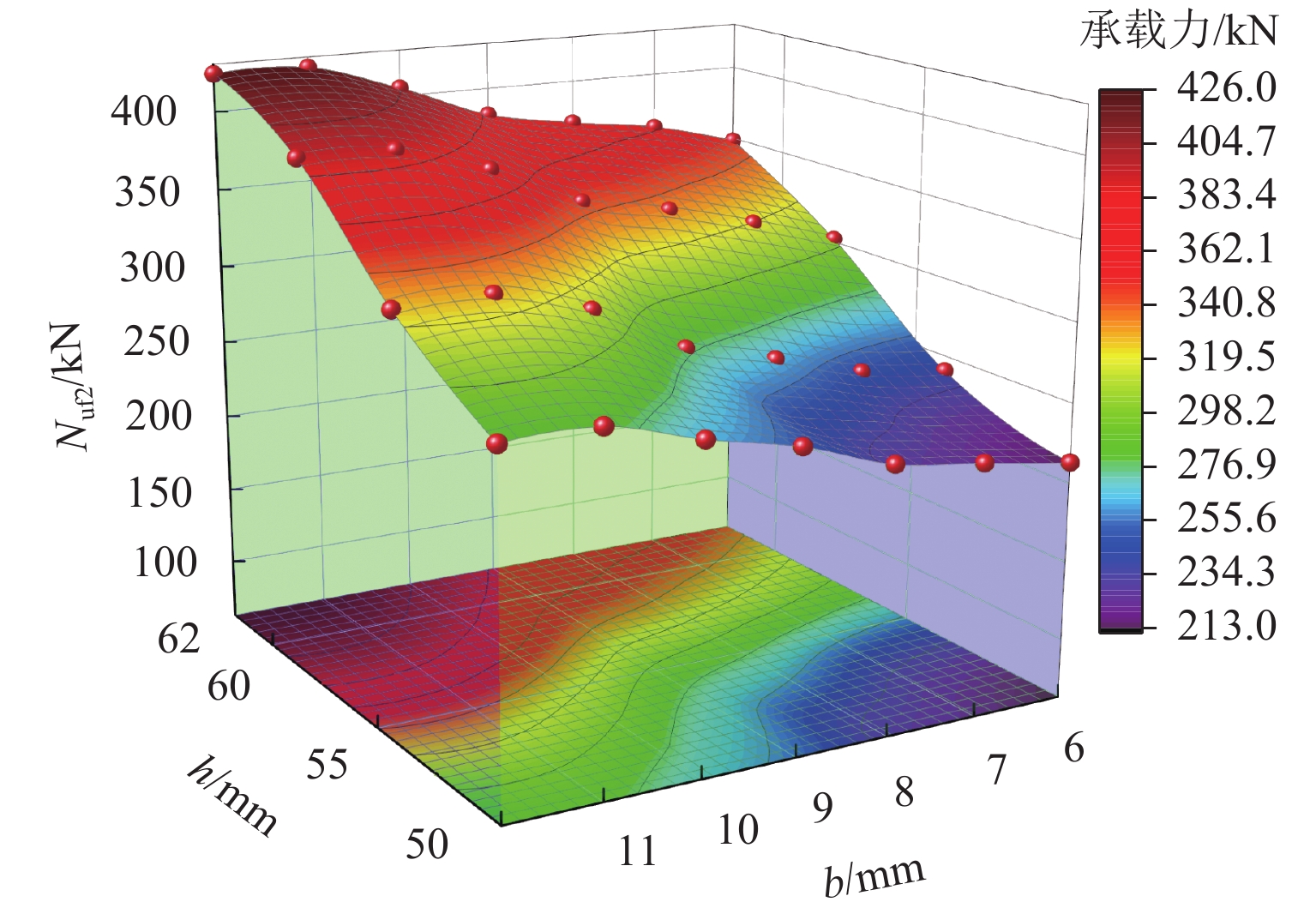
Table 4. Parameter expansion results
节点编号 h/mm b/mm Nuf1/kN Nuf2/kN A-1 50 6 70.9 213.1 A-2 7 78.1 222.3 A-3 8 82.1 231.1 A-4 9 88.2 248.5 A-5 10 90.6 264.6 A-6 11 94.1 281.3 A-7 12 94.9 287.9 B-1 55 6 85.1 251.1 B-2 7 96.3 261.1 B-3 8 100.3 278.3 B-4 9 106.5 292.8 B-5 10 108.8 325.7 B-6 11 111.4 341.7 B-7 12 112.1 342.4 C-1 60 6 105.1 334.8 C-2 7 118.5 351.4 C-3 8 120.6 363.3 C-4 9 123.1 373.2 C-5 10 125.9 395.2 C-6 11 128.6 413.4 C-7 12 129.7 416.6 D-1 62 6 112.6 348.3 D-2 7 124.9 363.3 D-3 8 128.9 371.7 D-4 9 132.3 382.3 D-5 10 134.5 405.2 D-6 11 136.4 423.4 D-7 12 136.7 424.9 -
[1] DUAN H B. Emissions and temperature benefits: the role of wind power in China[J]. Environmental Research, 2017, 152: 342-350. doi: 10.1016/j.envres.2016.07.016 [2] 张兰娣,张龙君,马轶群,等. 风电高塔架的前景分析[J]. 河北建筑工程学院学报,2018,36(3): 97-99,104.ZHANG Landi, ZHANG Longjun, MA Yiqun, et al. An analysis of the prospect of high tower of wind turbine[J]. Journal of Hebei institute of Architecture and Civil Engineering, 2018, 36(3): 97-99,104. [3] ADAM Z, WOLNIEWICZ K. The impact of supporting tower on wind turbine noise emission[J]. Applied Acoustics, 2019, 155: 260-270. [4] HUANG X G, LI B K, ZHOU X H, et al. Geometric optimisation analysis of steel-concrete hybrid wind turbine towers[J]. Structures, 2022, 35: 1125-1137. doi: 10.1016/j.istruc.2021.08.036 [5] 董崇海. 钢-混凝土组合结构风电塔架力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. [6] 刘海锋,朱彬荣,张宏杰,等. 钢管格构式和圆筒式塔架对风力机尾流扰动特性对比研究[J]. 太阳能学报,2019,40(7): 2036-2044.LIU Haifeng, ZHU Binrong, ZHANG Hongjie, et al. Comparative study on disturbance properties of tubular latticed and pipe tower on wake of wind turbines[J]. Acta Energiae Solaris Sinica, 2019, 40(7): 2036-2044. [7] 陈娟,聂建国,周成野. 钢管混凝土T形相贯节点应力集中系数研究[J]. 建筑结构学报,2018,39(3): 149-157.CHEN Juan, NIE Jianguo, ZHOU Chengye. Study on stress concentration factor of concrete-filled steel tubular T-joints[J]. Journal of Building Structures, 2018, 39(3): 149-157. [8] 高春彦,史治宇,牛丽华,等. 圆钢管混凝土K型焊接管板节点试验研究和有限元分析[J]. 中南大学学报(自然科学版),2017,48(3): 769-778.GAO Chunyan, SHI Zhiyu, NIU Lihua. Experimental study and finite element analysis of concrete-filled circular steel tubular K-type welded tube-gusset joints[J]. Journal of Central South University, 2017, 48(3): 769-778. [9] 赵必大,刘成清,章圣冶,等. Y型圆钢管相贯节点轴向刚度计算模型[J]. 西南交通大学学报,2015,50(5): 872-878.ZHAO Bida, LIU Chengqing, ZHANG Shengye, et al. Calculation model for axial rigidity of CHS Y-type joints[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 872-878. [10] 宋谦益. 圆钢管混凝土-钢管K形节点的力学性能研究[D]. 北京: 清华大学, 2010. [11] 王鹏,王湛,潘建荣,等. 空间隔板焊接X形圆钢管相贯节点受力性能试验研究[J]. 建筑结构学报,2019,40(3): 221-229.WANG Peng, WANG Zhan, PAN Jianrong, et al. Investigation on mechanical behavior of X-shaped welded spatial partition plate tubular joints[J]. Journal of Building Structures, 2019, 40(3): 221-229. [12] 蔡健,王永琦,陈庆军,等. 一种新型单层网壳节点的力学性能研究[J]. 西南交通大学学报,2019,54(1): 145-153.CAI Jian, WANG Yongqi, CHEN Qingjun, et al. Research on mechanical behaviours of new joints of single-layer reticulated shells[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 145-153. [13] MUSA I A, MASHIRI F R. Stress concentration factor in concrete-filled steel tubular K-joints under balanced axial load[J]. Thin-Walled Structures, 2019, 139: 186-195. doi: 10.1016/j.tws.2019.03.003 [14] LI F, DENG H Z, HU X Y. Resistance of gusset-tube DK-joints stiffened by 1/2 annular plates in transmission towers[J]. Journal of Constructional Steel Research, 2019, 159: 560-573. doi: 10.1016/j.jcsr.2019.05.013 [15] 李斌,赵振中,程亚超. 钢管混凝土格构式风电塔架节点力学性能对比分析[J]. 重庆理工大学学报(自然科学),2020,34(7): 108-113,175.LI Bin, ZHAO Zhengzhong, CHENG Yachao. Comparative analysis of mechanical properties of concrete-filled steel tubular lattice wind turbine tower joints[J]. Journal of Chongqing University of Technology (Natural Science), 2020, 34(7): 108-113,175. [16] 韩林海. 钢管混凝土结构: 理论与实践[M]. 3版. 北京: 科学出版社, 2016. -




 下载:
下载: