Mechanism of High-Speed Train Crosswind Overturning Stability Based on Frequency Domain Analysis
-
摘要:
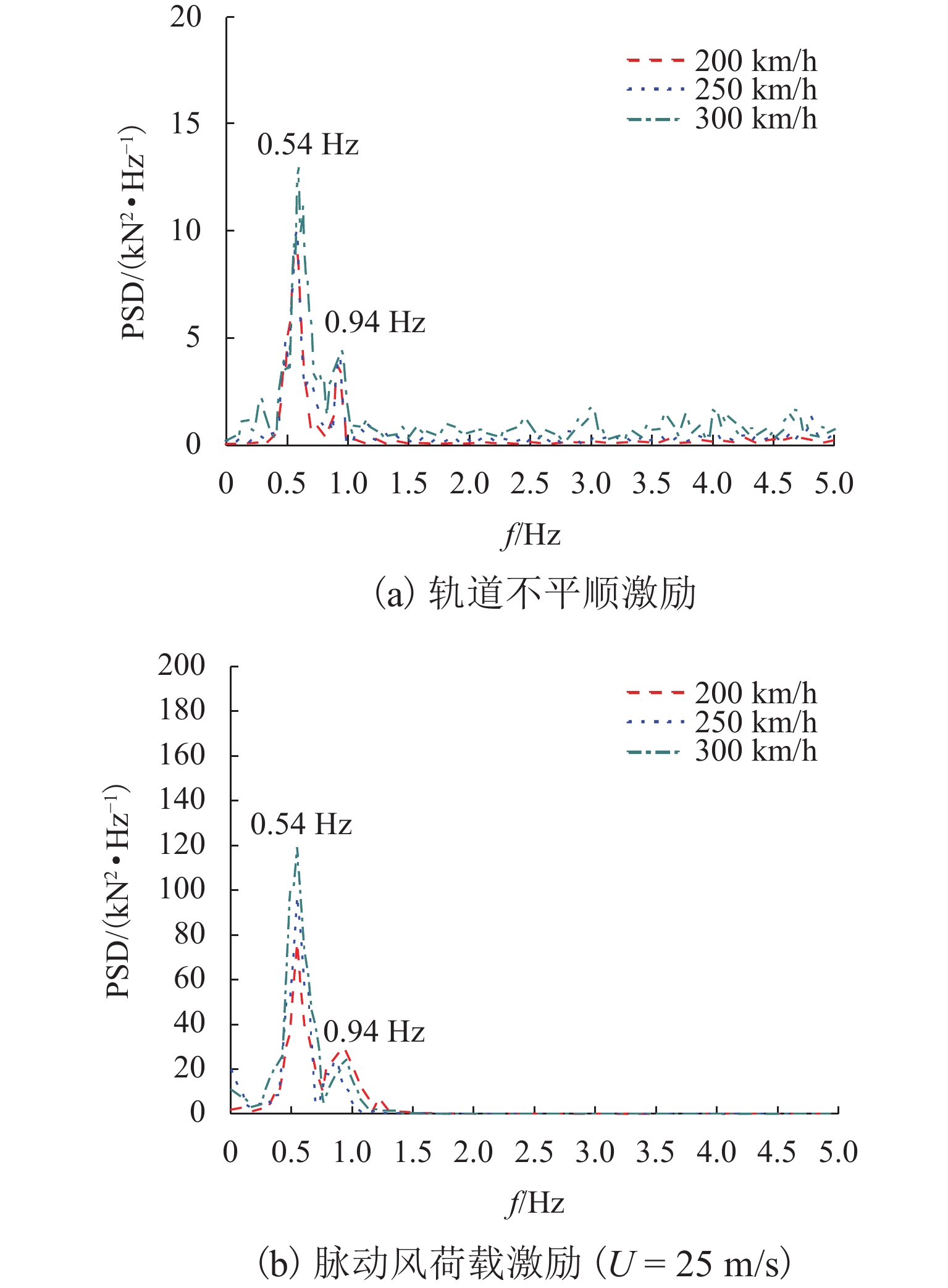
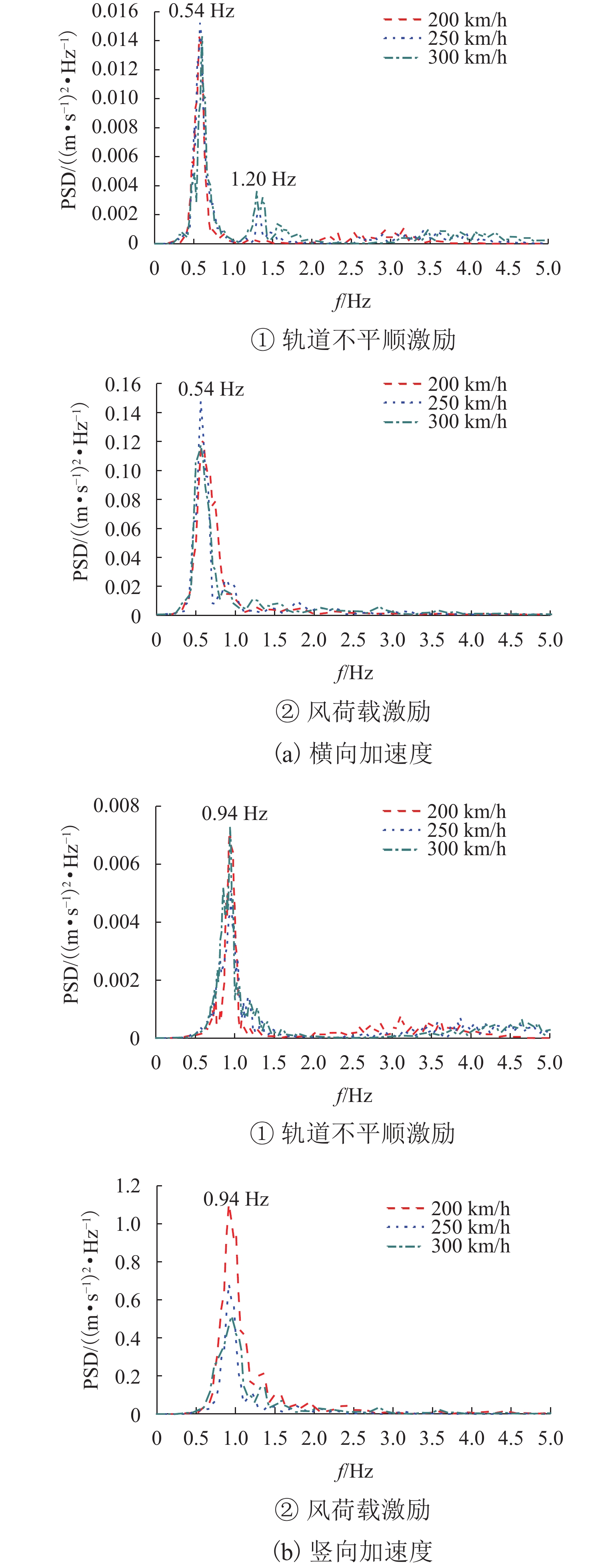
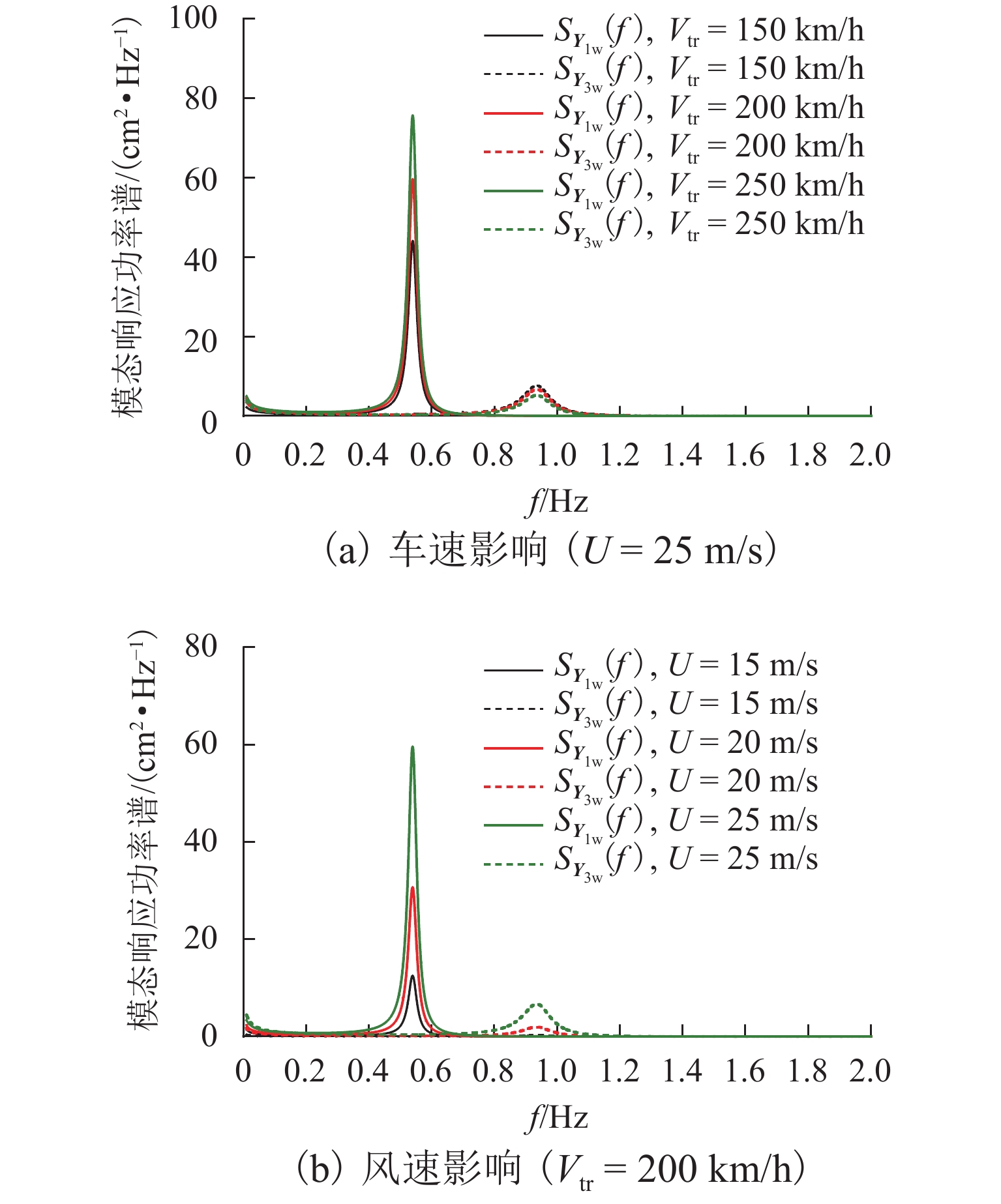
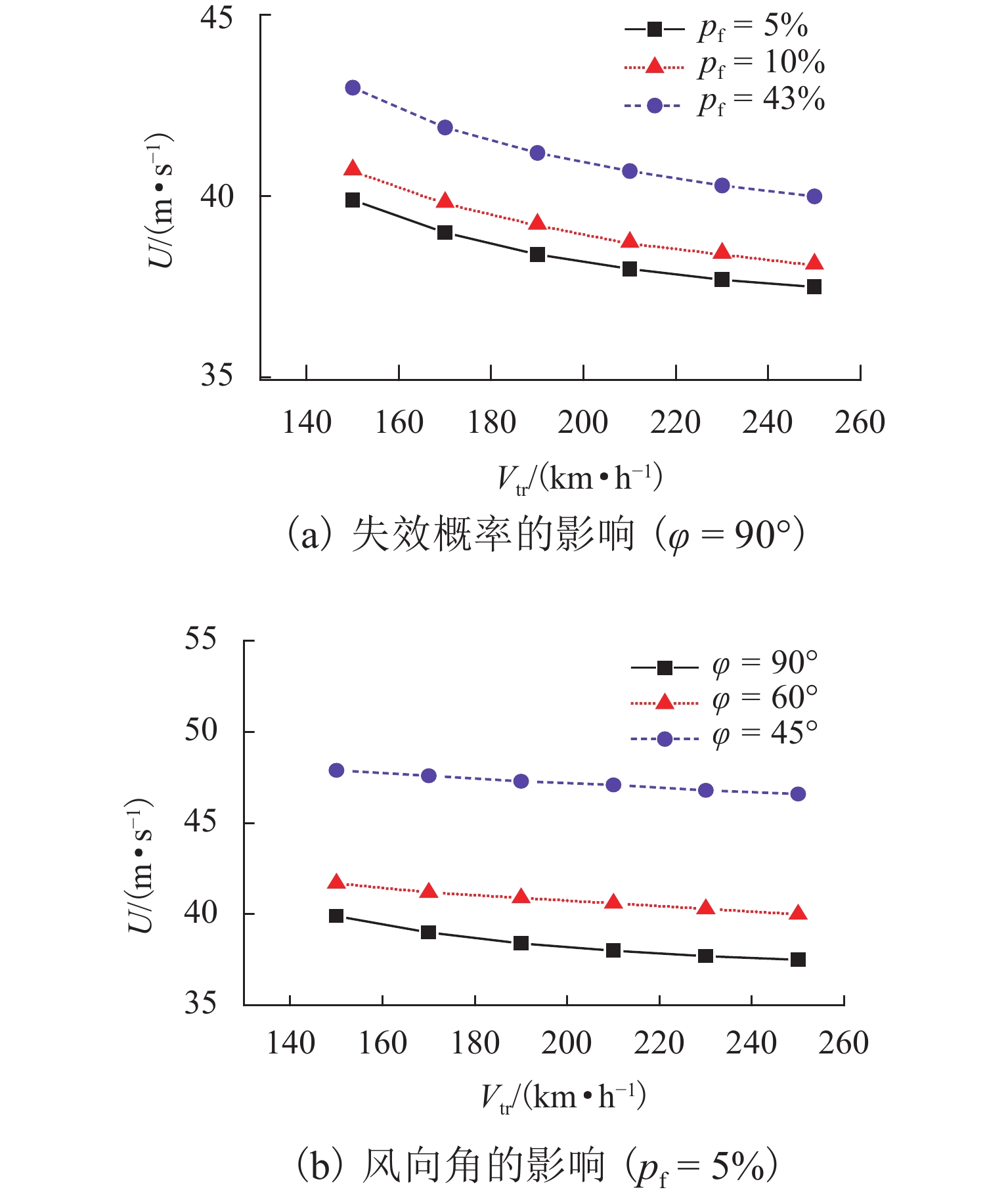
侧风作用下列车的动态环境以轮轨相互作用为主向，以空气动力作用为主演变，列车的侧风倾覆行为成为威胁列车行车安全性的主要诱因. 首先，采用精细化车-轨耦合模型开展列车侧风倾覆的频域特性分析，以明确侧风倾覆响应对列车模型的敏感性；基于考虑模态特性的频域分析框架，推导脉动风及轨道不平顺与列车倾覆动力响应间的传递函数，结合相应参数进行分析，以直观揭示列车的侧风倾覆机理. 结果表明：列车倾覆行为受绕车体下心侧滚模态和车体沉浮模态控制影响，其风荷载影响要明显大于轨道不平顺；在轨道不平顺激励下，第一阶模态贡献主要由轨向不平顺引起，第二阶模态贡献主要由高低不平顺引起，在脉动风荷载激励下，其顺风向脉动风分量起主要贡献；车速、风速和风向角的增大都会引起列车动力响应的增大，进而降低列车安全运营时的最大允许风速；失效概率的增大会降低动力响应的极值，进而提高安全运营风速.
Abstract:The dominant factor impacting the dynamic performance of a train under a crosswind changes from wheel-rail interactions to the aerodynamic force, making the crosswind overturning risk the main threat to safe train operation. This study first analyzes the train overturning stability using a refined coupling model to reveal its sensitivity to the train model. On the basis of a frequency domain framework accounting for the modal characteristic, transfer functions between the wind turbulence and track irregularities and the overturning responses are derived. The mechanism of train crosswind overturning is then intuitively interpreted via a parameter analysis. The results show that the overturning behavior of a train is controlled by the rolling mode around the lower center of the car body and the floating mode of the car body and that the influence of the wind load is significantly greater than that of track irregularities. Under track irregularity excitation, the first modal response primarily arises from the alignment component, while the second modal response arises from the vertical component. Under a wind load, the longitudinal fluctuating wind component plays a major role. Increasing the train speed, wind velocity, and wind direction angle increases the dynamic response of the train and reduces the maximum allowable wind speed to safely run the train. An increase in the failure probability can reduce extreme responses and increase the wind speed for safe operation.
-
Key words:
- wind effects /
- high-speed train /
- overturning risk /
- frequency domain analysis /
- analytical models
-
图 2 顺风向随机风场模拟及列车风速时程提取
Figure 2. Longitudinal turbulence field and the time history of train wind speed
图 6 轨道不平顺激励下模态频响函数及响应功率谱密度
Figure 6. Modal transfer function and PSDs under track irregularities excitations
图 7 风荷载激励下模态频响函数及响应功率谱密度
Figure 7. Modal transfer function and PSDs under turbulence wind excitation
图 8 模态响应功率谱密度参数分析
Figure 8. Parameter analysis of PSDs under turbulence wind excitation
图 9 失效概率及风向角对概率特征风速曲线的影响
Figure 9. Effects of failure probability and wind angle on PCWCs
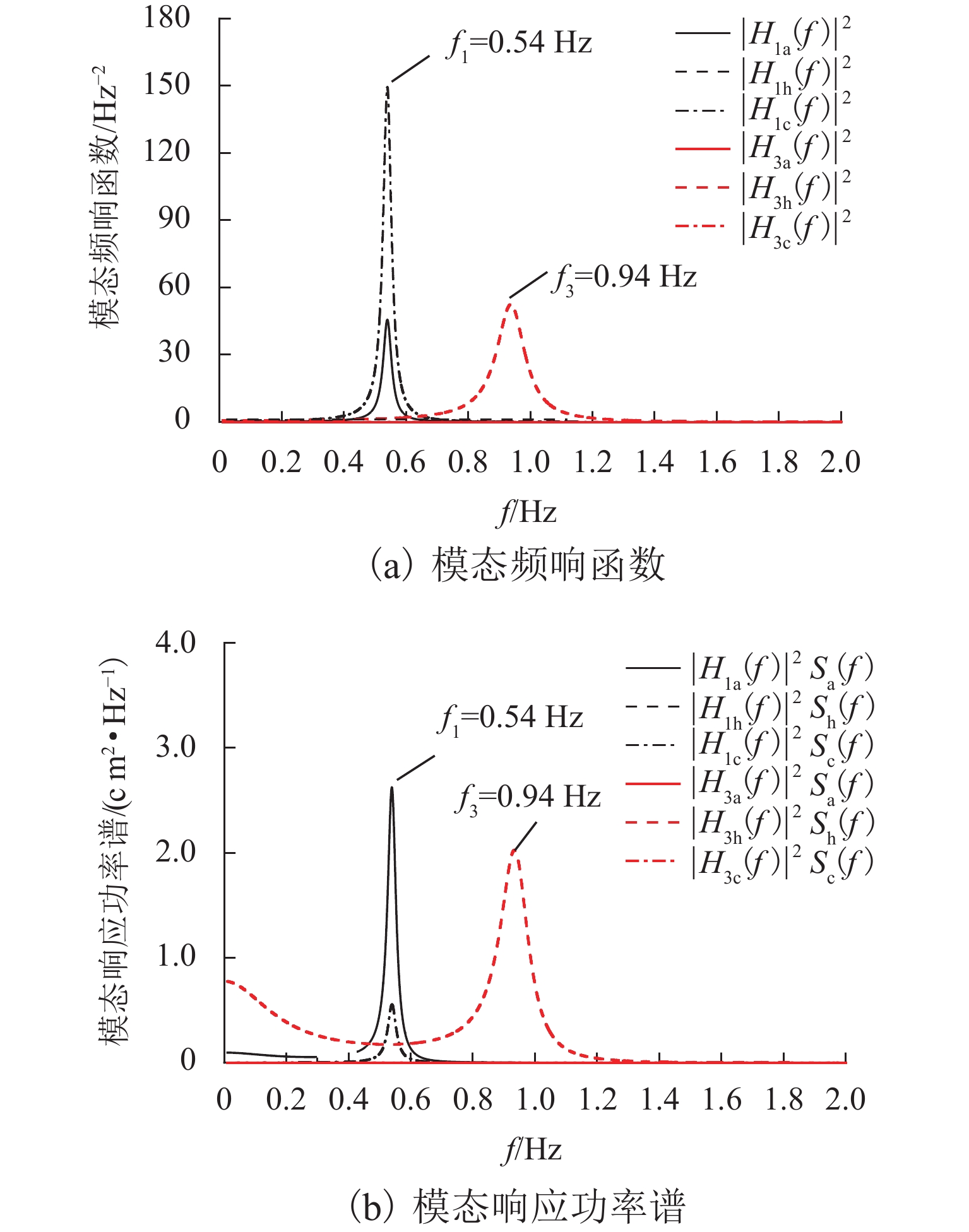
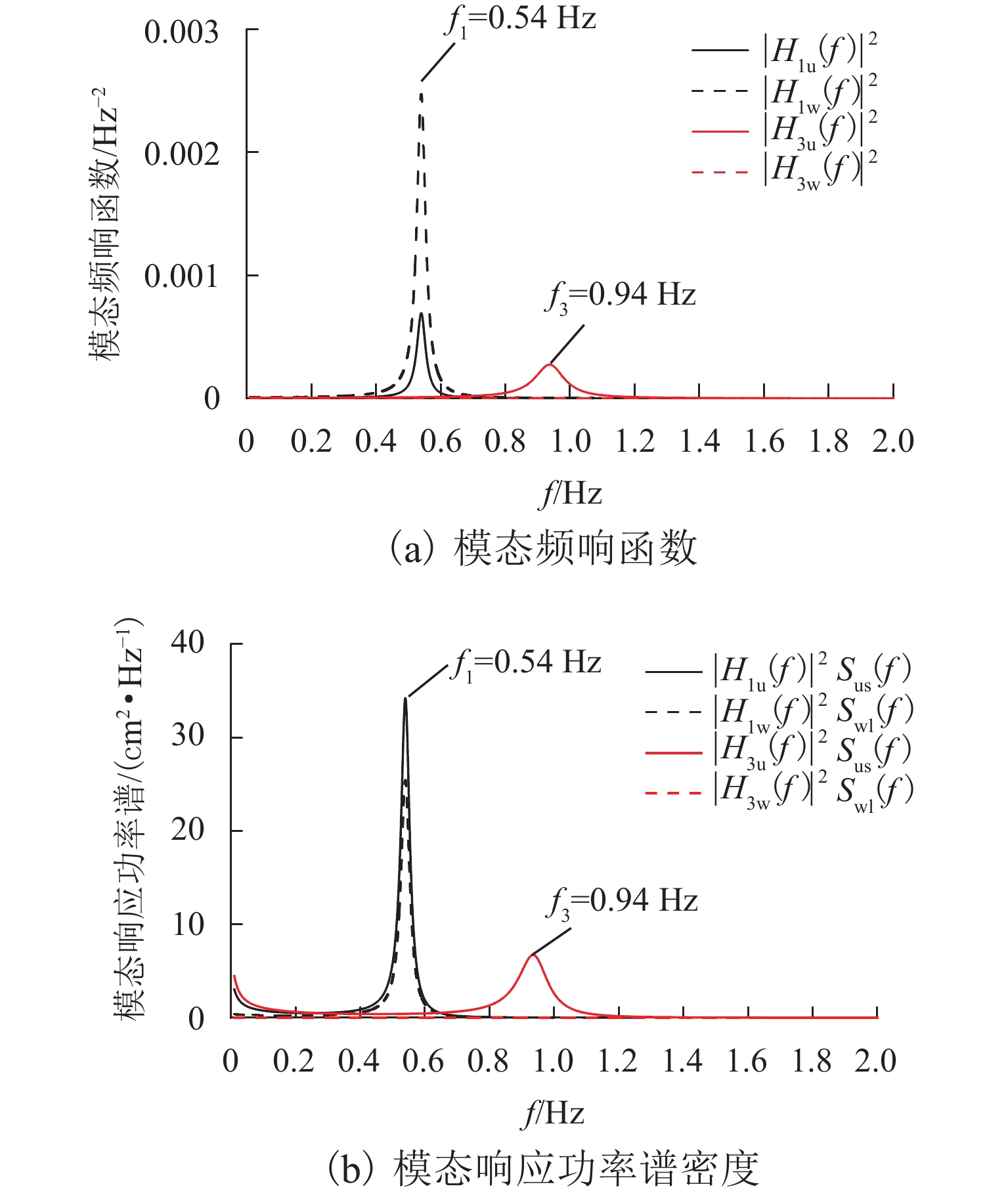
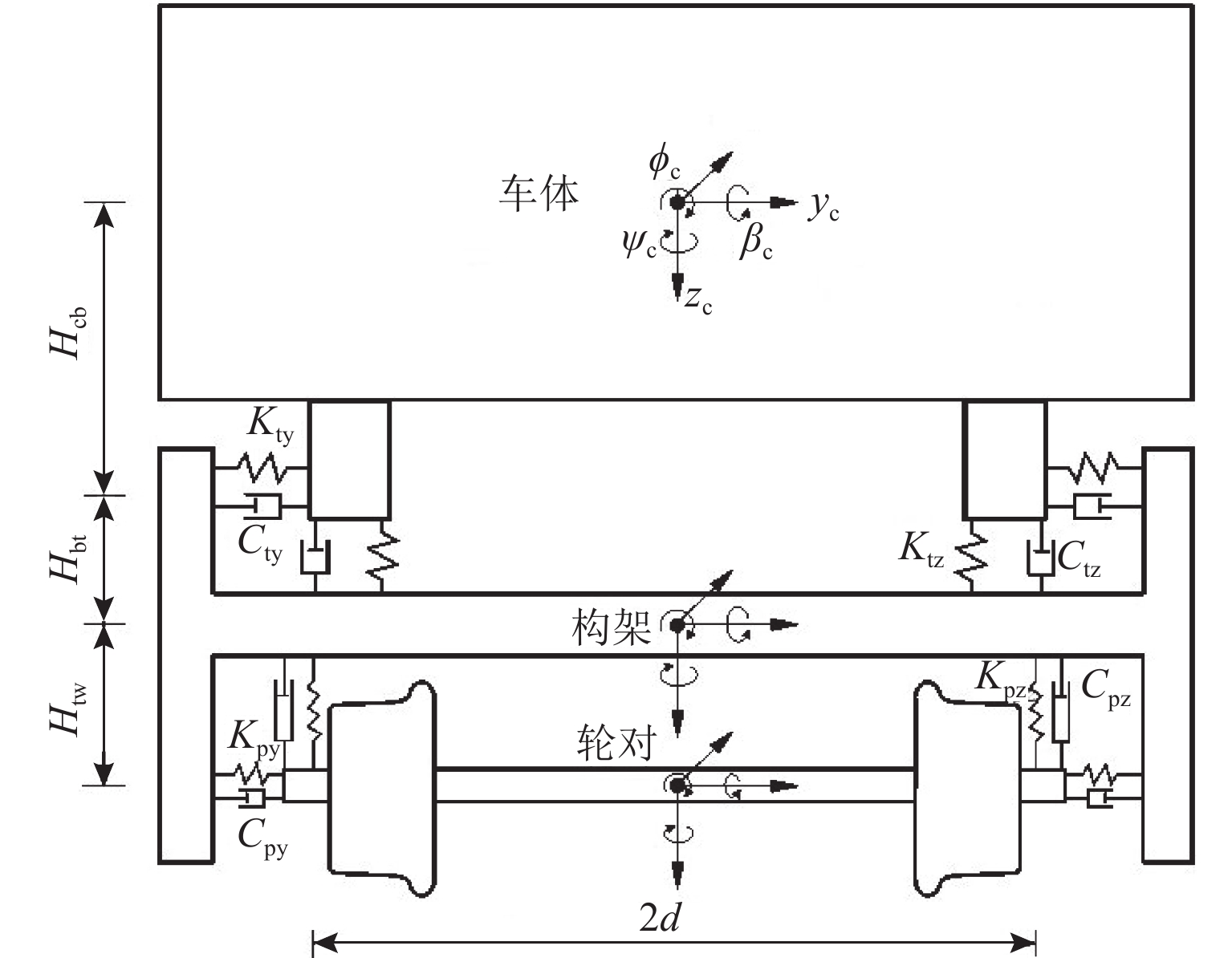
表 1 车体自振特性及振型描述
Table 1. Natural frequencies and modes of carbody
阶数 频率/Hz 振型描述 1 0.54 绕车体下心侧滚 2 0.86 车体摇头 3 0.94 车体沉浮 4 1.12 车体点头 5 1.20 绕车体上心侧滚 
下载: 导出CSV
-
[1] CHRISTINA R, RUNG T, WU D. Computational modelling of cross-wind stability of high-speed trains[J]. European Congress on Computational Methods in Applied Sciences and Engineering, 2004(7): 24-28. [2] 航空鉄道事故調査委員会. 西日本旅客鉄道株式会社福知山線塚口駅～尼崎駅間列車脱線事故[M]. 东京: 航空·鉄道事故調査委員会, 2007. [3] 金学松,郭俊,肖新标,等. 高速列车安全运行研究的关键科学问题[J]. 工程力学,2009,26(增2): 8-22,105.JIN Xuesong, GUO Jun, XIAO Xinbiao, et al. Key scientific problems in the study on running safety of high speed trains[J]. Engineering Mechanics, 2009, 26(S2): 8-22,105. [4] 翟婉明, 夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011. [5] YU M G, LIU J L, LIU D W, et al. Investigation of aerodynamic effects on the high-speed train exposed to longitudinal and lateral wind velocities[J]. Journal of Fluids and Structures, 2016, 61: 347-361. doi: 10.1016/j.jfluidstructs.2015.12.005 [6] CHELI F, CORRADI R, TOMASINI G. Crosswind action on rail vehicles: a methodology for the estimation of the characteristic wind curves[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106: 248-255. [7] 国枝正春. 鉄道車両の転ぷくに関する力学的理論解析[J]. 鉄道技術研究報告,1972(2): 1-15. [8] 高广军. 强侧风作用下列车运行安全性研究[D]. 长沙: 中南大学, 2008. [9] BAKER C. A framework for the consideration of the effects of crosswinds on trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 130-142. doi: 10.1016/j.jweia.2013.09.015 [10] 严乃杰. 横向风作用下移动列车风场特性、气动荷载及倾覆危险性研究[D]. 成都: 西南交通大学, 2019. [11] YAN N J, CHEN X Z, LI Y L. Assessment of overturning risk of high-speed trains in strong crosswinds using spectral analysis approach[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 174: 103-118. doi: 10.1016/j.jweia.2017.12.024 [12] WANG M, CHEN X Z, LI X Z, et al. A frequency domain analysis framework for assessing overturning risk of high-speed trains under crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 202: 104196.1-104196.14. [13] 王开文. 车轮接触点迹线及轮轨接触几何参数的计算[J]. 西南交通大学学报,1984,19(1): 89-99.WANG Kaiwen. The track of wheel contact points and the calculation of wheel/rail geometric contact parameters[J]. Journal of Southwest Jiaotong University, 1984, 19(1): 89-99. [14] CARRARINI A. Reliability based analysis of the crosswind stability of railway vehicles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(7): 493-509. doi: 10.1016/j.jweia.2006.10.001 [15] TSI H. Technical specification for interoperability relating to the ‘rolling stock’ sub-system of the trans-european high-speed rail system[R]. Aberdeen: Official Journal of the European Union, 2008. [16] DIEDRICHS B, EKEQUIST M, STICHEL S, et al. Quasi-static modelling of wheel-rail reactions due to crosswind effects for various types of high-speed rolling stock[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(2): 133-148. doi: 10.1243/0954409041319614 [17] CHEN X Z, KAREEM A. Equivalent static wind loads for buffeting response of bridges[J]. Journal of Structural Engineering, 2001, 127(12): 1467-1475. doi: 10.1061/(ASCE)0733-9445(2001)127:12(1467) -
下载:
点击查看大图
计量
- 文章访问数: 392
- HTML全文浏览量: 118
- PDF下载量: 84
- 被引次数: 0