Optimal Reconfiguration of Distribution Network Based on Backtracking Search Algorithm Under the Background of Non-cooperative Game Theory
-
摘要:
为缓解分布式电源大规模接入对配电网安全稳定运行的影响，提出一种考虑分布式电源输出功率的不确定性的有源配电网优化重构方法. 首先，采用非合作博弈理论研究电网调度人员与“大自然”之间的博弈关系，将配电网系统中光伏单元的不确定性视为“大自然”博弈方；其次，以有功网损、负荷均衡度、电压偏差最小为目标函数，建立有源配电网优化重构模型，通过回溯搜索算法（backtracking search algorithm，BSA）进行迭代求解，得到最优重构方案；最后，在IEEE33节点系统进行仿真分析，验证模型的正确性及求解算法的有效性. 研究结果表明，相较传统重构方法，本文方法更充分考虑了分布式电源输出功率的不确定性，并且在最恶劣的情况发生时，得到的重构策略能够使配电网系统的有功网损、负荷均衡度、电压偏差指标分别降低0.31%、0.59%、0.48%.
Abstract:To mitigate the impact of large-scale integration of distributed generation (DG) on the secure and stable operation of distribution networks, we propose an active distribution network optimal reconfiguration method that considers the uncertainty of distributed power generation output, based on non-cooperative game theory. Firstly, non-cooperative game theory is employed to analyze the game relationship between the distribution network topology and DG output, considering the uncertainty of photovoltaic units in the distribution network system as a player. Secondly, an optimal reconfiguration model with the objective functions of minimizing active network loss, balancing load and minimizing voltage deviation is established. The model is solved iteratively using the backtracking search algorithm (BSA) to obtain the optimal reconfiguration solution. Finally, simulation analysis is conducted using the IEEE33-node system to verify the correctness of the proposed model and the effectiveness of the algorithm. The results indicate that, compared to traditional reconfiguration methods, the proposed optimal reconfiguration approach in this study comprehensively addresses the uncertainty of distributed power generation output. In the most adverse scenario, the reconfiguration strategy can lead to a reduction of 0.31%, 0.59%, and 0.48% in active power loss, load balancing, and voltage deviation indices within the distribution network system.
-
图 1 有源配电网优化重构求解流程
Figure 1. Flowchart of optimal reconfiguration for active distribution network
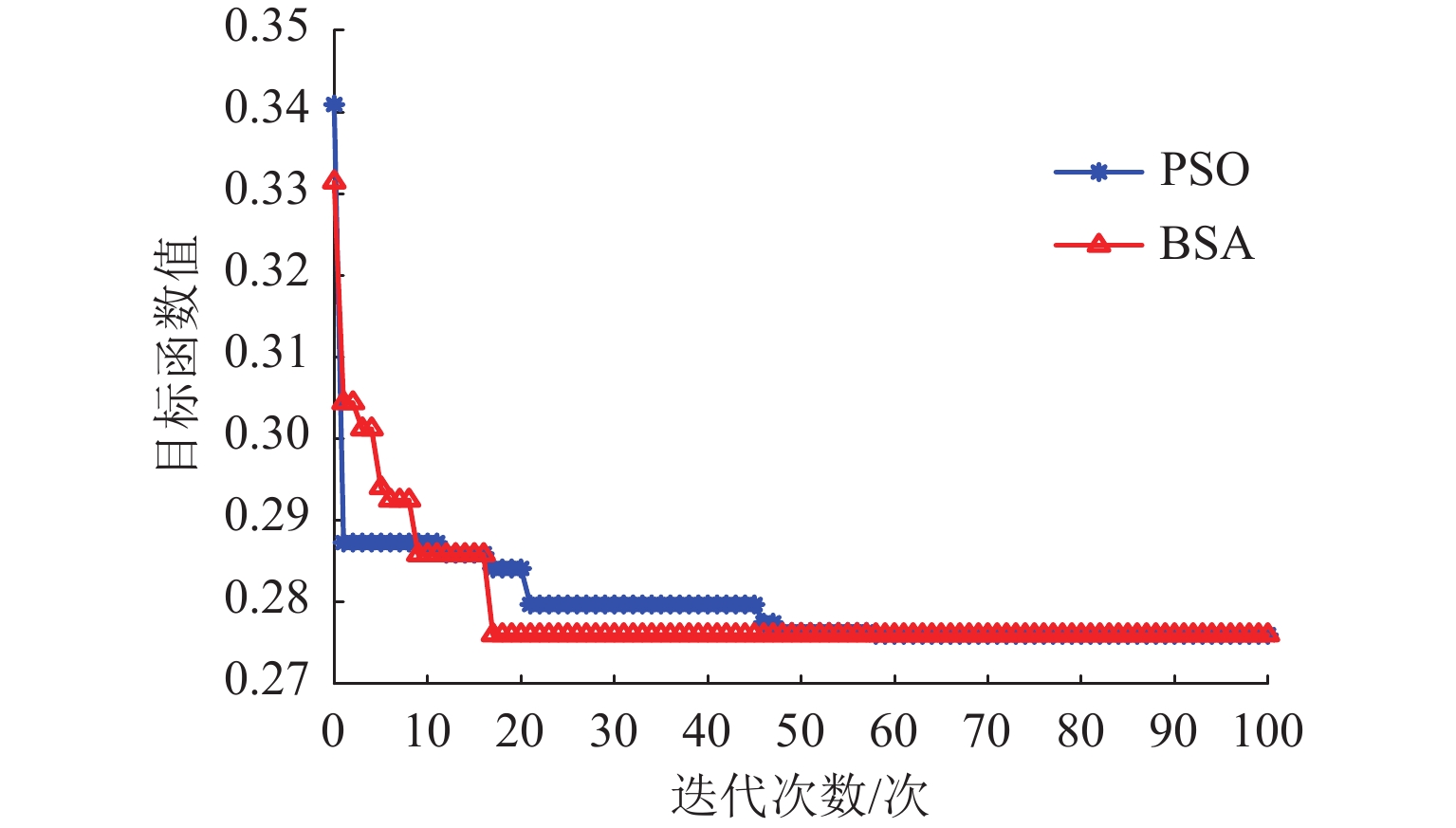
表 1 BSA和PSO各运行指标对比结果
Table 1. Comparison results of operation indexes between BSA and PSO
算法 断开支路 目标值 求解时间/s 寻优
率/%BSA 7—8, 9—10, 14—15, 17—18, 28—29 0.2760 272.189 100 PSO 7—8, 9—10, 14—15, 17—18, 28—29 0.2760 407.893 60 
下载: 导出CSV
表 2 不同情形下配电网系统的各个指标变化情况
Table 2. Index changes of the distribution network system in different situations
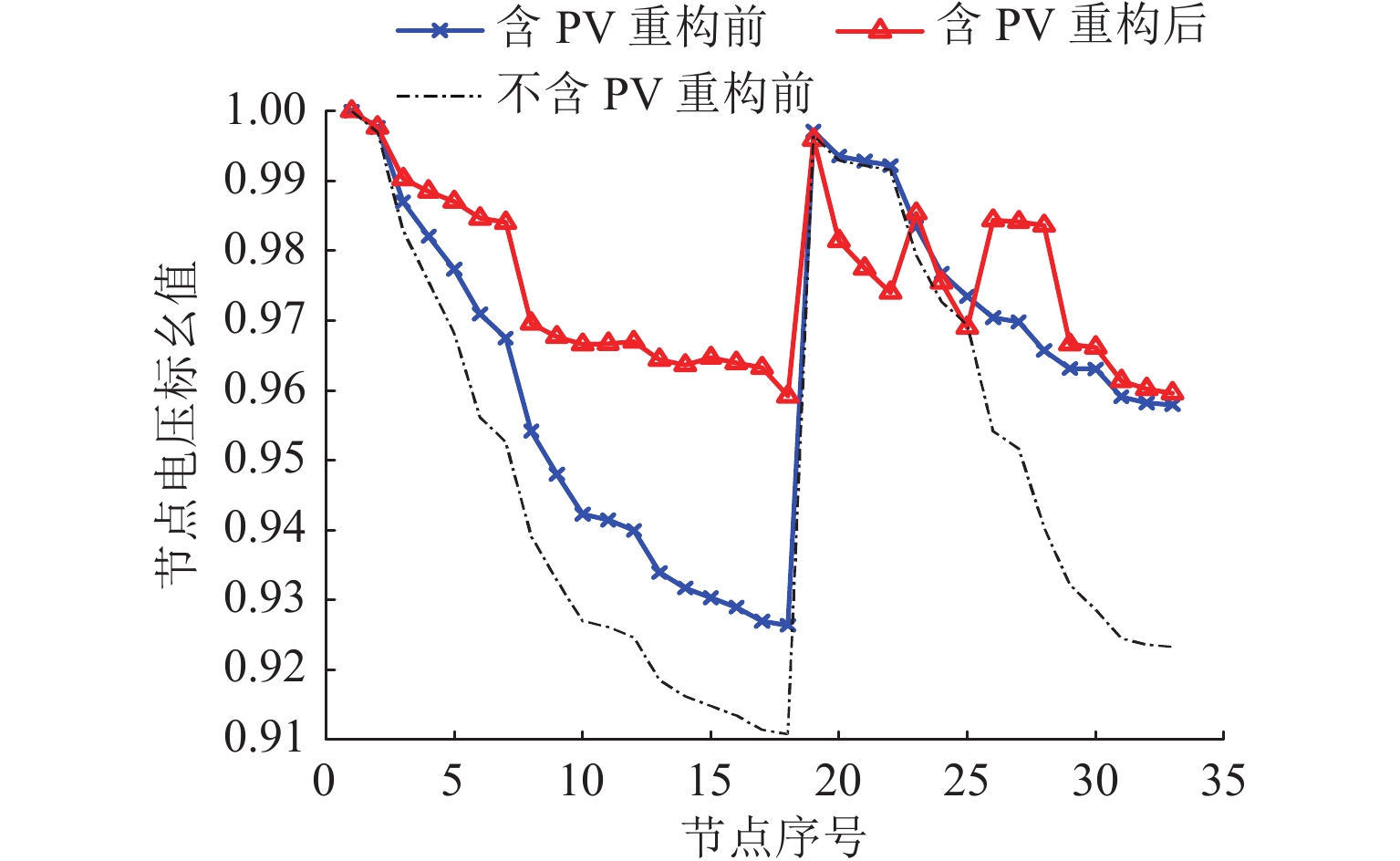
项目 断开支路 网损
/kW负荷
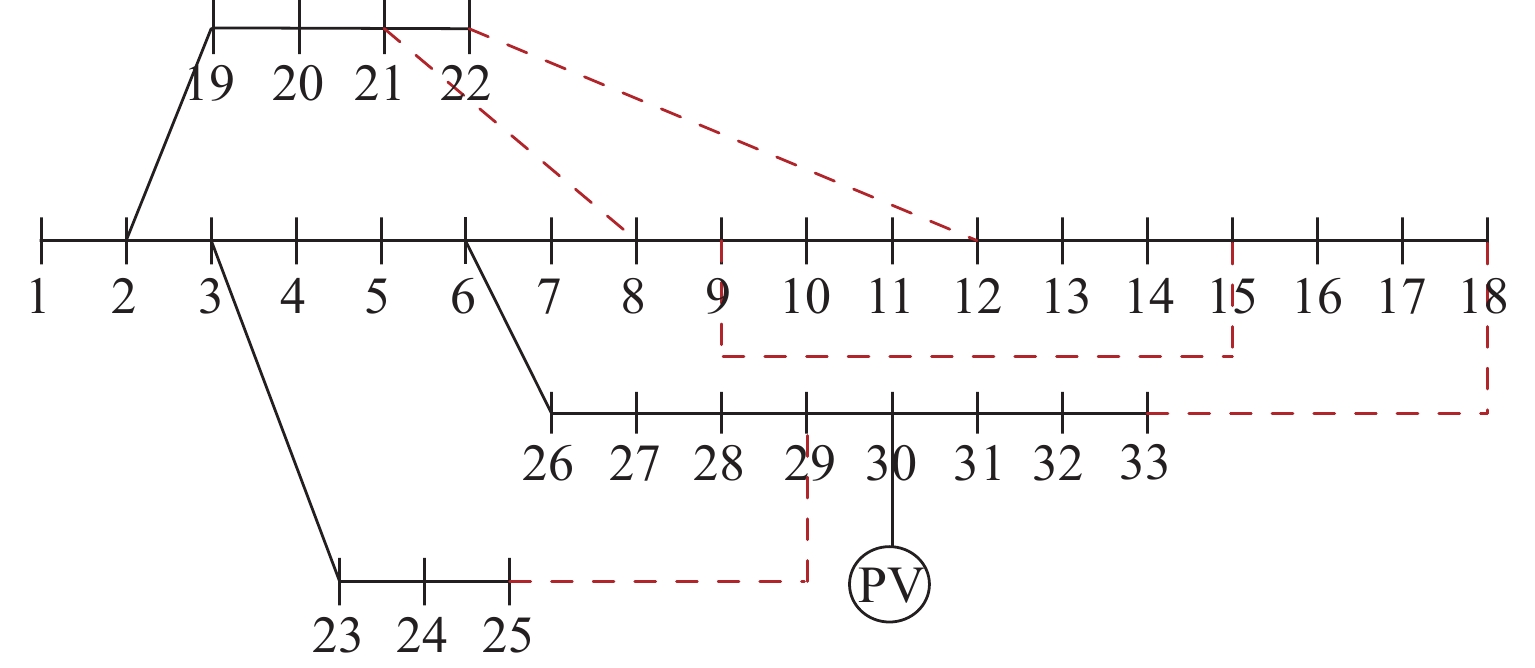
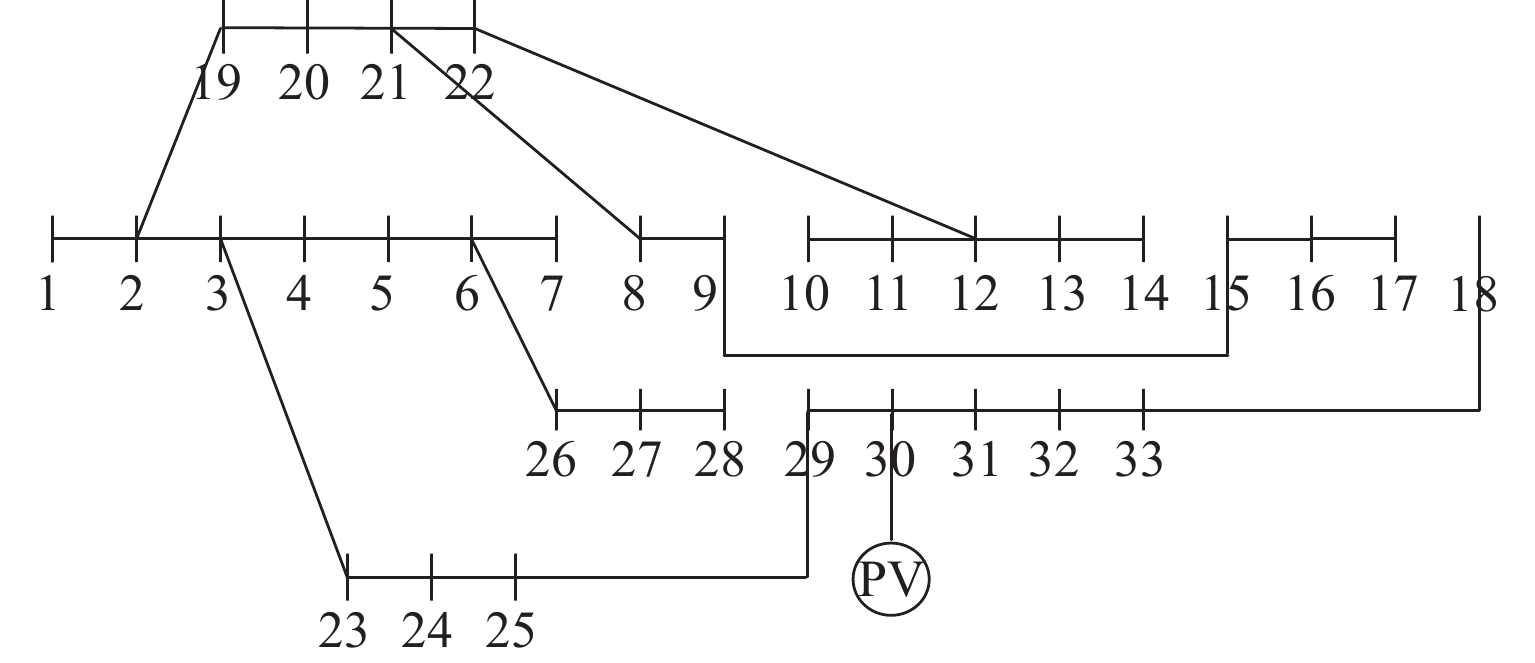
均衡度电压偏差标幺值 无 PV 8—21, 9—15, 12—22, 18—33, 25—29 208.46 0.758 1.661 重构前 8—21, 9—15, 12—22, 18—33, 25—29 132.98 0.476 1.197 重构后 7—8, 9—10, 14—15, 17—18, 28—29 90.26 0.334 0.826
下载: 导出CSV
表 3 不同情况下的重构策略对比
Table 3. Optimal reconfiguration results of different situations
方法 断开支路 非合作博弈 7—8，9—10，14—15，17—18，28—29 确定性优化 7—8，10—11，14—15，16—17，28—29
下载: 导出CSV
表 4 2种重构策略下各目标值
Table 4. Objective functions for the two methods
方法 网损/
kW负荷
均衡度电压偏差标幺值 加权
目标值非合作博弈 90.26 0.334 0.826 0.2760 确定性优化 90.54 0.336 0.830 0.2775
下载: 导出CSV
-
[1] 张运洲,张宁,代红才,等. 中国电力系统低碳发展分析模型构建与转型路径比较[J]. 中国电力,2021,54(3): 1-11.ZHANG Yunzhou, ZHANG Ning, DAI Hongcai, et al. Model construction and pathways of low-carbon transition of China’s power system[J]. Electric Power, 2021, 54(3): 1-11. [2] TAN C X, GENG S P, TAN Z F, et al. Integrated energy system-Hydrogen natural gas hybrid energy storage system optimization model based on cooperative game under carbon neutrality[J]. Journal of Energy Storage, 2021, 38: 102539.1-102539.14. [3] XING X T, LIN J, SONG Y H, et al. Modeling and operation of the power-to-gas system for renewables integration: a review[J]. CSEE Journal of Power and Energy Systems, 2018, 4(2): 168-178. doi: 10.17775/CSEEJPES.2018.00260 [4] LI J L, XUE Y S, TIAN L T, et al. Research on optimal configuration strategy of energy storage capacity in grid-connected microgrid[J]. Protection and Control of Modern Power Systems, 2017, 2(1): 1-7. doi: 10.1186/s41601-016-0032-y [5] 林清源,薛毓强,曾乙宸. 配电网重构研究综述[J]. 电气开关,2021,59(1): 3-8.LIN Qingyuan, XUE Yuqiang, ZENG Yichen. Overview of research on distribution network reconfiguration[J]. Electric Switchgear, 2021, 59(1): 3-8. [6] 陈正鹏,黄纯,张亚萍,等. 基于改进双种群遗传算法的含分布式电源配电网重构[J]. 电力系统及其自动化学报,2017,29(4): 78-83.CHEN Zhengpeng, HUANG Chun, ZHANG Yaping, et al. Distribution network reconfiguration with different distributed generations based on improved dual population genetic algorithm[J]. Proceedings of the CSU-EPSA, 2017, 29(4): 78-83. [7] 许喆,潘金生,樊淑娴,等. 基于改进萤火虫算法的含DG配电网重构方法[J]. 电力系统保护与控制,2018,46(14): 26-32.XU Zhe, PAN Jinsheng, FAN Shuxian, et al. A distribution network reconfiguration method with distributed generation based on improved firefly algorithm[J]. Power System Protection and Control, 2018, 46(14): 26-32. [8] 袁玉松,钟建伟,李沁,等. 混合型粒子群算法在含分布式电源配电网重构中的应用[J]. 电气自动化,2019,41(6): 55-57,99.YUAN Yusong, ZHONG Jianwei, LI Qin, et al. Application of hybrid particle swarm optimization to the reconfiguration of distribution networks with distributed generation[J]. Electrical Automation, 2019, 41(6): 55-57,99. [9] WU T C. Multi-objective distribution network reconstruction based on decimal coding[J]. IOP Conference Series: Earth and Environmental Science, 2021, 631(1): 012123.1-012123.6. [10] 陈光,戴攀,周浩,等. 计及入网电动汽车和分布式电源的配电系统重构[J]. 电网技术,2013,37(1): 82-88.CHEN Guang, DAI Pan, ZHOU Hao, et al. Distribution system reconfiguration considering distributed generators and plug-in electric vehicles[J]. Power System Technology, 2013, 37(1): 82-88. [11] SINGH J, TIWARI R. Electric vehicles reactive power management and reconfiguration of distribution system to minimise losses[J]. IET Generation, Transmission & Distribution, 2020, 14(25): 6285-6293. [12] 潘本仁,王和春,张妍,等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制,2020,48(15): 102-107.PAN Benren, WANG Hechun, ZHANG Yan, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107. [13] 钱科军,刘乙,张新松,等. 考虑电动汽车充电负荷的配电系统场景概率潮流分析[J]. 电力系统保护与控制,2020,48(24): 62-70.QIAN Kejun, LIU Yi, ZHANG Xinsong, et al. Scenario-based probabilistic power flow calculation of distribution systems with electric vehicle charging loads[J]. Power System Protection and Control, 2020, 48(24): 62-70. [14] SONG Y, ZHENG Y, LIU T, et al. A new formulation of distribution network reconfiguration for reducing the voltage volatility induced by distributed generation[J]. IEEE Transactions on Power Systems, 2020, 35(1): 496-507. doi: 10.1109/TPWRS.2019.2926317 [15] 梅生伟,魏韡,刘锋. 电力系统控制与决策中的博弈问题——工程博弈论初探[J]. 控制理论与应用,2018,35(5): 578-587.MEI Shengwei, WEI Wei, LIU Feng. Game theoretical perspective of power system control and decision making: a brief review of engineering game theory[J]. Control Theory & Applications, 2018, 35(5): 578-587. [16] 梅生伟,郭文涛,王莹莹,等. 一类电力系统鲁棒优化问题的博弈模型及应用实例[J]. 中国电机工程学报,2013,33(19): 47-56,20.MEI Shengwei, GUO Wentao, WANG Yingying, et al. A game model for robust optimization of power systems and its application[J]. Proceedings of the CSEE, 2013, 33(19): 47-56,20. [17] BADRAN O, MEKHILEF S, MOKHLIS H, et al. Optimal reconfiguration of distribution system connected with distributed generations: a review of different methodologies[J]. Renewable and Sustainable Energy Reviews, 2017, 73: 854-867. doi: 10.1016/j.rser.2017.02.010 [18] CIVICIOGLU P. Backtracking search optimization algorithm for numerical optimization problems[J]. Applied Mathematics and Computation, 2013, 219(15): 8121-8144. doi: 10.1016/j.amc.2013.02.017 [19] NGUYEN T T, PHAM H N, TRUONG A V, et al. A backtracking search algorithm for distribution network reconfiguration problem[C]//AETA 2015: Recent Advances in Electrical Engineering and Related Sciences. Cham: Springer, 2016: 223-234. [20] 郭腾云,刘艳. 基于博弈方法的含分布式电源配电网重构优化[J]. 电力系统保护与控制,2017,45(7): 28-34.GUO Tengyun, LIU Yan. Game theory based reconfiguration optimization for distribution network with distributed generations[J]. Power System Protection and Control, 2017, 45(7): 28-34. -
下载:
点击查看大图
计量
- 文章访问数: 231
- HTML全文浏览量: 131
- PDF下载量: 31
- 被引次数: 0