PEC柱-型钢梁框架异型内节点的抗剪性能试验研究

李补拴; 周伟; 赵冲; 路瑶; 赵根田; 陈明

doi:10.3969/j.issn.0258-2724.20210545

PEC柱-型钢梁框架异型内节点的抗剪性能试验研究

doi: 10.3969/j.issn.0258-2724.20210545

李补拴^{1, 2,},
周伟¹,
赵冲¹,
路瑶¹,
赵根田^{1, 2, ,},
陈明¹

1.
内蒙古科技大学土木工程学院，内蒙古包头 014010
2.
内蒙古科技大学土木工程安全与耐久重点实验室，内蒙古包头 014010

基金项目: 国家自然科学基金（51268042，51768055）

详细信息

作者简介:
李补拴（1986—），男，工程师，研究方向为新型组合结构及复合材料，E-mail： libushuan@163.com

通讯作者:
赵根田（1962—），男，教授，博士，研究方向为新型组合结构，E-mail： zhaogentian93110@sina.com

中图分类号: TU398.9
计量
- 文章访问数: 310
- HTML全文浏览量: 93
- PDF下载量: 33
- 被引次数: 0
出版历程
- 收稿日期: 2021-07-04
- 修回日期: 2021-11-19
- 网络出版日期: 2023-02-22
- 刊出日期: 2021-12-05

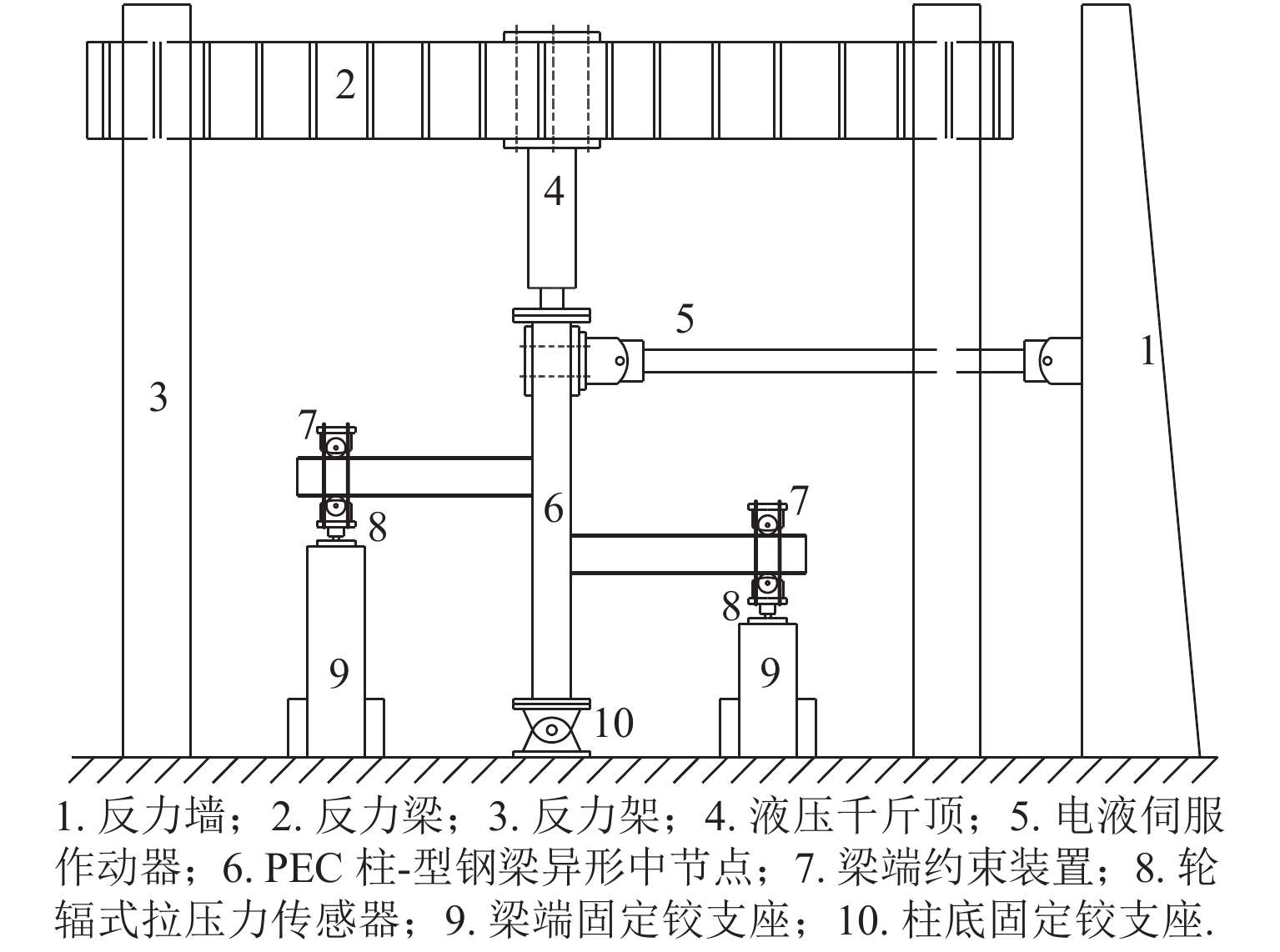
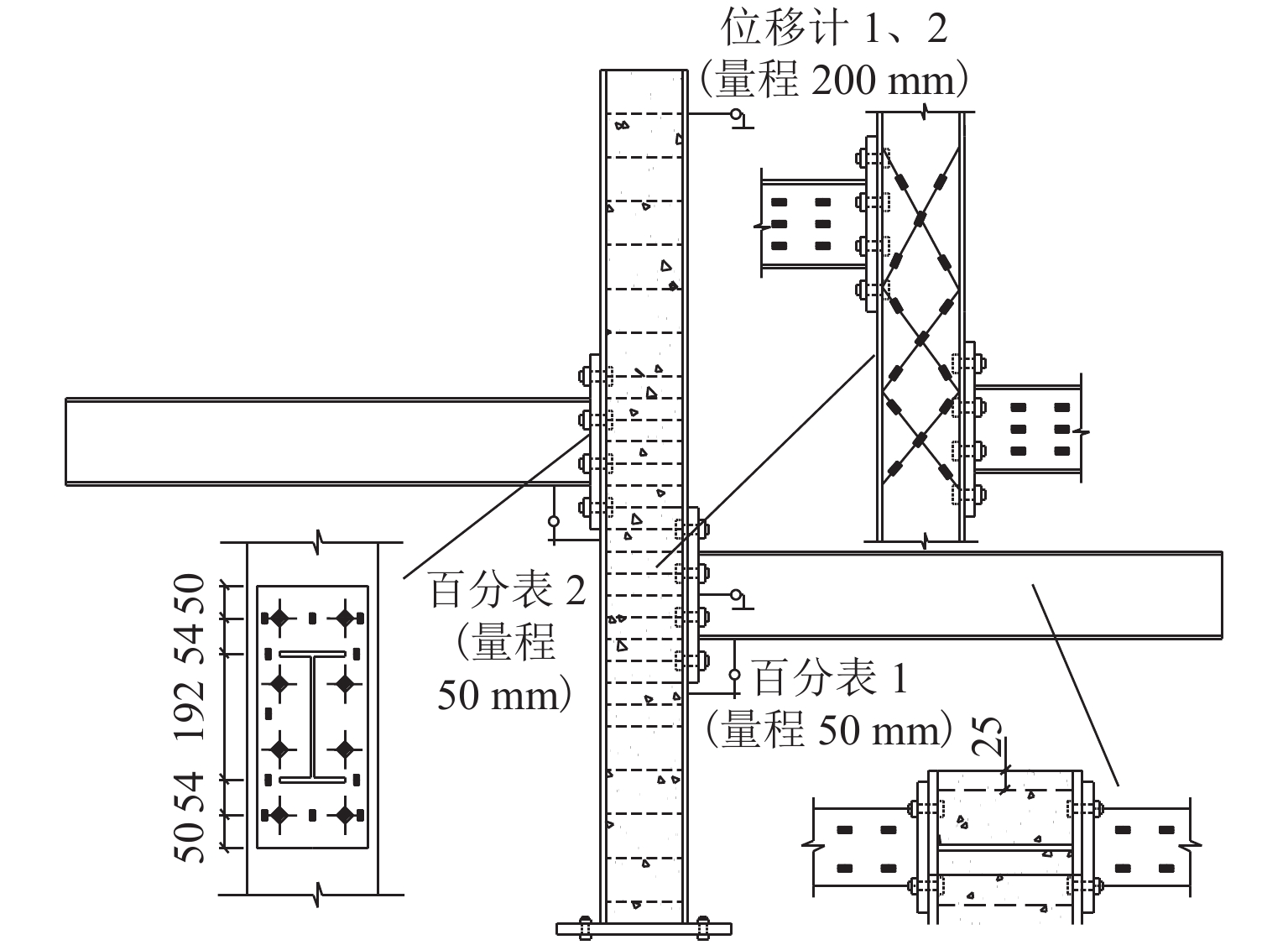
Experimental Study on Shear Resistance of Abnormal Internal Joints in Partially-Encased Concrete Column-Steel Beam Frame

LI Bushuan^{1, 2
,},
ZHOU Wei¹,
ZHAO Chong¹,
LU Yao¹,
ZHAO Gentian^{1, 2
, ,},
CHEN Ming¹

1.
School of Civil Engineering, Inner Mongolia University of Science & Technology, Baotou 014010, China
2.
Key Laboratory of Safety and Durability for Civil Engineering, Inner Mongolia University of Science & Technology, Baotou 014010, China

摘要

摘要:
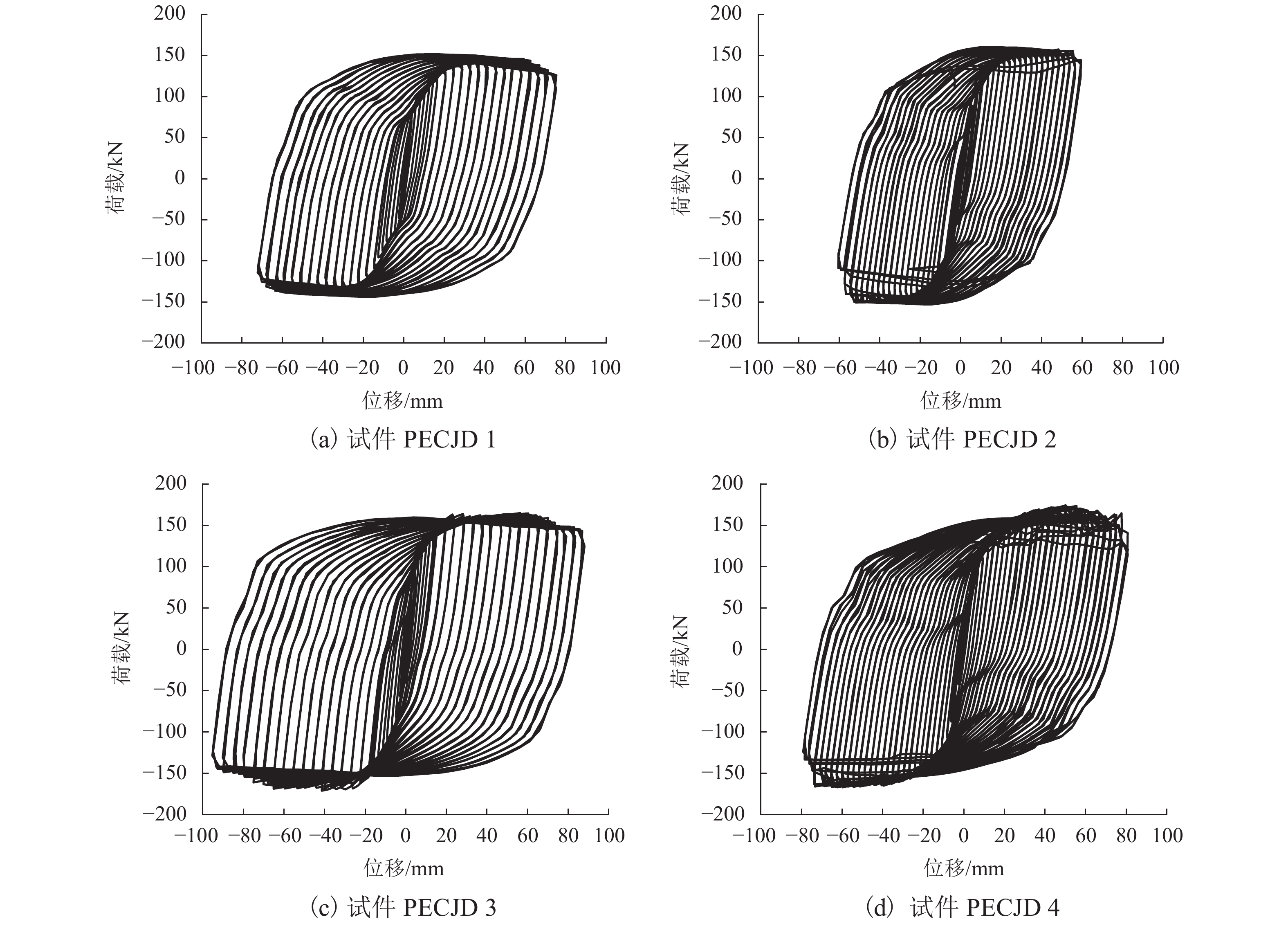
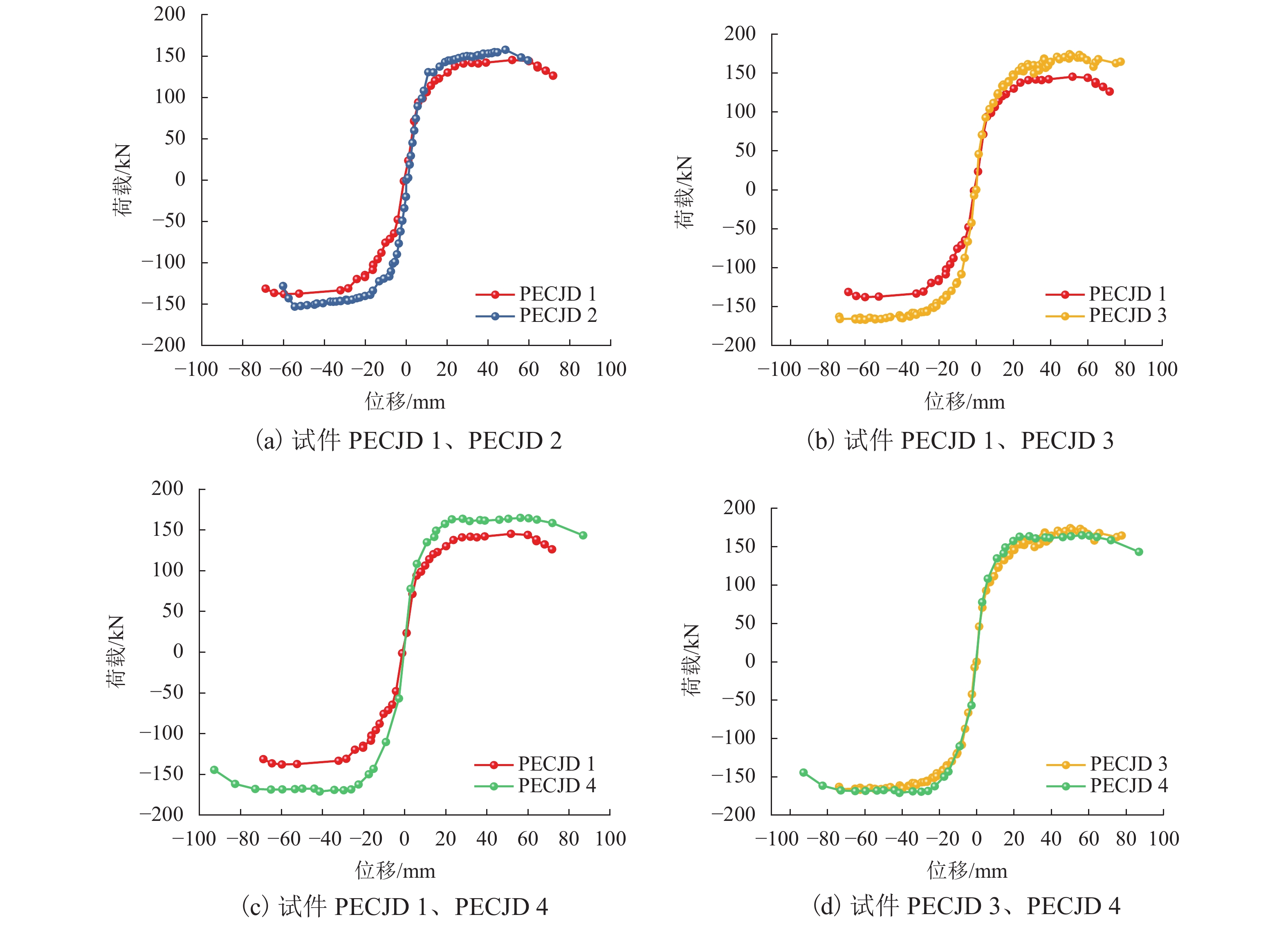
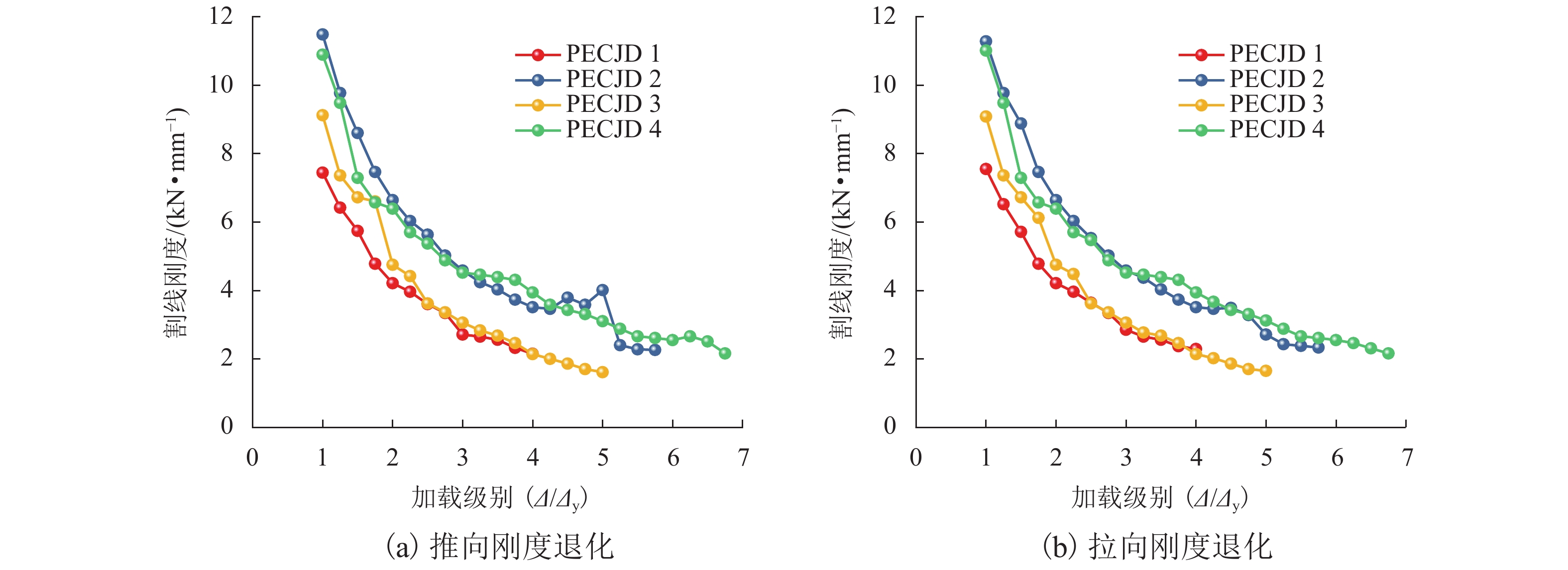
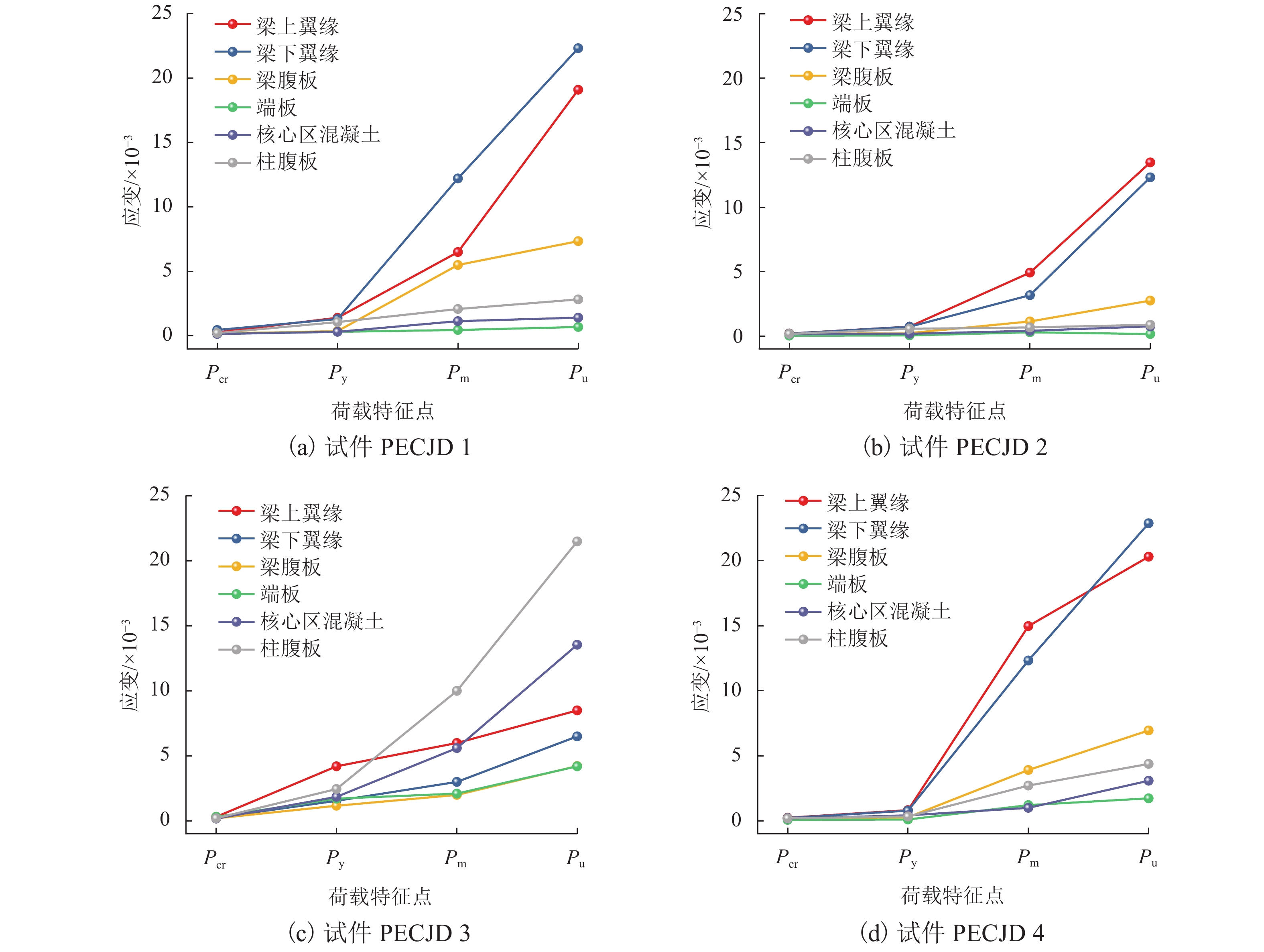
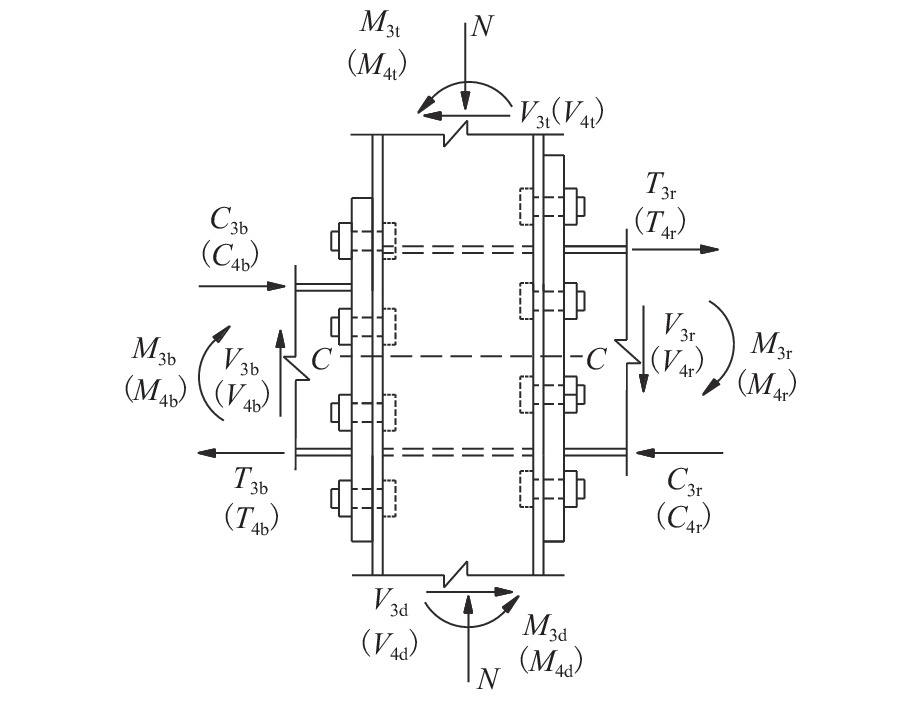
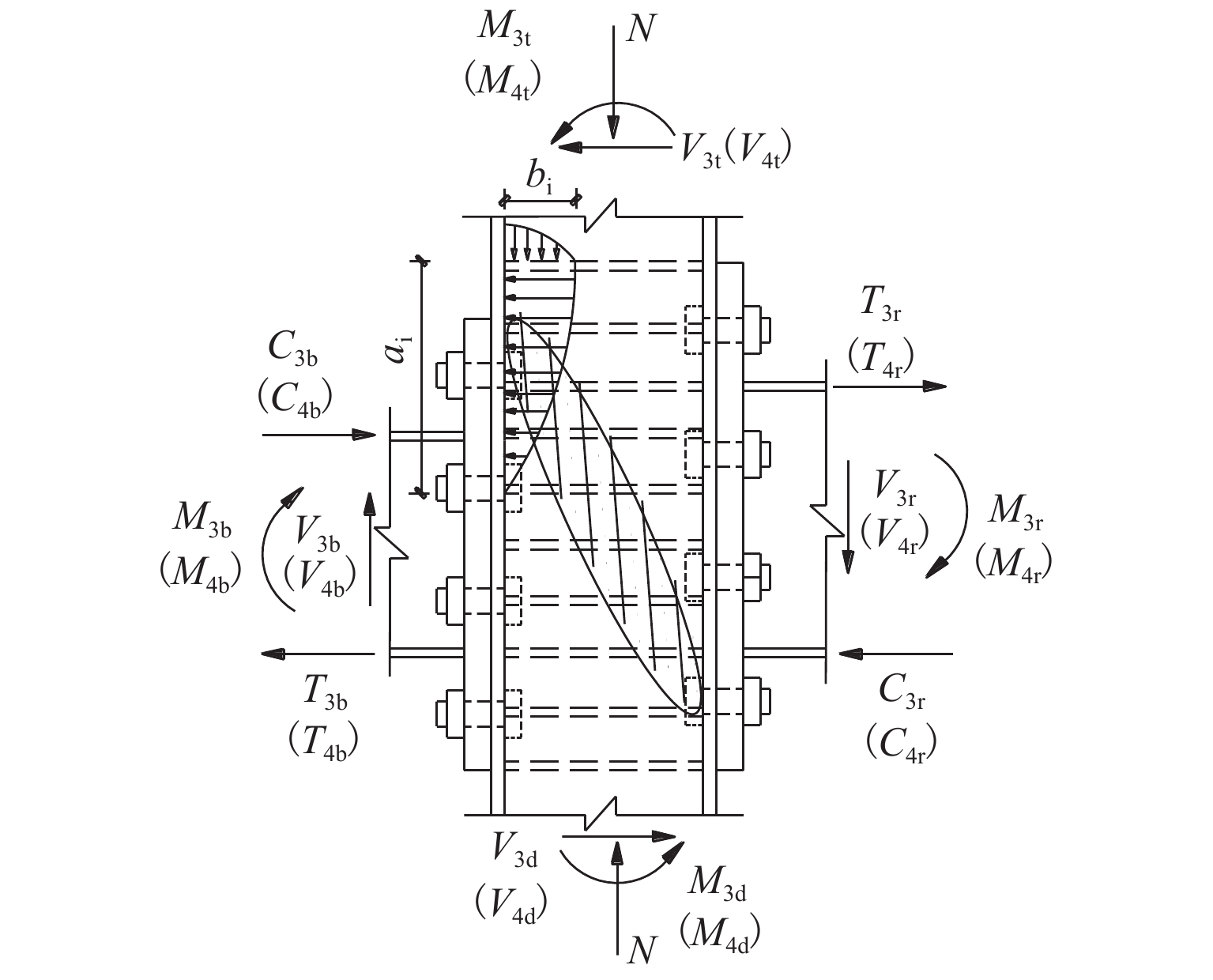
由于民用建筑外观及工业建筑生产工艺要求，部分包覆钢-混凝土结构因错位、变梁变柱等会形成异型内节点. 为研究该类异型内节点的抗剪性能，以柱两侧梁错位高度、单侧梁截面高度增大等为变量参数，按1∶2缩尺比例设计制作了1个常规内节点和3个异型内节点模型试件，并完成低周往复荷载试验，分析了内节点的破坏形态、滞回耗能、承载能力、延性性能等指标. 试验研究结果表明：各试件滞回曲线均呈现对称饱满的梭形；等效黏滞阻尼系数在0.598～0.618，位移延性系数在3.28～4.96，表现出良好的耗能性能及变形性能；因错位、变梁形成的异型内节点与常规内节点相比，承载力分别提升约6.1%、14.0%、15.0%；位移延性系数提升了约−26.6%、11.0%、−14.1%，延性性能规律不明显，耗能能力、强度和刚度退化变化不大；对于左右梁截面尺寸相同且完全错开（即错位高度大于梁高）的Ⅰ类异型内节点，可按T形边节点进行设计；基于节点域传力机理，建立了Ⅱ类异型内节点抗剪计算模型，并提出了抗剪承载力计算公式，试验结果与理论计算结果吻合较好.
- 错位 /
- 变梁 /
- 部分外包混凝土柱 /
- 异型内节点 /
- 低周往复加载试验 /
- 抗剪性能
Abstract:
Due to the requirements for the appearance of civil buildings and the production process of industrial buildings, abnormal internal joints may be formed in the partially-encased steel-concrete composite structures due to misalignment and change of beams and columns. In order to investigate the shear resistance of this type of abnormal internal joints, low circumferential reciprocal load tests were conducted on one conventional internal joint and three profiled internal joints with 1∶2 scale-down model specimens. The damage morphology, hysteretic energy dissipation, load bearing capacity, and ductility properties of the internal joints were analyzed using the height of the beam dislocation on both sides of the column and the height of the single side beam section as variable parameters. The experimental results show that the hysteresis curves of all specimens present a symmetrical and full shuttle shape. The equivalent viscous damping coefficient is between 0.598 and 0.618 and the displacement ductility coefficient is between 3.28 and 4.96, showing good performance in energy dissipation and deformation. Compared to the conventional internal joint, the load bearing capacity of the three profiled internal joints formed due to misalignment and variable beams is increased by 6.1%, 14.0% and 15.0%, respectively, and their displacement ductility factor is increased by approximately −26.6%, 11.0% and −14.1%, respectively, with insignificant ductility performance patterns and little change in energy dissipation capacity, strength and stiffness degradation. For class Ⅰ heterogeneous internal joints with the same cross-sectional dimensions of the left and right beams but completely staggered (i.e., the dislocation height greater than the beam height), they can be designed according to T-shaped edge joints. Based on the joint domain force transfer mechanism, a shear calculation model for class Ⅱ heterogeneous internal joints was established, a formula for calculating the shear bearing capacity was proposed, and the test results agreed well with the theoretical calculation results.
- split-level /
- varying depth beam /
- partially encased concrete (PEC) column /
- profiled interior joint /
- low-cyclic reversed loading test /
- shear resistance performance

HTML全文

图 1 试件设计与制作

Figure 1. Design and fabrication of specimens

下载: 全尺寸图片幻灯片

图 2 试验加载装置

Figure 2. Loading equipment of specimens

下载: 全尺寸图片幻灯片

图 3 测试仪表布置

Figure 3. Layout of testing instruments

下载: 全尺寸图片幻灯片

图 4 试件破坏形态

Figure 4. Failure mode of specimens

下载: 全尺寸图片幻灯片

图 5 柱顶部荷载-位移滞回曲线

Figure 5. Load-displacement hysterics loops of specimens

下载: 全尺寸图片幻灯片

图 6 试件荷载-位移骨架曲线

Figure 6. Load-displacement skeleton curves of specimens

下载: 全尺寸图片幻灯片

图 7 强度退化曲线

Figure 7. Strength degradation curves

下载: 全尺寸图片幻灯片

图 8 刚度退化曲线

Figure 8. Stiffness degradation curves

下载: 全尺寸图片幻灯片

图 9 节点各阶段应变变化曲线

Figure 9. Strain variation curves of joints in different stages

下载: 全尺寸图片幻灯片

图 10 节点受力示意

Figure 10. Force distribution of joints

下载: 全尺寸图片幻灯片

图 11 节点传力机理

Figure 11. Force transfer mechanism of joints

下载: 全尺寸图片幻灯片

表 1 试件基本参数

Table 1. Parameters of specimens

试件编号	柱截面尺寸/mm	梁截面尺寸/mm		错位高度/mm	左右梁截面高度差/mm	左右梁线刚度	n_t
试件编号	柱截面尺寸/mm	非加载侧	加载侧	错位高度/mm	左右梁截面高度差/mm	左右梁线刚度	n_t
PECJD 1	200/200/8.0/12	HN 200/100/5.5/8	HN 200/100/5.5/8	0	0	i₁=i₂	0.35
PECJD 2	200/200/8.0/12	HN 200/100/5.5/8	HN 200/100/5.5/8	400	0	i₁=i₂	0.35
PECJD 3	200/200/8.0/12	HN 200/100/5.5/8	HM 244/175/7.0/11	0	44	2.7i₁=i₂	0.35
PECJD 4	200/200/8.0/12	HN 200/100/5.5/8	HM 248/124/5.0/8	0	48	i₁=i₂	0.35
注：HN为窄翼缘H型钢，HM为中翼缘H型钢；错位高度定义为柱两侧梁翼缘中心线之间的距离；n_t为试验轴压比；i₁（i₂）为左（右）梁线刚度；第2～4列的数据分别为型钢截面高度、翼缘宽度、腹板厚度、翼缘厚度.

下载: 导出CSV

表 2 试件材性实测指标

Table 2. Measured values of material properties of specimens

类型	t(ϕ)/mm	f_y/MPa	f_u/MPa	E/GPa	ε_y/ × 10⁻³	A/%
钢板	5.0	305	463	204	1.496	39.0
	5.5	307	448	196	1.568	36.0
	7.0	297	423	180	1.650	30.0
	8.0	320	420	210	1.525	28.5
	12.0	319	437	220	1.451	26.0
	18.0	301	457	191	1.576	27.5
钢筋	8.0	335	522	210	1.594	30.0
注： t、ϕ、f_y、f_u、E、ε_y、A分别为钢板厚度、钢筋直径、钢材屈服强度、抗拉强度、弹性模量、屈服应变和断后伸长率.

下载: 导出CSV

表 3 试件在各特征点试验结果

Table 3. Experimental results of specimens at various feature points

试件编号	加载方向	开裂荷载P_cr/kN	开裂位移Δ_cr/mm	屈服荷载P_y/kN	Δ_y/mm	峰值荷载P_m/kN	峰值位移Δ_m/mm	破坏荷载P_u/kN	破坏位移Δ_u/mm	位移延性系数均值
PECJD 1	正向	101.01	9.82	122.20	15.20	151.80	57.32	129.03	75.39	4.47
PECJD 1	反向	−98.99	−11.42	−121.20	−17.64	−144.00	−58.83	−122.40	−70.12	4.47
PECJD 2	正向	91.10	6.98	142.60	18.99	160.60	53.99	136.51	59.48	3.28
PECJD 2	反向	−105.60	−7.01	−138.90	−17.62	−153.20	−54.51	−130.22	−60.27	3.28
PECJD 3	正向	129.10	10.79	149.20	16.65	165.80	56.42	140.93	86.96	4.96
PECJD 3	反向	−113.40	−9.19	−148.80	−19.71	−172.20	−41.35	−146.37	−92.75	4.96
PECJD 4	正向	110.30	8.75	144.00	18.50	173.20	55.54	147.22	75.74	3.84
PECJD 4	反向	−103.10	−7.10	−142.50	−17.94	−167.10	−62.42	−142.04	−64.42	3.84

下载: 导出CSV

表 4 等效黏滞性阻尼系数

Table 4. Equivalent viscous damping coefficients of specimens

试件编号	屈服荷载时	峰值荷载时	破坏荷载时
PECJD 1	0.261	0.481	0.610
PECJD 2	0.153	0.534	0.618
PECJD 3	0.248	0.469	0.600
PECJD 4	0.179	0.436	0.598

下载: 导出CSV

表 5 节点核心区剪力和受剪承载力

Table 5. Shear and shear bearing capacity in core area of joints

试件编号	V_j/kN	V_j1/kN	V_j/V_j1	破坏模式
PECJD 3	840.8	766.1	1.098	核心区剪切破坏
PECJD 4	697.0	768.0	0.908	梁端弯曲破坏和节点轻微剪切破坏并存
SRCIJ-7^[21]	965.1	977.5	0.987	核心区剪切破坏
SRCIJ-8^[21]	906.2	842.85	1.075	核心区剪切破坏

下载: 导出CSV

参考文献(21)

[1]	CHICOINE T, TREMBLAY R, MASSICOTTE B, et al. Behavior and strength of partially encased composite columns with built-up shapes[J]. Journal of Structural Engineering, 2002, 128(3): 279-288. doi: 10.1061/(ASCE)0733-9445(2002)128:3(279)
[2]	BEGUM M, DRIVER R G, ELWI A E. Behaviour of partially encased composite columns with high strength concrete[J]. Engineering Structures, 2013, 56: 1718-1727. doi: 10.1016/j.engstruct.2013.07.040
[3]	武志勇．焊接H型钢部分包裹混凝土组合短柱偏心受力性能研究[D]．包头: 内蒙古科技大学, 2009.
[4]	胡鳅文. H型钢部分包裹混凝土组合短柱弱轴方向偏压性能试验研究[D]．包头: 内蒙古科技大学, 2015.
[5]	JAMKHANEH M E, ALI KAFI M. Experimental and numerical investigation of octagonal partially encased composite columns subject to axial and torsion moment loading[J]. Civil Engineering Journal, 2017, 3(10): 939-955.
[6]	EBADI JAMKHANEH M, ALI KAFI M, KHEYRODDIN A. Behavior of partially encased composite members under various load conditions: experimental and analytical models[J]. Advances in Structural Engineering, 2019, 22(1): 94-111.
[7]	Canada Standards Association. Design of steel structures: CSA-S16-09[S]. Missisauga: Canada Standards Association, 2009.
[8]	European Committee for Standardization. Eurocode 4: design of composite steel and concrete structures, part 1-1: general rules and rules for buildings: EN 1994-1-1 [S]. Brussels: European Committee for Standardization, 2004.
[9]	方有珍,顾强,申林,等. 薄板混凝土组合截面部分外包组合柱(弱轴)滞回性能足尺试验研究[J]. 建筑结构学报,2012,33(4): 113-120. doi: 10.14006/j.jzjgxb.2012.04.001 FANG Youzhen, GU Qiang, SHEN Lin, et al. Hysteretic behavior of full scale partially encased composite columns (weak axis) fabricated with thin-walled built-up section[J]. Journal of Building Structures, 2012, 33(4): 113-120. doi: 10.14006/j.jzjgxb.2012.04.001
[10]	方有珍,陆佳,马吉,等. 薄壁钢板组合PEC柱(强轴)滞回性能试验研究[J]. 土木工程学报,2012,45(4): 48-55. doi: 10.15951/j.tmgcxb.2012.04.013 FANG Youzhen, LU Jia, MA Ji, et al. Hysteretic behavior of PEC columns (strong axis) with thin steel plate composite section[J]. China Civil Engineering Journal, 2012, 45(4): 48-55. doi: 10.15951/j.tmgcxb.2012.04.013
[11]	赵根田,王姗,狄昊,等. 焊接H型钢PEC柱-钢梁端板连接的滞回性能[J]. 土木工程学报,2014,47(增2): 74-78. doi: 10.15951/j.tmgcxb.2014.s2.012 ZHAO Gentian, WANG Shan, DI Hao, et al. Hysteretic behavior on connection of PEC columns-steel beam with end plates[J]. China Civil Engineering Journal, 2014, 47(S2): 74-78. doi: 10.15951/j.tmgcxb.2014.s2.012
[12]	马吉,方有珍,陆承铎,等. 薄钢板PEC柱-钢梁端板对拉螺栓连接滞回性能试验研究[J]. 工程力学,2013,30(6): 107-115,123. doi: 10.6052/j.issn.1000-4750.2012.02.0071 MA Ji, FANG Youzhen, LU Chengduo, et al. Hysteretic behavior study on connection of PEC columns-steel beam with end plates and pretension high-strength penetrating bolts[J]. Engineering Mechanics, 2013, 30(6): 107-115,123. doi: 10.6052/j.issn.1000-4750.2012.02.0071
[13]	方有珍,顾强,姚江峰,等. 新型卷边钢板组合PEC柱-钢梁中节点抗震性能试验研究[J]. 土木工程学报,2014,47(7): 53-62. doi: 10.15951/j.tmgcxb.2014.07.033 FANG Youzhen, GU Qiang, YAO Jiangfeng, et al. Experimental study on seismic performance of interior connections between new crimping thin-walled built-up section PEC column and steel beam[J]. China Civil Engineering Journal, 2014, 47(7): 53-62. doi: 10.15951/j.tmgcxb.2014.07.033
[14]	曹芙波,卢志明,赵根田,等. PEC柱-型钢梁框架中节点抗震性能试验研究[J]. 建筑结构学报,2020,41(10): 30-41. doi: 10.14006/j.jzjgxb.2018.0545 CAO Fubo, LU Zhiming, ZHAO Gentian, et al. Experimental research on seismic performance of PEC column-steel beam frame interior joints[J]. Journal of Building Structures, 2020, 41(10): 30-41. doi: 10.14006/j.jzjgxb.2018.0545
[15]	方有珍,戴雅萍,王辰宇,等. 薄钢板PEC柱-削弱截面钢梁框架层间抗震试验研究[J]. 西南交通大学学报,2017,52(4): 715-724. doi: 10.3969/j.issn.0258-2724.2017.04.009 FANG Youzhen, DAI Yaping, WANG Chenyu, et al. Test study on seismic performance of PEC column fabricated with thin-walled steel plates-steel beam (reduced beam section) composite frame[J]. Journal of Southwest Jiaotong University, 2017, 52(4): 715-724. doi: 10.3969/j.issn.0258-2724.2017.04.009
[16]	白国良,赵金全,杜宁军,等. 型钢混凝土异型中节点抗震性能试验研究及设计建议[J]. 建筑结构学报,2018,39(7): 33-45. doi: 10.14006/j.jzjgxb.2018.07.005 BAI Guoliang, ZHAO Jinquan, DU Ningjun, et al. Experimental study on seismic behavior of SRC abnormal interior joints and design advice[J]. Journal of Building Structures, 2018, 39(7): 33-45. doi: 10.14006/j.jzjgxb.2018.07.005
[17]	中华人民共和国建设部. 建筑抗震试验方法规程: JGJ 101—1996[S]. 北京: 中国建筑工业出版社, 1997.
[18]	贾金青,朱伟庆,王吉忠. 型钢超高强混凝土框架中节点抗剪承载力研究[J]. 土木工程学报,2013,46(10): 1-8. doi: 10.15951/j.tmgcxb.2013.10.013 JIA Jinqing, ZHU Weiqing, WANG Jizhong. Shear strength of interior steel reinforced high strength concrete beam-column joints[J]. China Civil Engineering Journal, 2013, 46(10): 1-8. doi: 10.15951/j.tmgcxb.2013.10.013
[19]	LIN C M, RESTREPO J I. Seismic behaviour and design of reinforced concrete interior beam-column joints[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2002, 35(2): 108-128. doi: 10.5459/bnzsee.35.2.108-128
[20]	ELNASHAI A S, ELGHAZOULI A Y. Performance of composite steel/concrete members under earthquake loading. Part I: Analytical model[J]. Earthquake Engineering & Structural Dynamics, 1993, 22(4): 315-345.
[21]	赵金全. 核电厂型钢混凝土框排架异型节点抗震性能与设计方法研究[D]. 西安: 西安建筑科技大学, 2018.