Identification of Vulnerable Lines in Power Grid Based on Power Flow Correlation Network
-
摘要:
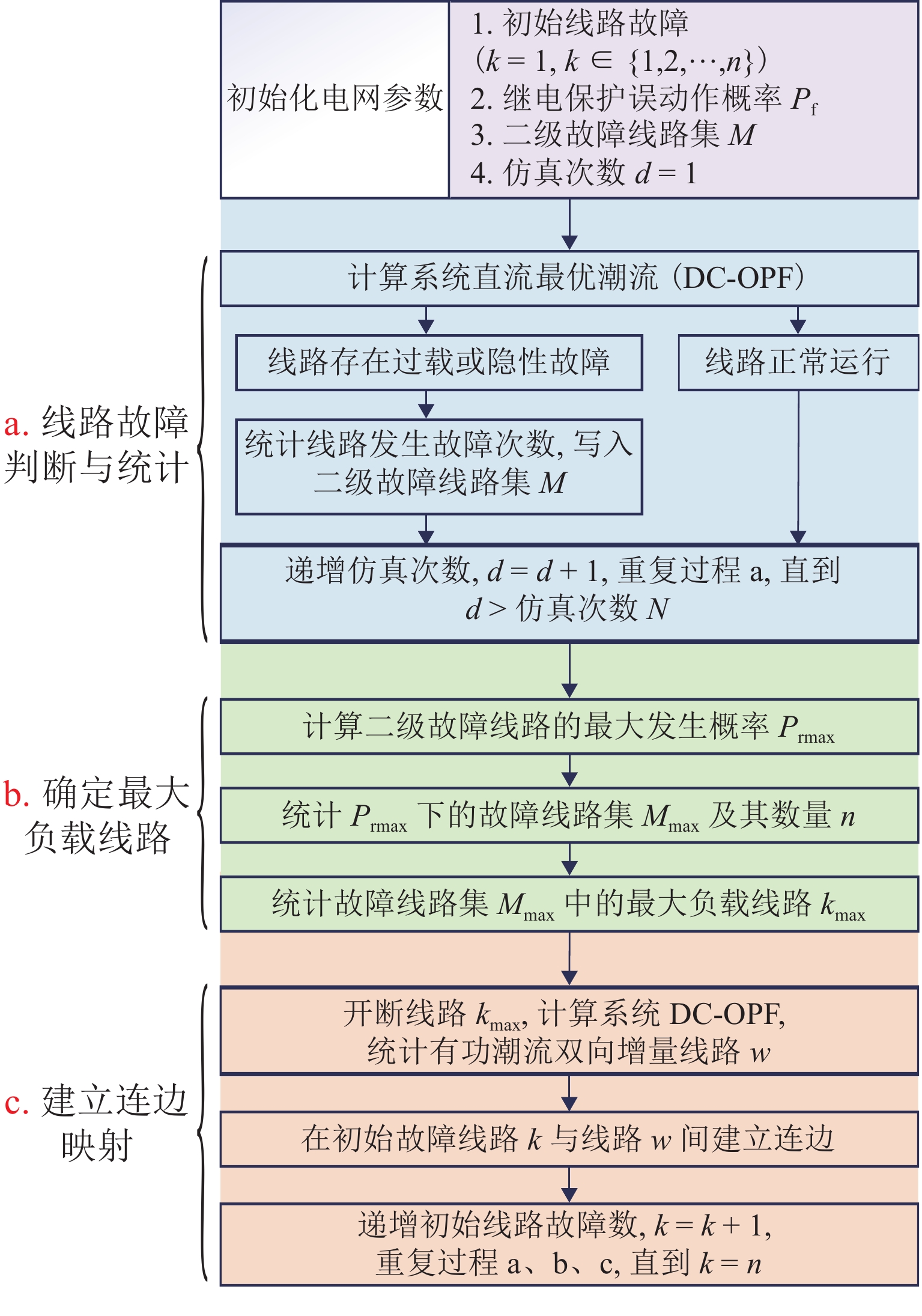
国内外大停电事故表明，电力系统中的脆弱线路会带来极大的运行风险，直接导致系统安全性下降. 鉴于此，本文根据二级连锁故障发生时有功潮流的转移特征进行电力系统脆弱线路识别. 首先，从系统运行角度，以电力系统发生二级连锁故障时有功潮流的转移量为系统线路间关系进行赋权，并构建双向加权潮流相关性网络；随后，为量化线路在连锁故障中的脆弱性，提出一种基于改进
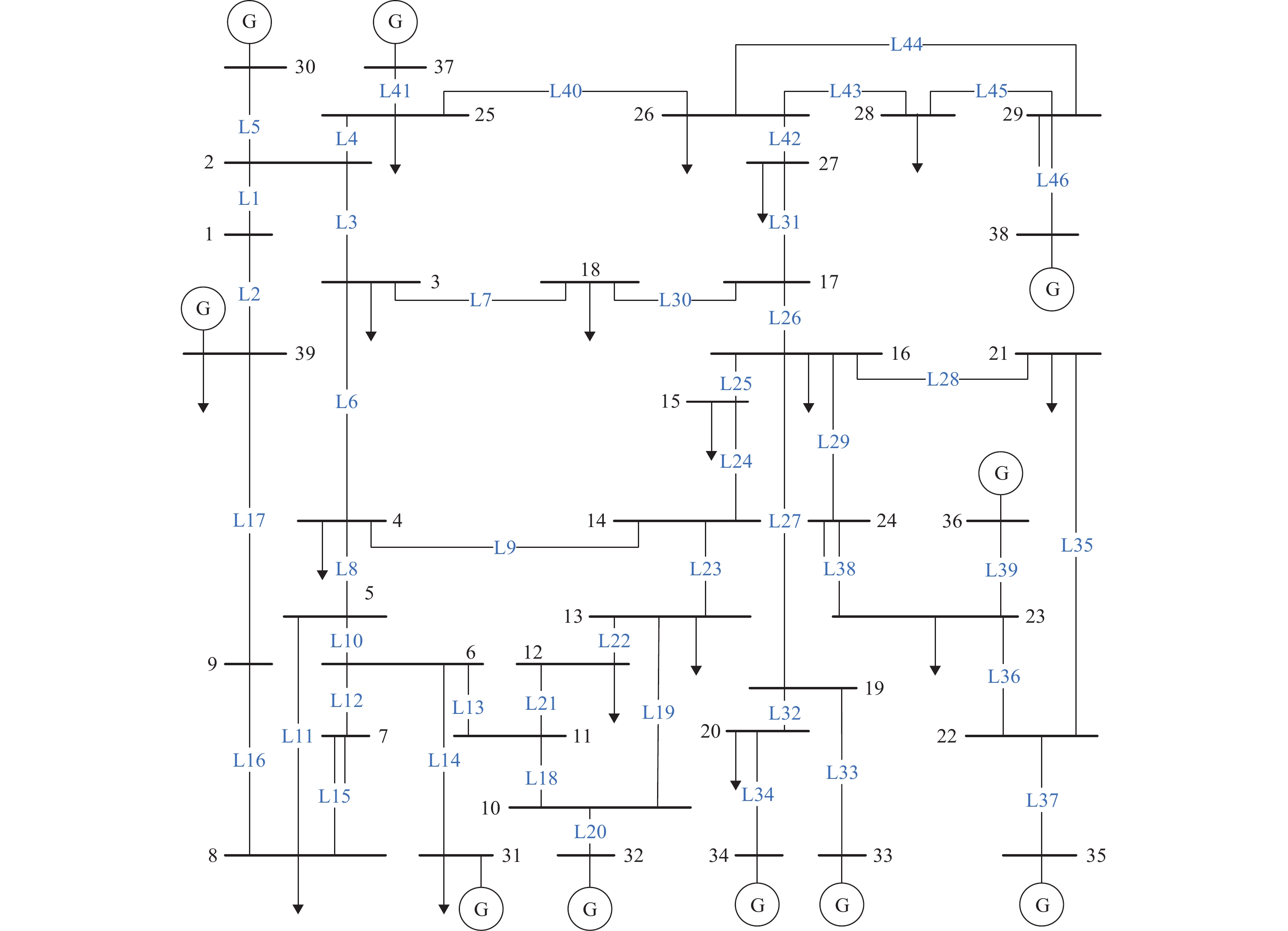
E 指数的脆弱线路识别方法. 研究表明：针对IEEE-39节点系统，依据本文方法识别结果中前8条脆弱线路的平均风险价值指数和平均条件风险价值指数分别为3453.73 MW与187.82 MW，远高于其他方法所得结果；静态蓄意攻击后所得的系统剩余负荷率仅为43.4%，系统子电气岛数量快速增长.Abstract:Global blackouts have indicated that vulnerable lines in the power system would bring great operation risk and threaten system security. In view of this, the identification of vulnerable lines in the power system was carried out according to the transfer characteristics of the active power flows in the case of a two-stage cascading failure. First, from the perspective of system operation, the relationship between the lines was weighted in terms of the transferred active power flows when the power system had a two-stage cascading failure, and a bidirectional weighted power flow correlation network was constructed. Then, an improved
E -index-based identification method for vulnerable lines was proposed to quantify line vulnerability in cascading failures. The results show that the average value at risk and the average conditional value at risk of the top eight vulnerable lines in the identified results are 3 453.73 MW and 187.82 MW respectively for the IEEE-39 bus system, which are much higher than those obtained from other methods. Meanwhile, the residual load rate of the system is only 43.4% after the static intentional attack, and the number of power islands in the system increases rapidly. -
图 4 不同隐性故障概率下蓄意攻击后系统剩余负荷率变化
Figure 4. Variation in residual load rates of system after intentional attacks under different hidden failure probabilities
图 5 不同方法下蓄意攻击后的系统剩余负荷率变化
Figure 5. Variation in residual load rates of system after intentional attacks with different methods
图 6 不同方法下蓄意攻击后的系统电气孤岛数量变化
Figure 6. Number of power islands in system after intentional attacks with different methods
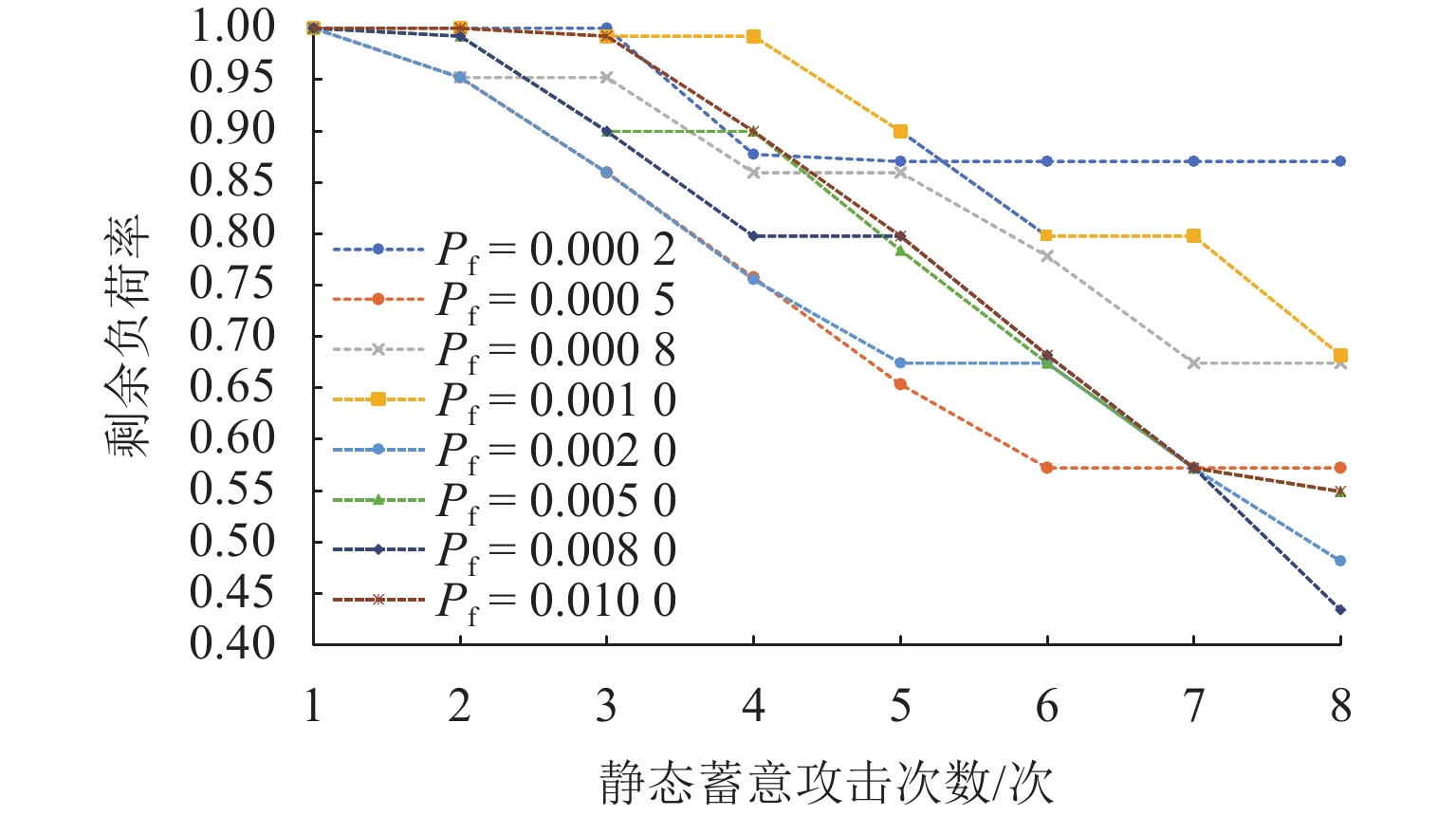
表 1 不同隐性故障概率下的脆弱线路排序
Table 1. Vulnerable line ranking under different hidden failure probabilities
Pf = 0.0020 Pf = 0.0050 Pf = 0.0100 线路 剩余负荷率 线路 剩余负荷率 线路 剩余负荷率 L37 1.00000 L34 1.00000 L34 1.00000 L20 0.95216 L33 0.99245 L38 1.00000 L39 0.85942 L39 0.89971 L33 0.99245 L33 0.75517 L35 0.89971 L39 0.89971 L34 0.67394 L20 0.78379 L14 0.79774 L38 0.67394 L37 0.67394 L20 0.68182 L14 0.57165 L14 0.57165 L37 0.57198 L41 0.48147 L38 0.54903 L35 0.54936 L46 0.34316 L46 0.43334 L46 0.43367 L27 0.30590 L10 0.43334 L27 0.38465 
下载: 导出CSV
表 2 不同方法的脆弱线路的风险价值比较
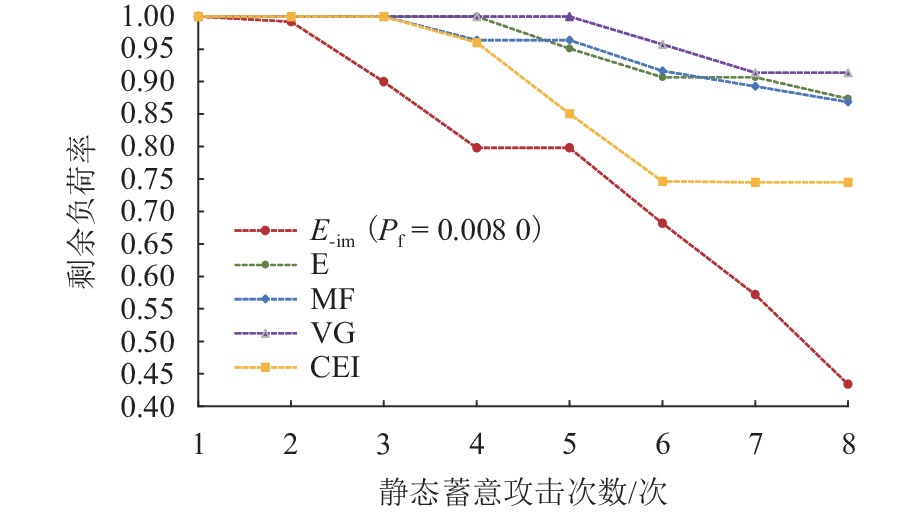
Table 2. Comparison of values at risk of vulnerable lines with different methods
攻击
序列E-im （Pf = 0.008） E 指数 VG CEI MF 线路 $ {{ \overline V_{\mathrm{aR}}}} $ ${{ \overline C_{\mathrm{VaR}}}} $ 线路 $ {{\overline V_{\mathrm{aR}}}} $ ${{ \overline C_{\mathrm{VaR}}}} $ 线路 ${{ \overline V_{\mathrm{aR}}}} $ $ {{\overline C_{\mathrm{VaR}}}} $ 线路 $ {{ \overline V_{\mathrm{aR}}}} $ ${{ \overline C_{\mathrm{VaR}}}} $ 线路 ${{ \overline V_{\mathrm{aR}}}} $ $ {{\overline C_{\mathrm{VaR}}}} $ 1 L34 3453.73 187.82 L41 3214.74 181.27 L10 2977.26 169.02 L35 3421.79 186.57 L26 3223.94 170.71 2 L33 L28 L25 L14 L37 3 L39 L29 L1 L23 L30 4 L14 L25 L3 L20 L33 5 L35 L38 L9 L37 L29 6 L20 L35 L40 L33 L38 7 L37 L43 L11 L13 L27 8 L46 L45 L4 L19 L7
下载: 导出CSV
-
[1] 何剑,屠竞哲,孙为民,等. 美国加州“8•14”、“8•15”停电事件初步分析及启示[J]. 电网技术,2020,44(12): 4471-4478.HE Jian, TU Jingzhe, SUN Weimin, et al. Preliminary analysis and lessons of California power outage events on August 14 and 15, 2020[J]. Power System Technology, 2020, 44(12): 4471-4478. [2] 孙为民,张一驰,张晓涵,等. 欧洲大陆同步电网“1•8”解列事故分析及启示[J]. 电网技术,2021,45(7): 2630-2637.SUN Weimin, ZHANG Yichi, ZHANG Xiaohan, et al. Analysis and lessons of disconnection accident of synchronous power grid in continental european area on January 8[J]. Power System Technology, 2021, 45(7): 2630-2637. [3] 马志远,刘锋,沈沉,等. 基于PageRank改进算法的电网脆弱线路快速辨识(一): 理论基础[J]. 中国电机工程学报,2016,36(23): 6363-6370.MA Zhiyuan, LIU Feng, SHEN Chen, et al. Rapid identification of vulnerable lines in power grid using modified PageRank algorithm—part I: theoretical foundation[J]. Proceedings of the CSEE, 2016, 36(23): 6363-6370. [4] 徐林,王秀丽,王锡凡. 电气介数及其在电力系统关键线路识别中的应用[J]. 中国电机工程学报,2010,30(1): 33-39.XU Lin, WANG Xiuli, WANG Xifan. Electric betweenness and its application in vulnerable line identification in power system[J]. Proceedings of the CSEE, 2010, 30(1): 33-39. [5] 刘文颖,梁才,徐鹏,等. 基于潮流介数的电力系统关键线路辨识[J]. 中国电机工程学报,2013,33(31): 90-98,11.LIU Wenying, LIANG Cai, XU Peng, et al. Identification of critical line in power systems based on flow betweenness[J]. Proceedings of the CSEE, 2013, 33(31): 90-98,11. [6] 张涛,孙晓伟,徐雪琴,等. 基于有功潮流介数的电网关键线路辨识[J]. 电网技术,2016,40(1): 193-198.ZHANG Tao, SUN Xiaowei, XU Xueqin, et al. Identification of critical lines in power grid based on active power flow betweenness[J]. Power System Technology, 2016, 40(1): 193-198. [7] 王涛,高成彬,顾雪平,等. 基于功率介数的电网关键环节辨识[J]. 电网技术,2014,38(7): 1907-1913.WANG Tao, GAO Chengbin, GU Xueping, et al. Power betweenness based identification of power grid critical links[J]. Power System Technology, 2014, 38(7): 1907-1913. [8] 蔡晔,曹一家,谭玉东,等. 基于标准化结构熵的电网结构对连锁故障的影响[J]. 电工技术学报,2015,30(3): 36-43.CAI Ye, CAO Yijia, TAN Yudong, et al. Influences of power grid structure on cascading failure based on standard structure entropy[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 36-43. [9] 鞠文云,李银红. 基于最大流传输贡献度的电力网关键线路和节点辨识[J]. 电力系统自动化,2012,36(9): 6-12.JU Wenyun, LI Yinhong. Identification of critical lines and nodes in power grid based on maximum flow transmission contribution degree[J]. Automation of Electric Power Systems, 2012, 36(9): 6-12. [10] 朱大锐,王睿,段建东,等. 考虑多影响因素的关键输电线路辨识[J]. 中国电机工程学报,2019,39(20): 5938-5947,6174.ZHU Darui, WANG Rui, DUAN Jiandong, et al. Identification of critical transmission lines considering multiple influencing factors[J]. Proceedings of the CSEE, 2019, 39(20): 5938-5947,6174. [11] 张至美,黄少伟,梅生伟,等. 基于合作博弈的电网支路脆弱性评估方法[J]. 电力系统自动化,2020,44(6): 9-16. doi: 10.7500/AEPS20190626005ZHANG Zhimei, HUANG Shaowei, MEI Shengwei, et al. Vulnerability assessment method of branch lines in power grid based on cooperative game[J]. Automation of Electric Power Systems, 2020, 44(6): 9-16. doi: 10.7500/AEPS20190626005 [12] 韦晓广,高仕斌,李多,等. 基于连锁故障网络图和不同攻击方式的输电线路脆弱性分析[J]. 中国电机工程学报,2018,38(2): 465-474,677.WEI Xiaoguang, GAO Shibin, LI Duo, et al. Cascading fault graph for the analysis of transmission network vulnerability under different attacks[J]. Proceedings of the CSEE, 2018, 38(2): 465-474,677. [13] 王涛,刘雨濛,顾雪平,等. 基于连锁故障时空图的电网脆弱线路辨识[J]. 中国电机工程学报,2019,39(20): 5962-5972,6176.WANG Tao, LIU Yumeng, GU Xueping, et al. Vulnerable lines identification of power grid based on cascading fault space-time graph[J]. Proceedings of the CSEE, 2019, 39(20): 5962-5972,6176. [14] 贾燕冰,何海丹. 基于绝对潮流介数和分布因子相关度的关键线路辨识方法[J]. 高电压技术,2017,43(1): 307-313.JIA Yanbing, HE Haidan. Identification of critical line in power systems based on absolute power flow betweenness and distribution factor correlation[J]. High Voltage Engineering, 2017, 43(1): 307-313. [15] 曾令康,姚伟,艾小猛,等. 基于双Q学习的考虑暂态稳定约束的电网薄弱线路辨识[J]. 中国电机工程学报,2020,40(8): 2429-2441.ZENG Lingkang, YAO Wei, AI Xiaomeng, et al. Double Q-learning based identification of weak lines in power grid considering transient stability constraints[J]. Proceedings of the CSEE, 2020, 40(8): 2429-2441. [16] 袁博,程林,陈亮,等. 考虑元件运行可靠性的电网脆弱性评估方法[J]. 电力系统及其自动化学报,2019,31(8): 102-107.YUAN Bo, CHENG Lin, CHEN Liang, et al. Evaluation method for power grid vulnerability considering operation reliability of components[J]. Proceedings of the CSU-EPSA, 2019, 31(8): 102-107. [17] 陈涛,杨秀中,陈冲,等. 考虑元件耐受性的电网关键元件辨识[J]. 电力系统及其自动化学报,2021,33(4): 62-70.CHEN Tao, YANG Xiuzhong, CHEN Chong, et al. Identification of critical components in power grid considering the resilience of components[J]. Proceedings of the CSU-EPSA, 2021, 33(4): 62-70. [18] 郝广涛,张逸,林清华,等. 基于输电线路利用率和连锁过载线路数量的关键输电线路辨识[J]. 武汉大学学报(工学版),2021,54(5): 429-437.HAO Guangtao, ZHANG Yi, LIN Qinghua, et al. Identification of key transmission lines based on power line utilization and interlocking overload line number[J]. Engineering Journal of Wuhan University, 2021, 54(5): 429-437. [19] 曹一家,江全元,丁理杰. 电力系统大停电的自组织临界现象[J]. 电网技术,2005,29(15): 1-5. doi: 10.3321/j.issn:1000-3673.2005.15.001CAO Yijia, JIANG Quanyuan, DING Lijie. Self-organized criticality phenomenon for power system blackouts[J]. Power System Technology, 2005, 29(15): 1-5. doi: 10.3321/j.issn:1000-3673.2005.15.001 [20] 顾雪平,刘雨濛,王涛,等. 基于结构平衡理论的电网自组织临界态辨识[J]. 电工技术学报,2018,33(17): 4136-4145.GU Xueping, LIU Yumeng, WANG Tao, et al. Self-organized critical state identification of power systems based on structural equilibrium theory[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4136-4145. [21] 曾凯文,文劲宇,程时杰,等. 复杂电网连锁故障下的关键线路辨识[J]. 中国电机工程学报,2014,34(7): 1103-1112.ZENG Kaiwen, WEN Jinyu, CHENG Shijie, et al. Critical line identification of complex power system in cascading failure[J]. Proceedings of the CSEE, 2014, 34(7): 1103-1112. [22] 马志远,刘锋,沈沉,等. 基于PageRank改进算法的电网脆弱线路快速辨识(二): 影响因素分析[J]. 中国电机工程学报,2017,37(1): 36-44.MA Zhiyuan, LIU Feng, SHEN Chen, et al. Rapid identification of vulnerable lines in power grid using modified PageRank algorithm—part Ⅱ: factors affecting identification results[J]. Proceedings of the CSEE, 2017, 37(1): 36-44. [23] LÜ L Y, ZHOU T, ZHANG Q M, et al. The H-index of a network node and its relation to degree and coreness[J]. Nature Communications, 2016, 7: 10168.1-10168.7. [24] ZHANG Q, FAN W L, QIU Z Y, et al. A new identification approach of power system vulnerable lines based on weighed H-index[J]. IEEE Access, 2019, 7: 121421-121431. doi: 10.1109/ACCESS.2019.2937903 [25] 王梅英,刘雪立. h-指数及其扩展指标的研究进展[J]. 中国科技期刊研究,2011,22(2): 184-189.WANG Meiying, LIU Xueli. Research advances on h index and its expanded variants[J]. Chinese Journal of Scientific and Technical Periodicals, 2011, 22(2): 184-189. [26] ZHANG C T. The e-index, complementing the h-index for excess citations[J]. PLoS ONE, 2009, 4(5): e5429.1-e5429.4. [27] 隋桂玲. g指数与h指数、e指数的关系及其文献计量意义[J]. 图书情报工作,2013,57(23): 90-94. doi: 10.7536/j.issn.0252-3116.2013.23.015SUI Guiling. Relations among g, h and e indexes and its bibliometrics meaning[J]. Library and Information Service, 2013, 57(23): 90-94. doi: 10.7536/j.issn.0252-3116.2013.23.015 [28] WEI X G, GAO S B, HUANG T, et al. Identification of two vulnerability features: a new framework for electrical networks based on the load redistribution mechanism of complex networks[J]. Complexity, 2019, 2019: 3531209.1-3531209.14. [29] 张海瑞,韩冬,刘玉娇,等. 基于反熵权法的智能电网评价[J]. 电力系统保护与控制,2012,40(11): 24-29. doi: 10.3969/j.issn.1674-3415.2012.11.005ZHANG Hairui, HAN Dong, LIU Yujiao, et al. Smart grid evaluation based on anti-entropy weight method[J]. Power System Protection and Control, 2012, 40(11): 24-29. doi: 10.3969/j.issn.1674-3415.2012.11.005 [30] FAN W L, LI Q Y, XIAO Y Q, et al. Power system vulnerability analysis based on topological potential field theory[J]. Physica Scripta, 2021, 96(12): 125227.1-125227.12. [31] HU P, FAN W L. Mitigation strategy against cascading failures considering vulnerable transmission line in power grid[J]. Physica A Statistical Mechanics and Its Applications,2020,540:123230.1-123230.9. [32] 蔡晔,曹一家,李勇,等. 考虑电压等级和运行状态的电网脆弱线路辨识[J]. 中国电机工程学报,2014,34(13): 2124-2131.CAI Ye, CAO Yijia, LI Yong, et al. Identification of vulnerable lines in urban power grid based on voltage grade and running state[J]. Proceedings of the CSEE, 2014, 34(13): 2124-2131. [33] ROCCHETTA R, PATELLI E. Assessment of power grid vulnerabilities accounting for stochastic loads and model imprecision[J]. International Journal of Electrical Power & Energy Systems, 2018, 98: 219-232. [34] DWIVEDI A, YU X H. A maximum-flow-based complex network approach for power system vulnerability analysis[J]. IEEE Transactions on Industrial Informatics, 2013, 9(1): 81-88. doi: 10.1109/TII.2011.2173944 -
下载:
点击查看大图
计量
- 文章访问数: 233
- HTML全文浏览量: 109
- PDF下载量: 97
- 被引次数: 0