Image Processing Based Method for Measuring Contact Force in Pantograph-Catenary System
-
摘要:
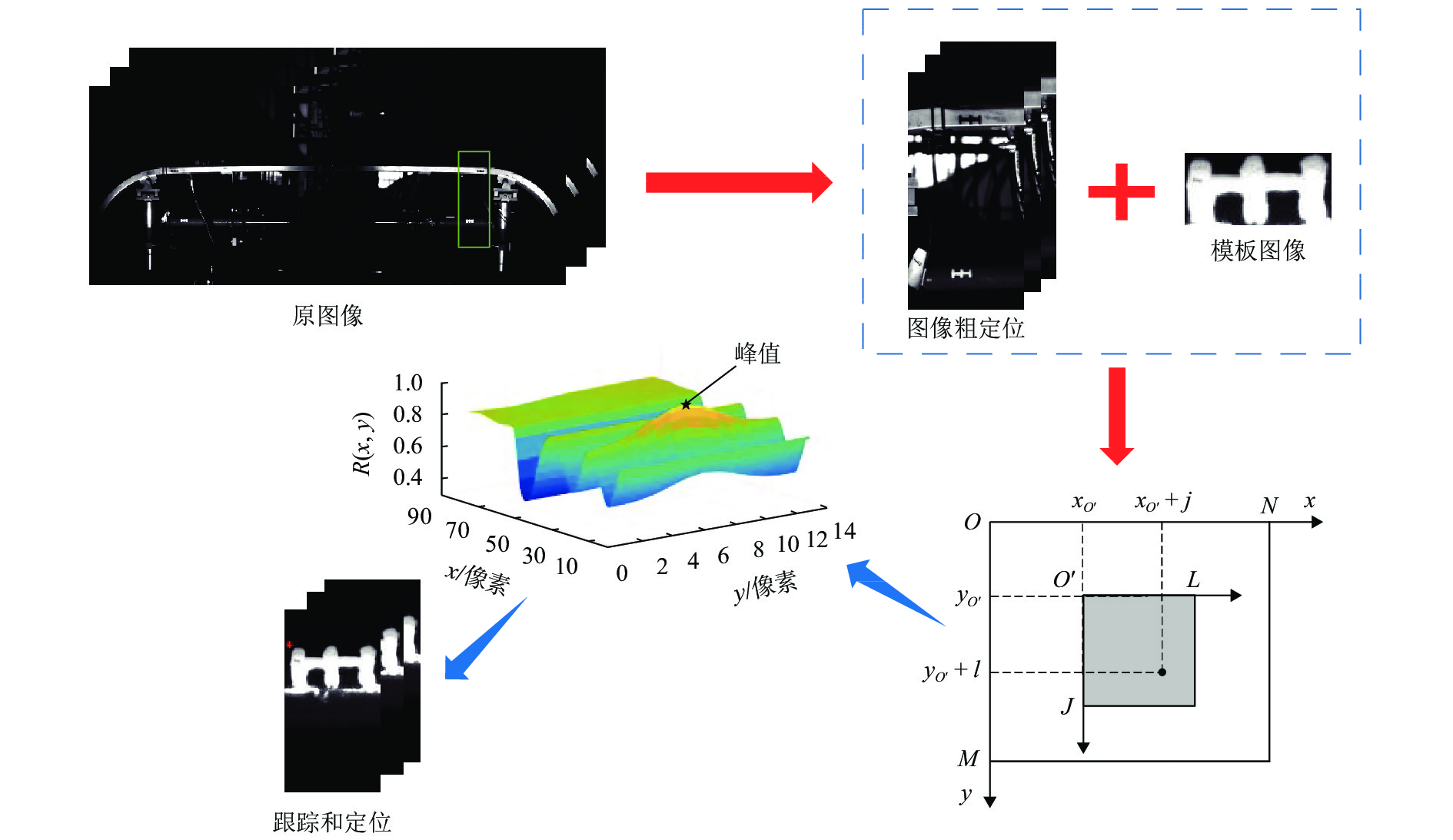
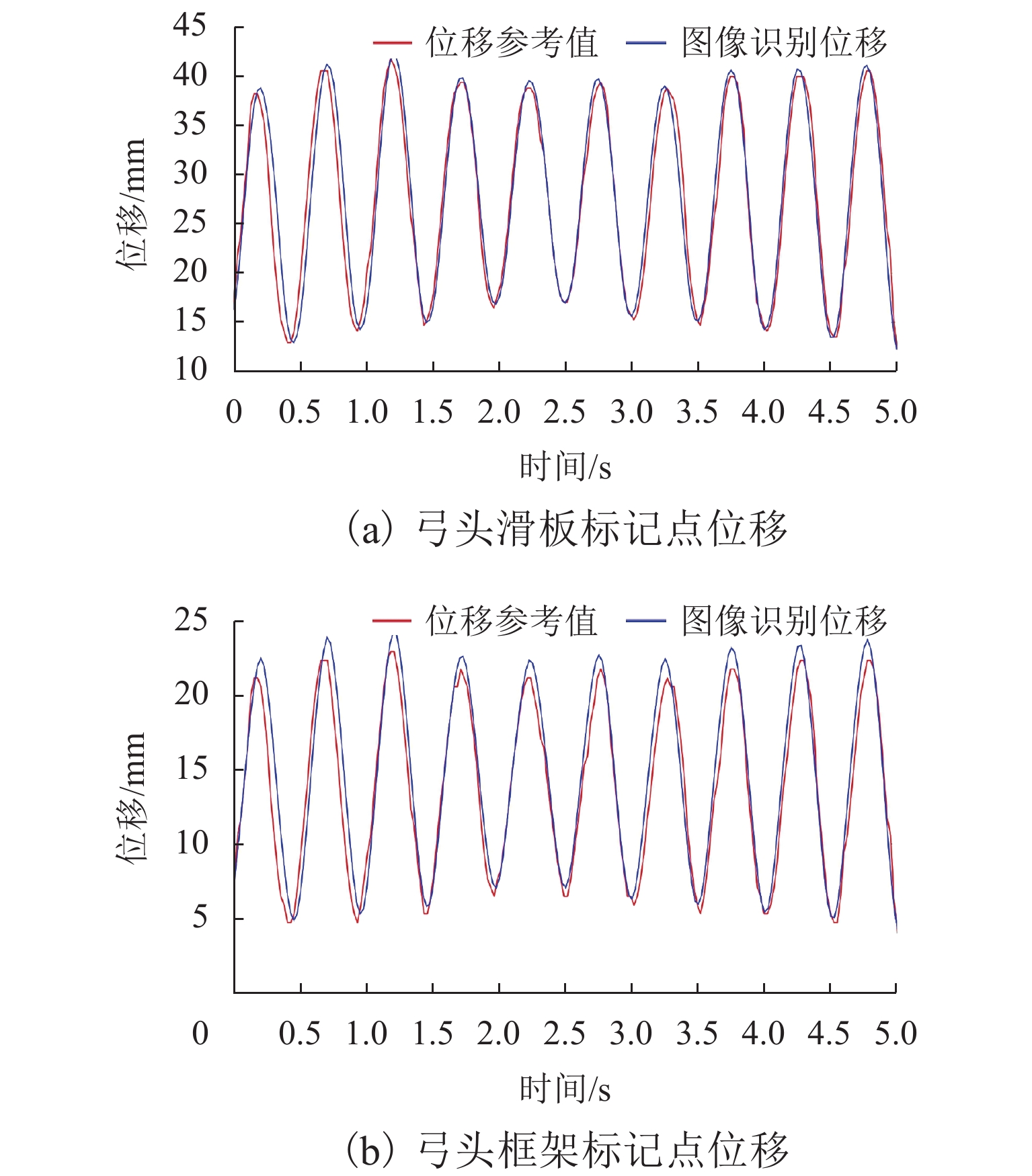
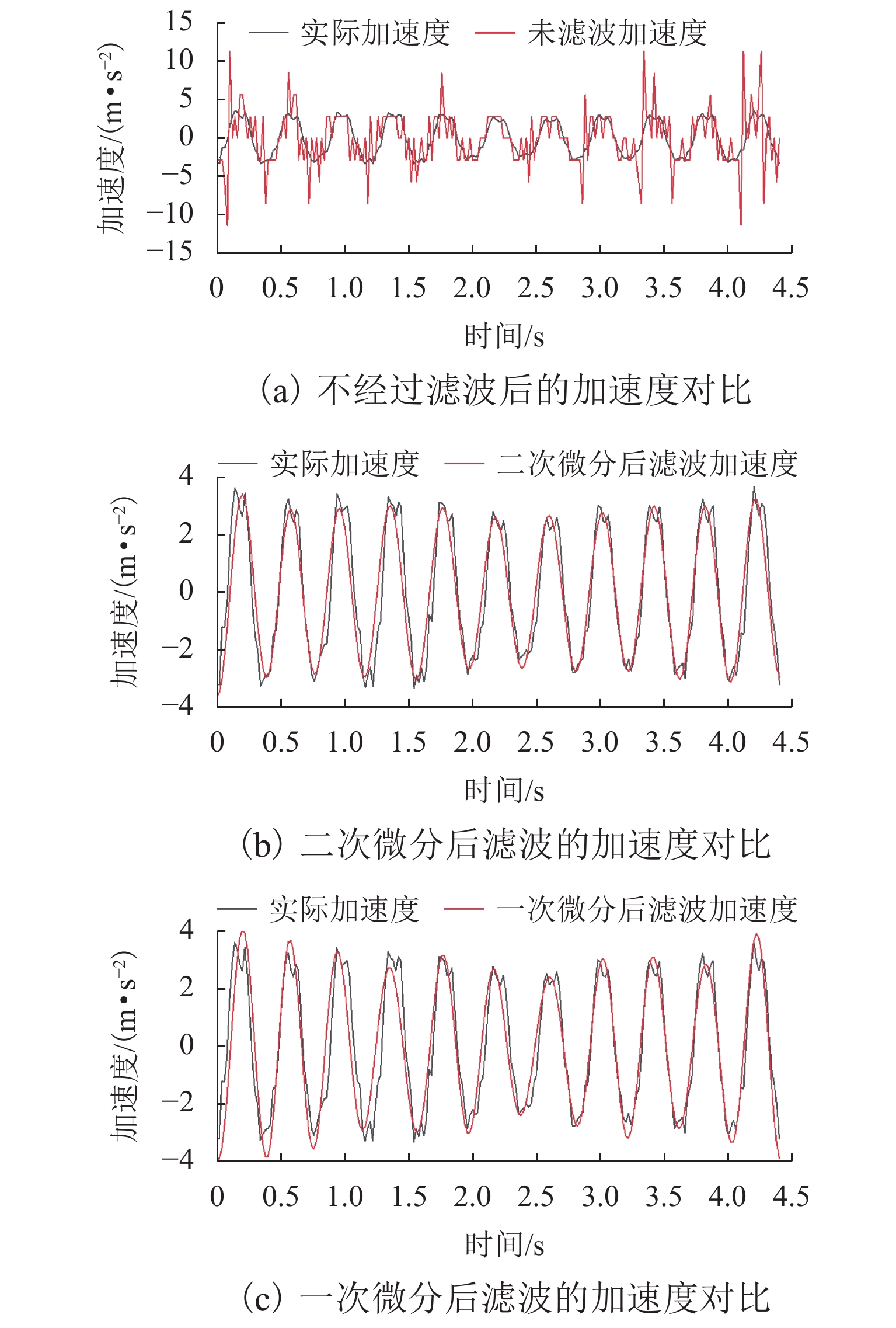
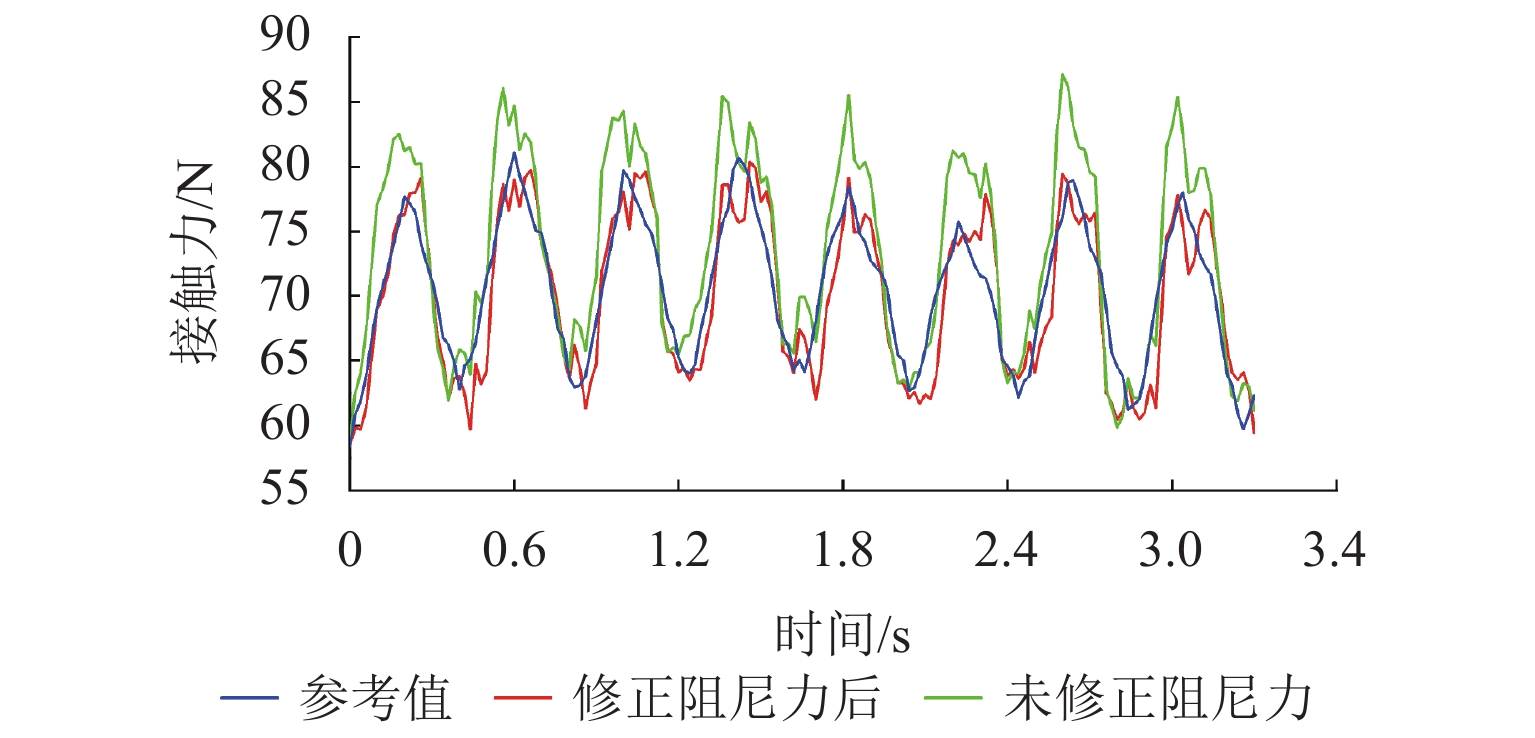
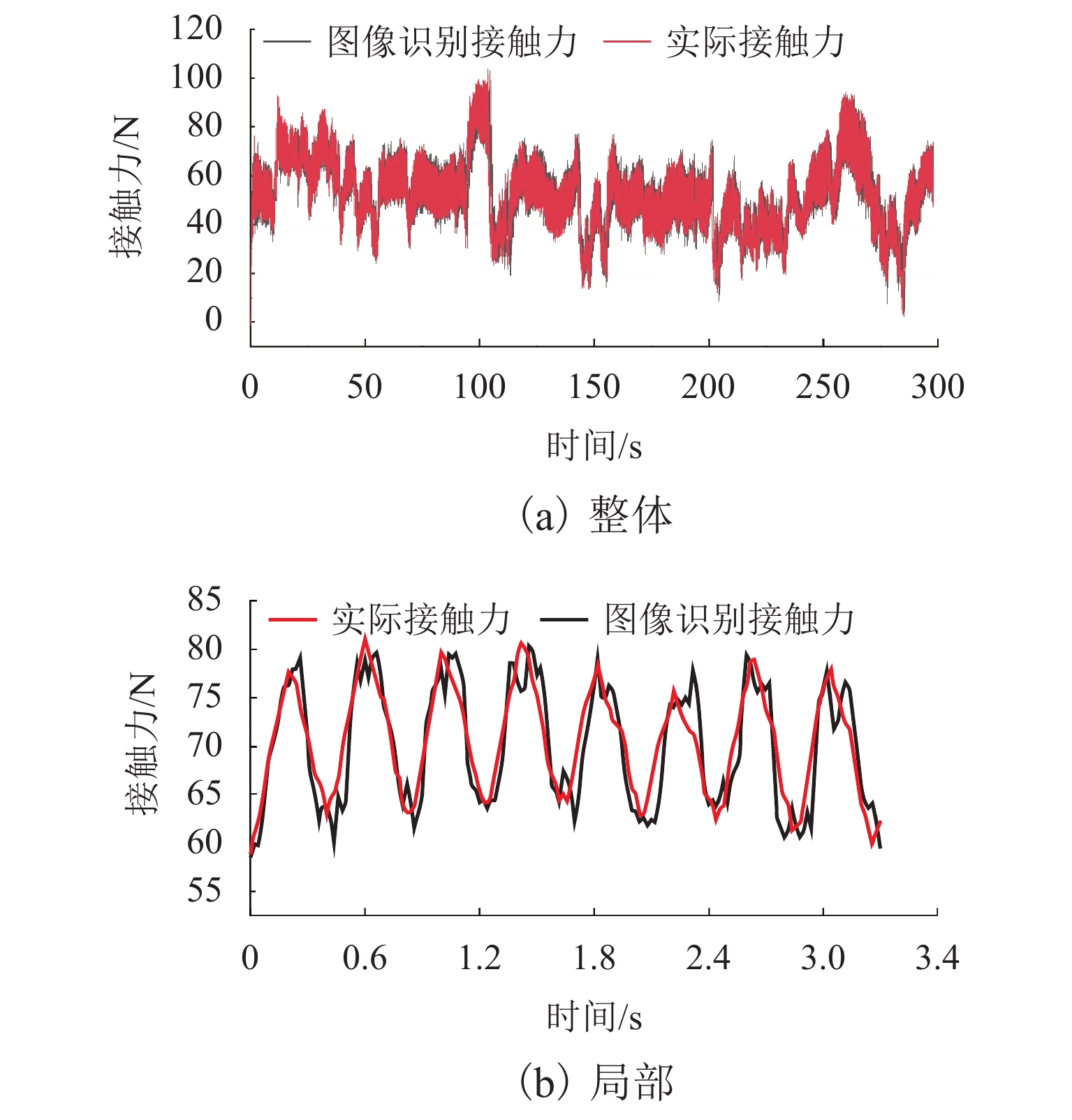
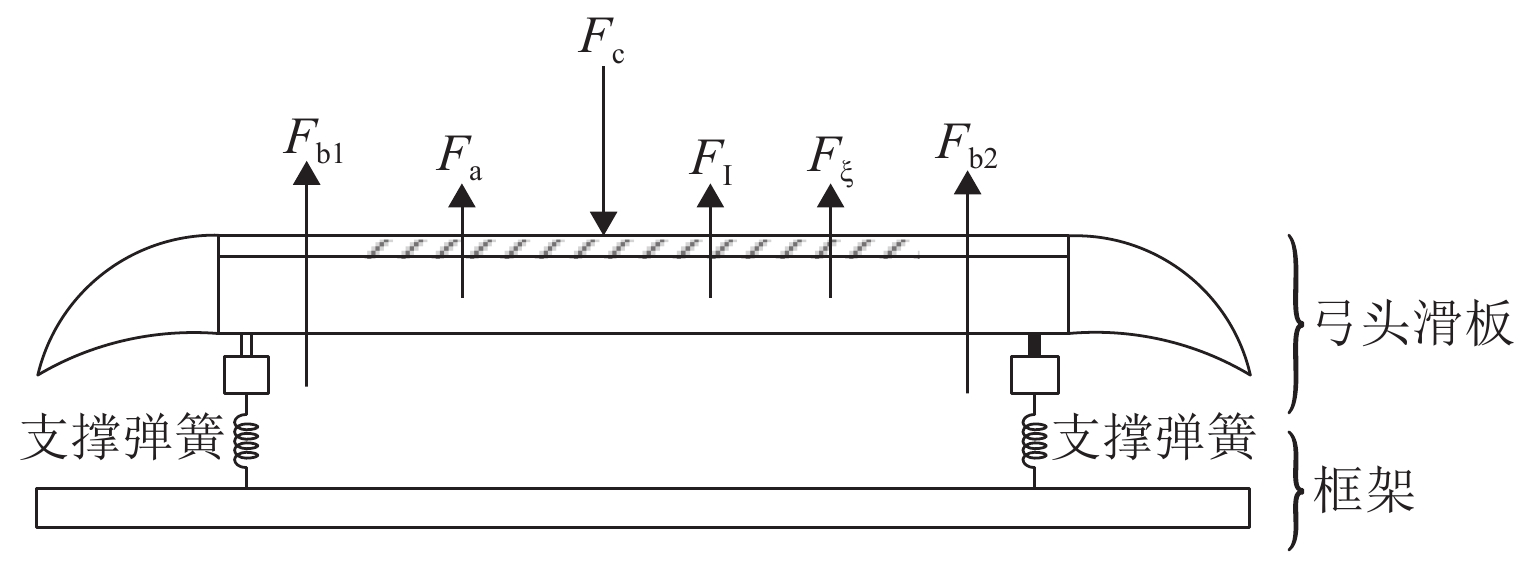
接触网和受电弓是电气化铁路供电系统中的重要组成部分，其中弓网之间的动态接触又是保证电力机车良好受流的关键条件，所以寻求良好的弓网关系是铁路供电系统设计的一个重点. 考虑到目前弓网接触力大多采用接触式检测手段，对于非接触检测的研究方法较少，故提出了一种基于图像处理算法检测弓网接触力的新方法. 简化受电弓弓头结构，分析了弓网接触力与弓头位移之间的关系，建立弓网接触力计算模型；并在弓网混合模拟试验台进行地面验证实验：首先，利用图像处理模块对采集到的图像进行标记点的目标跟踪与特征提取；然后，通过数据处理模块对得到的位移信息进一步分析得到弓头加速度等信息，修正得到加速度信号；最后，对经过惯性力和阻尼力修正后的接触力结果进行分析. 结果表明：通过图像处理检测得到的弓头位移最大测量误差仅为1.3 mm，精度较高；同时检测得到的弓网动态接触力的最大值、平均值和标准差的最大相对误差仅为5.46%、5.15%和4.58%，测量误差较小. 结果证实此方法检测弓网接触力是可行的，且检测精度满足要求.
Abstract:Catenary and pantograph are important parts in the power supply system for electrified railways. The dynamic contact between the pantograph and the catenary is pivotal to ensure that the electric locomotives acquire good electricity. Therefore, good dynamic contact between the pantograph and the catenary is a key in the design of the railway power supply system. Given that the contact detection method is common for pantograph catenary contact force at present, and there are few research methods for non-contact detection, a new method based on the image processing algorithm is proposed for detecting pantograph catenary contact force. First, the structure of the pantograph head is simplified, the relationship between the pantograph dynamic contact force and the pantograph head displacement is analyzed, and a new model for calculating the contact force is developed. Next, the ground validation test is conducted on the pantograph-catenary hybrid simulation platform. In tests, the image processing module is used for target tracking and feature extraction of marked points in the collected image. Then, the displacement information is further analyzed by the data processing module to obtain the pantograph head acceleration and other information, and the acceleration signal is corrected. Finally, the contact force results corrected by inertia force and damping force are analyzed. The test results show that the maximum error of the pantograph head displacement detected by image processing is 1.3 mm, showing a high accuracy. Meanwhile, the maximum relative errors of the maximum, average and standard deviation of the dynamic pantograph-catenary contact force are only 5.46%, 5.15% and 4.58%, demonstrating that the measurement error is small. Thus, this method is feasible in detecting the pantograph-catenary contact force and its detection accuracy meets the requirements.
-
Key words:
- pantograph /
- catenary /
- contact force /
- image processing /
- machine vision /
- template matching
-
无论堆煤还是采区遗煤在开采、运输和储存过程中均以颗粒状的松散煤体形式存在. 松散煤体自燃对空气质量、地表植被、地质条件造成了不同程度的影响[1-3]，同时粉尘、CO和SO2等有毒有害气体会伴随着煤体自燃大量涌入大气中，造成区域性空气污染，危害人体健康[4-9]，并且外界环境（如辐射、大气环境等）和内在因素（如煤体水分含量、粒径等）会对松散煤体的自燃特性造成影响[10-11]. 国内外学者对煤体自燃氧气浓度的演化进行了大量的研究.
目前，学者们多采用有限元[12]、回归模型[13]等方法对煤自燃温度场的模型进行组建与计算. 赵婧昱等[14-16]模拟松散煤体从常温到着火全过程，得出高温点首先出现在低氧浓度分布区，确定了高温氧化过程中的危险阶段为干裂—活性—增速温度阶段. 张九零等[17-18]模拟了火区自燃蔓延时温度场、一氧化碳浓度和速度场的分布情况，确定了露头自燃点下风侧方向是生成气体的主要集中区域. 此外，学者们还研究了煤体在不同热源温度[19]、粒度[20]、有效孔隙[21]等条件下氧气运移的规律特征. 郭兴明等[22-24]假设煤体为均匀介质，建立了氧气在松散煤体中扩散过程的数学模型；邓军等[25-26]对煤体自燃过程中的耗氧速率进行了理论分析，推导出了低温氧化阶段耗氧速率的量化模型；谭波等[27]基于煤自燃参数对煤自燃的影响分析，建立了煤自燃中温度场的数学模型并进行求解计算，得到了煤自燃数学一维模型.
由于煤自燃现场研究难度较大，研究人员多建立圆柱形煤火发生实验炉，进行煤自燃的传质、传热过程研究. 研究装置多为程序升温系统，持续进行热源和氧气供给，以维持良好的蓄热环境，但对于自然状态下煤火区域氧气与温度相互作用的效应探索较少. 由于煤体内非等温的温度场导致与外界产生热力压差，致使氧气通过裂隙渗入煤体，维持自燃反应，释放热能，推动高温区域向深部发展，致使燃烧愈加剧烈. 当煤体温度到达一定程度，松散煤体内部的氧浓度逐渐下降至极限氧浓度以下，开始形成煤体需氧量大而氧气浓度低的热环境，煤体开始主动吸附游离在空气中的氧气分子，此时存在煤体表面对氧气进行竞争状态，本文将这个竞争过程称为“煤体自然吸氧效应”. 在此基础上，采用自主研发的半封闭煤火演化实验系统，在自然通风的条件下，分析松散煤体自燃过程中的氧气及温度阶段性演化规律，从而建立高温贫氧条件下煤自燃耗氧速率的量化模型，并揭示其内在联系规律. 研究成果对开采、运输、储存状态下的松散煤体自然发火的防治提供理论基础.
1. 实验装置及实验条件
1.1 实验装置
本实验采用自主搭建半封闭煤火演化实验系统，模拟“自然吸氧效应”，不进行人为主动供氧，热源引燃煤体首层后，测试下五层煤体的自燃特征.
半封闭煤火演化实验系统包括以下装置：炉体、温度控制和监测平台、气体分析装置以及污染物处理装置等（如图1所示）. 实验炉体由耐高温纯纤维毯和碳钢材料压制组成，炉体整体为圆柱体，外部尺寸：半径300 mm × 高730 mm，炉膛内部尺寸：半径150 mm × 高600 mm，侧壁保温层厚度为150 mm，保温层由耐火砖和纤维的混合结构组成. 炉体顶部安装易于控制升温速率的不锈钢加热棒，直径14 mm，功率500 W，额定电压380 V，最大受热温度1100 ℃. 炉壁布置有直径为16 mm的通孔作为温度数据采集点和气体采集点，测温单元与温度记录仪装置连接，采用气相色谱仪对所采集的气体进行测试. 实验炉体顶部设有防潮盖，实验时，防潮盖为常开状态，保证实验为半封闭状态. 炉体为圆柱形设计，这里将横截面圆心位置来表征整个截面的温度变化，测温单元与测气单元布置于煤体正中心位置从上至下共五层；为反映煤体在燃烧过程中横向变化特征，在第三层的位置横向布置3个测点（如图2所示），中心位置5个测点从上至下分别编号为PTC1～PTC5，第三层两侧测点分别编号为PTC6、PTC7.
1.2 实验条件
半封闭煤火演化实验在常温、常压下完成. 煤样采自陕西孟村煤矿，从工作面采取后使用布袋密封运送至实验室，使用鄂式破碎机完成破碎，为模拟开采后煤堆粒径尺寸[28]，破碎的煤样粒径约为10 mm，实验条件、煤质分析分别如表1、2所示. 表中：Mad为水分含量；Aad为灰分产率；Vad为挥发分产率；FCad为固定碳含量.
表 1 实验条件Table 1. Experimental conditions项目 煤样 粒径/mm 室温/℃ 湿度/% 煤高/mm 装煤量/kg 参数 孟村 10 6 68 480 57.7 表 2 煤质分析Table 2. Coal quality analysis% 工业分析 元素成分分析 Mad Aad Vad FCad C H O N S 4.4 14.0 33.5 48.0 78.8 4.7 14.2 1.3 0.8 该实验无外部气源，通过实验装置留设的通孔布置测温热电偶、采气铜管和加热单元. 对煤体表面进行人为加热，主动提供火源，当顶层煤样开始出现明火时停止加热，之后松散煤体自发燃烧. 实验时采气间隔为1.0 h，当某层温度达到燃点温度，便改变该层采气间隔为2.0 h，所有煤层均达到燃点温度后，改变所有煤层采气间隔为4.0 h，当采集点裸露在空气中或最底层煤体温度达到室温后，不再采集气体.
通过热重分析法，确定了实验煤样自燃的特征温度. 样品粒径为80～120目，质量为5 mg，温度范围30.0～800.0 ℃，升温速率为5 ℃/min.
2. 自然吸氧变化特征
2.1 氧气浓度变化
松散煤体在燃烧过程中各测点氧气浓度变化情况如图3所示. 因首层煤样距空气位置较近，煤样反应发生较强，实验开始时，该层煤样相比于其他煤样氧气浓度低5.0%～10.0%. 推测实验初期上层煤样与空气接触面积较大，空气中游离的氧分子充足，更易于被煤体吸附，从而发生煤体“自然吸氧”反应，促使煤体温度升高. 将煤体主动吸收氧气的难易程度称为煤体“自然吸氧强度”. 实验进行至3.0 h后，各层煤样测点处煤体“自然吸氧强度”增高，氧气浓度下降速率开始加快，上层煤样几乎呈直线下降. 3.0 h时第二层测点氧气浓度下降至7.5%～10.0%，与实验初期首层煤样氧气浓度相似. 6.5 h后，首层煤样氧气浓度下降至1.0 %～3.0%，此为火区煤贫氧燃烧的极限氧浓度，此时煤体表面开始出现明火现象，燃烧开始，其后该测点氧气浓度基本保持不变. 7.0 h时第二层煤样测点处氧气浓度也下降至极限氧浓度. 总体来看，各层煤样测点变化趋势基本相似，但由于纵深变化的影响，实验初期，相较于上层煤样，底层煤样与空气接触面积较小，空气不易于流动，其“自然吸氧强度”也就弱于上层煤样，表现形式为氧气浓度开始下降时间的逐渐延后. 而此时，其他三层氧气浓度仍处于较高水平，直至14.0 h后，均下降至极限氧浓度以下.
在实验进行至4.0 h时，可以观察到第三层煤样3个测点之间氧气浓度下降程度略有不同，且在9.5 h后，第四层测点氧气浓度低于第三层. 推测因煤体自身裂隙发育的影响，使得该区域煤体与空气接触面积呈现出不同情况. 裂隙为氧气的扩散提供了通风线路，促进了其向裂隙扩展方向运移，从而导致同层不同测点之间氧气浓度下降程度的不均衡现象. 故煤体“自然吸氧强度”受氧气浓度、煤层高度、煤体温度及孔隙率共同影响.
2.2 自然吸氧强度计算模型
基于Krishnawamy等[29]提出的煤的动力学反应扩散模型求解煤在低氧浓度（氧气浓度小于3.0 %）下自燃时的自然吸氧强度. 假设高温低氧浓度区域是由相同粒径的煤颗粒所组成的，因此，自燃区域的耗氧速率即为煤颗粒的自然吸氧强度. 该区域的耗氧速率即为单位时间内煤体所消耗的氧气浓度，而在低氧浓度环境下煤体所消耗的氧气浓度等于单位时间内所供给的氧气浓度，推导得出自然吸氧强度为
r=ηkSr(1−ε)Vr(C−C1), (1) 式中：r为自然吸氧强度，mol/（m3·s）；η为效率因子；k为质量传输速率，kg/s；Sr为自燃区域底面积，m2；ε为煤体的孔隙率，%；Vr为燃烧区的体积，m3；C为外部环境中氧气浓度，mol/m3；C1为煤体中的氧气浓度，mol/m3.
由于在高温阶段煤体中的水分已经蒸发殆尽，煤体中的水分不会对氧气的供给产生影响，则其效率因子
$\eta $ 接近于1，可将该项忽略. 自燃曲的体积与表面积的关系可以化简为SrVr=SrSrH=1H, (2) 式中： H为自燃区域高度，m.
质量传输速率k可以根据舍伍德数求出，由半经验公式可得
k=Shd, (3) 式中：Sh为舍伍德数，无量纲，通常取0.3；d为煤粒粒径，m.
式（1）可简化为
r=ShD0(1−ε)dH(C−C1), (4) 式中：D0为热扩散系数，m2/s.
煤样不同测点的自然吸氧强度随时间变化曲线如图4所示. 由图4可知：自然吸氧强度与氧气浓度变化相反，当氧气浓度下降时，自然吸氧强度逐渐上升；火区低阶煤贫氧燃烧的极限氧浓度为1.0%～3.0%，当氧浓度小于极限氧浓度后，即高温燃烧过程将出现热解进程，此时自然吸氧强度趋于平缓；煤样同层不同测点自然吸氧强度变化规律近似于抛物线形式，第一、二层煤样在3.0 h前自然吸氧强度变化平稳，在3.0～6.5 h急剧提升，6.5 h后又趋于平稳；第三层煤样趋势稍缓，实验15.0 h后趋于平缓；第四、五层深煤样自然吸氧强度变化最慢，在整个阶段呈线性变化，这种现象取决于煤层深度的不同；纵向来看，由于氧气浓度、温度与煤体传热特征等原因，自然吸氧强度随深度的增加逐渐减小；同样地，同层煤样不同测点之间自然吸氧强度变化趋势也基本满足自然吸氧强度与氧气浓度变化相反.
图 4 自然吸氧强度变化与时间关系曲线Figure 4. Curves of natural absorption oxygen intensity versus time松散煤体在堆放、运输、储存过程中主要以自然通风为主，氧气供给充足，当温度达到一定条件之后容易发生自燃反应. 自燃开始形成后，燃烧便会由浅部向深部逐步发展，并不断向深部运移，同时内部环境与外部环境形成热力压差，促进煤体主动吸氧，使得游离在空气中的氧气分子被吸附于煤体内部，维持燃烧的进行. 松散煤体为多孔介质，各部位的传热是传导、辐射、对流共存的综合传热过程，属于不稳定传热. 随着自燃深度的加深，煤氧化学反应不断加剧，蓄热能力增强，传热作用显著增加，裂隙变化，温度发生变动.
3. 氧化自燃阶段分析
由氧气浓度变化可看出，煤体自燃拥有阶段性变化特征，为了更好地对温度运移与耗氧特征进行分析，选取热重曲线特征温度点[15]，根据特征温度对氧化自燃过程进行分阶段划分. 图5为实验煤样的热重（thermal gravity，TG）曲线及导数热重（derivative thermogravimetry，DTG）曲线，T1为吸氧增重起始温度点，此温度点之前为缓慢氧化阶段. T2为吸氧增重最大温度点，T1～T2为快速升温阶段. 吸氧增重最大温度点之后，煤氧化自燃开始从缓慢氧化阶段到高温自燃阶段过渡，煤氧反应更加剧烈，经历分界点着火点温度（T3）后，质量迅速下降，并达到DTG曲线谷值上的点T4 （最大失重速率的温度点），此后达到燃尽温度点（T5），煤体温度超过燃尽温度后，进入高温自燃阶段. 煤样3个不同氧化自燃阶段温度范围如表3所示.
表 3 不同氧化自燃阶段温度划分Table 3. Temperature levels in oxidized spontaneous combustion阶段 氧化自燃阶段 平均温度范围/℃ 第一阶段 缓慢氧化阶段 0～111.0 第二阶段 快速升温阶段 112.0～303.0 第三阶段 高温自燃阶段 304.0～604.0 4. 温度运移阶段性特征分析
第2节分析了从实验开始至煤体发生燃烧各层测点氧气浓度的变化趋势，而氧气是燃烧必不可少的反应物，氧气浓度的阶段性变化必然会引起温度的阶段性变化. 故本节对各层测点间温度变化趋势进行分析.
煤自燃在纵向发展过程中，随测点深度加深温度逐渐降低，达到最高温度点的时间依次延长. 测点各阶段的时间与温度如表4所示. 由图4、表4可知：第一层煤体在实验4.5 h左右达到121.0 ℃，随着实验的进行，温度逐渐向下传播，其余各层进入缓慢氧化阶段时间依次延后，第二层到第五层依次为12.0、14.0、19.5、32.5 h；其后，各测点温度上升速率逐渐加快，直至6.5 h时，首层煤样温度达到316.0 ℃，煤体表面出现明火现象，燃烧开始. 对于同测点温度变化时间要比氧气浓度变化时间相对延后，可证明氧气浓度的变化要先于温度的变化，在煤体自然过程中，氧气的变化为先决条件，煤体的“自然吸氧”效应使得游离在空气中的氧分子吸附于煤体之中，为自燃提供条件. 在氧气吸附的过程中，煤体温度逐渐升高，从而促使煤体“自然吸氧强度”增高，加快氧气的吸附，直到达到燃点，氧气浓度不再发生改变，于是可得出温度变化时间对氧气浓度变化时间具有一定的滞后性，而其滞后时间主要受煤层高度影响.
表 4 纵向测点到达各阶段的时间与温度Table 4. Time and temperature of longitudinal measuring points at each phase阶段 PTC1 PTC2 PTC3 PTC4 PTC5 时段/h 温度/℃ 时段/h 温度/℃ 时段/h 温度/℃ 时段/h 温度/℃ 时段/h 温度/℃ 第一阶段 0～4.5 121.0 0～12.0 132.0 0～14.0 120.0 0～19.5 115.0 0～32.5 121.0 第二阶段 4.5～6.5 316.0 12.0～13.5 314.0 14.0～16.0 308.0 19.5～21.0 301.0 23.5～48.0 302.0 第三阶段 6.5～23.0 602.0 13.5～24.0 598.0 16.0～48.0 577.0 21.0～43.0 492.0 48.0～73.0 476.0 所有测点处温度处于快速升温阶段的时间远小于缓慢氧化阶段，推测煤体“自然吸氧强度”使得氧气吸附在煤体的速率加快，由此可证明，氧气的变化引起温度的变化.
煤体纵向5个测点温度随时间变化曲线如图6所示，选取实验前24.0 h数据，温度变化与测点到煤体表面直线距离的关系曲线如图7所示. 由图可知：第一层煤体温度前24.0 h内均处于最高水平，这是由于其距表层最近，氧气浓度充足，同时距离加热层最近造成的；PTC2～PTC4的温度变化较快，曲线表现出从第6.0、12.0 h的凹状变为24.0 h的凸状；而第五层由于距离表层最远初始氧气浓度较低，且温度传播需要时间，所以其温度在前24.0 h内始终处于最低水平.
图 6 纵向温度变化与时间关系Figure 6. Relationship between longitudinal temperature change and time对温度随测点距煤体表面距离的变化曲线进行回归分析，得出温度与距离之间的关系为
t=Al3+Bl2+Cl+D, (5) 式中：t为温度，℃；l为距煤体表面距离，mm；A、B、C为回归方程系数；D为回归方程截距.
煤样所有测点虽距离煤体表面距离的不同，但温度变化曲线拟合均符合该回归方程，相关系数R2值均在0.9800左右，表现较好的相关性. 由此可知，煤体内部温度传播受纵深影响较大，深度越大，温度传播越慢，温度变化趋势越低. 同时做其温升速率变化如图8所示，可以看出随着深度的增加，各层测点温升速率达到峰值时间逐渐后移，峰值速率也逐渐降低，由此反向证明了拟合回归方程的正确性.
实验样本中第三层煤样3个测点的变化能够较为准确地反映整个实验的变化特征. 如图9所示，同层煤的不同测点展示出相同的变化规律. 由图可知：实验煤样同层测点的温度增长趋势一致，但到达各阶段的时间不同；PTC6经过13.0 h升至111.2 ℃，最先进入第二阶段，经15.0 h率先超过燃点温度达到312.2 ℃；PTC7温度变化慢于PTC3、PTC6，但实验48.0 h后，PTC7的温度下降速度最快，说明此测点氧气浓度较弱；312.0 h后，3个测点均处于低温状态. 煤体孔隙结构的变化能够直接影响氧气的吸附与渗流. 松散煤体为非均匀介质，在燃烧过程中由于温度的升高，煤体内部产生不规则裂隙，致使氧气随裂隙进入煤体内，从而促使燃烧加剧，且不同测点位置孔隙结构有所差异，同层煤不同测点的温度变化情况也因此各不相同.
5. 结 论
1） 通过对氧气浓度与温度迁移数据的分析可以表明煤火发展演化模拟实验装置能够较好地模拟和再现煤自燃“自然吸氧”过程.
2） 煤体自身“自然吸氧效应”为其燃烧提供动力，促使煤体内部氧气浓度发生改变. 随着煤层纵深的增加，氧气浓度下降开始时间逐渐增加，“自然吸氧强度”随也不断减弱.
实验过程中，氧气浓度的变化是温度变化的前提条件，温度变化时间滞后于氧气浓度变化，其滞后时间差随煤层纵深变化的增加而增加. 在水平方向上高温区域迁移趋势主要受煤体内部裂隙与孔隙分布的影响.
致谢：西安科技大学优秀青年科技基金项目（2020YQ3-02）.
-
图 9 图像识别与拉线位移传感器识别位移对比
Figure 9. Comparison between image recognition and wire displacement sensor
图 10 不同滤波策略的加速度信号对比
Figure 10. Comparison of acceleration signals with different filtering strategies
图 11 阻尼力修正前后局部接触力对比
Figure 11. Comparison of local contact force before and after damping force correction
图 12 整体与局部弓网动态接触压力对比
Figure 12. Comparison of dynamic contact pressure between overall and local pantograph-catenary
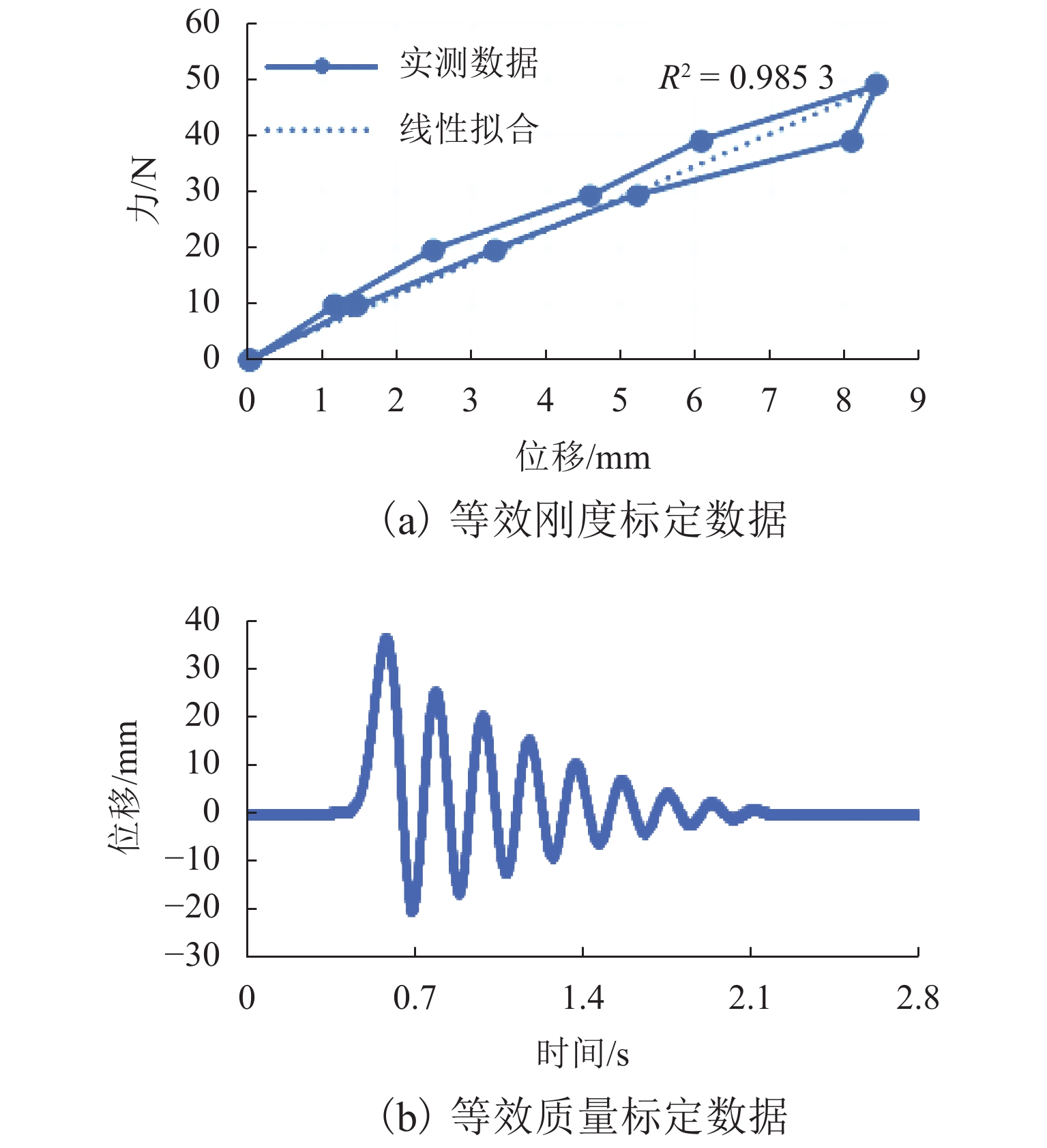
表 1 实验加载工况
Table 1. Loading conditions in tests
加载工况 力/N 位移/mm 1 9.8 1.1575 2 19.6 2.4888 3 29.4 4.5951 4 39.2 6.0655 5 49.0 8.4103 6 39.2 8.0725 7 29.4 5.2111 8 19.6 3.3035 9 9.8 1.4754 
下载: 导出CSV
表 2 标记点特征定位计算时间
Table 2. Calculation time for positioning markers
数据
类型图像大小
（宽×高）/
像素模板大小
（宽×高）/
像素图像
数量/
张计算
时间/
s平均每
帧计算
时间/s原图像 228×491 38×20 1000 265.87 0.26587 粗定位后图像 50×105 38×20 1000 9.39 0.00939
下载: 导出CSV
表 3 动态实验接触力统计结果
Table 3. Statistical results of contact forces from dynamical tests
修正类型 最小值 最大值 平均值 标准差 实际
值/N测量
值/N相对误
差/%实际
值/N测量
值/N相对误
差/%实际
值/N测量
值/N相对误
差/%实际
值/N测量
值/N相对误
差/%不考虑惯性力 −0.57 −2.40 321.10 103.67 119.82 15.58 52.61 55.32 5.15 15.49 23.67 52.81 考虑惯性力 −0.57 −1.63 185.96 103.67 109.33 5.46 52.61 55.32 5.15 15.49 16.20 4.58 不考虑阻尼力 −0.57 −1.70 198.25 103.67 108.38 4.54 52.61 55.31 5.13 15.49 16.41 5.94 考虑阻尼力 −0.57 −1.63 186.96 103.67 109.33 5.46 52.61 55.32 5.15 15.49 16.20 4.58
下载: 导出CSV
-
[1] 刘志刚,宋洋,韩烨,等. 高速铁路接触网研究进展[J]. 西南交通大学学报,2016,51(3): 495-518. doi: 10.3969/j.issn.0258-2724.2016.03.009LIU Zhigang, SONG Yang, HAN Ye, et al. Advances of research on high-speed railway catenary[J]. Journal of Southwest Jiaotong University, 2016, 51(3): 495-518. doi: 10.3969/j.issn.0258-2724.2016.03.009 [2] 周宁,蔚超,谭梦颖,等. 弓网系统动态及受流性能测试技术研究及应用[J]. 铁道学报,2020,42(3): 47-54.ZHOU Ning, WEI Chao, TAN Mengying, et al. Investigation on and application of measurement technology of dynamic performance and current collection quality of pantograph-catenary system[J]. Journal of the China Railway Society, 2020, 42(3): 47-54. [3] 张晓林,高晓蓉,王黎,等. 弓网接触力检测方法介绍[J]. 铁道技术监督,2010,38(8): 11-13,16. doi: 10.3969/j.issn.1006-9178.2010.08.004ZHANG Xiaolin, GAO Xiaorong, WANG Li, et al. Introduction on the detection of pantograph catenary contact force[J]. Railway Quality Control, 2010, 38(8): 11-13,16. doi: 10.3969/j.issn.1006-9178.2010.08.004 [4] 刘芳,王黎,高晓蓉,等. 受电弓与接触网间的接触压力检测研究[J]. 电力机车与城轨车辆,2006,29(6): 19-21,54.LIU Fang, WANG Li, GAO Xiaorong, et al. Study of measuring the contact force between pantograph and catenary[J]. Electric Locomotives & Mass Transit Vehicles, 2006, 29(6): 19-21,54. [5] 王亚春,徐超,杨才智. 弓网动态接触压力测量方法研究[J]. 铁道技术监督,2014,42(12): 41-43.WANG Yachun, XU Chao, YANG Caizhi. Research on the measurement method of pantograph-catenary dynamic contant force[J]. Railway Quality Control, 2014, 42(12): 41-43. [6] 谭梦颖,邹栋,李瑞平,等. 基于应变响应测量弓网接触力的新方法[J]. 西南交通大学学报,2017,52(6): 1208-1215.TAN Mengying, ZOU Dong, LI Ruiping, et al. New contact force measuring method for overhead catenary systems based on strain[J]. Journal of Southwest Jiaotong University, 2017, 52(6): 1208-1215. [7] SCHRÖDER K, ECKE W, KAUTZ M, et al. An approach to continuous on-site monitoring of contact forces in current collectors by a fiber optic sensing system[J]. Optics and Lasers in Engineering, 2013, 51(2): 172-179. doi: 10.1016/j.optlaseng.2012.08.007 [8] WAGNER R, MAICZ D, VIEL W, et al. A fibre optic sensor instrumented pantograph as part of a continuous structural health monitoring system for railway overhead lines[C]//7th European Workshop on Structural Health Monitoring. Nantes: HAL CCSD, 2014: 151-158. [9] KARAKOSE E, GENCOGLU M T, KARAKOSE M, et al. A new experimental approach using image processing based tracking for an efficient fault diagnosis in pantograph-catenary systems[J]. IEEE Transactions on Industrial Informatics, 2017, 13(2): 635-643. [10] 韩志伟,刘志刚,陈坤峰,等. 基于二代曲波系数定向映射的受电弓滑板裂纹检测技术[J]. 铁道学报,2011,33(11): 63-69. doi: 10.3969/j.issn.1001-8360.2011.11.011HAN Zhiwei, LIU Zhigang, CHEN Kunfeng, et al. Pantograph slide cracks detection technology based on curvelet coefficients directional projection (CCDP)[J]. Journal of the China Railway Society, 2011, 33(11): 63-69. doi: 10.3969/j.issn.1001-8360.2011.11.011 [11] 陈坤峰. 基于曲波变换的受电弓滑板裂纹故障检测[D]. 成都: 西南交通大学, 2011. [12] NA K M, LEE K, KIM H, et al. Implementation of image processing in studying contact conditions of overhead contact line-pantograph at 400 km/h[J]. Journal of Electrical Engineering & Technology, 2020, 15(2): 989-995. [13] MIN N K, KIWON L, KWON S S, et al. Detecting deformation on pantograph contact strip of railway vehicle on image processing and deep learning[J]. Applied Sciences-Basel, 2020, 10(23): 8509.1-8509.14. [14] AYDIN I, KARAKÖSE M, AKIN E. A new contactless fault diagnosis approach for pantograph-catenary system using pattern recognition and image processing methods[J]. Advances in Electrical and Computer Engineering, 2014, 14(3): 79-88. doi: 10.4316/AECE.2014.03010 [15] SHEN Y, PAN X, CHANG L N. Online intelligent perception of pantograph and catenary system status based on parameter adaptation[J]. Applied Sciences, 2021, 11(4): 1948.1-1948.19. [16] 蔚超. 适用于AC 25 kV 160 km/h刚性接触网的受电弓选型研究[D]. 成都: 西南交通大学, 2019. [17] 叶肖伟,董传智. 基于计算机视觉的结构位移监测综述[J]. 中国公路学报,2019,32(11): 21-39.YE Xiaowei, DONG Chuanzhi. Review of computer vision-based structural displacement monitoring[J]. China Journal of Highway and Transport, 2019, 32(11): 21-39. [18] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 轨道交通 受流系统 受电弓与接触网动态相互作用测量的要求和验证: GB/T 32592—2016[S]. 北京: 中国标准出版社, 2016. -
下载:
下载:
点击查看大图
计量
- 文章访问数: 896
- HTML全文浏览量: 256
- PDF下载量: 155
- 被引次数: 0