Influence of Maintenance Rail Position and Guide Vanes on Vortex-Induced Vibration Performance of Flat Box Girders
-
摘要:
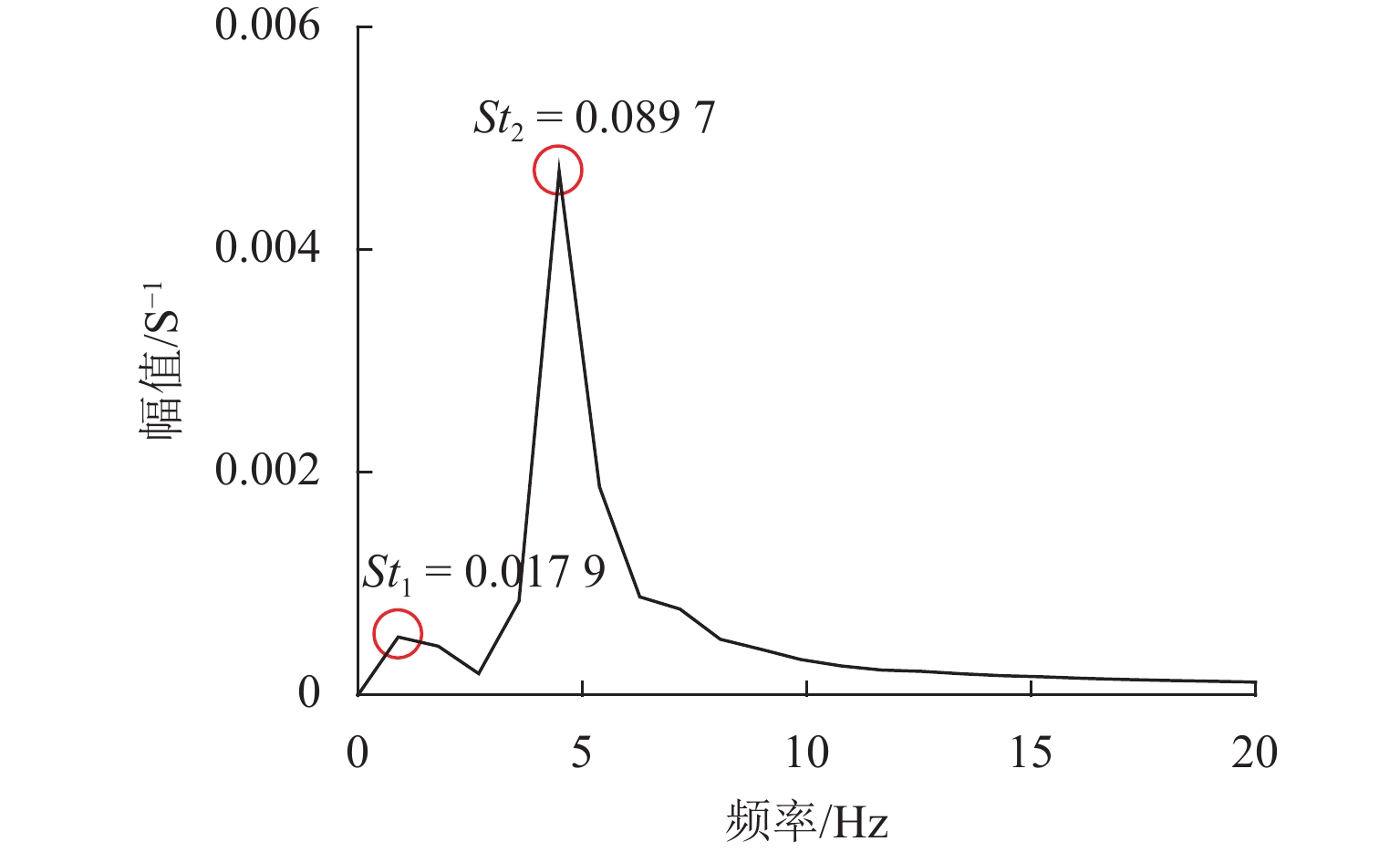
为研究检修车轨道位置与导流板对宽体扁平箱梁断面涡振性能的影响，以深中通道伶仃洋大桥（大跨度宽体扁平钢箱梁悬索桥）为背景，通过1∶25节段模型风洞试验测试了主梁的涡振响应，并采用计算流体动力学方法（CFD）对断面的二维流场进行了模拟. 结果表明：增大检修车轨道与主梁底板边缘之间距离
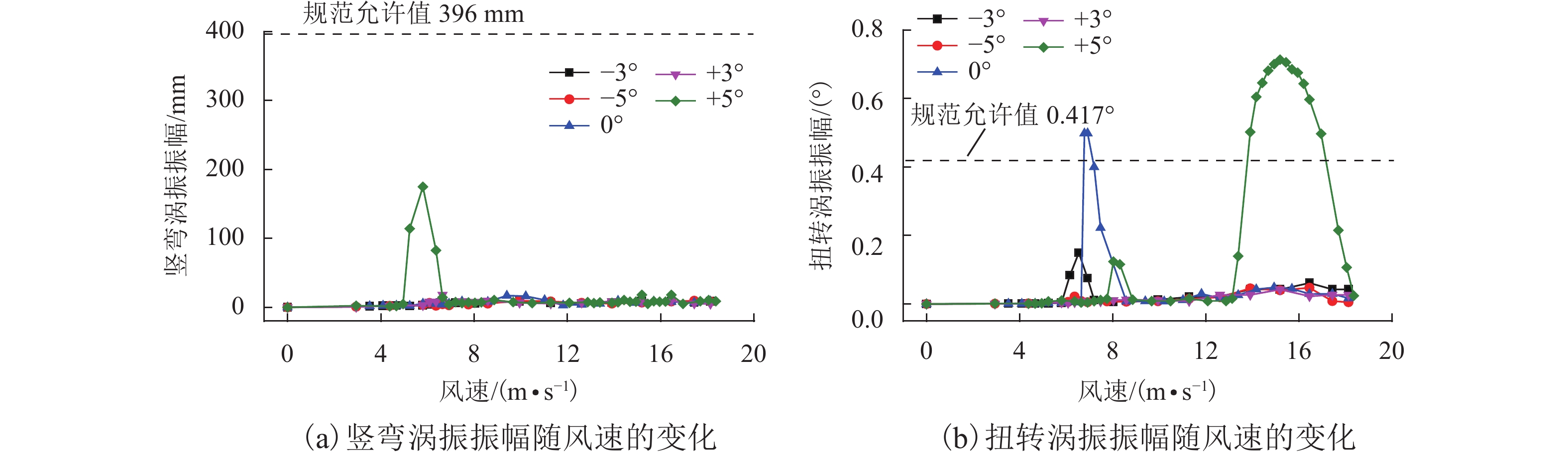
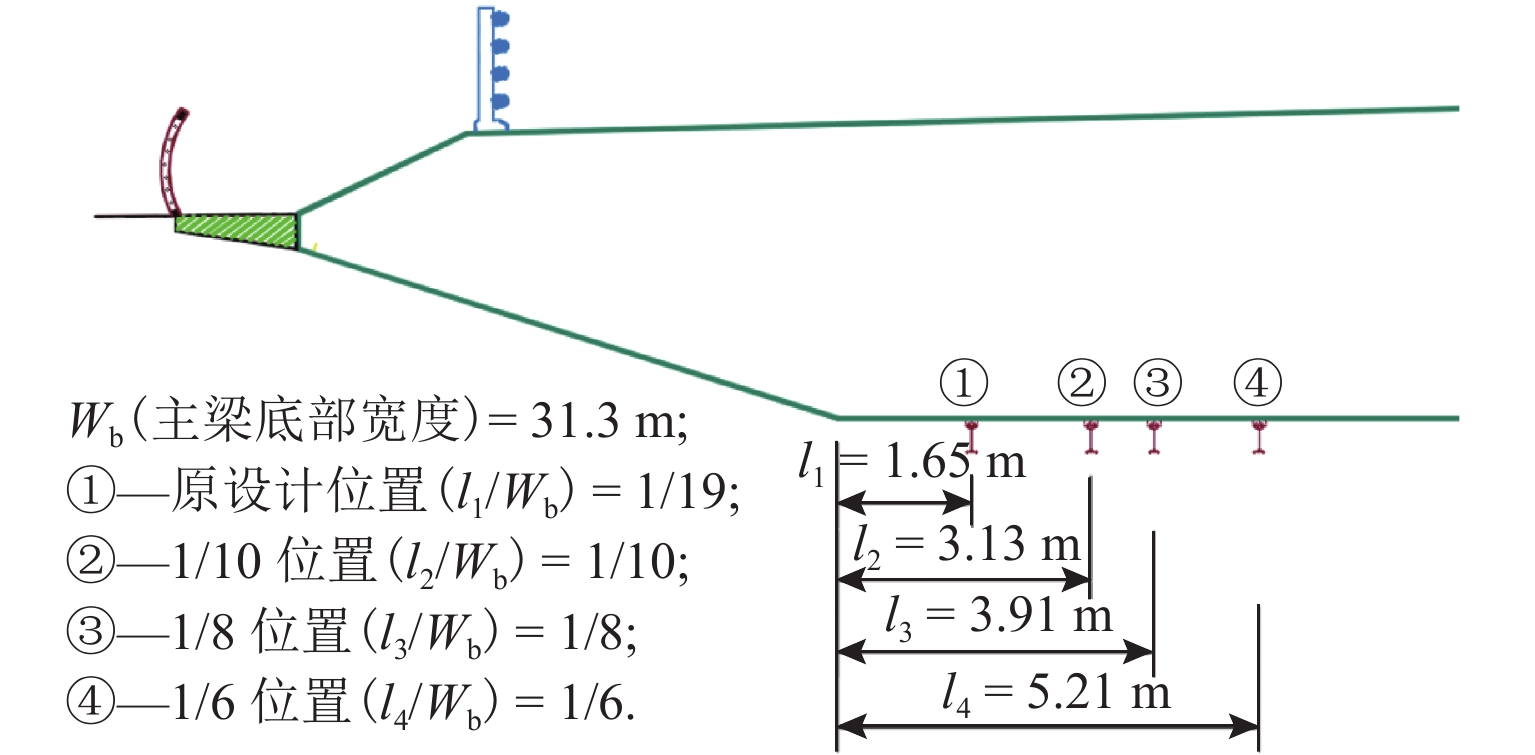
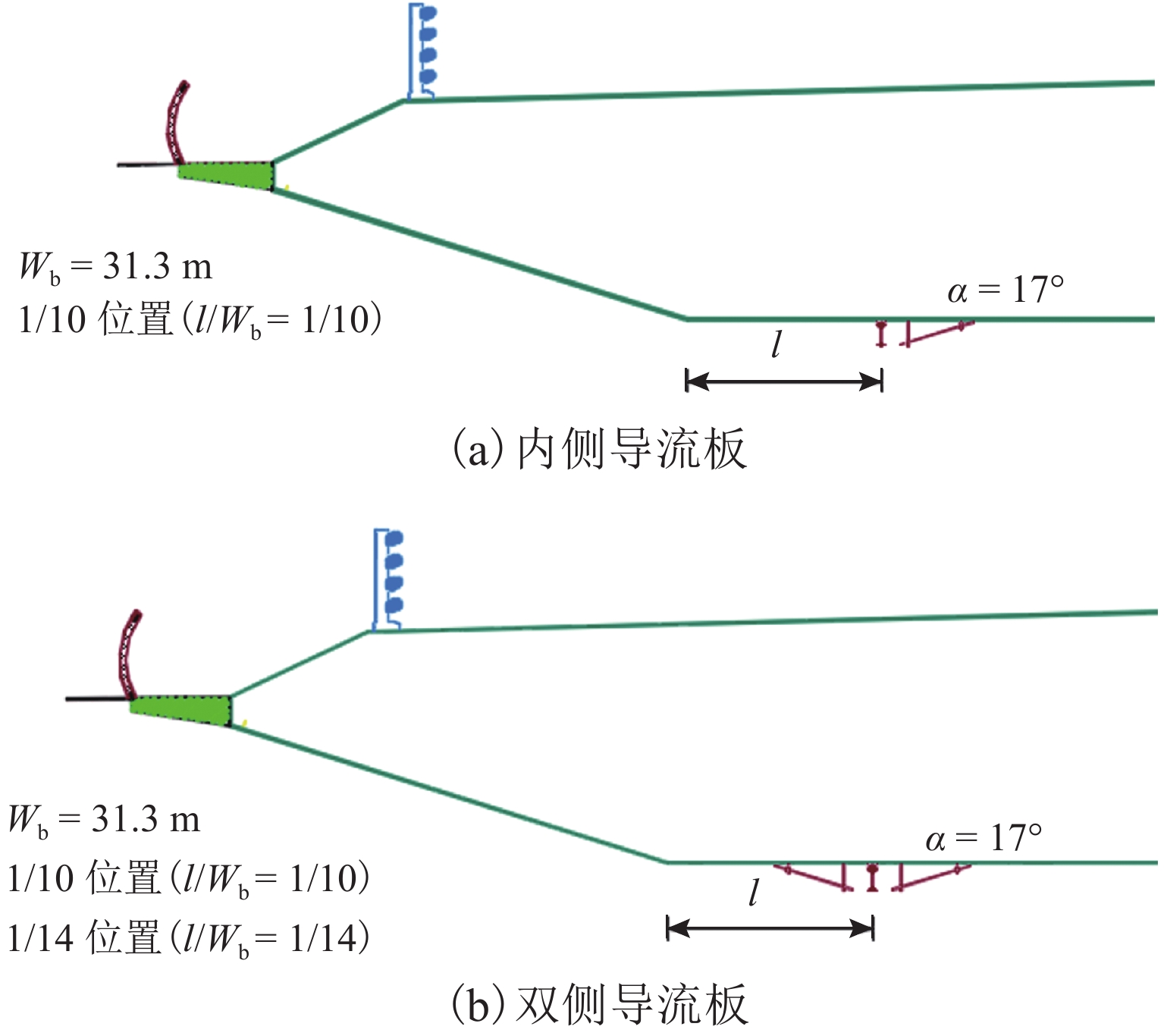
l 能够显著提高宽体扁平钢箱梁的涡振性能，当l⩾Wb/6 （Wb 为主梁底部宽度）时，可完全消除宽体扁平箱梁在各风攻角下的涡激振动；在检修车轨道处设置17° 倾角的内侧或双侧导流板均能够显著抑制梁体的涡激振动，且抑制效果相同，当l⩾Wb/10 时，布置导流板可完全消除梁体的涡激振动；增大检修车轨道与主梁底板边缘之间距离以及设置导流板均是通过消除断面下游斜腹板处的尾流漩涡，从而降低梁体受到的周期性涡激力，达到抑制主梁涡振的效果.Abstract:To study the influence of the maintenance rail position and the guide vanes on the vortex-induced vibration (VIV) performance of the wide flat box girder section, the Lingdingyang Bridge (a long-span suspension bridge with wide flat steel box girder) is taken as an example. The VIV of the main girder is studied using a 1∶25 scale section model wind tunnel test, and the two-dimensional flow field of the cross section is simulated using computational fluid dynamics. The test results show that increasing
l (the distance between the maintenance rail and the bottom edge of the main girder) can significantly improve the VIV performance of a wide flat box girder. Whenl⩾Wb/6 (Wb is the bottom width of the main girder), the VIV of the girder can be completely eliminated under different wind attack angles. Installing a guide vane with a 17° angle inside or on both sides of the maintenance rail can significantly suppress the VIV of the girder, and the suppression effect is the same. Whenl⩾Wb/10 , the installation of the guide vane can completely eliminate the VIV of the girder. The numerical simulation results show that increasing the distance between the maintenance rail and the bottom edge of the girder and setting a guide vane can both significantly reduce the periodic vortex-induced force of the main girder by eliminating the wake vortex at the inclined web downstream of the section, thereby suppressing the VIV of the girder. -
城市轨道交通具有运量大、节约环保、安全准时等特点. 截至2020年底，全国（不含港澳台）共有44个城市开通运营城市轨道交通线路233条，运营里程达7545.5公里，整体呈逐年上涨趋势. 目前城市轨道交通轨道结构主要采用现浇式，包括短枕式整体道床和长枕式整体道床：短轨枕式几何形位保持能力较差，施工精度较低；长枕式新旧混凝土接触面多，界面裂纹相对较多. 同时，现浇轨道结构均存在施工进度缓慢、混凝土质量控制难、作业环境恶劣、道床裂纹较多、维修困难、减振效果难以保证等诸多弊端[1-2].
为适应城市轨道交通的大规模建设，促进轨道结构技术创新，可结合国内高铁各类预制板式无砟轨道应用经验，引进并优化为适用于城市轨道交通的新型预制装配板式无砟轨道系统，解决目前现浇道床结构的各类缺点. 装配板式轨道相较于现浇式轨道具有七大优势：1） 工厂化预制质量更好、精度更高，在结构信息化方面优势明显；2） 机械化施工、现场拼装铺设轨道效率高、工期短；3） 施工占地小、城市交通压力小；4） 运营期间维修量少、可维修性好；5） 有减振需求时可快速实现减振升级改造；6） 能够应对我国即将到来的人力资源紧缺及人工成本持续提高的难题；7） 节能减排、降低能耗，能够有效降低施工对环境的污染. 此外，在轨道交通建设与运营中必须考虑减振问题，为最大限度减少振动造成对周围环境的影响，研发减振效果更好、结构更稳定的装配板式轨道十分必要[3-4].
目前已有部分学者对装配式轨道进行了相关研究. 李浩宇等[5]对城市轨道交通新型装配式无砟轨道的施工技术进行研究；冉丹丹等[6]对地铁装配式轨道板铺设的施工技术进行研究；李奇等[7]对装配式长型浮置板的静动力性能进行了研究；刘伟斌等[8-9]对城市轨道交通板式无砟轨道的设计应用进行相关研究；叶军等[10]对装配式轨道板的结构动力及减振特性进行研究；杨秀仁等[11]对城市轨道交通智能装配式减振轨道系统进行研究. 综上可知，既有针对城市轨道交通装配式轨道的研究主要集中在施工技术方面，对减振型装配式轨道设计研究相对较少，整体尚不够系统.
本文在系统总结分析装配式轨道设计需考虑因素的基础上，提出主要设计原则，并结合城市轨道交通减振需求，创新性提出一种减振型装配式无砟轨道设计方案，建立轨道动力分析模型和室内实尺试验模型，从理论和试验的角度对减振型装配式无砟轨道力学性能进行研究，以期为我国城市轨道交通减振型装配式无砟轨道结构设计提供参考.
1. 减振型装配式无砟轨道设计方案
1.1 设计原则
从既有城市轨道交通轨道结构运营实践来看，装配式轨道结构设计需考虑以下因素：
1） 小半径曲线适应性
城市轨道交通多运行在市区，受选线综合影响，小曲线半径较多，目前预制板式轨道结构在小半径曲线多利用扣件系统的调整量进行钢轨的圆矢度控制. 设计时需充分考虑针对小曲线应用需求，采用预制短板进行装配来适应线路调整，同时还需考虑外轨偏差、缓和曲线设置、轨道超高适应性等.
2） 施工吊装运输的便利性
城市轨道交通隧道地段铺设施工占比较大，预制轨道板尺寸及重量偏大时，在隧道内运输时需要专用吊装设备，洞内组装难度较大，施工效率偏低，平均铺设进度工效需进一步提升. 可在高速铁路轨道板设计尺寸参数等基础上进行优化调整，提高施工便利性和施工效率，兼顾施工质量与工效.
3） 桥上结构适应性
桥上铺设时需控制二期恒载，轨道结构长度需考虑温度效应. 对于露天路基地段及桥梁地段，轨道板运输及施工条件较好区域，轨道板长度可适当加长，进一步提高铺轨效率和轨道系统整体性能.
4） 减振区段适应性
城市轨道交通市区穿行，减振地段应用范围广泛，需充分考虑线路减振性能要求.
5） 排水适应性
受地下线盾构限界影响，现阶段预制板式轨道结构普遍采用双侧水沟，利用板两侧与隧道空隙设置排水沟，在小半径曲线地段内侧易造成排水沟尺寸较小，导致区间排水不畅，诱发相关病害. 可进一步优化轨道板结构尺寸，采用平板或框架板结构，适应中间排水与两侧排水应用需求.
6） 结构标准化
为进一步提升轨道建造经济性、降低轨道板制造费用，结合项目应用需求，考虑不同区段轨道板布置，通过优化结构尺寸及轨道板布置减少轨道板长度型号，形成标准化轨道板.
7） 运维便利性
城市轨道交通由于施工控制不佳或线路沉降超标，部分地段无法满足线路运营状态要求，需进行调整. 为降低对运营影响，需在天窗期实现单元板的切除、调运、更换、安装.
综合考虑上述因素，本文在城市轨道交通装配式无砟轨道设计时，主要遵循以下原则：1） 轨道结构简单、传力清晰，便于施工；2） 轨道结构各层匹配，无明显薄弱环节；3） 轨道结构采用工厂化制造、机械化施工，提高工程质量及施工工效；4） 具备较好的可维修性；5） 轨道结构减振实现方便且减振效果良好；6） 考虑一定的经济性；7） 充分考虑与相关工程的接口技术要求，系统设计.
1.2 设计方案
减振型装配式无砟轨道结构主要组成部件包括钢轨、扣件、预制轨道板、自密实混凝土层、减振垫、板间连接装配件、限位构件和基座等，如图1所示.
1） 钢轨及扣件
采用60 kg/m钢轨，材质为U75V. 采用无挡肩的DTVI2型扣件，如图2所示，扣件间距600 mm.
2） 轨道板
轨道板为工厂预制非预应力、单元分块式框架板结构. 板面设4对承轨台，板底设2排共14根门型筋，混凝土强度等级为C60. 轨道板分中间板和端板两种型式，中间标准轨道板宽2100 mm、厚200 mm、长2100 mm，端板长2200 mm. 板中间框架沿线路纵向长900 mm，沿横向宽800 mm，倒角半径200 mm. 框架板中间部分可作为排水沟检查使用，设置盖板作为疏散通道使用. 轨道板端部纵向预留2组共8根连接钢筋. 两块端板加上N块中间板通过板端连接钢筋和板间连接装配件装配形成较长的装配单元，如图3所示. 装配单元之间设100 mm伸缩缝，板端预埋接地端子.
3） 板间连接装配件
板间连接装配件为钢筋套筒，如图4所示. 板间连接装配件连接轨道板端外伸的连接钢筋装配形成一定长度的装配单元，形成的接头需符合《钢筋机械连接技术规程》[12]的Ⅰ级接头指标要求.
4） 自密实混凝土垫层
板下自密实混凝土垫层厚100 mm，强度等级为C40，起到调平、填充轨道板与下部基础的作用，如图5所示. 垫层宽度650 mm，与框架板两侧宽度相同，纵向与板长相同. 垫层内配置单层ϕ10钢筋网片，垫层混凝土浇筑施工时通过板一端向另一端进行灌注.
5） 减振垫
减振垫设置在自密实混凝土垫层与基座之间，可一定程度提高减振垫上部轨道结构的参振质量，提高减振效果. 减振垫采用聚氨酯发泡材料或者具有锥形突起结构的橡胶材料，减振层厚度为30 mm，减振垫刚度0.019 N/mm3.
6） 限位构件
限位构件现浇于装配单元中的中间板与中间板之间或中间板与端板之间，与自密实混凝土垫层共同浇筑形成整体. 限位构件分左右两块，如图6（a）所示，单块宽300 mm、长650 mm、高300 mm，起纵横向限位作用. 限位构件混凝土等级为C40，设钢筋笼，通过8根ϕ 20长540 mm的限位钢筋与下部混凝土基座相连，限位钢筋外包裹一层套筒，如图6（b）所示，钢筋可沿套筒长度方向自由伸缩，以此适应垂向减振的变形需求.
7） 基座
基座为现浇钢筋混凝土结构，混凝土强度等级为C40. 基座在限位构件位置植有限位钢筋，钢筋植入深度250 mm. 考虑到城市轨道交通曲线半径较小，超高较大，轨道结构超高通过基座实现.
总体来说，减振型装配式无砟轨道采用预制框架板型式，轨道板重量较轻，施工运输方便；板中框架可作为排水沟的观察孔和清理孔，盖上盖板还可作为疏散通道；单块轨道板在线路纵向上长度较短，对小曲线半径适应性较强；板与板之间通过装配形成较长的装配单元，结构施工精度高、整体性好、可靠性强，同时增加了轨道单元的整体长度，减振效果进一步加强；板端限位构件与自密实混凝土浇筑形成整体，限位能力强、稳定性能好；后期养护维修时，可通过解锁装配单元完成对轨道板单元的更换调整，可维修性较强.
2. 减振型装配式无砟轨道动力特性
结合轨道结构设计方案特点，建立可考虑新型装配式无砟轨道各结构层相互作用关系的车辆-轨道耦合动力分析模型，研究轨道结构在列车荷载作用下的动力特性.
2.1 新型装配式无砟轨道动力分析模型
基于车辆-轨道动力学耦合理论[13]，建立车辆-装配式无砟轨道空间耦合动力分析模型. 模型包括车辆、装配式无砟轨道、轮轨耦合、轨道不平顺共4个部分. 车辆采用整车模型，考虑车体和转向架的沉浮、横摆、点头、摇头、侧滚以及轮对的沉浮、摇头、横摆和侧滚共计31个自由度，车辆参数参照地铁B型车辆[14]. 新型装配式无砟轨道各组成部件的几何尺寸按设计取值，材料参数见表1.
表 1 轨道结构模型参数Table 1. Track structure model parameters部件 弹性模量/GPa 泊松比 密度/（kg·m−3） 钢轨 206.0 0.3 7800 轨道板 36.5 0.2 2500 混凝土垫层 34.0 0.2 2400 基座 34.0 0.2 2500 限位构件 34.0 0.2 2500 为更好反映各部件受力情况，钢轨、轨道板、板下自密实混凝土垫层、基座和限位构件均采用实体单元模拟. DTVI2型扣件采用三向非线性弹簧-阻尼单元模拟，考虑纵、横、垂3个方向的刚度，垂向刚度取30 kN/mm，切向静刚度取40 kN/mm[15]. 轨道板通过门型筋与自密实混凝土层相连，两界面采用绑定连接. 减振垫与自密实混凝土界面切向采用摩擦接触模拟，摩擦系数取0.6，法向采用硬接触模拟[16]，减振垫与基座界面采用绑定连接，减振垫刚度取0.019 N/mm3，以隧道地段为例，支撑刚度取1200 MPa/m[16-17]. 钢轨两端采用对称约束，轮轨间接触遵循Hertz非线性接触理论，轨道不平顺采用美国普通铁路的美国五级谱[18]. 综上，新型装配式无砟轨道车辆-轨道空间耦合动力有限元分析模型如图7所示.
2.2 轨道结构动力特性
行车速度100 km/h条件下，新型装配式无砟轨道的部分典型动力指标时程曲线如图8所示，系统动力响应汇总如表2、3所示.
表 2 车-轨动力响应统计Table 2. Statistics of vehicle-rail dynamic response动力响应指标 峰值 轮轨横向力/kN 5.457 轮轨垂向力/kN 73.115 脱轨系数 0.073 轮重减载率 0.108 表 3 系统动力响应统计Table 3. Statistics of system dynamic response项目 动力响应指标 峰值 车体 垂向加速度/（m·s−2） 0.429 横向加速度/（m·s−2） 0.285 钢轨 垂向加速度/（m·s−2） 190.380 垂向位移/mm 2.141 轨道板 垂向加速度/（m·s−2） 31.200 垂向位移/mm 0.812 混凝土垫层 垂向加速度/（m·s−2） 26.020 垂向位移/mm 0.761 基座 垂向加速度/（m·s−2） 1.160 垂向位移/mm 0.122 由图8和表2、3可知：新型装配式无砟轨道在行车速度100 km/h条件下，脱轨系数和轮重减载率最大分别为0.073、0.108，轮轨垂向力和横向力峰值分别为73.115 kN和5.457 kN，结果均未超限，满足行车安全要求；车体垂、横向加速度分别为0.429 m/s2和0.285 m/s2，满足《地铁设计规范》（GB 50157—2013）[19]垂向加速度az≤0.13g和横向加速度ay≤0.10g的行车安全性和乘坐舒适性指标要求；钢轨最大垂向位移为2.141 mm，轨道板垂向位移和自密实混凝土层相差不大，分别为0.812 mm和0.761 mm. 基座位移很小，约0.122 mm；钢轨、轨道板、自密实混凝土层和基座的振动加速度从上往下均有不同程度的衰减，垂向加速度峰值分别为190.380、31.200、26.020、1.160 m/s2.
综上可知，新型装配式无砟轨道结构在列车荷载作用下动力性能良好，满足行车安全性和舒适性要求.
3. 减振型装配式无砟轨道试验研究
借助试验室静动力加载装置以及落轴试验装置，对轨道结构进行静载试验、疲劳试验和落轴冲击试验，研究在静载、疲劳动载和落轴冲击载荷作用下，减振型装配式无砟轨道的力学性能，为新型装配板式无砟轨道的设计以及实际应用提供试验支撑. 减振型装配式无砟轨道实尺模型由3块轨道板（2块端板 + 1块中间板）组成，总长7.1 m. 现场部分测点布置如图9所示.
3.1 静载试验
轨道系统静载试验考虑的最大载荷为3Pj （Pj为列车静轮载，轴重17 t），包含规范推荐的设计垂向荷载2Pj. 从0加载至510 kN，在400 kN前每一级荷载为50 kN，在400 kN后每一级荷载为20 kN，记录每次载荷作用下轨道系统各测点的应变情况. 各级荷载作用下典型测点的混凝土应变变化曲线如图10所示，其中测点1、2分别位于轨道板横向两侧截面中间位置，测点3～6等间距分布于轨道板上表面板中位置.
由图10可知：各测点混凝土应变绝对值随荷载的增加整体呈线性增加趋势；在3Pj的静载作用下，轨道混凝土最大压应变为 −129.6 με，远小于混凝土极限应变值；在静载试验过程中轨道结构未出现开裂现象，减振型装配式轨道结构强度和刚度满足承载要求.
图11为各级荷载作用下轨道结构变形曲线. 由图11可知：各测点垂向位移均随着荷载的增大而增大，左、右两边钢轨最大垂向位移分别为2.44 mm和2.40 mm，轨道板两侧的最大垂向位移分别为1.32 mm和1.34 mm，数值相差不大，轨道结构两侧对称受力. 图12为加、卸载过程中钢轨位移变化曲线，由图12可知：在加载卸载过程中曲线总体平稳，未见位移的突变；卸载后基本没有残余位移，说明加载、卸载过程中轨道板主要处于弹性受力阶段，未出现较大的塑性变形，受力性能良好.
图 12 加载和卸载过程中钢轨位移变化曲线Figure 12. Rail displacement curves during loading and unloading3.2 疲劳试验
采用MTS疲劳试验机进行疲劳试验，疲劳荷载的上限按规范要求取为1.5Pj，疲劳荷载下限值按疲劳机最大加载能力的3%确定，即15 kN. 通过MTS作动器施加正弦荷载，加载频率为4 Hz，累计疲劳作用次数为200万次.
图13为钢轨和轨道板位移随疲劳试验次数变化曲线. 由图12可知：在1.5Pj的200万次疲劳荷载作用下，钢轨最大垂向位移为1.303 mm，轨道板最大垂向位移为0.843 mm；疲劳试验过程中，钢轨和轨道板位移在疲劳荷载作用下随疲劳次数的增加在一定范围内上下波动，200万次疲劳试验后钢轨最大垂向位移增加了0.180 mm，轨道板最大垂向位移增加了0.130 mm，整体变化量较小，表明装配式无砟轨道在经200万次疲劳荷载作用下的工作性能良好.
在疲劳试验过程中，轨道结构表面及层间界面未见肉眼可见裂缝，减振型装配式无砟轨道抵抗疲劳性能良好，新型装配式无砟轨道能够经受1.5Pj的疲劳荷载作用200万次的检验.
3.3 落锤冲击试验
采用力锤锤击法，分别测试一般地段和减振地段装配式无砟轨道结构在力锤脉冲荷载作用下的动力响应，对比分析轨道各部件在脉冲荷载作用下的Z振级，掌握减振型装配式无砟轨道振动传递特性和减振性能. 试验采用DFC-2型力锤，重量8 kg，力锤垂直下落高度为120 mm. 为避免轨道板纵向边界效应的影响，并且充分激发轨道板的垂向振动，将落锤点设置在轨道板板中截面.
力锤作用下一般地段和减振地段装配式无砟轨道基座垂向加速度1/3倍频程如图14所示.
由图14可知：减振型装配式无砟轨道具有显著的减振效果，频率为100～125 Hz，最大减振效果可达12.4 dB.
将力锤锤击试验工况下的轨道结构系统简化为单一激励输入的质量弹簧系统，分析力锤锤击激励输入与基座振动响应输出间的传递函数，对比一般地段与减振地段新型装配式无砟轨道传递函数幅值，如图15所示.
由图15可知：相比一般地段，减振地段的新型装配式无砟轨道可使力锤锤击激励与基座振动响应间的传递函数幅值大幅削减，减振型装配式无砟轨道减振效果较好；疲劳加载前、疲劳加载至100万次、200万次工况下的传递函数幅值曲线峰值起伏频率范围基本一致，表明轨道结构的减振特性经过疲劳加载后的稳定性较好.
4. 结 论
1） 减振型装配式无砟轨道结构在100 km/h的行车条件下，系统动力响应均在安全限值范围内，满足行车安全性和舒适性要求.
2） 轨道结构在静载试验过程中混凝土应变随荷载增加整体呈线性增加趋势，最大压应变为−129.6 με，远小于混凝土极限应变值，结构受力在强度允许范围内；卸载后残余变形很小，轨道弹性较好；静载试验过程中结构未见肉眼可见裂纹，结构承载能力和抗裂性能满足要求.
3） 在200万次疲劳荷载作用下，轨道结构整体受力变形较小，疲劳试验过程中变化幅值不大，轨道结构表面及层间界面未见裂缝，轨道结构抗疲劳性能良好.
4） 减振型装配式无砟轨道减振效果显著且减振稳定性较好，频率为100～125 Hz，最大减振效果可达12.4 dB.
致谢：中铁第四勘察设计院集团有限公司科技研发课题（2019K011，2020K155）.
-
图 4 原设计断面主梁涡振响应
Figure 4. Vortex-induced vibration displacement of the original section
图 8 1/19位置工况断面
CL(t) 频谱Figure 8.
CL(t) spectrum of section with maintenance rail on the 1/19 position
图 9 检修车轨道各位置工况断面涡量与迹线图
Figure 9. Vorticity magnitude and trace diagram around the section with different maintenance rail positions
图 10 数值模拟静力三分力时程图
Figure 10. Time-history diagram of the static coefficients in numerical simulation
图 13 各导流板工况断面涡量与迹线图
Figure 13. Vorticity magnitude and trace diagram around the section with different guide vanes
表 1 节段模型试验参数取值
Table 1. Section model test parameters
参数名称 实桥值 相似比 模型值 等效质量/（kg•m−1） 42156 1/252 67.45 等效质量惯性矩/
（kg•m2•m−1）10007344 1/254 25.62 竖弯频率/Hz 0.101 13.960 1.410 扭转频率/Hz 0.220 10.500 2.310 竖弯阻尼比/% 0.30 — 0.24 扭转阻尼比/% 0.30 — 0.10 
下载: 导出CSV
表 2 检修车轨道各位置工况涡振幅值
Table 2. VIV displacement of each working condition with different maintenance rail positions
风攻角/（°） 竖弯涡振振幅/mm 扭转涡振振幅/（°） 1/6 位置 1/8 位置 1/10 位置 1/19 位置 1/6 位置 1/8 位置 1/10 位置 1/19 位置 0 6.4 7.0 5.3 17.1 0.01 0.07 0.55 0.50 +3 6.9 7.9 6.4 18.1 0.02 0.01 0.02 0.04 +5 7.9 7.6 6.8 174.9 0.02 0.02 0.45 0.71 −3 6.5 7.7 7.5 8.5 0.01 0.21 0.02 0.15 −5 7.2 8.5 7.9 9.7 0.02 0.02 0.03 0.05
下载: 导出CSV
表 3 数值模拟参数设置
Table 3. Parameters of the numerical simulation
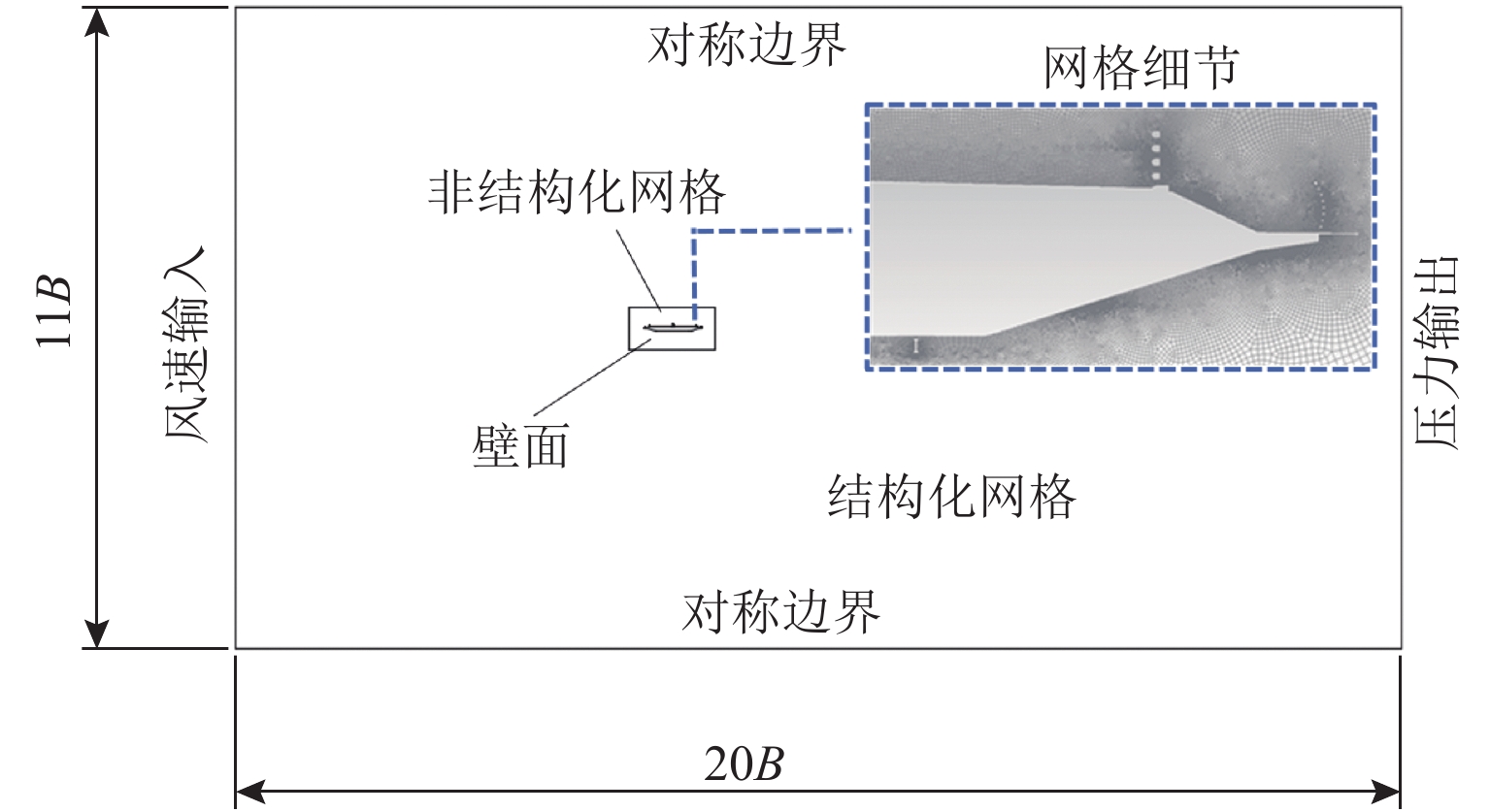
参数 湍流长度
尺度/m湍流强
度/%时间步长 算法 取值 0.08 0.5 0.00002 SIMPLE
下载: 导出CSV
表 4 各导流板工况涡振幅值
Table 4. VIV displacement of each working condition with different guide vanes
风攻角/（°） 竖弯涡振振幅/mm 扭转涡振振幅/（°） 1/14 位置双
侧导流板1/10 位置双
侧导流板1/10 位置内
侧导流板1/10 位置
无导流板1/14 位置双
侧导流板1/10 位置双
侧导流板1/10 位置内
侧导流板1/10 位置
无导流板0 38.4 5.3 5.5 5.3 0.37 0.01 0.01 0.55 +3 6.9 6.4 6.3 6.4 0.02 0.01 0.02 0.02 +5 12.2 8.3 7.5 6.8 0.45 0.02 0.02 0.45 −3 5.9 8.4 8.6 7.5 0.02 0.01 0.01 0.02 −5 7.3 8.8 8.7 7.9 0.02 0.01 0.01 0.03
下载: 导出CSV
表 5 全桥气弹模型试验参数取值
Table 5. Full bridge aeroelastic model test parameters
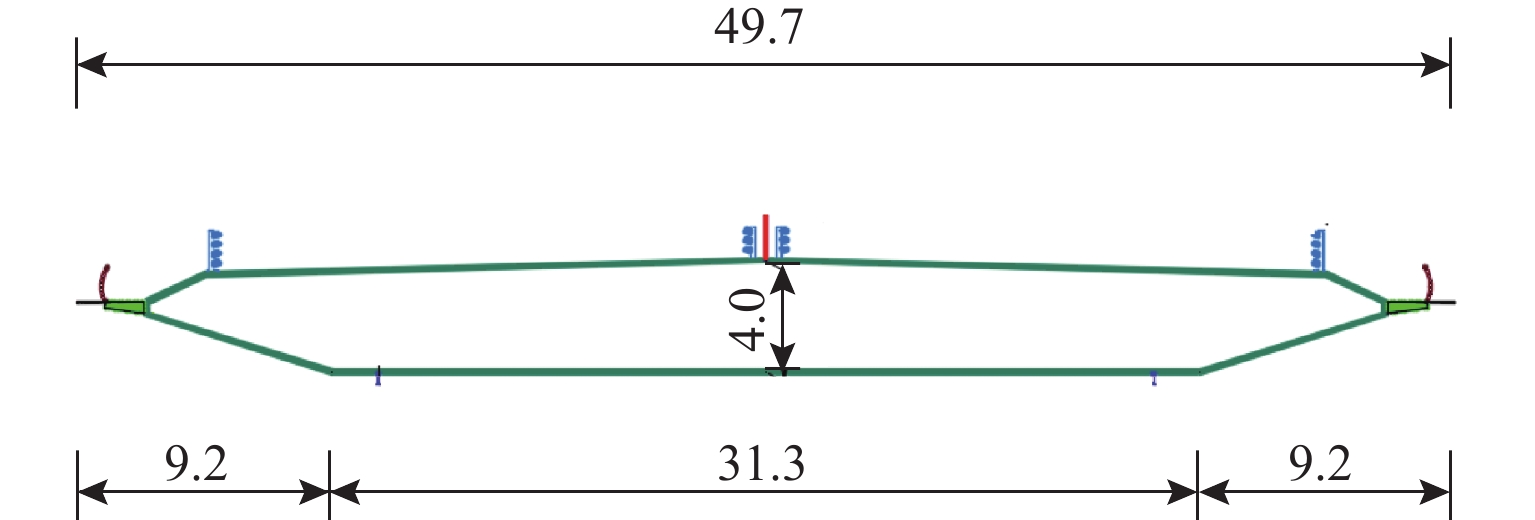
参数名称 实桥值 相似比 模型值 主梁长/m 1666 1/134 12.43 梁宽/m 49.7 1/134 0.371 梁高/m 4 1/134 0.030 单位长度质量/（kg•m−1） 32496 1/1342 1.8098 单位长度质量惯性矩/
（kg•m2•m−1）5722181 1/1344 0.0177
下载: 导出CSV
表 6 全桥气弹模型模态参数
Table 6. Modal testing parameters of full bridge aeroelastic model
振型 实桥频率/Hz 模型频率 阻尼比/% 要求值/Hz 实测值/Hz 误差/% V-S-1 0.1010 1.169 1.092 5.70 0.34 V-A-1 0.0960 1.112 1.121 1.10 0.32 T-S-1 0.2196 2.542 2.569 2.30 0.34 T-A-1 0.2263 2.62 2.6321 1.80 0.40 L-S-1 0.0564 0.661 0.6601 1.50 0.23 L-A-1 0.1345 1.557 1.5622 1.50 0.28
下载: 导出CSV
-
[1] 政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005. [2] 管青海,李加武,胡兆同,等. 栏杆对典型桥梁断面涡激振动的影响研究[J]. 振动与冲击,2014,33(3): 150-156. doi: 10.3969/j.issn.1000-3835.2014.03.029GUAN Qinghai, LI Jiawu, HU Zhaotong, et al. Effects of railings on vortex-induced vibration of a bridge deck section[J]. Journal of Vibration and Shock, 2014, 33(3): 150-156. doi: 10.3969/j.issn.1000-3835.2014.03.029 [3] 李春光,陈政清,韩阳. 带悬挑人行道板流线型箱梁涡振性能研究[J]. 振动与冲击,2014,33(24): 19-25. doi: 10.13465/j.cnki.jvs.2014.24.004LI Chunguang, CHEN Zhengqing, HAN Yang. Vortex induced vibration performance of a streamlined box girder with a cantilevered walking slab[J]. Journal of Vibration and Shock, 2014, 33(24): 19-25. doi: 10.13465/j.cnki.jvs.2014.24.004 [4] 杨阳,张亮亮,吴波,等. 宽体扁平钢箱梁气动力特性及涡振性能研究[J]. 桥梁建设,2016,46(1): 70-75.YANG Yang, ZHANG Liangliang, WU Bo, et al. Study of aerodynamic characteristics and vortex-induced vibration performance of wide flat steel box girder[J]. Bridge Construction, 2016, 46(1): 70-75. [5] LARSEN A, WALL A. Shaping of bridge box girders to avoid vortex shedding response[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106: 159-165. [6] LARSEN A, ESDAHL S, ANDERSEN J E, et al. Storebælt suspension bridge-vortex shedding excitation and mitigation by guide vanes[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2/3): 283-296. [7] NAGAO F, UTSUNOMIYA H, YOSHIOKA E, et al. Effects of handrails on separated shear flow and vortex-induced oscillation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71: 819-827. [8] CHEN Z S, LIU S M, YU X F, et al. Experimental investigations on VIV of bridge deck sections: a case study[J]. KSCE Journal of Civil Engineering, 2017, 21(7): 2821-2827. doi: 10.1007/s12205-017-0120-1 [9] ZHAN J, XIN D B, OU J P, et al. Experimental study on suppressing vortex-induced vibration of a long-span bridge by installing the wavy railings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 202(8): 104205.1-104205.13. [10] 李浩弘,吴波,张亮亮,等. 基于风洞试验及大涡模拟的宽体扁平箱梁涡振特性研究与优化[J]. 建筑结构学报,2018,39(增1): 29-35. doi: 10.14006/j.jzjgxb.2018.S1.005LI Haohong, WU Bo, ZHANG Liangliang, et al. Investigation and optimization on VIV performances of wide flat box girders based on wind tunnel tests and large eddy simulations[J]. Journal of Building Structures, 2018, 39(S1): 29-35. doi: 10.14006/j.jzjgxb.2018.S1.005 [11] 张建,郑史雄,唐煜,等. 基于节段模型试验的悬索桥涡振性能优化研究[J]. 实验流体力学,2015,29(2): 48-54. doi: 10.11729/syltlx20140037ZHANG Jian, ZHENG Shixiong, TANG Yu, et al. Research on optimizing vortex-induced vibration performance for suspension bridge based on section model test[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(2): 48-54. doi: 10.11729/syltlx20140037 [12] 刘君,廖海黎,万嘉伟,等. 检修车轨道导流板对流线型箱梁涡振的影响[J]. 西南交通大学学报,2015,50(5): 789-795. doi: 10.3969/j.issn.0258-2724.2015.05.004LIU Jun, LIAO Haili, WAN Jiawei, et al. Effect of guide vane beside maintenance rail on vortex-induced vibration of streamlined box girder[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 789-795. doi: 10.3969/j.issn.0258-2724.2015.05.004 [13] 李明,孙延国,李明水,等. 宽幅流线型箱梁涡振性能及制振措施研究[J]. 西南交通大学学报,2018,53(4): 712-719. doi: 10.3969/j.issn.0258-2724.2018.04.007LI Ming, SUN Yanguo, LI Mingshui, et al. Vortex-induced vibration performance of wide streamlined box girder and aerodynamic countermeasure research[J]. Journal of Southwest Jiaotong University, 2018, 53(4): 712-719. doi: 10.3969/j.issn.0258-2724.2018.04.007 [14] LI M, SUN Y G, JING H M, et al. Vortex-induced vibration optimization of a wide streamline box girder by wind tunnel test[J]. KSCE Journal of Civil Engineering, 2018, 22(12): 5143-5153. doi: 10.1007/s12205-018-0548-y [15] 朱思宇,李永乐,申俊昕,等. 大攻角来流作用下扁平钢箱梁涡振性能风洞试验优化研究[J]. 土木工程学报,2015,48(2): 79-86. doi: 10.15951/j.tmgcxb.2015.02.012ZHU Siyu, LI Yongle, SHEN Junxin, et al. Optimization of vortex-induced vibration of flat steel box girders at large attack angle by wind tunnel test[J]. China Civil Engineering Journal, 2015, 48(2): 79-86. doi: 10.15951/j.tmgcxb.2015.02.012 [16] 孙延国,廖海黎,李明水. 基于节段模型试验的悬索桥涡振抑振措施[J]. 西南交通大学学报,2012,47(2): 218-223,264. doi: 10.3969/j.issn.0258-2724.2012.02.008SUN Yanguo, LIAO Haili, LI Mingshui. Mitigation measures of vortex-induced vibration of suspension bridge based on section model test[J]. Journal of Southwest Jiaotong University, 2012, 47(2): 218-223,264. doi: 10.3969/j.issn.0258-2724.2012.02.008 [17] 胡传新,赵林,周志勇,等. 流线型闭口箱梁抑流板抑制涡振机理研究[J]. 振动工程学报,2020,33(1): 1-11. doi: 10.16385/j.cnki.issn.1004-4523.2020.01.001HU Chuanxin, ZHAO Lin, ZHOU Zhiyong, et al. Suppressing mechanism of spoilers on vortex-induced vibrations around a streamlined closed-box girder based on characteristics of aerodynamics forces and flow field[J]. Journal of Vibration Engineering, 2020, 33(1): 1-11. doi: 10.16385/j.cnki.issn.1004-4523.2020.01.001 [18] HU C X, ZHAO L, GE Y J. Mechanism of suppression of vortex-induced vibrations of a streamlined closed-box girder using additional small-scale components[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 189: 314-331. doi: 10.1016/j.jweia.2019.04.015 [19] SCHEWE G, LARSEN A. Reynolds number effects in the flow around a bluff bridge deck cross section[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 829-838. [20] SCHEWE G. Reynolds-number effects in flow around more-or-less bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14/15): 1267-1289. [21] 胡传新,赵林,陈海兴,等. 流线闭口箱梁涡振气动力的雷诺数效应研究[J]. 振动与冲击,2019,38(12): 118-125. doi: 10.13465/j.cnki.jvs.2019.12.017HU Chuanxin, ZHAO Lin, CHEN Haixing, et al. Reynolds number effects on aerodynamic forces of a streamlined closed-box girder during vortex-induced vibrations[J]. Journal of Vibration and Shock, 2019, 38(12): 118-125. doi: 10.13465/j.cnki.jvs.2019.12.017 [22] SCANLAN R H. Observations on low-speed aeroelasticity[J]. Journal of Engineering Mechanics, 2002, 128(12): 1254-1258. doi: 10.1061/(ASCE)0733-9399(2002)128:12(1254) [23] 李加武,张宏杰,韩万水. 斜拉桥风致响应的雷诺数效应[J]. 中国公路学报,2009,22(2): 42-47. doi: 10.3321/j.issn:1001-7372.2009.02.008LI Jiawu, ZHANG Hongjie, HAN Wanshui. Wind-induced response of cable-stayed bridge with consideration of Reynolds number effect[J]. China Journal of Highway and Transport, 2009, 22(2): 42-47. doi: 10.3321/j.issn:1001-7372.2009.02.008 [24] 熊龙,孙延国,廖海黎. 钢箱梁在高低雷诺数下的涡振特性研究[J]. 桥梁建设,2016,46(5): 65-70.XIONG Long, SUN Yanguo, LIAO Haili. Study of vortex-induced vibration characteristics of steel box girder at high and low Reynolds numbers[J]. Bridge Construction, 2016, 46(5): 65-70. [25] 董浩天,葛耀君,杨詠昕. 闭口钢箱梁悬索桥涡振多尺度模型风洞试验[J]. 结构工程师,2018,34(4): 94-100. doi: 10.3969/j.issn.1005-0159.2018.04.014DONG Haotian, GE Yaojun, YANG Yongxin. Multi-scale model tests of vortex-induced vibration of a suspension bridge with closed steel box girders[J]. Structural Engineers, 2018, 34(4): 94-100. doi: 10.3969/j.issn.1005-0159.2018.04.014 [26] 任若松,梁新华,刘小兵,等. 准流线型桥梁断面气动力特性的雷诺数效应研究[J]. 工程力学,2020,37(增1): 139-144,167.REN Ruosong, LIANG Xinhua, LIU Xiaobing, et al. Study on Reynolds number effect of aerodynamic characteristics of quasi-streamlined bridge section[J]. Engineering Mechanics, 2020, 37(S1): 139-144,167. [27] 交通运输部. 公路桥梁抗风设计规范: JTG/T 3360-01—2018[S]. 北京: 人民交通出版社, 2018. [28] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. doi: 10.2514/3.12149 [29] 熊龙,廖海黎,李明水,等. 马普托桥颤振稳定性的风洞试验研究[J]. 防灾减灾工程学报,2017,37(2): 321-326. doi: 10.13409/j.cnki.jdpme.2017.02.021XIONG Long, LIAO Haili, LI Mingshui, et al. Wind tunnel test study on flutter stability of Maputo bridge[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(2): 321-326. doi: 10.13409/j.cnki.jdpme.2017.02.021 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 392
- HTML全文浏览量: 151
- PDF下载量: 30
- 被引次数: 0