Analysis of Ground Settlement Induced by Shallow Tunnel Excavation in Composite Layered Strata
-
摘要:
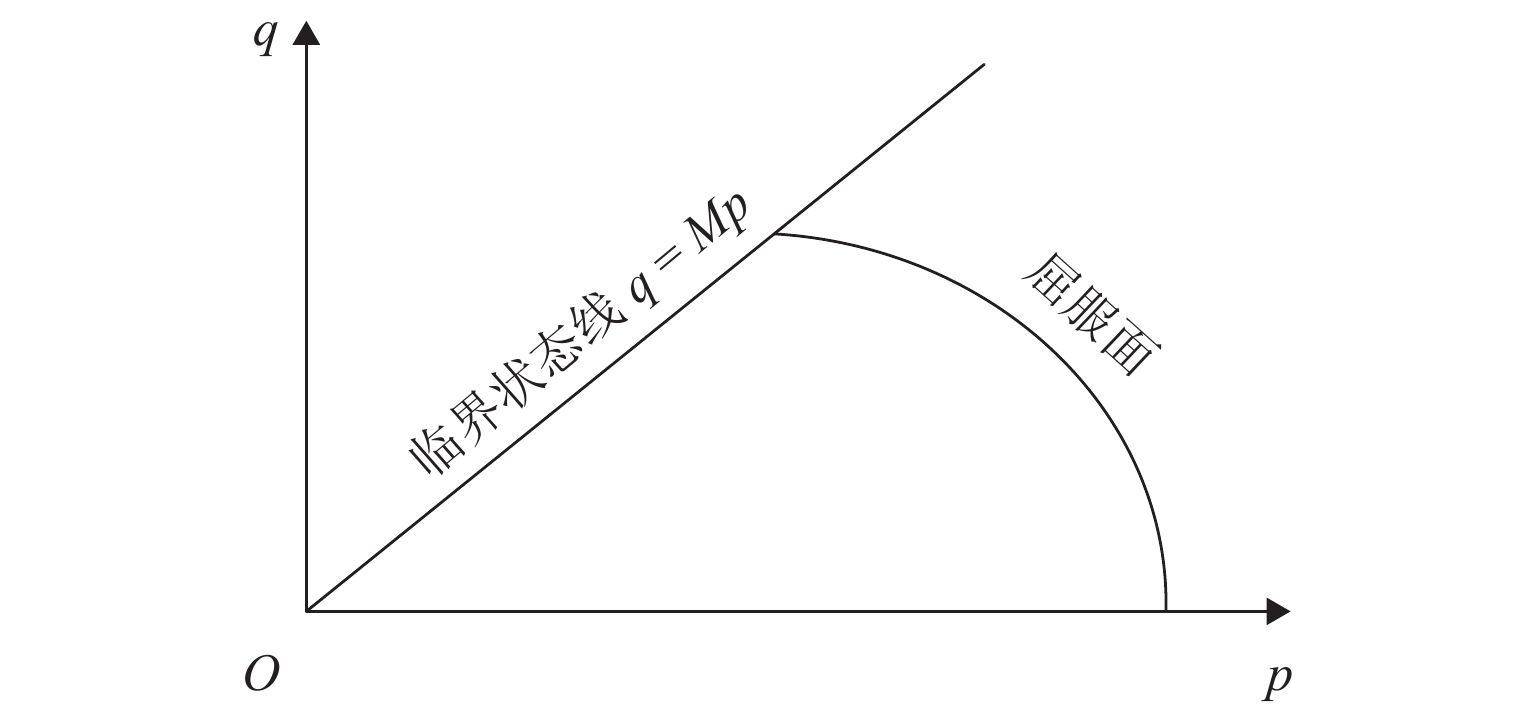
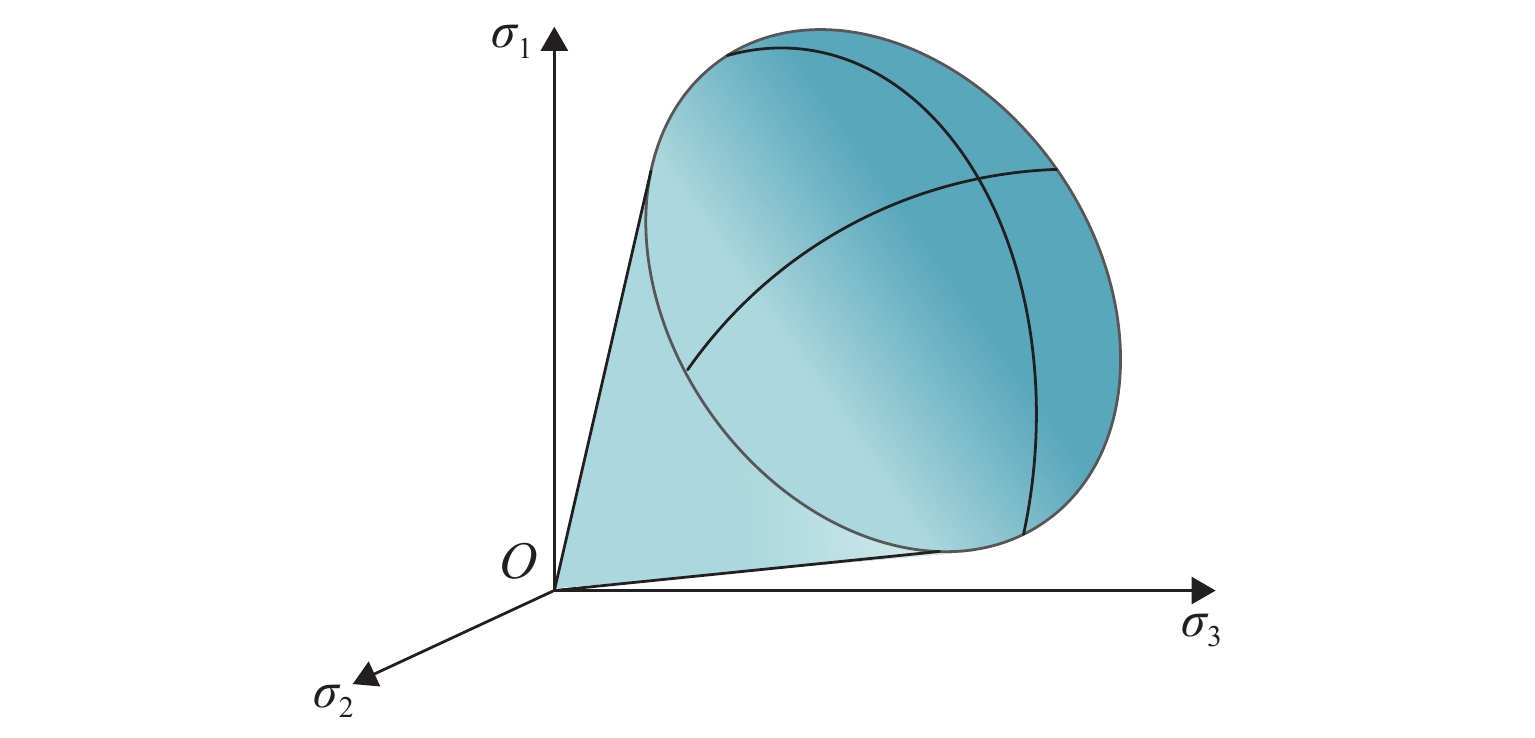
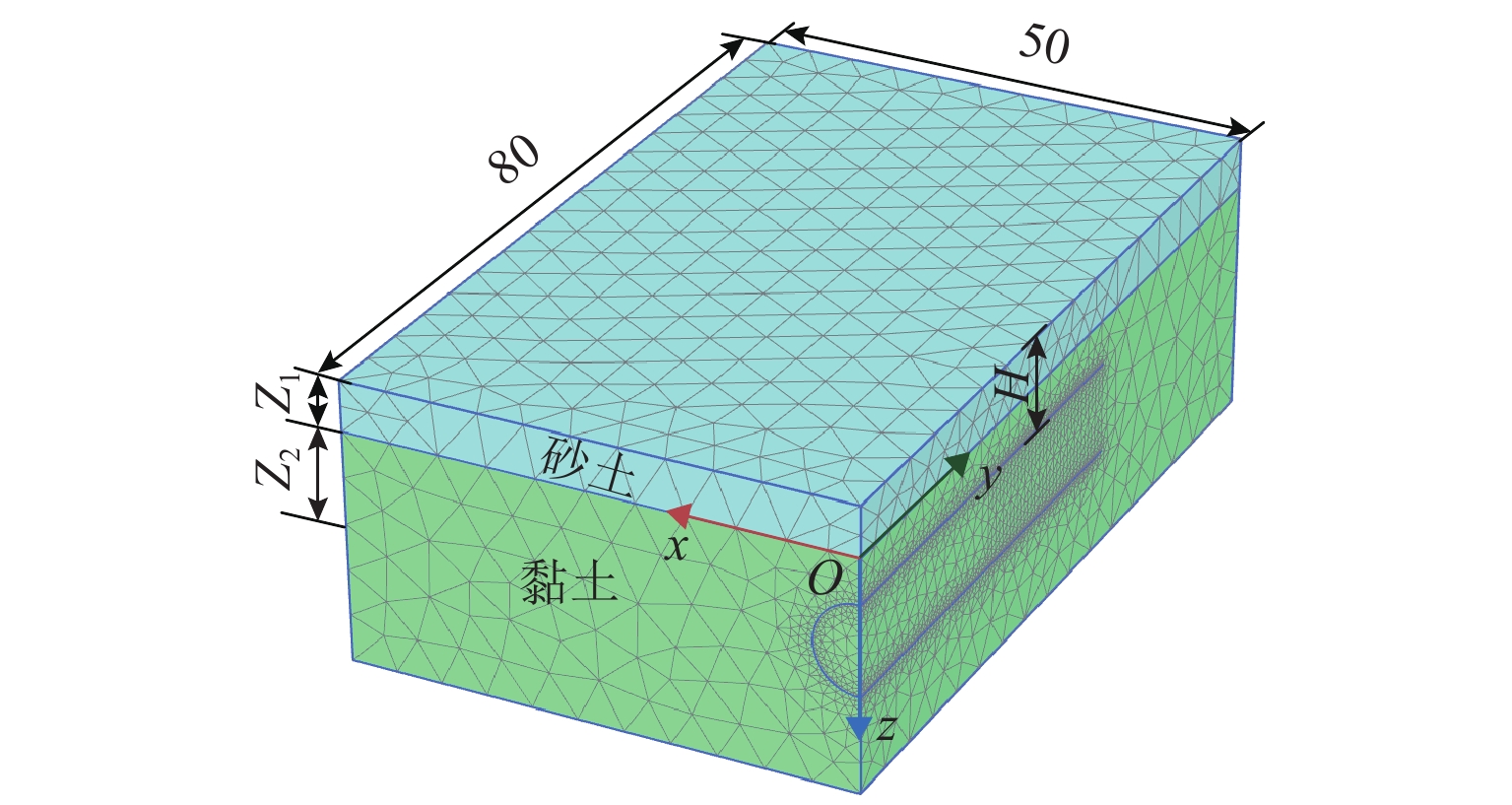
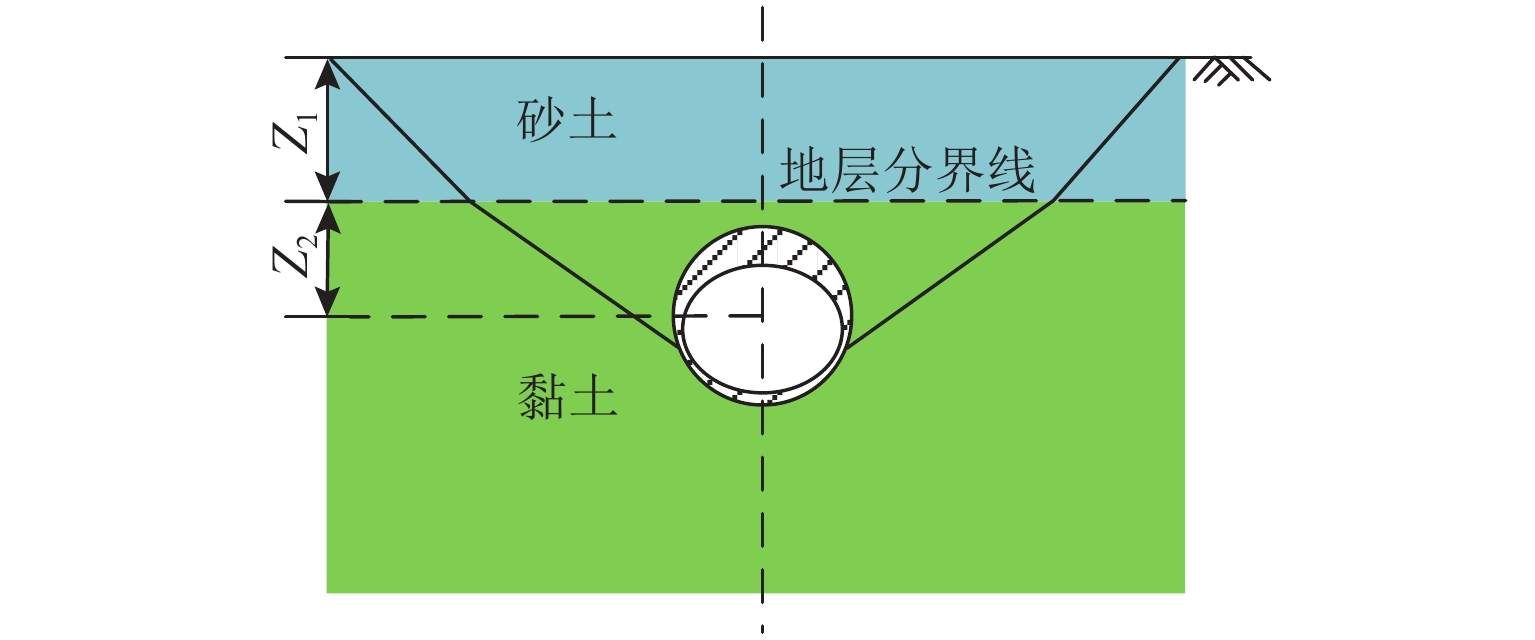
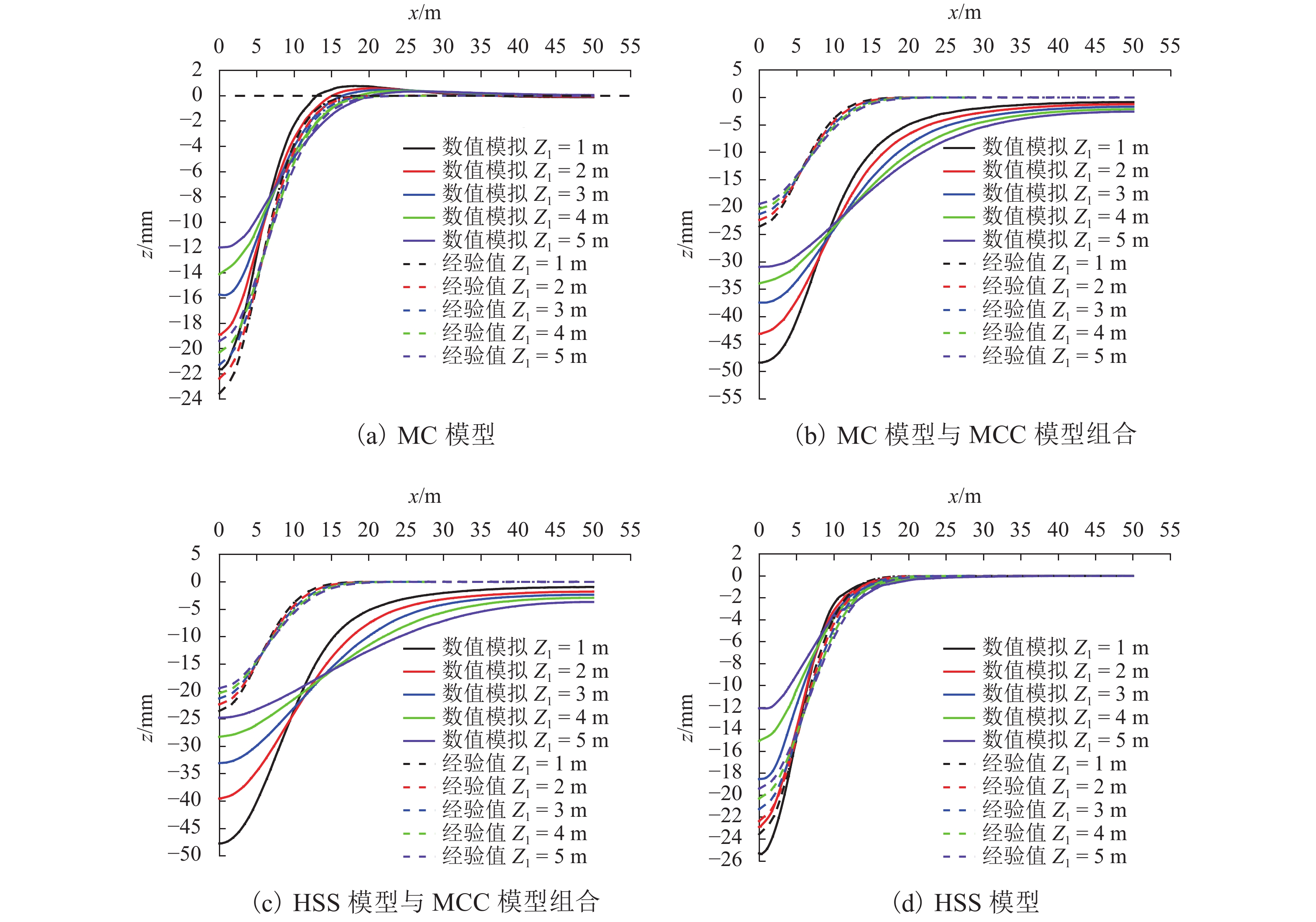
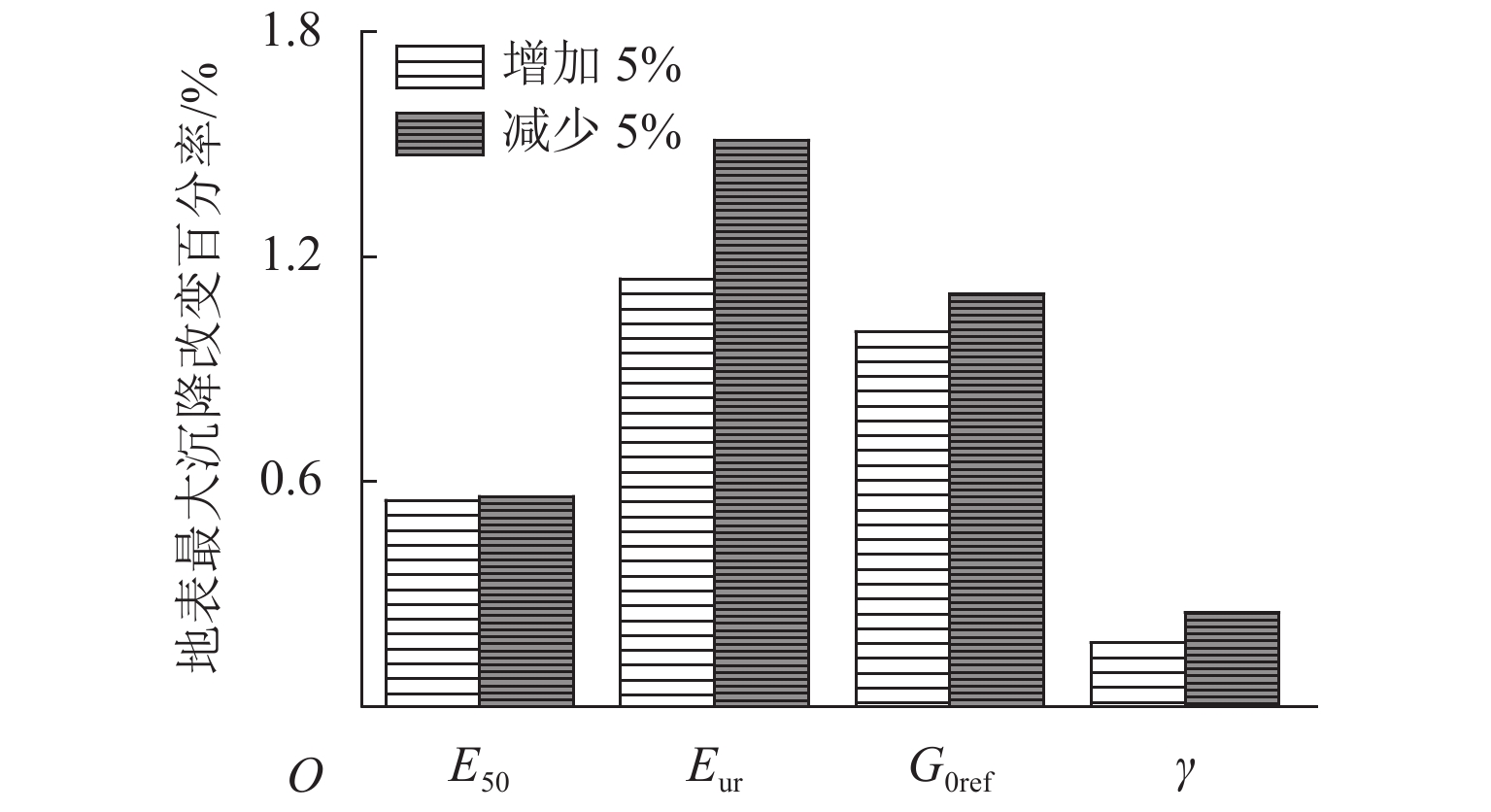
为探究本构模型对浅埋隧道开挖诱发地表沉降规律的影响，考虑摩擦性与临界状态土体本构模型，对复合成层地层浅埋隧道开挖诱发的地表沉降槽进行了分析. 首先，基于PlAXIS 3D有限元平台建立砂-黏复合地层浅埋隧道数值模型，材料模型选用3类本构模型（莫尔库伦（MC）、修正剑桥（MCC）、硬化小应变（HSS））及其组合模型；其次，利用参数等值转换关系，深入探讨了本构模型的选取对隧道开挖地表沉降槽宽度与深度的影响；最后，结合经验公式计算并对比分析，研究基于3类本构模型及其组合模型的沉降槽数值模拟与经验计算结果存在差异的原因. 结果表明：上、下地层均采用HSS模型时，最大沉降量及沉降槽宽度与经验公式的计算结果吻合度较高，最大沉降量相差不超过7.3 mm；上、下地层均采用MC模型时，出现地表隆起的不合理现象；下卧地层采用MCC模型、上伏地层分别采用MC模型和HSS模型，即采用MC -MCC模型和HSS -MCC模型时，其数值预测的最大沉降量高于经验公式计算值，达24.8 mm，而沉降槽形状相对于经验公式预测结果“窄而陡”；在针对HSS模型的参数敏感性分析中发现，若卸载再加载模量与初始剪切模量变化值为5%，将导致地表最大沉降量分别改变1.5%和1.0%.
Abstract:In order to explore the influence of constitutive models on the surface settlement induced by shallow tunnel excavation, the surface settlement trough induced by shallow tunnel excavation in composite layered strata was analyzed considering the friction and critical state soil constitutive model. Firstly, a numerical model of shallow buried tunnel in sand clay composite stratum is constructed on the finite element platform PLAXIS 3D. Three types of constitutive models (i.e., the Mohr-Coulomb model (MC), the modified Cam-Clay model (MCC), and the hardening small strain model (HSS)) and their combinations are utilized. Secondly, the influence of the constitutive model on the width and depth of the ground settlement trough in tunnel excavation is discussed using the parameter equivalent transformation relationship. Finally, the numerical simulation and empirical calculation results of the settlement trough based on the three types of constitutive models and their combined models are compared, and the reasons for their differences are analyzed. The results show that when the HSS model is used for both the upper and lower strata, the maximum settlement and the width of settling trough obtained by numerical simulation are in good agreement with the calculated results by empirical formula, and the difference in the maximum settlement between the two approaches is less than 7.3 mm; when the MC model is used for both the upper and lower strata, an unreasonable phenomenon of surface uplift appears; when the MCC model is used for the lower stratum while the MC model and HSS model are used for the upper stratum, respectively (i.e., when the MC-MCC and HSS-MCC combined models are used), the maximum settlement predicted by numerical simulation is 24.8 mm higher than that calculated by empirical formula, while the settlement trough is "narrow and steep" compared with the empirical result. According to the parametric sensitivity analysis of the HSS model, it is found that a change of 5% in the unloading and reloading modulus and initial shear modulus will lead to a change of 1.5% and 1.0% in the maximum ground settlement, respectively.
-
Key words:
- shallow tunnel /
- constitutive model /
- surface subsidence /
- numerical simulation
-
图 6 不同本构模型的地表沉降数值计算值与经验公式计算值对比
Figure 6. Comparison of numerical values of land subsidence calculated by different constitutive models with those calculated by empirical formulas
图 7 HSS模型改变砂土厚度竖向位移分布（Z1=5 m，Z2=9 m）
Figure 7. Contour of vertical displacement of HSS model changing sand thickness （Z1=5 m, Z2=9 m）
表 1 模型分析工况
Table 1. Working conditions for model analysis
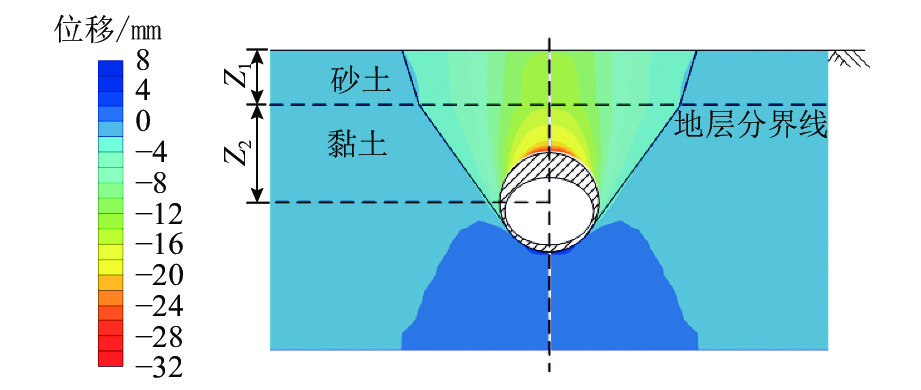
m 工况 Z1 Z2 H 模型高度 1 1 9 5.5 28 2 2 9 6.5 29 3 3 9 7.5 30 4 4 9 8.5 31 5 5 9 9.5 32 
下载: 导出CSV
土体类型 c/kPa φ/(°) ψ/(°) E/MPa v 砂土 1 33 3 120 0.3 黏土 10 20 0 50 0.2
下载: 导出CSV
土体类型 M λ κ e0 v 黏土 1 0.1 0.016 0.66 0.2
下载: 导出CSV
-
[1] ZHENG G, YANG X, ZHOU H, et al. Simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations[J]. Computers and Geotechnics, 2018, 95: 119-128. [2] 李涛,崔远,曹英杰,等. 岩-土复合地层暗挖隧道施工引起地表沉降计算方法[J]. 中国铁道科学,2020,41(2): 73-80. doi: 10.3969/j.issn.1001-4632.2020.02.09LI Tao, CUI Yuan, CAO Yingjie, et al. Calculation method of surface settlement caused by construction of mining tunnel in rock-soil composite strata[J]. China Railway Science, 2020, 41(2): 73-80. doi: 10.3969/j.issn.1001-4632.2020.02.09 [3] 黄茂松,张治国,王卫东. 基于位移控制边界单元法盾构隧道开挖引起分层土体变形分析[J]. 岩石力学与工程学报,2009,28(12): 2544-2553. doi: 10.3321/j.issn:1000-6915.2009.12.022HUANG Maosong, ZHANG Zhiguo, WANG Weidong. Response analysis of shield tunnelling-induced layered soil deformation based on deformation controlled boundary element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2544-2553. doi: 10.3321/j.issn:1000-6915.2009.12.022 [4] 王金麒,李林安,陈茜,等. 水平分层土质条件下浅埋隧道掌子面支护稳定性研究[J]. 防灾减灾工程学报,2016,36(2): 196-204.WANG Jinqi, LI Linan, CHEN Qian, et al. Suppporting security research of shallow tunnel face in horizontal layered soil condition[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(2): 196-204. [5] 王维. 土岩复合地层盾构施工参数对地层及隧道变形特性影响[J]. 铁道建筑技术,2019(5): 12-16,21. doi: 10.3969/j.issn.1009-4539.2019.05.003WANG Wei. Influence of shield construction parameters on deformation characteristics of stratum and tunnel in soil-rock composite strata[J]. Railway Construction Technology, 2019(5): 12-16,21. doi: 10.3969/j.issn.1009-4539.2019.05.003 [6] ROSCOE K H, BURLAND B. On the generalised stress-strain behaviour of an ideal wet clay[M]. Cambridge: Cambridge University Press, 1968. [7] 徐中华,王卫东. 敏感环境下基坑数值分析中土体本构模型的选择[J]. 岩土力学,2010,31(1): 258-264,326. doi: 10.3969/j.issn.1000-7598.2010.01.044XU Zhonghua, WANG Weidong. Selection of soil constitutive models for numerical analysis of deep excavations in close proximity to sensitive properties[J]. Rock and Soil Mechanics, 2010, 31(1): 258-264,326. doi: 10.3969/j.issn.1000-7598.2010.01.044 [8] BENX T. Small-strain stiffness of soils and its numerical consequences[D]. Stuttgart: University of Stuttgart, 2007. [9] MITCHELL J K. Fundamentals of soil behavior[J]. Soil Science Society of America Journal, 1976, 40(4): 827-866. [10] 宋天田,周顺华,徐润泽. 盾构隧道盾尾同步注浆机 理与注浆参数的确定[J]. 地下空间与工程学报,2008,4(1): 130-133.SONG Tiantian, ZHOU Shenhua, XU Runze. Mechanism and determination of parameters of synchronous grouting in shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(1): 130-133. [11] BRINKGREVE R B J, SWOLFS W M, BEUTH L, et al. PLAXIS 3D foundation material models manual[M]. 2nd ed. Delft: [s.n.], 2007. [12] MATHEW G V, LEHANE B M. Numerical back-analyses of greenfield settlement during tunnel boring[J]. Canadian Geotechnical Journal, 2013, 50(2): 145-152. doi: 10.1139/cgj-2011-0358 [13] 顾晓强,吴瑞拓,梁发云,等. 上海土体小应变硬化模型整套参数取值方法及工程验证[J]. 岩土力学,2021,42(3): 833-845.GU Xiaoqiang, WU Ruituo, LIANG Fayun, et al. On HSS model parameters for Shanghai soils with engineering verification[J]. Rock and Soil Mechanics, 2021, 42(3): 833-845. [14] SELBY A R. Surface movements caused by tunnelling in two-layer soil[J]. Geological Society London Engineering Geology Special Publications, 1988, 5(1): 71-77. doi: 10.1144/GSL.ENG.1988.005.01.05 -
下载:
点击查看大图
计量
- 文章访问数: 467
- HTML全文浏览量: 179
- PDF下载量: 54
- 被引次数: 0