车轮多边形对重载机车轮轨相互作用及接触损伤的影响分析

张波; 杨云帆; 凌亮; 王开云

doi:10.3969/j.issn.0258-2724.20210448

车轮多边形对重载机车轮轨相互作用及接触损伤的影响分析

doi: 10.3969/j.issn.0258-2724.20210448

张波^{1, 2,},
杨云帆²,
凌亮^2, ,,
王开云²

1.
中车株洲电力机车有限公司重载快捷大功率电力机车全国重点实验室，湖南株洲 412001
2.
西南交通大学轨道交通运载系统全国重点实验室，四川成都 610031

基金项目: 国家自然科学基金（U2268210, 52072317, 51825504）

详细信息

作者简介:
张波（1988―），男，高级工程师，研究方向为车辆动力学及轮轨关系，E-mail：zb20064120@126.com

通讯作者:
凌亮（1986―），男，研究员，研究方向为轨道车辆服役安全与控制，E-mail：liangling@swjtu.edu.cn

中图分类号: U270.1；U211.5
计量
- 文章访问数: 321
- HTML全文浏览量: 97
- PDF下载量: 53
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-01
- 修回日期: 2021-09-23
- 网络出版日期: 2023-09-18
- 刊出日期: 2021-09-29

Wheel−Rail Interaction and Rolling Fatigue Damage of Heavy-Haul Locomotive Subjected to Wheel Polygonal Wear

ZHANG Bo^{1, 2
,},
YANG Yunfan²,
LING Liang^{2
, ,},
WANG Kaiyun²

1.
The State Key Laboratory of Heavy-duty and Express High-power Electric Locomotive, CRRC Zhuzhou Locomotive Co.,Ltd., Changsha 412001, China
2.
State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要:
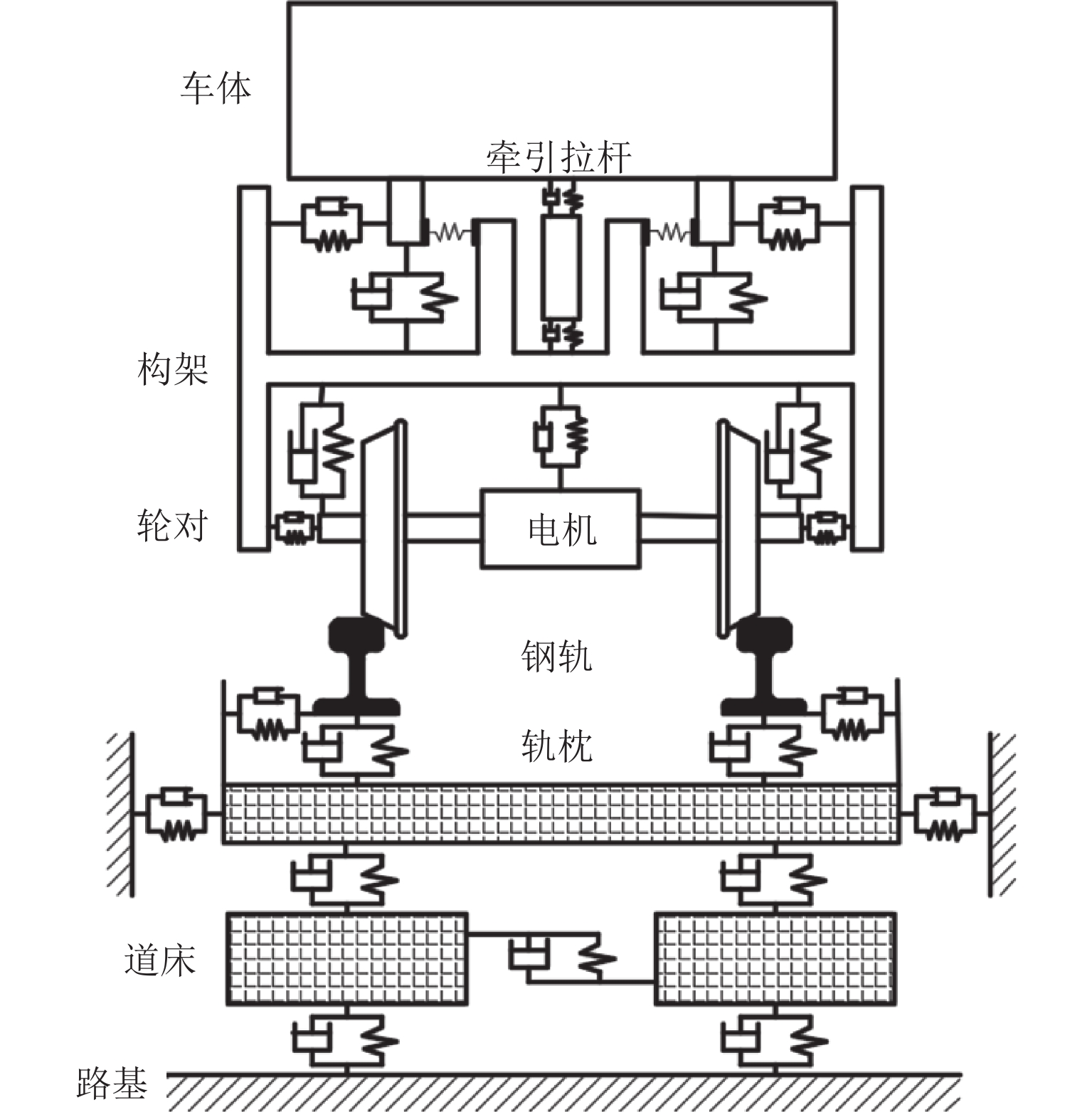
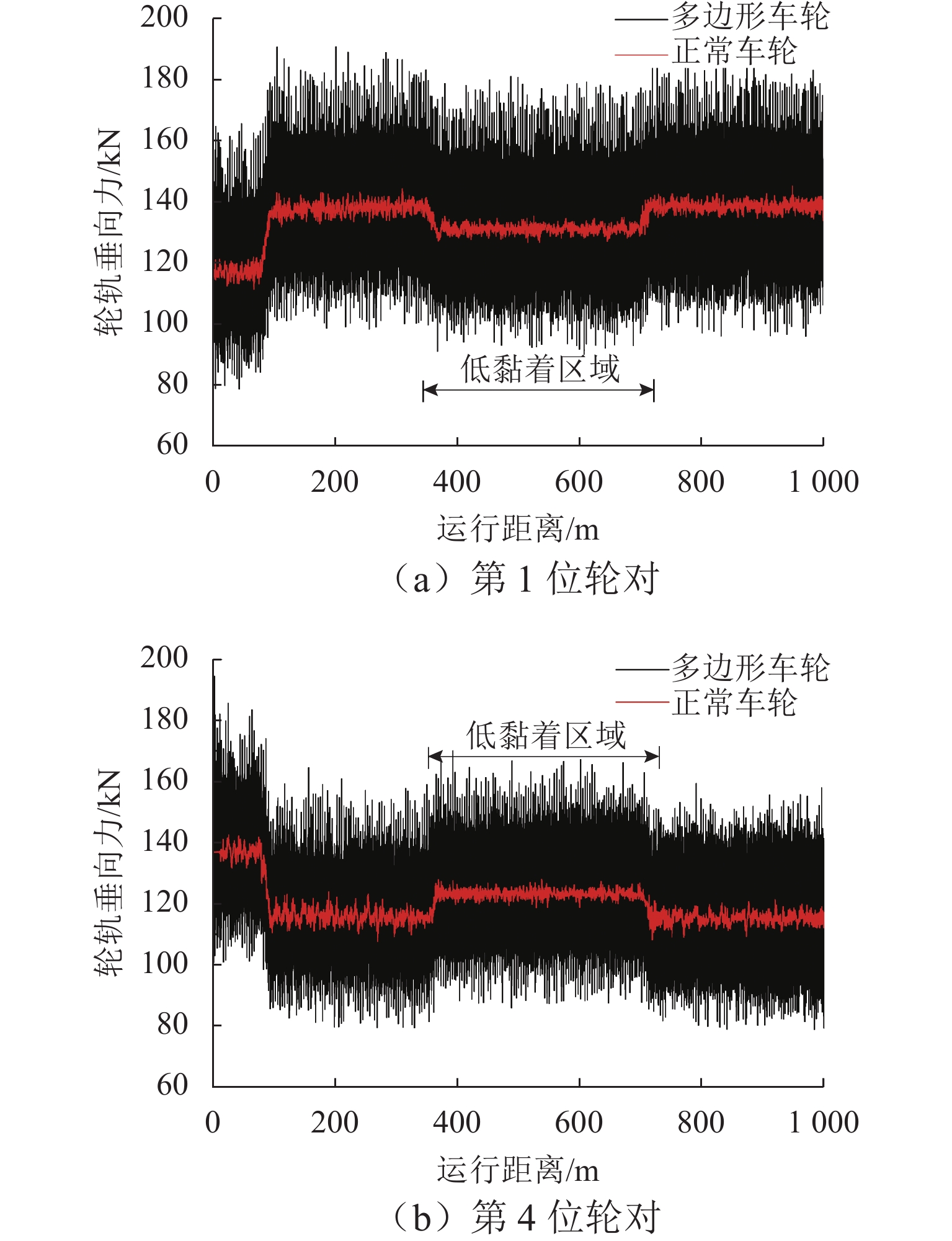
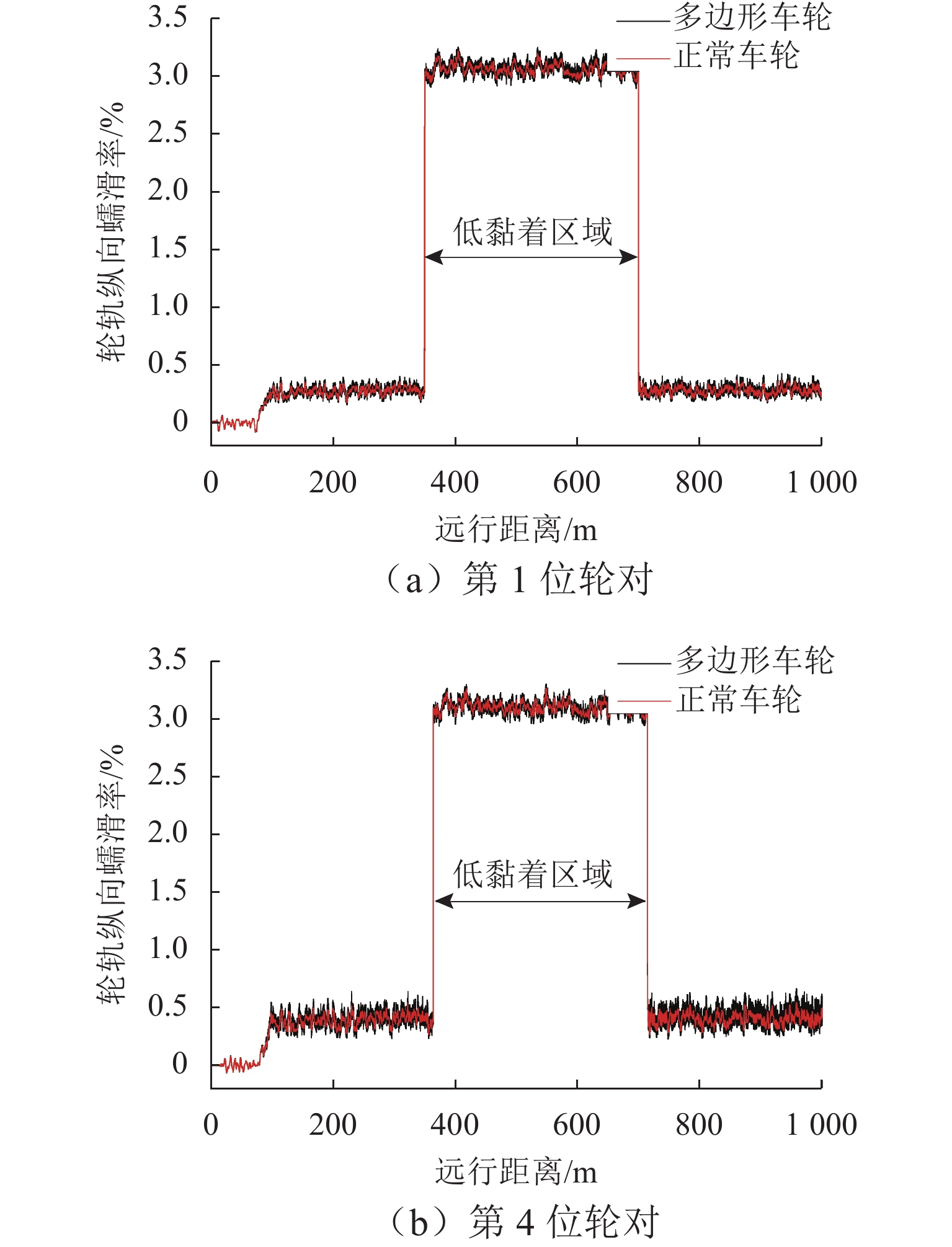
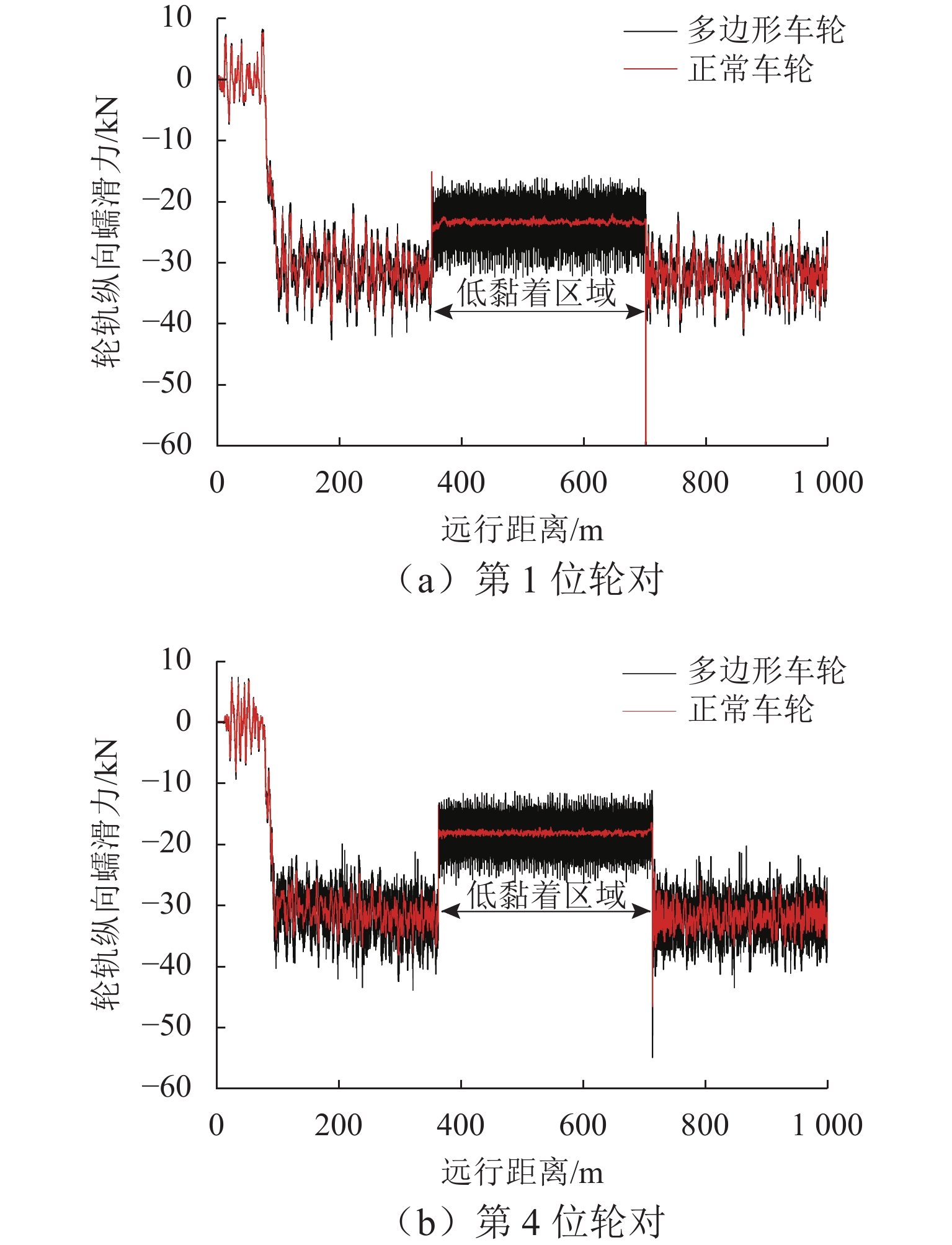
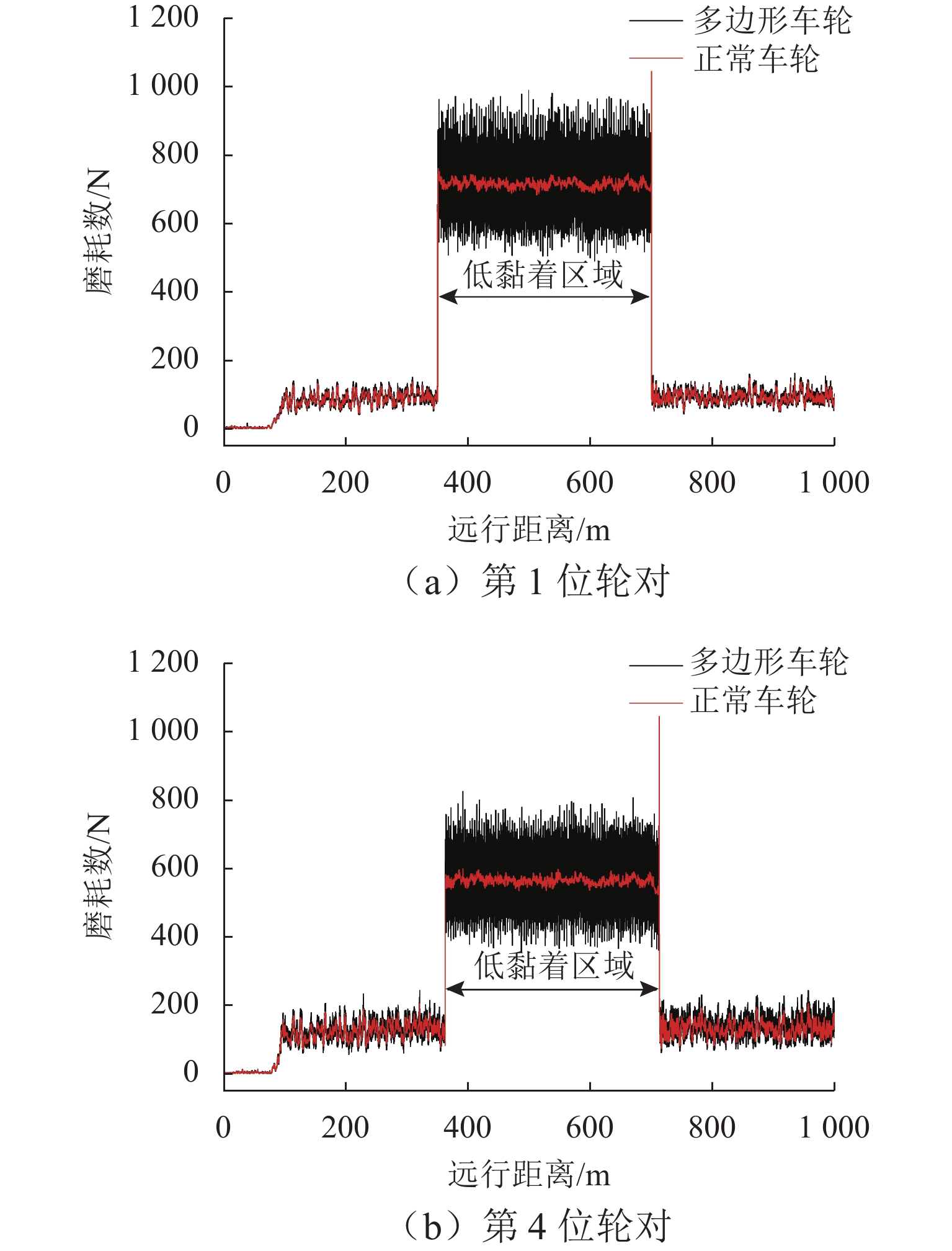
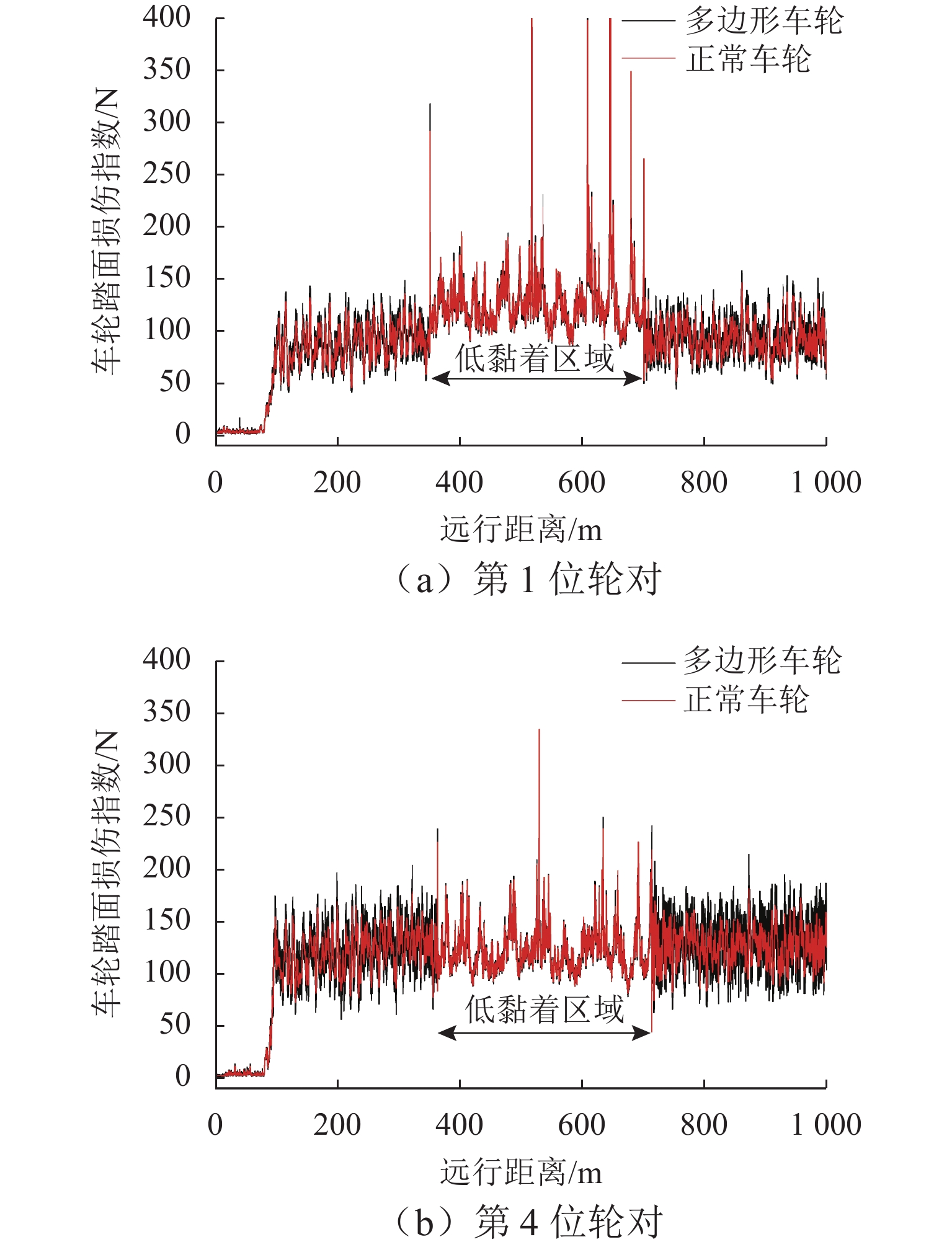
为了研究重载机车轮轨接触损伤问题，建立重载列车-轨道三维耦合动力学模型，研究车轮多边形与多种轨面摩擦条件下的机车轮轨系统动态相互作用行为. 在此基础上，建立基于轮轨系统动力学响应的车轮踏面疲劳损伤预测模型，研究制动工况和轮轨接触表面变摩擦条件下车轮多边形磨耗对车轮表面磨损的影响. 结果表明：严重的车轮多边形磨耗不仅加剧轮轨动态相互作用，也会增大轮轨接触界面磨耗损伤；在干燥接触条件下，车轮多边形会加剧车轮踏面疲劳损伤，车轮多边形导致机车第1位轮对和第4位轮对的损伤指数波动范围较正常车轮损伤指数的波动范围增大19.59%和39.43%；在低黏着接触条件下，车轮多边形会加剧车轮磨耗，车轮多边形导致轮轨蠕滑力波动增大5.85倍，使得机车第1位轮对和第4位轮对的磨耗数波动范围增大6.44倍和6.22倍.
- 重载机车 /
- 车轮疲劳损伤 /
- 车轮多边形 /
- 车辆-轨道耦合动力学 /
- 损伤指数
Abstract:
In order to study the rolling fatigue damage (RCF) of heavy-haul locomotive wheels, the three-dimensional heavy-haul locomotive–track coupled dynamics model was established, and the dynamic interaction behavior of locomotive wheel–rail system under the condition of wheel polygonal wear and different rail surface frictions was studied. On this basis, a wheel tread RCF prediction model based on the dynamic responses of the wheel–rail system was established, and the effect of wheel polygonal wear on the wheel surface wear was studied under the changing wheel–rail friction conditions with the braking effort. The results suggest that the wheel polygonal wear not only intensifies wheel–rail dynamic interaction but also increases wheel–rail interface wear and damage. The wheel polygonal wear can aggravate the wheel tread RCF under the dry contact condition. The fluctuation range of the damage index of the locomotive with one and four wheelsets increases by 19.59% and 39.43% compared with that of a normal wheel. Under the low-adhesion contact condition, the wheel polygonal wear can aggravate the wheel wear, and the fluctuation range of wheel–rail creep force increases 5.85 times. The fluctuation range of the wear number of the locomotive with one and four wheelsets improves 6.44 times and 6.22 times, respectively.
- heavy-haul locomotive /
- rolling fatigue damage of wheels /
- wheel polygonal wear /
- locomotive–track coupled dynamics /
- damage index

HTML全文

图 1 机车车轮踏面滚动接触疲劳仿真流程

Figure 1. Simulation flow of wheel-tread RCF of locomotive

下载: 全尺寸图片幻灯片

图 2 机车车辆-轨道耦合动力学模型

Figure 2. Locomotive–track coupled dynamics model

下载: 全尺寸图片幻灯片

图 3 不同接触条件下轮轨黏着特性曲线

Figure 3. Wheel–rail adhesion feature curves under different contact conditions

下载: 全尺寸图片幻灯片

图 4 实测车轮多边形

Figure 4. Tested wheel polygonal wear

下载: 全尺寸图片幻灯片

图 5 轴箱振动加速度对比分析结果

Figure 5. Comparison results of vibration accelerations of the axlebox

下载: 全尺寸图片幻灯片

图 6 制动力矩

Figure 6. Braking torque

下载: 全尺寸图片幻灯片

图 7 轮轨垂向力

Figure 7. Wheel–rail vertical forces

下载: 全尺寸图片幻灯片

图 8 轮轨纵向蠕滑率

Figure 8. Wheel–rail longitudinal creepage

下载: 全尺寸图片幻灯片

图 9 轮轨纵向蠕滑力

Figure 9. Wheel–rail longitudinal creep force

下载: 全尺寸图片幻灯片

图 10 磨耗数

Figure 10. Wear number

下载: 全尺寸图片幻灯片

图 11 车轮踏面损伤指数

Figure 11. Damage index of wheel tread

下载: 全尺寸图片幻灯片

表 1 不同轮轨摩擦条件下接触参数

Table 1. Contact parameters under different wheel–rail friction conditions

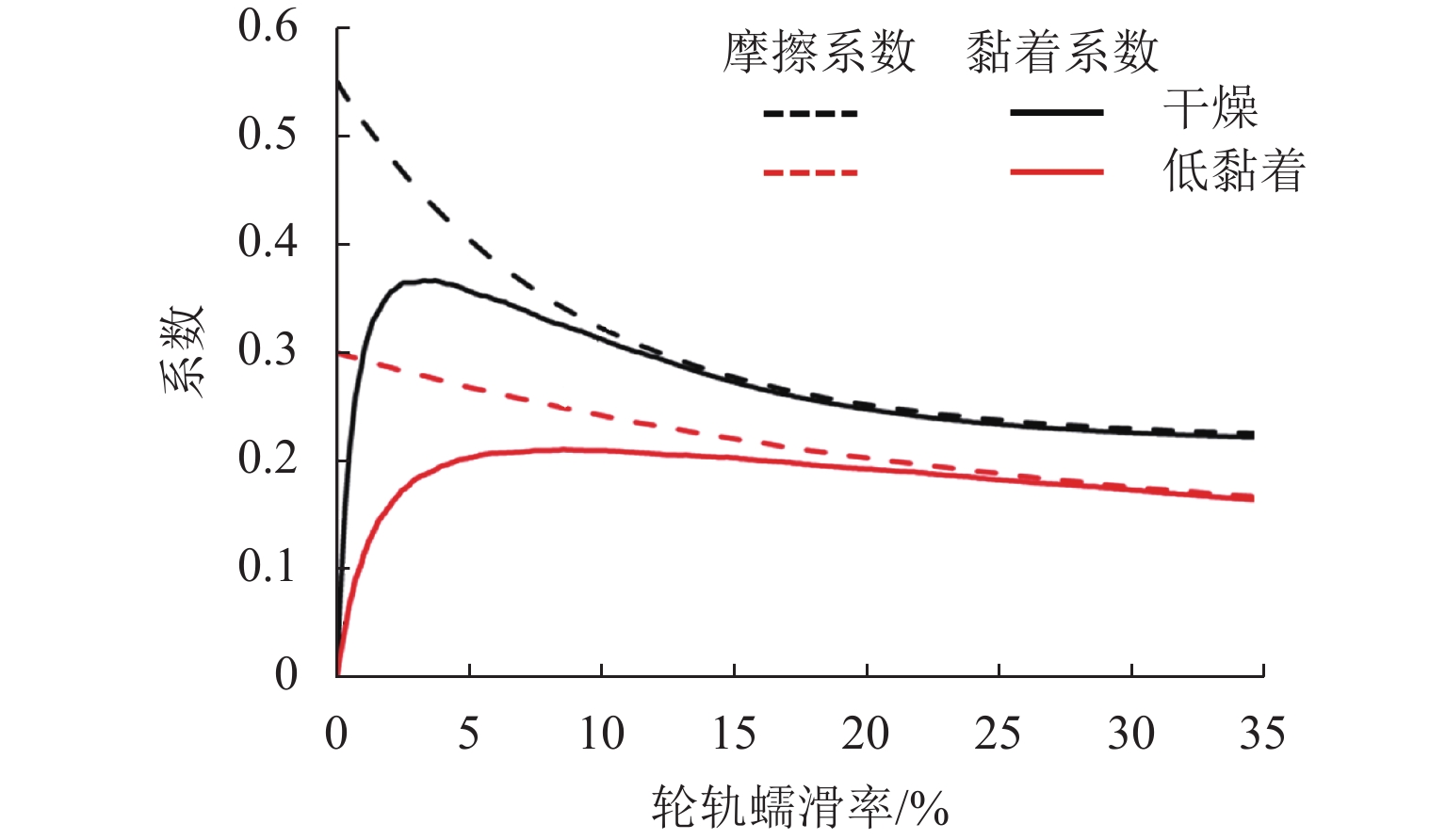
条件 μ₀ μ_∞ B /（s·m⁻¹） K_A K_S

干燥 0.55 0.22 0.60 1.00 0.40
低黏着 0.30 0.12 0.20 0.30 0.10

下载: 导出CSV

参考文献(25)

[1]	刘鹏飞,王开云,翟婉明. 驱动工况下重载机车与轨道动态相互作用[J]. 西南交通大学学报,2014,49(1): 15-20. doi: 10.3969/j.issn.0258-2724.2014.01.003 LIU Pengfei, WANG Kaiyun, ZHAI Wanming. Dynamics interaction between heavy-haul locomotive and track under driving conditions[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 15-20. doi: 10.3969/j.issn.0258-2724.2014.01.003
[2]	赵鑫,温泽峰,王衡禹,等. 中国轨道交通轮轨滚动接触疲劳研究进展[J]. 交通运输工程学报,2021,21(1): 1-35. doi: 10.19818/j.cnki.1671-1637.2021.01.001 ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. Research progress on wheel/rail rolling contact fatigue of rail transit in China[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 1-35. doi: 10.19818/j.cnki.1671-1637.2021.01.001
[3]	郭立昌,杨斌,何成刚,等. 基于接触斑能量耗散轮轨磨损与损伤机制研究[J]. 西南交通大学学报,2018,53(5): 945-950. doi: 10.3969/j.issn.0258-2724.2018.05.010 GUO Lichang, YANG Bin, HE Chenggang, et al. Wear and damage mechanism of wheel-rail materials based on contact zone energy dissipation[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 945-950. doi: 10.3969/j.issn.0258-2724.2018.05.010
[4]	王军平,周宇,沈钢. 钢轨硬度对疲劳裂纹萌生和钢轨磨耗的影响[J]. 西南交通大学学报,2021,56(3): 611-618. WANG Junping, ZHOU Yu, SHEN Gang. Effect of rail hardness on fatigue cracks initiation and rail wear[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 611-618.
[5]	杨逸凡,凌亮,杨云帆,等. 重载机车车轮擦伤下的轮轨动态响应[J]. 工程力学,2020,37(12): 213-219. doi: 10.6052/j.issn.1000-4750.2020.01.0033 YANG Yifan, LING Liang, YANG Yunfan, et al. Wheel/rail dynamic responses due to the wheel flat of heavy-haul locomotives[J]. Engineering Mechanics, 2020, 37(12): 213-219. doi: 10.6052/j.issn.1000-4750.2020.01.0033
[6]	ZHAO X, WANG Z, WEN Z F, et al. The initiation of local rolling contact fatigue on railway wheels: an experimental study[J]. International Journal of Fatigue, 2020, 132: 105354.1-105354.14.
[7]	CHEN Y Z, HE C G, ZHAO X J, et al. The influence of wheel flats formed from different braking conditions on rolling contact fatigue of railway wheel[J]. Engineering Failure Analysis, 2018, 93: 183-199. doi: 10.1016/j.engfailanal.2018.07.006
[8]	LI Y, CHEN J J, WANG J X, et al. Study on the effect of residual stresses on fatigue crack initiation in rails[J]. International Journal of Fatigue, 2020, 139: 105750.1-105750.7.
[9]	于荣泉,李强,李娜,等. 车轮滚动接触疲劳裂纹萌生寿命预测[J]. 铁道学报,2015,37(12): 20-24. doi: 10.3969/j.issn.1001-8360.2015.12.004 YU Rongquan, LI Qiang, LI Na, et al. Numerical analysis on prediction of rolling contact fatigue crack initiation life of wheel[J]. Journal of the China Railway Society, 2015, 37(12): 20-24. doi: 10.3969/j.issn.1001-8360.2015.12.004
[10]	EKBERG A, KABO E. Fatigue of railway wheels and rails under rolling contact and thermal loading—an overview[J]. Wear, 2005, 258(7/8): 1288-1300.
[11]	EKBERG A, SOTKOVSZKI P. Anisotropy and rolling contact fatigue of railway wheels[J]. International Journal of Fatigue, 2001, 23(1): 29-43. doi: 10.1016/S0142-1123(00)00070-0
[12]	EKBERG A, ÅKESSON B, KABO E. Wheel/rail rolling contact fatigue—Probe, predict, prevent[J]. Wear, 2014, 314(1/2): 2-12.
[13]	KHAN S A, PERSSON I, LUNDBERG J, et al. Prediction of top-of-rail friction control effects on rail RCF suppressed by wear[J]. Wear, 2017, 380/381: 106-114. doi: 10.1016/j.wear.2017.03.010
[14]	LIU Y F, JIANG T, ZHAO X, et al. Effects of axle load transfer on wheel rolling contact fatigue of high-power AC locomotives with oblique traction rods[J]. International Journal of Fatigue, 2020, 139: 105748.1-105748.13.
[15]	LYU K K, WANG K Y, LING L, et al. Influence of wheel diameter difference on surface damage for heavy-haul locomotive wheels: measurements and simulations[J]. International Journal of Fatigue, 2020, 132: 105343.1-105343.10.
[16]	金学松,吴越,梁树林,等. 车轮非圆化磨耗问题研究进展[J]. 西南交通大学学报,2018,53(1): 1-14. doi: 10.3969/j.issn.0258-2724.2018.01.001 JIN Xuesong, WU Yue, LIANG Shulin, et al. Mechanisms and countermeasures of out-of-roundness wear on railway vehicle wheels[J]. Journal of Southwest Jiaotong University, 2018, 53(1): 1-14. doi: 10.3969/j.issn.0258-2724.2018.01.001
[17]	杨云帆,刘志强,高贤波,等. 电力机车车轮非圆化磨耗特征及其对轮轨动态冲击作用影响分析[J]. 机械工程学报,2021,57(4): 130-139. doi: 10.3901/JME.2021.04.130 YANG Yunfan, LIU Zhiqiang, GAO Xianbo, et al. Analysis on essential characteristics of the polygonal wear of locomotive wheels and its effect on wheel/rail dynamic impact[J]. Journal of Mechanical Engineering, 2021, 57(4): 130-139. doi: 10.3901/JME.2021.04.130
[18]	LAN Q Q, DHANASEKAR M, HANDOKO Y A. Wear damage of out-of-round wheels in rail wagons under braking[J]. Engineering Failure Analysis, 2019, 102: 170-186. doi: 10.1016/j.engfailanal.2019.04.019
[19]	翟婉明. 车辆-轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007.
[20]	TIAN Y, LIU S, DANIEL W J T, et al. Investigation of the impact of locomotive creep control on wear under changing contact conditions[J]. Vehicle System Dynamics, 2015, 53(5): 692-709. doi: 10.1080/00423114.2015.1020815
[21]	关庆华,赵鑫,温泽峰,等. 基于Hertz接触理论的法向接触刚度计算方法[J]. 西南交通大学学报,2021,56(4): 883-890. GUAN Qinghua, ZHAO Xin, WEN Zefeng, et al. Calculation method of Hertz normal contact stiffness[J]. Journal of Southwest Jiaotong University, 2021, 56(4): 883-890.
[22]	SH SICHANI M, ENBLOM R, BERG M. An alternative to FASTSIM for tangential solution of the wheel-rail contact[J]. Vehicle System Dynamics, 2016, 54(6): 748-764. doi: 10.1080/00423114.2016.1156135
[23]	POLACH O. Creep forces in simulations of traction vehicles running on adhesion limit[J]. Wear, 2005, 258(7/8): 992-1000.
[24]	DIRKS B, ENBLOM R. Prediction model for wheel profile wear and rolling contact fatigue[J]. Wear, 2011, 271(1/2): 210-217.
[25]	SPANGENBERG U, FRÖHLING R D, ELS P S. Influence of wheel and rail profile shape on the initiation of rolling contact fatigue cracks at high axle loads[J]. Vehicle System Dynamics, 2016, 54(5): 638-652. doi: 10.1080/00423114.2016.1150496