基于紧密堆积理论的混凝土弹性模量与徐变控制

李福海; 唐慧琪; 李继芸; 刘梦辉; 王江山; 陈爽; 徐腾飞

doi:10.3969/j.issn.0258-2724.20210431

基于紧密堆积理论的混凝土弹性模量与徐变控制

doi: 10.3969/j.issn.0258-2724.20210431

1.
西南交通大学土木工程学院，四川成都 610031
2.
云南建设基础投资股份有限公司，云南昆明 650000

基金项目: 四川省科技厅中央引导地方科技发展专项（2020ZYD011）；四川省科技厅项目（2021YJ0545）；红河州元蔓高速公路投资建设开发有限公司科技项目（ZX[2020]YMGS03）

详细信息

作者简介:
李福海（1979—），男，副教授，博士，研究方向为混凝土材料及耐久性，E-mail： lifuhai2007@home.swjtu.edu.cn

通讯作者:
徐腾飞（1983—），男，副教授，博士，研究方向为高性能混凝土与桥梁结构，E-mail：soarl120@gmail.com

中图分类号: TU528.1
计量
- 文章访问数: 243
- HTML全文浏览量: 183
- PDF下载量: 45
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-25
- 修回日期: 2022-05-19
- 网络出版日期: 2023-10-11
- 刊出日期: 2022-07-07

Concrete Elastic Modulus and Creep Control Based on Dense Packing Theory

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
Yunnan Infrastructure Investment Co., Ltd., Kunming 650000, China

摘要

摘要:
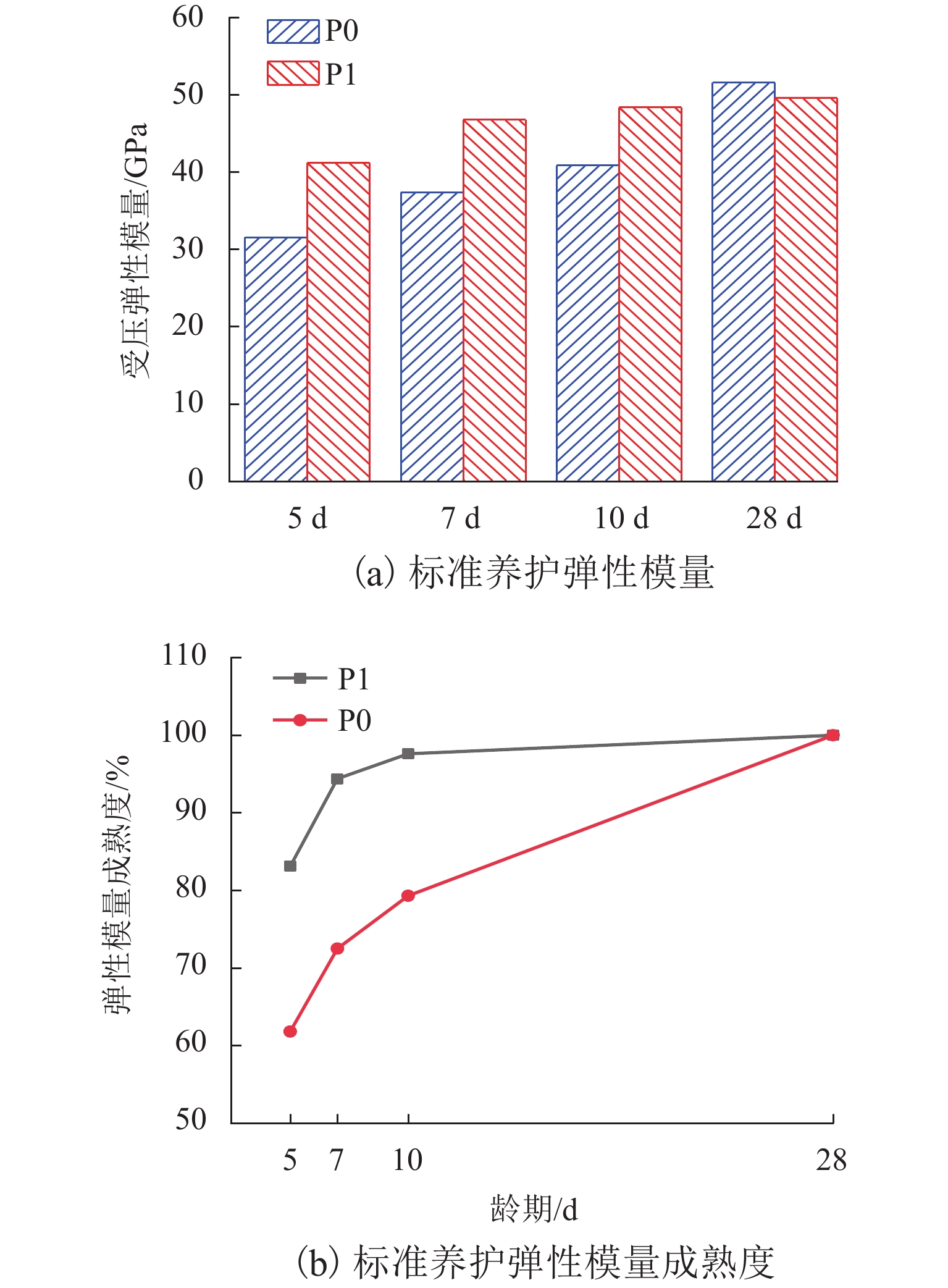
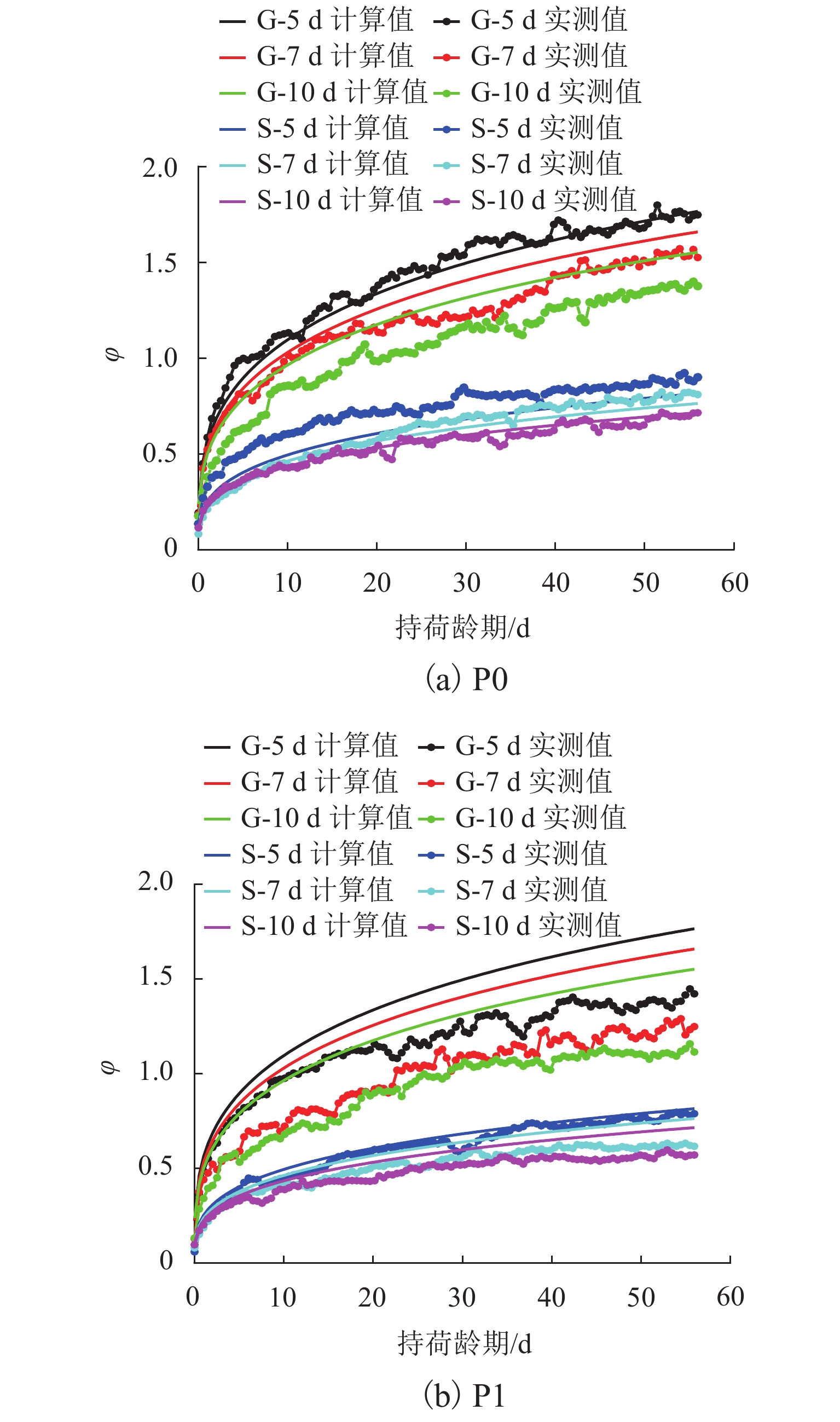
为降低连续刚构桥跨中下挠幅度，针对弹性模量与徐变2种影响因素，提出一种基于骨料紧密堆积理论的配合比优化控制方法，并对比原配合比研究了优化控制方法对不同龄期与环境下的弹性模量与徐变的影响；结合SEM （scanning electron microscope）与MIP （mercury intrusion porosimetry）试验，从混凝土微观层面分析优化机理，以CEB-FIP （1990）模型为基础，提出考虑弹性模量成熟度的修正模型. 结果表明：优化控制方法对早龄期混凝土弹性模量具有明显的控制效果，但界面过渡区面积的增加限制了后期弹性模量的发展；相同条件下，优化后混凝土徐变系数较原配合比降低了12%～23%；环境对混凝土徐变影响与优化控制方法相比占主导作用，不同环境下混凝土徐变变化幅度在45%～60%；混凝土徐变随加载龄期延长而减小，且优化后混凝土在较小加载龄期时，徐变仍比较大加载龄期的原配合比混凝土徐变降低3%～13%；优化后混凝土早龄期内部孔隙与微裂缝数量减少，改善了混凝土内部结构；修正后的CEB-FIP （1990）模型对徐变预测精度更高.
- 紧密堆积理论 /
- 弹性模量 /
- 徐变 /
- CEB-FIP （1990）模型 /
- 微观结构
Abstract:
In order to reduce the deflection amplitude of the continuous rigid frame bridge span, an optimized control method of mix proportion based on the dense packing theory of aggregates was proposed for the two influencing factors of elastic modulus and creep. In addition, the original mix proportion was studied to analyze the influence of the optimized control method on the elastic modulus and creep under different ages and environments. At the same time, the optimization mechanism was analyzed from the microscopic level of concrete in combination with scanning electron microscope (SEM) and mercury intrusion porosimetry (MIP) experiments. Based on the CEB-FIP (1990) model, a modified model considering the maturity of elastic modulus was proposed. The results show that the optimized control method can effectively control the elastic modulus of concrete at an early age, but the increase in the area of the interface transition zone limits the later development of the elastic modulus. Under the same conditions, the creep coefficient of the optimized concrete is reduced by 12%–23% compared with the original mix proportion. Moreover, the influence of the environment on the concrete creep is dominant compared with the optimized control method. The variation range of concrete creep under different environments is between 45% and 60%. Concrete creep decreases with the loading age, and the creep of optimized concrete at a small loading age is still 3%–13% lower than the original mix proportion of the concrete at a large loading age. After optimization, the number of internal pores and micro-cracks in the concrete at an early age is reduced. Therefore, the internal structure of the concrete is improved. The modified CEB-FIP (1990) model has higher accuracy in predicting creep.
- dense packing theory /
- elastic modulus /
- creep /
- CEB-FIP (1990) model /
- microstructure

HTML全文

图 1 骨料级配曲线

Figure 1. Aggregate grading curve

下载: 全尺寸图片幻灯片

图 2 HYT-FAC-1000C型弹簧式混凝土徐变仪

Figure 2. HYT-FAC-1000C spring-type concrete creep meter

下载: 全尺寸图片幻灯片

图 3 优化控制方法对混凝土弹性模量的影响

Figure 3. Influence of optimized control method on concrete elastic modulus

下载: 全尺寸图片幻灯片

图 4 各组混凝土徐变系数发展曲线

Figure 4. Development curves of concrete creep coefficient of different groups

下载: 全尺寸图片幻灯片

图 5 CEB-FIP （1990）模型计算值与实测值对比

Figure 5. Calculated and measured values of CEB-FIP (1990) model

下载: 全尺寸图片幻灯片

图 6 修正CEB-FIP （1990）模型计算值与实测值对比

Figure 6. Calculated and measured values of modified CEB-FIP (1990) model

下载: 全尺寸图片幻灯片

图 7 混凝土试样累计汞侵入量与对数微分汞侵入量

Figure 7. Cumulative mercury intrusion and logarithmic differential mercury intrusion of concrete samples

下载: 全尺寸图片幻灯片

图 8 混凝土试样微观形貌

Figure 8. Micro morphology of concrete sample

下载: 全尺寸图片幻灯片

表 1 混凝土配合比设计

Table 1. Concrete mix proportion design

编号	浆骨比	水/ （kg·m⁻³）	水泥/ （kg·m⁻³）	矿渣/ （ kg·m⁻³）	砂/ （ kg·m⁻³）	小石/ （kg·m⁻³）	大石/（ kg·m⁻³）	减水剂/ （kg·m⁻³）	28 d 抗压强度/MPa
P0	34.0∶66.0	160	453	80	860	352	655	7.9	62.6
P1	32.5∶67.5	156	442	78	722	217	866	7.8	61.8

下载: 导出CSV

表 2 徐变设计分组

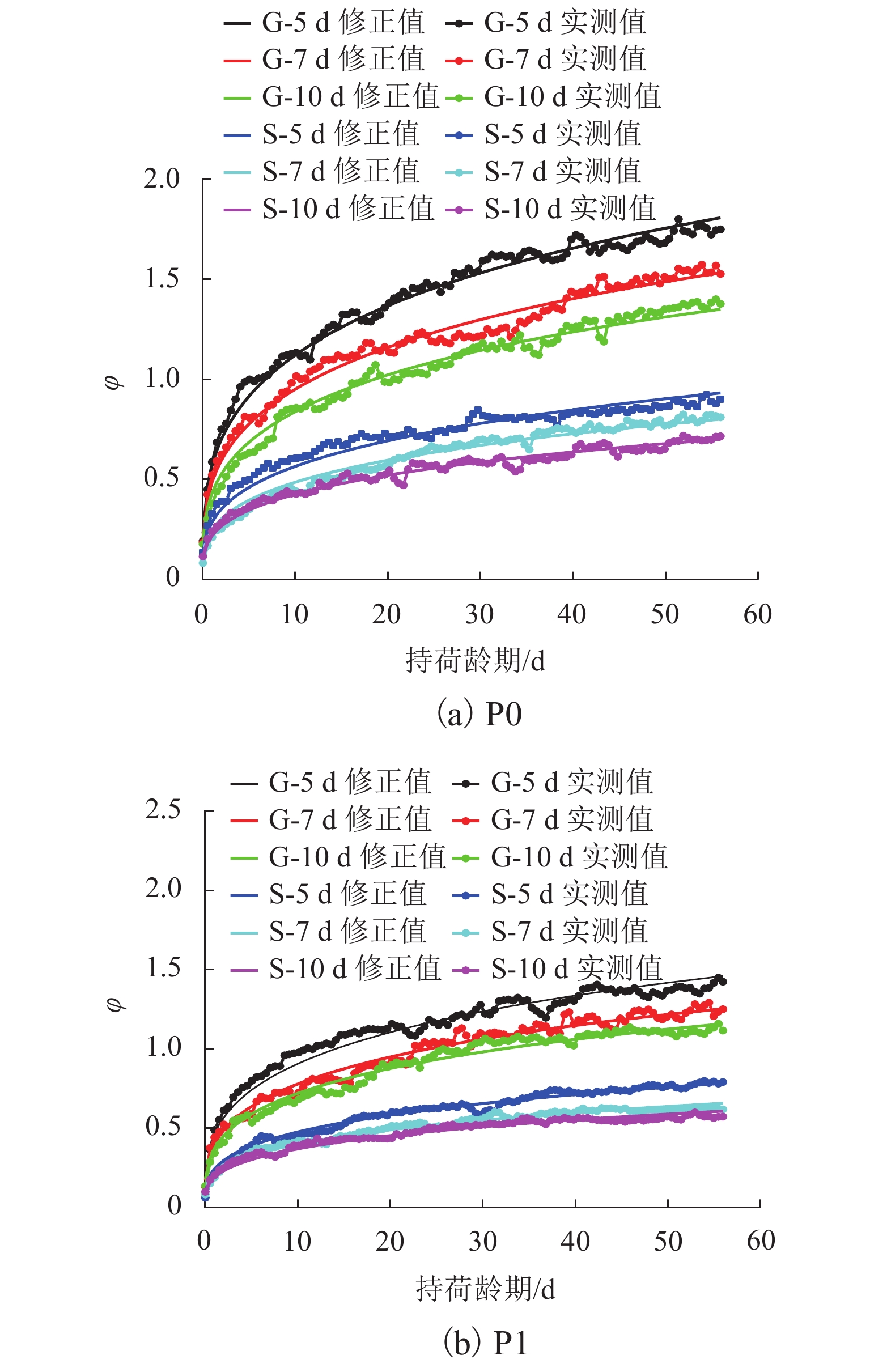
Table 2. Creep design group

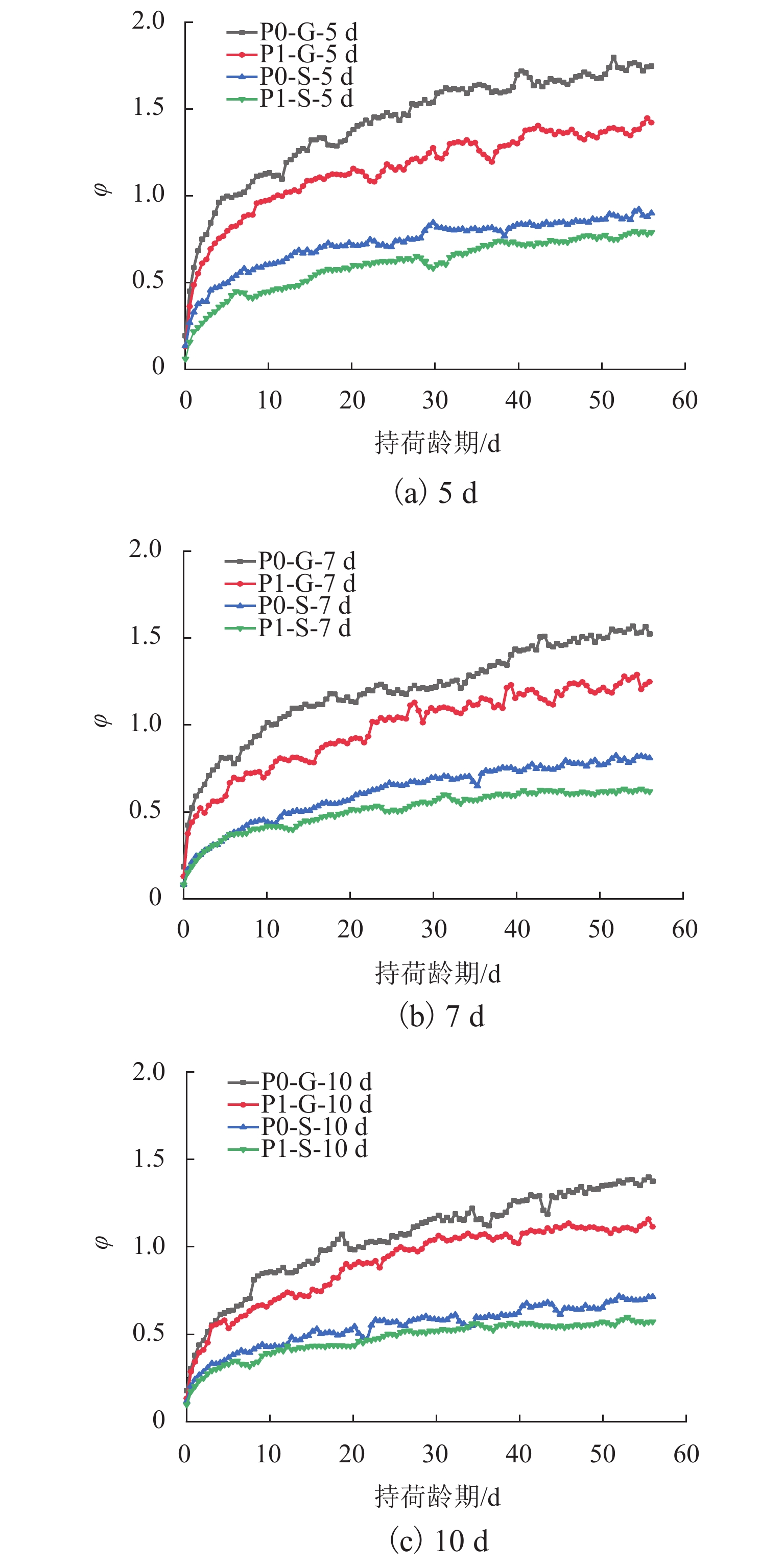
工况名称		编号	加载龄期/d	抗压强度/MPa
大风干燥	水雾养护	编号	加载龄期/d	抗压强度/MPa
P0-G-5 d	P0-S-5 d	P0	5	47.1
P0-G-7 d	P0-S-7 d		7	50.6
P0-G-10 d	P0-S-10 d		10	55.2
P1-G-5 d	P1-S-5 d	P1	5	49.7
P1-G-7 d	P1-S-7 d		7	52.1
P1-G-10 d	P1-S-10 d		10	56.3

下载: 导出CSV

参考文献(26)

[1]	朱世峰. 多跨连续刚构桥结构线形控制与合拢技术研究[D]. 重庆: 重庆交通大学, 2008.
[2]	卢志芳. 考虑时变性和不确定性的混凝土桥梁收缩徐变及预应力损失计算方法[D]. 武汉: 武汉理工大学, 2011.
[3]	黄国兴, 惠荣炎, 王秀军. 混凝土徐变与收缩[M]. 北京: 中国电力出版社, 2012: 3-4.
[4]	罗剑均. 混凝土弹性模量对连续刚构桥跨中下挠影响的研究[D]. 重庆: 重庆交通大学, 2017.
[5]	蒋正武,周磊,李文婷. 石灰岩骨料混凝土弹性模量与强度相关性研究[J]. 建筑材料学报,2014,17(4): 649-653. doi: 10.3969/j.issn.1007-9629.2014.04.016 JIANG Zhengwu, ZHOU Lei, LI Wenting. Study on the correlation between elastic modulus and strength of concrete made with limestone aggregate[J]. Journal of Building Materials, 2014, 17(4): 649-653. doi: 10.3969/j.issn.1007-9629.2014.04.016
[6]	陈洪光,许将. C50泵送混凝土弹性模量影响因素的试验研究[J]. 隧道建设,2012,32(6): 802-805. CHEN Hongguang XU Jiang. Test on factors influencing elatic modulus of C50 concrete[J]. Tunnel Construction, 2012, 32(6): 802-805.
[7]	HAILE BEZAWIT F, JIN D W, YANG B, et al. Multi-level homogenization for the prediction of the mechanical properties of ultra-high-performance concrete[J]. Construction and Building Materials, 2019, 229: 116797.1-116797.17.
[8]	郭光玲. 钢纤维增强混凝土的制备及力学性能研究[J]. 功能材料,2020,51(11): 11165-11170. doi: 10.3969/j.issn.1001-9731.2020.11.024 GUO Guangling. Preparation and mechanical properties of steel fiber reinforced concrete[J]. Journal of Functional Materials, 2020, 51(11): 11165-11170. doi: 10.3969/j.issn.1001-9731.2020.11.024
[9]	LI H, WEE T H, WONG S F. Early-age creep and shrinkage of blended cement concrete[J]. Materials Journal, 2002, 99(1): 3-10.
[10]	BROOKS J J, MEGAT JOHARI M A. Effect of metakaolin on creep and shrinkage of concrete[J]. Cement and Concrete Composites, 2001, 23(6): 495-502. doi: 10.1016/S0958-9465(00)00095-0
[11]	HE Z H, LI L Y, DU S G. Mechanical properties, drying shrinkage, and creep of concrete containing lithium slag[J]. Construction and Building Materials, 2017, 147: 296-304. doi: 10.1016/j.conbuildmat.2017.04.166
[12]	VAN DAMME H. Concrete material science: past, present, and future innovations[J]. Cement and Concrete Research, 2018, 112: 5-24. doi: 10.1016/j.cemconres.2018.05.002
[13]	MARIO M, RANGEL C S, PEPE M, et al. Optimization of normal and high strength recycled aggregate concrete mixtures by using packing model[J]. Cement and Concrete Composites, 2017, 84: 83-92. doi: 10.1016/j.cemconcomp.2017.08.016
[14]	Standards Australia. Determination of creep of concrete cylinders in compression: S1012.16[S]. Sydney: Standards Australia Limited, 1996.
[15]	中华人民共和国住房和城乡建设部, 国家市场监督管理总局. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019.
[16]	黄维蓉,杨玉柱,刘延杰,等. 含粗骨料超高性能混凝土的力学性能[J]. 硅酸盐学报,2020,48(11): 1747-1755. doi: 10.14062/j.issn.0454-5648.20200118 HUANG Weirong YANG Yuzhu LIU Yanjie et al. Mechanical properties of ultra-high performance concrete containing coarse aggregate[J]. Journal of the Chinese Ceramic Society, 2020, 48(11): 1747-1755. doi: 10.14062/j.issn.0454-5648.20200118
[17]	李华,汪洋,王育江,等. 膨胀剂对混凝土早期基本徐变的影响[J]. 建筑材料学报,2022,25(3): 256-262. doi: 10.3969/j.issn.1007-9629.2022.03.006 LI Hua, WANG Yang, WANG Yujiang, et al. Effect of expansive additives on basic creep of early-age concrete[J]. Journal of Building Materials, 2022, 25(3): 256-262. doi: 10.3969/j.issn.1007-9629.2022.03.006
[18]	张雄,高鹏. 骨料对混凝土干缩性能的影响[J]. 粉煤灰综合利用,2014,27(2): 3-7. doi: 10.3969/j.issn.1005-8249.2014.02.001 ZHANG Xiong, GAO Peng. Influence of aggregate on dry shrinkage of concrete[J]. Fly Ash Comprehensive Utilization, 2014, 27(2): 3-7. doi: 10.3969/j.issn.1005-8249.2014.02.001
[19]	杨杨,吴炎平,李鹏,等. 加载龄期和养护温度对高性能混凝土早期拉伸徐变的影响[J]. 混凝土与水泥制品,2010(4): 10-14. doi: 10.3969/j.issn.1000-4637.2010.04.003
[20]	白国良,祁豪,刘超. 再生混凝土徐变试验与预测模型研究[J]. 建筑结构学报,2016,37(增2): 121-126. doi: 10.14006/j.jzjgxb.2016.s2.018 BAI Guoliang QI Hao LIU Chao. Study on creep test and prediction model of recycled aggregate concrete[J]. Journal of Building Structures, 2016, 37(S2): 121-126. doi: 10.14006/j.jzjgxb.2016.s2.018
[21]	American Concrete Institute (ACI). Prediction of creep, shrinkage, and temperature effects inconcrete structures[M]. Farminton Hills: ACI Committee 318, 2008.
[22]	Committee Euro-International Beton and Federation International De La Precontitute. CEB-FIP model code for concrete structures 1990[S]. London: Thomas Teloford Services Ltd., 1990.
[23]	International Federation for Structural Concrete (FIB). Fib model code for concrete structures 2010[M]. Hoboken: Ernst & Sohn, 2010.
[24]	Standards Australia. Australian standard AS 3600: 2018[S]. Sydney: Standards Australia Limited, 2018.
[25]	BAZAN ZDENĚK P, SANDEEP B . Justification and refinements of model B3 for concrete creep and shrinkage 2. Updating and theoretical basis[J]. Materials and Structures, 1995, 28(8): 488-495.
[26]	GARDNER N J. Comparison of prediction provisions for drying shrinkage and creep of normal-strength concretes[J]. Materials Science, 2004, 31(5): 767–775.