Longitudinal Vibration Characteristics of Deep Sea Mining Pipe Based on ABAQUS
-
摘要:
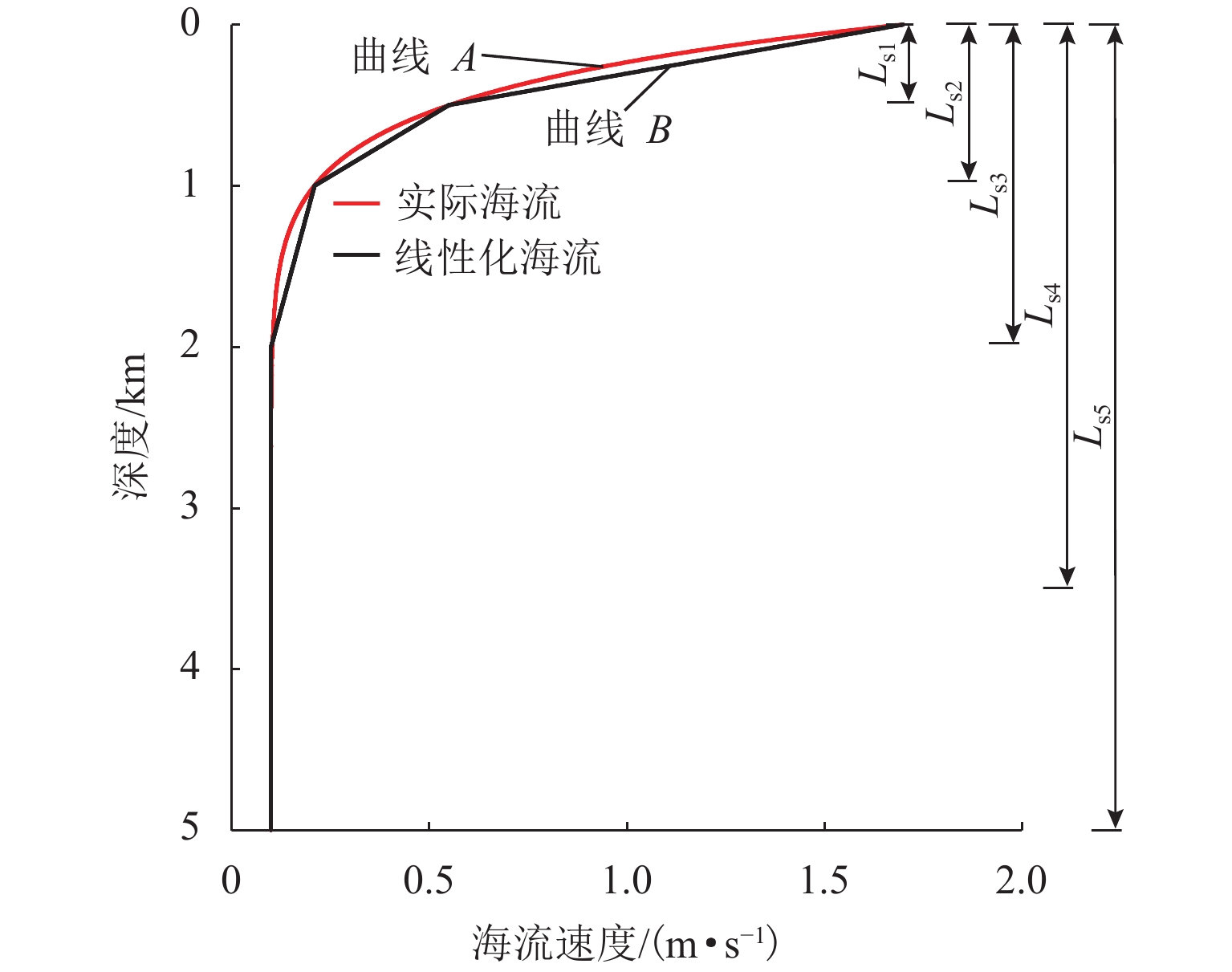
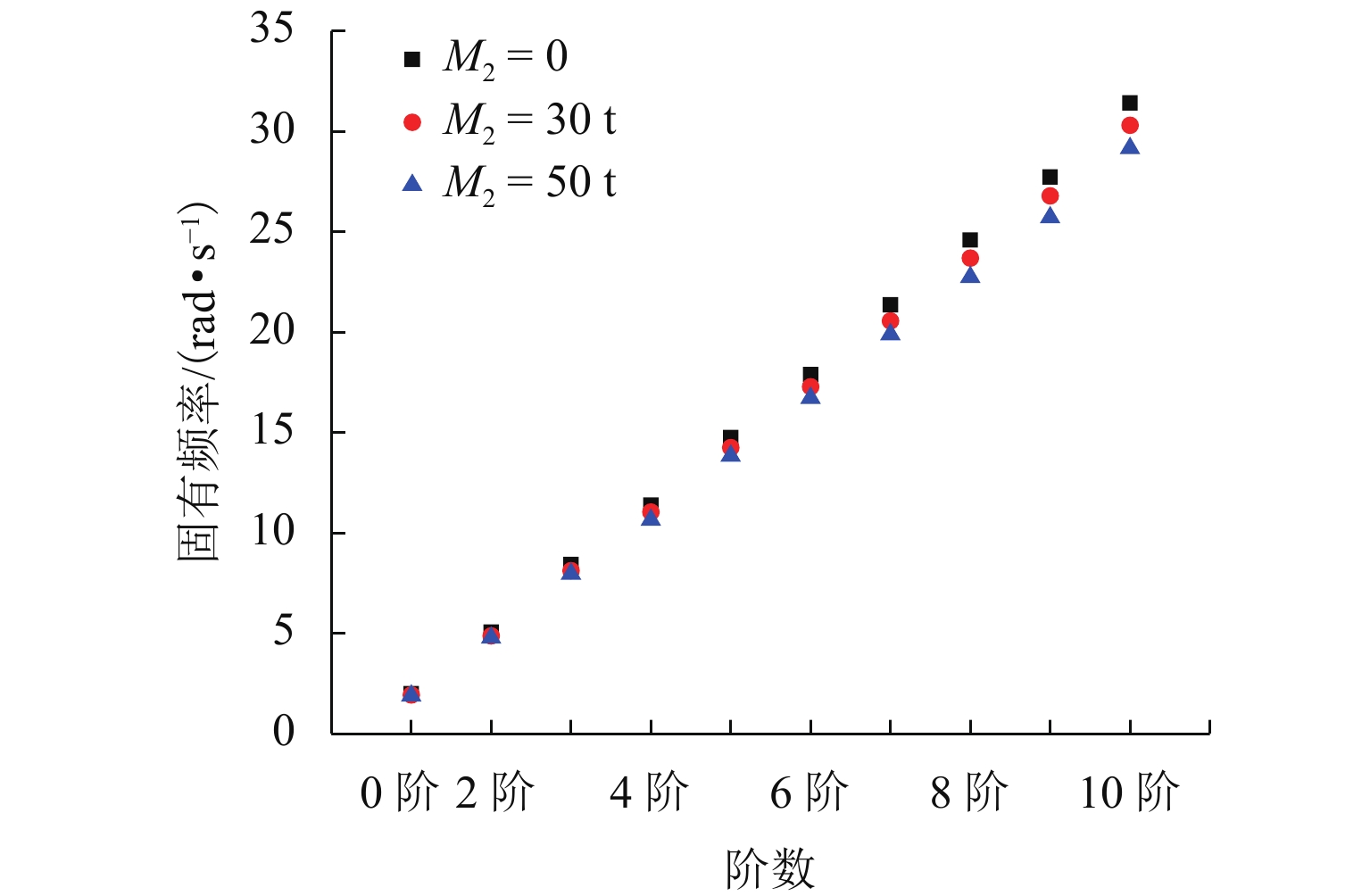
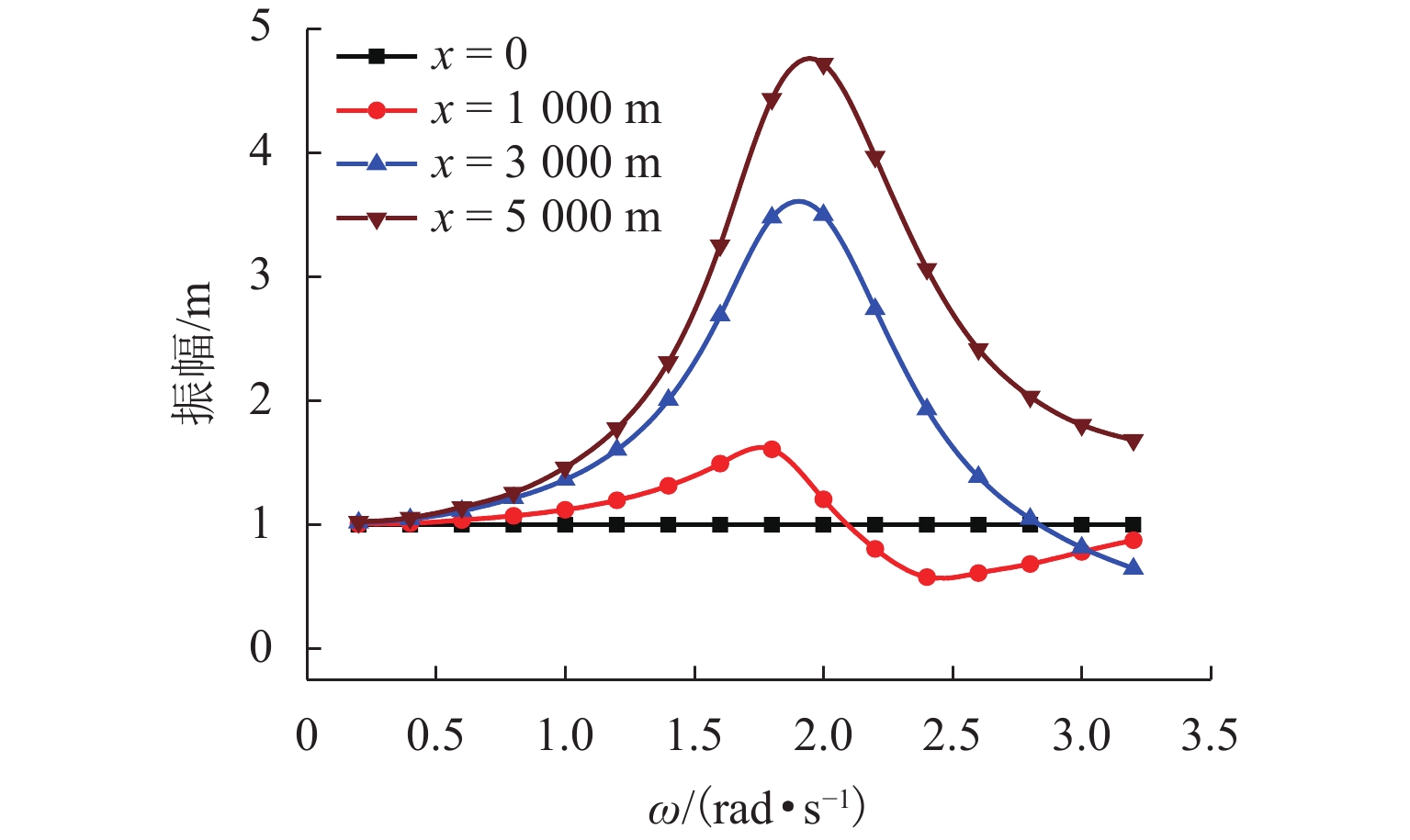
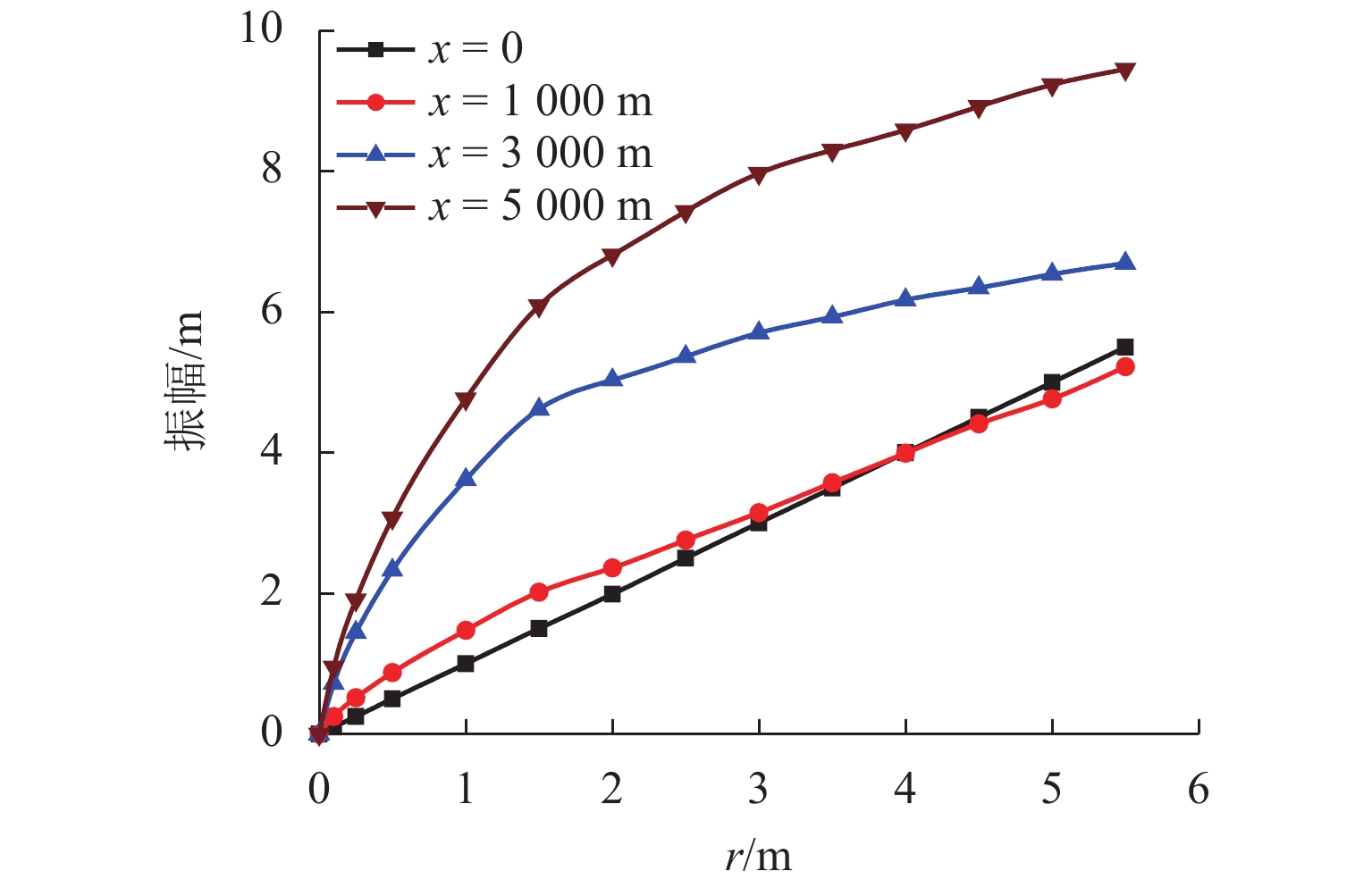
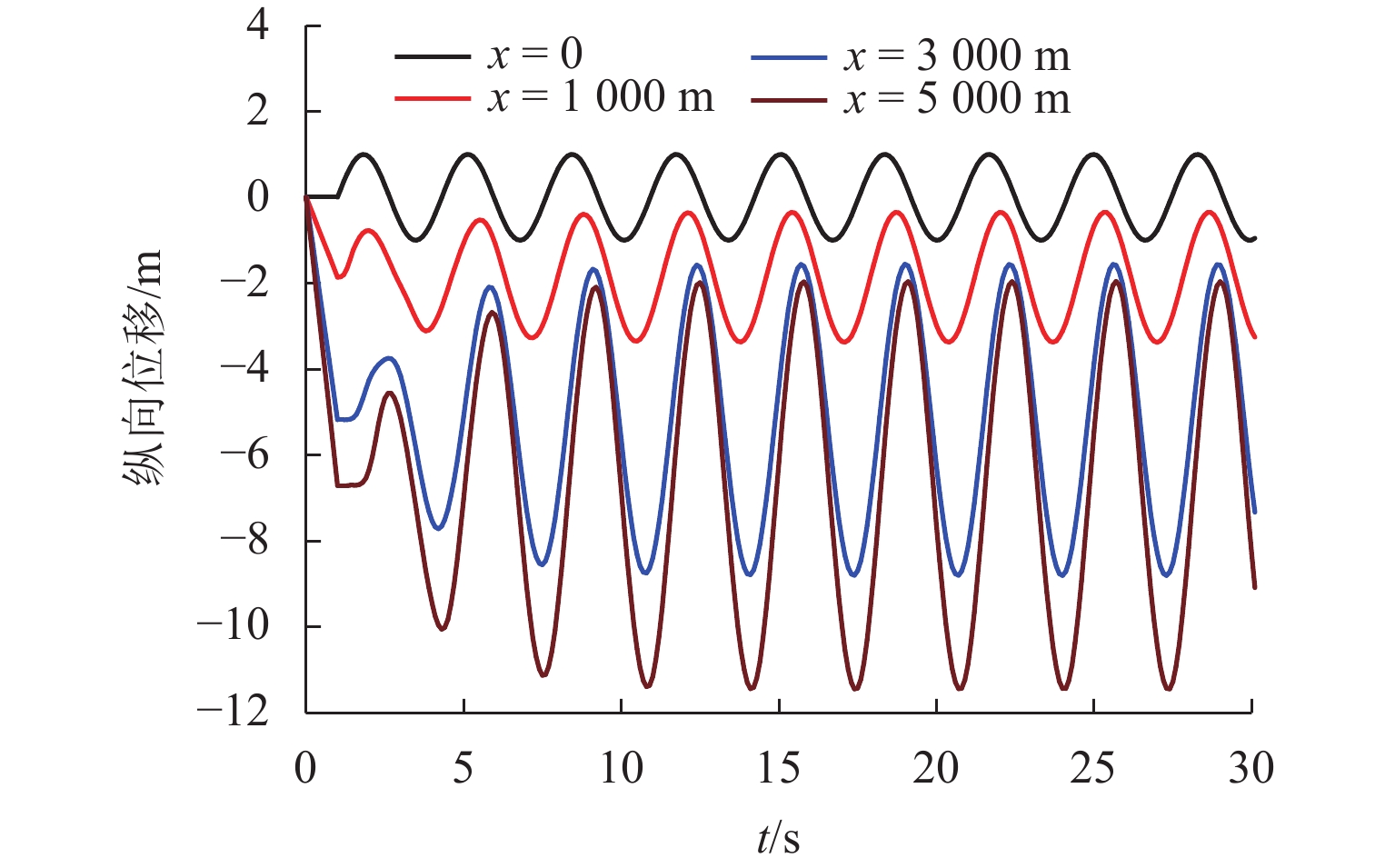
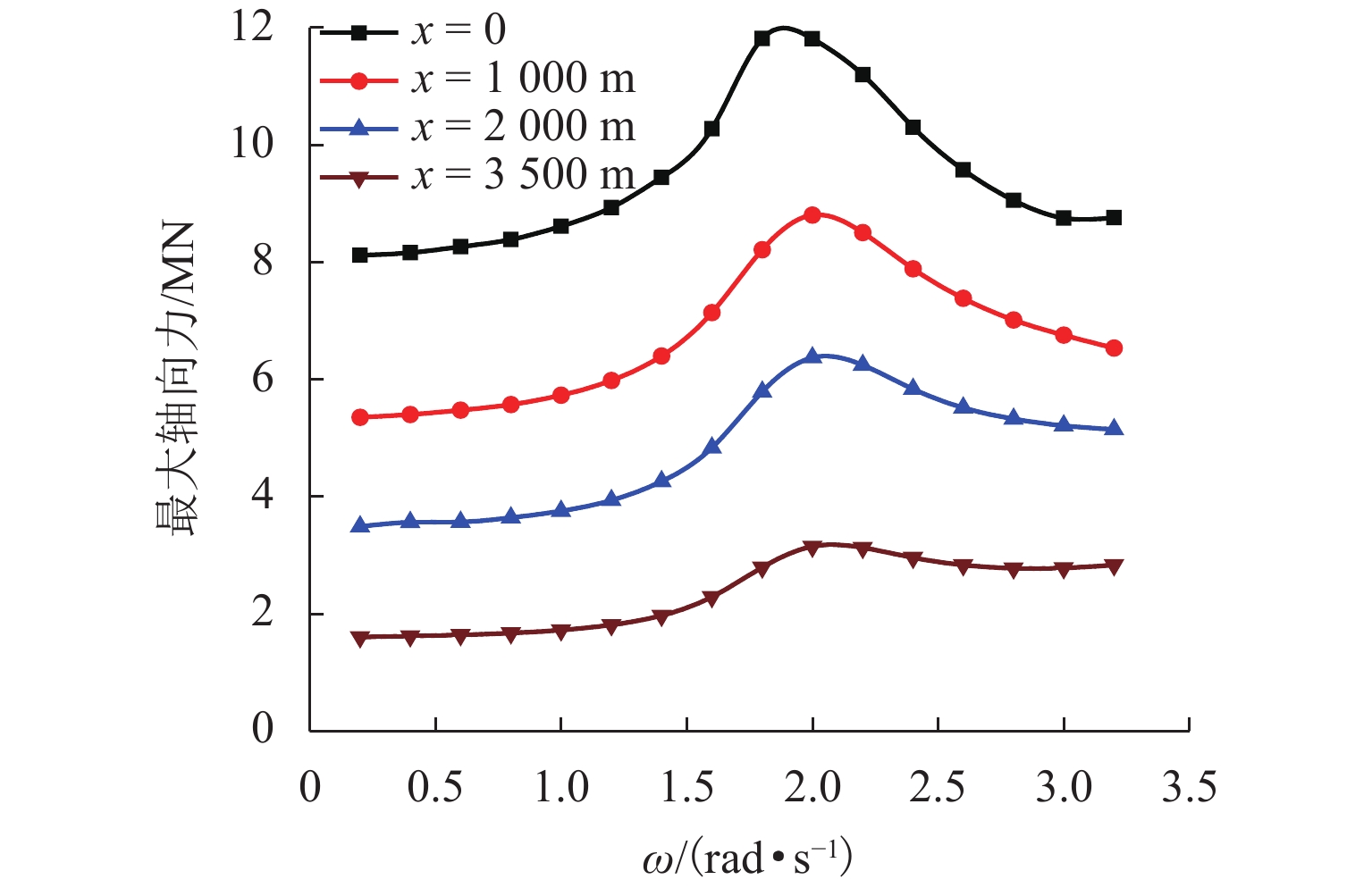
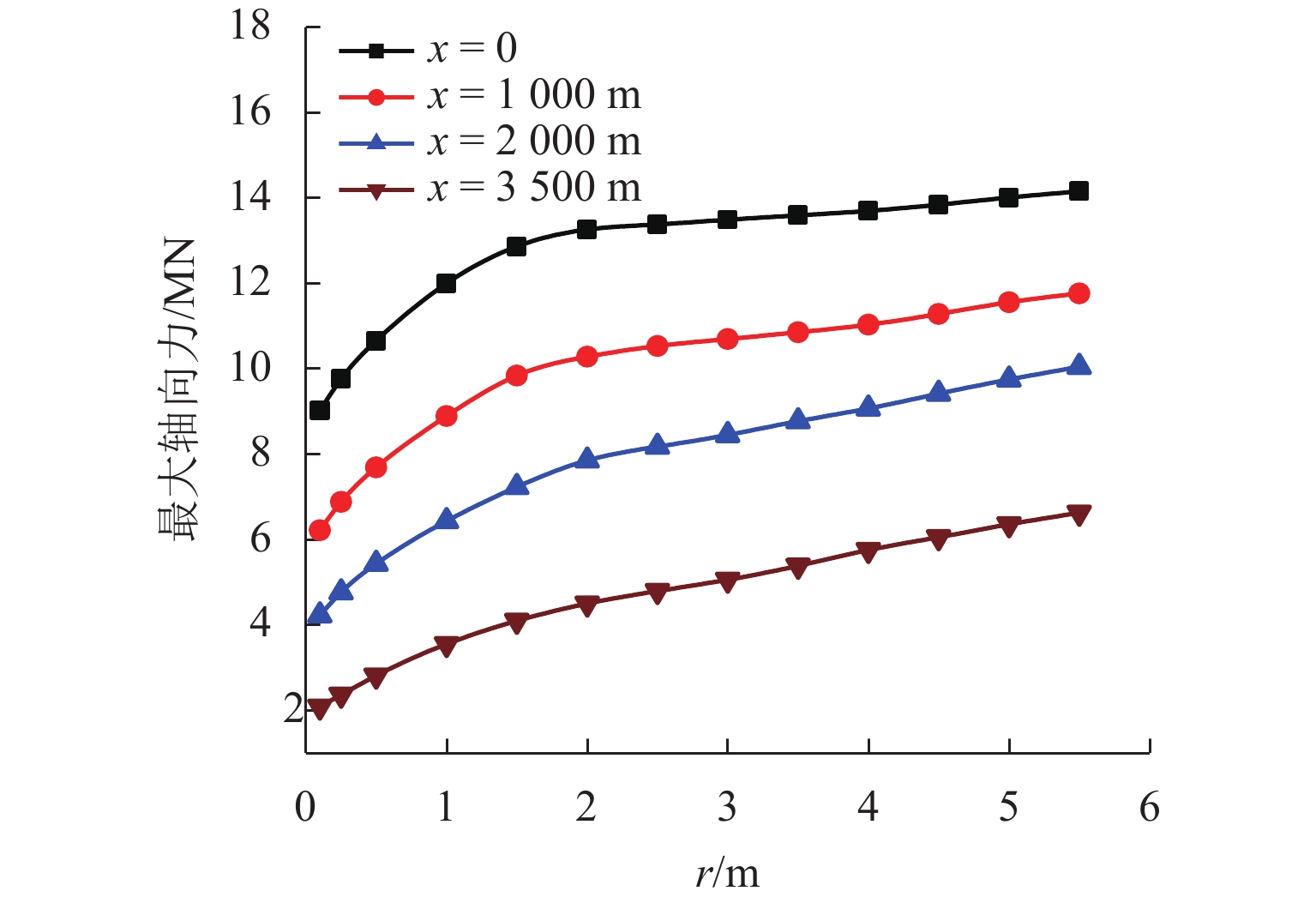
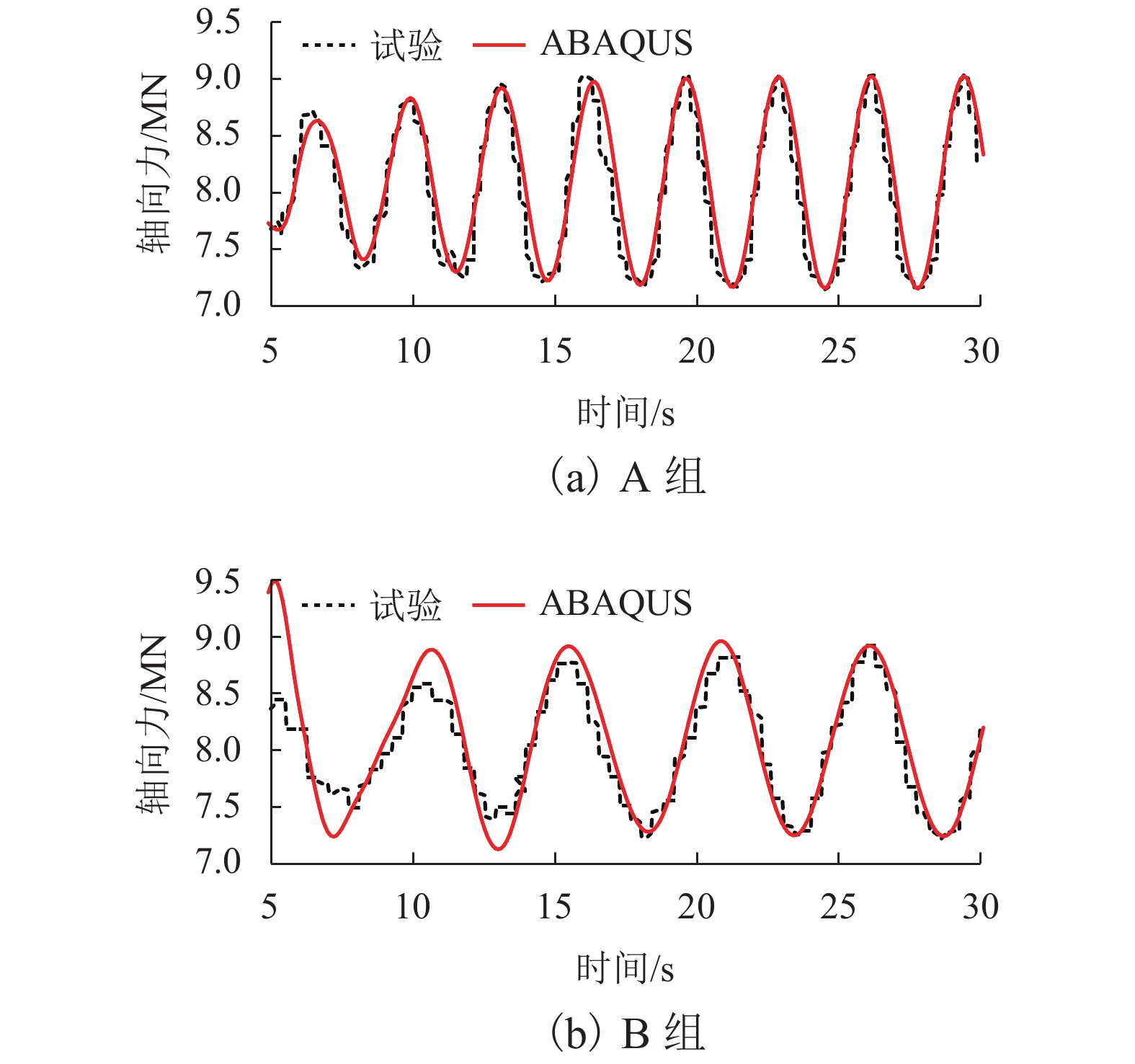
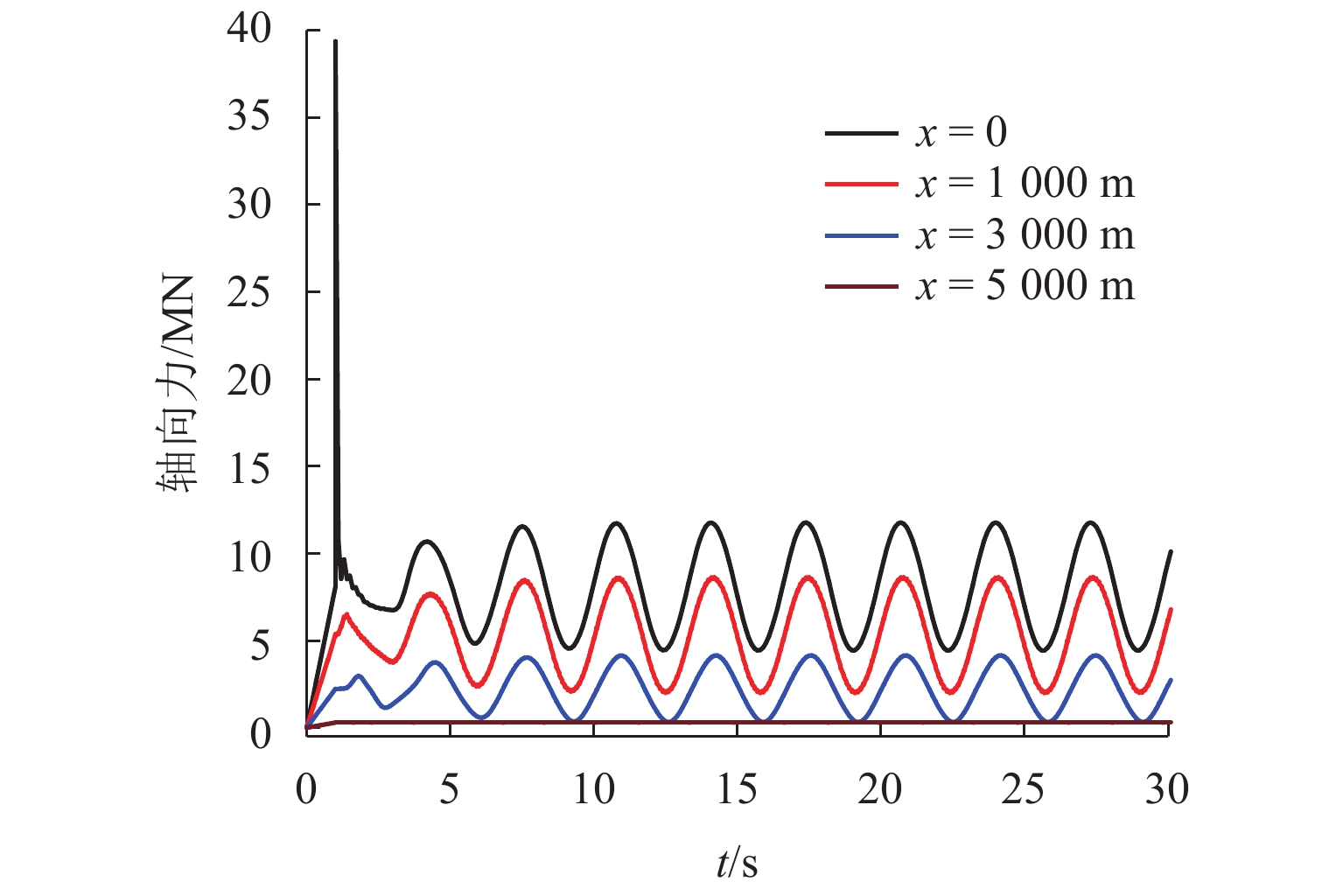
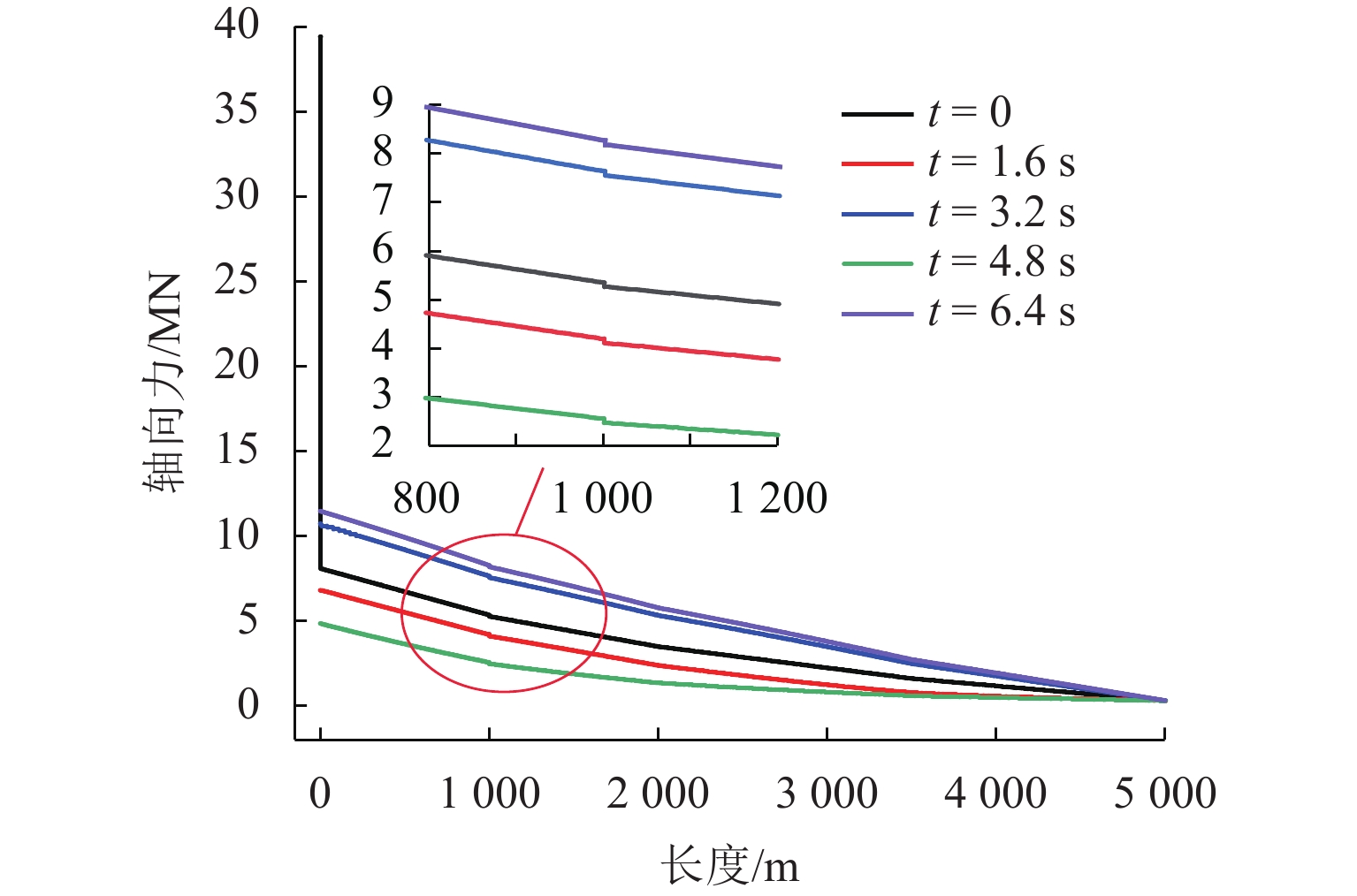
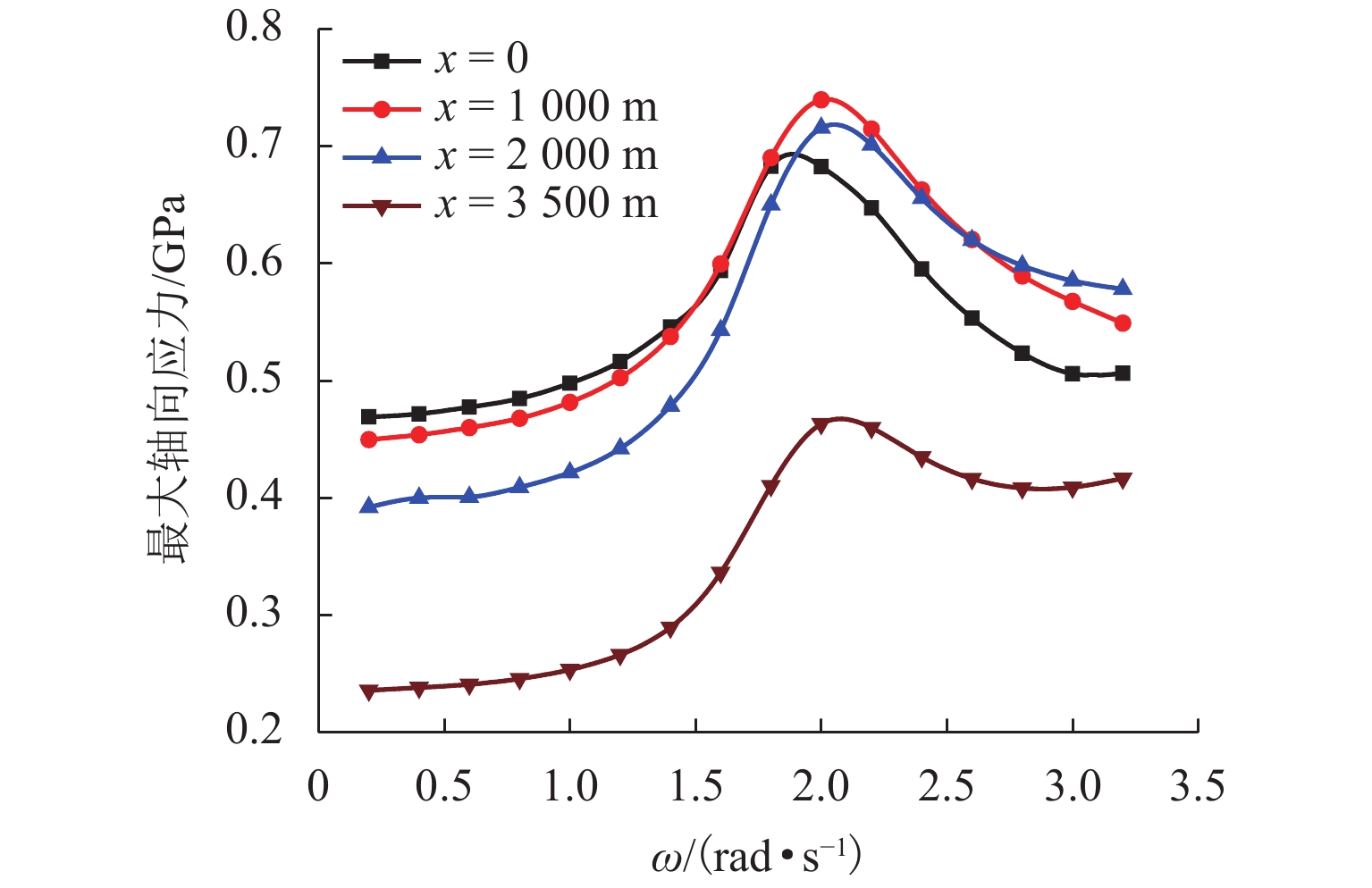
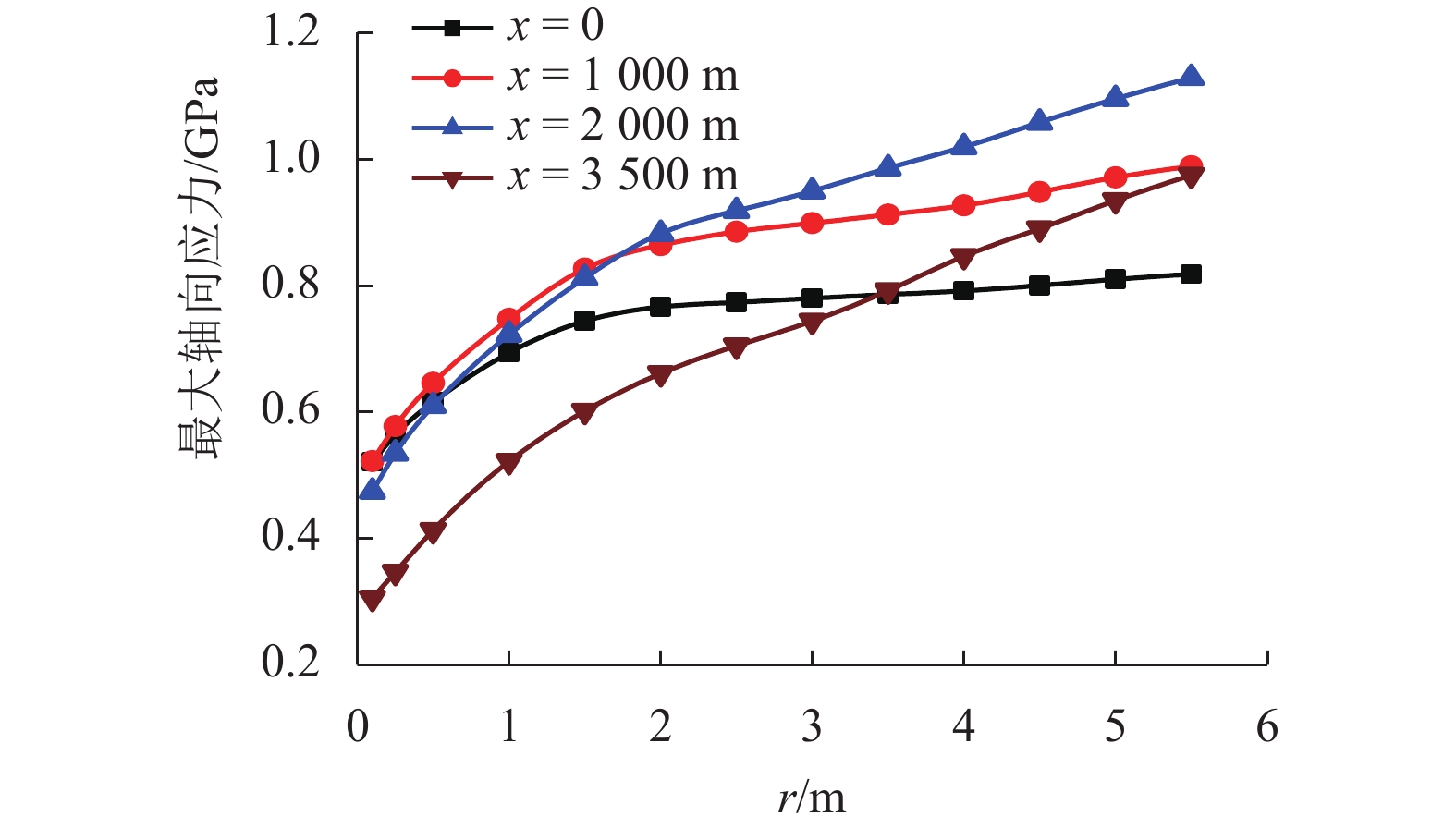
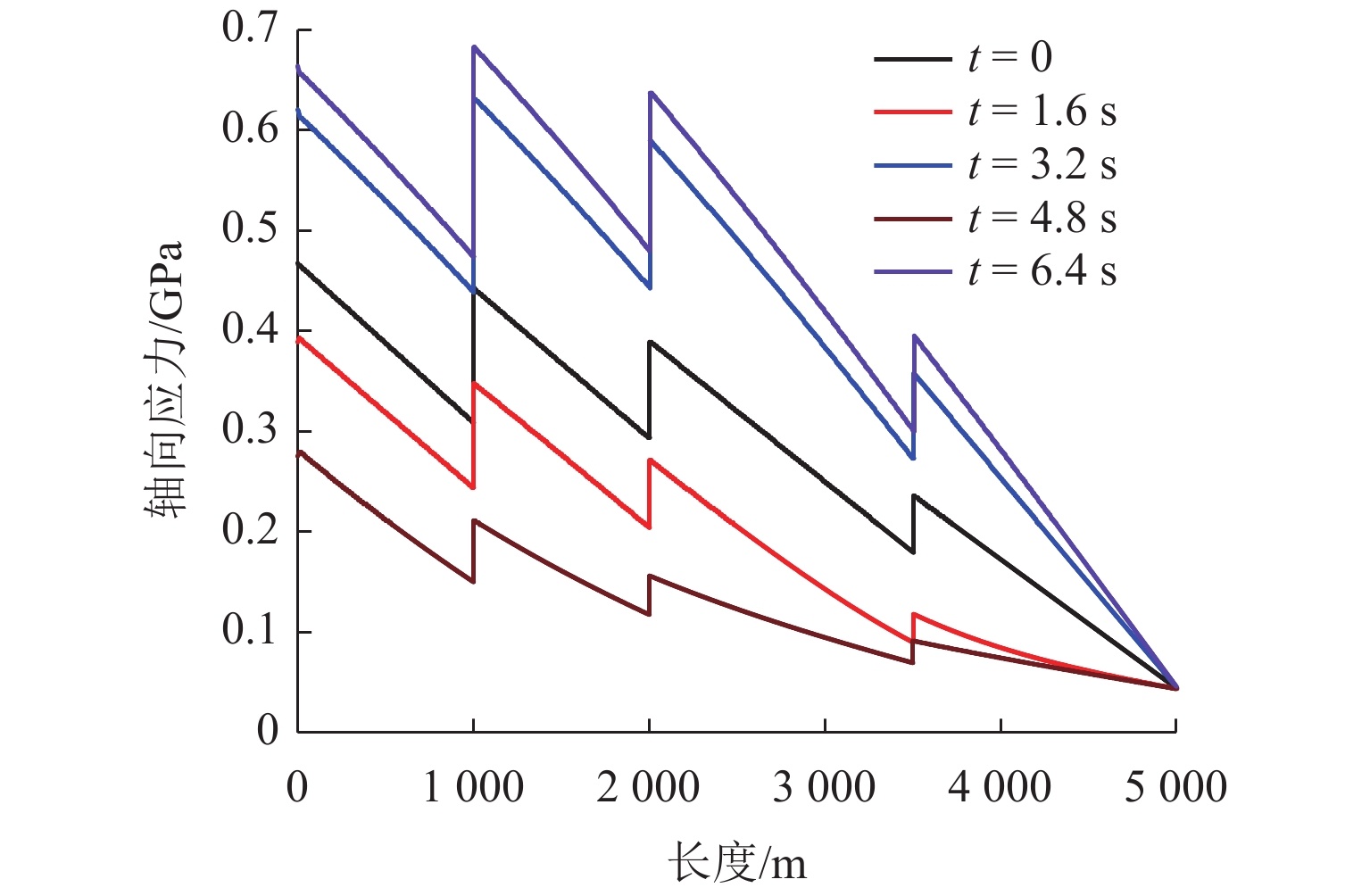
为了研究复杂阶梯状扬矿管在采矿船升沉运动和海流作用下的纵向振动特性，利用连续弹性杆振动理论，对5 000 m长扬矿管纵向振动性能进行分析. 首先，根据达朗贝尔原理建立扬矿管纵向振动数学模型，采用分离变量法推导管道固有频率方程；然后，进行振型的质量归一化处理；最后，利用ABAQUS软件建立扬矿管有限元模型，对管道的纵向动态响应进行研究. 研究结果表明：扬矿管的一阶纵向共振频率处于矿区海浪能量集中的频带内，随着中间矿仓质量的增加扬矿管固有频率减小，中间矿仓质量对高阶固有频率的影响更加明显；随着海浪频率的增加，纵向振幅、轴向力和轴向应力先增大后减小，并在一阶固有频率时达到峰值，其峰值分别发生在扬矿管5 000、0、1 000 m处；随着采矿船升沉幅值的增加，扬矿管的动态响应逐渐增大，当升沉幅值大于1.5 m时，扬矿管动态响应的增长速度变缓；扬矿管发生一阶纵向共振时，振动位移和轴向力先增大后作等幅稳态振荡；随着海水深度的增加，沿管长方向的振动幅值逐渐增大，振动平衡位置发生下移，振动响应时间发生延迟，同时轴向力和轴向应力逐渐减小，且轴向应力在每两级阶梯管间急剧变大.
Abstract:In order to study the longitudinal vibration characteristics of the stepped lifting pipe with a complex structure under the action of the ocean current and mining vessel heave motion, the longitudinal vibration performance of a 5000 m long lifting pipe was analyzed using the vibration theory of continuous elastic rod. Firstly, a mathematical model of the longitudinal vibration of the lifting pipe was established according to the D’Alembert principle, and the natural frequency equation of the pipeline was derived by the method of separating variables. Then, the mass normalization of the vibration mode was carried out. Finally, a finite element model of the lifting pipe was established using ABAQUS software to study the longitudinal dynamic response of the pipeline. The results show that the first-order longitudinal resonance frequency of the lifting pipe is in the frequency band where the wave energy is concentrated in the mining area. With an increase in the buffer mass, the natural frequency of the lifting pipe decreases gradually, and the influence of the buffer mass on the high-order natural frequencies becomes more obvious. With the wave frequency increasing, the longitudinal amplitude, axial force and axial stress first increase and then decrease, and reach their peaks at the first-order natural frequency, which occurs at 5000, 0 and 1000 m along the lifting pipe length, respectively. As the heave amplitude of the mining vessel increases, the dynamic response of the lifting pipe increases gradually; after the heave amplitude is greater than 1.5 m, the growth rate of the dynamic response of the lifting pipe slows down. When the first-order longitudinal resonance occurs in the lifting pipe, the vibration displacement and axial force first increase and then make constant-amplitude steady-state oscillation. With the increase of seawater depth, the vibration amplitude along the length of the pipe increases gradually, the vibration equilibrium position moves down, and the vibration response time is delayed; meanwhile, the axial force and axial stress decrease gradually, and the axial stress between each pipe string segment increases sharply.
-
Key words:
- deep sea mining /
- lifting pipe /
- ABAQUS /
- longitudinal vibration characteristics /
- resonance response
-
图 5 不同频率时扬矿管的振幅（
$ r $ =1.0 m）Figure 5. Amplitude of lifting pipe at different frequencies（
$ r $ =1.0 m）
图 6 不同升沉幅值时扬矿管的振幅（
$ \omega = 1.92 $ rad/s）Figure 6. Amplitude of the lifting pipe at different heave amplitudes （
$ \omega = 1.92 $ rad/s）
图 9 不同频率时扬矿管的最大轴向力（
$ r $ =1.0 m）Figure 9. Maximum axial force of lifting pipe at different frequencies （
$ r $ =1.0 m）
图 10 不同升沉幅值时扬矿管的最大轴向力（
$ \omega = 1.92 $ rad/s）Figure 10. Maximum axial force of lifting pipe at different heave amplitudes （
$ \omega = 1.92 $ rad/s）
图 11 轴向力的试验与仿真结果对比
Figure 11. Comparison of test and simulation results of axial force
图 14 不同频率时扬矿管的最大轴向应力（
$ r $ =1.0 m）Figure 14. Maximum axial stress of lifting pipe at different frequencies （
$ r $ =1.0 m）
图 15 不同升沉幅值时管道最大轴向应力（
$ \omega = 1.92 $ rad/s）Figure 15. Maximum axial stress of lifting pipe at different heave amplitudes （
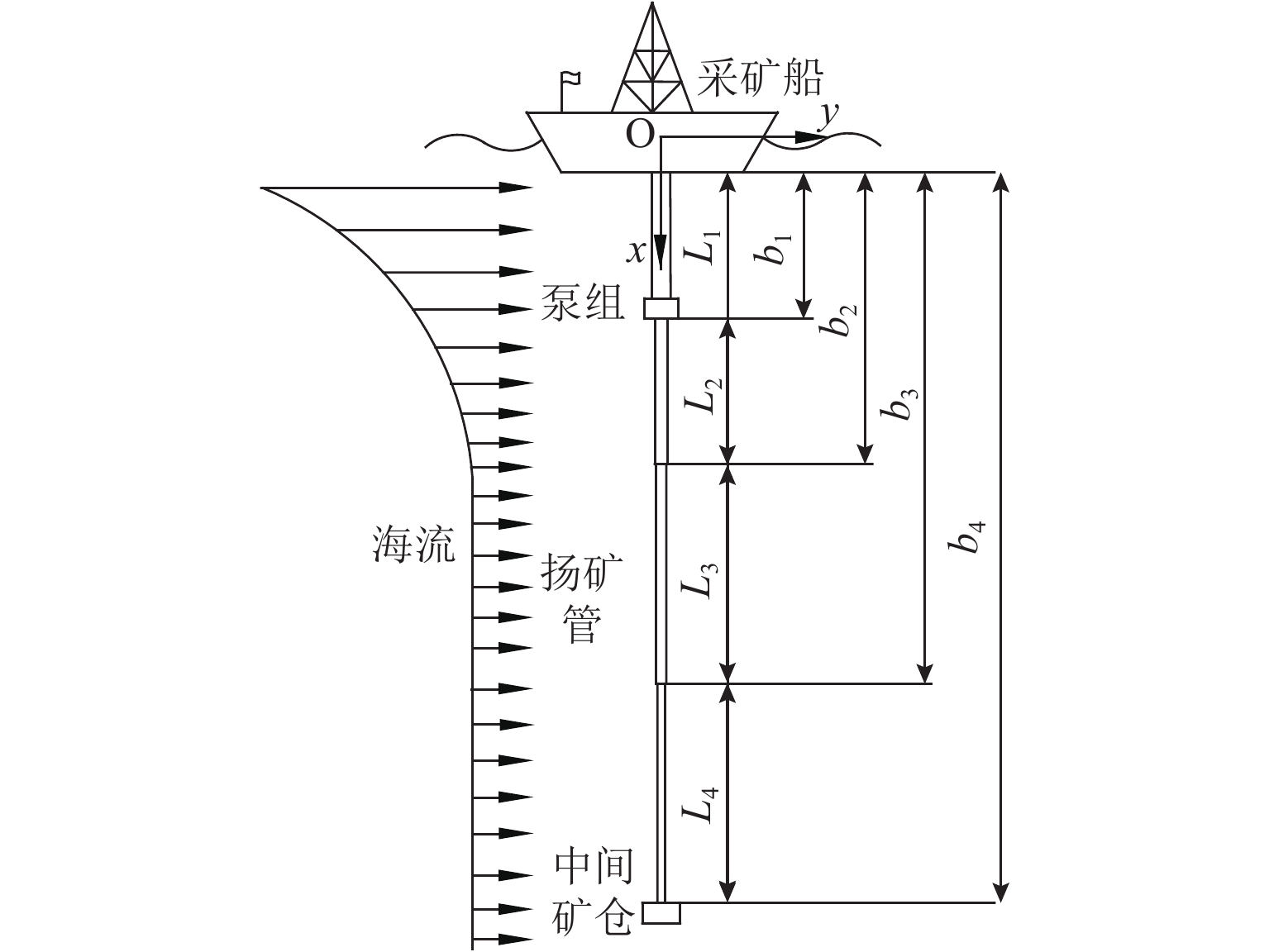
$ \omega = 1.92 $ rad/s）表 1 阶梯扬矿管的参数
Table 1. Parameters of stepped lifting pipe
i 长度/
m外径/
mm内径/
mm单位长度
质量 /（kg•m−1）弹性
模量/GPa1 1 000 254 206 390.02 206 2 1 000 240 206 267.84 206 3 1 500 232 206 134.10 206 4 1 500 226 206 101.74 206 
下载: 导出CSV
表 2 扬矿管前5阶固有频率
Table 2. The first five natural frequencies of lifting pipe
阶数 1 阶 2 阶 3 阶 4 阶 5 阶 固有频率/（rad•s−1） 1.92 4.86 8.11 11.03 14.24
下载: 导出CSV
-
[1] 韩春杰. 深水平台钻井钻柱耦合振动及模拟分析[D]. 大庆: 大庆石油学院, 2010. [2] WU Q, YANG J M, LU H N, et al. Effects of heave motion on the dynamic performance of vertical transport system for deep sea mining[J]. Applied Ocean Research, 2020, 101: 102188. doi: 10.1016/j.apor.2020.102188 [3] WANG Y B, GAO D, FANG J. Longitudinal vibration analysis of marine riser during installation and hangoff in ultra deepwater[J]. Computer Modeling in Engineering & Sciences, 2016, 111(4): 357-373. [4] WANG S W, XU X S, LU X. Movement optimization of freely-hanging deepwater risers in reentry[J]. Ocean Engineering, 2016, 116: 32-41. doi: 10.1016/j.oceaneng.2016.02.029 [5] LIU J, ZHAO H L, LIU Q Y, et al. Dynamic behavior of a deepwater hard suspension riser under emergency evacuation conditions[J]. Ocean Engineering, 2018, 150: 138-151. doi: 10.1016/j.oceaneng.2017.12.050 [6] THORSEN M J, CHALLABOTLA N R, SAEVIK S, et al. A numerical study on vortex-induced vibrations and the effect of slurry density variations on fatigue of ocean mining risers[J]. Ocean Engineering, 2019, 174: 1-13. doi: 10.1016/j.oceaneng.2019.01.041 [7] 邱显焱,汤迎红. 附加单个动力吸振器的扬矿子系统纵向振动仿真分析研究[J]. 机械强度,2014,36(3): 335-339.QIU Xianyan, TANG Yinghong. Simulation study of longitudinal vibration for lifting pipe with single dynamic vibration absorber[J]. Journal of Mechanical Strength, 2014, 36(3): 335-339. [8] 肖林京,左帅,于志豪. 深海采矿扬矿管的纵向振动分析[J]. 科学技术与工程,2020,20(18): 7213-7219.XIAO Linjing, ZUO Shuai, YU Zhihao. Longitudinal vibrations analysis of lifting pipe in deep-sea mining[J]. Science Technology and Engineering, 2020, 20(18): 7213-7219. [9] 肖林京,刘强,梁彬. 基于波流联合作用的深海采矿扬矿管纵向振动分析[J]. 矿业研究与开发,2019,39(11): 147-150.XIAO Linjing, LIU Qiang, LIANG Bin. Longitudinal vibration analysis of hoisting pipe in deep-sea mining based on combination action of wave and current[J]. Mining Research and Development, 2019, 39(11): 147-150. [10] LIU Q, XIAO L J. Analysis and research on longitudinal vibration characteristics of deep sea mining pipe based on finite element method[J]. Mathematical Problems in Engineering, 2020, 3: 8219794.1-8219794.18. [11] SPARKS C. Transverse modal vibrations of vertical tensioned risers. a simplified analytical approach[J]. Oil & Gas Science and Technology, 2002, 57(1): 71-86. [12] SOLTANAHMADI A. Determination of flexible riser natural frequencies using Fourier analysis[J]. Marine Structures, 1992, 5(2/3): 193-203. [13] CHENG Y, VANDIVER J K, MOE G. The linear vibration analysis of marine risers using the wkb-based dynamic stiffness method[J]. Journal of Sound and Vibration, 2002, 251(4): 750-760. doi: 10.1006/jsvi.2001.3843 [14] XI L Y, LI X F, TANG G J. Free vibration of standing and hanging gravity-loaded Rayleigh cantilevers[J]. International Journal of Mechanical Sciences, 2013, 66: 233-238. doi: 10.1016/j.ijmecsci.2012.11.013 [15] WU Q, YANG J M, GUO X X, et al. Influence of irregular waves on the dynamic response of a vertical transport system for deep sea mining[J]. Ocean Engineering, 2021, 229: 108443.1-108443.18. [16] 王明峰. 深海采矿船运动模拟平台系统控制方法研究[D]. 长沙: 中南大学, 2012. [17] SONG Q H, JIANG H Y, SONG Q J, et al. Vibration characteristics and reduction analysis of lifting pipe under ocean current[J]. Shock and Vibration, 2021, 2021: 2778243.1-2778243.20. [18] CHEN W M, LI M, GUO S X, et al. Dynamic analysis of coupling between floating top-end heave and riser’s vortex-induced vibration by using finite element simulations[J]. Applied Ocean Research, 2014, 48: 1-9. doi: 10.1016/j.apor.2014.07.005 [19] 操芹,夏鹏飞,汪轲,等. 基于模态分析的某皮卡发动机罩分析方法研究[J]. 汽车实用技术,2015(5): 1-3,6. doi: 10.3969/j.issn.1671-7988.2015.05.001CAO Qin, XIA Pengfei, WANG Ke, et al. Based on modal analysis of a pickup hood analysis method research[J]. Automobile Applied Technology, 2015(5): 1-3,6. doi: 10.3969/j.issn.1671-7988.2015.05.001 [20] 王文明. ABAQUS有限元分析与案例精通: 在海洋石油工程中的应用[M]. 北京: 机械工业出版社, 2017. -
下载:
点击查看大图
计量
- 文章访问数: 217
- HTML全文浏览量: 136
- PDF下载量: 19
- 被引次数: 0