哑铃型桥梁结构畸形波浪力水槽试验及简化算法

康啊真; 顾宇航; 张东明; 金可; 祝兵; 杨兵

doi:10.3969/j.issn.0258-2724.20210380

哑铃型桥梁结构畸形波浪力水槽试验及简化算法

doi: 10.3969/j.issn.0258-2724.20210380

康啊真^1,,
顾宇航¹,
张东明²,
金可¹,
祝兵^1, ,,
杨兵¹

1.
西南交通大学土木工程学院，四川成都 610031
2.
成都大学建筑与土木工程学院，四川成都 610106

基金项目: 国家自然科学基金（52178167，52278221）；四川省应用基础面上项目（2021YJ0039）；四川省重点研发项目（2021YFS0323）

详细信息

作者简介:
康啊真（1986—），女，副教授，研究方向为深水桥梁基础，桥梁风浪耦合动力学，E-mail： xiaokang_198610@163.com

通讯作者:
祝兵（1965—），男，教授，研究方向为桥梁结构动力学及桥梁风浪耦合动力学，E-mail：Zhubing126@126.com

中图分类号: U446.1
计量
- 文章访问数: 332
- HTML全文浏览量: 151
- PDF下载量: 33
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-10
- 修回日期: 2022-02-14
- 网络出版日期: 2023-04-14
- 刊出日期: 2022-03-24

Wave Flume Test and Simplified Algorithm for Freak Wave Forces on a Dumbbell-Shaped Bridge Structure

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031
2.
School of Architecture and Civil Engineering, Chendu University, Chengdu 610106

摘要

摘要:
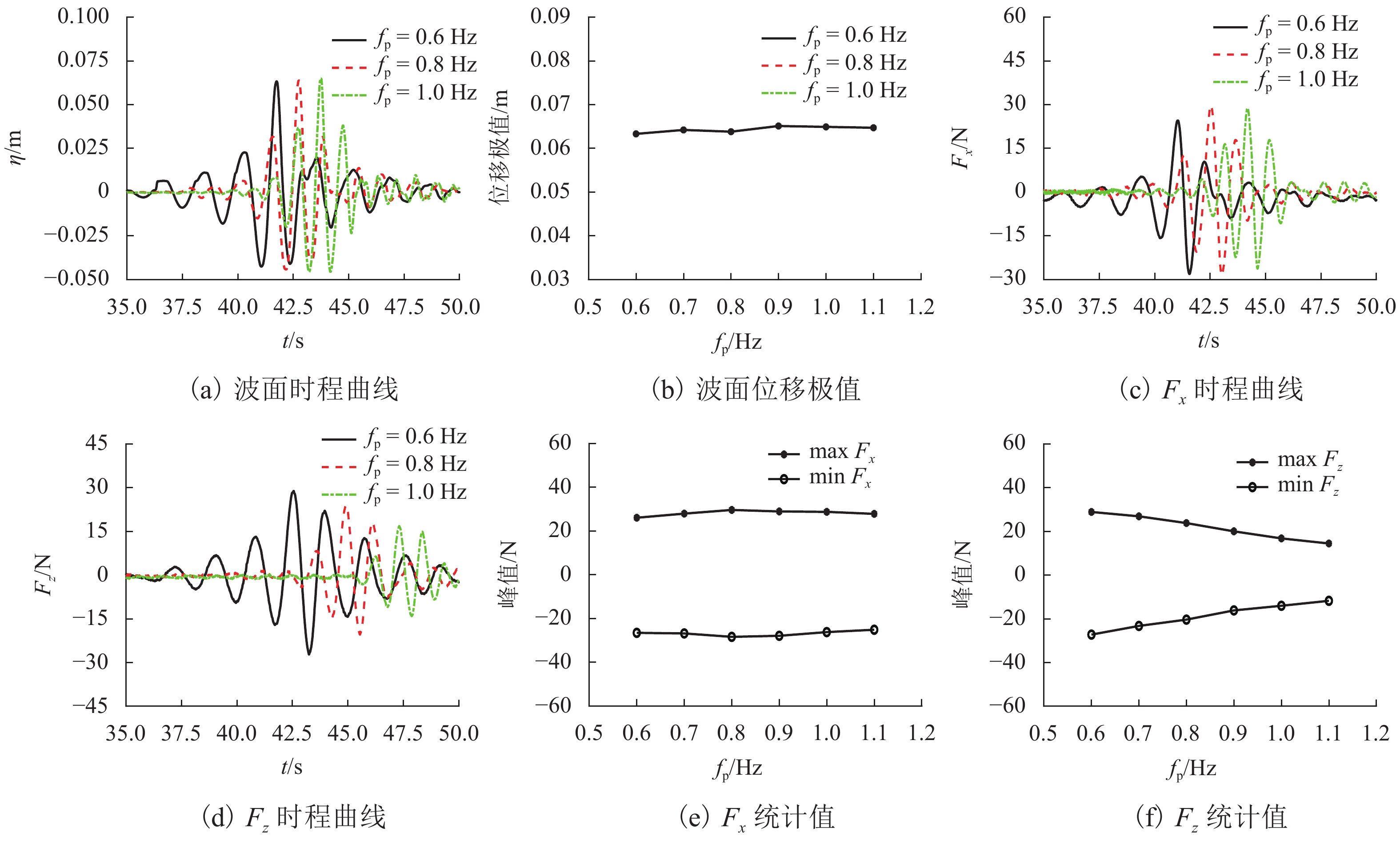
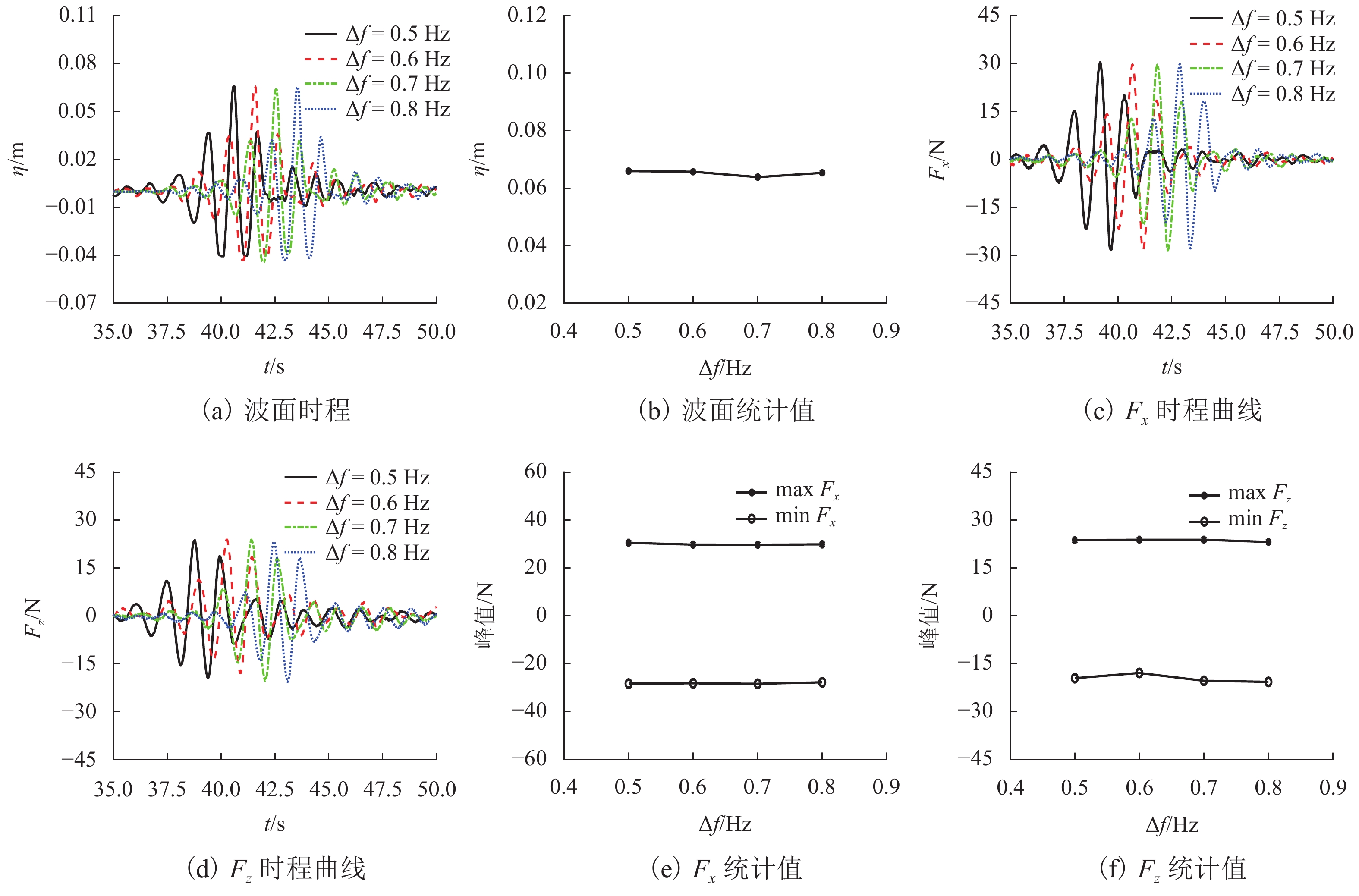
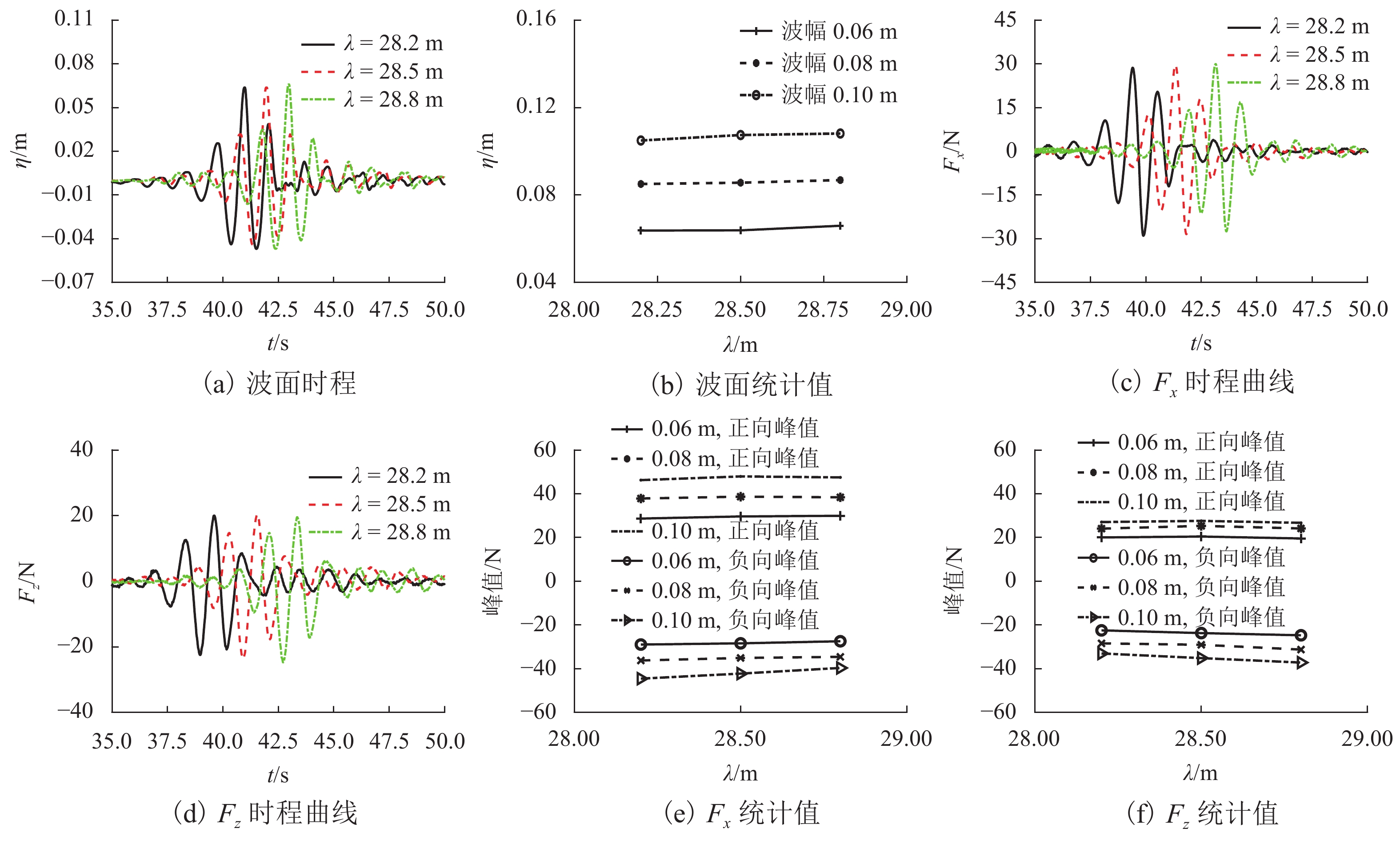
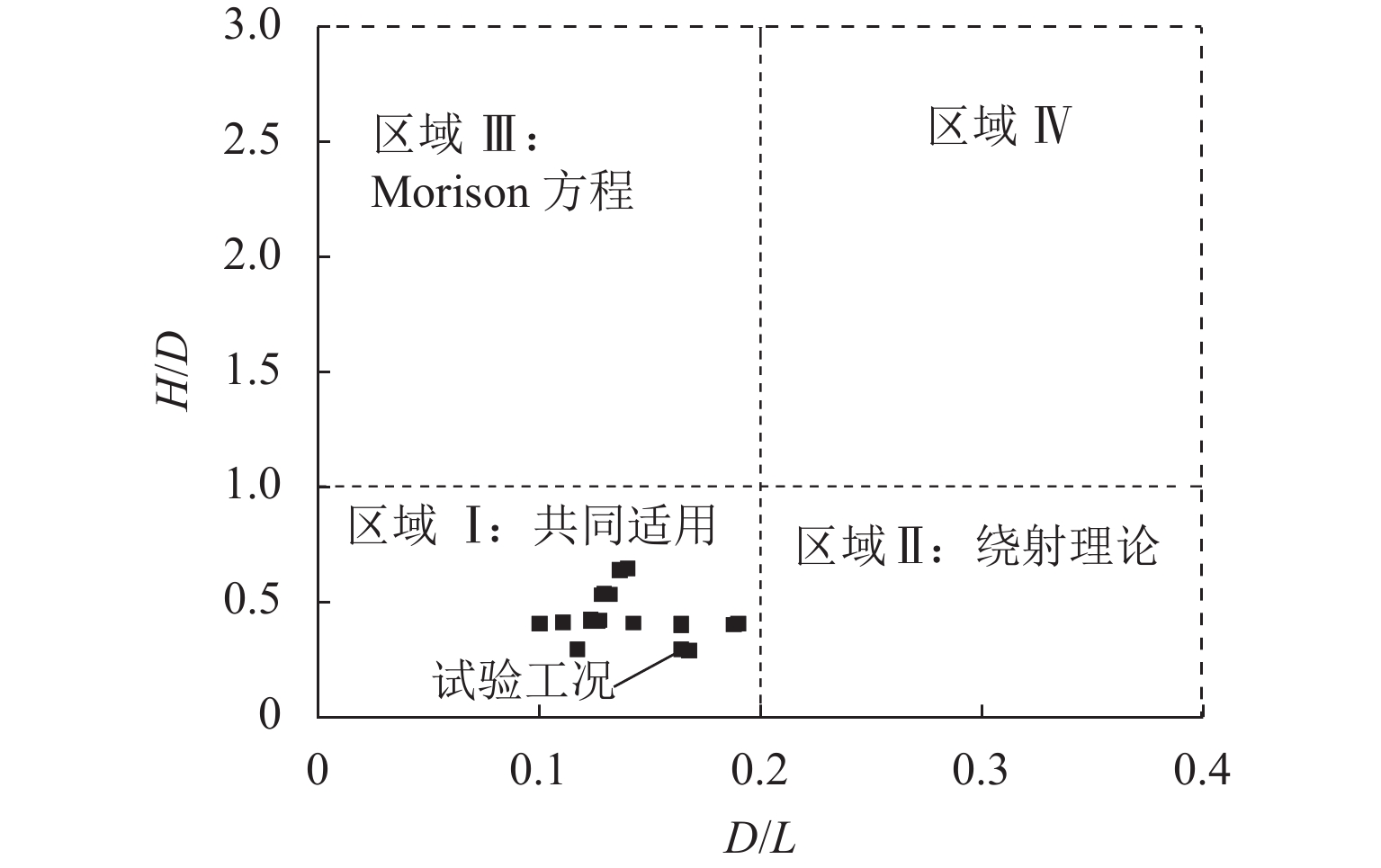
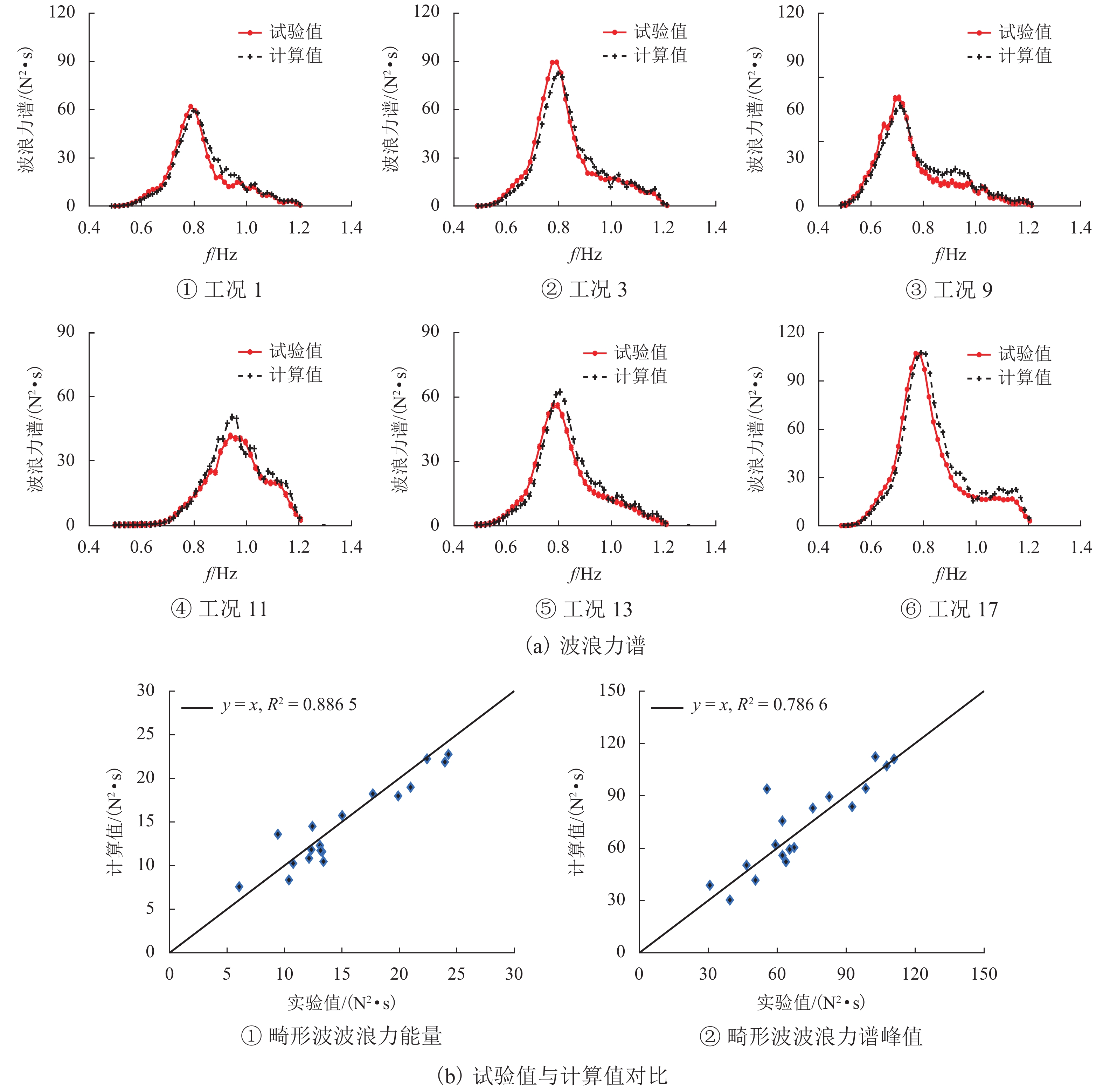
为研究畸形波浪参数对新型哑铃型桥梁结构波浪力的影响，开展一系列波流水槽模型试验. 首先，分析谱峰频率、频率范围及聚焦位置对哑铃型桥梁结构周围的波面时程图及波峰的影响；其次，阐明上述波浪参数对结构畸形波浪力时程图及波浪力峰值的影响规律；最后，基于经典绕射理论，提出适用于新型哑铃型桥梁结构畸形波浪力谱的简化计算方法. 研究结果表明：谱峰频率、聚焦位置及频率范围对结构周围的波面位移影响均较小，差异均小于3%. 谱峰频率和聚焦位置对哑铃型桥梁结构畸形波浪力有较大影响，当谱峰频率从0.6 Hz增加到1.1 Hz时，顺波向波浪力呈先增后减的变化趋势，变化幅度最高达11.0%，垂向浮托力则下降了57.0%；当频率范围从0.5 Hz增加到0.8 Hz时，顺波向波浪力下降了2.1%，垂向浮托力增大了5.9%；当聚焦位置从结构物的迎浪侧移动到背浪侧时，引起的结构顺波向波浪力变化幅度小于5%，垂向浮托力变化幅度小于3%. 经过试验数据和理论分析结果的对比表明，基于绕射理论提出的简化算法可有效计算畸形波作用下哑铃型桥梁结构的波浪力谱模型.
- 哑铃型桥梁结构 /
- 畸形波 /
- 波浪力 /
- 水槽试验 /
- 绕射理论
Abstract:
In order to study the effects of freak wave parameters on the wave force of a new dumbbell-shaped bridge structure, a series of wave flume model tests were conducted. Firstly, the influences of peak frequency, frequency bandwidth and focusing position on wave elevation time history and wave crest around the dumbbell-shaped bridge were analyzed. And the influences of the wave parameters mentioned above on the freak wave force time history and the statistical peak value were investigated. Finally, based on the classical diffraction theory, a simplified calculation method for the freak wave force spectrum on the new dumbbell-shaped bridge structure was proposed. The results show that the peak frequency, focusing positions and frequency bandwidth have little influence on the wave elevation around the dumbbell-shaped bridge structure with a small difference of less than 3%. The peak frequency and focusing positions have great influence on the freak wave force of dumbbell-shaped bridge structure. When the peak frequency increases from 0.6 Hz to 1.1 Hz, the horizontal wave force increases first and then decreases with a maximum range of 11.0%, while the vertical wave force decreases by 57.0%. When the frequency bandwidth increases from 0.5 Hz to 0.8 Hz, the horizontal wave force decreases by 2.1% and the vertical wave force increases by 5.9%. When the focusing position moves from the surge side of the structure to the back/opposite side, the change amplitude of horizontal wave force is less than 5%, and that of vertical wave force is less than 3%. The comparison of experimental data and theoretical analysis proves that the simplified algorithm based on the diffraction theory can effectively estimate the wave force spectrum of dumbbell-shaped bridge structure under freak waves.
- dumbbell-shaped bridge structure /
- freak waves /
- wave forces /
- wave flume tests /
- diffraction theory

HTML全文

图 1 波浪水槽布局图（单位：m）

Figure 1. Layout of the wave flume (unit：m)

下载: 全尺寸图片幻灯片

图 2 f_p对测点V波面位移及畸形波波浪力影响

Figure 2. Influence of peak frequency f_p on wave elevations at point V and freak wave forces

下载: 全尺寸图片幻灯片

图 3 Δf对测点V波面位移及畸形波波浪力影响

Figure 3. Influence of frequency bandwidth Δf on wave elevations at point V and freak wave forces

下载: 全尺寸图片幻灯片

$\lambda$ 对测点V波面位移及畸形波波浪力影响

Influence of focal location $\lambda$ on wave elevations at point V and freak wave forces

下载: 全尺寸图片幻灯片

图 5 畸形波计算方法判定^[15]

Figure 5. Judgment of the freak wave calculation method^[15]

下载: 全尺寸图片幻灯片

图 6 传递函数估算：

Figure 6. Estimation of transfer function

下载: 全尺寸图片幻灯片

图 7 波浪力谱估算

Figure 7. Estimation of wave force spectrum

下载: 全尺寸图片幻灯片

表 1 试验工况

Table 1. Test conditions

工况	A_max/m	Δf/Hz	f_p/Hz	λ/m
1	0.04	0.5～1.2	0.8	28.5
2	0.06	0.5～1.2	0.8	28.5
3	0.08	0.5～1.2	0.8	28.5
4	0.10	0.5～1.2	0.8	28.5
5	0.06	0.6～1.1	0.8	28.5
6	0.06	0.6～1.2	0.8	28.5
7	0.06	0.5～1.3	0.8	28.5
8	0.06	0.5～1.2	0.6	28.5
9	0.06	0.5～1.2	0.7	28.5
10	0.06	0.5～1.2	0.9	28.5
11	0.06	0.5～1.2	1.0	28.5
12	0.06	0.5～1.2	1.1	28.5
13	0.06	0.5～1.2	0.8	28.2
14	0.06	0.5～1.2	0.8	28.8
15	0.08	0.5～1.2	0.8	28.2
16	0.08	0.5～1.2	0.8	28.8
17	0.10	0.5～1.2	0.8	28.2
18	0.10	0.5～1.2	0.8	28.8

下载: 导出CSV

参考文献(17)

[1]	张立超. 平潭海峡公铁两用大桥通航孔桥桥塔墩承台施工技术[J]. 桥梁建设,2017,47(6): 1-6. ZHANG Lichao. Construction techniques for pile caps of pylon piers of navigable span bridges of Pingtan Straits rail-cum-road bridge[J]. Bridge Construction, 2017, 47(6): 1-6.
[2]	王东辉. 平潭海峡公铁两用大桥航道桥基础设计与施工创新技术[J]. 铁道标准设计,2017,61(9): 68-75. WANG Donghui. Innovative technology in channel bridge foundation design and construction of pingtan strait hi-rail bridge[J]. Railway Standard Design, 2017, 61(9): 68-75.
[3]	黄宇. 复杂海况下哑铃型承台钢吊箱围堰设计与施工[J]. 公路,2020,65(1): 128-134.
[4]	刘勇,祝兵,张程然,等. 哑铃形咬合桩围堰水流力作用试验研究[J]. 铁道标准设计,2020,64(10): 72-76. LIU Yong, ZHU Bing, ZHANG Chengran, et al. Experimental study on current force of dumbbell type occluded pile cofferdam[J]. Railway Standard Design, 2020, 64(10): 72-76.
[5]	黄博,段伦良,祝兵. 三维波浪作用下钢吊箱围堰下放过程受力研究[J]. 西南交通大学学报,2018,53(3): 525-532. HUANG Bo, DUAN Lunliang, ZHU Bing. Study of three-dimensional wave forces on lowering of steel-suspending cofferdam[J]. Journal of Southwest Jiaotong University, 2018, 53(3): 525-532.
[6]	KANG A Z. Experimental and numerical study of wave-current interactions with a dumbbell-shaped bridge cofferdam[J]. Ocean Engineering, 2020, 210: 107433.1-107433.19. doi: 10.1016/j.oceaneng.2020.107433
[7]	祝兵,张家玮,潘良,等. 跨海桥梁哑铃形围堰规则波浪力试验研究[J]. 桥梁建设,2019,49(5): 21-26. doi: 10.3969/j.issn.1003-4722.2019.05.004 ZHU Bing, ZHANG Jiawei, PAN Liang, et al. Experimental study of regular wave forces on dumbbell-shaped cofferdam of sea-crossing bridge[J]. Bridge Construction, 2019, 49(5): 21-26. doi: 10.3969/j.issn.1003-4722.2019.05.004
[8]	OHL C O G, TAYLOR P H, EATOCK TAYLOR R, et al. Water wave diffraction by a cylinder array. Part 2. Irregular waves[J]. Journal of Fluid Mechanics, 2001, 442: 33-66. doi: 10.1017/S0022112001004943
[9]	CHIEN H, KAO C C, CHUANG L Z H. On the characteristics of observed coastal freak waves[J]. Coastal Engineering Journal, 2002, 44(4): 301-319. doi: 10.1142/S0578563402000561
[10]	康啊真,祝兵,韩嘉怡,等. 聚焦波浪对哑铃型跨海桥梁围堰作用的试验研究[J]. 土木工程学报,2019,52(10): 93-100. KANG Azhen, ZHU Bing, HAN Jiayi, et al. Experimental study of focused wave actions on dumbbell-shaped sea-crossing bridge cofferdam[J]. China Civil Engineering Journal, 2019, 52(10): 93-100.
[11]	KHARIF C, PELINOVSKY E. Physical mechanisms of the rogue wave phenomenon[J]. European Journal of Mechanics-B/Fluids, 2003, 22(6): 603-634. doi: 10.1016/j.euromechflu.2003.09.002
[12]	GODA Y. A comparative review on the functional forms of directional wave spectrum[J]. Coastal Engineering Journal, 1999, 41(1): 1-20. doi: 10.1142/S0578563499000024
[13]	孙一艳. 二维聚焦波浪及其与直立圆柱作用的研究[D]. 大连: 大连理工大学, 2010.
[14]	DENG Y F, YANG J M, ZHAO W H, et al. Freak wave forces on a vertical cylinder[J]. Coastal Engineering, 2016, 114: 9-18. doi: 10.1016/j.coastaleng.2016.03.007
[15]	GARRISON C J, CHOW P Y. Wave forces on submerged bodies[J]. Journal of the Waterways, Harbors and Coastal Engineering Division, 1972, 98(3): 375-392. doi: 10.1061/AWHCAR.0000157
[16]	MACCAMY R C, FUCHS R A. Wave forces on piles: A diffraction theory[J]. Beach Erosion Board, 1954, 69: 75-86.
[17]	王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013: 182-183.